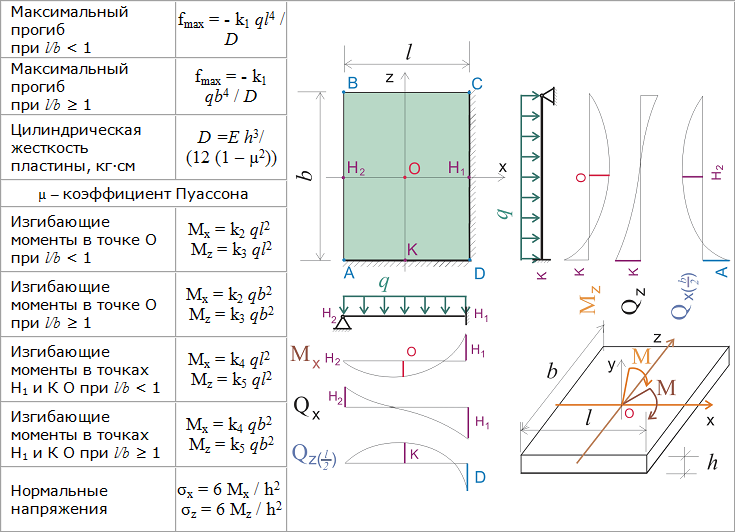
alexxlab | Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный | |||||||||||||||
| Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны | |||||||||||||||
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) | ||
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
| Заделка-консоль Заделка-заделка Заделка-шарнир Шарнир-шарнир |
| Длина стойки L, м : | Нагрузка P, кг : |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров — ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P — действующая нагрузка,
- Fp — плошадь поперечного сечения стойки,
- Ry — расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения «В» того же СНиПа;
- Yc — коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.
Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi — коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) — некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr — расчётная длина стержня;
- i — радиус инерции поперечного сечения стержня (стойки,колонны).
Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I — момент инерции сечения,
- Fp — его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu — коэфф., зависящий от схемы её крепления:
- «заделка-консоль»(свободный конец) — Mu = 2;
- «заделка-заделка»-Mu = 0.5;
- «заделка-шарнир» -Mu = 0.7;
- «шарнир-шарнир»-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра — относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора «Вид, назначение стоек…». Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке «РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ»; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
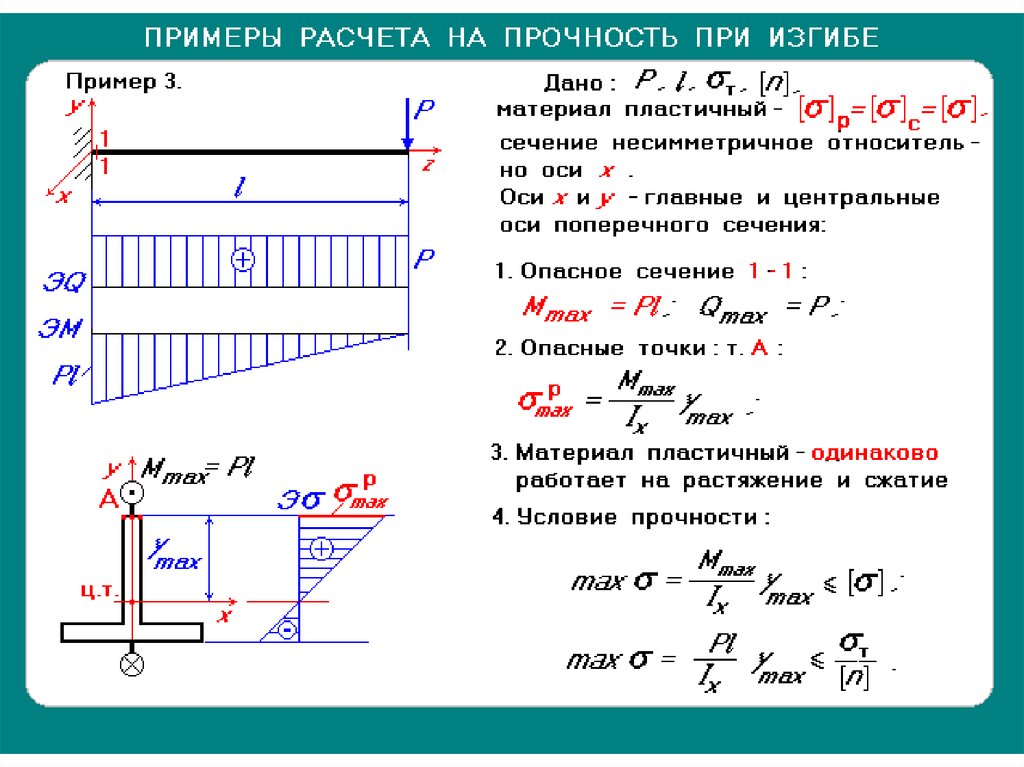
Расчет балки (3 участка) на изгиб онлайн. (при наличии администратора на месте) Полный вариант работы (расчитываются все пункты) Перейти на страницу выбора балок…
Расчет балки (3 участка) на изгиб онлайн. (при наличии администратора на месте)
Полный вариант работы (расчитываются все пункты)
Перейти на страницу выбора балок (выбор числа участков и сложности расчета)
Решение: Определим реакции опор.
Составим уравнения статики. Сумма момментов относительно опоры
равна 0
Сумма момментов относительно опоры
равна 0
Сделаем проверку расчетов
Сумма сил на ось Y равна 0
Построим эпюры поперечных сил и изгибающих моментов. Для этого определим поперечные силы и изгибающие моменты на участках
1 участок
при
Подставляя числовые значения, получим
при
при
2 участок
при
Подставляя числовые значения, получим
при
при
3 участок
при
Подставляя числовые значения, получим
при
при
По условию прочности подбираем рациональный профиль из семи заданных ниже форм
Допустимое нормальное напряжение
Из условия прочности
тогда расчетный осевой момент сопротивления сечения балки
Определяем размеры наиболее распространенных балок
а) прямоугольник
б) квадрат
в) круг
г) кольцо
д) треугольник
при вычислении напряжения в вершине треугольника
пусть
тогда
e) швеллер
При требуемом моменте сопротивления
Выберем:
Номер швеллера —
момент сопротивления швеллера
момент инерции
число швеллеров —
Площадь одного швеллера
ж) двутавр
Выберем:
Номер двутавра
момент сопротивления двутавра
момент инерции двутавра
число двутавров
Площадь одного двутавра
Очевидно , что самое оптимальное сечение у
который имеет минимальное значение совокупной площади поперечного сечения
Оцениваем материалоемкость балок с подобранными сечениями, принимая площадь наимеьшего сечения за 100%
Для выбранной балки вычисляем максимальное рабочее напряжение
которое меньше допускаемого напряжения на
Наибольшие касательные напряжения возникают в точках нейтралльной линии опасного сечения балки, где
Предварительно по таблицам сортамента для
проверяем прочность балки по касательным напряжениям
при
Условие прочности балки по касательным напряжениям выполняется
Выбор опасного сечения.
В рассматриваемом примере опасным являестя сечение где действует момент
и действует поперечная сила
Построение эпюры нормальных напряжений в опасном сечении.
Нормальные напряжения в опасном сечении вычисляются по формуле
Поскольку в опасном сечении
, то слои, рапсположенные выше нейтральной линии, будут испытывать
ниже нейтральной линии —
Построение эпюры касательных напряжений в опасном сечении
Представим условно выбранную фигуру состоящей из трех прямоугольников: двух полок размером
— стенки размером
выбираемыми из таблицы сортамента в расчетных точках определяются по формуле Д.И. Журавского
Размеры профиля:
в дальнейших расчетах эти величины переводим в метры, чтобы исключить ошибку.
1. Точка D
следовательно
касательное напряжение
нормальное напряжение
2 . Точка Е
3 . Точка F
4 . Точка G
поскольку эпюра касательных напряжений симметрична оси х и эпюра нормальных напряжений имеет также симметрию (только знак меняется на противоположный), то расчет в точках K,L,M можно не выполнять.
Проверяем прочность балки по эквивалентным напряжениям
Наиболее опасными с точки зрения прочности по эквивалентным напряжениям являются точки F и K. Условие прочности для точки F по третьей теории прочности запишется
где
Составим универсальное уравнение углов поворота
Просьба вместо `z писать z
граничные условия
при этом
при этом
получим систему уравнений
тогда начальные параметры
Расчитываем прогибы и углы поворота балки
при
при
при
при
при
при
при
Допустимый прогиб
Максимальное значение прогиба
Как видно, условие жесткости выполняется
Новый калькулятор свободного луча SkyCiv
15.02.2023
SkyCiv — поставщик облачного программного обеспечения для проектирования конструкций и API-технологий. Бесплатный калькулятор балок компании — один из самых популярных бесплатных ресурсов среди студентов и специалистов по проектированию строительных конструкций.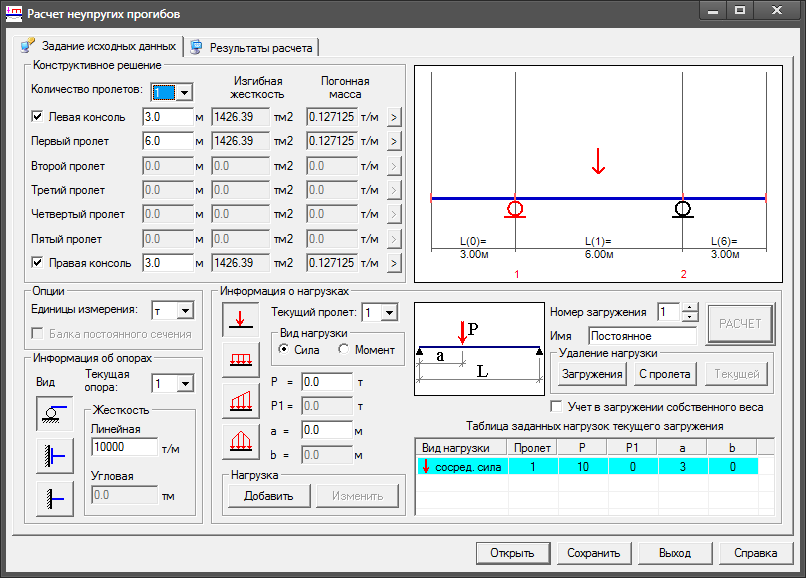
Это веб-инструмент, который позволяет пользователям выполнять структурный анализ и проектные расчеты для простых и консольных балок. Бесплатный инструмент рассчитывает изгибающие моменты, силы сдвига, прогибы и реакции для заданной геометрии балки и условий нагрузки, помогая студентам и профессиональным инженерам проектировать безопасные и эффективные конструкции. Лучше всего то, что он абсолютно бесплатен и доступен через ваш веб-браузер.
Последнее обновление SkyCiv Free Beam Calculator
Недавно SkyCiv выпустила обновленную версию Free Beam Calculator с улучшенным пользовательским интерфейсом, обещая еще лучший пользовательский интерфейс. Теперь он удобен для мобильных устройств, что позволяет пользователям легко анализировать и рассчитывать лучи прямо со своих телефонов.
Благодаря новому интерфейсу этот бесплатный инструмент для работы с лучами еще никогда не был таким простым в использовании!
Калькулятор свободной балки также имеет несколько новых функций, облегчающих пользователям расчет диаграмм изгибающего момента и поперечной силы в секундах.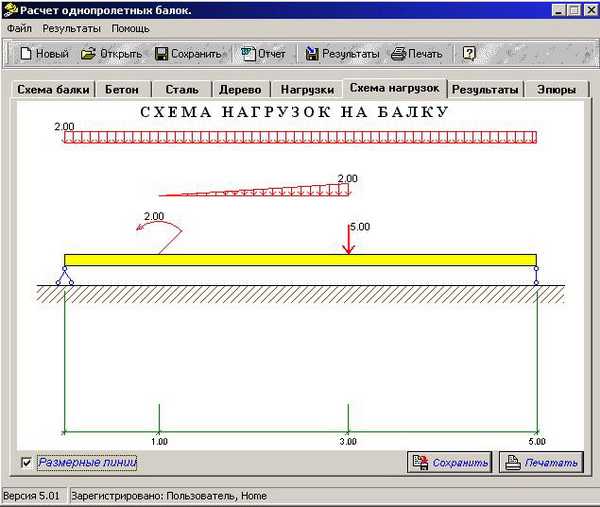
Например, теперь пользователи могут щелкать и перетаскивать, чтобы перемещать грузы:
Вместе с широким спектром сокращенных вводов, таких как ввод с разделителями-запятыми, математические выражения и сочетания клавиш, теперь сложный ввод уходит в прошлое!
SkyCiv Free Beam Calculator Особенности
SkyCiv Free Beam Calculator — это мощный инструмент для инженеров, подрядчиков и всех, кому необходимо выполнять расчеты луча. Калькулятор может генерировать реакции, диаграммы поперечной силы (SFD), диаграммы изгибающего момента (BMD), прогиб и расчет напряжения для консольной или просто опертой балки. Калькулятор помогает пользователям выполнить профессиональный рабочий процесс расчета балки, позволяя им просматривать и определять, соответствуют ли их расчеты региональным нормам проектирования.
Калькулятор реакции балки
Калькулятор также имеет калькулятор реакции балки, который легко вычисляет реакции на опорах как для консольных, так и для простых балок.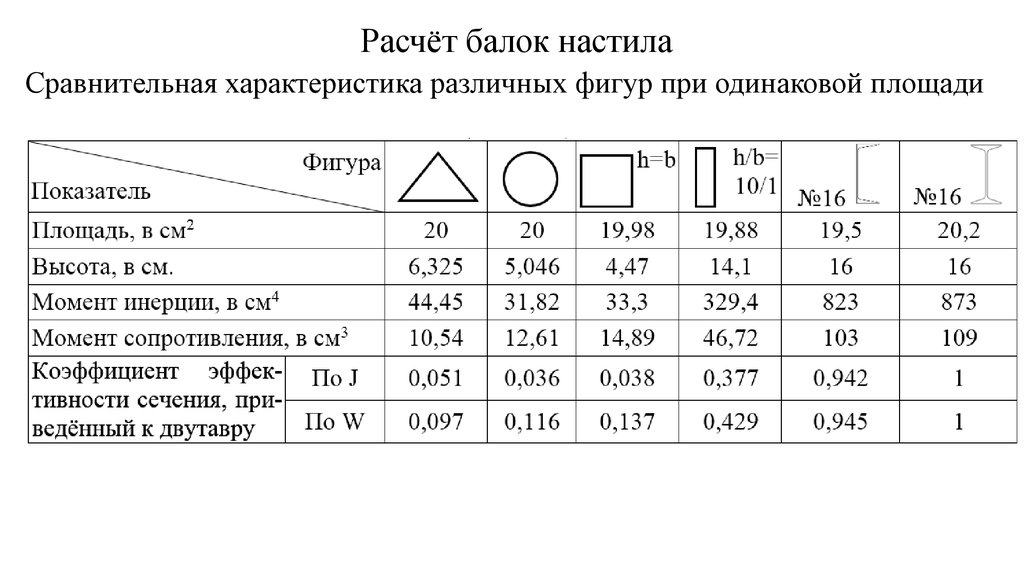
Калькулятор включает реакции для консольных балок, в том числе реакции изгибающего момента и силы реакции x,y. Реакции на опорах полезны для определения общей силы, приложенной к конструкции.
Калькулятор изгибающего момента и силы сдвига
Еще одной ключевой функцией калькулятора свободной балки SkyCiv является калькулятор изгибающего момента и силы сдвига. Этот универсальный инструмент для проектирования конструкций используется для расчета изгибающего момента в алюминиевых, деревянных или стальных балках. Его также можно использовать в качестве калькулятора несущей способности балки, рассчитывая напряжение изгиба или напряжение сдвига. Калькулятор может учитывать до 2 различных сосредоточенных точечных нагрузок, 2 распределенных нагрузок и 2 моментов, которые могут быть организованы как равномерно распределенные нагрузки (UDL), треугольные распределенные нагрузки или трапециевидные распределенные нагрузки. Калькулятор может учитывать наиболее распространенные ситуации расчета балки, так как все нагрузки и моменты могут быть направлены как вверх, так и вниз по величине.
Калькулятор отклонения луча
Наконец, калькулятор свободного луча SkyCiv также имеет калькулятор отклонения луча (или калькулятор смещения луча). Эта функция позволяет пользователям наблюдать расчетный прогиб свободно опертой балки или консольной балки. Калькулятор также может добавлять формы и материалы сечений, что делает его полезным в качестве калькулятора деревянных балок или калькулятора стальных балок для проектирования низкоуровневых балок или двутавровых балок. Эта функция в настоящее время доступна только в программном обеспечении SkyCiv Beam, которое предлагает еще больше возможностей для проектирования деревянных, бетонных и стальных балок.
Оцените последнюю версию SkyCiv Free Beam Calculator прямо сейчас — лучший бесплатный онлайн-инструмент для расчета момента, сдвига и отклонения балок. Если вы присматриваетесь к программному обеспечению SkyCiv, это идеальное место, чтобы познакомиться с тем, что может предложить SkyCiv Beam!
О SkyCiv
SkyCiv предлагает широкий спектр облачного программного обеспечения для структурного анализа и проектирования для инженеров.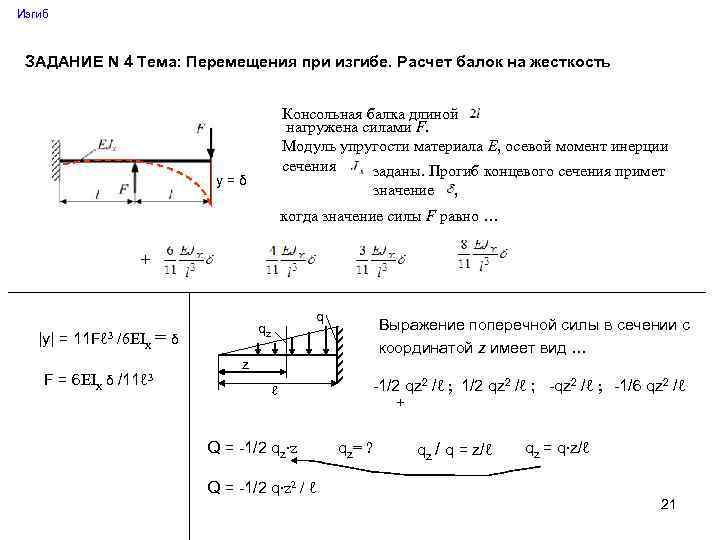
Как постоянно развивающаяся компания, SkyCiv стремится внедрять инновации и улучшать существующие рабочие процессы, чтобы сэкономить время инженеров в их рабочих процессах и проектах.
Источник: SkyCiv Beam Calculator
Моделирование отклонения луча
ВВЕДЕНИЕ:
Это симулятор/калькулятор для отклонения луча с использованием теории пучка Эйлера-Бернулли.
Раздел BEAM EDITOR содержит элементы управления для проектирования балки.
Раздел УРАВНЕНИЯ содержит уравнения, используемые для построения диаграмм.
Элементы управления:
- — Тип балки: Это выпадающее меню изменяет сценарий для моделирования/расчета.
- — Кнопки масштабирования:
Обе кнопки регулируют уровни масштабирования диаграммы, чтобы графики были видны.
- — «диаграмма» Масштаб: Изменяет уровень масштабирования связанной диаграммы.
- — Нагрузка ( F ) (кН): Изменяет значение точечных нагрузок.
- — Распределенная нагрузка ( w ) (кН/м): Изменяет значение распределенных нагрузок.
- — Момент ( M 0 ) (кНм): Изменяет значение моментов.
- — Положение нагрузки ( и ) (м): Изменяет положение различных грузов.
- — Длина балки ( L ) (м): Изменяет длину луча.
- — Момент инерции ( I ) (мм 4 ): Изменяет момент инерции балки относительно нейтральной оси.
- — Модуль Юнга ( E ) (ГПа):
Изменяет модуль Юнга балки.
- — Форма луча: Это выпадающее меню изменяет форму проектируемого луча.
- — Размер «переменный» (мм): Изменяет значение связанного измерения.
Обучающее видео:
Ваш браузер не поддерживает видео тег.
ВВОД:
Тип балки:
Консольная торцевая нагрузкаКонсольная промежуточная нагрузкаКонсольная равномерная распределенная нагрузкаКонсольная треугольная распределенная нагрузкаКонсольный конечный моментПросто поддерживаемая промежуточная нагрузкаПростой поддерживаемая центральная нагрузкаПросто поддерживаемая равномерная нагрузкаПростой поддерживаемая равномерная распределенная нагрузкаПростой поддерживаемый момент при каждой поддержкеПросто поддерживаемый момент в одной поддержкеПростой поддерживаемый центральный моментFix ed-Fixed Center LoadFixed-Fixed Равномерная распределенная нагрузка
Загрузка масштабирования: Масштаб отклонения: Масштаб сдвига: Момент Зум:
% % % %
Нагрузка ( F ) (кН):
Распределенная нагрузка ( w ) (кН/м):
Момент ( M 900 86 0 ) (кНм):
Нагрузка Положение ( a ) (м):
Длина балки ( L ) (м):
Момент инерции ( I ) (мм 4 ):
Модуль Юнга ( E 90 074 ) (ГПа):
Материал SelectAluminium: 69 ГПаБереза: 15 ГПа Армированный углеродным волокном пластик: 150 ГПа Алмаз: 1220 ГПа Железо: 210 ГПа Сталь, конструкционная ASTM-A36: 200 ГПа Вольфрам: 410 ГПа Уран: 170 ГПа
BEAM EDITOR:
Форма луча:
ПрямоугольникПолый прямоугольникКругПолый кругДвутавровая балка
Размер b (мм):
Размер c (мм):
Размер d (мм):
УРАВНЕНИЯ:
Ниже приведены уравнения, используемые для построения диаграмм.