Сколько вагонки в кубе штук: Сколько вагонки в кубе: онлайн-калькулятор

Сколько вагонки в кубе: правила расчета и калькулятор

Главная » Материалы » Дерево

Содержание

1. На что влияет объем стройматериала
2. Расчет по простой формуле
3. Из кубического в квадратные метры
4. Можно ли визуально узнать объем
5. Помощь калькуляторов
6. Подводим итоги

При покупке строительных и отделочных материалов нужно заранее рассчитать необходимое количество. Плохо, когда материала оказывается слишком мало. Еще хуже, если их будет чрезмерно много. Это лишние потраченные деньги, а также нежелательные поездки по магазинам для докупки или сдачи. Потому лучше предварительно разобраться в том, сколько вагонки в кубе.

Да, сегодня говорим именно про расчет вагонки. Обычно с ее помощью выполняется внутренний отделочный процесс. Вагонка обладает уникальными декоративными, а также эксплуатационными свойствами.

Помимо того, что деревянная ламель должна соответствовать всем требованиям и подходить для поставленных задач, ею еще и требуется покрыть всю площадь помещений.

Вагонка — это особая деревянная доска, которая может продаваться по цене за 1 кубический метр. А поскольку длина и другие габаритные параметры у доски разные, да и помещение может обладать различной площадью, то при покупке 1 м3 и более важно понимать, какое количество штук вагонки в кубе.

Конечно, вы можете взять на вооружение онлайн калькулятор вагонки. Но это один из вариантов расчета.

На что влияет объем стройматериала

Перед тем как рассчитать вагонку, скажу несколько слов относительно того, почему важно все определить максимально верно.

Объем материала влияет на ряд факторов:

• стоимость деревянных изделий;
• цена доставки;
• необходимые лакокрасочные материалы;
• количество расходников и креплений.

Цена пиломатериалов зависит от нескольких пунктов, включая тип древесины, ее сорт, сырье для производства, а также габаритные размеры.

Если рассчитать общий требуемый объем материала, то можно будет определить общую стоимость и свои расходы на закупку.

Расчет по простой формуле

Теперь к вопросу о том, сколько содержит в себе куб вагонки.

Начнем с того, сколько досок вагонки в кубе. И для этого существует довольно простая формула. Выглядит она следующим образом:

1/(ШхТхД)

Здесь нужно подставить следующие значения:

• Ш — это ширина одной ламели;
• Т— означает толщину;
• Д — указывает на параметры длины.

Теперь будет легко определить, сколько штук вагонки в кубе. Конечно же, если все ламели одинаковые.

Допустим, доска имеет габаритные размеры 150х25х2000 мм.

Расчеты проводим в метрах, поскольку 1 это как раз 1м3.

Нужно умножить 0,15х0,025х2. И на единицу разделить полученное значение. В нашем примере это 1/0,0072. Получается 133,3. Всегда округляем в большую сторону. Вот так можно узнать, сколько досок вагонки в кубе. Здесь это 134 штуки.

А если вы знаете, сколько стоит 1 м3, и сумели определить общее число досок, просто разделите стоимость на это количество.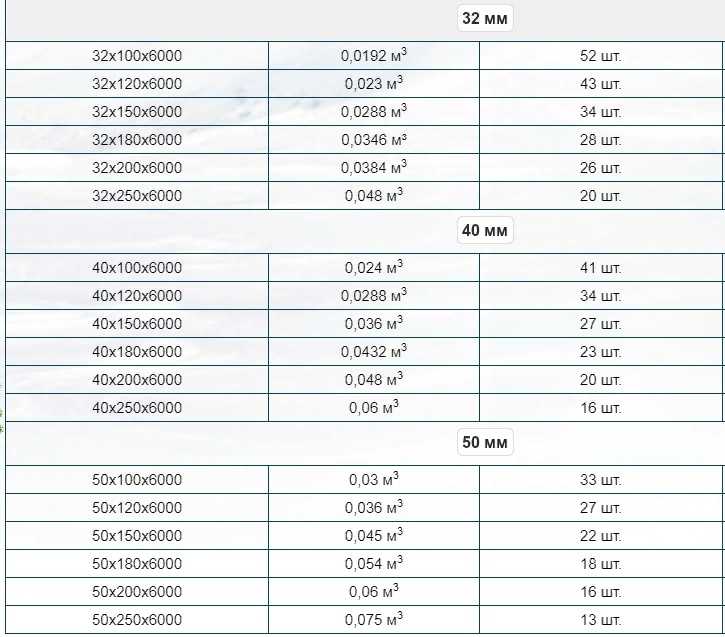 Получите цену за 1 изделие.

Из кубического в квадратные метры

Еще один вопрос связан с тем, сколько квадратных метров в 1 кубе вагонки.

Объем не является метражом. Объем обычно используют, чтобы рассчитать стоимость материала, а также стоимость доставки.

Если же вы планируете облицевать стены или потолок, нужно знать, сколько квадратных метров в кубе вагонки.

Для этого нужно кубометры перевести в квадратные метры.

Возьмем простой пример.

• Для обшивки стен используется доска толщиной 0,025 м или 25 мм;
• Если 1 м2 разделить на 0,025, получим площадь, которую можно обшить с помощью кубометра такого материала. 1/0,025 будет 40 м2;
• Теперь считаем площадь стен. Допустим, это 2 стены размером 2,5х4 метра. Получаем 20 м2;
• Если 40 разделить на 20, то это и будет объем необходимой для покупки деревянной доски.

При этом вы также можете определить, сколько ламелей в штуках потребуется для обшивки стен.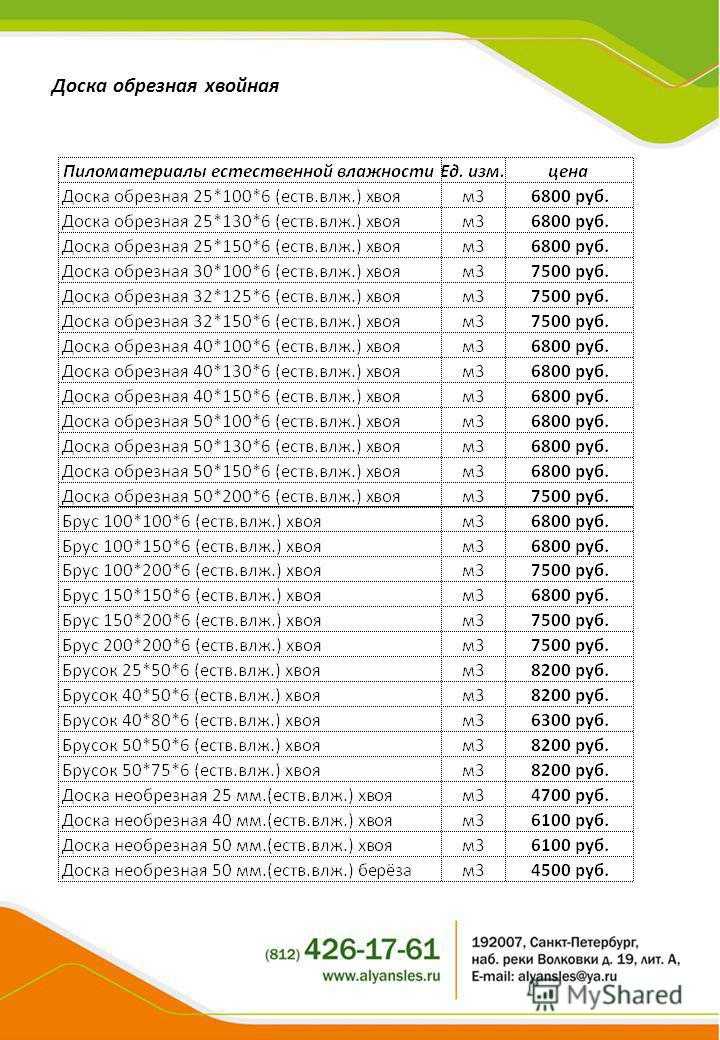

Для этого просто умножьте длину, ширину и высоту 1 изделия. Теперь полученный ранее объем разделите на это число. В нашем случае мы 0,5 делим на 0,0072. Получится 69,4 штуки. Округляем в большую сторону.

Делаем вывод, что для обшивки двух стен площадью 20 м2 нам потребуется 0,5 м3 деревянных изделий или же 70 штук ламелей.

Можно ли визуально узнать объем

Определить, сколько вагонки в упаковке в штуках возможно, если знать некоторые исходные данные.

Но визуально понять, сколько штук вагонки в кубе, особенно 3 метровой, довольно проблематично, если вы новичок в этом деле.

Чтобы быстро и более менее правильно рассчитать значения, вооружитесь рулеткой. Измерьте показатели высоты, длины и ширины. Далее умножьте значения. Так вы узнаете, не пытается ли вас продавец обмануть.

А опытные строители даже на глаз могут примерно понять, сколько изделий содержится в пачке или кубе. Все это приходит лишь с опытом. Поэтому без измерений лучше не покупать этот материал.

Проще всего рассчитать нужное количество и объем материала, когда каждая стена помещения имеет одинаковое значение по высоте. В этом случае можно заказывать пиломатериалы одинаковой длины. Следовательно, толщина и ширина также будут идентичными. Один тип деревянной вагонки на все помещение.

Куда сложнее, если нужно использовать ламели с разными характеристиками. Тут придется сделать отдельно расчет для каждого типа материалов.

Помощь калькуляторов

Чтобы узнать, сколько вагонки в кубе, не обязательно брать лист бумаги, ручку и проводить какие-то математические вычисления.

Отличное решение — это калькулятор вагонки для стен и потолка.

При этом можно найти и выбрать как калькулятор площади вагонки, так и определить с помощью подобного инструмента, сколько штук деревянных панелей в пачке.

Достаточно ввести несколько исходных данных, и все. Система автоматически все рассчитает.

Подобный расчет вагонки по площади, кубическим метрам и по штукам обычно применяют люди, занимающиеся реализацией, либо регулярными закупками.

Представленная формула, как и онлайн калькуляторы, являются универсальными. С их помощью можно рассчитывать:

• пластиковые панели;
• МДФ;
• ламели;
• деревянные доски;
• сайдинг;
• брус и т.п.

Подходит как для штучных изделий, так и для материалов по площади и по объему.

Подводим итоги

Теперь и вы знаете, сколько вагонки в кубе и квадратном метре. Сделать расчеты оказалось вовсе не так сложно, как многим могло показаться изначально.

Использовать расчетные формулы, либо вооружиться онлайн калькуляторами, тут уже решайте сами.

Обязательно воспользуйтесь инфографикой производителя, загляните на его официальный сайт, познакомьтесь с выпускаемой продукцией.

Если же вы покупаете пиломатериалы на обычном строительном рынке, тогда настоятельно рекомендуем вам брать с собой рулетку, и включать калькулятор на телефоне. Либо через какой-нибудь сайт воспользуйтесь их онлайн калькулятором. Иначе есть вероятность, что вас попытаются обмануть. А никому не хочется платить больше денег, а также лишаться части ламелей, за которые заплатили.

А вам приходилось вести подобные расчеты? Что использовали для определения количества материала? Насколько удобными были предлагаемые онлайн калькуляторы? Сложно ли посчитать самостоятельно?

Жду ваших ответов, а также историй из личного опыта.

На этом пока все. Будем прощаться. Спасибо за внимание!

Подпишитесь, оставьте комментарий, задайте вопрос и расскажите о проекте друзьям!

Ваша оценка очень важна!

( Пока оценок нет )

Поделитесь с друзьями

Как рассчитать количество досок и вес деревянной вагонки?

Автор admin На чтение 3 мин Просмотров 539 Опубликовано 14. 10.2021

Деревянная вагонка производится путем распила стволов деревьев на доски, с последующей обработкой поверхности (нанесение профиля и замковой впадины). Реализуется она в упаковках, производители чаще всего формируют пачки по 10 штук, герметично запаивая их термоусадочной пленкой, а расчет стоимости производится из расчета кубометра древесины. Отправляясь в магазин, нужно точно знать какое количество материала вам необходимо, чтобы не пришлось докупать одну-две штуки. О том, как рассчитать количество вагонки, расскажет наша статья.

Стандартные размеры

Согласно ГОСТу 8242-88 размер досок должен быть таким: ширина до 150 мм, толщина от 12 до 25 мм, длина от 500 до 6000 мм. Для внутренней отделки, как правило, используется материал толщиной до 16 мм. Для наружных работ используется вагонка толщиной от 16 до 25 мм.

Кроме обычной стандартной на рынке представлена и евровагонка, которая имеет следующие параметры: ширина 80, 100, 110, 120 мм, толщина 13, 16, 19 мм, длина от 500 до 6000 мм.

Вес вагонки зависит от типа древесины, из которой изготавливают доски, а также от степени влажности. Обычно рассчитывается вес сухого или воздушно-сухого материала. Один кубометр весит:

• из кедра, ели, пихты – 450-500 кг,
• сосновая, ольховая или осиновая – 500-550 кг,
• из лиственницы или березы – 600-650кг,
• из дуба, бука, граба, ясеня – до 800 кг.

Как узнать, сколько нужно досок, и каково их количество в одном кубе?

Прежде чем оформлять покупку, вам нужно знать, сколько конкретно материала вам понадобится. Для этого вы должны знать точную площадь, которую придется покрывать. Кроме этого, нужно учитывать и другие параметры, например длину доски. Если высота помещения, которое предстоит отделать 2, 5 м, а длина вагонки 3 м, вам придется покупать материал со значительным запасом, ведь 0, 5 м будет срезано с каждой полоски. При горизонтальном набивании расчет будет другим, если ширина помещения 3 м, то соответственно обрезков практически не будет.

Расчет количества будет проводиться по простой математической формуле:

• Ширина стены /Ширина вагонки = Количество досок

Например (если вагонка широкая), 3 000 мм/ 150 мм = 20 досок, если в помещении будут оббиты все стены, то соответственно эту цифру нужно умножить еще на 4. Если вы выберите более узкую, то соответственно количество увеличится. Обычно при покупке рассчитывают +10% материала про запас, на случай порчи или замены доски при необходимости.

Чтобы посчитать, сколько штук вагонки в кубе, нужно сделать следующий расчет. Например, если вы хотите купить вагонку длиной 3000 мм, толщиной 16 мм и шириной 150 мм, разделите 1000 на 16 – так вы узнаете, сколько досок в высоту (в данном случае 62, 5), затем разделите 1000 на 150 – так вы узнаете, сколько штук помещается в ширину (в данном случае 6, 66). Умножив 62, 5 на 6, 66 вы получите количество материала в кубометре (в данном случае 416 досок).

Базовый тетраэдр для куба

Базовый тетраэдр для куба

Предварительные занятия: симметрия квадрата

Квадрат имеет 8 симметрий, 4 отражения линий и 4 вращения кратно из 90 градусов. На этом рисунке линиями симметрии являются две диагональные линии. и две линии, соединяющие середины противоположных сторон. Эти строки ломаются разделить квадрат на 8 равных равнобедренных прямоугольных треугольников. Если мы возьмем один из эти треугольники и преобразовать его каждой из 8 симметрий квадрата, треугольники изображения заполнят квадрат.

Это можно увидеть в физическом эксперименте, поместив два шарнирных зеркала с их петля в центре квадрата и два зеркала по двум сторонам одного из восьми треугольников, который окрашен. Одного взгляда на калейдоскоп изображение, образованное двумя зеркалами, кажется квадратом того же цвета.

Обратите внимание, что если длина стороны квадрата s, то длины сторон треугольника AM = MF = s/2 (синяя сторона) и AF = (s/2)*sqrt 2 (черная сторона).

Плоскости симметрии куба

Симметрии куба со стороной s включают два вида плоских отражений.

Есть 3 симметрии, которые являются отражениями в плоскости, параллельной паре грани куба. Каждая из этих 3 плоскостей пересекает 4 ребра в их средних точках; это перпендикулярная биссектриса 4 параллельных ребер. Плоскость симметрии разрезает поверхность куба на квадрат со стороной s. Каждая из плоскостей пересекается 4 квадратных лица. Он пересекает каждую грань по линии симметрии грани. соединяющая середины противоположных ребер. Такая плоскость не содержит ни одного из вершины куба.

Остальные 6 плоских отражений находятся в плоскостях, пересекающих две противоположные грани кубы по диагоналям. Такая плоскость содержит два противоположных ребра куба и 4 вершины. Каждая такая плоскость разрезает поверхность куба прямоугольником ширина = s и длина = s*sqrt 2.

На приведенном выше квадратном рисунке, если квадрат является гранью куба, то два из 3 плоскости симметрии первого типа разрезают квадрат по двум линиям симметрии через середины сторон. Кроме того, два из 6 самолетов Симметрия второго типа разрезает квадрат по линиям симметрии, которые являются диагоналями квадрата.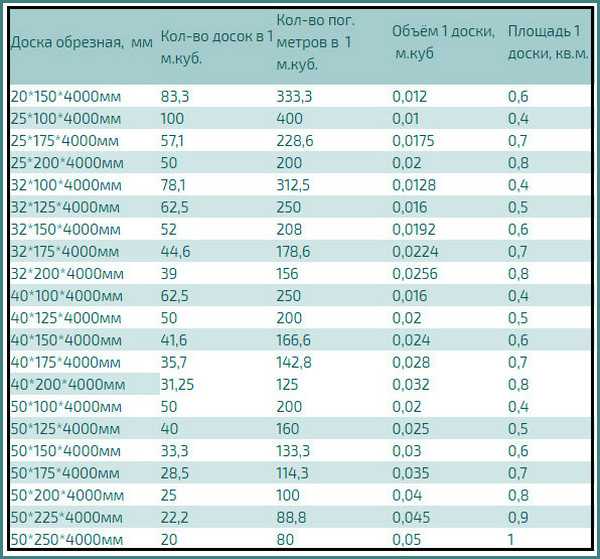

Обратите внимание, что первые линии красные, а диагональ линии зеленые.

Сравните это с изображением куба ниже. Красные сегменты представляют пересечения 3-х плоскостей симметрии первого типа с 3-мя видимыми грани куба. Зеленые пунктирные сегменты представляют собой пересечения 6 плоскостей симметрии второго типа с 3 видимыми гранями куб. Обратите внимание, что каждый из этих сегментов расположен вдоль одной из линий симметрии. квадратного лица.

Таким образом, эти плоскости разрезают каждую грань куба на одинаковые 8 конгруэнтных равнобедренных прямоугольные треугольники, которые были фундаментальными областями симметрии квадрата. Поскольку граней шесть, поверхность куба разделена на 48 равных частей. равнобедренные прямоугольные треугольники.

Основные области куба

Мы видели, как поверхность куба разрезана на 48 прямоугольных треугольников. плоскости симметрии куба.

внутренность куба разрезать на твердые многогранные куски. Так как все плоскости симметрии проходят через центр O куба, куб разделен на 48 пирамид с вершиной O и с основанием на 48 треугольников.

Каждая пирамида представляет собой неправильный тетраэдр. Одна грань — это один из 48 треугольников на гранях куба. Три другие грани — треугольники; каждый имеет вершину в точке O. Каждая из этих граней пирамиды представляет собой треугольник в одной из плоскостей симметрии куба. Мы видим, что одна из этих плоскостей симметрии тип, параллельный паре граней куба. Два других — каждый самолет которые содержат пару ребер.

На рисунке вершины одного из 48 треугольников обозначены АСМ. затем грани пирамиды треугольник АФМ (на грани куба), треугольник OFM (на плоскости симметрии, параллельной двум граням куба и перпендикулярной линия АМ), треугольник ОМА (на плоскости симметрии, содержащей О и линию АМ) и треугольник OAF (в плоскости симметрии, пересекающей грань по линии AF).

Если мы рассмотрим ребра пирамиды дальше, мы увидим, что ребро OF перпендикулярно грани АСМ.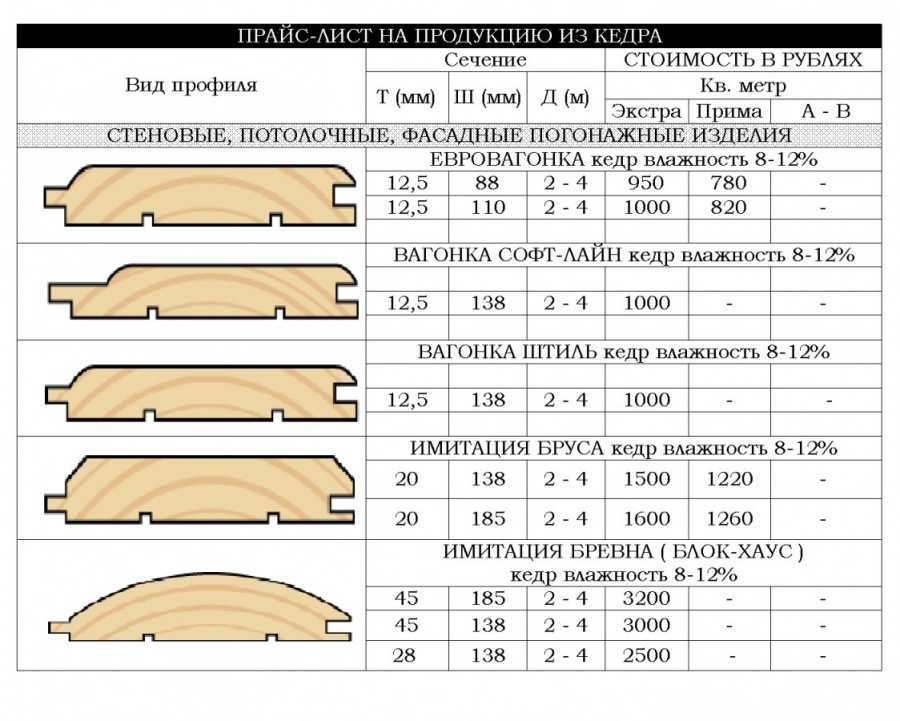

Также длины 3 ребер пирамиды равны s/2; это АМ = МР = ФО. Два ребра являются диагоналями квадратов, поэтому AF = OM = (s/2)*sqrt 2. конечное ребро составляет половину диаметра куба OA = (s/2)*sqrt 3 (OA — это диагональ «углового куба»).

Таким образом, мы видим, что среди четырех граней тетраэдра есть две пары из равных треугольников. Два равнобедренных прямоугольных треугольника с катетами = s/2 и два прямоугольных треугольника, которые являются половинами прямоугольника с шириной s/2 и длина (s/2)*sqrt 2. (Обратите внимание на цветовую маркировку приведенных ниже длин и длин на рисунке выше.) Параллелограмм и прямоугольник внизу можно вырезать и сложить по указанной диагонали, а затем сложить, чтобы сформировать пирамиду.

Легко проверить, что объем одной из этих пирамид равен 1/48 объема объем куба.

Наконец, есть физический эксперимент, показывающий симметрию куба. Можно построить трехмерный калейдоскоп, соединив 3 зеркала в пространстве так, чтобы зеркала образуют 3 стороны пирамиды, которые встречаются в точке O.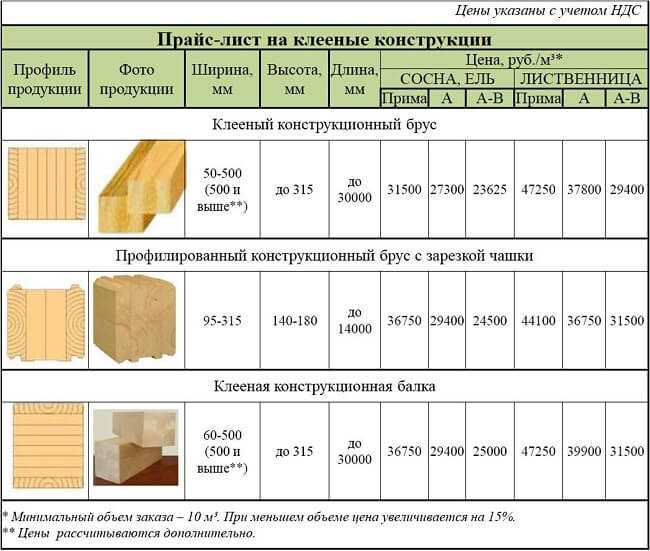 Тогда, если построить модель одной из 48 пирамид и бросает ее в калейдоскоп, каждый видит, что кажется целым кубом.

Кубик Рубика Решение: Nerd Paradise

Это простое решение кубика Рубика, состоящее из различных методов, которые я объединил вместе, и которые, по моему мнению, были самыми простыми для начинающих. Некоторые решения требуют некоторого запоминания и небольшого размышления. Другие требуют много размышлений, но мало запоминания. Другие требуют много обоих, но очень быстро. Представленное здесь решение относится к низкому уровню мышления, слабому запоминанию, но довольно медленной части спектра. Поэтому вы не сможете пойти и собрать кубик Рубика сразу после прочтения этой страницы только один раз. Это потребует хорошего запоминания, но это не невозможно. Я видел, как люди запоминали это решение за день. Если вы тщательно изучите это решение, ваше лучшее время может быть около минуты или полутора минут. Как только вы достаточно хорошо освоите этот метод и захотите поработать над временем решения, я предлагаю вам изучить метод Фридриха или другой метод измерения скорости. Гугл твой друг.

Аксиомы, которые следует помнить:

• Куб состоит из 21 движущейся части. К ним относятся 1 тройная ось, 12 кромок и 8 угловых деталей.
• Центральный квадрат всегда останется центральным квадратом, как бы вы ни поворачивали куб. Крайняя часть всегда останется краевой, независимо от того, как вы поворачиваете куб.
• Угловая часть всегда останется угловой, как бы вы ни поворачивали куб. Центральные части никогда не меняют своего положения по отношению друг к другу. Они только крутятся на месте, хотя кажется, что меняются местами.
• На кромке есть две наклейки. Эти две наклейки всегда будут оставаться рядом друг с другом. Если вы хотите переместить один из цветов в другую позицию, другой тоже должен прийти. Та же идея касается и угловых элементов.

Отклеивание наклеек не является решением (на самом деле, если вы начнете отклеивать некоторые из наклеек, но так и не закончите ставить остальные на свои места, вы, скорее всего, получите невозможную комбинацию и сделаете куб неразборным). Даже если вы закончите заменять наклейки, вы сделаете сборку куба более сложной и неудобной для человека, который действительно знает, как его собрать, поскольку цвета не находятся в одном и том же месте по отношению друг к другу.

Сторона A Примечание:

Существует разница между ориентированным и позиционированным. Если сегмент находится в неправильном месте, говорят, что он находится в неправильном положении. Если сегмент находится в правильном месте, но обращен не в ту сторону, то он ориентирован неправильно.

Шаг 1. Решение одной стороны

Решение верхней строки — самая сложная часть решения, хотите верьте, хотите нет. Имейте в виду, что когда вы решаете одну сторону, вы должны одновременно решать соседний ряд. Это означает, что если вы решили сначала решить синее лицо, оно должно выглядеть примерно так, как на картинке выше. Обратите внимание, как красиво выстроены красные и зеленые квадраты в верхнем ряду. Готовы принять вызов? Вот так…

Пошаговые инструкции:

• Не паникуйте
• Выберите цвет из шести (в большинстве примеров я буду использовать синий, поэтому всякий раз, когда я говорю «синий», я имею в виду верхний цвет).
• Найдите наклейку того цвета, которая находится в центре лица. Это будет ваш топ.
• Переместите соответствующие ребра и угловые части этого цвета рядом с центральным кубом, убедившись, что цвета верхнего внешнего ряда выровнены (пусть мыслительные соки текут).

Давайте разберем последнюю часть…

То, что вы в основном пытаетесь сделать, это:

Когда вы пытаетесь сделать это в первый раз, всегда полезно сначала решить крайние части. , так что у вас есть крест сверху, вот так…

Это облегчит позиционирование углов.

Однако иногда вы столкнетесь с этой маленькой дилеммой…

Вот что делать, если это произойдет:

Щелкните здесь, чтобы просмотреть анимацию приведенной выше последовательности.

Перемещая кромку на место, убедитесь, что пока вы поворачиваете стороны, она не мешает уже установленным кромкам. Переместите верхнюю сторону, чтобы не испортить то, что вы уже сделали.

Всегда следите за тем, чтобы цвета на сторонах краев совпадали с цветами других центральных квадратов (ОЧЕНЬ ВАЖНО). ..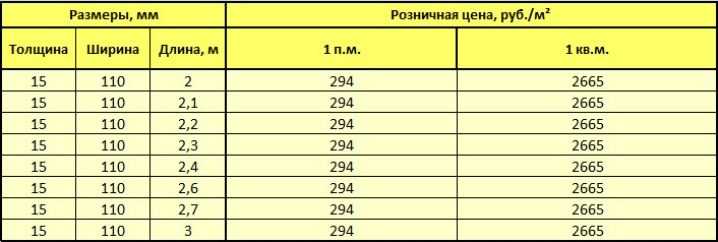

Когда вы это сделаете, вы можете перейти к решению углов.

Если угол, который вы хотите переместить, находится в нижнем ряду, переместите его прямо под нужное место. Помните, что цвета должны совпадать, когда он попадает в верхний ряд. Поэтому не перемещайте угловой элемент с синим, желтым и оранжевым цветом непосредственно под сине-красным и сине-зеленым краями.

НЕПРАВИЛЬНО:

ПРАВИЛЬНО:

Есть три способа переместить этот угол в верхний ряд, не нарушая ни одной кромки. В зависимости от того, как ориентирован угол, вы можете решить, как его переместить.

«2» означает повернуть эту сторону на 180 градусов. Неважно, каким образом.

Синяя наклейка обращена вправо:

Синяя наклейка обращена влево:

Синяя наклейка направлена ​​вниз:

Что делать, если нужный угол уже находится в верхнем ряду, но находится не в том месте или имеет неправильную ориентацию? Делайте это, удерживая куб так, чтобы нужный угол был впереди:

Нужная деталь теперь находится в нижнем ряду где-то слева. Кризис решен.

Посмотрите, что вы только что сделали:

Шаг 2: средний ряд

Теперь поверните верхнюю грань так, чтобы центральный куб на каждой соседней грани совпадал по цвету с тремя квадратами над ним, образуя маленькие буквы «Т». с каждой стороны, вот так.

Вы можете сказать, что краевой элемент с зеленым цветом на одной стороне и оранжевым на другой стороне находится в середине изображения выше, чтобы он выглядел следующим образом:

Посмотрите на нижнюю грань на твой куб. Выясните, каким будет ваш нижний цвет; он должен быть того же цвета, что и центральная наклейка внизу.

Теперь посмотрите на крайние части внизу и попытайтесь найти ту, на которой нет нижнего цвета. Это означает, что эта кромка должна идти в среднем ряду.

Следующие два алгоритма показывают, как переместить фишку из нижнего ряда в средний ряд. Имейте в виду, что приведенные цвета являются лишь примерами того, как может выглядеть цветовая схема вашего куба. (красный спереди, зеленый справа)

→

→

Если фигура находится в среднем ряду, но не на своем месте или неправильно ориентирована, например, вот этот красно-зеленый край…

…тогда выберите случайную фигуру из нижнего ряда. Представьте, что эта случайная фигура из нижнего ряда — красно-зеленая крайняя фигура, и решите ее. Как только вы поместите эту неправильную фишку на место красно-зеленой, настоящая красно-зеленая фишка упадет обратно в нижний ряд. Как только настоящая красно-зеленая фигура окажется в нижнем ряду, вы можете расположить ее обычным образом, используя шаги, описанные выше.

Шаг 3: Ориентация нижних углов

Этот следующий шаг является одним из наиболее часто неправильно истолковываемых шагов во всем решении, поэтому обратите особое внимание…

Далее вы должны сориентировать четыре угла. Сравните четыре угла в нижней части куба с этими картинками. Не обращайте внимания на неугловые части в нижней части куба. Пропустите этот шаг, если все они ориентированы правильно. Весь смысл сравнения дна в том, чтобы определить, как удерживать кубик для следующего хода. Черные точки представляют собой нижний цвет вашего куба. Это все возможные комбинации ориентации углов. Выясните, какой из них выглядит как нижние углы вашего куба. Теперь держите куб так, чтобы он выглядел точно так, как здесь. Возможно, вам придется повернуть его, чтобы он совпадал.

Примечание : Помните, что «2» означает дважды повернуть указанную грань. Неважно, в какую сторону вы его повернете. В любом случае кончится одинаково.

Теперь вернитесь к началу этого шага и продолжайте делать это, пока все четыре угла не будут правильно ориентированы. Если вы все сделаете правильно, максимум, что вам придется сделать, это три раза. Иногда получается с первой попытки. Иногда вам может повезти, и вы можете вообще пропустить этот шаг.

Как добраться:

Шаг 4: Ориентация нижних краев

На этом шаге есть только 4 варианта ориентации нижних краев. Если ваш куб не соответствует ни одному из них, значит, кто-то отклеил ваши наклейки. Этот шаг довольно прост. Игнорировать серые квадраты; белые квадраты — это те, которые нужно сориентировать. Держите куб так, как показано на картинке. Если вы не держите его так, чтобы белый цвет на картинке точно соответствовал тому, где находятся дезориентированные края, вы можете сделать некоторые ходы, разрушительные для вашего прогресса.

Эти приемы довольно легко запомнить, потому что они всегда следуют следующей схеме:

Влево вверх, вправо вверх, повернуть куда-нибудь вперед,
Влево вниз, вправо вниз, поверните где-нибудь дно,
Повторение.

Загляните под куб, чтобы сопоставить его с одной из диаграмм ниже. Белые квадраты представляют края, которые неправильно ориентированы.

2 Неправильные части рядом друг с другом

(Вторая половина этого хода почти точно повторяет первую!)

2 Неправильные части друг напротив друга

Все 4 ребра неправильные

Очень близко.