Сколько в квадрате кубов: Сколько метров в кубе посчитать онлайн калькулятор

Сколько метров в кубе посчитать онлайн калькулятор

Очень часто нужно быстро рассчитать количество необходимых пиломатериалов. Формулы расчета просты, но не всегда под рукой есть калькулятор. Наш онлайн-калькулятор призван помочь решить эту проблему. Вопросы о том, сколько метров в кубе и другие подобные им  решаются путем перетаскивания ползунков нижеприведенной формы.  Приведенная форма помогает легко рассчитать количество досок в 1 м.кв. зная их ширину и длину.  А если добавить толщину доски, то легко можно вычислить такие величины, как количество квадратных метров или досок в 1 м.куб.  Просто перетаскивайте ползунки и нажимайте кнопку «Посчитать».

Онлайн-калькулятор расчета количества пиломатериалов

Некоторые результаты расчета для самопроверки приводим в следующих таблицах.

 Расчет количества доски в 1 м.куб.

толщина, мм	ширина, мм	длина, м	кол-во, шт	м. кв.	м.куб	шт в м.кв.	шт в м.куб.	кв.м. в кубе
18	100	1,5	1	0,15	0,003	6,67	370,37	55,56
20	120	2,0	1	0,24	0,005	4,17	208,33	50,00
20	140	3,0	1	0,42	0,008	2,38	119,05	50,00
35	70	3,0	1	0,21	0,007	4,76	136,05	28,57
40	70	3,0	1	0,21	0,008	4,76	119,05	25,00
27	120	4,0	1	0,48	0,013	2,08	77,16	37,04
35	140	6,0	1	0,84	0,029	1,19	34,01	28,57

Расчет количества бруса в 1 м.куб.

Количество доски на забор можно рассчитать в нашем калькуляторе расчета заборной доски

Для более точного расчета количества пиломатериалов исходя из их наличия и ассортимента  лучше связаться с нашими представителями по телефонам, указанным в шапке сайта.

Сколько в квадратном метре газоблока, Сколько газоблоков в

Сколько в квадратном метре газоблока? Сколько газоблоков в 1 куб метре?

Давайте разберемся сколько штук газоблоков в 1 м³. Для этого необходимо на калькуляторе 1 (единицу) поделить на высоту блока в метрах (например 0,3 для высоты 300мм), поделить на ширину газоблока в метрах (например 0,2 для ширины 200мм) и поделить на 0,6 (стандартная длинна блоков 600мм). Получаем:

1/0,3/0,2/0,6=27,77 шт в 1 м

³ для блока 300х200х600мм
Актуальный прайс-лист

Для блока 400х250х600мм имеем 1/0,4/0,25/0,6= 16,66 шт. И еще разок для газоблока 100х288х600мм — 1/0,288/0,1/0,6= 57,87 шт.

Ура! Теперь мы можем легко посчитать сколько штук газоблоков м³ или сколько в кубе шт. Стоимость газоблока

Немножко тяжелее разобраться как посчитать сколько газоблока в 1 м

2 или куб газоблока сколько метров? Начнем с вопроса сколько газоблоков в 1м² кладки. Нужно на калькуляторе 1 (единицу) поделить на ВЫСОТУ блока в метрах (например 0,3 для высоты 300мм) и поделить на 0,6 (стандартная длинна блоков 600мм). Для блока 200х300х600 мм (толщина стены 200мм) получаем

1/0,3/0,6=5,55 шт в 1м

²

Мы уже знаем, что в 1м³ 200х300х600мм блока — 27,77 шт, и следовательно 27,77/5,55=5,00м² (пять метров квадратных) кладки мы получим из блока 200*300*600мм при толщине стены 200мм.

Для этого же блока 200х300х600мм при толщине стены в 300мм имеем: 1/0,2/0,6=8,33 шт газоблоков в 1м², 27,77/ 8,33= 3,33 м² кладки из 1м³. Еще раз Ура! Теперь мы можем легко посчитать сколько газоблока в квадрате 1м².

И легкое, высчитать кубатуру газоблока или как посчитать куб газоблока? Для примера возьмем блок 375х250х600мм.

Объем одного блока равен 0,375*0,25*0,6= 0,05625 м³. Если теперь 1 (единицу) поделить на 0,05625 то мы получим 17,77. Это количество штук блока в 1м³.

Закрепим на примере:имеем стеновой газобетон 400х200х600 мм (толщина стены 400мм) и перегородочный газоблок 100х200х600мм.

Сколько газоблоков 1 куб метре: для стенового 1/0,4/0,2/0,6=20,83шт, для перегородочного газобетона 1/0,1/0,2/0,6=83,33шт.

Сколько в квадратном метре газоблока (расход газоблока на 1м²): для стенового 1/0,2/0,6= 8,33шт, для перегородочного 1/0,2/0,6= как видим тоже 8,33шт.

Сколько квадратов в кубе газоблока: для блока 400х200х600мм при толщине стены 400мм 1/0,4=2,5м², для блока 100х200х600мм 1/0,1=10м²

Заказать газоблок с доставкой

Возможно Вас также заинтересует:

Please enable JavaScript to view the comments powered by Disqus.

» Калькулятор

Мы смело можем заявить, что наш калькулятор является самым удобным и точным.

Мы разработали для Вас калькулятор, который быстро Вам поможет перевести необходимое вам количество кубических метров, квадратных метров или упаковок в другие единицы измерения. Возможно перевести как метры квадратные в метры кубические или упаковки, так и наоборот: метры квадратные в метры кубические и упаковки.

С помощью калькулятора можно рассчитать, сколько досок евровагонки понадобится вам для отделки конкретного количества квадратных метров поверхности.

При заказе не стоит забывать об отходах при монтаже пиломатериалов, величина которых может составлять до 10% и стоит заранее взять материалы с запасом хотя бы на 5-10%.

Если вам необходимо рассчитать кубические или квадратные метры для изделий отличных от пиломатериалов, вы можете воспользоваться нашими универсальными калькуляторами, представленными ниже.

Первый, синий калькулятор переводит из квадратных метров в кубические, вы только указываете толщину.

Второй, зеленый калькулятор переводит из кубических метров в квадратные, так же вы должны указать толщину.

Пример
Задача: Понять сколько в кубах будет доска пола толщиной 30 мм на площадь помещения 25 м2?

Решение: Вы хотите купить доску для пола толщиной 30 мм на площадь 25 м2, то есть надо перевести из квадратных метров в кубические,  для этого вы в синем калькуляторе всего лишь вводите необходимую Вам площадь 25 квадратных метром и толщину половой доски 30 мм или любого предполагаемого пиломатериала, далее нажимаете кнопку рассчитать. В итоге вы получаете необходимое количество кубических метров для Вашей площади при заданной толщине.

Если Вам требуется наоборот понять сколько квадратных метров в кубе при заданной толщине, то всего лишь используйте второй, зеленый калькулятор, который делает перевод из кубических метров в квадратные.

Пользоваться калькулятором очень просто, для перевода вам необходимо всего лишь знать толщину изделия.

Можно выбрать единицы измерения толщины: миллиметры, сантиметры, дюймы и метры.

Сколько кирпичей в квадрате и кубе кладки

Подсчёт сметы – это начальный этап строительства. От его точности зависит то, появятся ли лишние растраты, успеют ли строители закончить проект в срок, хватит ли материалов.

Подсчёт сметы – это начальный этап строительства. От его точности зависит то, появятся ли лишние растраты, успеют ли строители закончить проект в срок, хватит ли материалов.

Когда речь идёт о кирпичах, рассчитывать смету следует в двух параметрах – сколько кирпичей в кладке в кубе и квадрате. Задача усложняется тем, что в учёте учувствуют габариты кирпича, которые различны. Поэтому в первую очередь следует определить, какого размера будет кирпич, применяемый в данном строительстве.

Сколько кирпичей в квадрате кладки

Квадратными метрами измеряется площадь. Для того, чтобы определить сколько кирпичей в 1м2 кладки необходимо произвести простые расчёты:

1. Вычислить площадь одного кирпича. Для этого умножить его ширину на длину. Допустим, 250 мм. на 120 мм. = 30 000 кв.мм.
2. Этот результат нужно перевести из квадратных миллиметров в квадратные метры. Для этого нужно поделить его на 1 000 000 (потому что 1кв.м.=1 000 000 кв.мм.). Получается 30 000 кв.мм./1 000 000 = 0,03 кв.м. – это площадь одного кирпича.
3. Затем, чтобы узнать, сколько кирпича в м2 кладки, следует разделить этот квадрат на площадь одного кирпича. То есть 1кв.м./0,03 кв.м. = 33,3 кирпича. Рекомендуется округлять в большую сторону – 34 кирпича на один квадрат.

Сколько кирпичей в кубе кладки

Кубическими метрами измеряете объём. Для определения количества кирпича в 1м3 кладки, потребуются результаты вычисления пощади:

1. Чтобы узнать объём, требуется умножить длину на высоту и ширину. Так как произведение длины и ширины есть площадь, вычисление которой было рассмотрен выше, то берём этот готовый показатель (то есть 0,03 кв.м) и умножаем его на ширину кирпича в метрах 0,065 м. – 0,03кв.м х 0,065м. = 0,00195 куб.м. – объём одного кирпича.
2. Вычисляем, сколько кирпича в м3 кладки простым действием – 1куб.м./0,00195 куб.м. = 512,8 кирпичей. И округляем снова в большую сторону – 513 кирпичей в кубе кладки.
То, сколько кирпичей в кубе кладки может зависеть от раствора, который их соединяет, если речь идёт о более точном подсчёте. Это касается и расчёта площади тоже. В некоторых случаях учитывает показатель толщины этого раствора. И здесь коэффициент может быть разным, так как это зависит от качества и количества веществ, применяемых в составлении раствора. Но чаще всего можно обойтись и без учёта данного параметра.
В данных примерах был взять стандартный кирпич размером 250х120х65 мм. Если в стройке используется другой размер, то результаты, естественно, будут иными.

Объем и размеры резервуаров – как выбрать подходящую емкость

Наша компания является производителем резервуаров различных типов и назначения. Мы предлагаем емкости разной формы и объема, при этом на посвященных им страницах всегда указываем исчерпывающую информацию по характеристикам конкретной продукции, включая:

• объем в м3;
• форму – цилиндрическая, квадратная, прямоугольная;
• расположение – горизонтальное, вертикальное.

Тем не менее, мы достаточно часто получаем вопросы, связанные с габаритами наших изделий и их объемом. Поэтому рассмотрим данный вопрос более подробно.

Связь между объемом и формой резервуара

Всем, кто прилежно изучал школьный курс физики, известно, что минимальной площадью поверхности при максимальном объеме обладает сосуд в форме шара. Но шарообразные емкости сложны в изготовлении и непрактичны, поэтому производители изготавливают емкости в форме цилиндра или куба (прямоугольника).

Цилиндрические емкости

Могут располагаться горизонтально или вертикально. Объем рассчитывается по формуле V=πr2h. То есть умножаем число π (3,14159) на радиус в квадрате и на высоту h цилиндра.

Пример: есть вертикальный цилиндрический резервуар диаметром 3 метра и высотой 5 метров. Рассчитываем объем: Радиус – 1,5 метра, в квадрате будет 2,25. Умножаем: 3,14159 ×2.25 ×5 (высота) = 35,34 м3. Итого, рабочий объем нашего резервуара будет равен 35 кубическим метрам, или 35 000 литрам (в 1 кубе – 1000 литров).

На практике конкретные размеры резервуара рассчитываются с учетом его функциональности. Например, горизонтальный резервуар диаметром 1 метр и длиной 10 метров будет просто неудобен в использовании. Его объем составит 7,8 куба. Если нам нужен резервуар такого объема, уместнее увеличить его диаметр и уменьшить длину – например, сделать диаметр 2 метра при длине 3 метра. Получим те же 7,8 куба при гораздо более функциональных размерах.

Прямоугольные емкости

Здесь все еще проще. Чтобы узнать полный объем, достаточно длину емкости умножить на ее ширину и высоту. Например, кубический резервуар со стороной 1 метр будет вмещать 1 куб жидкости. Емкость размером 3000 мм × 2000 мм × 2500 мм будет иметь объем 15 кубометров.

Почему большинство резервуаров имеют не квадратную или прямоугольную, а цилиндрическую форму? Потому что конструктивно такие емкости являются более прочными. Чтобы сварить куб, нужны 6 листов стали и 12 сварных швов. Цилиндрическая емкость имеет всего 3 поверхности: два круглых дна и цилиндрический корпус.

Корпус может быть сварен из одного листа металла, свернутого в цилиндр, для этого нужен всего 1 сварной шов. Плюс еще два круговых шва, чтобы приварить днища. Итого, в идеальном варианте всего 3 сварных шва – вместо 12 у куба.

Зачем тогда делают прямоугольные емкости? У них есть свои сферы использования. Например, их применяют в качестве пожарных емкостей – они обладают отличной эргономикой и хорошо вписываются в помещения, занимая минимум места.

В нашей компании вы можете заказать резервуар практически любого типа, формы и назначения. Мы предлагаем как типовые варианты, так и изготавливаем продукцию на заказ. Зная основные принципы расчета размеров и объема резервуаров, вы можете оценить, какой вариант для вас окажется наиболее подходящим.

Как перевести кубический метр в квадратный, и наоборот

В реальной жизни часто возникает необходимость соотнесения разных мер измерения: перевести кубический метр в квадратный.

Если это касается площади, то желательно знать не только правило, но и его особенности, и даже скрытый смысл, о котором в конце поста.

Интуитивный способ перевода кубического метра в квадратный и наоборот

Пользоваться выражением «а, вдруг, не хватит» означает потратить деньги на материал, который не будет использован. Тогда результат работы может не только огорчить, но и создать проблему: куда деть новое, что куплено как не нужное. Например, выбирая кафельную плитку, рулонные утеплители, сыпучие строительные материалы, не стоит ориентироваться на глаз.

Как процесс перевода выглядит в голове человека с образным мышлением.
Сначала он пытается представить себе куб.

Далее этот куб мысленно разрезает на три плоскости, которые на рисунке обозначены черным, зеленым и синим.

 

Потом, переводя мысленно кубический метр в квадратный, он размещает разноцветные квадраты так

 

или так

 

В зависимости от формы площади, которую нужно застелить.

Обратная последовательность перевода квадратного метра в кубический становится понятной, если эти рисунки рассматривать снизу-вверх.

Математическое правило перевода кубического метра в квадратный и наоборот

С точки зрения математики существует уравнение, согласно которому один квадратный метр условно равен 0,33 части одного кубического метра. Это значит, что, например, продается упаковка, содержащая 1 кубический метр утеплителя. Чтобы узнать, сколько это будет квадратных метров, нужно 1 разделить на 0,33, и получится 3.03.

Следовательно, одной упаковки, в которой содержится 1 кубический метр, хватит, чтобы в один слой застелить поверхность, которая равна 3 квадратным метрам, и еще должно остаться 3 сантиметра. В реальной жизни следует разделить цифру, указанную на упаковке в кубических метрах, на 0,33, и узнать количество квадратных метров, ведь утеплитель не пакуют именно по одному метру кубическому.

А что такое квадратный метр, и как его измерить? Для начала нужно понимать, что квадратный метр, это условно определенная целостная горизонтальная, вертикальная, любого наклона, поверхность, у которой длина каждой стороны равна одному метру.

Внимание! Переводя кубический метр в квадратный следует помнить о следующем. Особенно, если речь о материалах, которые планируется самостоятельно переводить из кубических метров в квадратные. То есть вручную разрезать по слоям, чтобы далее накрыть поверхность, и, хотя-бы утеплить балкон.

Например изовер,  минеральная вата. Они бывают толщиной 15 см, и предполагается острым ножом разрезать, чтобы сделать несколько пластов. Мы же помним, что 0,33+0,33+0,33=0,99. Это значит, что после разрезания на пласты не получится целый квадратный метр. К сожалению, не хватает всего одного сантиметра. Похоже, что это ерунда, но чем-то её придется закрыть, или учесть на начальном этапе перевода кубического метра в квадратный.

При проведении обратной операции, переводя из квадратных метров в кубические, останется хвостик. Что с ним делать — решайте сами.
Как мне удалось, за один выходной, выбрать, подогнать по размеру, и установить на окно купленные в магазине жалюзи Вы узнаете из новой бесплатной книги «Жалюзи: подобрать, подогнать, установить».

Игорь

  Все получается!

ВВЕДИТЕ СВОЙ Е-МЕЙЛ — ПРОСМОТРИТЕ КНИГУ!

 

БЕСПЛАТНАЯ КНИГА

Поделиться ссылкой:

Понравилось это:

Нравится Загрузка…

Похожее

Как перевести квадратные метры в другие единицы площади

Как перевести метры в квадратные метры

Один метр — это длина пути, проходимого светом в вакууме за 1/299792458 секунды (где-то 1 широкий шаг достаточно высокого человека).

Один квадратный метр — это площадь квадрата со стороной в 1 метр. Чтобы узнать площадь комнаты или участка земли в квадратных метрах, нужно сосчитать сколько в них уместится квадратов метр на метр (1 м × 1 м).

масштаб 1 : 100

Длина: 1 мПлощадь: 1 м²Площадь: 6 м²Длина: 3 мШирина: 2 м

Нельзя конвертировать метры в квадратные метры, но можно зная длину и ширину прямоугольника найти его площадь в квадратных метрах.

Предварительно все значения нужно привести к одной требуемой единице измерения.

Например, если нужно вычислить размер стены в квадратных метрах, то её длину в 3 метра и 20 сантиметров нужно заменить на 3,2 метра.

3 м 20 см × 2м = 3,2 м × 2 м = 6,4 м²

Зная формулы из уроков геометрии, можно рассчитать площадь фигуры любой другой формы, например, треугольной.

масштаб 1 : 100

a: 4 мb: 3 м 60 смc: 2 м 50 см

1/4 √(a + b + c)(b + c - a)(a + c - b)(a + b - c) = 1/4 √(4 + 3,6 + 2,5)(4 + 2,5 - 3,6)(3,6 + 2,5 - 4)(4 + 3,6 - 2,5) = 1/4 √10,1 × 2,9 × 2,1 × 5,1 = 1/4 √313,6959 = 1/4 × 17,711 = 4,43 м²

Калькулятор квадратных метров

1 см	=	10 мм	1 см²	=	100 мм²
1 дм	=	10 см	1 дм²	=	100 см²
1 м	=	10 дм	1 м²	=	100 дм²
			1 а	=	100 м²
			1 га	=	100 а (ар или сотка)
1 км	=	1000 м	1 км²	=	100 га = 1000000 м²

В один квадрат со стороной в 1 метр помещается 100 квадратов со стороной в 1 дециметр.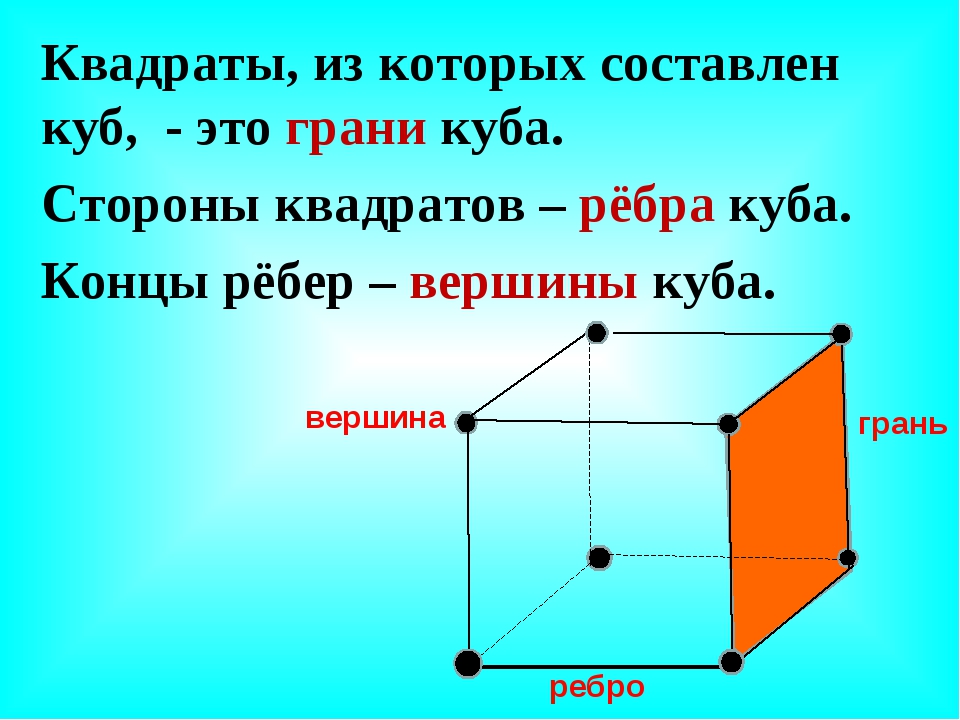

масштаб 1 : 10

1м = 10 дмДлина: 1 дмДлина: 1 м1м² = 1 м × 1 м = 10 дм × 10 дм = 100 дм²Площадь: 1 дм²Площадь: 1 м²

В каждый из 100 квадратов со стороной в 1 дециметр помещается 100 квадратов со стороной в 1 сантиметр.

масштаб 1 : 10

1м = 100 смДлина: 1 смДлина: 1 м1м² = 10 дм × 10 дм = 100 см × 100 см = 10000 см²Площадь: 1 см²Площадь: 1 м²

Послесловие: если информации оказалось недостаточно для решения вопроса, в комментариях можно оставить дополнения или пожелания относительно содержания статьи.

Головоломка с числами в виде квадратов и кубов

Головоломка с числами из квадратов и кубов

Автор: Дэвид, 2 мая 2018 г. Головоломка

Когда вы умножаете целое число само на себя, вы получаете квадратное число. Если вы возьмете три копии целого числа и умножите их все вместе, вы получите кубическое число.

Есть только одно двузначное число, которое одновременно является квадратом и кубом.Вы можете определить, какой это номер?

Для тех, кто ищет вызов, можете ли вы найти единственное трехзначное число, которое одновременно является квадратом и кубом?

Прокрутите вниз, чтобы найти ответ!

Ответ на головоломку

Есть много способов решить эту головоломку. Один из способов — перечислить все квадратные числа двумя цифрами: 16, 25, 36, 49, 64, 81.

Затем перечислите все числа куба двумя цифрами: 27, 64.

Ответ — единственное число в обоих списках: 64.

Есть и более хитрый способ решить эту головоломку, который упрощает решение проблемного вопроса. Он основан на математическом факте: если вы умножите два квадрата вместе, вы получите квадрат! Если вы не уверены в этом факте, попробуйте привести несколько примеров, чтобы понять, что происходит.

Мы начнем с квадрата и используем его, чтобы сделать квадрат, который также является кубом. Начнем с небольшого квадрата: 4.

Мы знаем, что 4 x 4 = 16 — это квадрат из приведенного выше факта, а также из-за того, что означает квадрат.Но мы можем пойти еще дальше. 4 x 16 = 64 — это произведение двух квадратов, поэтому это тоже квадрат. Но вы также можете записать его как 64 = 4 x 4 x 4, превратив его в куб.

Используя этот метод, мы можем вычислить следующий квадрат, который является кубом, повторяя этот процесс. На этот раз начните со следующего наименьшего квадрата: 9. Во-первых, 9 x 9 = 81.

9 x 81 = 729, это произведение двух квадратов, поэтому оно также является квадратом. Вы также можете записать его как 729 = 9 x 9 x 9, превратив его в куб.

Следовательно, ответ на вызов — 729.

Чтобы получить больше головоломок и головоломок для детей, подпишитесь на журнал Double Helix!

кубоидов, прямоугольных призм и кубов

Перейти к площади или объему поверхности.

Кубоид — объект прямоугольной формы.

У него шесть плоских граней, и все углы прямые.

И все его грани — прямоугольники.

Это также призма, потому что она имеет одинаковое поперечное сечение по длине.Фактически это прямоугольная призма .

Примеры кубоидов

Кубоиды очень распространены в нашем мире, от коробок до зданий мы видим их повсюду. Мы можем даже поместить их в другие кубоиды!

Дом
Коробка с
слот как ручка
Кубоиды в
кубовидная комната
Ящики для модельных поездов
Вот это просто глупо!

Квадратная призма

Если по крайней мере две длины равны, ее также можно назвать квадратной призмой .

(Примечание: мы все еще можем назвать это прямоугольной призмой, если захотим!)

Куб

Когда все три длины равны, он называется кубом (или шестигранником)
, и каждая грань представляет собой квадрат.

Куб по-прежнему является призмой.

А куб — одно из Платоновых Тел.

Так:

• Куб — это просто частный случай квадратной призмы, а
  
• Квадратная призма — это просто частный случай прямоугольной призмы, а
  
• Все они кубоиды!

Примечание. Название «кубоид» происходит от «куб» и -oid (что означает «похожий на или похожий») и, таким образом, гласит: «это , как куб».

Другое использование -оида — это когда мы говорим о том, что Земля является сфероидом (не совсем сферой, но близко).

Площадь

Площадь поверхности определяется по формуле:

Площадь = 2 × Ширина × Длина + 2 × Длина × Высота + 2 × Ширина × Высота

Что можно сократить до:

А = 2WL + 2LH + 2HW

Пример: Найдите площадь поверхности этого кубоида

А	=	2WL + 2LH + 2HW
	=	2 × 4 × 10 + 2 × 10 × 5 + 2 × 5 × 4
	=	80 + 100 + 40
	=	220

Объем

Объем кубоида находится по формуле:

Объем = длина × ширина × высота

Что можно сократить до:

V = д × ш × в

Или проще:

V = lwh

Пример: Найдите объем этого кубоида

V = lwh = 10 × 4 × 5 = 200

Что такое Unit Cube? — Определение, факты и пример

Игры с юнит-кубом

Объем с использованием юнит-кубов

Единичный куб — это куб, имеющий объем или емкость 1 юнит.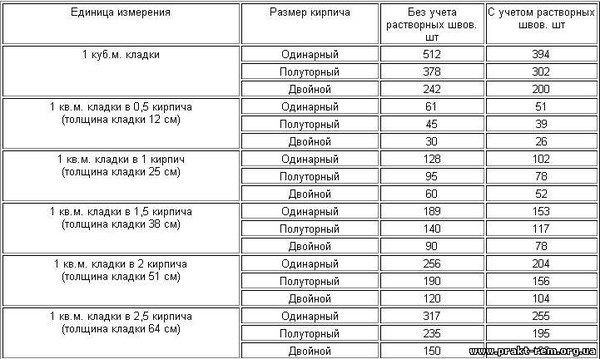 Вы можете подсчитать количество единичных кубиков, которые могут поместиться в твердое тело, чтобы определить его объем.

охватывает Common Core Curriculum 5.MD.5.aИграть сейчасПосмотреть все игры по геометрии >>

Учитесь с полной программой обучения математике K-5

Что такое Unit Cube?

В геометрии единичный куб — это куб, каждая сторона которого имеет длину 1 единицу.

Объем Количество места, которое что-то занимает, называется его объемом.

Объем единичного куба:

У куба все стороны одинаковой длины. Единичный куб имеет все стороны длиной 1 единицу. Итак,

объем единичного куба = Сторона × Сторона × Сторона

= 1 единица × 1 единица × 1 единица

= 1 кубическая единица

Объем единичного куба равен одной кубической единице.

Если твердая фигура сделана из единичных кубов, то объем фигуры равен количеству единичных кубов, составляющих фигуру.

Это тело состоит из 6 единичных кубов.

Следовательно, его объем равен 6 куб.

Площадь Общая площадь, которую покрыла бы поверхность трехмерного объекта, если бы его стороны были плоскими, называется площадью поверхности. Площадь поверхности измеряется в квадратных единицах.

Площадь единичного куба

У куба 6 квадратных граней. Единичный куб имеет 6 квадратных граней, каждая из которых имеет длину 1 единицу.Итак, площадь каждой стороны куба = 1 единица × 1 единица = 1 квадратная единица

Поскольку все 6 граней куба имеют одинаковую площадь,

Площадь поверхности единичного куба = 6 × площадь одной грани

= 6 × 1 квадратная единица

= 6 квадратных единиц

Следовательно, площадь поверхности единичного куба составляет 6 квадратных единиц.

Интересные факты Чтобы найти объем объектов с помощью единичных кубов, заполните объект единичными кубами. Количество единичных кубов, которые умещаются в объекте, — это его объем.

Использование линейных, квадратных и кубических мер соответственно

Результаты обучения

• Для объекта измерения определите, будете ли вы использовать линейные, квадратные или кубические единицы
• Вычислить периметр и площадь прямоугольника

Когда вы измеряете свой рост или длину садового шланга, вы используете линейку или рулетку (см. Ниже).Рулетка может напоминать вам линию — вы используете ее для линейной меры, которая измеряет длину. Дюйм, фут, ярд, миля, сантиметр и метр — единицы линейного измерения.

Эта рулетка измеряет дюймы сверху и сантиметры снизу.

Если вы хотите узнать, сколько плитки нужно для покрытия пола или размер стены, которую нужно покрасить, вам нужно знать площадь, меру области, необходимой для покрытия поверхности. Площадь измеряется в квадратных единицах. Мы часто используем квадратные дюймы, квадратные футы, квадратные сантиметры или квадратные мили для измерения площади.Квадратный сантиметр — это квадрат, каждая сторона которого равна одному сантиметру (см). Квадратный дюйм — это квадрат, каждая сторона которого составляет один дюйм (см. Ниже).

Квадратные меры имеют стороны, каждая из которых имеет длину [латекс] 1 [/ латекс] единицу.

На следующем изображении показан прямоугольный коврик длиной [латекс] 2 [/ латекс] и шириной [латекс] 3 [/ латекс]. Каждый квадрат имеет [латекс] 1 [/ латекс] фут в ширину, [латекс] 1 [/ латекс] фут в длину или [латекс] 1 [/ латекс] квадратный фут. Коврик изготовлен из [латексных] 6 [/ латексных] квадратов.Площадь ковра [латекс] 6 [/ латекс] квадратных футов.

Коврик состоит из шести квадратов [латекс] 1 [/ латекс] квадратного фута каждый, поэтому общая площадь ковра составляет [латекс] 6 [/ латекс] квадратных футов.

Когда вы измеряете, сколько требуется для заполнения контейнера, например количество бензина, которое может поместиться в бак, или количество лекарства в шприце, вы измеряете объем. Объем измеряется в кубических единицах, таких как кубические дюймы или кубические сантиметры. При измерении объема прямоугольного твердого тела вы измеряете, сколько кубиков заполняет контейнер.Мы часто используем кубические сантиметры, кубические дюймы и кубические футы. Кубический сантиметр — это куб, который имеет размер по одному сантиметру с каждой стороны, а кубический дюйм — это куб, который измеряет один дюйм с каждой стороны (см. Ниже).

Кубические меры имеют стороны длиной 1 [латекс] [латекс].

Предположим, куб на изображении ниже имеет размеры [латекс] 3 [/ латекс] дюймов с каждой стороны и вырезан по показанным линиям. Сколько в нем маленьких кубиков? Если бы мы разобрали большой куб, мы бы нашли [латексные] 27 [/ латексных] маленьких кубиков, каждый размером один дюйм со всех сторон.Итак, каждый маленький кубик имеет объем [латекс] 1 [/ латекс] кубический дюйм, а объем большого куба — [латекс] 27 [/ латекс] кубических дюймов.

Куб размером [латекс] 3 [/ латекс] с каждой стороны состоит из [латексных] 27 [/ латексных] однодюймовых кубов или [латексных] 27 [/ латексных] кубических дюймов.

Выполнение математического упражнения «Визуализация площади и периметра» поможет вам лучше понять разницу между площадью фигуры и ее периметром.

пример

Для каждого элемента укажите, будете ли вы использовать линейную, квадратную или кубическую меру:
1.количество коврового покрытия, необходимое в комнате
2. длина удлинителя
3. количество песка в песочнице
4. длина карниза
5. количество муки в канистре
6. размер крыши собачьей будки.

Решение

1. Вы измеряете, какую площадь покрывает ковер, то есть площадь.	квадратный метр
2. Вы измеряете длину удлинителя, то есть длину.	линейная мера
3.Вы измеряете объем песка.	мера кубическая
4. Вы измеряете длину карниза.	линейная мера
5. Вы измеряете объем муки.	мера кубическая
6. Вы измеряете площадь крыши.	квадратный метр

Многие геометрические приложения включают определение периметра или площади фигуры.В повседневной жизни также существует множество применений периметра и площади, поэтому важно убедиться, что вы понимаете, что каждое из них означает.
Представьте себе комнату, которой нужна новая напольная плитка. Плитки состоят из квадратов, каждая сторона которых составляет один фут — один квадратный фут. Сколько таких квадратов нужно, чтобы покрыть пол? Это площадь пола.
Затем подумайте о том, чтобы положить в комнату новый плинтус после того, как выложили плитку. Чтобы выяснить, сколько полосок понадобится, необходимо знать расстояние по комнате.Вы можете использовать рулетку, чтобы измерить количество футов в комнате. Это расстояние — периметр.

Периметр и площадь

Периметр — это мера расстояния вокруг фигуры.
Площадь — это мера поверхности, покрытой фигурой.

На изображении ниже показана квадратная плитка толщиной [латекс] 1 [/ латекс] дюйм с каждой стороны. Если бы муравей прошел по краю плитки, он прошел бы [латекс] 4 [/ латекс] дюйма. Это расстояние — периметр плитки.

Поскольку плитка представляет собой квадрат размером [латекс] 1 [/ латекс] дюйм с каждой стороны, ее площадь составляет один квадратный дюйм. Площадь фигуры измеряется путем определения количества квадратных единиц, покрывающих фигуру.

[латекс] \ begin {array} {c} \ text {Perimeter} = 4 \ text {дюймы} \\ \ text {Area} = 1 \ text {квадратный дюйм} \ end {array} [/ latex]

Когда муравей полностью обходит плитку по ее краю, он отслеживает периметр плитки. Площадь плитки [латекс] 1 [/ латекс] квадратный дюйм.

Выполнение математического задания «Измерение площади и периметра» поможет вам лучше понять, как измерять площадь и периметр фигуры.

пример

Каждая из двух квадратных плиток имеет [латекс] 1 [/ латекс] квадратный дюйм. Две плитки показаны вместе.
1. Каков периметр фигуры?
2. Что это за площадь?

Показать решение

Решение
1. Периметр — это расстояние вокруг фигуры. По периметру [латекс] 6 [/ латекс] дюймов.
2. Площадь — это поверхность, покрытая фигурой. Есть плитки [латекс] 2 [/ латекс] квадратных дюйма, поэтому площадь составляет [латекс] 2 [/ латекс] квадратных дюйма.

Геометрия

— количество кубов, которые можно уместить в два больших куба

геометрия — Количество кубов, которые можно разместить в двух больших кубах — Mathematics Stack Exchange

Сеть обмена стеков

Сеть Stack Exchange состоит из 176 сообществ вопросов и ответов, включая Stack Overflow, крупнейшее и пользующееся наибольшим доверием онлайн-сообщество, где разработчики могут учиться, делиться своими знаниями и строить свою карьеру.

Посетить Stack Exchange

2. 0
3. +0
6. Авторизоваться Зарегистрироваться

Mathematics Stack Exchange — это сайт вопросов и ответов для людей, изучающих математику на любом уровне, и профессионалов в смежных областях.Регистрация займет всего минуту.

Зарегистрируйтесь, чтобы присоединиться к этому сообществу

Кто угодно может задать вопрос

Кто угодно может ответить

Лучшие ответы голосуются и поднимаются наверх

Спросил 6 лет, 6 месяцев назад

Просмотрено 1к раз

$ \ begingroup $

У меня следующая проблема

Сколько кубиков, каждый площадью 36 кв. Сантиметров.необходимы для образования 2 кубиков, каждый площадью 144 кв. сантиметра

На мой взгляд, я бы просто разделил 144 * 2/36, чтобы получить 8 кубиков, однако результат дает 16 как правильный ответ. Какая логика мне не хватает?

Создан 08 окт.

$ \ endgroup $ 1 $ \ begingroup $

Вы не можете напрямую разделить области, потому что, когда вы объединяете кубы вместе, некоторые грани входят внутрь, а учитываются только те, которые остались снаружи.Итак, сначала вы найдете длины сторон кубиков, которые равны $ \ sqrt6 $ и $ 2 \ sqrt6 $ соответственно.

Проявив немного воображения, вы можете увидеть, что 8 кубиков меньшего размера вместе образуют один куб большего размера, длина стороны которого вдвое больше, чем у меньших. Итак, для двух из них вам нужно всего 16 кубиков.

Создан 08 окт.

Najayaznajayaz

1,9779 золотых знаков1616 серебряных знаков4545 бронзовых знаков

$ \ endgroup $ $ \ begingroup $

Куб с площадью поверхности $ 36 $ кв. См имеет длину стороны $ \ sqrt {6} $ см, а куб с площадью поверхности $ 144 $ кв. См имеет длину стороны $ \ sqrt {24} = 2 \ sqrt {6} $ см. .3 = 8 $.

Следовательно, мы можем уместить 8 маленьких кубиков в большой куб и $ 16 $ в два из них.

Создан 08 окт.

$ \ endgroup $ Mathematics Stack Exchange лучше всего работает с включенным JavaScript

Ваша конфиденциальность

Нажимая «Принять все файлы cookie», вы соглашаетесь с тем, что Stack Exchange может хранить файлы cookie на вашем устройстве и раскрывать информацию в соответствии с нашей Политикой в ​​отношении файлов cookie.

Принимать все файлы cookie Настроить параметры

Площадь поверхности куба — объяснение и примеры

Определение площади поверхности объекта важно, если вы хотите определить, сколько материала необходимо для покрытия поверхности объекта.

Например, компаниям, которые упаковывают товары в картонные коробки, требуется площадь поверхности, чтобы определить, сколько картона потребуется для изготовления коробки.

Площадь поверхности куба — это общая сумма площадей всех шести квадратов, покрывающих квадрат.

В этой статье мы узнаем, как найти площадь поверхности куба, используя формулу площади поверхности куба.

Как найти площадь поверхности куба?

Напомним, что куб — это трехмерная фигура с 6 равными квадратными гранями, 8 ребрами и 8 вершинами.Поскольку куб имеет шесть граней, площадь поверхности куба определяется умножением площади одной квадратной грани на 6.

Что касается других площадей, площадь поверхности объекта измеряется в квадратных единицах, то есть в миллиметрах ² , см ² , м ² .

Площадь поверхности формулы куба

На приведенном выше рисунке площадь поверхности куба равна:

Площадь поверхности куба = a ² + a ² + a ² + a ² + a ² + a ²

Следовательно, площадь поверхности по формуле куба задается как:

Площадь поверхности куба = 6a ²

, где a = любая длина стороны куб.

Давайте решим несколько примеров задач, связанных с площадью поверхности куба.

Пример 1

Найдите площадь поверхности куба с длиной стороны 10 см.

Решение

По формуле

Площадь куба = 6a ²

= 6 x 10 ²

= 6 x 100

= 600 см

67

Пример 2

Найдите поверхность куба объемом 343 м ³ .

Решение

Учитывая

Объем куба, a ³ = 343 м ³

Сначала найдите длину куба

a = ³ √343

a = 7 м 9000

SA = 6a ²

= 6 x 7 ²

= 6 x 49

= 294 м ²

Пример 3

Площадь поверхности куба составляет 150 квадратных футов . Какая длина куба?

Решение

Учитывая площадь поверхности = 150 футов ²

SA = 6a ²

150 = 6a ²

Разделите обе стороны на 6, чтобы получить,

25 = ²

√a = 5

Следовательно, длина куба составляет 5 футов.

Пример 4

Сплошной куб длиной 10 м должен быть нарисован на 6 гранях. Если стоимость покраски составляет 10 долларов за квадратный метр, найдите общую стоимость покраски куба.

Решение

Чтобы найти общую стоимость рисования куба, мы умножаем площадь поверхности куба на скорость рисования.

SA = 6a ²

= 6 x 10 ²

= 6 x 100

= 600 м ²

Стоимость покраски = 600 м ² x 10 долларов за м ²

= 6000 долларов США.

Пример 5

Высота кубического резервуара составляет 12 футов. Найдите площадь поверхности резервуара.

Решение

SA = 6a ²

= 6 x 12 ²

= 6 x 144

= 864 фута ²

Пример 6

Длина

стороны куба, площадь поверхности которого равна его объему?

Решение

Дано:

Площадь поверхности куба = объем куба

6a ² = a ³

Разделите обе стороны на ²

6a67 ^{2 2 2 = a 3 / a 2}

6 = a

Следовательно, длина куба составляет 6 единиц.

Пример 7

Найдите площадь поверхности куба с диагональю 12 ярдов.

Решение

Для куба длина диагонали = √ 3a

, где a = длина стороны куба.

Следовательно,

12 = √ 3a

Возвести обе стороны в квадрат и затем разделить на 3.

144 = 3a

a = 48

Теперь вычислим площадь поверхности куба

SA = 6a ²

= 6 x 48 x 48

= 13824 квадратных ярда

Пример 8

Прямоугольный картон равен 0.5 м в длину и 0,3 м в ширину. Сколько кубических коробок длиной 5 см можно сделать из картона?

Раствор

Площадь прямоугольного картона = 0,5 x 0,3

= 0,15 м ² ⇒ 1500 см ²

Площадь кубической коробки = 6a ²

= 6 x 5 ²

= 6 x 25

= 150 см ²

Чтобы получить количество ящиков, разделите площадь карты на площадь поверхности куба

Количество ящиков = 1,500/150

= 10 коробок.

Пример 9

Стоимость 1 м ² карты составляет 0,5 доллара США. Найдите стоимость изготовления 60 кубических коробок длиной 0,4 м.

Решение

Сначала определите площадь поверхности 60 коробок

SA коробки = 6a ²

= 6 x 0,4 ²

= 6 x 0,16

= 0,96 м ²

Площадь 60 коробок = 0,96 x 60

= 57,6 м ²

Стоимость изготовления 60 коробок = 57.6 x 0,5

= 28,8 долларов США

Пример 10

Площадь поверхности куба составляет 1014 дюймов ² . Каков объем куба?

Решение

SA = 6a ²

1014 = 6a ²

a ² = 169

a = √169

64 a = 13

Объем 905 куб. 3

= 13 x 13 x 13

= 2197 дюймов ³ .

Предыдущий урок | Главная страница | Следующий урок

Сколько квадратов на кубике рубика?

ВеликийСолтан сказал…

6 * [9 (1×1) +12 (2×1) +6 (3×1) +4 (2×2) +4 (3×2) +1 (3×3)] = 216

22 мая 2011 г., 16:32

Анонимный сказал…

Квадраты = 1 * 6 + 9 * 6 + 4 * 6 = 84
Прямоугольники = 6 (9 + 12 + 6 + 4 + 4 + 1) = 6 * 36 = 196

22 мая 2011 г., 18:12

Секретный Сквиррел сказал…

216 прямоугольников, из которых 84 квадраты.

24 мая 2011 г., 17:55

Неизвестный сказал…

У куба 6 граней, и каждая грань имеет 4 прямые, пересекающие 4 другие.

Итак, чтобы сделать прямоугольник, нам нужно выделить 2 горизонтальные и 2 вертикальные линии.

Итак, возможное число: 6 * (4C2 * 4C2) = 216

27 мая 2011 г., 18:02

вайшнави сказал…

84 квадрата

28 мая 2011 г., 16:41

EMPORiO сказал…

да его 84..

4 июня 2011 г., 14:29

Электронная почта компании сказал…

Я считаю, что его 297.

9 июня 2011 г., 2:46

Анонимный сказал…

если квадраты считаются прямоугольниками … разве это не будет 216 прямоугольников плюс 84 квадрата? (300 прямоугольников и квадратов)

16 июня 2011 г., 2:31

Анонимный сказал…

Один единственный квадрат — это как квадрат, так и прямоугольник.т.е. квадрат 1
2 * 2 квадрата будет иметь 4 + 1 квадрата и 4 прямоугольника, то есть квадраты 1 + квадраты 2 будут количеством квадратов и квадратов, а прямоугольники вместе будут кубом 2, что составит общее число девять. куб № 2
3 * 3 квадрата будет иметь 14 квадратов и 22 прямоугольника, всего 36, т.е. общее количество квадратов = квадрат 1 + квадрат 2 + квадрат 3, в то время как сумма квадратов и прямоугольников будет 36, т.е. [1 + 2 + 3]
Таким образом можно подсчитать общее количество квадратов и прямоугольников.

19 июня 2011 в 12:41

Анонимный сказал…

Один единственный квадрат — это как квадрат, так и прямоугольник. т.е. квадрат 1
2 * 2 квадрата будет иметь 4 + 1 квадрата и 4 прямоугольника, то есть квадраты 1 + квадраты 2 будут количеством квадратов и квадратов, а прямоугольники вместе будут кубом 2, что составит общее число девять. Куб из квадрата № 1 + 2
3 * 3 будет иметь 14 квадратов и 22 прямоугольника, всего 36, т.е. общее количество квадратов = квадрат 1 + квадрат 2 + квадрат 3, а сумма квадратов и прямоугольников будет 36 i .e квадрат [1 + 2 + 3]
Таким образом можно вычислить общее количество квадратов и прямоугольников.

19 июня 2011 г. 12:41

19 июня 2011 в 12:43

Сурендра сказал…

84 кв.

23 сентября 2011 в 13:47

Вирадж Шах сказал…

Я могу собрать куб 3×3 менее чем за 2 минуты, поверьте, я занимаюсь этим 2 года, а для человека, занимающегося этим 2 года, я очень медленно, но есть 27 кубетов, это кусок.(1 кубок = 1 штука) или, если вы хотите, сколько наклеек вы бы использовали по этой формуле.

9х6 не так уж и сложно равно 54

23 ноября 2011 г., 7:11

Акас Ахмед сказал…

Если вы нашли или играете в онлайн-пазлы, пожалуйста,
посетите наш сайт и наслаждайтесь пазлами.

24 декабря 2011 г., 21:58

Анонимный сказал…

как насчет квадратов с каждой стороной на разных гранях куба? : D

9 октября 2012 в 22:31

Неизвестный сказал…

Правильный ответ — 84

31 мая 2015 в 13:36

Неизвестный сказал…

Правильный ответ — 84

31 мая 2015 в 13:38

Неизвестный сказал…

Правильный ответ — 240

31 мая 2015 в 14:08

.