Расчет на прочность и жесткость балки онлайн: СОПРОМАТ ГУРУ. Расчет балки онлайн. Построение эпюр

Содержание

Расчет балки

Подробный ход решения — расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 6·2 = 12кН

Составим уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + M + Q1 · 3 — R_E · 6= + 12 · 2 + 8 + 12 · 3 — R_E · 6=0

Σ M_E = — P · 4 + M — Q1 · 3 + R_A · 6= — 12 · 4 + 8 — 12 · 3 + R_A · 6=0

Из этих уравнений находим реакции опор

R_A = 12.67кН.

R_E = 11.33кН.

Записываем уравнения поперечных сил и изгибающих моментов на участках балки , используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 12.67 = 12.667 кН

M(z₁) = + R_A · z = + 12.67 · z

M(0) = 0 кНм

M(2) = 25.333 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 12.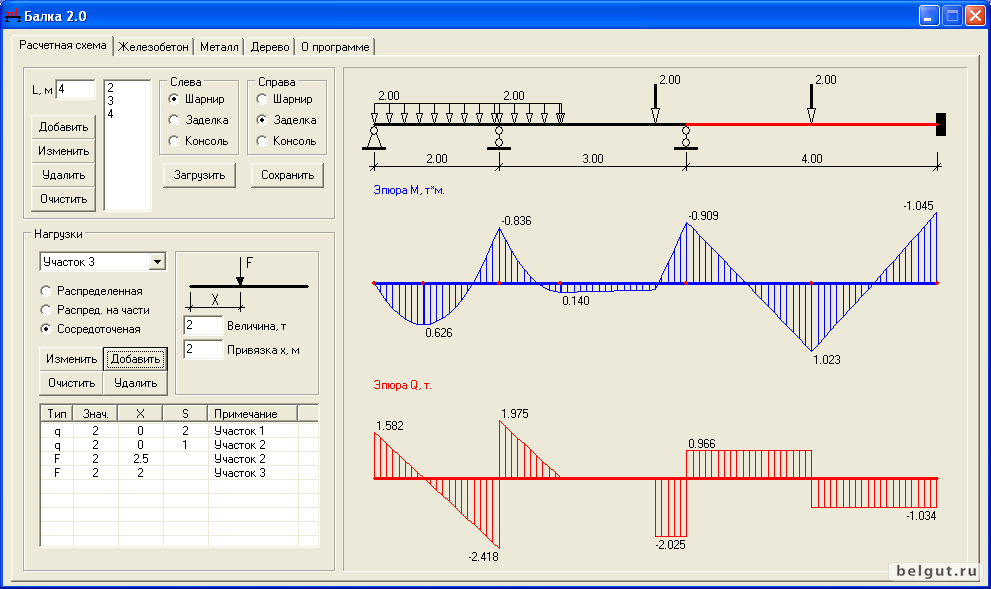

67 — 12 — 6·(z — 2)

Q(2) = 0.667 кН

Q(4) = -11.333 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)²/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)²/2

M(2) = 25.333 кНм

M(4) = 14.667 кНм

Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M

M(2.11) = 25.4 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₃) = + R_A · z — P·(z — 2) — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)

M(4) = 14.667 кНм

M(5) = 3.333 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₄) = + R_A · z — P·(z — 2) + M — Q

1·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)

M(5) = 11. 333 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M_max = 25.4 кНм. По этому значению подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

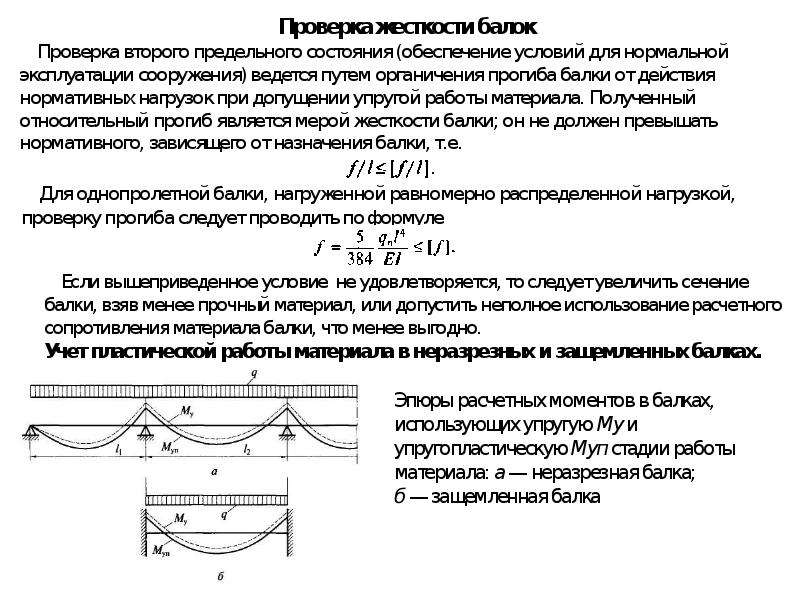
Полный расчет балки на прочность и жесткость

Пример решения задачи полного расчета на прочность и жесткость стальной двутавровой балки для заданной системы изгибающих нагрузок.

Задача

Произвести полный расчет на прочность и проверить жесткость статически определимой двутавровой двухопорной балки (рис. 1) при следующих данных: F=40кН, q=30 кН/м, a=0,8 м, l=4м, допустимые нормальные и касательные напряжения: [σ]=160 МПа и [τ]=100 МПа, допустимый прогиб балки [f]=

l/400

Рис. 1

Другие примеры решений >
Помощь с решением задач >

Решение

Определение опорных реакций

Подробно, пример определения опорных реакций для балки рассмотрен здесь

А также в нашем коротком видеоуроке:

Из Σm_в=0

Из Σm_А=0

Построение эпюр Q и М

Подробный пример построения эпюр поперечных сил Q и изгибающих моментов M для балки

Видео про расчет значений Q и M для построения эпюр:

В пролете балки 0 ≤ z₂ ≤ l

Q_II= — R_B+ qz₂= -52+30∙z₂
Q_II(z=0)= -52 кН
Q_II(z=l)= -52+30∙4=68 кН

M_II=R_B∙z₂-qz₂²/2=52z₂-30∙z₂²/2
M_{II (z=0)}= 0
M_{II (z=l)}= -32 кНм

На консоли l ≤ z₁≤ (l+a)

Q_I= — R_B+ ql — R_A=-52+30∙4-108=-40 кН

M_I=R_B z₁-ql(z₁-l/2)+R_A(z₁-l)=52z₁-30∙4(z₁-4/2)+108(z₁-4)
M_{I (z=l)}= -32 кНм
M_{I (z=l+a)}= 0

По этим данным построены эпюры Q и М.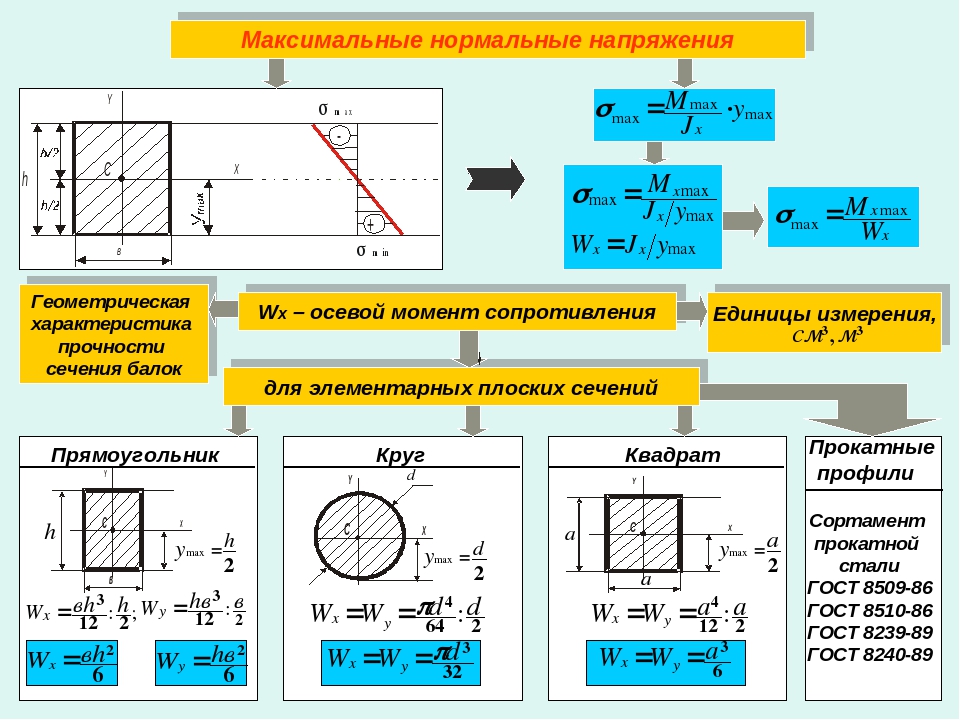

Короткое видео о том, как надо строить эпюры:

Так как М_mах = 45 кНм, то

W_x≥M_max

/ [σ] = 45∙10³ / 160∙10⁶= 0,281 м³= 281 см³.

О том, как подбирается сечение балки

По сортаменту выбираем двутавр № 24, для которого W_x = 289 см³, I_x= 3460 см⁴, S_max = 163 см³, h = 24 см, b_п = 11,5 см, t = 0,95 см, d = b_c = 0,56 см, h₀ = h-2t = 22,1 см.

Этот двутавр будет работать при максимальном нормальном напряжении в крайнем волокне опасного сечения.

σ_max = M_max / W_x = 45∙10³ / 289∙10^-6= 156∙10⁶ Па = 156 МПа

Проверка сечения балки по касательным напряжениям

Так как Q_max = 68 кН, то

Построение эпюр нормальных σ и касательных τ напряжений в неблагоприятном сечении балки:

Построение эпюры нормальных напряжений

Построение эпюры касательных напряжений

В отношении главных напряжений неблагоприятным является сечение над левой опорой, в котором:

М = -32 кНм и Q = 68 кН.

Значение напряжений в различных точках по высоте двутавра сведены в таблицу 1

Таблица 1

Результаты расчета в примере

Проверка прочности балки по главным напряжениям

Наиболее опасной точкой в неблагоприятном сечении является точка 3. В этой точке σ₁=118 МПа и σ₃= -16 МПа. Проверяем прочность в этой точке по третьей гипотезе прочности согласно неравенству σ₁ — σ₃≤ [σ].

Так как 118 — ( -16) = 134 < 160, то выбранное сечение удовлетворяет условию прочности и по главным напряжениям.

Расчет перемещений сечений (прогибов балки)

Универсальные уравнения МНП для сечения z:

Опорные условия:

1) при z=0: y(z)=0, следовательно, y₀=0

2) при z=l: y(z)=0 находим θ₀

откуда θ₀= -8,48∙10

-3 радиан.

Прогиб в пролете при z=l/2=4/2=2 м.

Аналогично определяется прогиб на конце консоли при z = l + a =4+0,8 = 4,8 м.

Проверка жесткости балки

— пролетной части:

y_c=0,98 см < 1/400 = 400/400 = 1 см

— консольной части:

y_D=0,33 см < 2a/400 = 2∙80/400 = 0,4 см.

Следовательно, принятая двутавровая балка удовлетворяет требуемому условию жесткости.

Другие примеры решения задач >

Расчет балки онлайн с расчетом на прочность и построение эпюр онлайн с решением. —

Расчет балки

Подробный ход решения — расчет балки, построение эпюр

Заменим распределенную нагрузку равнодействующей

Q₁ = 6·2 = 12кН

Составим
уравнения равновесия для определения реакций опор

Σ M_A = + P · 2 + M + Q1 · 3 — R_E · 6= + 12 · 2 + 8 + 12 · 3 — R_E · 6=0

Σ M_E = — P · 4 + M — Q1 · 3 + R_A · 6= — 12 · 4 + 8 — 12 · 3 + R

A · 6=0

Из этих уравнений находим реакции опор

R_A = 12. 67кН.

R_E = 11.33кН.

Записываем уравнения поперечных сил и изгибающих моментов на
участках балки
, используя метод сечений

На участке AB: (0 ≤ z₁ ≤ 2 м )

Q(z₁) = + R_A = + 12.67 = 12.667 кН

M(z₁) = + R_A · z = + 12.67 · z

M(0) = 0 кНм

M(2) = 25.333 кНм

На участке BC: (2 ≤ z₂ ≤ 4 м )

Q(z₂) = + R_A — P — q₁·(z — 2) = + 12. 67 — 12 — 6·(z — 2)

Q(2) = 0.667 кН

Q(4) = -11.333 кН

M(z₂) = + R_A · z — P·(z — 2) — q₁·(z — 2)²/2 = + 12.67 · z — 12·(z — 2) — 6·(z — 2)²/2

M(2) = 25.333 кНм

M(4) = 14.667 кНм

Поскольку поперечная сила на участке пересекает ноль при z = 2.11 м, в этой точке будет экстремум на эпюре M

M(2.11) = 25.4 кНм

На участке CD: (4 ≤ z₃ ≤ 5 м )

Q(z₃) = + R_A — P — Q₁ = + 12. 67 — 12 — 12 = -11.333 кН

M(z₃) = + R_A · z — P·(z — 2) — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) — 12·(z — 3)

M(4) = 14.667 кНм

M(5) = 3.333 кНм

На участке DE: (5 ≤ z₄ ≤ 6 м )

Q(z₄) = + R_A — P — Q₁ = + 12.67 — 12 — 12 = -11.333 кН

M(z₄) = + R_A · z — P·(z — 2) + M — Q₁·(z — 3) = + 12.67 · z — 12·(z — 2) + 8 — 12·(z — 3)

M(5) = 11. 333 кНм

M(6) = 0 кНм

Максимальный момент в балке составляет M

max = 25.4 кНм. По этому значению
подбираем сечение балки.

Условие прочности при изгибе σ = M_max / W ≤ [σ]

Отсюда, минимально необходимый момент сопротивления вычисляем по формуле W_min=M_max / [σ]

Расчет опорных реакций балки на двух опорах онлайн

Расчет выполняется по следующей методике:

1. Заменяем распределенную нагрузку ее равнодействующей, которая является сосредоточенной силой. Для равномерно распределенной нагрузки равнодействующая равна произведению интенсивности нагрузки q на длину участка L, на котором она действует: Fq = q*L.

2. Обозначаем опоры. Общепринято их обозначать буквами А и В. Простая балка имеет одну шарнирно-неподвижную и одну шарнирно-подвижную опоры.

3. Освобождаемся от опор и заменяем их действие на балку реакциями.

Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида:
M_A = 0; M_B = 0,

Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия:
Y = 0,

Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Q_x. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.

В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Q_лев и Q_прав.

Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:

а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;

б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.

Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Q_x.

7. Строим эпюру изгибающих моментов М_x. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.

В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М_лев и М_прав. В точках приложения сил определяется одно значение изгибающего момента.

Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:

а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;

б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Пример решения балки:

Построение эпюр усилий онлайн

Інструкція.

Программа позволяет определить опорные реакции и построить эпюры внутренних усилий для двухопорной и консольной балки.

Дальнейшие инструкции будут приведены на примере балки на двух опорах.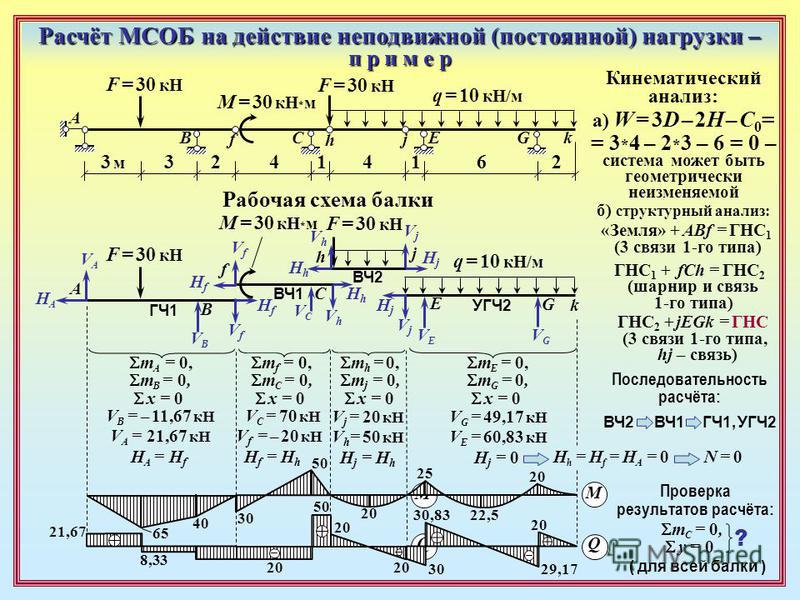

1. Выберите условия крепления концов балки. Возможны варианты — свободный, шарнир и жесткое. В нашем примере левый и правый конец стержня не имеют креплений, поэтому выбираем вариант «свободный».

Если по ошибке был выбран другой вариант, нажимаем на кнопку «Новая схема».

2. Указываем длину балки и координаты опор. Длина балки равна «13», а координаты опор от левого конца балки, в соответствии к опоры A — «2» и к опоре B — «11».

3. Указываем нагрузку.
Выбираем количество сосредоточенных моментов — «2». В таблице вводим значения моментов и их координаты от левого конца балки. M₁=40, a₁=6 и M₂=-20, a₂=13
(момент который вращается против часовой стрелки — положительный, по — отрицательный).
Выбираем количество сосредоточенных сил — «2». В таблице вводим значение сил и их координаты. F₁=9, b₁=0
и F₂=6. 93, b₂=9 (сила направленная вниз — положительная, вверх — отрицательная).
Выбираем количество равномерно распределенной нагрузки — «1». В таблице вводим значение РРН, координаты начала
и конца РРН. q₁=12, c₁=2 та d₁=8 (РРН направлена вниз — положительная, вверх — отрицательная).

4. Нажимаем на кнопку «Построить эпюры». После нажатия определяются опорные реакции и строятся эпюры усилий. Если нужно определить усилия в произвольном сечении, введите координату в форму. Если нужно, задайте точность
расчета и выберите правое или левое сечение.

Скриншот к примеру:

Скриншот к примеру (эпюра поперечных сил):

Скриншот к примеру (эпюра изгибающих моментов):

Онлайн расчет статически неопределенной балки

Расчет выполняется методом сил

Канонические уравнения метода сил:

Где коэффициенты системы определяются:

Принцип ввода данных, рассмотрим с помощью следующего примера:

1. Задание длины (12м) и условий закрепления стержня. Левый конец стержня свободен, а правый — жестко закрепленный. Задаем координаты опор (отсчет ведется от левого конца стержння). Первая опора имеет координату 2м, вторая — 7м.

2. Задаем нагрузки, использовав соответствующие правила знаков:

3. В случае, если жесткость балки переменная, задайте необходимые пропорции (нажмите на кнопку «Изменить жесткость»):

4. Для начала расчета нажмите на кнопку «Построить эпюры».

Для расчета балок используется следующая основная система (ОС). Выбрать ОС невозможно.

Решение системы уравнений:

Опорные реакции:

Расчет онлайн для разнотипных балочных конструкций.

Строительство зданий – сложная работа, требующая точных расчетов и качественного выполнения работы. Основным материалом в строительстве жилых домов является древесина. Несущие конструкции изготавливаются из этого материала. Рассмотрим способы расчета балки онлайн.

Разновидности перекрытий

Назначение:

Межэтажные.
Прочное, надежное перекрытие. Между двумя материалами складываются звуко- и теплоизоляционные наполнители.
Чердачное.
Является частью стропильной конструкции крыши. Чердак оборудован изоляцией от шума и пара.
Цокольное.
Выносят высокие нагрузки. Делаются с теплоизоляцией.

Балки бывают двух видов:

цельные;
клееные.

Слабым звеном монолитных балок является ограниченная длина. Не могут быть больше 5 метров.

Преимуществами клееных балок над цельными являются:

перекрытие больших пролетов;
легкость установки;
маленькая масса;
длительная эксплуатация;
пожароустойчивые;
не деформируются.

Каким образом определяется длина балки?

Обычно размещаются параллельно самой маленькой стене. Размеры зависят от материалов, из которых изготавливаются блоки и от общего объема материала. Для крепления используют металлические крепежи (кронштейны, уголки, пластинки с перфорацией, плитки). Если применяете один из этих видов крепежа, то длина балки должна соответствовать пролету комнаты.

Также балки могут быть частью стропильных элементов. Конструкция опирается на мауэрлат. Данный способ увеличивает длину исходного материала на метр.

Советы для правильного расчета:

Учитывайте глубину введения материалов в стену. Глубина вхождения для стен из кирпича составляет от 150 мм для балок из бруса и 100 мм для досок. В домах из дерева – от 70 мм.
Длина балки составляет минимум 6 м.

Инструкция для подсчета:

замерьте пролет;
выберите закрепляющие элементы;
рассчитайте влияющую нагрузку;
подберите шаг и сечение.

При строительстве можно выпустить балки наружу на 31- 60 см. Таким образом, формируется свес крыши.

Определение действующей нагрузки

В жилом помещении имеется два дверных пролета. Обычно отличаются по размерам, но в квадратной комнате могут быть одинаковыми.

Перемычки укладывают в более коротком проеме ,длиной 3-4 метра. По стандарту, стороны должны соотноситься в пропорции семь к пяти. Так исключается деформация. Если не соблюдать этих пропорций, балки прогнутся. Возможный деформация – два см на четыре метра.

Для устранения провисания бруса, изготовьте снизу на несколько см, при этом придав форму арки.

Прогиб можно рассчитать по формуле f(нор)= L/200

L –длина пролета,

200 – расстояние на единицу погружения дерева.

Нагрузка на любую конструкцию определяется по нескольким формулам.

Первая – геометрическая характеристика сечения стержнями:

W≥M/R . M – время относительно нейтральной оси сечения балки или другого твердого тела,

R – рассчитываемое сопротивление, которое нужно взять из справочника исходя из основы.

Для стержней прямоугольной формы формула выглядит так:

W_Z =b∙ h 2/6,

b – ширина балки,

h – высота.

Перекрытие во многих случаях является кровлей и полом следующего и предшествующего этажей. Объединяйте, учитывая нагрузку мебели на поверхности. Если неправильно распределить, появляется риск разрушения конструкций. Не следует применять уж очень широкий шаг промеж балками и отказываться от лагов. Учитывайте, что пространство между основами зависит от толщины досок. Если имеются лаги, то расстояние посередине должно составлять метр.

Совет! Предусмотрите массу утеплителя. Цокольное перекрытие, длиной 1 м2, весит 100 килограммов. Увеличивает вдвое одну и ту же массу опилкобетон. Керамзит еще тяжелее.

Выяснение сечения и шага балки

Параметры балок строго регламентированы. Так, соразмерность – 1:1:4. Широта – с 5 до 21 сантиметра, высота – от 10 до 31 сантиметра. Учитывайте утеплитель! Бревна перекрытия должны иметь диаметр от 11 до 31 сантиметра.
Установочный шаг – примерно 30–120 сантиметров. При каркасном строении шаг соответствует дистанции промеж твердыми основами.

Требования, предъявляемые к конструкциям:

влагосодержание материала – максимум 15%;
нельзя использовать испорченную древесину, то есть синюшную, поражённую грибком, насекомыми, грызунами;
обработка антисептическим составом;
размерное отношение – 7:5 для брусьев;
чем больше высота лаг, тем больше нагрузка, выдерживаемая балкой;
для ровного перекрытия сделайте подъем ярусов;
брусья и бревна замените досками, уложенными на ребро, если укладка интенсивная.

Онлайн калькулятор для расчета деревянных балок

Высота балки (мм)
Ширина балки (мм)
Материал древесины
Пролет (м)
Шаг балок (м)

Произвести расчет балки возможно самостоятельно: рассчитать нагрузки, воздействующие на перекрытие по формулам и параметрам или воспользоваться онлайн калькулятором. Также можно выбрать подходящую конструкцию, исходя из имеющихся условий.

Бесплатный Калькулятор Луча | Изгибающий момент, Калькулятор поперечной силы и прогиба

Добро пожаловать в наш бесплатный онлайн калькулятор изгибающего момента и диаграммы силы сдвига, который может генерировать реакции, Диаграммы силы сдвига (SFD) и диаграммы изгибающих моментов (BMD) консольной балки или опертой балки. Используйте этот калькулятор балок, чтобы определить реакции на опорах, нарисуйте диаграмму сдвига и момента для балки и рассчитайте прогиб стали или дерево луч. Бесплатный онлайн лучевой калькулятор для генерации реакций, расчет прогиба стальной или деревянной балки, составление диаграмм сдвига и момента для балки. Это бесплатная версия нашей полной SkyCiv. Beam Software. Доступ к нему можно получить в любом из наших Платные аккаунты, который также включает программное обеспечение для полного структурного анализа.

Используйте интерактивную рамку выше для просмотра и удаления длины луча, поддерживает и добавляет нагрузки. Любые сделанные изменения автоматически перерисовывают диаграмму свободного тела любым простым или консольным лучом.. Калькулятор реакции луча и расчеты изгибающего момента будут запущены, как только «Решить» нажата кнопка и автоматически сгенерирует диаграммы моментов сдвига и изгиба. Вы также можете нажать отдельные элементы этого калькулятора луча LVL, чтобы редактировать модель.

Калькулятор пролета луча легко рассчитает реакции на опорах. Умеет рассчитывать реакции на опорах для консольных или простых балок.. Это включает в себя расчет реакций для балки кантилевера, который имеет реакцию изгибающего момента, а также х,у сил реакции.

Вышеуказанный калькулятор балок со стальной балкой — это универсальный инструмент для расчета конструкций, используемый для расчета изгибающего момента в алюминии., деревянная или стальная балка. Его также можно использовать в качестве калькулятора грузоподъемности балки, используя его в качестве калькулятора напряжения изгиба или напряжения сдвига. Может вместить до 2 различные сосредоточенные точечные нагрузки, 2 распределенные нагрузки и 2 моменты. Распределенные нагрузки могут быть расположены так, чтобы они были равномерно распределенными нагрузками. (UDL), треугольные распределенные нагрузки или трапециевидные распределенные нагрузки. Все нагрузки и моменты могут иметь как восходящее, так и нисходящее направление по величине. , которые должны быть в состоянии учитывать наиболее распространенные ситуации анализа пучка. Расчет изгибающего момента и силы сдвига может занять до 10 секунд, чтобы появиться и, пожалуйста, обратите внимание, что вы будете перенаправлены на новую страницу с реакциями, Диаграмма силы сдвига и диаграмма изгибающего момента балки.

Одна из самых мощных функций использует его в качестве калькулятора отклонения луча (или калькулятор смещения луча). Это может быть использовано для наблюдения расчетного отклонения балки с простой опорой или балки кантилевера. Возможность добавлять формы и материалы раздела, это делает его полезным в качестве калькулятора для деревянных балок или в качестве калькулятора для стальных балок для LVL-лучей или I-лучевой конструкции. На данный момент, эта функциональность доступна в SkyCiv Beam который имеет гораздо больше функциональных возможностей для древесины, конструкция из бетона и стальных балок.

SkyCiv предлагает широкий спектр программного обеспечения для анализа и проектирования облачных вычислений для инженеров. Как постоянно развивающаяся технологическая компания, мы стремимся к инновациям и стимулированию существующих рабочих процессов, чтобы сэкономить время инженеров в их рабочих процессах и проектах.

Расчет балки на прогиб — онлайн калькулятор

Онлайн калькулятор по определению прогиба балки.

Для расчета вам необходимо:

1. Выбрать форму поперечного сечения

2. Выбрать материал (при использовании металлических балок — можно использовать сортамент)

3. Выбрать необходимую расчетную схему

4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)

5. Указать геометрические размеры, указанные на картинках

6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)

Из возможных поперечных сечений в данном онлайн калькуляторе выбраны само часто встречающиеся сечения: круг, труба, двутавр, швеллер, уголок, прямоугольник, квадрат и профильная труба.

В расчет входят такие материалы как дерево, сталь, железобетон, алюминий, медь и стекло.

Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка и заделка-свободный конец.

После того, как прогиб балки рассчитается – появится кнопка Подробнее, нажав на которую, можно узнать площадь сечения рассчитываемого элемента, его массу, распределенную нагрузку от собственного веса и момент инерции заданного сечения).

Зная значение длины пролета балки по СП 20.13330.2016 «Нагрузки и воздействия» для таких конструкций как балка, ферма, ригель, прогон, плита, настил покрытий и перекрытий, рассчитывается предельный прогиб, который можно сравнить с получившимся прогибом и принять решение о сечении вашей конструкции (для уменьшения прогиба в 1-ую очередь надо увеличивать высоту сечения).

При расчете балки программа уже учитывает собственный вес.

Помимо того, что Вы рассчитаете балку на прогиб, нужно ее проверить и на прочность здесь .

Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц. сети, а также посмотреть другие
строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.

Последние изменения:

— Добавлен расчет предельного прогиба балки

— Добавлена возможность загружения балки сосредоточенной силой

— Исправлены графические замечания с расположением швеллера

— Добавлен расчет таврого сечения

— Исправлено положение прямоугольного сечения

— Добавлена возможность поворота швеллера

— Добавлена возможность ввода своих значений модуля упругости и плотности материала

— Исправлено отображение толщины стенки и полки швеллера

Калькулятор отклонения балки

КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ УЧАСТНИКОВ
Калькулятор	Определение
	Расчет элементов сжатия (продольного изгиба)
ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА
	Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами
	Балка с простой опорой и сосредоточенной нагрузкой в любой точке
	Просто поддерживаемая балка с двумя Точечные нагрузки
	Балка с простой опорой и частично распределенной промежуточной нагрузкой
	Балка с простой опорой и двумя частично распределенными промежуточными нагрузками
	Балка с простой опорой и моментом
	Балка с простой опорой и двумя моментами
КАНТИЛЬВЕРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА
	Консольная балка с множественными точечными / распределенными нагрузками и моментами
	Консольная балка с одинарной нагрузкой
	Распределенная нагрузка консольной балки
	Консольная балка с одним моментом
КАЛЬКУЛЯТОРЫ ПРОБЕГА ФИКСИРОВАННОЙ ЛУЧИ
	Фиксированный -Фиксированная балка с множественными точечными / распределенными нагрузками и моментами
	Фиксированная — фиксированная балка с одинарной нагрузкой
	Фиксированный — Неподвижная балка с распределенной нагрузкой
	Фиксированная — фиксированная балка с одним моментом

Калькулятор отклонения балки

Этот калькулятор отклонения балки поможет вам определить максимальное отклонение балки для балок с простой опорой и консольных балок, несущих простых конфигураций нагрузки .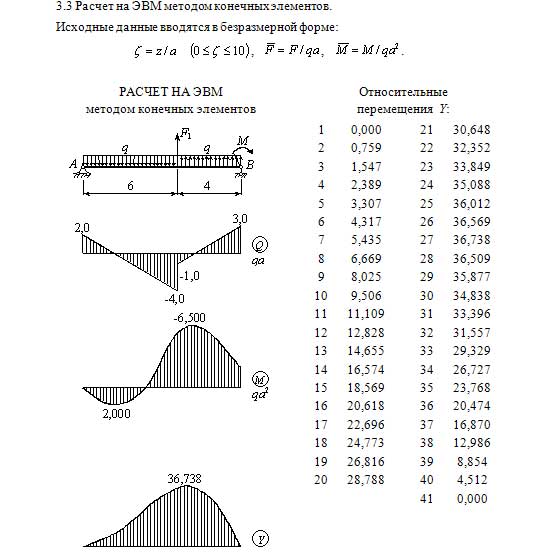 Вы можете выбрать один из нескольких типов нагрузки, которые могут воздействовать на балку любой длины по вашему желанию. Величина и расположение этих нагрузок влияют на то, насколько балка изгибается. В этом калькуляторе отклонения балки вы узнаете о различных формулах отклонения балки , используемых для расчета отклонений балок с жесткой опорой и балок консольных балок. Вы также узнаете, как модуль упругости балки и момент инерции ее поперечного сечения влияют на расчетный максимальный прогиб балки.

Что такое прогиб балки и изгиб балки

В строительстве мы обычно используем каркасные конструкции , которые удерживаются на месте фундаментом в земле. Эти каркасные конструкции подобны каркасам зданий, домов и даже мостов. В кадре мы называем вертикальное обрамление колонн , а горизонтальные балки . Балки — это длинные элементы конструкции, которые несут нагрузки, создаваемые горизонтальными плитами конструкций, включая перекрытия и крыши.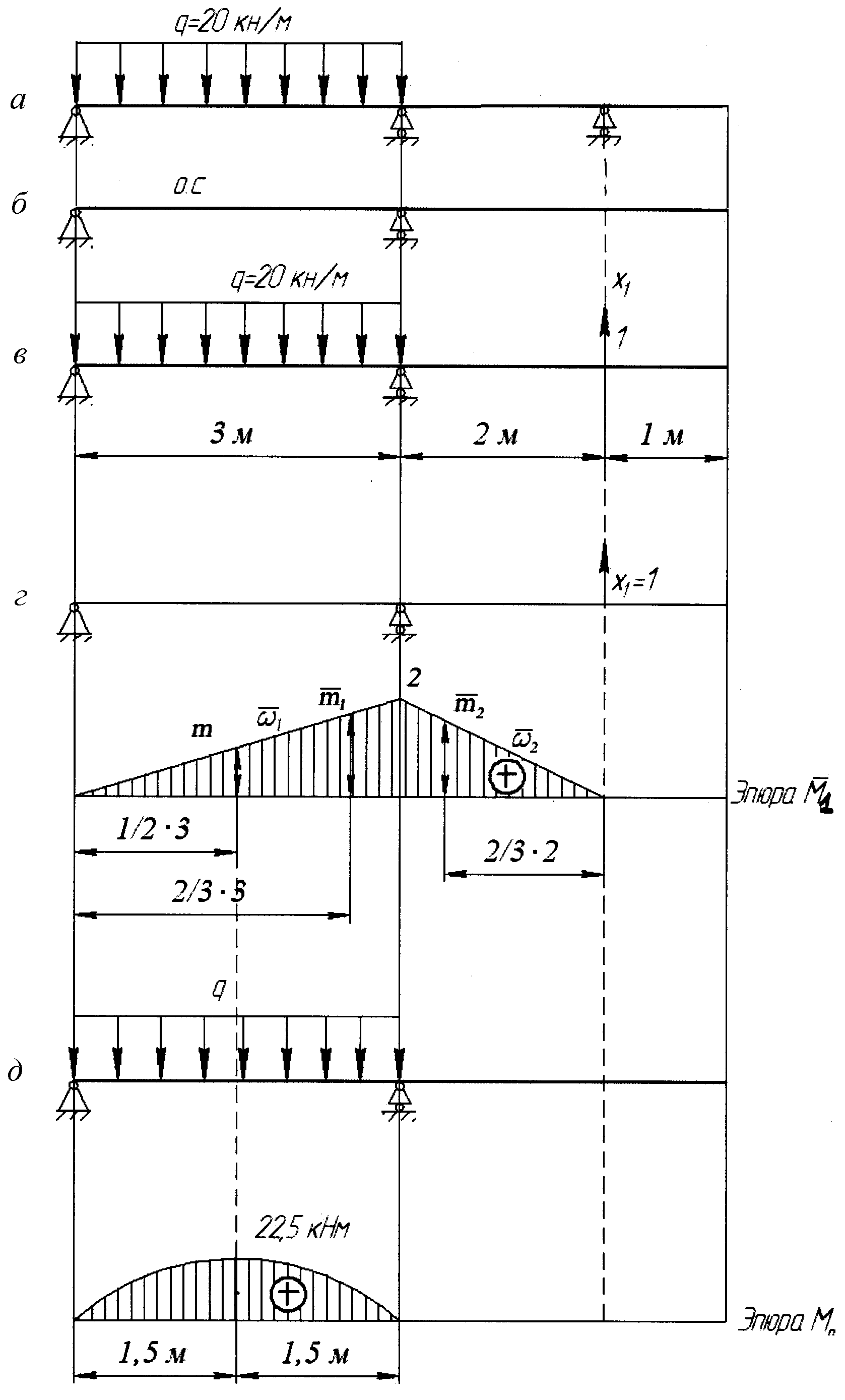

Когда балки несут слишком тяжелые для них нагрузки, они начинают гнуться. Мы называем величину изгиба балки , прогиб балки . Отклонение балки — это вертикальное смещение точки вдоль центра тяжести балки. Мы также можем рассматривать поверхность балки как опорную точку, если нет изменений в высоте или глубине балки во время изгиба.

Как рассчитать максимальный прогиб балки

Мы снабдили наш калькулятор прогиба балки формулами, которые инженеры и студенты-инженеры используют для быстрого определения максимального прогиба, который будет испытывать конкретная балка из-за нагрузки, которую она несет.Однако эти формулы могут решать только простые нагрузки и их комбинацию. Мы составили для вас таблицы этих формул, как показано ниже:

Формулы прогиба балок без опоры

Формулы отклонения консольной балки

Метод наложения

Для расчета максимального прогиба балки с комбинацией нагрузок мы можем использовать метод наложения .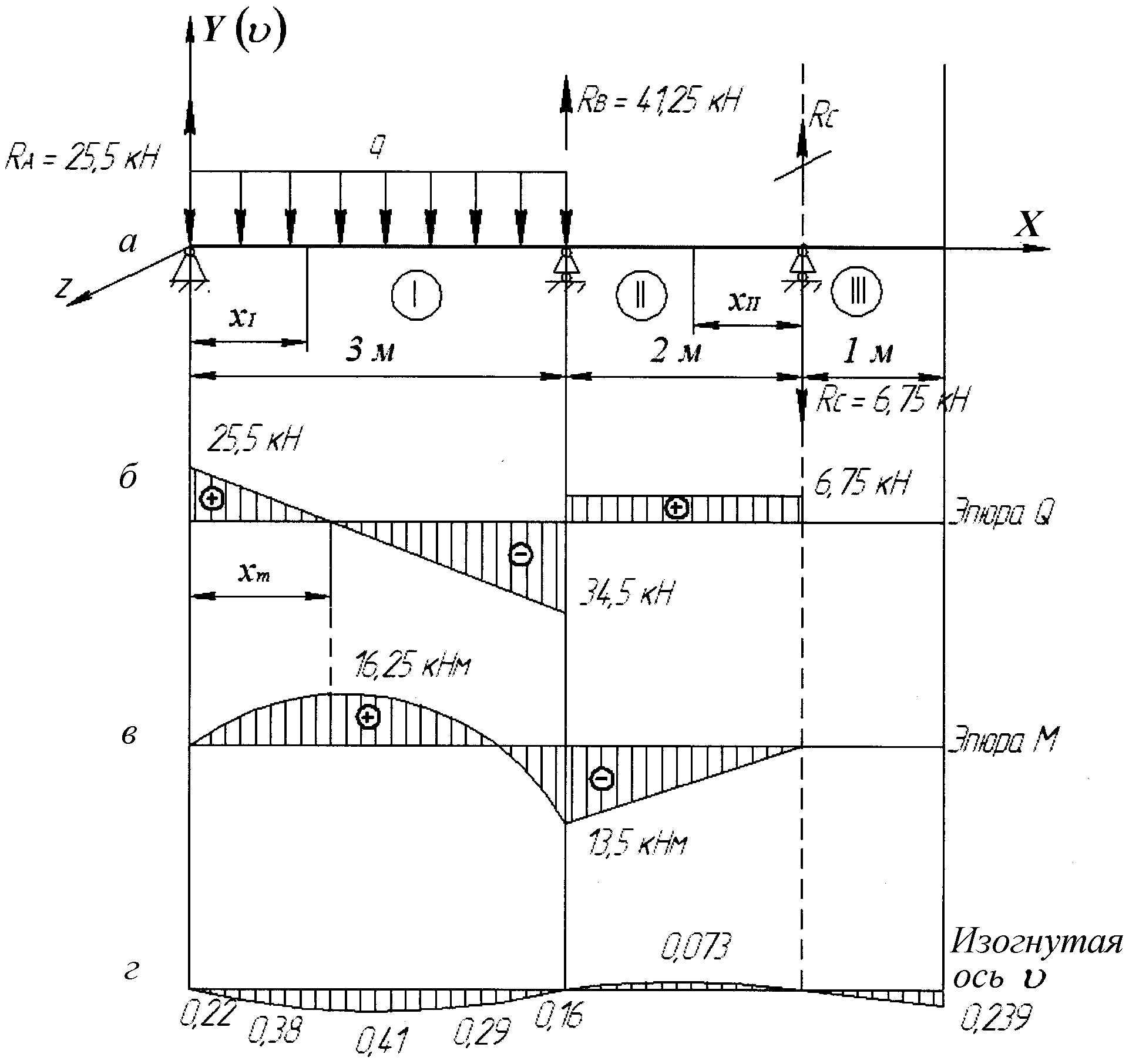 Метод наложения утверждает, что мы можем приблизительно оценить полное отклонение балки, сложив вместе все отклонения, вызванные каждой конфигурацией нагрузки.Однако этот метод дает нам лишь приблизительное значение фактического максимального прогиба. Расчет сложных нагрузок потребует от нас использования так называемого метода двойного интегрирования .

Жесткость балки

Для расчета прогиба балки необходимо знать жесткость балки и величину силы или нагрузки, которые могут повлиять на изгиб балки. Мы можем определить жесткость балки, умножив модуль упругости балки , E , на ее момент инерции , I .Модуль упругости зависит от материала балки. Чем выше модуль упругости материала, тем больше прогиб может выдержать огромные нагрузки, прежде чем достигнет предела разрушения. Модуль упругости бетона составляет 15-50 ГПа (гигапаскалей), а у стали — около 200 ГПа и выше. Эта разница в значениях модуля упругости показывает, что бетон может выдерживать лишь небольшой прогиб и трескается быстрее, чем сталь.

Вы можете узнать больше о модуле упругости, воспользовавшись нашим калькулятором напряжений.С другой стороны, чтобы определить момент инерции для определенного поперечного сечения балки, вы можете воспользоваться нашим калькулятором момента инерции. Момент инерции представляет собой величину сопротивления материала вращательному движению. Момент инерции зависит от размеров поперечного сечения материала.

Момент инерции также зависит от оси вращения материала. Чтобы лучше понять эту концепцию, давайте рассмотрим поперечное сечение прямоугольной балки шириной 20 см и высотой 30 см.Используя формулы, которые вы также можете увидеть в нашем калькуляторе момента инерции, мы можем вычислить значения момента инерции этого поперечного сечения следующим образом:

Iₓ = ширина * высота³ / 12
= 20 * (30³) / 12
= 45000 см⁴

Iᵧ = высота * ширина³ / 12
= 30 * (20³) / 12
= 20,000 см⁴

Обратите внимание на два значения момента инерции. Это потому, что мы можем рассматривать изгиб балки по вертикали (по оси x, то есть Iₓ) или по горизонтали (по оси y, то есть Iᵧ).Поскольку мы учитываем отклонение балки при вертикальном изгибе, для расчетов всегда нужно использовать Iₓ . Полученные нами значения говорят нам о том, что балку труднее изгибать при вертикальной нагрузке и легче изгибать при горизонтальной нагрузке. Эта разница в значениях момента инерции является причиной того, что мы видим балки в этой конфигурации, в которой ее высота больше, чем ее ширина.

Понимание формул прогиба балки

Теперь, когда мы знаем концепции модуля упругости и момента инерции, мы можем теперь понять, почему эти переменные являются знаменателями в наших формулах отклонения балки.Формулы показывают, что чем жестче балка, тем меньше будет ее прогиб. Однако, изучив наши формулы, мы также можем сказать, что длина балки также напрямую влияет на прогиб балки. Чем длиннее балка, тем больше она может изгибаться и тем больше может быть прогиб.

С другой стороны, нагрузки

влияют на отклонение балки двумя способами: направление отклонения и величина отклонения . Нисходящие нагрузки склонны отклонять балку вниз.Нагрузки могут быть в виде точечной нагрузки, линейного давления или моментной нагрузки. Формулы в этом калькуляторе ориентированы только на нисходящие или восходящие направления для точечной нагрузки и распределенных нагрузок. Распределенные нагрузки аналогичны давлению, но учитывают только длину балки, а не ширину балки. Формулы в этом калькуляторе также учитывают момент или крутящий момент нагрузки как по часовой стрелке, так и против часовой стрелки. Просто проконсультируйтесь по направлениям стрелок на соответствующем изображении формулы, чтобы выяснить, в каком направлении имеется положительное значение нагрузки.

Пример расчета прогиба балки

Для примера расчета прогиба балки рассмотрим простую деревянную скамью с ножками на расстоянии 1,5 метра друг от друга в их центрах. Допустим, у нас есть доска из восточной белой сосны толщиной 4 см и шириной 30 см, которая служит сиденьем для этой скамейки. Мы можем рассматривать это сиденье как балку, которая отклоняется, когда кто-то садится на скамейку. Зная размеры этого сиденья, мы можем вычислить его момент инерции, как в нашем примере выше.Поскольку нам нужно рассчитать Iₓ, его момент инерции будет:

Iₓ = ширина * высота³ / 12
= 30 * (4³) / 12
= 160,0 см⁴ или 1,6x10⁻⁶ м⁴

Сосна восточная белая имеет модуль упругости 6800 МПа (6,8x10⁹ Па) , что является значением, которое мы получили из Справочника по древесине. Вы также можете легко получить значение модуля упругости для других материалов, таких как сталь и бетон, в Интернете или в местной библиотеке.Теперь, когда мы знаем эти значения, давайте рассмотрим нагрузку, которую будет нести этот стенд. Предположим, что ребенок 400 N сидит в центре скамейки. Теперь мы можем рассчитать прогиб сиденья скамейки из-за точечной нагрузки в его центре:

δₘₐₓ = P * L³ / (48 * E * I)
δₘₐₓ = (400 Н) * (1,5 м) ³ / (48 * 6,8x10⁹ Па * 1,6x10⁻⁶ м⁴)
δₘₐₓ = 0,002585 m = 2,5850 мм

Это означает, что многоместное сиденье прогнется примерно на 2. 6 миллиметров на от исходного положения, когда ребенок сидит посередине скамейки.

Если вы нашли эту тему интересной и хотели бы узнать больше о прочности материалов, вам также может понравиться наш калькулятор запаса прочности. Вы также можете воспользоваться нашим конвертером силы, если хотите изучить различные единицы измерения точечных нагрузок и расчета сил.

Калькулятор балок: реакции опор, изгибающий момент, напряжения

Этот онлайн-калькулятор балки рассчитывает силы и моменты , , , в двух подшипниках (= опорные реакции), а также углы наклона статически определенных или
статически неопределимые балки.Кроме того, поперечная сила , изгибающий момент , , напряжение изгиба и
отклонение может быть определено в желаемом месте. Изгибающий момент, поперечная сила и прогиб как функция длины x показаны.
графически в виде двух диаграмм . Расчет максимального изгибающего момента , максимального напряжения изгиба ,
максимальное отклонение и соответствующее положение также возможно.

Подшипники могут быть выполнены в виде неподвижного подшипника, подвижного подшипника, фиксированного зажима или свободного конца. В качестве нагрузки, равной нагрузки или точечной нагрузки, или их комбинации, или треугольной нагрузки.
(влево или вправо) можно выбрать.

* Чтобы ввести эти значения, выберите в разделе «Поперечное сечение A» -> «Другие профили» -> «Собственный профиль».

** Модуль упругости вводится автоматически при выборе материала и может быть изменен в любой момент; подходящих значений вы можете найти, например, в википедии.

Осторожно:

Для профилей с отверстием только I, W и максимальное напряжение изгиба правильно рассчитываются с помощью дополнительных функций. Для других значений выберите профиль без отверстия!

С помощью этого калькулятора можно рассчитать опорные силы как статически определенных, так и статически неопределенных систем. Возможны следующие комбинации:

Страница создана в августе 2019 года. Последнее изменение: 24 октября 2020 года.

Калькулятор для инженеров — изгибающий момент и поперечное усилие для балки с простой опорой

Избранные ссылки

Калькулятор преобразования напряжения
Расчет главного напряжения, максимального напряжения сдвига и их плоскостей

Калькулятор для анализа подвижной нагрузки
Для определения абсолютного макс. Б.М. из-за движущихся грузов.

Калькулятор момента инерции
Расчет момента инерции плоских сечений e.грамм. швеллер, уголок, тройник и др.

Калькулятор железобетона
Расчет прочности железобетонной балки

Калькулятор распределения моментов
Решение неопределенных балок

Калькулятор прогиба и уклона
Расчет прогиба и уклона свободно опертой балки для многих случаев нагружения

Калькулятор фиксированной балки
Инструмент для расчета изгибающего момента и поперечной силы для фиксированной балки для многих случаев нагружения

Калькулятор BM и SF для консоли
Расчет SF и BM для консоли

Калькулятор прогиба и наклона консоли
Для многих случаев нагружения консоли

Вычислитель выступающей балки
Для SF и BM многих случаев нагружения выступающей балки

Дополнительные ссылки

Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства

Научные статьи
Исследования, диссертации и диссертации

Небоскребы мира
Высокие здания мира

Предстоящие конференции
Список конференций, семинаров и практикумов по гражданскому строительству

Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями

Профессиональные общества
Всемирные профессиональные общества инженеров-строителей

Продолжайте посещать, чтобы получать обновления или присоединяйтесь к нашему списку рассылки, чтобы получать обновления

Поищите на нашем сайте больше…

Расскажите о нас своим друзьям

Другие полезные ссылки

Калькулятор изгибающего момента и поперечной силы

Bendingmomentdiagram. com — это бесплатный онлайн-калькулятор, который генерирует диаграммы изгибающего момента (BMD) и диаграммы поперечного усилия (SFD) для большинства простых балок. Калькулятор полностью настраивается для работы с большинством балок; эта функция недоступна в большинстве других калькуляторов. Программное обеспечение работает на базе SkyCiv, предлагая мощное программное обеспечение для структурного анализа и проектирования в облаке.

Инструмент полностью функциональный, поэтому посетите наше Бесплатное программное обеспечение Beam, чтобы начать работу! Он будет работать со всеми опорными, определяющими балками и способен воспринимать точечные нагрузки, сосредоточенные моменты и распределенные нагрузки. Кроме того, его можно легко настраивать и настраивать, чтобы вы могли создавать свои собственные лучи. Это чрезвычайно точный инструмент и, в отличие от современных калькуляторов, очень удобный. Это чрезвычайно полезный инструмент для студентов университетов, колледжей и старшеклассников, которым утомительно приходится перерисовывать BMD и SFD для заданий и практических / учебных вопросов.

У нас также есть Учебная страница, которая поможет студентам университетов с расчетами, ожидаемыми в их инженерной степени, а также школьникам. Эти студенты могут научиться рассчитывать и создавать диаграммы поперечной силы и изгибающего момента, и мы понимаем, что процесс анализа балки иногда может быть трудным, поэтому мы предоставили простое пошаговое руководство по расчету диаграмм изгибающего момента и поперечной силы. Включены простые уравнения и формулы изгибающего момента, которые хорошо помогают в ваших расчетах.Существуют также примеры и генераторы случайных балок, которые позволят вам поэкспериментировать с тем, как различные нагрузки влияют на расчет балки, а также на поперечную силу и изгибающий момент балки.

Схема

Bending Moment Diagram разработана командой SkyCiv Engineering, которая предлагает пакеты для студентов и профессионалов, которые предоставляют пользователям доступ к разнообразному программному обеспечению для проектирования конструкций для выполнения работы.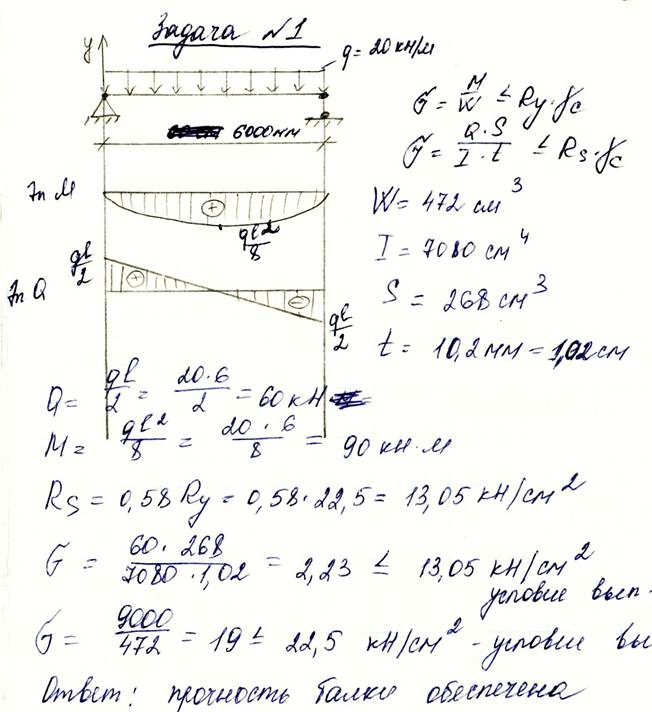 Все учетные записи основаны на подписке, поэтому вы можете ежемесячно оплачивать программное обеспечение по мере необходимости! Больше никаких проблем с установкой, загрузкой или лицензированием!

Калькулятор деревянных балок | Какой размер мне нужен?

Рассчитайте размер, необходимый для балки, фермы или заголовка, изготовленных из No.2 сосны или LVL. Охватывает любой пролет и любую нагрузку с высокой точностью. Дважды проверьте себя с помощью этих диаграмм. Работает только с равномерно распределенными нагрузками.

Есть два разных типа нагрузок. Это либо внешняя, либо внутренняя нагрузка. Другими словами, он будет либо на внешней стене, либо где-то внутри. Нагрузка на внешнюю стену с чистыми пролетными фермами составляет ровно половину нагрузки на каждую стену. Например, если размер здания составляет 24 x 24 дюйма, и в нем есть фермы, а нагрузка на крышу будет составлять 30 фунтов снеговой нагрузки, а потолок без хранилища будет таким.Это будет вдвое больше нагрузки на внешние стены по сравнению со зданием с центральной стеной. Калькулятор учитывает все это. Вам нужно только выбрать все применяемые нагрузки.

Большинство внутренних балок должны учитывать нагрузку на крышу. Если есть какие-либо вопросы по другому поводу, вам следует обратиться к поставщику или инженеру. Этот калькулятор соответствует 90% приложений в Международной книге кодов жилищного строительства 2012 года.

Здравый смысл

По моему опыту никогда не использовать балку меньше двухслойной 2 x 8.Независимо от того, что говорят спецификации. Эти небольшие области обычно представляют собой дверные проемы внутри, и людей учат, что эти области являются самым надежным местом в доме в случае возникновения чрезвычайной ситуации.

Подшипник

Согласно кодам IRC 2012 года любая балка, балка или коллектор никогда не должны иметь наклон менее 1 1/2 дюйма. Что-нибудь 5 ‘и выше мы всегда как минимум вдвое калечим. На более длинных пролетах балке может потребоваться гораздо больше места для опоры, как указано в этой таблице.

Крепление

Балки, состоящие из более чем одного слоя, необходимо скреплять вместе гвоздями или болтами.Код IRC 2012 года требует минимум 32 ″ O.C. в шахматном порядке с использованием гвоздя размером не менее 3 ″ на 120 ″. На собственном опыте мы научились использовать гвоздь с пазом размером не менее 3 1/4 дюйма x 131 дюйм в столбике из четырех на каждую ногу вниз по ламинату.

Единственный случай, когда вам когда-либо понадобится использовать болты, будет, если материал будет иметь такие серьезные деформации, как плохая «чашка», которую невозможно преодолеть гвоздями.

Онлайн калькулятор луча

| Калькулятор изгибающего момента и силы сдвига выступающей балки

NEWS | ПРОГРАММНОЕ ОБЕСПЕЧЕНИЕ | ЛИСТ

Бесплатный онлайн-калькулятор предназначен для расчета величины поперечной силы и изгибающего момента в точке свисающей балки, несущей равномерно распределенную нагрузку (UDL), или точечной нагрузки в любой точке по длине.

Он даже обеспечивает количество наивысшего изгибающего момента, в котором его местоположение появляется. Калькуляторы соответствуют установленным формулам для поперечной силы и изгибающего момента нависающей балки и предложены преподавателями колледжа.

В случае объединения нагрузок можно применить закон суперпозиции для вычисления результирующих величин.

Примеры нагрузки для выступающей балки: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, по отношению к точечной нагрузке на пролете.Вычисленные величины можно использовать для набросков изгибающего момента и поперечной силы.

Калькулятор также можно использовать для определения ординат диаграммы линий влияния для зданий.

Равномерная нагрузка на балку: калькулятор предлагает результаты для поперечной силы и изгибающего момента на части выступающей балки, вероятно, в отношении равномерно распределенной нагрузки на участке пролета. Пожалуйста, сделайте ссылку на представление и введите количество нагрузки и пролеты в форму, представленную ниже, а затем нажмите «Рассчитать».

Предполагается, что все восходящие рабочие нагрузки положительны, а нисходящие — отрицательны.

Онлайн-калькуляторы изгибающего момента и поперечной силы выступающей балки.

Прочтите следующий видеоурок, чтобы получить дополнительную информацию.

Лектор: Параг Пал

Расчет балки на прочность онлайн калькулятор

Балка длиной L загружена равномерно распределенной нагрузкой q либо сосредоточенной силой P, которые необходимо будет задать (как собрать нагрузки на балку можно получить тут Сбор нагрузок (калькулятор).
Все геометрические размеры сечения можно задать самому, поэтому в калькуляторе реализован огромный выбор самых различных балок: труба, швеллер, профильная труба, двутавр, уголок, пластина и др.
Расчет проходит по нормальным и касательным напряжениям, которые возникают из-за поперечной силы.
Касательные напряжения получаем по формуле Журавского и производим проверку с использованием главных напряжений по 3-ей теории прочности.
В онлайн расчет входят такие материалы, как сталь нескольких классов (С235, С245, С255, С345) и дерево трех сортов.

Для расчета вам необходимо:
1. Выбрать форму поперечного сечения (труба, швеллер, профильная труба, двутавр, уголок, пластина и др.)
2. Выбрать материал (сталь, дерево)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)

Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка, свободный конец балки.
Коэффициенты поправки расчетного сопротивления дерева на изгиб приняты следующие:
Mдл = 0.

66 — совместное действие постоянной и кратковременной снеговой нагрузок
Mв = 0.9 — нормальные условия эксплуатации дерева (влажность менее 12%)
Mт = 0.8 — эксплуатация дерева при температуре 50 градусов
Mсс = 0.9 — срок эксплуатации конструкции 75 лет

При расчете уже учитывается собственный вес конструкции.

Последние изменения
1. Добавлена возможность расчета балки при сосредоточенной нагрузке
— Добавлена проверка устойчивости стенки и полки двутавра, швеллера, уголка, профильной трубы
— Исправлено расчетное сопротивление дерева на изгиб согласно СП 64.13330.2017 «Деревянные конструкции»
— Исправлены расчетные сопротивления стали
— Исправлено допустимое эквивалентное напряжение при действии нормальных и касательных напряжений
— Добавлена возможность поворота швеллера

Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц. сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.

Расчет опорных реакций балки на двух опорах онлайн

Расчет выполняется по следующей методике:

3. Освобождаемся от опор и заменяем их действие на балку реакциями.
Реакции опор при такой нагрузке будут только вертикальными.

4. Составляем уравнения равновесия вида:
M_A = 0; M_B = 0,
Моментом силы относительно точки называется произведение этой силы на плечо — кратчайшее расстояние от этой точки приложения силы (в общем случае — до линии действия силы).

5. Выполним проверку решения. Для этого составим уравнение равновесия: Y = 0,
Если оно удовлетворено, то реакции найдены правильно, а если нет, но в решении допущена ошибка.

6. Строим эпюру поперечных сил Q_x. Для этого определяем значения поперечных сил в характерных точках. Напомним, что поперечная сила в сечении равна сумме проекций всех сил, расположенных только слева или только справа от рассматриваемого сечения, на ось, перпендикулярную оси элемента. Силу, расположенную слева от рассматриваемого сечения и направленную вверх, считают положительной (со знаком «плюс»), а направленную вниз — отрицательной (со знаком «минус»). Для правой части балки — наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных сил, в том числе в точках приложения опорных реакций, необходимо определить два значения поперечной силы: чуть левее рассматриваемой точки и чуть правее ее. Поперечные силы в этих сечениях обозначаются соответственно Q_лев и Q_прав.
Найденные значения поперечных сил в характерных точках откладываются в некотором масштабе от нулевой линии. Эти значения соединяются прямыми линиями по следующим правилам:
а) если к участку балки нет распределенной нагрузки, то под этим участком значения поперечных сил соединяются прямой линией, параллельной нулевой линии;
б) если на участке балки приложена распределенная нагрузка, то под этим участком значения поперечных сил соединяются прямой, наклонной к нулевой линии. Она может пересекать или не пересекать нулевую линию.
Соединив все значения поперечных сил по указанным правилам, получим график изменения поперечных сил по длине балки. Такой график называется эпюрой Q_x.

7. Строим эпюру изгибающих моментов М_x. Для этого определяем изгибающие моменты в характерных сечениях. Напомним, что изгибающий момент в рассматриваемом сечении равен сумме моментов всех сил (распределенных, сосредоточенных, в том числе и опорных реакций, а также внешних сосредоточенных моментов), расположенных только слева или только справа от этого сечения. Если любое из перечисленных силовых воздействий стремится повернуть левую часть балки по часовой стрелке, то оно считается положительным (со знаком «плюс»), если против — отрицательным (со знаком «минус»), а для правой части наоборот.
В сечениях, соответствующих точкам приложения сосредоточенных моментов, необходимо определить два значения изгибающего момента: чуть левее рассматриваемой точки и чуть правее ее. Изгибающие моменты в этих точках обозначаются соответственно М_лев и М_прав. В точках приложения сил определяется одно значение изгибающего момента.
Полученные значения откладываются в некотором масштабе от нулевой линии. Эти значения соединяются в соответствии со следующими правилами:
а) если на участке балки нет распределенной нагрузки, то под этим участком балки два соседних значения изгибающих моментов соединяются прямой линией;
б) если к участку балки приложена распределенная нагрузка, то под этим участком значения изгибающих моментов для двух соседних точек соединяются по параболе.

Пример решения балки:

Подбор сечения балок онлайн — Мастер Фломастер

При проектировании и изготовлении конструкций из металла и других материалов очень важно соблюдать и выполнять физико-механические расчеты на прочность, одним из которых является расчет балок на изгиб (прогиб). Выполнять расчет прогиба балки онлайн — очень удобно и быстро. Поэтому специалисты нашего предприятия подготовили онлайн калькулятор для расчетов.

Расчет прогиба балки онлайн

Площадь поперечного сечения профиля:

Расчетный вес профиля (балки):

Описание

При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].

Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.

Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.

Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)

По полученному значению требуемого момента сопротивления из сортамента принимаем сечение прокатного двутавра балочного по ГОСТ 26020-83 — №35Б2:

момент инерции относительно оси х

вес 1 погонного метра балки

радиус закругления проката

По принятым характеристикам поперечного сечения двутавра уточняем значение коэффициента для расчета на прочность элементов стальных конструкций с учетом развития пластических деформаций.

Определяем :

Согласно табл. Н.1 ДБН интерполяцией определяем =1,089

Проверка прочности балки

Проверка жесткости балки настила:

Сечение подобрано верно: двутавр балочный по ГОСТ 26020-83 I №35Б2

4. Расчет главной балки:

Материал главных балок — сталь С245 по ГОСТ 27772-88 с расчетным сопротивлением стали R_y = 240МПа — для листовой стали толщиной до 20мм.

Сбор нагрузок на главную балку:

В связи с частым расположением балок настила нагрузку на главную балку принимаем равномерно распределенной:

n₁=1,2 и n₂=1,05 — к-ты надежности по нагрузке для временной и постоянной

_г.б = 2…6 кН/м – предварительный вес главной балки.

Принимаем _г.б = 3 кН/м

q н = [19+1,218+3] ∙ 7 = 162,5 кН/м

q р = [1,2 ∙ 19+1,05 ∙ 1,218+1,05 ∙ 3] ∙ 7 = 190,60 кН/м

В связи с тем, что расположение балок настила частое, нагрузку на главную балку принимаем равномерно распределенную.

Определение расчетных усилий:

Упрощенно принимаем нагрузку на балку равномерно распределенной и

определяем расчетный и нормативный изгибающий момент.

Определение расчетных усилий

Расчетный изгибающий момент в балке:

Нормативный изгибающий момент в балке:

Расчетная поперечная сила в балке:

Подбор сечения:

Подбор сечения. Главную балку принимаем постоянного сечения по длине и рассчитываем без учета развития пластических деформаций.

R_y – расчетное сопротивление стали. R_y = 240 МПа = 24 кН/см 2 .

Определяем высоту балки. Задаемся предварительно толщиной стенки по эмпирической формуле:

Оптимальная высота главной балки:

Минимальная высота сечения балки:

где — — предельный относительный прогиб для главных балок.

Высоту балки стремимся принять близкую к оптимальной, но не менее минимальной. Окончательную высоту балки принимаем кратной модулю 100мм или с учетом ширины листов, поставляемых по сортаменту.

Принимаем высоту стенки балки h_w= 1240мм из прокатной стали 1250х12

Суммарную толщину полок — 2 x 30 = 60мм;

Общую высоту балки h = 1300мм.

Минимальная толщина стенки из условия среза:

Принимаем окончательно толщину стенки балки равной t_w= 12мм.

Компоновка поперечного сечения и определение геометрических размеров:

Определяем площадь полок балки (необходимую площадь пояса).

Принимаем пояс из универсальной широкополочной стали сечением

Отношение соответствует диапазону

Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки и позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с готовым решением. Удачи!

Сопромат. Решение задач. Онлайн решение

является одной из основных общетехнических дисциплин, определяющих уровень подготовки и составляющих необходимый «инженерный багаж» будущего бакалавра или специалиста.

При переходе на новые федеральные государственные образовательные стандарты, в условиях существенного сокращения числа аудиторных часов, выделенных в новых учебных планах на данную дисциплину, у студента увеличивается доля самостоятельной работы, а именно выполнение индивидуальных заданий (контрольных работ, расчетно-графических работ, расчетно-проектировочных работ).

На нашем сайте Вы найдете примеры решения задач по сопромату (сопротивлению материалов) на такие темы как:

Плоский изгиб балки- построение эпюр изгибающих моментов и поперечных сил, подбор поперечных сечений балок при плоском изгибе, определение перемещений в балках методом Верещагина, Симпсона, используя интеграл Мора, метод начальных параметров; плоский изгиб рамы-эпюры N, Q, M.
Центральное растяжение и сжатие стержней- построение эпюр продольных сил, напряжений, перемещений в статически определимых и статически неопределимых стержнях;
Геометрические характеристики поперечных сечений- определение геометрических характеристик: осевые моменты инерции, полярные моменты инерции, осевые моменты сопротивления, положение центра тяжести составных несимметричных и симметричных сечении;
Напряженное и деформированное состояние в точке- плоское напряженное состояние, величина и направление главных площадок;
Кручение вала, расчет на прочность- условия прочности и жесткости вала, абсолютные и относительные углы закручивания, кручение валов прямоугольного сечения, распределение касательных напряжений, изгиб с кручением;
Расчет статически неопределимых балок и рам- используя метод сил, каноническое уравнение метода сил, способ Верещагина, Симпсона;
Косой изгиб, сложное сопротивление-расчет на прочность при косом изгибе, положение нулевой линии при косом изгибе, расчет пространственного стержня на прочность;
Внецентренное растяжение и сжатие- положение нулевой линии, напряжения в точках сечения;
Устойчивость сжатых стержней, стержень Эллера — допускаемая и критическая силы, гибкость стержня, минимальный радиус инерции, условие устойчивости по допускаемым напряжениям, подбор поперечного сечения сжатой стойки, коэффициенты приведения длины;
Динамическое действие нагрузок- расчеты на удар, коэффициент динамичности, статический прогиб, круговая частота свободных колебаний;

А так же поможем с решением задач по сопромату (сопротивлению материалов), онлайн решение задач по сопротивлению материалов, строительной механике, теоретической механике

Онлайн помощь по сопромату включает в себя оперативное решение задачи (в кратчайшие сроки, время на решение от 5 минут) на такие темы:

Построение эпюр в балке;
Расчет рамы;
Расчет фермы;
Геометрические характеристики;
Растяжение -сжатие;
Напряжения в точках сечения;
Кручение вала;
Расчет на удар;
Стержень Эллера;
Косой изгиб;
Метод сил;
Статически неопределимая балка;
Статически неопределимая рама;
Теоретическая механика;
Строительная механика;

Выполняли работы в большинство основных государственных университетов России, в такие города как:

Москва, Новосибирск, Волгоград, Тюмень, Липецк, Орел, Санкт-Петербург, Уфа, Пермь, Иваново, Псков, Казань, Ижевск, Тверь, Белгород, Воронеж, Курск, Архангельск, Вологда, Ростов-на-Дону, Челябинск.

[свернуть]

Калькулятор для расчета прочности прямоугольной балки

Калькулятор расчета прочности прямоугольной балки для расчета нормального напряжения, напряжения сдвига и напряжения Фон Мизеса для заданного твердого прямоугольного поперечного сечения. Калькулятор также рисует графики изменения напряжения в зависимости от расстояния от нейтральной оси.

Поперечная нагрузка на прямоугольную балку может привести к нормальному и поперечному напряжения одновременно на любом поперечном сечении конструкции прямоугольный брус.Нормальное напряжение на данном поперечном сечении изменяется в зависимости от относительно расстояния y от нейтральной оси, и он наибольший на самом дальнем точка от нервной оси. Нормальное напряжение также зависит от изгибающего момента. в сечении и максимальное значение нормальных напряжений в прямоугольных балках возникает там, где изгибающий момент наибольший. Максимальное напряжение сдвига возникает на нейтральная ось прямоугольного сечения балки, где сила сдвига максимальна.

Конструкция прямоугольных балок обычно определяется максимальным изгибающим моментом. В случае коротких структурных балок конструкция может приводиться в движение максимальной силой сдвига.

Примечание. Для получения дополнительной информации о предмет, пожалуйста, обратитесь к главе «Расчет балок и валов на прочность» механики материалов. .

Примечание: V и M — поперечная сила и изгибающий момент в сечении, как показано на фигура.Визит » «Калькуляторы прогиба и напряжения несущей балки». Для расчета поперечной силы и изгибающего момента.

Примечание. Предполагается, что на несущую балку действует вертикальная сила сдвига в вертикальной плоскости симметрии.

РЕЗУЛЬТАТЫ
Параметр	Стоимость
Площадь поперечного сечения [A]	—	мм ^ 2 см ^ 2 дюйма ^ 2 фута ^ 2
Первый момент площади для части поперечного сечения над точкой y [Q]	—	мм ^ 3 см ^ 3 дюйма ^ 3 фута ^ 3
Второй момент площади [I _zz]	—	мм ^ 4 см ^ 4 дюйма ^ 4 фута ^ 4
Нормальное напряжение в точке y [σ _x]	—	МПапсикси
Напряжение сдвига в точке y [τ _xy]	—
Напряжение фон Мизеса в точке y [σ _v]	—
Максимальное нормальное напряжение [σ _макс]	—
Максимальное напряжение сдвига [τ _макс]	—
Максимальное напряжение по Мизесу [σ _{v_max}]	—

Примечание: используйте точку «.»как десятичный разделитель.

Примечание. Напряжения являются положительными числами, и это величины напряжений в луч. Он не делает различий между растяжением и сжатием конструкции. луч.

Нормальное напряжение

Напряжение сдвига

Напряжение фон Мизеса

Нормальное напряжение: Напряжение действует перпендикулярно поверхности (поперечному сечению).

Второй момент области: способность поперечного сечения противостоять изгибу.

Принцип Сен-Венана: Напряжения на поверхности, находящиеся на значительном удалении от нагрузка на тело существенно не изменяется, если эта нагрузка изменяется на статическую эквивалентную нагрузку. Распределение напряжений и деформаций изменяется только вблизи областей действия нагрузки.

Напряжение сдвига: Напряжение, действующее параллельно поверхности (поперечному сечению), имеет режущий характер.

Напряжение: Среднее усилие на единицу площади, которое приводит к деформации материала.

Прочность материалов | Механика материалов

ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.

Сопротивление материалов , также известный как Механика материалов , ориентирован на анализ напряжений и прогибов в материалах под нагрузкой.Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки.

Напряжение и деформация

Когда к конструктивному элементу прикладывается сила, в этом элементе в результате силы возникают как напряжение, так и деформация. Напряжение — это сила, переносимая элементом на единицу площади, и типичными единицами измерения являются фунт-сила / дюйм ² (фунт / кв. Дюйм) для стандартных единиц США и Н / м ² (Па) для единиц СИ:

где F — приложенная сила, а A — площадь поперечного сечения, на которую действует сила.Приложенная сила вызовет деформацию конструктивного элемента на некоторую длину, пропорциональную его жесткости. Деформация — это отношение деформации к исходной длине детали:

где L — деформированная длина, L ₀ — исходная недеформированная длина, а δ — деформация (разница между ними).

Существуют различные типы нагрузки, которые приводят к различным типам напряжений, как показано в таблице ниже:

Тип нагрузки	Тип напряжения	Иллюстрация
Осевая сила	Осевое напряжение (общий случай) Растягивающее напряжение (если сила растяжения) Напряжение сжатия (если сила сжимающая)
Сила сдвига	Напряжение поперечного сдвига
Изгибающий момент	Напряжение изгиба
Кручение	Напряжение скручивания

Осевое напряжение и изгибающее напряжение являются формами нормального напряжения , σ, поскольку направление силы перпендикулярно области, противодействующей силе.Поперечное напряжение сдвига и напряжение скручивания являются формами напряжения сдвига , τ, поскольку направление силы параллельно области, противодействующей силе.

Нормальное напряжение
Осевое напряжение:
Напряжение изгиба:

Напряжение сдвига
Поперечное напряжение:
Торсионное напряжение:

В уравнениях для осевого напряжения и поперечного напряжения сдвига F — это сила, а A — площадь поперечного сечения элемента.В уравнении для изгибающего напряжения M — изгибающий момент, y — расстояние между центральной осью и внешней поверхностью, а I _c — центроидный момент инерции поперечного сечения относительно соответствующей оси. В уравнении для напряжения кручения T — это кручение, r — радиус, а J — полярный момент инерции поперечного сечения.

В случае осевого напряжения на прямом участке напряжение распределяется равномерно по всей площади.В случае напряжения сдвига распределение максимально в центре поперечного сечения; однако среднее напряжение определяется как τ = F / A, и это среднее напряжение сдвига обычно используется при расчетах напряжений. Более подробное обсуждение можно найти в разделе о касательных напряжениях в балках. В случае напряжения изгиба и скручивания максимальное напряжение возникает на внешней поверхности. Более подробное обсуждение можно найти в разделе о напряжениях изгиба в балках.

Так же, как основными типами напряжения являются нормальное напряжение и напряжение сдвига, основными типами деформации являются нормальная деформация и деформация сдвига .В случае нормальной деформации деформация перпендикулярна области, на которую действует сила:

В случае деформации поперечного сдвига деформация параллельна области, на которую действует сила:

где γ — деформация сдвига (безразмерная) и & phiv; — деформированный угол в радианах.

В случае деформации кручения элемент поворачивается на угол & phiv; вокруг своей оси.Максимальная деформация сдвига возникает на внешней поверхности. В случае круглого стержня максимальная деформация сдвига определяется как:

где & phiv; — угол закручивания, r — радиус стержня, а L — длина.

Деформации сдвига пропорциональны внутренней части стержня и связаны с максимальной деформацией сдвига на поверхности следующим образом:

где ρ — радиальное расстояние от оси стержня.

Закон Гука

Напряжение пропорционально деформации в упругой области кривой напряжения-деформации материала (ниже предела пропорциональности, когда кривая является линейной).

Нормальное напряжение и деформация связаны между собой:

σ = E & varepsilon;

где E — модуль упругости материала, σ — нормальное напряжение, а & varepsilon; это нормальный штамм.

Напряжение сдвига и деформация связаны между собой:

τ = G γ

где G — модуль сдвига материала, τ — напряжение сдвига, а γ — деформация сдвига.Модуль упругости и модуль сдвига связаны соотношением:

где ν — коэффициент Пуассона.

Закон Гука аналогичен уравнению силы пружины F = k δ. По сути, все можно рассматривать как пружину. Закон Гука можно перестроить, чтобы получить деформацию (удлинение) в материале:

Осевое удлинение (от нормального напряжения)
Угол скручивания (от напряжения сдвига / скручивания)

Энергия деформации

Когда к конструктивному элементу прикладывается сила, этот элемент деформируется и накапливает потенциальную энергию, как пружина.Энергия деформации (то есть количество потенциальной энергии, накопленной из-за деформации) равна работе, затраченной на деформацию элемента. Полная энергия деформации соответствует площади под кривой отклонения нагрузки и имеет единицы дюйм-фунт-сила в обычных единицах США и Н-м в единицах СИ. Энергия упругой деформации может быть восстановлена, поэтому, если деформация остается в пределах упругого предела, то вся энергия деформации может быть восстановлена.

Энергия деформации рассчитывается как:

Общая форма:	U = Работа = ∫ F dL	(площадь под кривой нагрузки-прогиб)
В пределах предела упругости:		(площадь под кривой нагрузки-прогиб)
В пределах предела упругости:		(потенциальная энергия пружины)

Обратите внимание, что есть два уравнения для энергии деформации в пределах упругого предела.Первое уравнение основано на площади под кривой прогиба нагрузки. Второе уравнение основано на уравнении для потенциальной энергии, запасенной в пружине. Оба уравнения дают один и тот же результат, просто они выводятся несколько по-разному.

Более подробную информацию об энергии деформации можно найти здесь.

Жесткость

Жесткость, обычно называемая жесткостью пружины, — это сила, необходимая для деформации элемента конструкции на единицу длины.Все конструкции можно рассматривать как совокупность пружин, а силы и деформации в конструкции связаны уравнением пружины:

F = k δ _макс

где k — жесткость, F — приложенная сила, а δ _max — максимальное отклонение при прогибе в элементе.

Если прогиб известен, то жесткость элемента можно найти, решив k = F / δ _max. Однако максимальный прогиб обычно неизвестен, поэтому жесткость необходимо рассчитывать другими способами.Таблицы прогиба балки можно использовать в общих случаях. Два наиболее полезных уравнения жесткости, которые необходимо знать, — это уравнения для балки с приложенной осевой нагрузкой и для консольной балки с концевой нагрузкой. Обратите внимание, что жесткость зависит от модуля упругости материала E, геометрии детали и конфигурации нагрузки.

Торсионный эквивалент уравнения пружины:

Т = к & phiv;

Особый интерес представляет жесткость вала при скручивающей нагрузке:

	Жесткость [дюйм * фунт-сила / рад]	Максимальный прогиб [рад]	Иллюстрация
Вал с крутильной нагрузкой:

Конструкция с несколькими путями нагружения

Если в конструкции есть несколько путей загрузки (т.е. в конструкции есть несколько элементов, которые разделяют нагрузку), нагрузка будет выше в более жестких элементах. Чтобы определить нагрузку, воспринимаемую любым отдельным элементом, сначала вычислите эквивалентную жесткость элементов на пути нагружения, рассматривая их как пружины. В зависимости от их конфигурации они будут рассматриваться как некоторая комбинация пружин, включенных последовательно, и пружин, включенных параллельно.

Если элементы на пути нагружения нельзя рассматривать только как пружины, включенные последовательно или как пружины, включенные параллельно, а скорее представляют собой комбинацию пружин, включенных последовательно и параллельно, тогда проблему необходимо будет решать итеративно.Найдите подгруппу элементов, которые находятся либо последовательно, либо параллельно, и используйте приведенные уравнения для расчета эквивалентной жесткости, силы и прогиба в этой подгруппе. Затем подгруппу можно рассматривать как одну пружину с рассчитанными жесткостью, силой и прогибом, и эту пружину затем можно рассматривать как часть другой подгруппы пружин. Продолжайте группировать участников и решать, пока не будет достигнут желаемый результат.

Концентрации напряжений

Можно подумать, что силы и напряжения протекают через материал, как показано на рисунке ниже.Когда геометрия материала изменяется, линии потока перемещаются ближе друг к другу или дальше друг от друга, чтобы приспособиться. Если в материале имеется разрыв, такой как отверстие или выемка, напряжение должно течь вокруг неоднородности, и линии потока будут уплотняться вместе вблизи этого разрыва. Это внезапное уплотнение потоковых линий приводит к резкому скачку напряжения — это пиковое напряжение называется концентрацией напряжений . Элемент, вызывающий концентрацию напряжений, называется подъемником напряжений .

Концентрации напряжений учитываются с помощью коэффициентов концентрации напряжений . Чтобы найти фактическое напряжение в вязкости несплошности, рассчитайте номинальное напряжение в этой области и затем увеличьте его с помощью соответствующего коэффициента концентрации напряжений:

σ _макс = K σ _ном

где σ _max — фактическое (масштабированное) напряжение, σ _nom — номинальное напряжение, а K — коэффициент концентрации напряжений.При расчете номинального напряжения используйте максимальное значение напряжения в этой области. Например, на рисунке выше должна использоваться наименьшая площадь у основания галтеля.

Многие справочные руководства содержат таблицы и кривые коэффициентов концентрации напряжений для различных геометрических форм. Двумя наиболее полными наборами факторов концентрации напряжения являются факторы концентрации напряжения Петерсона и формулы Рорка для напряжения и деформации. MechaniCalc также предоставляет набор интерактивных графиков для общих факторов концентрации стресса.

По мере того, как мы удаляемся от источника стресса, концентрация стресса рассеивается. Принцип Сен-Венана — это общее практическое правило, гласящее, что расстояние, на котором рассеивается концентрация напряжений, равно наибольшему размеру поперечного сечения, несущего нагрузку.

Расчет концентрации напряжений особенно важен, когда материалы очень хрупкие или когда существует только один путь нагрузки. В пластичных материалах местная податливость позволит перераспределить напряжения и снизит напряжение вокруг стояка.По этой причине коэффициенты концентрации напряжений обычно не применяются к элементам конструкции из пластичных материалов. Коэффициенты концентрации напряжений также обычно не применяются при наличии избыточного пути нагружения, и в этом случае податливость одного элемента позволит перераспределить силы на элементы на других путях нагружения. Примером этого является набор болтов. Если один болт начинает прогибаться, другие болты в шаблоне принимают на себя большую нагрузку.

Комбинированные напряжения

В любой точке нагруженного материала общее состояние напряжения можно описать тремя нормальными напряжениями (по одному в каждом направлении) и шестью напряжениями сдвига (по два в каждом направлении):

Индексы нормальных напряжений σ указывают направление нормальных напряжений.Индексы касательных напряжений τ состоят из двух компонент. Первый указывает направление нормали к поверхности, а второй указывает направление самого напряжения сдвига.

Обычно напряжения в одном направлении равны нулю, так что полное напряжение возникает в одной плоскости, как показано на рисунке ниже. Это называется напряжением в плоскости . Плоское напряжение возникает в тонких пластинах, но оно также возникает на поверхности любой нагруженной конструкции. Напряжения на поверхности обычно являются наиболее критическими напряжениями, поскольку напряжение изгиба и скручивания максимизируется на поверхности.

На рисунке выше σ _x и σ _y — нормальные напряжения, а τ — напряжение сдвига. Напряжения уравновешиваются, так что точка находится в статическом равновесии. Поскольку напряжения сдвига все одинаковы по величине, для простоты индексы опущены. (Обратите внимание, однако, что знак напряжений на грани x будет противоположен знаку напряжений на грани x ).

Правильные условные обозначения показаны на рисунке.Для нормального напряжения растягивающее напряжение положительное, а сжимающее — отрицательное. Для напряжения сдвига значение по часовой стрелке положительное, а против часовой стрелки — отрицательное.

Если напряжения из рисунка выше известны, можно найти нормальное напряжение и напряжение сдвига в плоскости, повернутой на некоторый угол θ относительно горизонтали, как показано на рисунке ниже. Уравнения преобразования ниже дают значения нормального напряжения и напряжения сдвига на этой повернутой плоскости.

Нормальное напряжение:
Напряжение сдвига:

Обратите внимание, что на рисунке выше θ отсчитывается от оси x, а положительное значение θ — против часовой стрелки.

В любой точке материала можно найти углы плоскости, при которых нормальные напряжения и напряжения сдвига максимизируются и минимизируются.Максимальное и минимальное нормальные напряжения называются главными напряжениями . Максимальные и минимальные касательные напряжения называются крайними касательными напряжениями . Углы главных напряжений и крайних касательных напряжений находятся путем взятия производной каждого уравнения преобразования по θ и нахождения значения θ, при котором производная равна нулю.

Углы главного напряжения:
Экстремальные углы напряжения сдвига:

Указанные выше углы можно подставить обратно в уравнения преобразования, чтобы найти значения главных напряжений и экстремальных касательных напряжений:

Основные напряжения:
Экстремальные напряжения сдвига:

Углы, при которых возникают основные напряжения, составляют 90 ^° друг от друга.Главные напряжения всегда сопровождаются нулевым напряжением сдвига. Углы возникновения экстремальных касательных напряжений составляют 45 ^° от углов главных напряжений. Экстремальные напряжения сдвига сопровождаются двумя равными нормальными напряжениями (σ _x & plus; σ _y) / 2.

Вот пара полезных отношений:

σ ₁ & plus; σ ₂ = σ _x и плюс; σ _y	Сумма нормальных напряжений постоянна.
	Максимальное напряжение сдвига составляет половину разницы главных напряжений.

Круг Мора

Круг Мора — это способ визуализировать состояние напряжения в точке нагруженного материала. Это дает интуитивное представление о уравнениях преобразования напряжений и показывает, как напряжения на элементе изменяются в зависимости от угла поворота θ. Из круга Мора также становится ясно, каковы основные напряжения, экстремальные напряжения сдвига и углы, под которыми возникают эти напряжения.Пример круга Мора показан на рисунке ниже:

Чтобы построить круг Мора, сначала найдите центр круга, взяв среднее значение нормальных напряжений:

Поместите точки на окружности, представляющие напряжения на гранях x и y элемента напряжения. Напряжения на грани x будут иметь координаты (σ _x, −τ), а напряжения на грани y будут иметь координаты (σ _y, τ).Поместите точки на окружности для главных напряжений. Максимальное главное напряжение будет иметь координаты (σ ₁, 0), а минимальное главное напряжение будет иметь координаты (σ ₂, 0). Поместите точки на окружности для экстремальных касательных напряжений. Максимальное экстремальное напряжение сдвига будет иметь координаты (σ _c, τ ₁), а минимальное экстремальное напряжение сдвига будет иметь координаты (σ _c, τ ₂).

Все точки будут лежать по периметру круга.Круг имеет радиус, равный величине предельных касательных напряжений:

Напряженное состояние на гранях x и y элемента напряжения представлено черной линией в круге Мора, соединяющим точки (σ _x, −τ) и (σ _y, τ). Эта линия в круге Мора соответствует невращающемуся элементу на рисунке ниже. Если эту линию повернуть на некоторый угол, то значения точек на конце повернутой линии дадут значения напряжения на гранях x и y повернутого элемента.Важно отметить, что 360 градусов круга Мора эквивалентны 180 градусам на элементе напряжения. Например, точки для грани x и грани y расположены на 180 градусов друг от друга на круге Мора, но они всего на 90 градусов на элементе напряжения.

Чтобы получить более интуитивное представление о том, как круг Мора связывает напряжения в элементе напряжения и как состояние напряжения изменяется в зависимости от угла поворота, см. Прилагаемый калькулятор круга Мора.

Приложения

Есть много структурных компонентов, которые обычно подвергаются анализу напряжений. Подробности анализа этих компонентов приведены в других разделах:

Расчет допустимого напряжения

Знание напряжений и прогибов позволяет безопасно проектировать конструкции, способные выдерживать предполагаемые нагрузки. Всегда желательно, чтобы напряжения в конструкции оставались в пределах прочности конструкции.Предел текучести материала обычно выбирается как предел прочности, с которым сравниваются расчетные напряжения.

Коэффициент запаса прочности , FS, рассчитывается как:

где σ _{фактическое} — это расчетное напряжение в конструкции, а предел — это максимальный предел напряжения, обычно прочность материала, например предел текучести (S _ty). Коэффициент запаса прочности показывает, насколько фактическое напряжение ниже предельного напряжения.Значение FS должно быть больше или равно 1, чтобы конструкция не вышла из строя, но инженеры почти всегда будут проектировать с некоторым требуемым коэффициентом безопасности, превышающим 1. Требуемый коэффициент безопасности будет варьироваться в зависимости от критичности конструкции (т. Е. последствия разрушения конструкции), а также условия нагружения (т. е. какие типы нагрузок применяются, насколько они предсказуемы и т. д.). Высокое значение FS приведет к очень безопасной конструкции, но если значение FS слишком велико, конструкция может стать настолько большой и тяжелой, что больше не сможет успешно выполнять свою функцию.Поэтому при выборе подходящего запаса прочности приходится идти на компромиссы. Типичные значения FS варьируются от 1,15 до 10.

Запас прочности рассчитывается как:

В приведенном выше уравнении любое значение выше нуля указывает на то, что фактическое напряжение ниже предельного напряжения. Хотя запасы прочности обычно указываются в виде десятичных значений, гораздо более интуитивно понятно думать о запасах в процентах. Например, если предельное напряжение конструкции равно 1.В 5 раз превышающее фактическое напряжение, запас прочности составляет 50% (MS = 0,5).

Когда сообщается о факторах безопасности и запасах прочности, иногда требуемый коэффициент безопасности будет «вплетен» в указанные факторы. Например, инженеры могут потребовать, чтобы конструкция поддерживала коэффициент безопасности не менее 2, так что FS _req = 2. Чтобы обеспечить требуемый коэффициент безопасности, сообщаемые FS и MS рассчитываются как:

Обратите внимание, что при включении необходимого коэффициента безопасности, FS _req, сообщаемые FS и MS фактически являются запасами по отношению к FS _req, а не по напряжению.

PDH Classroom предлагает курс повышения квалификации, основанный на этой справочной странице о прочности материалов. Этот курс можно использовать для выполнения требований к кредитам PDH для поддержания вашей лицензии PE.

Теперь, когда вы прочитали эту справочную страницу, получите за нее кредит!

Список литературы

Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е издание
Доулинг, Норман Э., «Механическое поведение материалов: инженерные методы деформации, разрушения и усталости», 3-е издание.
Гир, Джеймс М., «Механика материалов», 6-е издание
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е издание
Пилки, Уолтер Д. и Пилки, Дебора Ф., «Факторы концентрации стресса Петерсона», 3-е издание.
«Формулы Рорка для стресса и деформации», 8-е издание

Калькулятор прочности и прогиба балки

Балка или стержень — это любой элемент конструкции, длина которого значительно превышает ширину или глубину.Однако термин «существенно» означает разные вещи для разных людей. Некоторые люди считают, что длина в два раза больше, другие считают, что длина в пять раз больше, чем длина, и поэтому считают такой элемент пластиной, каркасом или конструкцией. Процедуры расчета балок не накладывают таких ограничений или различий.

Балки обычно используются для несения нагрузки, в то время как пролетные опоры находятся на достаточном расстоянии друг от друга, например, пол (см. Калькулятор этажей CalQlata). При указании балки вы должны определить ее максимальную грузоподъемность (т.е. его прочность) и максимально допустимый прогиб.

Прочность и жесткость балки

Прочность балки зависит от предела текучести материала, из которого изготовлена балка, тем самым определяя максимальную нагрузку, которая может быть приложена до того, как она деформируется (или сломается, если она сделана из хрупкого материала), и

, его жесткость зависит от второго момента площади поперечного сечения балки (например, канал, двутавровая балка, двутавровая балка, угол и т. Д.) вместе с модулем Юнга материала, тем самым определяя ожидаемый прогиб балки для любой заданной нагрузки

Обе вышеуказанные характеристики определяют поведение балки под нагрузкой.

Спроектировать балку

Предположим, у вас есть равномерно распределенная нагрузка в 4000 Н на длине балки 4 м (1 Н / мм) и максимально допустимый прогиб, скажем, 1/200 длины балки (20 мм).

Используя Beams, вы вводите информацию, которую знаете, и изменяете второй момент площади (I), пока не получите желаемое отклонение (20 мм в середине балки, где ее отклонение будет наибольшим), что в этом случае дает вам значение для I около 800000 мм².

Предполагая, что вы планируете использовать секцию канала, отсортировав каналы в базе данных CalQlata Steel Sections, вы обнаружите, что размер вашей балки должен быть сечением «3×6», которое является наименьшим сечением балки со значением I выше 800000 мм², и найдите значение для « y ‘(расстояние от нейтральной оси балки до внешней части ее сечения), которое в данном случае составляет 38,1 мм.

Вы возвращаетесь в раздел «Балки», вводите правильное значение для I (863 264 мм²), а также вводите значение 38,1 мм для «d», чтобы установить максимальное напряжение в материале балки, которое в данном случае составляет 88 Н / мм².

Если это значение находится в пределах требований вашего запаса прочности, то ваш луч приемлем. Если нет, но вы должны работать с данным материалом, вам следует изменить (увеличить) сечение балки, тем самым уменьшив допустимый прогиб до тех пор, пока напряжение не станет приемлемым.

Калькулятор прогиба балки — Техническая помощь

Рис. 1. Диаграмма нагрузки на балку

Предполагается, что любая нагрузка в калькуляторе прочности балок одинаково распространяется через плоскость или сечение балки во всех направлениях, перпендикулярных (другими словами, под углом 90 ° к) к ее продольной оси.

Если нагрузка локализована в поперечном сечении балки (т. Е. Неравномерно распределена по ней), могут потребоваться дополнительные расчеты для определения локальных (сосредоточенных) реакций и напряжений (см. Калькуляторы CalQlata Plates and Sheets).

Напряжение изгиба

Изгибающие напряжения в балках применяются к балке на заданном расстоянии (d) от ее нейтральной оси. Эта входная переменная (‘d’) используется только в расчетах для напряжения (σx) и деформации (ex). Если вы оставите поле пустым или установите его на ноль, балки не будут вычислять напряжение или деформацию в указанном вами месте вдоль балки (рис. 1 ‘x’).Никакие другие результаты не будут затронуты.

Условия одновременной / множественной нагрузки

Если у вас есть балка с более чем одной приложенной нагрузкой, вы просто складываете результаты вместе в указанном месте.

Пример расчета прочности балки (рис. 2):

Детали балки:
L = 2000 мм
I = 1.2E + 08 мм⁴
E = 2.07E + 05 Н / мм²
y = 200 мм
Условия нагрузки 1:
wA & wB = 450 Н / мм
l = 0
Условия нагрузки 2:
F = 150000 Н
l = 700 мм
Расстояние по балке до выхода:
x = 1000

Шаг 1:
Введите данные для балки и условия нагрузки 1 (простая фиксированная / распределенная нагрузка), задав для параметра wA (/ L) и wB (/ L) значение 450 ‘, скопируйте список данных и вставьте в электронную таблицу.

Шаг 2:
Введите условие нагрузки 2 (простая фиксированная / точечная нагрузка), установив значение F на 150000, скопируйте список данных и вставьте в ту же электронную таблицу.

Шаг 3:
Добавьте результаты обоих калькуляторов, и вы получите условия в нужном месте.

Рис. 2. Процедура расчета нагрузки смеси

Ограничения

Эти расчеты действительны только в том случае, если материал по всей длине и толщине сечения подчиняется закону Гука.
Результаты остаются действительными для этого калькулятора, если прогиб таков, что на длину балки существенно не влияют условия нагрузки.
Калькулятор больших отклоняющих балок CalQlata (гибкие балки) следует использовать, если длина балки изменяется более чем на 5% в результате приложенной нагрузки.

Дополнительная литература

Дополнительную информацию по этому вопросу можно найти в справочных публикациях ^{(2, 3 и 4)}

ИНЖИНИРИНГ.com | Калькуляторы прогиба балки

Калькуляторы прогиба балки — сплошные прямоугольные балки, полые прямоугольные балки, сплошные круглые балки

Введите значение и нажмите «Рассчитать». Результат будет отображаться

Расчет прогиба для сплошных прямоугольных балок
Расчет прогиба для полых прямоугольных балок
Расчет прогиба для сплошных круглых балок
Расчет прогиба для круглых трубчатых балок

Расчет прогиба сплошных прямоугольных балок

фунтов стерлингов

Введите свои значения:

Длина:	Дюймы
Ширина:	Дюймы
Высота:	Дюймы
Сила:
Материал:


Результатов:
Прогиб:	Дюймы
Напряжение изгиба:	PSI

Расчет прогиба для полых прямоугольных балок

фунтов стерлингов

Введите свои значения:

Длина:	Дюймы
Ширина:	Дюймы
Высота:	Дюймы
Толщина стенки:	Дюймы
Сила:
Материал:


Результат:
Прогиб:	Дюймы
Напряжение изгиба:	PSI

Расчет прогиба сплошных круглых балок

фунтов стерлингов

Введите свои значения:

Длина:	Дюймы
Диаметр:	Дюймы
Сила:
Материал:


Результатов:
Прогиб:	Дюймы
Напряжение изгиба:	PSI

Расчет прогиба для круглых трубных балок

фунтов стерлингов

Введите свои значения:

Длина:	Дюймы
Диаметр:	Дюймы
Толщина стенки:	Дюймы
Сила:
Материал:


Результат:
Прогиб:	Дюймы
Напряжение изгиба:	PSI

Как рассчитать прочность на изгиб

Обновлено 28 января 2020 г.

Ли Джонсон

Проверено: Lana Bandoim, B.S.

Определение силы, которую объект может выдержать до разрушения, может пригодиться во многих ситуациях, особенно для инженеров. Это должно быть определено на основе экспериментальных результатов, которые, по сути, включают в себя воздействие на материал возрастающей силы до тех пор, пока он не сломается или не изгибается навсегда. Но выполнение реальных расчетов для определения прочности материала на изгиб может показаться действительно сложной задачей. К счастью, если у вас под рукой нужная информация, вы можете легко выполнить расчет.

Определение прочности на изгиб

Прочность на изгиб (или модуль разрыва ) — это величина силы, которую объект может выдержать без разрушения или постоянной деформации. Если это сложно понять, подумайте о деревянной доске, поддерживаемой с двух концов.

Если вы хотите узнать, насколько прочна древесина, один из способов ее проверки — это надавить все сильнее и сильнее на центр доски, пока она не сломается. Максимальное толкающее усилие, которое древесина может выдержать до разрушения, — это ее прочность на изгиб.Если бы другой кусок дерева был сильнее, он выдержал бы большую силу, прежде чем сломался бы.

Прочность на изгиб действительно говорит вам о максимальной величине напряжения, которое может выдержать материал (так что вы также можете видеть ссылки на «напряжение изгиба»), и она указывается как сила (в ньютонах или фунт-силах) на единицу площади (в метрах в квадрате или квадратном дюйме).

Испытания по трем или четырем точкам

Есть два метода испытания прочности на изгиб, но они очень похожи. Длинный прямоугольный образец материала опирается на торцы, поэтому посередине нет опоры, но концы крепкие.Затем к средней секции прикладывают нагрузку или силу до тех пор, пока материал не разорвется.

Для трехточечного испытания на прочность на изгиб к центру образца прикладывают постоянно увеличивающуюся нагрузку до тех пор, пока в материале не произойдет излом или остаточный изгиб. Машина для испытания на изгиб может прилагать увеличивающееся количество силы и точно записывать величину силы в точке разрушения.

Испытание на четырехточечный изгиб очень похоже, за исключением того, что нагрузка прикладывается одновременно в двух точках, опять же по направлению к центру образца.Легче всего рассчитать прочность на изгиб, когда одна нагрузка или сила прикладываются на одной трети расстояния между опорами, а вторая — на двух третях расстояния между ними. Таким образом, в этом примере к средней трети образца будут приложены силы с обеих сторон.

Расчет прочности на изгиб при трехточечном испытании

Для трехточечного испытания прочность на изгиб (с учетом символа σ ) можно рассчитать с помощью:

Сначала это может показаться пугающим, но если вы знаете, что каждый символ означает, что это довольно простое уравнение.

F означает максимальное приложенное усилие, L — длина образца, w — ширина образца и d — глубина образца. Итак, чтобы рассчитать прочность на изгиб ( σ ), умножьте силу на длину образца, а затем умножьте это на три. Затем умножьте глубину образца на себя (то есть возведите его в квадрат), умножьте результат на ширину образца, а затем умножьте его на два. Наконец, разделите первый результат на второй.

В единицах СИ длина, ширина и глубина будут измеряться в метрах, а сила — в ньютонах, с результатом в паскалях (Па) или ньютонах на квадратный метр. В британских единицах измерения длина, ширина и глубина будут измеряться в дюймах, а сила — в фунтах-силах, а результат — в фунтах на квадратный дюйм.

Расчет прочности на изгиб при четырехточечном испытании

При четырехточечном испытании используются те же символы, что и при расчете трехточечного испытания. Но если предположить, что две нагрузки или силы приложены так, что они разделяют образец на три части, это выглядит намного проще:

Обратите внимание, что это в точности то же самое, что и формула напряжения изгиба для трехточечных испытаний, но без коэффициента 3/2.Просто умножьте прилагаемую силу на длину, а затем разделите полученное значение на ширину материала, умноженную на его глубину в квадрате.

Прогнозирование прочности древесины на изгиб и изменения жесткости в поперечном сечении на основе местной ориентации древесных волокон

Результаты и обсуждение, представленные ниже, разделены на две части. В первом представлены и обсуждаются статистические результаты для измеренных и вычисленных свойств, определенных выше, которые представляют общий интерес для целей классификации прочности.Во второй части представлены и обсуждаются дополнительные результаты и наблюдения, касающиеся конкретной серии тестов, состоящей из 105 плат. Эти результаты указывают на потенциал дальнейшего развития метода.

Статистические зависимости общих свойств платы и новых IP от прочности на изгиб

В таблице 2 показаны средние значения и стандартные отклонения прочности на изгиб, локальной и глобальной MOE, соответственно, динамической продольной MOE, плотности платы и определенных новых IP. выше.Замечено, что новые кандидаты IP E _{б, не менее}, E _{б, мин, 80}, E _{b, мин, 80, w} и E _{a, мин} значительно ниже средних значений для E _метр, E _{м, г} и E _A1.Для самого низкого MOE, рассчитанного для сечения вдоль балки, E _{б, не менее}, среднее значение составляет всего 7,1 ГПа, то есть только 57% от среднего значения E _A1. Среднее значение E _{б, мин, 80} составляет 9,4 МПа, т.е. 76% от среднего значения E _A1.Это дает представление о том, насколько ниже жесткость на изгиб на локальном уровне по сравнению со средней жесткостью платы.

Таблица 2 Табл. 2 Средние значения и стандартные отклонения для различных свойств 105 плит Mittelwerte und Standardabweichungen verschiedener Eigenschaften der 105 Bretter
В таблице 3 показаны коэффициенты определения между теми же свойствами, что и в таблице 2. Особый интерес представляют коэффициенты определения между IP и прочностью на изгиб (выделены жирным шрифтом в таблице 3).Осевая динамическая жесткость E _A1 часто используется в качестве IP при коммерческой сортировке, и для оцениваемых здесь плит он дает коэффициент определения прочности на изгиб 0,59. IP E _{б, не менее} дает лучший результат, R ² = 0,64, но дополнительное улучшение было достигнуто за счет использования минимальной жесткости на изгиб на расстоянии 80 мм вместо использования самого низкого значения в отдельной секции балки.Для E _{б, мин, 80} коэффициент определения прочности на изгиб составил 0,68. Были предприняты попытки для более коротких и более длинных расстояний, т.е. с другими значениями δ в E . _{b, мин, δ, w}, но 80 мм дали самый высокий коэффициент определения. Учитывая, что внешние части плит, ближе к концам, чем 7 d , не могут быть подвергнуты максимальному изгибающему моменту при испытании в соответствии с EN 408, корреляция между IP и прочностью на изгиб была еще больше улучшена. E _{b, мин, 80, w} дает коэффициент детерминации 0,71. При практическом оценивании: E _{b, мин, 80, w} не следует использовать в качестве IP, поскольку части из разных плат могут быть соединены вместе пальцевым соединением, а слабая часть рядом с концом одной исходной сортированной платы может оказаться в критическом положении собранной платы, но она представлена здесь, чтобы проиллюстрировать возможности предлагаемого метода.На практике E _{б, мин, 80} — более подходящий IP. На рисунке 7 показаны диаграммы разброса, коэффициенты детерминации и уравнения для линий регрессии между E . _A1 и σ _метр и между E _{b, мин, 80, w} и σ _метр соответственно.
Таблица 3 Табл. 3 Коэффициенты определения R ² между различными свойствами 105 плит Bestimmtheitsmaße R² für die Beziehung zwischen verschiedenen Materialeigenschaften der 105 Bretter Рис. 7 Рис. 7
Диаграммы рассеяния, коэффициенты детерминации и уравнения для линий регрессии между ( слева ) E _A1 и σ _метр и ( правый ) E _{b, мин, 80, w} и σ _метр
Streudiagramme, Bestimmtheitsmaße und Gleichungen der Regressionsgeraden zwischen (ссылки) E _a1 und σ _m sowie (rechts) E _{b, min, 80, w} und σ _m
Дополнительные результаты и наблюдения
Для 105 плат исследовали часть каждой платы, включая наихудший дефект, т.е.е. узел или группа узлов, которые должны были вызвать разрушение, по возможности располагались в зоне максимального изгибающего момента, когда прочность на изгиб определялась в соответствии с EN 408. Если эта часть находилась так близко к концу, что ее нельзя было расположить в этой зоне. В зоне максимального изгибающего момента второй наихудший дефект и так далее. Для всех досок было задокументировано расположение опор и точечных нагрузок, и, таким образом, известно, какая часть каждой доски подвергалась максимальному изгибающему моменту.Кроме того, для каждой платы было задокументировано место инициализации сбоя, хотя в некоторых случаях было трудно точно определить это положение на сломанной плате.
Зная, как каждая плата была размещена в испытательной машине, и рассчитав профиль жесткости на изгиб для каждой отдельной платы, можно было создать модель конечных элементов (FE) для той части каждой платы, которая фактически подвергалась изгибу. и для моделирования нагружения четырехточечного изгиба.Используемая здесь модель FE состоит из ряда балочных элементов длиной примерно 2 см каждый. На основе перемещений, полученных при расчете КЭ, MOE, обозначенные здесь E . _{м, с} и E _{м, г, с}, соответственно, были рассчитаны по аналогии с E _метр и E _{м, г} получено из измеренных прогибов во время испытаний.В таблице 4 показаны коэффициенты определения между этими различными MOE, основанные на измерениях во время испытаний и на основе расчетов FE, соответственно, но представляющие одну и ту же древесину, то есть те же 18 d = 2610 мм частей досок при четырехточечном изгибе. . Коэффициенты определения между этими MOE и прочностью на изгиб также показаны в таблице 4. MOE на основе измеренных прогибов, E _метр и E _{м, г}, значительно лучше коррелируют с прочностью на изгиб ( R ² = 0.74 и 0,72 соответственно), чем то, что MOE на основе расчетных прогибов, E _{м, с} и E _{м, г, с}, сделать ( R ² = 0,61 для обоих случаев). Однако существует довольно сильная корреляция между MOE на основе измеренных и рассчитанных прогибов, коэффициенты детерминации равны 0,85 в обоих случаях между E . _метр и E _{м, с} и между E _{м, г} и E _{м, г, с}.
Таблица 4 Табл. 4 Коэффициенты детерминации, R ², между прочностью на изгиб и MOE на основе измерений и расчетов, соответственно
Поскольку оба MOE, основанные на измеренных и рассчитанных прогибах, представляют одни и те же физические части древесины, любые различия между E _метр и E _{м, с}, или между E _{м, г} и E _{м, г, с}, обнаруживает некоторую неточность при попытке вычислить истинный профиль жесткости на изгиб на основе спроецированных углов волокон, использованной схемы интегрирования и продольного динамического возбуждения.Предлагаемый подход кажется достаточно точным, чтобы дать очень хорошую корреляцию между предлагаемыми IP и прочностью на изгиб, но результаты, представленные в таблице 4, показывают, что существует значительный потенциал для дальнейшего улучшения корреляции. Если высокое разрешение профилей жесткости на изгиб (которое можно быстро рассчитать на основе результатов сканирования) может достигать точности измеренной жесткости на изгиб на ребре (т. Е. Измеренной на более или менее общем уровне во время четырехточечного изгиба), то это Вероятно, что коэффициент детерминации между одиночным IP и прочностью на изгиб может приблизиться или даже превысить R ² = 0.80. В какой степени существуют различия между E ? _метр и E _{м, с}, и между E _{м, г} и E _{м, г, с} зависят (1) от того факта, что используются спроецированные углы волокон на поверхности, а не от истинного трехмерного углового поля волокон внутри деревянного элемента, (2) от упрощающего предположения, что параметры древесного материала, относящиеся к системе lrt, постоянны. внутри деревянного элемента (3) при условии, что жесткость может быть определена достаточно точно с помощью модели балки, или при некоторых других условиях следует изучить в ходе дальнейших исследований.
Последнее замечание касается положения вдоль каждой балки, где фактически был инициирован отказ по отношению к тому месту, где он должен был произойти, то есть, где расчетная жесткость на изгиб была самой низкой по отношению к приложенному изгибающему моменту. В 70% досок расстояние между фактическим положением разрушения и прогнозируемым положением было менее 5 см, а для 78% досок расстояние было менее 10 см. Это указывает на высокую вероятность отказа в непосредственной близости от секции с самой низкой жесткостью на изгиб.Однако можно отметить, что многие доски имеют вторую слабую секцию и, возможно, даже третью, с расчетной жесткостью на изгиб, почти такой же низкой, как и самая слабая.
% PDF-1.5 % 885 0 объект > эндобдж xref 885 85 0000000016 00000 н. 0000003220 00000 н. 0000003370 00000 н. 0000003941 00000 н. 0000004078 00000 н. 0000004210 00000 н. 0000004349 00000 п. 0000004491 00000 н. 0000004518 00000 н. 0000005188 00000 п. 0000005398 00000 н. 0000005959 00000 н. 0000006156 00000 п. 0000006193 00000 п. 0000006768 00000 н. 0000006880 00000 н. 0000006994 00000 н. 0000007207 00000 н. 0000007603 00000 н. 0000008080 00000 н. 0000008107 00000 н. 0000008134 00000 п. 0000008630 00000 н. 0000009382 00000 п. 0000009894 00000 н. 0000010605 00000 п. 0000011298 00000 п. 0000012005 00000 п. 0000012138 00000 п. 0000012287 00000 п. 0000012314 00000 п. 0000012808 00000 п. 0000012835 00000 п. 0000013255 00000 п. 0000013946 00000 п. 0000014608 00000 п. 0000015271 00000 п. 0000015356 00000 п. 0000036914 00000 п. 0000037207 00000 п. 0000037606 00000 п. 0000037692 00000 п. 0000079126 00000 п. 0000079409 00000 п. 0000079979 00000 п. 0000080049 00000 п. 0000080119 00000 п. 0000080200 00000 н. 0000087193 00000 п.