Расчет на изгиб онлайн: Расчет балки на прогиб и прочность

Содержание

Формулы для расчетов на изгиб

Подборка формул для расчета балок и рам на изгиб и решения задач сопротивления материалов по расчету внутренних сил, напряжений, деформаций и перемещений при изгибе.

Обозначения:

σ — нормальные напряжения,
τ — касательные напряжения,
Q_y – внутренняя поперечная сила,
M_x – внутренний изгибающий момент,
I_x – осевой момент инерции сечения балки,
W_x – осевой момент сопротивления сечения,
A — площадь поперечного сечения,
[σ], [τ] – соответствующие допустимые напряжения,
E – модуль упругости I рода (модуль Юнга),
y — расстояние от оси x до рассматриваемой точки сечения балки.

Расчет внутренних поперечных сил и изгибающих моментов

Формула кривизны балки в заданном сечении

Расчет нормальных напряжений в произвольной точке сечения балки при изгибе

Условие прочности по нормальным напряжениям при изгибе (проверочный расчет)

Осевые моменты инерции I и сопротивления W

прямоугольного сечения

h – высота сечения,
b – ширина сечения балки.
круглого сечения балки

D — диаметр сечения

Касательные напряжения в произвольной точке сечения при изгибе определяются по формуле Журавского:

Здесь:

S_x^* — статический момент относительно оси x отсеченной части сечения

b — ширина сечения на уровне рассматриваемой точки

Другие видео

Условие прочности балки по касательным напряжениям

Дифференциальное уравнение линии изогнутой оси балки

Уравнения метода начальных параметров (МНП)

θ_z, y_z — соответственно угол наклона и прогиб сечения балки на расстоянии z от начала координат,
θ₀, y₀ — соответственно угол наклона и прогиб сечения балки в начале координат,
m, F, q — соответственно все изгибающие моменты, сосредоточенные силы и распределенные нагрузки приложенные к балке,

a, b — расстояние от начала координат до сечений где приложены моменты и силы соответственно,
c — расстояние от начала координат до начала распределенной нагрузки q.

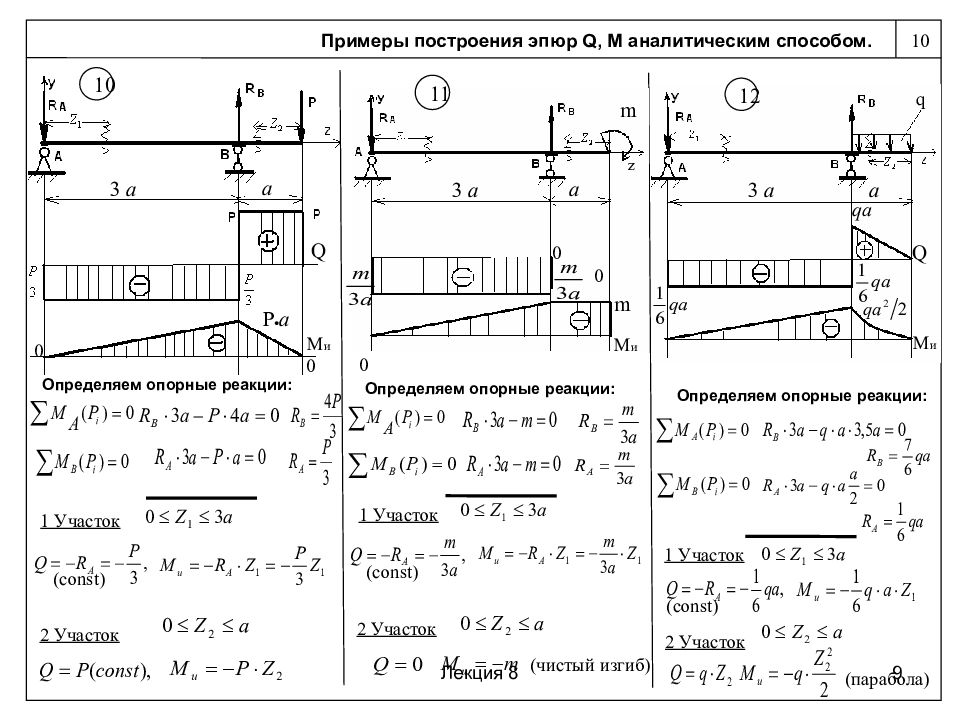
Пример расчета перемещений в балке методом начальных параметров >

Другие формулы >
Примеры решения задач >
Краткая теория >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.
Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

На нашем сайте можно бесплатно скачать:

— Рамки A4 для учебных работ

— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Сохранить или поделиться с друзьями

Заказать решение

Поиск формул и решений задач

Расчет прогиба пластины в Excel

Опубликовано 26 Мар 2016
Рубрика: Механика | 126 комментариев

/Файл с программой дополнен расчетами круглых пластин P. S. (27.03.2022)./

При выполнении расчетов стенок емкостей, стенок конструкций или различных покрытий возникает задача определения напряжений и прогибов. Хочется получить быстрый ответ на простые вопросы — …

…на сколько и как выгнется пластина под нагрузкой, и не разрушится ли она? Теория предлагает по заданной известной функции нагрузки найти функцию прогибов. Для этого нужно решить неоднородное бигармоническое дифференциальное уравнение четвертого порядка в частных производных. От одного прочтения предыдущего предложения, я думаю, многим читателям стало грустно и тоскливо. А если добавить, что для практической реализации одного из методов предстоит решить систему из 15-и уравнений и найти 15 неизвестных, то большинство на этом просто прекратят чтение и потеряют всякий интерес к теме, либо продолжат поиск программ, выполняющих автоматически подобные расчеты. Эти программы, выполняющие расчет прогиба пластин, чаще всего реализуют приближенные численные методы конечных элементов и конечных разностей и стоят приличных денег.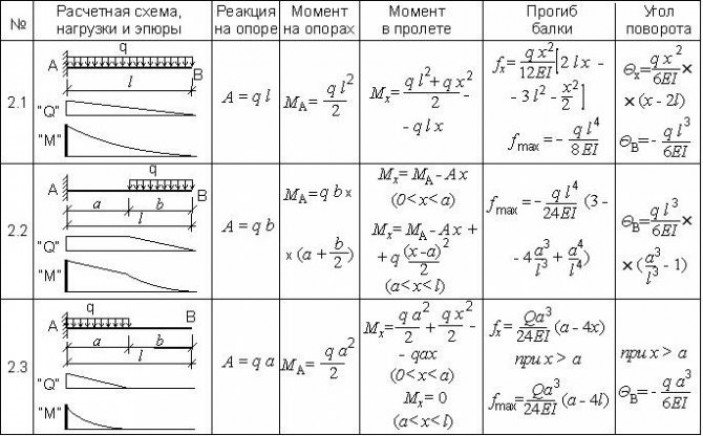

Но есть и другой путь… (Как известно, выходов всегда не меньше двух…) Эта дорога старая, заросшая лесом новых теорий, но не до конца забытая!

Этот путь является достаточно узким и индивидуальным для различных форм пластин, способов закрепления контуров и относительных величин прогибов. Для каждой расчетной схемы – свои таблицы коэффициентов к расчетным формулам! Расчет прогиба пластины по старым методикам прост – это несомненный плюс, но не универсален – это существенный минус.

Цель данной статьи – рассказать, как наши деды — инженеры прошлого века — решали такие практические вопросы, и показать простой пример модернизированного расчета в Excel задачи об изгибе пластины для одного из наиболее распространенных случаев в практике.

Из-за отсутствия каких-либо машин для выполнения рутинных сложных расчетов (кроме светлой головы, листка бумаги, карандаша, таблиц функций и логарифмической линейки ничего не было) ученые в начале и в середине 20-ого века стремились вооружить простого инженера короткими и понятными алгоритмами, «привязанными» к рассчитанным в НИИ номограммам и таблицам. Такой подход обеспечивал значительное упрощение и ускорение работы инженеров, хотя и не давал им полного понимания теории.

Расчет прогиба пластины изучается в общей теории оболочек, которая является сложным самостоятельным разделом механики, давно выделившимся из недр классического сопромата.

Теория тонких пластин распространяется на листы и плиты, у которых толщина h менее 20% от наименьшего габаритного размера в плане a.

Тонкие пластины делят на 3 класса в зависимости от величины максимального прогиба w:

жесткие — w<0,25h

гибкие — 0,25h<w<5h

абсолютно гибкие — w>5h

Попадание конкретной пластины в тот или иной класс, как видите, зависит от прогиба, а значит — от величины нагрузки. Важно отметить, что одна и та же пластина при разных нагрузках может быть отнесена к разным классам, и расчет её будет производиться по различным формулам.

Далее в примере рассматривается тонкая жесткая пластина.

Расчет в Excel прогиба пластины. Пример.

Прямоугольная пластина из изотропного материала (Сталь Ст3) жестко закреплена по всему контуру. В перпендикулярном направлении к плоскости пластины приложена равномерно распределенная по всей площади нагрузка.

Требуется вычислить наибольший прогиб пластины от действия нагрузки и найти максимальные возникающие в теле листа напряжения.

Исходные данные:

Первые три параметра являются справочными характеристиками свойств материала пластины.

1. Предел текучести для пластичных материалов или прочности для хрупких материалов [σ] в Н/мм² записываем

в ячейку D3: 245

Этот параметр не участвует в расчетах и нужен лишь для сравнения с полученными в результате расчета напряжениями. Правильнее вместо него использовать допускаемые напряжения материала с учетом всех запасов для конкретного случая применения.

2. Модуль упругости или модуль Юнга E в Н/мм² заносим

в D4: 210000

3. Коэффициент Пуассона μ вписываем

в D5: 0,28

В примечаниях к ячейкам D4 и D5 приведены значения модулей упругости и коэффициентов Пуассона для некоторых материалов.

4.,5.,6. Далее вводим в таблицу размеры пластины h, a и b в мм

в ячейку D6: 5,0

в D7: 500

в D8: 1000

В примечаниях к ячейкам D6, D7 и D8 записаны ограничения, которые должны соблюдаться. В случае их нарушения цифры окрашиваются инверсным белым цветом, а поле ячейки – красным, сообщая пользователю об ошибке ввода данных.

7. Значение распределенной равномерно по всей площади нагрузки q в Н/мм² вносим

в D9: 0,016

Ссылка на скачивание файла с программой: raschet-progiba-plastiny-NEW (xlsx 174KB).

Результаты расчета:

8. Цилиндрическую жесткость пластины D в Н*мм (аналог EI – линейной жесткости для стержней) вычисляем

в ячейке D11: D=(E*h³)/(12*(1- μ²)=2373589

9.,11. Безразмерные коэффициенты k₁ и k₂, зависящие от формы и размеров пластины, а также от способов закрепления контурных сторон, можно найти в таблицах старых справочников (Тимошенко С.П., Войновский-Кригер С. Пластины и оболочки; Вайнберг Д.В, Вайнберг Е.Д. Расчет пластин). Правда, k₂ зависит еще и от μ, а в таблицах приведены значения только для стали μ≈0,3 и бетона μ≈1/6, но, проанализировав ряд таблиц, можно увидеть, что эта зависимость не очень значительная…

Выполнив аппроксимацию в Excel табличных данных, получим аналитические выражения для расчетов коэффициентов

в ячейке D12: при 0,5<a/b<1

k₁=0,16747*(a/b)⁶-0,766*(a/b)⁵+1,4455*(a/b)⁴-1,4342*(a/b)³+0,78433*(a/b)²-0,22506*(a/b)+0,029239=0,0254

при 0<a/b<0,5

k₁=-0,00012*(a/b)+0,0026=0,0254

в D14: при 0,5<a/b<1

k₂=0,71922*(a/b)⁶-3,1489*(a/b)⁵+5,6353*(a/b)⁴-5,1372*(a/b)³+2,3658*(a/b)²-0,50294*(a/b)+0,12003=0,0829

при 0<a/b<0,5

k₁=-0,0008*(a/b)+0,0833=0,0829

Точность аппроксимации очень и очень высокая. Об этом можно судить как по абсолютным Δ_абс и относительным Δ_отн погрешностям, так и по величине достоверности R².

10. Максимальный прогиб пластины w в мм будет в рассматриваемой схеме в центре пластины в точке O; вычисляем его

в ячейке D13: w=k₁*q*a⁴/D=1,07

Расчет прогиба в MS Excel выполнен. Величина прогиба не превышает четверти толщины листа, следовательно применение использованных формул правомерно.

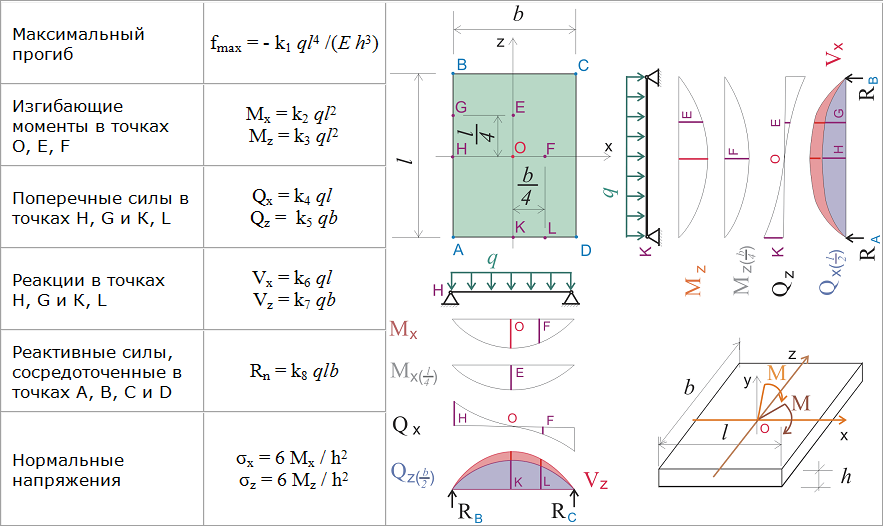
12. Наибольшие моменты на единицу длины сечения пластины M_max возникают в рассматриваемой схеме по серединам больших сторон контура в точках A и A’.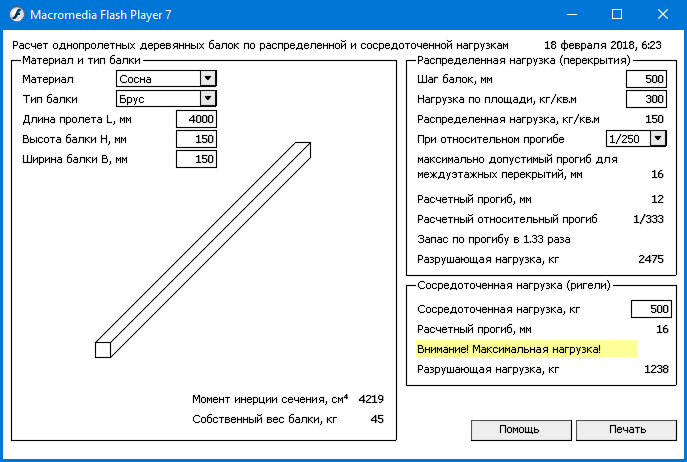 Вычисляем их в Н*мм/мм

в ячейке D15: M_max=k₂*q*a²=332

13. Наибольшие напряжения в пластине σ_max в точках действия максимального момента вычисляем в Н/мм²

в ячейке D16: σ_max=6* M_max/h²=80

Напряжения не превышают предела текучести. Деформации листа являются упругими, после снятия нагрузки пластина вернется в исходное плоское состояние.

Заключение.

По предложенной программе в Excel можно выполнять расчет прогиба тонкой жесткой прямоугольной пластины из любого изотропного материала – стекла, пластмассы, бетона, любого металла при жестком закреплении контура.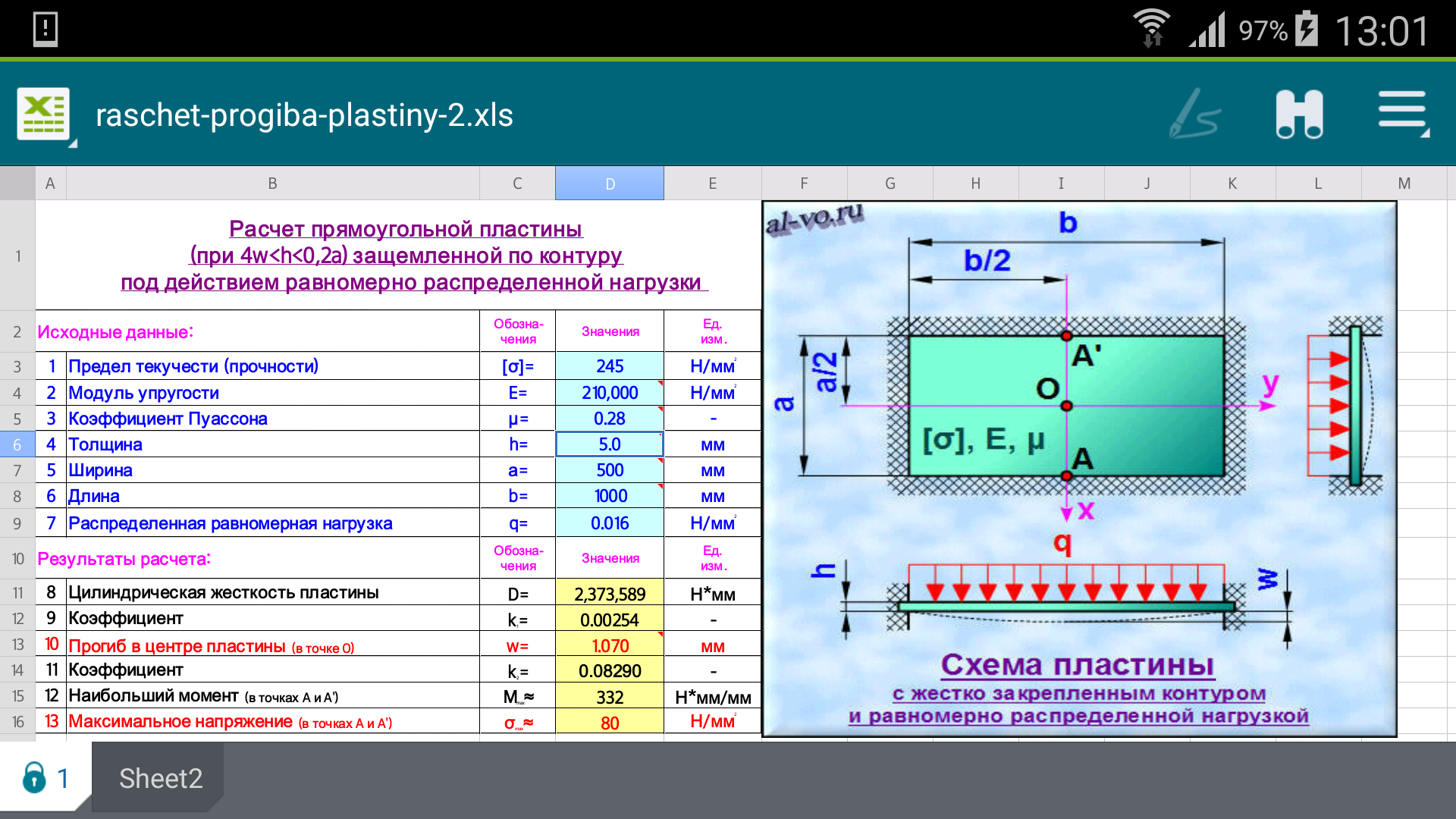

Прогиб вычисляется точно для любых материалов. Напряжения рассчитываются точно только для стали. Чем значительней коэффициент Пуассона материала отличается от коэффициента Пуассона стали, тем больше будет ошибка в определении действующих напряжений.

Так как способов закрепления контура пластины, видов форм пластины, сочетаний нагрузок — очень много, то задача расчета прогибов при рассмотренном подходе к решению распадается на сотни индивидуальных задач, в которых значения коэффициентов k₁ и k₂ также индивидуальны!

В продолжение темы «Расчет прогиба пластины» может быть в одной из будущих публикаций попробую рассмотреть более универсальный подход – метод конечных разностей с использованием MS Excel.

P. S. (27.03.2022)

В файл с расчетами добавлены вычисления максимальных прогибов и напряжений по двум схемам для круглых пластин.

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Калькулятор гибки листового металла

(бесплатно)

9 мая 2023 г. / Автор: Shane / 3 минуты чтения

Что такое гибка листового металла?
Калькулятор гибки листового металла
- Инструкции:
Часто задаваемые вопросы

Хотите погрузиться в мир гибки листового металла, но не знаете, с чего начать?

Посмотрите наш исчерпывающий справочник по листогибочным прессам и гибочным станкам. От различных типов гибочных машин и пресс-форм до важнейших параметров, которые вам необходимо знать для успешных расчетов гибки, наше руководство поможет вам.

С помощью нашего бесплатного онлайн-калькулятора гибки листового металла вы можете быстро и легко определить К-фактор, Y-фактор, допуск на изгиб, вычет изгиба, длину дуги и размер развернутой плоскости для вашего конкретного проекта.

Кроме того, наш удобный раздел часто задаваемых вопросов ответит на все ваши животрепещущие вопросы о расчетах гибки листового металла.

Являетесь ли вы опытным профессионалом или только начинаете, в нашем руководстве есть все, что вам нужно знать, чтобы получить идеальную трехмерную форму для вашего проекта из листового металла.

Так зачем ждать? Ознакомьтесь с нашим руководством сегодня и начните сгибаться как профессионал!

Что такое гибка листового металла?

Гибка листового металла представляет собой процесс преобразования плоского листового металла в трехмерную форму с использованием оборудования, работающего под давлением, и специальных пресс-форм.

Конкретный тип гибочного станка, используемых верхних и нижних форм и специальных форм зависит от материала, толщины, длины и ширины листа, а также желаемой формы и угла.

Для достижения желаемых результатов необходимы различные гибочные машины с разным тоннажем и давлением, формы с различной высотой, формой и V-образными отверстиями, а также формы с уникальными формами.

См. также:

Листогибочный пресс 101: все, что вам нужно знать
Плашки листогибочного пресса (инструменты): полное руководство 011
Калькулятор гибки листового металла
Наш бесплатный онлайн-калькулятор гибки листового металла позволяет быстро определить важнейшие параметры при расчетах гибки листового металла, такие как К-фактор, Y-фактор, припуск на изгиб, вычет изгиба, длина дуги и размер развернутой плоскости.
Связанное чтение:
- Как рассчитать допуск на изгиб, вычет изгиба и К-фактор?
- Калькулятор коэффициента К
- Калькулятор коэффициента Y
- Калькулятор допуска на изгиб
- Калькулятор уменьшения изгиба
Инструкции:
- Затем введите угол изгиба, чтобы получить длина дуги, допуск на изгиб и уменьшение изгиба .
- Затем введите длины сторон A и B, чтобы получить плоский размер листа.
Часто задаваемые вопросы
1. Что такое калькулятор гибки листового металла?
Калькулятор гибки листового металла — это инструмент, позволяющий быстро определить важные параметры при расчетах гибки листового металла.
2. Какие параметры можно рассчитать с помощью калькулятора гибки листового металла?
Калькулятор гибки листового металла может рассчитать такие параметры, как К-фактор, Y-фактор, допуск на изгиб, уменьшение изгиба, длина дуги и размер развернутой плоскости.
3. Что такое К-фактор в расчетах на изгиб листового металла?
К-фактор — это константа, представляющая положение нейтральной оси по отношению к толщине изгибаемого материала.
4. Что такое Y-фактор в расчетах на изгиб листового металла?
Коэффициент Y — это константа, представляющая величину пружинения, возникающего в процессе гибки.
5. Что такое припуск на изгиб в расчетах на изгиб листового металла?
Припуск на изгиб представляет собой длину нейтральной оси в изгибе и представляет собой количество материала, необходимого для размещения изгиба.
6. Что такое вычет изгиба при расчете изгиба листового металла?
Уменьшение сгиба — это количество материала, которое необходимо удалить с плоской заготовки, чтобы получить желаемый размер гнутой детали.
Профессиональная информация
Получить консультацию специалиста по металлообрабатывающим станкам
Позвольте нашим специалистам помочь вам выбрать правильный металлообрабатывающий станок для ваших нужд.
Запросить предложение
Калькулятор гибки листового металла для производства листового металла
Калькулятор гибки листа используется для расчета допусков на гибку листа, вычетов изгиба, исходного размера пластины для гибки листа
Калькулятор гибки листа очень полезен в производстве листового металла, процесса производство оборудования, производство тяжелого оборудования и производство листового металла.
Термины, используемые в калькуляторе гибки листового металла
Угол изгиба (θ)
Угол изгиба (θ) — это угол, измеряемый от линии горизонтальной плоскости до внешней стороны изгибаемой пластины. это обозначается θ. Вы можете сослаться на стандартное эталонное входное изображение, показанное в этом калькуляторе, для лучшего понимания этого значения угла. Вы можете использовать любые размерные единицы, такие как дюймы или мм, в соответствии с вашими предпочтениями. если вы используете дюймы в качестве единиц для ваших входных значений, пожалуйста, обратитесь к таблице десятичных дробей, чтобы ввести правильные входные значения.
Радиус изгиба (R)
Радиус изгиба (R) — это внутренний радиус, при котором происходит изгиб пластины. радиус изгиба также является важным параметром, слишком малый радиус изгиба приводит к развитию трещины на листе, поэтому выбор радиуса изгиба также требует внимания, обычно он равен толщине для листа малой толщины. обычно это зависит от конфигурации изгиба. Вы можете сослаться на стандартное эталонное входное изображение, показанное в этом калькуляторе, для лучшего понимания этого значения угла. Вы можете использовать любые размерные единицы, такие как дюймы или мм, в соответствии с вашими предпочтениями. если вы используете дюймы в качестве единиц для ваших входных значений, пожалуйста, обратитесь к таблице десятичных дробей, чтобы ввести правильные входные значения.
Длина пластины (L)
Длина пластины (L) — это внешняя длина гибочной пластины. Он обозначается L1 и L2 для длины левой и правой пластин соответственно. Вы можете обратиться к стандартному справочному входному изображению, показанному в этом калькуляторе, для лучшего понимания этого значения угла. Вы можете использовать любые единицы измерения, такие как дюймы или мм, в соответствии с вашими предпочтениями. . если вы используете дюймы в качестве единиц для ваших входных значений, пожалуйста, обратитесь к таблице десятичных дробей, чтобы ввести правильные входные значения.
Коэффициент К материала (K)
Значения коэффициента К материала зависят от типа материалов и толщины изгибаемого материала. Вы можете ввести коэффициент k материала, известный для вашего материала, или вы также можете обратиться к таблице коэффициента k материала, щелкнув ссылку диаграммы коэффициента k материала. В норме он находится в диапазоне от 0,33 до 0,55. для большинства приложений используется 0,55.
Толщина листа (T)
Толщина листа (T) — это толщина изгибаемого материала. это обозначено буквой T. Вы можете обратиться к стандартному справочному входному изображению, показанному в этом калькуляторе, для лучшего понимания этого значения угла. Вы можете использовать любые единицы измерения, такие как дюймы или мм, в соответствии с вашими предпочтениями. если вы используете дюймы в качестве единиц для ваших входных значений, пожалуйста, обратитесь к таблице десятичных дробей, чтобы ввести правильные входные значения.
Как использовать этот калькулятор гибки листа
1. Сначала перейдите к калькулятору гибки листа
2. Вы должны обратиться к стандартному входному изображению форм гибки листа и составить список размеров, необходимых в этом калькуляторе, и держать эти размеры под рукой.
3. Выберите входные размеры Stanarad Units на панели выбора единиц измерения. если вы используете дюймы в качестве размеров, пожалуйста, обратитесь к примечанию ниже выбора ввода, чтобы ознакомиться с таблицей выбора десятичного коэффициента.
4. Введите все необходимые размеры в данные поля ввода в соответствии с выбранной вами единицей измерения. Все размеры необходимо заполнить, прежде чем двигаться дальше.
5. для материала k-factor вы можете просмотреть диаграмму, щелкнув ссылку Material k-factor Chart. после обращения к этой диаграмме введите значение k-фактора корректирующего материала в поле ввода.
6. после заполнения всех данных поля ввода нажмите кнопку расчета, чтобы сгенерировать вывод этого калькулятора гибки листа.
7. Если вы оставили какое-либо поле ввода пустым, оно покажет вам уведомление об ошибке, поэтому, если вы получаете это уведомление, проверьте все свои пустые поля и введите правильные данные для получения результатов.
8. Перейдите ниже, чтобы вычислить кнопку, чтобы увидеть сгенерированные выходные данные этого калькулятора.
9. Обратитесь к выходному изображению, чтобы понять значения размеров маркировки, чтобы точно отметить линию изгиба.
, если вы хотите узнать о методе маркировки схемы изготовления соединений трубных отводов, нажмите здесь, чтобы загрузить нашу электронную книгу «Мастер разработки схемы изготовления». В этой книге все как геометрические, так и численные методы изготовления компоновок всех типов соединений патрубков.
Зачем использовать этот Калькулятор гибки листа
1. Калькулятор гибки листа полезен для расчета допусков на изгиб, вычетов при изгибе и требуемого размера листа для этих гибочных пластин
2. Калькулятор гибки листов обеспечивает полное решение для расчетов гибки листов.
3. Вы можете сэкономить на стоимости материалов с помощью этого калькулятора.
4. Вы можете сэкономить время на процессе компоновки изготовления.
5. Простой и быстрый способ расчета изгиба.
Область применения калькулятора гибки листа
Калькулятор гибки листа полезен для производства листового металла, производства сосудов под давлением, производства резервуаров для хранения, производства воздуховодов, производства изоляции, производства технологического оборудования, производства тяжелого оборудования или любого другого аналогичный Industry
Нажмите здесь, чтобы загрузить приложение для Android-устройства.