Расчет балки прогиб: Расчет балки на прогиб и прочность

Расчет балки на прогиб — онлайн калькулятор

Онлайн калькулятор по определению прогиба балки.
Для расчета вам необходимо:
1. Выбрать форму поперечного сечения
2. Выбрать материал (при использовании металлических балок — можно использовать сортамент)
3. Выбрать необходимую расчетную схему
4. Выбрать вид нагрузки (распределенная по длине балки либо сосредоточенная)
5. Указать геометрические размеры, указанные на картинках
6. Задать нагрузку (нагрузку можно рассчитать онлайн здесь)

Из возможных поперечных сечений в данном онлайн калькуляторе выбраны само часто встречающиеся сечения: круг, труба, двутавр, швеллер, уголок, прямоугольник, квадрат и профильная труба.
В расчет входят такие материалы как дерево, сталь, железобетон, алюминий, медь и стекло.
Также есть возможность выбора расчетной схемы: шарнир-шарнир, заделка-шарнир, заделка-заделка и заделка-свободный конец.
После того, как прогиб балки рассчитается – появится кнопка Подробнее, нажав на которую, можно узнать площадь сечения рассчитываемого элемента, его массу, распределенную нагрузку от собственного веса и момент инерции заданного сечения).
Зная значение длины пролета балки по СП 20.13330.2016 «Нагрузки и воздействия» для таких конструкций как балка, ферма, ригель, прогон, плита, настил покрытий и перекрытий, рассчитывается предельный прогиб, который можно сравнить с получившимся прогибом и принять решение о сечении вашей конструкции (для уменьшения прогиба в 1-ую очередь надо увеличивать высоту сечения).

При расчете балки программа уже учитывает собственный вес.

Помимо того, что Вы рассчитаете балку на прогиб, нужно ее проверить и на прочность здесь .

Если данный калькулятор оказался Вам полезен – не забывайте делиться им с друзьями и коллегами ссылкой в соц.сети, а также посмотреть другие строительные калькуляторы онлайн, они простые, но здорово облегчают жизнь строителям и тем, кто решил сам строить свой дом с нуля.

Последние изменения:
— Добавлен расчет предельного прогиба балки
— Добавлена возможность загружения балки сосредоточенной силой
— Исправлены графические замечания с расположением швеллера
— Добавлен расчет таврого сечения
— Исправлено положение прямоугольного сечения
— Добавлена возможность поворота швеллера
— Добавлена возможность ввода своих значений модуля упругости и плотности материала
— Исправлено отображение толщины стенки и полки швеллера

Расчет прогиба балки на двух опорах

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

• Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
• Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
• Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

1. Имеет прямоугольное сечение S=b*h, длина опирающейся части составляет L;
2. Линейка нагружена силой Q, проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ, с прогибом относительно начального горизонтального положения, равным f;
3. Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ, где Е – справочная величина, R— усилие, Δ— величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е).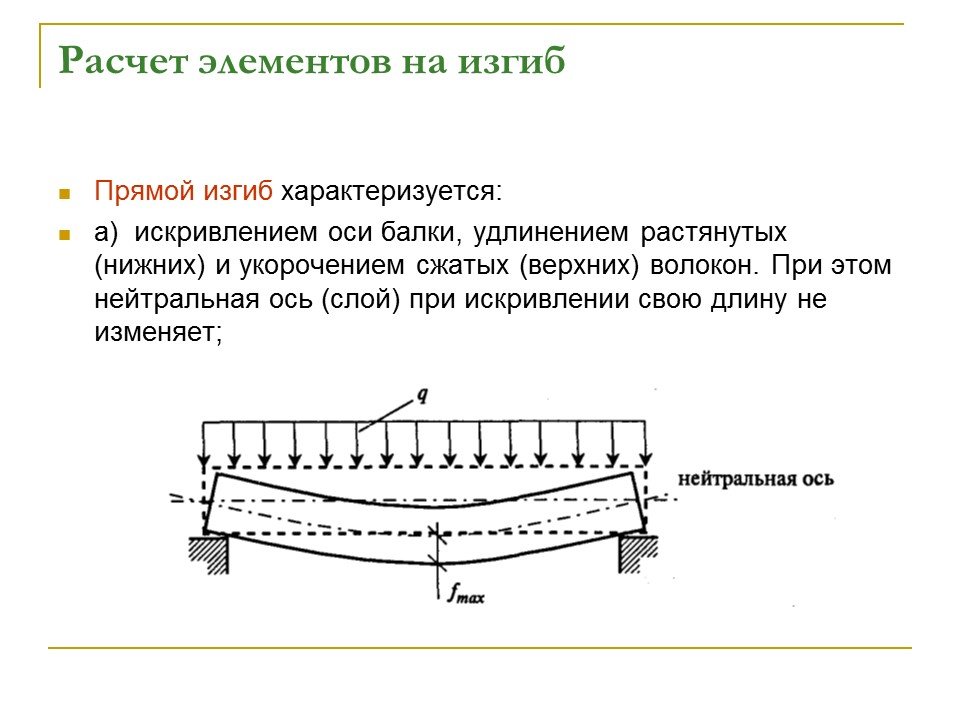 Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е).

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е).

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8, соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е). Величину b·h²/6 называют моментом инерции и обозначают W. В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L

2/8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h³/12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.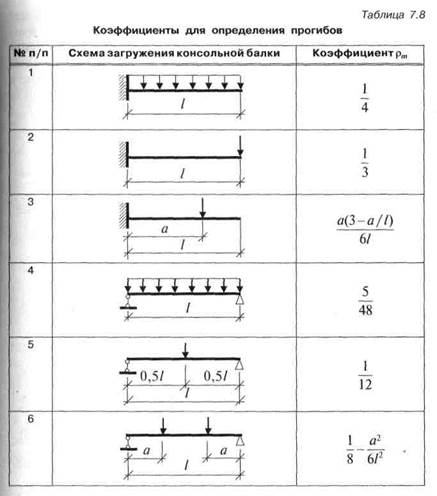

Совет! В вопросе расчета предельного состояния балки по величине прогиба неоценимую услугу оказывают требования СНиПа. Устанавливая предел прогиба в относительной величине, например, 1/250, строительные нормы существенно облегчают определение аварийного состояния балки или плиты.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

• Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
• По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
• По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

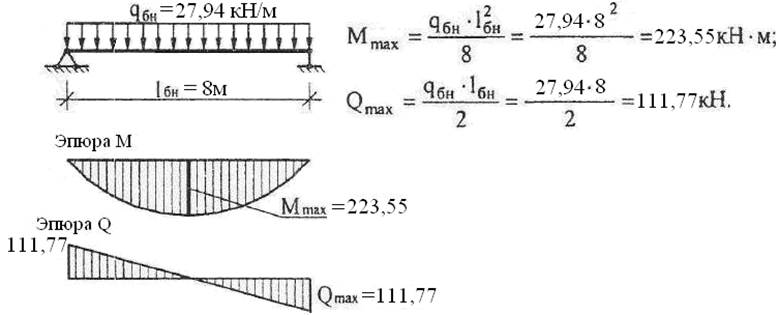
Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L²/(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ  прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Совет! Используйте в своих расчетах существующие ведомственные сборники различных проектных организаций, в которых в сжатом виде сведены все необходимые формулы для определения и расчета предельного нагруженного состояния.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Что еще почитать по теме?

Автор статьи:

Сергей Новожилов — эксперт по кровельным материалам с 9-летним опытом практической работы в области инженерных решений в строительстве.

Понравилась статья? Поделись с друзьями в социальных сетях:

Facebook

Twitter

Вконтакте

Одноклассники

Google+

Расчет балки на изгиб | Блог Александра Воробьева

Опубликовано 28 Апр 2013
Рубрика: Механика | 94 комментария

Расчет балки на изгиб «вручную», по-дедовски, позволяет познать один из важнейших, красивейших, четко математически выверенных алгоритмов науки сопротивление материалов. Использование многочисленных программ типа «ввел исходные данные…

…– получи ответ» позволяет современному инженеру сегодня работать гораздо быстрее, чем его предшественникам сто, пятьдесят и даже двадцать лет назад. Однако при таком современном подходе инженер вынужден полностью доверять авторам программы и со временем перестает «ощущать физический смысл» расчетов. Но авторы программы – это люди, а людям свойственно ошибаться. Если бы это было не так, то не было бы многочисленных патчей, релизов, «заплаток» практически к любому программному обеспечению. Поэтому, мне кажется, любой инженер должен уметь иногда «вручную» проверить результаты расчетов.

Справка (шпаргалка, памятка) для расчётов балок на изгиб представлена ниже на рисунке.

Давайте на простом житейском примере попробуем ей воспользоваться. Допустим, я решил сделать в квартире турник. Определено место – коридор шириной один метр двадцать сантиметров. На противоположных стенах на необходимой высоте напротив друг друга надежно закрепляю кронштейны, к которым будет крепиться балка-перекладина – пруток из стали Ст3 с наружным диаметром тридцать два миллиметра. Выдержит  ли эта балка мой вес плюс дополнительные динамические нагрузки, которые возникнут при выполнении упражнений?

Чертим схему для расчета балки на изгиб. 2

По прочности на изгиб расчет показал трехкратный запас прочности – турник можно смело делать из имеющегося прутка диаметром тридцать два миллиметра и длиной тысяча двести миллиметров.

Таким образом, вы теперь легко можете произвести расчет балки на изгиб «вручную» и сравнить с результатами, полученными при расчете по любой из многочисленных программ, представленных в Сети.

Прошу УВАЖАЮЩИХ труд автора ПОДПИСАТЬСЯ на анонсы статей.

Другие статьи автора блога

На главную

Статьи с близкой тематикой

Отзывы

Расчет балки на прочность: онлайн-калькуляторы, пример, последовательность действий

Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение.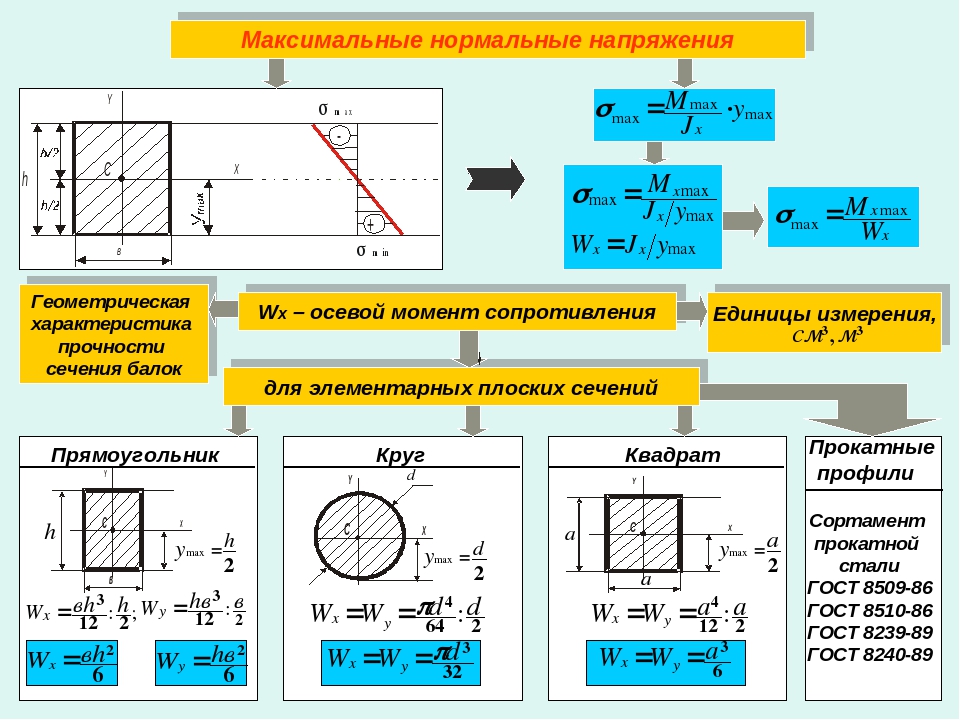 В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.

Как рассчитывать балки на прочность

Расчет балки на прогиб, калькулятор для которого можно найти в интернете, можно произвести следующими методами:

• Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
• Подобрать сечение;
• Проверочный перерасчет по максимальным значениям напряжения.

Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.

Последовательность действий

Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:

1. Заделка — шарнир;
2. Заделка — заделка;
3. Шарнир — шарнир;
4. Заделка — свободный конец.

Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.

Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.

Сравнение полученных напряжений с напряжением материалов

Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.

Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности.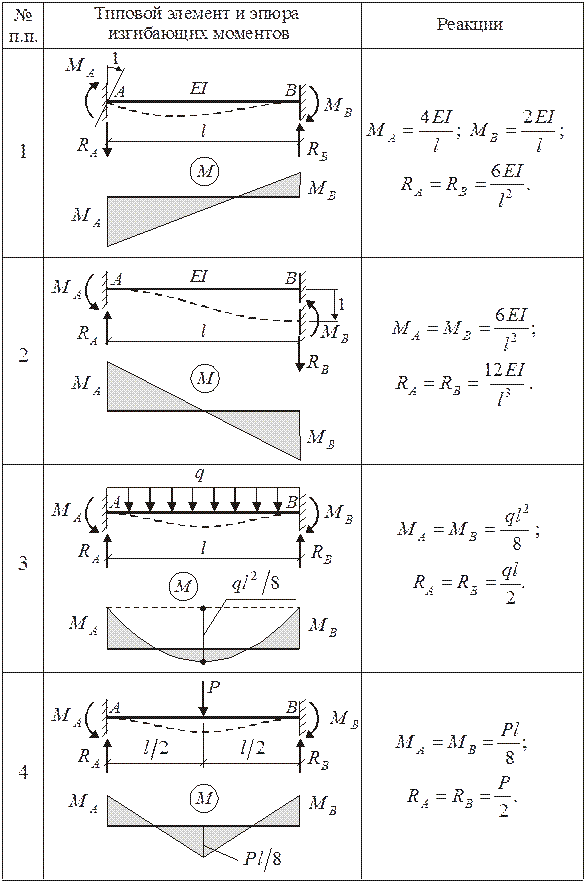 Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.

Пример расчета

Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:

• Выбираем расчетную схему, в этом случае заделка — свободный конец;
• Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
• Находим по таблице сортаментов для данного двутавра момент сопротивления;
• Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0. 0000397 = 45,34 Мпа;
• Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.

Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.

Онлайн-калькуляторы

Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.

Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.

Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения. Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.

В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.

Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза. Удачных расчетов на прочность!

Расчет стальной балки на прогиб

При расчете стальных балок по II-й ГПС (по прогибам) необходимо создавать раскрепления для прогибов:

Информация из справки LIRA SAPR (Справка\Пояснения Сталь\Проверки прогибов):

Проверка прогиба осуществляется сопоставлением реально определенного относительного прогиба (L/f) с максимально возможным для данного конструктивного элемента прогибом.

В данной версии проверка выполняется только для балок на основании состава загружений во всех сочетаниях. Учитываются коэффициенты надежности по нагрузке (заданные при формировании РСУ в среде ПК ЛИРА-САПР) и коэффициенты сочетания.

Перемещения, вызванные загружениями с долей длительности 0, в данном расчете не используются.

Прогибы находятся для каждого сечения на основании распределения MY1, MZ1, QY1, QZ1 по длине элемента. Соответственно, увеличение количества расчетных сечений способствует более точному определению прогибов (особенно, если воздействуют сосредоточенные силовые факторы).

В режиме локального расчета элемента (см. справочную систему СТК-САПР) имеется возможность расчета прогибов по огибающим эпюрам изгибающего момента в запас. Это может потребоваться, когда редактируются расчетные сочетания усилий (или нагрузок) и теряется связь с результатами расчета на ПК ЛИРА-САПР основной схемы.

Важно: Предусмотрена возможность определять не чистые перемещения (относительно локальных осей Y и Z в недеформированной схеме), а прогиб относительно двух выбранных условно неподвижных точек – точек раскрепления (в случае консоли, например, относительно одной точки).

Схема к определению прогибов балки с раскреплениями и без раскреплений

На приведенном фрагменте показан механизм определения прогибов (они обозначены как di и dk) в конструктивном элементе с наложенными раскреплениями на элементы.

Если раскрепления не наложены, то прогиб принимается равным полному расстоянию до оси X.

Важно: Если балка (ригель) разбита по длине промежуточными узлами, то для нее необходимо создать конструктивный элемент и раскрепления для проверки прогибов создавать как для конструктивного элемента (т.е. для балки как единого целого). В расчете стальных конструкций коэффициент расчетной длины (и для балок, и для колонн, и для ферм) применяется к длине конечного элемента (КЭ), если не задан конструктивный элемент (КоЭ). Если задан КоЭ, то коэффициент расчетной длины применяется к полной длине КоЭ.

Пример расчета однопролетной балки

Расчётная модель рамы с цельным ригелем и разбитым на отдельные элементы

Согласно нормативной документации прогиб определяется от действия нормативных нагрузок. Поскольку в LIRA SAPR все нагрузки прикладываются к узлам и элементам их расчётными значениями, при определении прогибов программа определяет нормативное значение нагрузок путём деления их на коэффициент надёжности.

Посмотреть какие приняты коэффициенты надёжности, а также ввести их вручную, если это необходимо, можно в окне параметров расчёта.

Окно параметров расчёта, вызываемое из окна задания параметров для стальных конструкций

Подробнее о корректировке коэффициентов надёжности для расчета прогибов вручную читайте в статье «Коэффициенты к временным нагрузкам при проверке прогиба»

Мозаика результатов проверки назначенных сечений по 2 предельному состоянию

Предельно допустимый L/200=6000/200=30мм

Без задания раскреплений (по абсолютному перемещению узлов балки):
((39,8мм/ к-т надежности по нагрузке)/ 30мм))*100%=((39,8/1,1)/30)*100%=120,6%

С заданием раскреплений (по относительному перемещению узлов балки за вычетом перемещений опорных узлов):
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Ручной ввод расчётной длины балки для расчёта прогибов

В диалоговом окне задания характеристик расчёта стальной балки присутствует группа параметров Расчёт по прогибу.

Информация из справки ЛИРА САПР:
Расчет по прогибу – данные для расчета прогиба. Длина пролета авто – вычисляется по положению раскреплений. Длина пролета точно – длина пролета при расчете приравнивается этому числу.

Рассмотрим раму из предыдущего примера, только теперь раскрепления для прогибов назначим для всех конструкций, а расчётные длины будем для первого случая задавать автоматическим способом, а для второго ручным.

Расчётная модель с информацией о назначенных расчётных длинах балок

Результаты расчётов прогибов балок

Предельно допустимый прогиб при длине 6 м L/200=6000/200=30мм

Предельно допустимый прогиб при длине 4 м L/200=4000/200=20мм

Проценты использования по предельному прогибу

Длина балки 6 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/30)*100%=92,9%

Длина балки 4 м:
((39,8мм-9,14)/ к-т надежности по нагрузке)/30мм))*100%=(((39,8-9,14)/1,1)/20)*100%=139,4%

Расчёт прогибов стрельчатой арки

Пример — рама переменного сечения (РПС) пролётом 18 м. Соединение полурам в коньке — шарнирное, опирание полурам на фундамент — шарнирное.

Расчётная модель рамы

При этом в параметрах «Дополнительные характеристики» необходимо указать вручную пролет, с которым программа будет сравнивать прогиб (автоматическое определение пролета возможно только для линейных балок, где все конечные элементы (КЭ) конструктивного элемента (КоЭ) лежат на одной оси):

Эпюра перемещений fz ригеля одной полурамы (вдоль местной оси Z1 стержня)

Мозаика перемещений узлов по Z и «Раскрепления для прогибов» (раскреплён только ригель №4)

Результаты определения прогибов в СТК-САПР:

Результаты определения прогибов ригелей №2 и №4

Предельно допустимый L/200=17664/200=88.32 мм

Без задания раскреплений (по абсолютному значению на эпюре прогибов fz):
96.7/17644=1/182 — совпадает с результатом расчёта элемента №2

С заданием раскреплений (по относительному значению на эпюре прогибов fz):
(96.7-(-6.46))/17644=1/171 — совпадает с результатом расчёта элемента №4

Без задания раскреплений (по абсолютному значению перемещений узлов):
99.8/17644=1/177 — не совпадает ни с чем

Вывод: Расчёт на прогибы выполняется в местной системе координат стержня. Прогиб стрельчатых и цилиндрических арок, а также любых криволинейных конструкций, нужно определять по перемещениям узлов в глобальной системе координат и вручную сравнивать с предельно допустимыми значениями.

Расчёт прогибов цилиндрической арки

Пример – цилиндрическая арка пролётом 18 м, стрелой подъёма f = 9 м. Соединение всех элементов между собой — жёсткое, опирание на фундамент — шарнирное.

Нагрузки на арку приложены их расчётными значениями. Значения нагрузок для определения прогибов принимаются согласно СП 20.13330.2016 Нагрузки и воздействия, таблица Д.1 Приложения Д. В данном примере арка является конструкцией покрытия, прогиб которой должен определяться от постоянных и длительных нагрузок (п.2 табл. Д.1). Для визуализации перемещений от нормативных значений нагрузок, необходимо создать особое РСН с нормативными длительными значениями нагрузок. Нагрузки в данном РСН нужно поделить на коэффициент надёжности, с учётом длительности. На конструкцию действуют два загружения:

Загружение 1 — постоянное, коэффициент надёжности 1.1;
Загружение 2 — кратковременное, коэффициент надёжности 1.2, доля длительности 0.35;

Вычислим коэффициенты для перехода к нормативным значениям

Загружение 1 Kn=1/1.1=0.91;
Загружение 2 Kn=1/1.2*0.35=0.292

Таблица РСН с сочетаниями расчётных и нормативных значений нагрузок с учётом длительности.

Мозаика перемещений узлов цилиндрической арки от РСН2

Предельно допустимый прогиб L/200=18000/200=90 мм

Фактический прогиб (по абсолютному значению перемещений узлов): 32.2/18000=1/559 – меньше предельно допустимого значения.

Примечание: если подобная конструкция стоит на своих опорах, то перемещения опорных точек (для получения относительных перемещений) удобно получить через «Мозаику относительных перемещений», указав реперный узел.

Мозаика перемещений узлов в глобальной СК (абсолютных)

Мозаика перемещений узлов в глобальной СК относительно реперного узла

Балки под сосредоточенной нагрузкой | Онлайн калькулятор

В данном разделе можно выполнить онлайн расчеты статически определимых балок в условиях прямого поперечного изгиба под действием сосредоточенной нагрузки. Расчеты определяют прогиб, угол поворота и изгибающий момент в произвольно заданной точке балки при различных граничных условиях. Определив наибольший изгибающий момент и соответствующее опасное сечение балки легко подобрать его размеры исходя из допускаемых напряжений в сечении.

Исходные данные:

L — длина балки, в миллиметрах;

a — координата точки приложения сосредоточенной нагрузки, в миллиметрах;

X — координата точки нахождения изгибающего момента, угла поворота и прогиба балки, в миллиметрах;

F — нагрузка, в ньютонах;

I_x — момент инерции сечения относительно оси, перпендикулярной действию нагрузки, в метрах ⁴;

Е — модуль упругости материала балки, в паскалях.

Расчет балки # 1.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке консольно закрепленной балки под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 — реакция опоры в крайней левой точке;

M_L = 0 — изгибающий момент в крайней левой точке;

θ_R = 0 — угол поворота в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

Расчет балки # 2.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и скользящей опорой под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 — реакция опоры в крайней левой точке;

θ_L = 0 — угол поворота в крайней левой точке;

θ_R = 0 — угол поворота в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

Расчет балки # 3.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленным концом и шарнирной опорой под действием сосредоточенной нагрузки.

Граничные условия:

М_L = 0 — изгибающий момент в крайней левой точке;

Y_L = 0 — прогиб балки в крайней левой точке;

θ_R = 0 — угол поворота в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

Расчет балки # 4.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c защемленными концами под действием сосредоточенной нагрузки.

Граничные условия:

θ_L = 0 — угол поворота в крайней левой точке;

Y_L = 0 — прогиб балки в крайней левой точке;

θ_R = 0 — угол поворота в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

Расчет балки # 5.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирными опорами под действием сосредоточенной нагрузки.

Граничные условия:

М_L = 0 — изгибающий момент в крайней левой точке;

Y_L = 0 — прогиб балки в крайней левой точке;

М_R = 0 — изгибающий момент в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

Расчет балки # 6.1

Расчет изгибающего момента, угла поворота и прогиба в произвольно заданной точке балки c шарнирной и скользящей опорами под действием сосредоточенной нагрузки.

Граничные условия:

R_L = 0 — реакция опоры в крайней левой точке;

θ_L = 0 — угол поворота балки в крайней левой точке;

М_R = 0 — изгибающий момент в крайней правой точке;

Y_R = 0 — прогиб балки в крайней правой точке.

©ООО»Кайтек», 2020. Любое использование либо копирование материалов или подборки материалов сайта, может осуществляться лишь с разрешения автора (правообладателя) и только при наличии ссылки на сайт www.caetec.ru

несущая способность, на двух опорах, пример

В современном индивидуальном строительстве деревянные балки используются почти в каждом проекте. Найти постройку, в которой не используются деревянные перекрытия, практически невозможно. Деревянные балки применяются и для устройства полов, и в качестве несущих элементов, как опоры для межэтажных и чердачных перекрытий.

Формула расчета прогиба балки.

Известно, что деревянные балки, как и любые другие, могут прогибаться под воздействием различных нагрузок. Эта величина – стрелка прогиба – зависит от материала, характера нагрузки и геометрических характеристик конструкции. Небольшой прогиб вполне допустим. Когда мы ходим, например, по деревянному настилу, то чувствуем, как пол слегка пружинит, однако если такие деформации незначительны, то нас это мало беспокоит.

Насколько можно допустить прогиб, определяется двумя факторами:

1. Прогиб не должен превышать расчетных допустимых значений.
2. Прогиб не должен мешать эксплуатации здания.

Чтобы узнать, насколько будут деформироваться деревянные элементы в конкретном случае, нужно произвести расчеты на прочность и жесткость. Подробные и детальные расчеты такого рода – это работа инженеров-строителей, однако, имея навык математических вычислений и зная несколько формул из курса сопротивления материалов, вполне можно самостоятельно рассчитать деревянную балку.

Вспомогательная таблица для расчета количества балок.

Любая постройка должна быть прочной. Именно поэтому балки перекрытия проверяют в первую очередь на прочность, чтобы конструкция могла выдерживать все необходимые нагрузки, не разрушаясь. Кроме прочности конструкция должна обладать жесткостью и устойчивостью. Величина прогиба является элементом расчета на жесткость.

Прочность и жесткость неразрывно связаны между собой. Вначале делают расчеты на прочность, а затем, используя полученные результаты, можно сделать расчет прогиба.

Чтобы правильно спроектировать собственный загородный дом, необязательно знать полный курс сопротивления материалов. Но углубляться в слишком подробные вычисления не стоит, как и просчитывать различные варианты конструкций.

Чтобы не ошибиться, лучше воспользоваться укрупненными расчетами, применяя простые схемы, а высчитывая нагрузки на несущие элементы, всегда делать небольшой запас в большую сторону.

Алгоритм вычисления прогиба

Рассмотрим упрощенную схему расчета, опуская некоторые специальные термины, и формулы для расчета двух основных случаев нагружения, принятых в строительстве.

Нужно выполнить следующие действия:

1. Составить расчетную схему и определить геометрические характеристики балки.
2. Определить максимальную нагрузку на этот несущий элемент.
3. При необходимости проверить брус на прочность по изгибающему моменту.
4. Вычислить максимальный прогиб.

Расчетная схема балки и момент инерции

Расчетную схему сделать довольно просто. Нужно знать размеры и форму поперечного сечения элемента конструкции, способ опирания, а также пролет, то есть расстояние между опорами.4.

Здесь нужно обратить внимание на то, что момент инерции прямоугольного сечения зависит от того, как оно сориентировано в пространстве. Если брус положить широкой стороной на опоры, то момент инерции будет значительно меньше, а прогиб – больше. Этот эффект каждый может прочувствовать на практике. Все знают, что доска, положенная обычным способом, прогибается гораздо сильнее, чем та же доска, положенная на ребро. Это свойство очень хорошо отражается в самой формуле для вычисления момента инерции.

Определение максимальной нагрузки

Для определения максимальной нагрузки на балку нужно сложить все ее составляющие: вес самого бруса, вес перекрытия, вес обстановки вместе с находящимися там людьми, вес перегородок. Все это нужно сделать в пересчете на 1 пог.м балки. Таким образом, нагрузка q будет состоять из следующих показателей:

Расчет на смятие опорных участков балки.

• вес 1 пог.м балки;
• вес 1 кв.м перекрытия;
• временная нагрузка на перекрытие;
• нагрузка от перегородок на 1 кв.3/48*E*J, где:

  F – сила давления на брус, например, вес печи или другого тяжелого оборудования.

  Модуль упругости Е для разных видов древесины различен, эта характеристика зависит не только от породы дерева, но и от вида бруса – цельные балки, клееный брус или оцилиндрованное бревно имеют различные модули упругости.

  Подобные вычисления могут производиться с различными целями. Если вам нужно просто узнать, в каких пределах будут находиться деформации элементов конструкции, то после определения стрелки прогиба дело можно считать завершенным. Но если вас интересует, насколько полученные результаты соответствуют строительным нормам, то необходимо выполнить сравнение полученных результатов с цифрами, приведенными в соответствующих нормативных документах.

  Отклонение луча: как рассчитать

  В приложениях, связанных с перемещением, существует множество ситуаций, когда линейная направляющая или привод не полностью поддерживается по всей своей длине. В этих случаях прогиб (из-за собственного веса компонента и из-за приложенных нагрузок и сил) может повлиять на ходовые качества подшипников и вызвать плохую работу в виде преждевременного износа и заедания.

  Изделия, которые могут быть смонтированы только с концевыми опорами, такими как линейные валы или приводы в сборе, или в консольной ориентации, например телескопические подшипники, обычно имеют спецификацию для максимально допустимого отклонения.Важно проверить приложение и убедиться, что это максимальное отклонение не превышено. К счастью, большинство линейных направляющих и приводов можно смоделировать как балки, а их отклонение можно рассчитать с помощью обычных уравнений отклонения балки.

  Соображения, касающиеся материалов и конструкции

  При расчете прогиба необходимо знать свойства направляющей или привода и условия приложенной нагрузки. Что касается направляющей или привода, важными критериями являются модуль упругости и планарный момент инерции компонента.Модуль упругости является мерой жесткости материала, и его обычно можно найти в каталоге продукции. Момент инерции описывает сопротивление объекта изгибу и иногда предоставляется производителем компонента. Если момент инерции не указан, его можно разумно аппроксимировать, используя уравнение момента инерции для сплошного или полого цилиндра (для линейного круглого вала) или прямоугольника (телескопический подшипник или линейный привод).

  ---

  Модуль упругости, также известный как модуль Юнга или модуль упругости при растяжении, можно определить как отношение напряжения (силы на единицу площади) на оси к деформации (отношение деформации по длине) вдоль этой оси.

  Планарный момент инерции (также называемый вторым моментом площади или моментом инерции площади) определяет, как точки области распределяются относительно произвольной плоскости и, следовательно, ее сопротивление изгибу.

  ---

  С точки зрения применения и конструкции критериями, влияющими на прогиб балки, являются тип опоры на концах направляющей или привода, приложенная нагрузка и длина без опоры. Когда компонент является консольным, его можно смоделировать как фиксированную балку, а когда он поддерживается с обоих концов, он обычно может быть смоделирован как балка с простой опорой.Для консольных балок максимальное отклонение будет происходить, когда нагрузка находится на свободном конце балки, в то время как для балок с простой опорой максимальное отклонение будет иметь место, когда нагрузка находится в центре балки.

  При определении общего отклонения имейте в виду, что будут иметь две нагрузки, , которые вызывают отклонение: вес направляющей или самого привода и приложенная нагрузка. Собственный вес компонента почти всегда можно смоделировать как равномерно распределенную нагрузку, оценивая приложенную нагрузку как точечную нагрузку в месте максимального прогиба (на свободном конце консольной балки или в центре балки с простой опорой). обычно обеспечивает наихудший сценарий полного прогиба.

  Прогиб консольных балок

  Телескопические подшипники часто являются консольными, а некоторые конфигурации декартовых роботов приводят к консольному приводу на оси Y или Z. В этом случае вес балки, который достаточно однороден по длине, вызывает максимальный прогиб на конце балки.

  Изображение предоставлено: wikipedia.org

  Этот прогиб рассчитывается как:

  Где:

  q = сила на единицу длины (Н / м, фунт-сила / дюйм)

  L = длина без опоры (м, дюйм)

  E = модуль упругости (Н / м ² , фунт-сила / дюйм ² )

  I = планарный момент инерции (м ⁴ , дюйм ⁴ )

  Для создания наихудшего сценария прогиба мы рассматриваем приложенную нагрузку как точечную нагрузку (F) на конце балки, и результирующий прогиб можно рассчитать как:

  Сложив прогиб из-за равномерной нагрузки и прогиб из-за приложенной (точечной) нагрузки, получаем общий прогиб на конце балки:

  Прогиб свободно опертых балок

  Линейные валы и приводы часто закрепляются на концах, оставляя длину без опоры, как у балки с простой опорой.Равномерная нагрузка на балку (собственный вес вала или привода) вызовет максимальный прогиб в центре балки, который можно рассчитать как:

  Поскольку это балка с простой опорой, приложенная нагрузка может быть смоделирована как точечная нагрузка в центре балки для наихудшего сценария.

  Изображение предоставлено: wikipedia.org

  Прогиб из-за приложенной нагрузки в этом состоянии рассчитывается как:

  Полный прогиб в центре балки:

  Прогиб валов с двумя подшипниками

  Когда два подшипника используются на балке с простой опорой, как это обычно бывает с круглыми направляющими вала, приложенная нагрузка распределяется между двумя подшипниками, и максимальное отклонение происходит в двух местах: в положении на каждом подшипнике , когда подшипниковый узел (иногда называемый кареткой или столом) находится в середине вала.

  Изображение предоставлено: Thomson Linear

  Расчет отклонения балки для этого условия:

  Опять же, мы должны добавить прогиб из-за собственного веса балки плюс прогиб из-за приложенной нагрузки, чтобы получить общий прогиб:

  ---

  Существуют дополнительные сценарии монтажа и нагружения, которые могут возникнуть в некоторых приложениях, например, в приводе с фиксированной опорой на обоих концах. Но, как и в приведенных выше примерах, их можно оценить с помощью стандартных уравнений отклонения балки.Полный список сценариев опор балки и уравнений отклонения можно найти на этой странице Корнельского университета.

  Изображение предоставлено: wikipedia.org

  Калькулятор прогиба балки

  КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ УЧАСТНИКОВ
  Калькулятор	Определение
  	Расчет элементов сжатия (продольного изгиба колонны)
  ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОБЕГА
  	Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами
  	Балка с простой опорой и сосредоточенной нагрузкой в ​​любой точке
  	Просто поддерживаемая балка с двумя Точечные нагрузки
  	Балка с простой опорой и частично распределенной промежуточной нагрузкой
  	Балка с простой опорой и двумя частично распределенными промежуточными нагрузками
  	Балка с простой опорой и моментом
  	Балка с простой опорой и двумя моментами
  КАНТИЛЬВЕРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГНОЗА
  	Консольная балка с множественными точечными / распределенными нагрузками и моментами
  	Консольная балка с одинарной нагрузкой
  	Распределенная нагрузка консольной балки
  	Консольная балка с одним моментом
  КАЛЬКУЛЯТОРЫ ПРОГИБА ФИКСИРОВАННОЙ ЛУЧИ
  	Фиксированный -Фиксированная балка с множественными точечными / распределенными нагрузками и моментами
  	Фиксированная — фиксированная балка с одинарной нагрузкой
  	Фиксированный — Неподвижная балка с распределенной нагрузкой
  	Фиксированная — неподвижная балка с одним моментом

  Прогиб балки

  от Расс Эллиот Благодарности : Существует ряд стандартных работ, касающихся принципов отклонения балки.Особенно хорошее изложение, на котором основаны приведенные здесь уравнения, содержится в книге Mechanics of Materials (четвертое издание SI) , написанной Дж. М. Гиром и С. П. Тимошенко, Стэнли Торнсом, ISBN 0 7487 3998 X. Следует сделать ссылку на эта работа для вывода уравнений. Введение Прогиб пружинной балки зависит от ее длины, формы поперечного сечения, материала, места приложения отклоняющей силы и того, как балка поддерживается. Уравнения, приведенные здесь, относятся к однородным, линейно упругим материалам, в которых вращение балки невелико. В следующих примерах рассматриваются только нагрузки, действующие в одной точке или отдельных точках — точка приложения силы F на схемах предназначена для обозначения рупорного блока модели локомотива (или буксы транспортного средства), способного перемещаться вертикально. в рупорной направляющей и действуя против силы пружинной балки, прикрепленной к локомотиву или основным шасси транспортного средства или переносимых ими.Доля общего веса, действующего на каждую ось локомотива или транспортного средства, будет зависеть от положения его центра тяжести по отношению к оси (или точек крепления уравновешивающих балок шасси, если они используются). Приложение для моделирования рожковых блоков локомотивов Как видно из уравнений, толщина материала ( h или d ) очень важна, и, следовательно, увеличивающиеся размеры в диапазоне доступных гитарных струн делают их очень привлекательными для использования в качестве пружинные балки.Также существует значительная разница в прогибе балки для данной силы, в зависимости от того, как она поддерживается и фиксируется, а также от того, поддерживается ли она только на одном конце или на обоих концах. Предполагается, что конструкция должна быть основана на заданном прогибе рогового блока, а затем определить, какая длина, толщина и стиль балки наиболее подходят для конкретной силы, которая должна восприниматься каждой осью. Для локомотивов, вес которых составляет от 4 до 6 граммов на тонну прототипа, массы, поддерживаемые каждым отдельным роговым блоком локомотива, вероятно, будут находиться в диапазоне от 30 до 60 граммов (что соответствует нагрузке прототипа от 14 до 20 тонн на тонну). ось). Выбор значения отклонения Для разумного мелкого пути в масштабе 4 мм рекомендуемое значение прогиба рогового блока, δ , при конечной нагрузке локомотива составляет 0,5 мм. Приведенная выше рекомендация, как известно, является чрезмерно упрощенным и, возможно, неверным предположением о том, каким должно быть расчетное значение прогиба, и вызвала серьезные споры. Приветствуется любой опыт применения этой рекомендации в реальной практике моделирования шасси — цель этой статьи — начало обсуждения, а не его заключение.Щелкните здесь, чтобы ознакомиться с вопросами по этому поводу. Момент инерции, I Момент инерции прямоугольного сечения I = bh 3 ∕ 12 где h — размер в плоскости изгиба, т. Е. По оси, по которой действует изгибающий момент Момент инерции круглого сечения I = π r 4 ∕ 4 = π d 4 ∕ 64 , где r и d — радиус и диаметр соответственно Все приведенные ниже уравнения содержат I , момент инерции балки, который является константой, определяемой формой и толщиной поперечного сечения балки.Момент инерции не зависит от длины или материала балки. Здесь рассматриваются только прямоугольные и круглые цельные сечения. Пояснения к схемам прогиба и обозначениям На схемах показаны два типа опор: фиксированная и простая. На неподвижной опоре балка удерживается жестко, а угловой прогиб в точке крепления равен нулю. На простой опоре балка может скользить по опоре и вращаться в соответствии с силой, приложенной к балке. L = длина балки a = промежуточная длина балки δ = прогиб балки F = сила (т. Е. Доля веса локомотива, которому оказывает сопротивление букса) E = модуль Юнга I = момент инерции балки Уравнения и диаграммы прогиба Примечание к схемам и уравнениям .Приведенные здесь диаграммы были перевернуты по сравнению с их обычным описанием в учебниках, чтобы отразить их применение для моделей локомотивов и буксовых ящиков транспортных средств. Однако, хотя уравнения для отклонения были согласованы с их учебным представлением, нормальное соглашение о знаках (+ или -, чтобы указать отклонения по вертикальной оси y от опорной линии балки) было проигнорировано, поскольку мы здесь обеспокоены только с абсолютной величиной прогиба балки. Концевая нагрузка на консольную балку с одинарной неподвижной опорой δ = FL 3 ∕ 3 EI Это уравнение также следует использовать для отклонения уравнительной балки, вращающейся вокруг фиксированной оси и опирающейся на два рупорных блока по обе стороны от оси поворота. Двойные нагрузки на балку с двумя простыми опорами (примеры применения этой конфигурации) Это может быть применено для двух роговых блоков, прижимающихся к единой балке. Прогиб на расстоянии a от соседней опоры составляет: δ = Fa 2 (3 L — 4 a ) ∕ 6 EI Свисающая нагрузка на балку, ограниченная двумя простыми опорами δ = Fa 2 ( L + a ) ∕ 3 EI Промежуточная / центральная нагрузка на балку с одной фиксированной и одной простой опорой Отклонение по длине a от неподвижной опоры составляет: δ = Fa 3 ( L — a ) 2 (4 L — a ) ∕ 12 EIL 3 Для нагрузки в центре балки, подставив a = L ∕ 2 в вышеприведенное уравнение, прогиб составит: δ = 3.5 FL 3 ∕ 384 EI Центровка нагрузки на балку с двумя неподвижными опорами δ = FL 3 ∕ 192 EI При нагрузке в центре отклонение на расстоянии a от фиксированной опоры (где a меньше чем или равно L ∕ 2 ): δ = Fa 2 (3 L — 4 a ) ∕ 48 EI Промежуточная нагрузка на балку с двумя неподвижными опорами Отклонение на расстоянии a от неподвижной опоры: δ = 2 Fa 3 ( L — a ) 2 ∕ 3 EI (2 а + Д ) 2 Значения модуля Юнга, E Бериллий медь 124 ГПа 1 Латунь, твердость 70/30 117.2 ГПа Латунь неуточненная от 96 до 110 ГПа Нейзильбер 132,5 ГПа (127 ГПа 1 ) Бронза фосфористая, 5%, твердая 131,8 ГПа Фосфорная бронза (92% Cu / 8% Sn, или CuSn8) 111 ГПа 1 Сталь мягкая или инструментальная 212 ГПа Сталь мягкая, низкоуглеродистая 210 ГПа Сталь мягкая (закаленная) 201.4 ГПа Сталь нержавеющая 215,2 ГПа (190 ГПа 1 ) Сталь инструментальная (закаленная) 203,2 ГПа Следует отметить, что это теоретические значения. Типичное значение для стальной гитарной струны можно принять равным 205 ГПа. Значения, указанные для фосфористой бронзы, различаются: кажется, что они будут зависеть от материала типа «пружинный» или «экстрапружинный», состоящий из фосфористой бронзы 92% Cu / 8% Sn. обычно используется в переключателях с защелкой. 1 Шигли, инженер-конструктор машиностроения, 1980, McGraw Hill Примечания к агрегатам и размерам 1 Па = 1 Н · м -2 = 10 -6 Н · мм -2 = 10 -6 кг · м · с -2 · мм -2 = 1 г · мм -1 · с -2 Чтобы получить силу F в приведенных выше уравнениях, массу нужно умножить на гравитационную постоянную г (9.81 м · с -2 , или, что нам удобнее, 9810 мм · с -2 ) Размеры модуля Юнга E составляют ML -1 T -2 Размеры усилия F составляют L 2 ML -1 T -2 = MLT -2 Размеры момента инерции I — L 4 © Расс Эллиотт , впервые опубликовано 19 апреля 2000 г .; небольшая редакционная правка, август 2001 г .; уравнение для промежуточной нагрузки на балку с двумя фиксированными опорами исправлено, и уравнение прогиба для промежуточной / центральной нагрузки на балку с одной фиксированной и одной простой опорой повторно выражено, январь 2005 г .; Пересмотренная диаграмма для нависающей нагрузки на балку, стесненную двумя простыми опорами, 8 октября 2009 г .; Уравнение промежуточной нагрузки на балку с двумя неподвижными опорами исправлено, 30 декабря 2010 г.

  Лучшее руководство по определению прогиба в балках переменного поперечного сечения — опытный инженер

  Таблицы балок дают информацию и предполагают, что прогиб расчет основан на постоянном сечении.Итак, что делать, если у нашей балки есть крест сечение, которое меняется по длине балки?

  Чтобы определить величину отклонения в балка переменного сечения, необходимо интегрировать формулу прогиба балки с моментом инерции, являющимся переменной по отношению к длине и применить граничные условия. Луч Формула отклонения: v ’’ = M (x) / [E * I (x)].

  Непрерывный или дискретный — Есть два типа секций балки: непрерывная и дискретная.Большинство балок представляют собой непрерывные балки и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Кровельные балки в больших стальных зданиях — отличный пример непрерывной переменной балки. Балка относительно короткая на концах и очень высокая посередине.

  Дискретные балки балки которые имеют внезапные разрывы в разрезе. Вы не поверите, но иногда это проще для расчета, потому что дискретные участки обычно постоянны, что приводит к более легкий расчет.

  Формула отклонения балки является универсальной формула, которая позволяет настраивать несколько нагрузок и балку разделы. Предупреждаю, что чем больше чем точнее должны быть ваши расчеты, тем сложнее будет выполнить математику. Упрощение здесь сэкономит много времени и усилия. Как упоминалось ранее, формула:

  в ’’ = M (x) / [E * I (x)]

  Где v ’’ — вторая производная отклонения ( ускорение прогиба), M — момент, который обычно является функцией положение по длине балки, x. E — модуль упругости, I — момент инерции поверхности луч. Все табличные балки будут считайте это постоянной величиной, и поэтому ни одна из формул прогиба может быть использован.

  Теперь, когда мы проинтегрируем приведенное выше уравнение, мы будем выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C _n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный В этом случае у нас будет два или более уравнений.

  Граничные условия — это требования, которым должна соответствовать формула прогиба балки, когда она находится в окончательном виде. Окончательная форма приходит только тогда, когда мы используем граничные условия для решения констант образованный неопределенным интегралом. Общий случаи: концы балки с опорой должны быть равны 0 (дюймы, мм и т. д.) или наклон консольной балки должен быть 0 радиан.

  В этой статье мы рассмотрим три примера распространенных балок переменного сечения.

  1. Двухсекционная консольная балка с точечной нагрузкой на конце.
  2. Двухсекционная балка, свободно поддерживаемая собственным весом.
  3. Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.

  Лучшее руководство по минимизации отклонения луча

  Пример 1. Двухсекционная консольная балка с точечной нагрузкой на конце.

  Эта проблема состоит из 100-дюймового консольная стальная балка с нагрузкой 500 фунтов.4.

  Теперь мы определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я решил, что моя система координат (переменная x) начинается с основания. Это немного усложняет интегрирование, но переменные C ₁ и C ₂ будут уравновешиваться из-за граничных условий 1 и 2. Вы увидите через секунду.

  Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ в уравнениях.Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

  Теперь, когда проблема определена, давайте установим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки составляли 0 дюймов и 0 радиан. Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этом положении должны быть одинаковыми.

  Решим граничные условия 1 и 2

  Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, когда я выберу, чтобы система координат начиналась с база.

  Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

  Обратите внимание на чек, который я поставил в блок поиска, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = s ₂ на 50 дюймовЭто подтверждает что положение и наклон в этой точке будут непрерывными.

  Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v ₁ не имеет прогиба или наклона в основании.

  Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

  Как видите, отклонение быстро увеличивается после 50 дюймов от основания. Это четко указано на обоих графиках.

  4 лучших способа улучшить характеристики торсионной балки

  Пример 2: Двухсекционная стальная балка с простой опорой под собственным весом.

  Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов с распределенной нагрузкой 30 фунтов / дюйм на левом конце. На правом конце распределенная нагрузка составляет 50 фунтов.4.

  Теперь определим момент и проинтегрируем уравнение отклонения балки дважды каждый раз, добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Их связывает:

  г = L-x

  Я выбрал эту систему координат, так что C ₂ и C ₄ будет сокращаться, когда мы решаем граничные условия 1 и 2. Это также упрощает математику. чрезвычайно.Вы увидите через секунду.

  Мне нужно выполнить интегрирование только для одного из разделов, а затем изменить I ₁ на I ₂ и w ₁ на w ₂ в уравнениях. В уравнениях правого сечения я также заменю «y» на «x». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.

  Теперь, когда проблема определена, давайте установим граничные условия.Нам нужно, чтобы концы балки были отклонены на 0 дюймов (BC 1 и 2). Также нам понадобятся еще два граничных условия на стыке сегментов. Наклон и положение в этой позиции должны быть такими же, как и в месте соединения сегментов.

  Решим граничные условия 1 и 2

  Как упоминалось выше, я предвидел, что переменные C ₂ и C ₄ будет равно 0, если я выберу координату система запускается на базе.

  Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.

  Обратите внимание на чек, который я поставил в блок поиска, чтобы чтобы мы могли проверить, что v ₁ = v ₂ и s ₁ = s ₂ при 200 дюйм. Это подтверждает что положение и наклон в этой точке будут непрерывными.

  Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине.Мы ищем четыре граничных условия, которые должны быть выполнены.

  Ой, что случилось !? Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов прогиб, но они не касаются на пересечении. Я не только показываю силу график решения для точности, но также демонстрируя, что с помощью двух разные системы координат создают проблему. Согласно уравнениям склоны приближаются к месту расположения стык на равном по величине нисходящем склоне.Однако сделать эту работу одной из склонов на самом деле нужно подойти. Мы можем исправьте эту проблему, внеся одно небольшое изменение.

  с ₁ = -s ₂

  Давайте внесем это изменение и приступим к решению.

  Да, намного лучше! Наконец, мы объединим два графика вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

  Как и ожидалось, более длинная и жесткая секция меньше прогибается.

  Как рассчитать данные о пучке, если вашего случая нет в таблице

  Пример 3: Постоянно изменяющаяся неразрезная балка с простой опорой и постоянной распределенной нагрузкой.

  Эта проблема состоит из стальной балки с простой опорой длиной 300 дюймов с распределенной нагрузкой 1000 фунтов / дюйм поперек балки. Сечение начинается на высоте 10 дюймов, линейно увеличивается к центру, где достигает высоты 24 дюйма. Затем он снова сужается до 10 дюймов.

  Чтобы определить, как момент инерции изменяется относительно x, мы будем моделировать в Solidworks и делать сечения каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним линию.

  Теперь вы, наверное, заметили, что я сделал таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию для упрощения этой сложной задачи. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела прогиб 0 дюймов, а наклон в середине балки был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае координата x будет идти слева направо.

  Здесь вы можете видеть, что вычисленные значения I (x) точно соответствуют тому, что указано в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, верхняя и нижняя части имеют переменную «x», и интегрировать это будет очень весело. Итак, вам нужно знать обо мне одну вещь. У меня есть ограничения относительно того, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!

  Как видите, очень утомительная работа по интеграции была замалчена, и мы смогли напрямую решить для нашей границы условия.В уравнениях s (x) и v (x), на самом деле были натуральные бревна и каким-то образом появилась обратная касательная (не показано). Я до сих пор не жалею позволяя MathCAD делать всю работу.

  Следующим шагом является проверка результатов. Это делается в два этапа. Первый — построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.

  Наконец, мы отразим графики вместе, образуя окончательное уравнение для отклонения нашей консольной балки.

  Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.

  Лучшее руководство по решению статически неопределимых балок

  Заключение

  В этой статье рассматриваются три популярных варианта нагружения, когда балка имеет переменное поперечное сечение. Хотя это действительно связано с исчислением, часто это очень легко сделать вручную, потому что это многочлены. Если нет, то будьте благодарны за такие надежные программы, как MathCAD, которые сделают это за вас.Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа подобных балок. Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.

  Связанные

  Отклонение луча — S.B.A. Изобретатель

  Существует несколько способов определения прогиба балки из-за нагрузки, которая на нее воздействует. Я собираюсь обсудить, как использовать функции интеграции и прерывания.В соответствующих статьях. Однако, прежде чем идти дальше, если вы не знаете, как создать диаграмму моментов или как рассчитать момент инерции площади, я предлагаю вам сначала обратиться к этим справочным страницам.

  В таблицах ниже представлены максимальные отклонения и уклон для 6 уникальных настроек.

  . Прогиб за счет интеграции

  Если вы знаете, что представляет собой уравнение момента, которое представляет конкретную интересующую балку, вы можете использовать двойной интеграл, чтобы определить, каково отклонение балки.2} $ символизирует двойную производную для переменной x

  Еще одна вещь, которую необходимо учитывать при связывании уравнения момента с прогибом, — это модуль Юнга материала. Причина этого в том, что закон Хука связывает напряжение и деформацию, поэтому эффективно модуль Юнга используется для преобразования напряжения в деформацию, чтобы можно было определить прогиб. Уравнения 3-5 показывают, как использовать расчет и модуль Юнга вместе с теорией балки для определения прогиба и наклона с момента.2} = M (x)

  долл. США

  (уравнение 4) $ EI \ frac {dv} {dx} = θ (x) $

  (уравнение 5) $ EIv = v (x) $

  $ v $ = прогиб

  $ θ $ = уклон

  Пример показан ниже.

  Функции прерывания

  Другой метод, который можно использовать для определения прогиба, — это использование функций неоднородности; также известный как функции Маколея. Функции разрыва используются, чтобы обойти этап построения диаграммы моментов для определения момента.3} = V (x)

  долл. США Пример использования функций неоднородности для определения отклонения балки показан ниже.

  (Прогиб — TotalConstructionHelp)

  Балки и перемычки на самом деле являются просто балками. Балка — это конструктивный элемент, который обычно размещается горизонтально и может выдерживать нагрузки, в первую очередь за счет сопротивления изгибу. Изгибающая сила индуцируется в материале балки в результате нагрузок, в том числе ее собственный вес (вес балки) и дополнительные нагрузки (другие нагрузки, называемые временными нагрузками) и статические нагрузки, такие как люди и мебель).Эти нагрузки производят то, что называемые изгибающими моментами в балке, и могут также иметь изгибающие моменты на каждом поддерживаемый конец, когда концы прикреплены к концевым опорам. Фиксированный означает, что они прикреплены таким образом, что некоторая нагрузка на балку переносится на торцевые соединения (например, стены или колонны). Балки бывают разных размеров и форм. Обычно они либо однородные, либо однородные. или составной.Однородный пучок — это пучок, состоящий из одного материала, например, дерево или сталь. Композит — это композит, сделанный из материалов, которые не совпадают, например как, бетонная балка со стальной арматурой. Некоторые типы балок: Погрузка балки и опоры:

  Все это может показаться ошеломляющим, но это не так. Некоторые эксперты говорят, что инженерия — это на 80% логика и на 20% приложение. Некоторые могут обсудить это. но здесь мы предоставим вам основную инженерную информацию и приложения, которые не всегда доступны. Пока балки нагружаются по-разному. Балка с простой опорой — это обычно используемая балка (как показано выше). Ниже вам будет показано, как все это работает, и как выбрать балку (дерево или сталь). Мы также касаемся выбора бетонной балки в секции балки. Простая опорная балка с равномерно распределенной нагрузкой с уравнениями и решениями: В приведенном выше примере есть шаги, необходимые для выбора и проектирования дерева. Луч. Если вы хотите выбрать и спроектировать стальную балку, выполните следующие действия: тем же.Меняются несколько вещей, например, напряжение изгиба в Материал, момент инерции, модуль упругости и сечение Модуль. Все остальные уравнения были бы такими же, если бы у вас было такое же нагрузка (W) и пролет (L). Обычные этапы проектирования балки: Решите, какой материал вы хотите использовать (дерево или сталь). Мы не проектируем Бетонные балки в разделе сайта. Если нагрузка будет тяжелой, вы можете использовать сталь, так как она иметь возможность принимать большую нагрузку на тот же пролет. Если пролет короткий, вероятно, лучше будет использовать дерево. Иногда полевые условия диктуют, что лучше использовать. Определите, какие нагрузки будут на балку. Нагрузка обычно берется из Строительных норм. Кодекс содержит список из того, что минимальные нагрузки для большинства типов использования. В жилых помещениях Кодекс обычно требует, чтобы минимум 40 фунтов на квадратный фут использовался для называется «Жилые помещения». Будьте осторожны, потому что код имеет гораздо большую загрузку Требования к балконам и лестницам. Предоставляется ссылка на Строительный кодекс. в разделе Строительных норм на этом веб-сайте. Иногда условия нагрузки превышают указанные в Кодексе. Имейте в виду, что Кодекс предусматривает минимальные требования, и вы можете превысить минимум. Проверьте пролет (длину) и то, что будет поддерживать балку на каждом конце. Пролет — это расстояние между одной опорой и другой опорой на каждом конце. луча. Как только у вас будет вся вышеуказанная информация, вы запустите Actual Beam. Дизайн. Уравнение Общая нагрузка = Ш x Д предназначено для определения полной нагрузки на балку. Получив полную нагрузку на балку, ее делят на 2, чтобы определить нагрузка, передаваемая на каждый конец балки, которая переносится либо на стена или колонна.Это важно, так как вам нужно убедиться, что стена или колонна может нести нагрузки. Получите момент, максимальный момент должен быть получен, по этой причине Моменты в других точках Луча игнорируются. Мы хотим, чтобы луч быть спроектированным для максимальной безопасности. Для балки с простой опорой и Равномерно распределенная нагрузка M = WL 2 / 8. Итак, у нас есть нагрузка и момент балки. Теперь нам нужно знать будет ли Луч будет деревянным или стальным. Если балка деревянная, то в зависимости от для древесины типичное значение fb (напряжение изгиба) может варьироваться от 1000 фунтов на квадратный дюйм. (фунт на квадратный дюйм) до 1200 фунтов на квадратный дюйм. Как правило, консервативное значение будет около 1000 фунтов на квадратный дюйм, если вы используете пихту или болиголов, это также можно получить из Строительного кодекса для различных пород дерева.Точно так же, если вы намерены для использования стали значение Fy = 36000 Steel будет fb = 24000 psi (где, fb = 0,66 x Fy). Как видно, Сталь — 24000, а Дерево — 1000, что указывает на то, что сталь примерно в 24 раза прочнее древесины при изгибе. Что также указывало на то, что стальная балка будет меньше деревянной балки. Так если у вас ограниченное пространство, стальная балка может быть лучшим выбором. Теперь нам нужно вычислить Sx (модуль сечения), который требуется для кода. Этот выполняется с использованием уравнения Sx = M / fb. У нас есть М (момент) из нашего вычисления. Просто примените расчеты. Этот расчет — это то, что есть требуется и должно быть минимально допустимым. Вы можете выбрать деревянную балку. из Таблицы сечений древесины, которые доступны в большинстве Руководств по дереву, или из наш веб-сайт, или вы аналогичным образом выбираете стальную балку таким же образом.Естественно, вы можете выбрать деревянный стержень, а затем рассчитать модуль сечения для этого Член, как показано в примере. Модуль сечения должен быть равен или больше чем рассчитанный модуль сечения. Остается один последний шаг — найти отклонение луча, вызванное загрузка. Когда вы кладете груз на балку, она изгибается вниз, и это вертикальное смещение вниз называется прогибом и измеряется в дюймы (или мм).Как видно из примера, мы вычислили максимальное значение Прогиб в центре луча. В примере максимальное отклонение разрешено контролируется Кодексом. Различные допустимые отклонения показаны на пример. Чтобы вычислить отклонение, нам нужна дополнительная информация, который представляет собой E (модуль упругости) материала и I (момент Инерция) для выбранного элемента. (См. Раздел о вычислении момента инерции на этом веб-сайте) Модуль упругости (E) древесины колеблется в районе 11 , для этих в примерах использовалось значение 119000.Если используется сталь, то значение E будет около 2 00, как показано в примерах. Момент инерции (I) может быть вычислен или выбран из таблиц. предоставлено или вычислено. (См. Раздел о вычислении момента инерции) Допустимый прогиб: опорные перекрытия и потолки L / 360, опорные Крыши с уклоном менее 3 дюймов 12 L / 240 и несущие крыши больше чем 3 в 12, наклон L / 180.L = пролеты, например: 12 футов, умножить 12 футов на 12 дюймов = 144 дюйма, разделенные на 360, 240 или 180, в зависимости от того, что применимо. Наконец, сравните вычисленное отклонение с допустимым отклонением. Если Расчетное отклонение больше допустимого отклонения, тогда вы должны выберите больший элемент балки и произведите перерасчет. Простая сосредоточенная балка с опорной точкой с уравнениями и решениями:

  конструкций — Как рассчитать прогиб простой балки с нагрузкой в ​​центре?

  Я имею в виду деревянную балку… Википедия предлагает мне также знать «момент инерции площади поперечного сечения», но я не знаю, как это получить.

  Если вы используете пиломатериалы стандартных размеров, Американский совет по древесине (AWC) публикует таблицу различных размеров и свойств сечения в Приложении NDS 2015, раздел 3.1. Например, рассмотрим скриншот ниже

  .

  Если вы использовали балку 6×12, ее момент инерции, $ I_x $, равен 697,1 на ⁴ вокруг ее главной оси.Это одна часть измерения жесткости балки или ее сопротивления прогибу — другая часть — это ее модуль упругости , как вы уже определили.

  ---

  Если у вас еще нет формулировки, прогиб балки с простой опорой при точечной нагрузке в середине пролета определяется следующим образом (согласно 14-му изданию AISC. Руководство по стальным конструкциям ):

  Вы решаете переменную $ \ Delta_ {max} $.Как вы сказали, у вас есть все детали, необходимые для расчета прогиба, за исключением $ I $. Ответ @GlenH7 уже дает вам формулировку для определения $ I $, если у вас есть форма, не охваченная дополнением NDS, поэтому я не буду повторять эту информацию здесь.

  Обратите внимание, что NDS содержит код для проектирования деревянных конструкций. Этот или другой подобный код обычно является сводом правил для деревянных конструкций, спроектированных в Соединенных Штатах. Есть дополнительные положения, которые следует учитывать, если вы выполняете «правильный» анализ прогиба в соответствии с кодом, которые выходят за рамки этого вопроса, но я чувствую, что вам действительно не нужно вдаваться в подробности.