▖Квадратные 🧊Кубические метры в Сантиметры Миллиметры Дециметры
Краткий Курс школьной физики
СУПЕР АКЦИЯ!!!
Перевод единиц измерения в квадрате и кубе
В этой статье мы рассмотрим три правила, благодаря которым вам будет гораздо проще переводить любые единицы площади и объема.
Итак, для начала вспомним, что в Cистеме СИ единицей измерения площади является метр квадратный, а объема — метр кубический.
Также, вспомните таблицу приставок, которая помогает образовывать разнообразные единицы измерения.
Это важно вспомнить для того, чтобы применять наши правила.
Первое правило
поможет вам перевести единицы площади в квадратные метры (м²) или единицы объема в кубические метры (м³).
Второе правило
покажет, как квадратные (м²) и кубические метры (м³) переводить в другие единицы измерения.
И наконец, третье правило
объединяет в себе первые два правила и необходимо для перевода, например, квадратных сантиметров (см²) в квадратные дециметры (дм²) или кубических миллиметров (мм³) в кубические сантиметры (см³).
Что ж, теперь понятно, что нам предстоит сегодня разобрать. Не переживайте, все проще, чем вы могли бы подумать.
Правило №1
Чтобы перевести любые единицы площади в квадратные метры, нужно множитель соответствующий приставки возвести во вторую степень. А чтобы перевести какие-либо единицы объема в кубические метры, нужно множитель возвести в третью степень.
Например, переведем четыре квадратных километра в квадратные метры. Четыре просто переписываем и умножаем на множитель приставки «кило», а это десять в третьей степени. И так как площадь измеряется в квадратных метрах, то множитель возводим в квадрат. По свойству степени получаем: четыре умножить на десять в шестой степени метров квадратных.
Аналогично поступаем с единицами измерения объема. Ноль целых две десятых кубических километра перевести в кубические метры. Ноль целых две десятых переписываем и умножаем на множитель приставки «кило», который возводим в третью степень. Получаем: ноль целых две десятых на десять в девятой степени, уже метров кубических.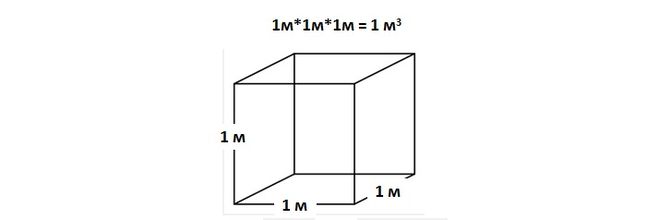
Триста сорок квадратных сантиметров переведем в квадратные метры. Это значит, что триста сорок нужно умножить на множитель приставки «санти», десять в минус второй степени, который нужно возвести в квадрат. Получаем: триста сорок умножить на десять в минус четвертой степени метров квадратных. На этом можно остановиться, а можно продолжить и записать: равно ноль целых тридцать четыре тысячных метров квадратных.
Двадцать пять кубических дециметров переведем в кубические метры. Это будет двадцать пять умножить на множитель приставки «деци»: десять в минус первой степени, который возведем в третью степень. Получаем: двадцать пять на десять в минус третьей степени кубических метров. Это можно записать как ноль целых двадцать пять тысячных кубических метров.
ВСЯ ГЕОМЕТРИЯ за 7 класс
ВСЯ ГЕОМЕТРИЯ за 8 класс
Как решать НЕРАВЕНСТВА
Правило №2
Вот так быстро и неожиданно мы подошли к Правилу №2. Теперь квадратные и кубические метры будем переводить в другие единицы измерения, то есть в не системные единицы. Все делаем аналогично, только меняем знак показателя степени нужного множителя на противоположный.
Все делаем аналогично, только меняем знак показателя степени нужного множителя на противоположный.
Две тысячи пять квадратных метров перевести в квадратные километры. Две тысячи пять пишем без изменений. У множителя приставки «кило» меняем знак показателя степени на минус. Потом, десять в минус третьей степени возводим в квадрат и получаем две тысячи пять умножить на десять в минус шестой степени километров квадратных. В стандартном виде это: две целых пять тысячных на десять в минус третьей степени квадратных километров.
Сто тридцать тысяч метров кубических перевести в кубические километры. Сто тридцать тысяч умножить на десять в минус третьей степени. Множитель возводим в третью степень. Получаем: сто тридцать тысяч умножить на десять в минус девятой степени кубических километров. А это можно записать в стандартном виде: одна целая три десятых на десять в минус четвертой степени кубических километров.
Аналогично переведем метры квадратные в миллиметры квадратные. Одна целая три сотых переписываем. У множителя приставки «милли» меняем знак показателя степени на противоположный и возводим его во вторую степень. Получаем: одна целая три сотых на десять в шестой степени квадратных миллиметров.
У множителя приставки «милли» меняем знак показателя степени на противоположный и возводим его во вторую степень. Получаем: одна целая три сотых на десять в шестой степени квадратных миллиметров.
Кубические метры переведем в кубические сантиметры. Ноль целых шесть тысячных умножаем на десять в шестой степени. Это множитель приставки «санти», в котором мы поменяли знак показателя степени и возвели в куб. В стандартном виде это будет: шесть на десять в третьей степени кубических сантиметров.
Правило №3
А тем временем мы с вами представим ситуацию, что нам вдруг потребовалось перевести, например, квадратные сантиметры в квадратные дециметры или кубические миллиметры в кубические сантиметры. Если вам сложно сделать такой перевод напрямую, то можно это сделать в два приема. Это будет Правило №3.
Сначала нужно будет единицы перевести в Cистему СИ по первому правилу, а затем в нужные единицы по второму правилу.
Давайте попробуем перевести девятьсот квадратных миллиметров в квадратные дециметры. Девятьсот умножаем на множитель приставки «милли». Это десять в минус третьей степени. Отлично, это мы с вами перевели в метры, а теперь по второму правилу умножаем на множитель приставки «деци», изменив знак показателя степени. Это десять в первой степени.
Девятьсот умножаем на множитель приставки «милли». Это десять в минус третьей степени. Отлично, это мы с вами перевели в метры, а теперь по второму правилу умножаем на множитель приставки «деци», изменив знак показателя степени. Это десять в первой степени.
А теперь возводим эти множители во вторую степень. Это девятьсот умножить на десять в минус четвертой степени квадратных дециметров. Не поняли, как мы пришли к такому показателю степени?
Посмотрите наш Курс «Перевод единиц измерения» с самого начала, и все станет понятно. Полученный ответ можно оставить в таком виде, а можно записать в стандартном виде: девять умножить на десять в минус второй степени.
Аналогично поступаем с единицами объема, только скобку с множителями нужно будет возвести в третью степень. Пусть ноль целых пятьдесят четыре тысячных кубических дециметров нужно перевести в кубические миллиметры.
Ноль целых пятьдесят четыре тысячных умножаем на множитель приставки «деци» — десять в степени минус один. Это будут метры. А теперь умножаем на десять в степени три, это множитель приставки «милли», в котором мы поменяли знак показателя степени.
Это будут метры. А теперь умножаем на десять в степени три, это множитель приставки «милли», в котором мы поменяли знак показателя степени.
Не забываем скобку возвести в третью степень. Получаем десять в шестой степени. В стандартном виде это будет: пять целых четыре десятых на десять в четвертой степени кубических миллиметров.
А теперь попробуйте поупражняться сами, без наших подсказок.
Для того, чтобы разобраться в этой теме более подробно, предлагаем посмотреть наш курс!
КУрс «Перевод единиц измерения»
В школе вам такое вряд ли расскажут…
Посмотреть бесплатный курс!
Куб дроби. Дробь в третьей степени.
- Альфашкола
- Статьи
Какие действия необходимо сделать, чтобы выполнить возведение в куб дроби? Для этого стоит определить какая дробь смешанная или обыкновенная, десятичная или недясятичная.
- Для того чтобы возвести обыкновенную дробь в куб надо числитель и знаменатель возвести в степень. Пример :
- Для того чтобы возвести смешанную дробь в куб надо ее перевести в неправильную дробь, а затем числитель и знаменатель возвести в степень и в полученной дроби выделить целую часть.
Пример:
- При возведении в третью степень десятичного числа надо вычислить произведение трех ее множителей, равных самой дроби. Пример:
Дробь: ————
———-
Больше уроков и заданий по математике вместе с преподавателями нашей онлайн-школы «Альфа».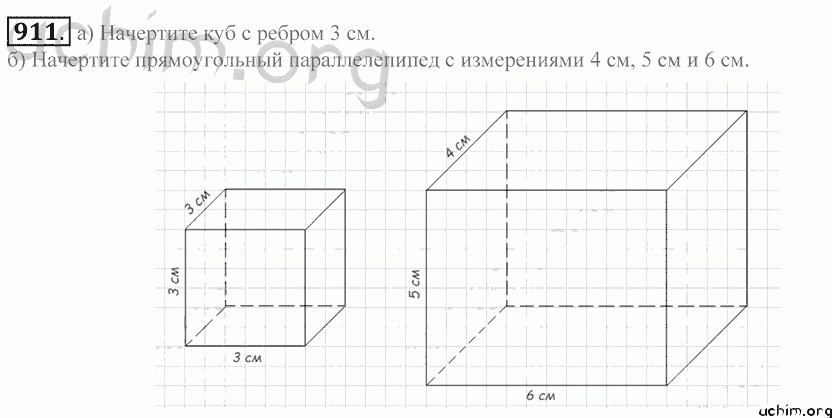 Запишитесь на пробное занятие уже сейчас!
Запишитесь на пробное занятие уже сейчас!
Запишитесь на бесплатное тестирование знаний!
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Наши преподаватели
Виктория Игоревна Лаптик
Репетитор по математике
Стаж (лет)
Образование:
Мозырский государственный педагогический университет им. И.П. Шамякина
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 1-4 классов. Могу проводить урок как на русском языке так и на английском. Преподаю предмет так, как хотела бы, чтоб учили моего ребенка. Могу весело и интересно преподнести сложный материал учащимся. Я люблю математику за точность, а не приблизительность, за возможность предугадать будущий результат, а не полагаться на нечто неконтролируемое.
Буду рада видеть на своих уроках!
Могу проводить урок как на русском языке так и на английском. Преподаю предмет так, как хотела бы, чтоб учили моего ребенка. Могу весело и интересно преподнести сложный материал учащимся. Я люблю математику за точность, а не приблизительность, за возможность предугадать будущий результат, а не полагаться на нечто неконтролируемое.
Буду рада видеть на своих уроках!
Людмила Владимировна Киселева
Репетитор по математике
Стаж (лет)
Образование:
Армавирский государственный университет, Днепропетровский государственный университет
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор 5-11 классов. Имею большой опыт работы со школьниками. Профессионально устраню любые пробелы в знаниях, доходчиво объясню учебный материал, подготовлю к ОГЭ, ГВЭ, ЕГЭ, поступлению в лицей, колледж, ВУЗ. В работе использую ИК — технологии. Смогу помочь понять математику как не сложную науку, а как интересную и нужную.
Имею большой опыт работы со школьниками. Профессионально устраню любые пробелы в знаниях, доходчиво объясню учебный материал, подготовлю к ОГЭ, ГВЭ, ЕГЭ, поступлению в лицей, колледж, ВУЗ. В работе использую ИК — технологии. Смогу помочь понять математику как не сложную науку, а как интересную и нужную.
Елена Сергеевна Журова
Репетитор по математике
Стаж (лет)
Образование:
Белорусский государственный педагогический университет им. М. Танка
Проведенных занятий:
Форма обучения:
Дистанционно (Скайп)
Репетитор по математике и русскому языку 1-4 классов.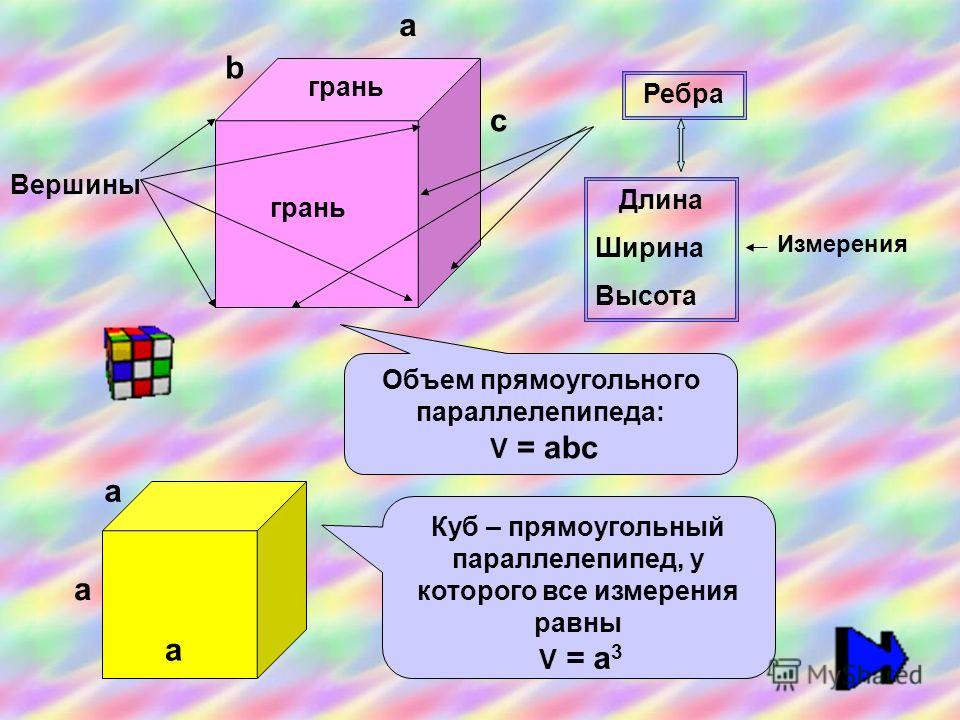 Создаю компьютерные игры для тех, кто любит математику, кто хочет быстро выучить таблицу умножения, легко решать задачи и освоить навыки устного счета. Никогда не объясняю одну и ту же тему разным ученикам одинаково. Каждому подбираю его личное, понятное только ему объяснение. Учиться можно легко.
Создаю компьютерные игры для тех, кто любит математику, кто хочет быстро выучить таблицу умножения, легко решать задачи и освоить навыки устного счета. Никогда не объясняю одну и ту же тему разным ученикам одинаково. Каждому подбираю его личное, понятное только ему объяснение. Учиться можно легко.
Похожие статьи
- Что такое рациональные числа
- Распределительное свойство умножения
- МФТИ: факультеты и специальности, проходной балл, вступительные испытания
- ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 2)
- ЕГЭ по математике, базовый уровень. Текстовые задачи (вариант 5)
- Работа по математике
-
Решаем олимпиадные задачи.

- Отпусти меня, мама, я уже взрослый
Нажимая кнопку «Записаться» принимаю условия Пользовательского соглашения и Политики конфиденциальности
Перевести кубы в литры | Перевод кубов в литры и обратно
Математика
Как перевести кубы в литры? Ответ на этот вопрос вы узнаете прочитав данную статью.
Содержание статьи:
- Сколько в 1 кубе литров?
- Формула перевода объема куба в литры
- Формула перевода литров в метры кубические
- Примеры перевода литров в кубы
- Примеры перевода кубов в литры
Частенько у учащихся возникают сложности с переводом одних единиц измерения в другие. Отсюда и множество вопросов вроде:
- Сколько литров в кубе?
- 1 куб – сколько это литров?
- Сколько литров в кубе воды?
- Сколько литров в кубе газа, пропана, бензина, песка, земли, керамзита?
- Сколько в кубе литров метана, сжиженного газа?
- Как перевести см в кубе (см3) или дм куб (см3) в литры?
- Куб бетона, бензины, солярки, дизельного топливо — это сколько литров?
Далее можно выделить группу вопросов более конкретных, к примеру, сколько литров в кубе воды, а в ванне? Или сколько кубов в бочке, объемом 200 литров, а в ведре, а в 10 литрах? А 40 литров сухого водорода это сколько кубов? Данные вопросы актуальны как для учащихся при решении различных задач, так и в практических целях, например, при покупке какой-нибудь емкости для воды. Разберемся же в этом вопросе основательно, вспомним, так сказать, матчасть, чтобы в любой момент с легкостью можно перевести кубы в литры, ну и конечно обратно.
Разберемся же в этом вопросе основательно, вспомним, так сказать, матчасть, чтобы в любой момент с легкостью можно перевести кубы в литры, ну и конечно обратно.
Обратим в первую очередь внимание на тот факт, что вне зависимости от вещества, размещаемое в емкости перевод из литров в кубы всегда будет одинаков, будь то вода, газ, песок или бензин.
Сколько в 1 кубе литров?
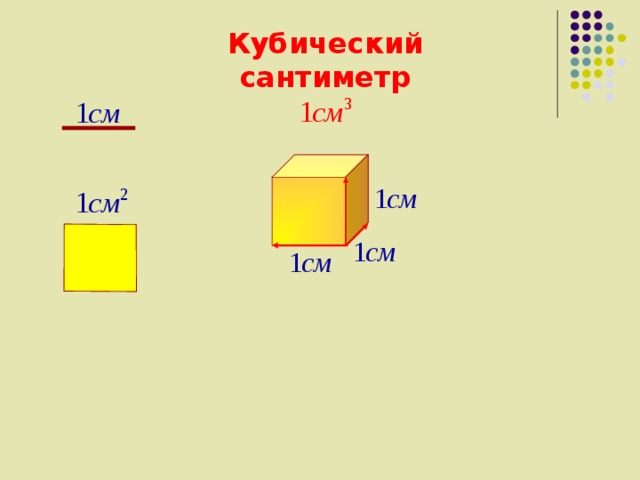
Начнем с лирического отступления, а именно с курса школьной физики. Известно, что общепринятая единица измерения объема – это кубический метр. 1 кубический метр – это объем куба, сторона которого равна ровно одному метру.
Эта единица не всегда является удобным и именно по этой причине очень часто используются другие – литры – они же кубические дециметры и кубические сантиметры.
Как показала практика, наиболее удобной оказалась единица измерения объема – литр, которая представляет собой объем куба, длина которого 1 дм или 10 см. Таким образом получаем, что все вопросы как перевести дм куб в кубы равносильны вопросу: как перевести литры в кубы, ведь 1 дм. куб = 1 литр.
куб = 1 литр.
Формула перевода объема куба в литры
1 куб. м = 1000 л (формула объема куба в литрах)
Формула перевода литров в метры кубические
1 л = 0,001 куб. м
Примеры перевода литров в кубы
А теперь вооружившись всеми необходимыми знаниями, можем переходить непосредственно к расчетам.
| Задача #1: Сколько литров в 0,5 кубах? Решение: Используя, приведенную выше формулу получаем: 0,5* 1000 = 500 литров. Ответ: в 0,5 кубах 500 литров. | Задача #6: Сколько литров в 300 кубах? Решение: 300 * 1000 = 300 000 литров Ответ: в 300 кубах 300 тыс. литров. |
| Задача #2: В 1 куб м сколько литров? (самое простое) Решение: 1 * 1 000 = 1 000 литров. Ответ: в 1 кубе 1 000 литров. | Задача #7: 5 кубов — сколько литров? Решение: 5 * 1000 = 5 000 литров Ответ: 5 кубов – это 5 тыс.  литров. литров. |
| Задача #3: 2 куба – это сколько литров? Решение: 2 * 1 000 = 2 000 литров. Ответ: в 2 кубах 2 000 литров. | Задача #8: 6 кубов – это сколько литров? Решение: 6 * 1000 = 6 000 литров. Ответ: в 6 кубах 6 тыс. литров. |
| Задача #4: Сколько литров в 10 кубах? Решение: 10 * 1000 = 10 000 литров Ответ: в 10 кубах 10 тыс. литров. | Задача #9: 4 куба сколько литров? Решение: 4 * 1000 = 4 000 литров Ответ: в 4 кубах 4 тыс. литров. |
| Задача #5: 20 кубов – это сколько литров? Решение: 20 * 1000 = 20 000 литров Ответ: в 20 кубах 20 тыс. литров. | Задача #10: 500 куба сколько литров? Решение: 500 * 1000 = 500 000 литров Ответ: в 500 кубах 500 тыс. литров. |
Примеры: как перевести кубы в литры?
Рассмотрим теперь обратные задачи о нахождении количества кубов в указанном количестве литров.
| Задача #1: Сколько кубов в 100 литрах? Решение: 100 * 0,001 = 0,1 куб. метр. Ответ: 100 литров – это 0,1 метра куб. | Задача #6: Сколько кубов в 1500 литрах? Решение: 1500 * 0,001 = 1,5 метров кубических. Ответ: в 1500 литров 1,5 метров кубических. |
| Задача #2: Сколько кубов в 200 литрах? Решение: 200 * 0,001 = 0,2 куб. метра. Ответ: в 200 литров 0,2 м. метра. | Задача #7: Сколько кубов в 3000 литрах? Решение: 3000 * 0,001 = 3 метров кубических. Ответ: в 3000 литрах — 3 метров кубических. |
| Задача #3: Сколько кубов в 140 литрах? Решение: 140 * 0,001 = 0,14 кубометров. Ответ: в 140 литров 0,14 кубометров. | Задача #8: Сколько кубов в 5000 литрах? Решение: 5000 * 0,001 = 5 метров кубических. Ответ: в 5 000 литрах — 5 метров кубических.  |
| Задача #4: Сколько кубов в 500 литрах? Решение: 500 * 0,001 = 0,5 кубов. Ответ: в 500 литров 0,5 кубов. | Задача #9: Сколько кубов в 10 000 литрах? Решение: 10 000 * 0,001 = 10 куб. м. Ответ: в 10 000 литрах – 10 куб. м. |
| Задача #5: Сколько кубов в 1000 литрах? Решение: 1000 * 0,001 = 1 метр кубический. Ответ: в 1000 литрах 1 метр кубический. | Задача #10: Сколько кубов в 30 000 литрах? Решение: 30 000 * 0,001 = 30 куб. м. Ответ: в 30 000 литров 30 куб. м. |
Для быстроты расчетов предлагаем воспользоваться вам нашими онлайн калькуляторами:
- калькулятор перевода кубы в литры
- калькулятор перевода литров в кубы
Перейдите по соответствующим ссылкам и воспользуйтесь инструкциям.
Если остались какие-то вопросы по данной теме, или вам нужна помощь в решении задачи по переводу кубов в литры или литров в кубы, то оставляйте их внизу в комментариях.
Другие статьи по теме
Математика
Как переводить литры в кубические сантиметры. Как перевести см кубические в метры кубические? Перевод величин в кубе
Калькулятор переводит единицы измерения объема. К наиболее часто используемым метрическим относятся литр и метр кубический. Литр равен 1 дециметру кубическому, метр кубический равен 1 000 литров. Гектолитр равен 100 литров.
Англо-американская система использует исторические единицы, которые в Соединенных Штатах и Великобритании, несмотря на одинаковое название, представляют различный объем. В Америке, к тому же, до сих пор используется другая система единиц объема для жидкости и твердых тел (например, зерно). Например, одна пинта может представлять три различные значения объема. В таблице переводов отдельные системы четко разделены.
Конвертер
Введите объем и выберите единицы измерения
миллиметр (мм) кубический сантиметр (см) кубический дециметр (дм) кубический метр (м) кубический миллилитр (мл) сантилитр (сл) децилитр (дл) литр (л) гектолитр (гл) джилл (gi) пинта (pt) кварта (qt) галлон (gal) баррель (bl) джилл (gi) пинта (pt) кварта (qt) галлон (gal) баррель (bl) пинта (pt) кварта (qt) галлон (gal) пек (pk) бушель (bsh) квартер (qr)Округлить до знаков после запятой
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер плотности потока водяного пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др.
1 кубический метр [м³] = 1000000 кубический сантиметр [см³]
Исходная величина
Преобразованная величина
кубический метр кубический километр кубический дециметр кубический сантиметр кубический миллиметр литр эксалитр петалитр тералитр гигалитр мегалитр килолитр гектолитр декалитр децилитр сантилитр миллилитр микролитр нанолитр пиколитр фемтолитр аттолитр куб.см капля баррель (нефтяной) баррель американский баррель британский галлон американский галлон британский кварта США кварта британская пинта США пинта британская стакан американский стакан (метрический) стакан британский унция жидкая США унция жидкая британская столовая ложка амер. столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
Общие сведения
Объем — это пространство, занимаемое веществом или предметом. Также объем может обозначать свободное пространство внутри емкости.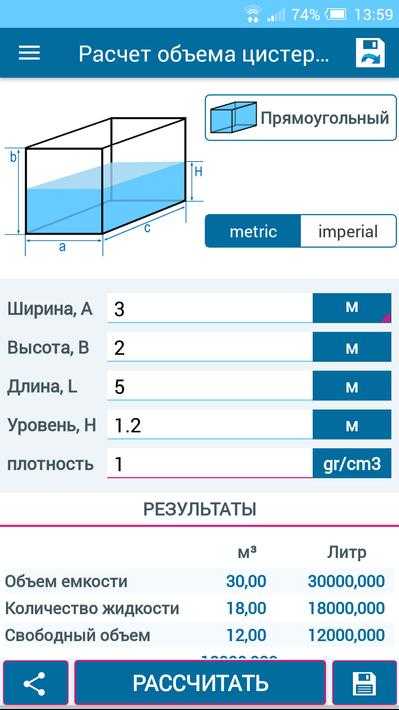 Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Единицы объема
Кубический метр
Единица измерения объема в системе СИ — кубический метр. Стандартное определение одного кубического метра — это объем куба с ребрами длиной в один метр. Также широко используются производные единицы, например, кубические сантиметры.
Литр
Литр — одна из наиболее часто используемых единиц в метрической системе. Он равен объему куба с ребрами длиной 10 см:
1 литр = 10 см × 10 см × 10 см = 1000 кубических сантиметров
Это все равно, что 0,001 кубических метров. Масса одного литра воды при температуре 4°C примерно равна одному килограмму. Часто используются также миллилитры, равные одному кубическому сантиметру или 1/1000 литра. Миллилитр обычно обозначают как мл.
Джилл
Джиллы — единицы объема, используемые в США для измерения алкогольных напитков. Один джилл — это пять жидких унций в Британской имперской системе или четыре в американской. Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Драм
Драм, или драхма — мера объема, массы, а также монета. В прошлом эта мера использовалась в аптекарском деле и равнялась одной чайной ложке. Позже стандартный объем чайной ложки изменился, и одна ложка стала равна 1 и 1/3 драхмы.
Объемы в кулинарии
Жидкости в кулинарных рецептах обычно измеряют по объему. Сыпучие и сухие продукты в метрической системе, наоборот, измеряют по массе.
Чайная ложка
Объем чайной ложки разный в разных системах измерения. Изначально одна чайная ложка была четвертью столовой, потом — одной третьей. Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Столовая ложка
Объем столовой ложки тоже колеблется в зависимости от географического региона. Так, например, в Америке, одна столовая ложка — это три чайных, пол-унции, примерно 14,7 миллилитра, или 1/16 американской чашки. Столовые ложки в Великобритании, Канаде, Японии, Южной Африке и Новой Зеландии — тоже содержат три чайных ложки. Так, метрическая столовая ложка — 15 миллилитров. Британская столовая ложка — 17.7 миллилитра, если чайная — 5,9, и 15, — если чайная — 5 миллилитров. Австралийская столовая ложка — ⅔ унции, 4 чайных ложки, или 20 миллилитров.
Чашка
Как мера объема, чашка не определяется так строго, как ложки. Объем чашки может варьировать от 200 до 250 миллилитров. Метрическая чашка — 250 миллилитров, а американская немного меньше, примерно 236,6 миллилитра. В американской диетологии объем чашки равен 240 миллилитрам. В Японии чашки еще меньше — всего 200 миллилитров.
Кварты и галлоны
Галлоны и кварты также имеют разную величину, в зависимости от географического региона, где они используются. В имперской системе измерения один галлон равен 4,55 литра, а в американской системе мер — 3,79 литра. В основном в галлонах измеряют топливо. Кварта равна четверти галлона и, соответственно, 1,1 литра в американской системе, и примерно 1,14 литра в имперской системе.
Пинта
В пинтах измеряют пиво даже в странах, где пинту не используют для измерения других жидкостей. В Великобритании в пинтах измеряют молоко и сидр. Пинта равна одной восьмой галлона. В некоторых других странах Содружества Наций и Европы также используют пинты, но, так как они зависят от определения галлона, а галлон имеет разный объем в зависимости от страны, пинты также не везде одинаковы. Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Жидкая унция
Имперская унция примерно равна 0,96 американской унции. Таким образом, в имперской унции содержится приблизительно 28,4 миллилитра, а в американской -29,6 миллилитра. Одна американская унция также приблизительно равна шести чайным ложкам, двум столовым, и одной восьмой чашки.
Вычисление объема
Метод вытеснения жидкости
Объем предмета можно вычислить с помощью метода вытеснения жидкости. Для этого его опускают в жидкость известного объема, геометрически вычисляют или измеряют новый объем, и разница этих двух величин и есть объем измеряемого предмета. Например, если при опускании предмета в чашку с одним литром воды, объем жидкости увеличится до двух литров, значит объем предмета — один литр. Таким способом можно вычислить только объем предметов, которые не впитывают жидкость.
Формулы для вычисления объема
Объем геометрических фигур можно вычислить при помощи следующих формул:
Призма:
произведение площади основания призмы на высоту.
Прямоугольный параллелепипед: произведение длины, ширины и высоты.
Куб: длина ребра в третьей степени.
Эллипсоид: произведение полуосей и 4/3π.
Пирамида: одна треть произведения площади основания пирамиды и высоты.
Параллелепипед: произведение длины, ширины и высоты. Если высота неизвестна, то ее можно вычислить, используя ребро и угол, который оно образует с основанием. Если мы назовем ребро а , угол А , длину — l , а ширину — w , то объем параллелепипеда V равен:
V = l w a cos(A )
Этот объем также можно вычислить, используя свойства прямоугольных треугольников.
Конус: радиус в квадрате, умноженный на высоту и ⅓π.
Шар: радиус в третьей степени, умноженный на 4/3π.
Цилиндр: произведение площади основания цилиндра, высоты, и π: V=π r² h, где r — радиус цилиндра и h — его высота
Соотношение между объемами цилиндр:шар:конус равно 3:2:1.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Стало быть в 1 м кубическом — 100 в кубе см кубических
А на дано: х м кубических — 1000 см кубических
Мы получили самую обыкновенную пропорцию, решаем е quot;крест-накрестquot;, получаем:
х= 1 * 1000/100 * 100 * 100 (100 в кубе)
Получается х= 0,001 или 1*10 в минус 3 степени (если так удобнее для решения задачи)
Известно, что в 1 дм — 10 см
Тогда в 1 дм кубическом — 10 в кубе см кубических (т.е. 10 * 10 * 10=1000)
Если речь идет о величине — кубических см или метрах, то просто возводим в соответствующую степень, в данном случае — 3.
Таким образом получаем следующее: в 1 куб. м будет 1 000 000 куб. см. Мы возвели в куб количество сантиметров в одном метре. Точно так же можно и поступить с другими величинами.
Я знаю, что в одном метре ровно 100 сантиметров. Далее в одном метре ровно 10 дециметров, ну а в одном дециметре ровно 10 сантиметров.
Далее в одном метре ровно 10 дециметров, ну а в одном дециметре ровно 10 сантиметров.
1 м. = 100 см. Отсюда 1 см. = 0.01 м.
1 дм. = 10 см. Отсюда 1 см. = 0.1 дм.
1 м. = 10 дм. Отсюда 1 дм. = 0.1 м.
Квадратное — значит возводим в квадрат, кубическое — возводим в куб. В итоге получается следующее:
В 1 куб. м. = 1 000 000 куб. см. То есть количество сантиметров в одном метре возвели в куб. Также и со всеми остальными величинами. В 1 куб. м. = 1 000 куб. дм. В 1 куб. дм. = 1 000 куб. см. Это же все математика.
Ну и наоборот, В 1 куб. см. = 0. 000 001 куб. м.
Для того, чтобы без расчетов воспользоваться готовыми ответами или проверить себя, можно воспользоваться специальным переводчиком, например здесь
1.Переводим кубические сантиметры в кубические метры или см3 в м3
100 см, таким образом в 1 см=1/100 м=0,01 м
Теперь, чтобы понятней объяснить подробно запишем так
1см3 =1см х 1см х 1 см =0,01 м х0,01 м х 0,01 м = 0,000 001 м3 ,
т. е. чтобы перевести см3 в м3 нужно количество см3 поделить на 1 000 000 (1 миллион)
е. чтобы перевести см3 в м3 нужно количество см3 поделить на 1 000 000 (1 миллион)
Примеры перевода 1000 см3 в м3:
вариант 1 1 000 см3= 1 000 х 1 см3= 1000 х 0,000 001 м3=0,001 м3
вариант 2 1 000 см3 =1 000/1 000 000 =0,001 м3
Примеры перевода 3000 см3 в м3:
вариант 1 3 000 см3= 3 000 х 1 см3= 3 000 х0,01м х0,01м х 0,01м= 3 000 х 0,000 001 м3=0,003 м3
вариант 2 3 000 см3 =3 000/1 000 000 =0,003 м3
____________________________________________________________________________ shy;______________________________
2.Переводим кубические метры в кубические сантиметры, то есть м3 в см3
3.Переводим кубические дециметры в кубические сантиметры или дм3 в см3
1 дм3 = 10 см х10 см х10 см =1000 см3 , то есть для перевода нужно количество дециметров умножить на 1000.
да ладно вам! вы что, в школе не учились???
известно, что в одном метре 100 сантиметров. когда мы имеем дело с объемом, то у нас величины растут в трех направлениях — по длине, ширине и высоте.
когда мы имеем дело с объемом, то у нас величины растут в трех направлениях — по длине, ширине и высоте.
Калькулятор перевода метров квадратных в метры кубические
поэтому чтобы перевести сантиметры кубические в метры кубические, надо делить величину не на 100, а на миллион, т.е. надо умножить на 10 в -6 степени.
соответственно, 1куб.м. равен миллиону кубических см.
а 1000куб.м. равно 1 миллиарду куб.см.
с дециметрами точно так же: т.к. в 1дециметре 10 сантиметров, то 1куб.дм. равен 1000 куб.см.
Чтобы перевести кубические сантиметры в кубические метры надо сантиметры поделить на 1000000 (один миллион). Например нам надо перевести 3000 кубических сантиметров в кубические метры, 3000 делим на 1000000 и получаем 0,3 метра кубических.
ООО этоже математика начальных классов*-*, о это великолепное время, когда мы были маленькие и нас только учили считать и переводить из метров в сантиметры и тд. Ну это так небольшое отступление:) Ну например вот: 1 000 см3= 1 000 х 1 см3= 1000 х 0,000 001 м3=0,001 м3
Урок 53 «Кубический дециметр и кубический сантиметр» (1 урок)
Предметные задачи:
— продолжение линии по изучению единиц измерения объёма — соотношение между кубическим дециметром и кубическим сантиметром:
1 куб.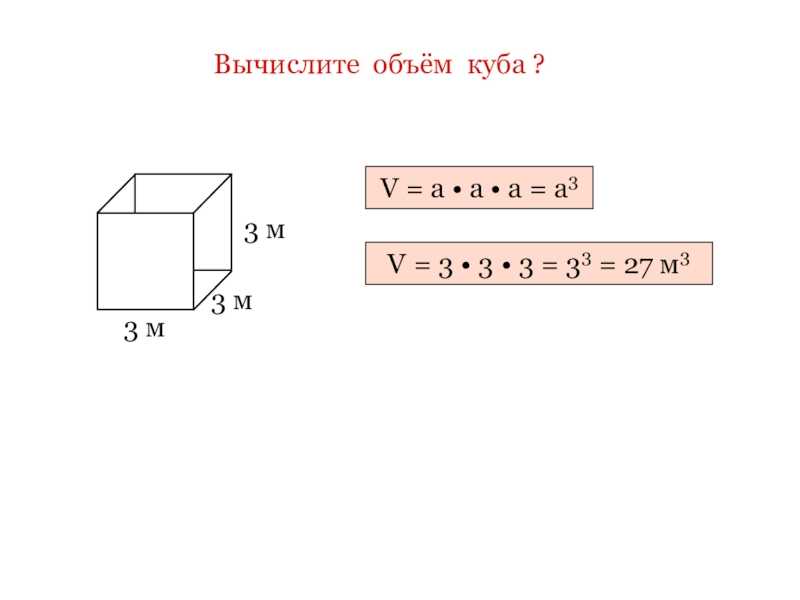 дм = 1000 куб.
дм = 1000 куб.
Конвертер величин
— решение задач с использованием изучаемых единиц измерения объёма:
1 куб см, куб. дм;
Формирование УУД: Познавательные УУД : использование таблиц, сравнение и сопоставление единиц измерения объёма в условиях выполнения заданий. Регулятивные: умение определять задачи урока, анализировать достигнутые результаты Коммуникативные: умение излагать своё мнение и аргументировать свою точку зрения, управлять действиями партнёраЛичностные: ориентация на самоанализ и самоконтроль результата, на анализ соответствия результатов требованиям конкретной задачи, на понимание предложений и оценок учителей, товарищей
Пропедевтика: измерение объемов геометрических фигур.
Повторение: алгоритм сложения и вычитания столбиком.
Методы и приемы организации деятельности учащихся
: беседа, организация самостоятельной работы учащихся по заданиям учебника. Учебно-методическое обеспечение: У-1
, Т-1.
Вводная часть урока
Учащиеся озвучивают тему урока, просматривают с.94 учебника и высказывают предположение о том, что на уроке мы узнаем, что 1 куб. дм = = 1000 куб. см., научимся выражать объем в кубических сантиметрах, данный в кубических дециметрах и кубических сантиметрах, выполнять кратное сравнение двух данных объемов.
Задаём вопросы из учебника, требуя развернутых ответов.
— Чему равен объём куба с ребром 1 см? (Объём куба с ребром 1 см равен 1 куб. см)
— Как можно назвать единицу объёма, представленную кубом с ребром 1 дм? (единицу объёма, представленную кубом с ребром 1 дм, можно назвать кубическим дециметром)
— Сколько сантиметров в 1 дециметре? (В одном дециметре 10 см)
Записываем на доске: 1 дм = 10 см
— Сколько квадратных сантиметров в 1 квадратном дециметре? (В 1 кв. дм – 100 кв. см)
Дополняем запись на доске: 1 дм = 10 см 1кв. дм = 100 кв. см
ДЕЦИМЕТР (с. 116) и ответить на вопрос: сколько кубических сантиметров в 1 КУБИЧЕСКОМ ДЕЦИМЕТРЕ? (1 куб дм – 1000 куб. см)
см)
Обращаем внимание учеников на голубую плашку и предлагаем доказать справедливость равенства: 1 куб дм – 1000 куб. см
Вызываем к доске ученика, который выполняет соответствующие преобразование: 1 куб. дм = 1 дм ∙ 1 дм ∙ 1 дм = 10 см ∙ 10 см ∙ 10 см =
1000 куб. см
Задание № 318 (У – 1, с. 94)
Спрашиваем, сколько кубиков со стороной 1 дм можно уложить на дно коробки, длина которой – 3 дм, а ширина – 2 дм? (3 куб. ∙ 2 ряда = 6 куб.) Выясняем, что высота коробки равна 1 дм, значит, в коробке будет
1 слой, в котором 6 кубиков , следовательно, коробка ВМЕЩАЕТ 6 кубиков Делаем вывод, что ВМЕСТИМОСТЬ коробки равна 6 кубическим дециметрам, так как объём одного кубика со стороной 1 дм равен 1 куб. дм.
Задание № 319 (У – 1, с. 94)
Ожидаемый ответ: отрезок нужно увеличить в 10 раз, так как 1 см ∙ 10 = 10 см = 1 дм
Ожидаемый ответ: выполняем кратное сравнение величин: 1 кв. дм: 1 кв. см = 100 кв. см: 1 кв. см = 100 (раз), значит, 1 кв.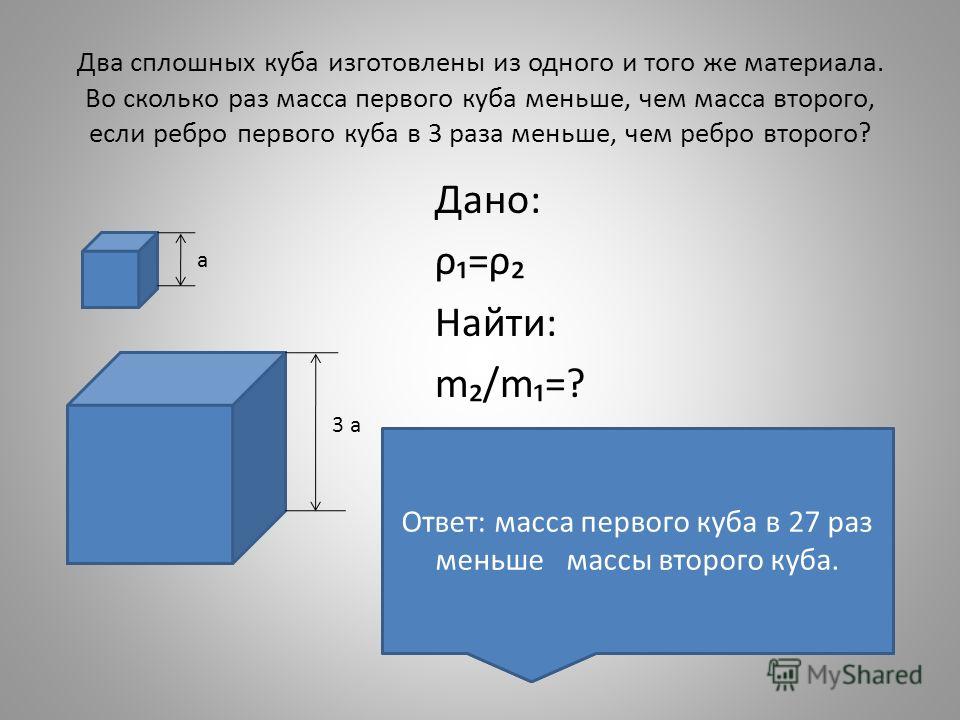 см меньше 1 кв. дм в 100 раз.
см меньше 1 кв. дм в 100 раз.
Предлагаем ученикам самостоятельно ответить на третье требование задания: во сколько раз 1 куб. см меньше 1 куб. дм? (пауза) Проверяем, вызывая к доске одного из учеников:
1 куб. дм: 1 куб. см = 1000 куб. дм: 1 куб. см = 1000 (раз), значит,
1 куб. см меньше 1 куб. дм в 1000 раз.
Задание № 320 (У – 1, с. 94)
Иллюстрируем образец оформления:
1 куб. дм + 500 куб. см = 1000 куб. см + 500 куб. см = 1500 куб. см Остальные задания учащиеся выполняют самостоятельно, затем сравнивают результаты.
Задание № 321 (У – 1, с. 94)
Учащиеся самостоятельно читают и выполняют задание. Даём время на выполнение, проверяем, проецируя на доску образцы решения: 326532 куб. дм + 867543 куб. дм = 1194075 куб.дм 326532
+ 867543
1785634 куб. дм – 1423156 куб. дм = 362478 куб.дм
— 1423156
Задание № 322 (У – 1, с. 95)
На доске иллюстрируем перевод кубических дециметров и кубических сантиметров в кубические сантиметры: 1 куб. дм 500 куб. см = 1 куб см + 500 куб. см == 1000 куб. см + 500 куб. см
= 1500 куб. см.
дм 500 куб. см = 1 куб см + 500 куб. см == 1000 куб. см + 500 куб. см
= 1500 куб. см.
Подчеркиваем те действия, которые можно выполнить устно, и предлагаем выполнить краткую запись:
1 куб. дм 500 куб. см = 1500 куб. см.
Организуем проверку посредством чтения развернутых решений по цепочке.
1 куб. дм 10 куб. см = 1000 куб. см + 10 куб. см = 1010 куб см
куб. дм 5 куб. см = 5000 куб. см.+ 5 куб. см = 5005 куб см
10 куб. дм 10 куб. см = 10000 куб. см.+ 10 куб см = 10010 куб. см
Задание № 323 (У – 1, с. 95)
Даём время на заполнение таблицы, проверяем устно чтением ответов по цепочке или проектируя ответы на доску:
Спрашиваем, сколько нужно взять чашек воды для того, чтобы получить 1 куб. дм воды?
Ожидаемый ответ: 4 чашки, так как 1 куб. дм = 1000 куб. см.
Задание № 324* (У – 1, с. 95)
Ученики читают задачу, озвучивают её своими словами и высказывают предположения о том, как можно вычислить размеры нового аквариума.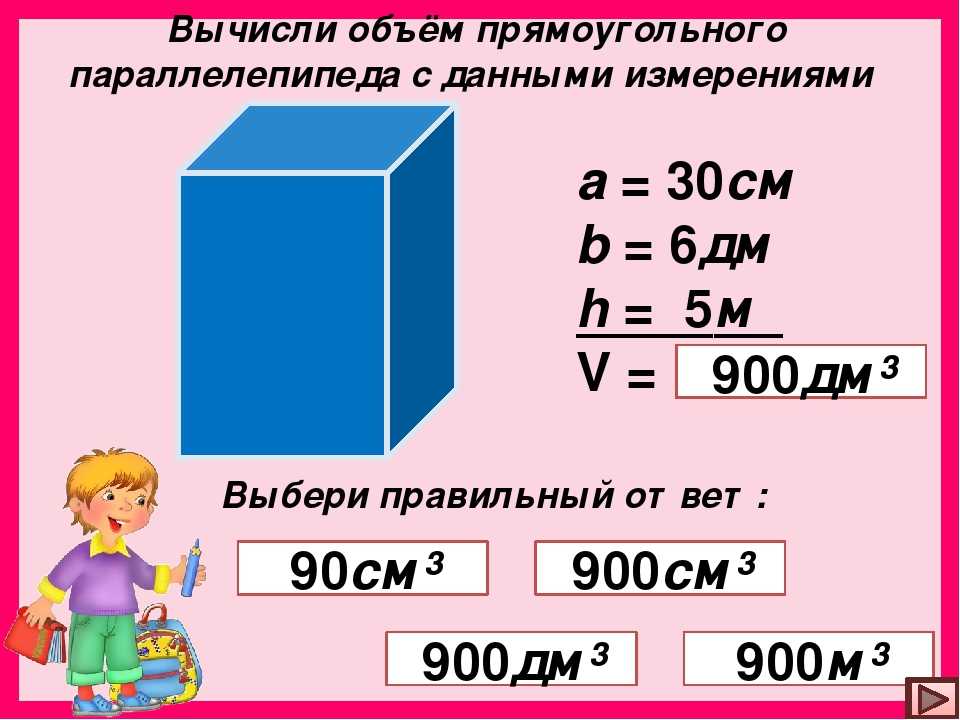 Ожидаемый ответ: данный аквариум заполнен водой наполовину. Для того, чтобы новый аквариум был полностью заполнен этим количеством воды, нужен аквариум меньшего размера. Это может быть аквариум, высота которого в 2 раза меньше данного аквариума. Записываем на доске краткую запись. решение и ответ задачи:
Ожидаемый ответ: данный аквариум заполнен водой наполовину. Для того, чтобы новый аквариум был полностью заполнен этим количеством воды, нужен аквариум меньшего размера. Это может быть аквариум, высота которого в 2 раза меньше данного аквариума. Записываем на доске краткую запись. решение и ответ задачи:
Длина – 6 дм
Ширина – 5 дм
Высота – 4 дм
4 дм: 2 = 2 дм – высота нового аквариума
Ответ: размеры нового аквариума: длина – 6 дм, ширина – 5 дм, высота – 2 дм.
Спрашиваем, можно ли решить по-другому? (да, можно уменьшить в 2 раза длину аквариума)
Записываем на доске другое решение и ответ задачи: 6 дм: 2 = 3 дм Ответ: размеры нового аквариума: длина – 3 дм, ширина – 5 дм, высота – 4 дм.
Спрашиваем, как ещё можно решить данную задачу? (можно уменьшить в
2 раза ширину аквариума)
Предлагаем ученикам самостоятельно записать решение и ответ задачи (пауза)
Проверяем, вызывая к доске одного из учеников: 5 дм: 2 = 50 см: 2 = 25 см Ответ: размеры нового аквариума: длина – 3 дм, ширина – 25 см, высота – 4 дм.
∙ Чтобы доказать правильность каждого из предложенных решений предлагаем ученикам проверить вместимость каждого нового аквариума.
Записываем на доске:
1 аквариум: 6 дм ∙ 5 дм ∙ 2 дм = 60 куб. дм
2 аквариум: 3 дм ∙ 5 дм ∙ 4 дм = 60 куб. дм
3 аквариум: 6 дм ∙ 25см ∙ 4 дм = 60 см ∙ 25 см ∙ 40 см = 60 000 куб. см =
Делаем вывод, если вместимость аквариумов одинаковая, значит, все три решения являются верными!
Задание № 325 (У – 1, с. 95)
Учащиеся самостоятельно читают задание. Спрашиваем, какие преобразования можно сделать для того, чтобы расположить данные объёмы в порядке возрастания?
Ожидаемый ответ: все объёмы можно выразить в кубических сантиметрах.
Пишем на доске и еще раз объясняем:
10 куб. дм 5 куб. см = 10000 куб. см + 5 куб. см = 10005 куб. см
Следующие преобразования учащиеся выполняют самостоятельно:
10 куб. дм 50 куб. см = 10000 куб. см + 50 куб. см = 10050 куб. см
10 куб. дм 555 куб. см = 10000 куб. см + 555 куб. см = 10555 куб. см
см + 555 куб. см = 10555 куб. см
Записываем на доске и синхронно в тетрадях все объёмы, но уже в одних и тех же единицах измерения: 10500 куб. см 10005 куб. см 10550 куб. см
10050 куб. см 15000 куб. см 10555 куб. см
Располагаем объёмы, выраженные в одних и тех же единицах, в порядке возрастания столбиком, а справа записываем ответ на требование задания, располагая объемы, выраженные разными единицами измерения, в порядке возрастания. Ответ:
10005 куб. см 10 куб. дм 5 куб. см
10050 куб. см 10 куб. дм 50 куб. см 10500 куб. см 10500 куб. см 10550 куб. см 10 куб. дм 50 куб. см
10555 куб. см 10 куб. дм 555 куб. см 15000 куб. см 15000 куб. см
Задание № 326 (У – 1, с. 95)
Выясняем, что для выполнения кратного сравнения данных объёмов нужно выразить их в одинаковых единицах измерения – кубических сантиметрах.
Записываем на доске: 10 куб. дм = 10000 куб. см
Задание на дом: № 135 – 136 (Т – 1, с. 73)
Перевод кубических сантиметров в кубические метры
Таблица перевода куба
Значительная часть строительных работ требует измерение в единицах объема. Это, прежде всего, бетонирование и кирпичная кладка, земля-ные работы. Зачастую, количество привезенных материалов измеряется в кубических единицах, также в них может измеряться объем вывезенного мусора. И при проектировании, и на строительстве, и в процессе лабораторных исследований пригодится настоящая таблица перевода единиц объема.
Это, прежде всего, бетонирование и кирпичная кладка, земля-ные работы. Зачастую, количество привезенных материалов измеряется в кубических единицах, также в них может измеряться объем вывезенного мусора. И при проектировании, и на строительстве, и в процессе лабораторных исследований пригодится настоящая таблица перевода единиц объема.
В таблице представлены следующие единицы: кубический метр, кубический дециметр, кубический сантиметр, кубический миллиметр, гекто-литр, декалитр, литр, децилитр, сантилитр, миллилитр и микролитр.
Некоторые из приведенных единиц на практике встречаются редко, но таблица без них не была бы полной.
Для каждой единицы объема составлена отдельная таблица перевода в другие единицы через коэффициенты.
Пример: Требуется выразить величину 0,6 м3 в других единицах измерения.
Рассмотрим таблицу соответствия 1 квадратного метра и поочеред-но перемножим наше значение на коэффициенты перевода.
- В результате расчетов определяем, что 0,6 м2 составляет:
- 600 кубических дециметров;
- 600000 или 6×105 кубических сантиметров;
- 6×108 кубических миллиметров;
- 6 гектолитров;
- 60 декалитров;
- 600 литров;
- 6000 децилитров;
- 60000 сантилитров;
- 600000 миллилитров;
- 6×108 микролитров.
Словарь строителя:: Вопросы по ремонту:: Калькуляторы:: Спецтехника:: Разное
2006 — 2017 © пользовательское соглашение:: связь с администрацией сайта [email protected]
Частенько у учащихся возникают сложности с переводом одних единиц измерения в другие. Отсюда и множество вопросов вроде:
- Сколько литров в кубе?
- 1 куб – сколько это литров?
- Сколько литров в кубе воды,
- Сколько литров в кубе газа, пропана, бензина, песка, земли, керамзита?
- Сколько в кубе литров метана, сжиженного газа?
- Как перевести см в кубе или дм куб в литры?
- Куб бетона, бензины, солярки, дизельного топливо — это сколько литров?
Далее можно выделить группу вопросов более конкретных, к примеру, сколько литров в кубе воды в ванне или сколько кубов в бочке 200 литров, в ведре в 10 литров? А 40 литров сухого водорода это сколько кубов? Данные вопросы актуальны как для учащихся при решении различных задач, так и в практических целях, например, при покупке какой-нибудь емкости для воды. Разберемся же в этом вопросе основательно, вспомним, так сказать, мат. часть, чтобы в любой момент с легкостью можно перевести кубы в литры, ну и конечно обратно.
Разберемся же в этом вопросе основательно, вспомним, так сказать, мат. часть, чтобы в любой момент с легкостью можно перевести кубы в литры, ну и конечно обратно.
Обратим в первую очередь внимание на тот факт, что вне зависимости от вещества, размещаемое в емкости перевод из литров в кубы всегда будет одинаков, будь то вода, газ, песок или бензин.
Сколько в 1 кубе литров?
Начнем с лирического отступления, а именно с курса школьной физики. Известно, что общепринятая единица измерения объема – это кубический метр.
1 кубический метр – это объем куба, сторона которого равна ровно одному метру. Эта единица не всегда является удобным и именно по этой причине очень часто используются другие – литры – они же кубические дециметры и кубические сантиметры.
Как показала практика, наиболее удобной оказалась единица измерения объема – литр, которая представляет собой объем куба, длина которого 1 дм или 10 см. Таким образом получаем, что все вопросы как перевести дм куб в кубы равносильны вопросу как перевести литры в кубы, ведь 1 дм. куб = 1 литр.
куб = 1 литр.
Формула перевода объема куба в литры
1 куб. м = 1000 л (формула объема куба в литрах)
Формула перевода литров в метры кубические
1 л = 0,001 куб. м
А теперь вооружившись всеми необходимыми знаниями, можем переходить непосредственно к расчетам.
| Задача #1: Сколько литров в 0,5 кубах? Решение: Используя, приведенную выше формулу получаем: 0,5* 1000 = 500 литров. Ответ: в 0,5 кубах 500 литров. |
Задача #6: Сколько литров в 300 кубах? Решение: 300 * 1000 = 300 000 литров Ответ: в 300 кубах 300 тыс. литров. |
| Задача #2: В 1 куб м сколько литров? (самое простое) Решение: 1 * 1 000 = 1 000 литров. Ответ: в 1 кубе 1 000 литров. |
Задача #7: 5 кубов — сколько литров? Решение: 5 * 1000 = 5 000 литров Ответ: 5 кубов – это 5 тыс. литров. |
| Задача #3: 2 куба – это сколько литров? Решение: 2 * 1 000 = 2 000 литров. Ответ: в 2 кубах 2 000 литров. 
|
Задача #8: 6 кубов – это сколько литров? Решение: 6 * 1000 = 6 000 литров. Ответ: в 6 кубах 6 тыс. литров. |
| Задача #4: Сколько литров в 10 кубах? Решение: 10 * 1000 = 10 000 литров Ответ: в 10 кубах 10 тыс. литров. |
Задача #9: 4 куба сколько литров? Решение: 4 * 1000 = 4 000 литров Ответ: в 4 кубах 4 тыс. литров. |
| Задача #5: 20 кубов – это сколько литров? Решение: 20 * 1000 = 20 000 литров Ответ: в 20 кубах 20 тыс. литров. |
Задача #10: 500 куба сколько литров? Решение: 500 * 1000 = 500 000 литров Ответ: в 500 кубах 500 тыс. литров. |
Сколько кубов в N литрах?
Рассмотрим теперь обратные задачи о нахождении количества кубов в указанном количестве литров.
| Задача #1: Сколько кубов в 100 литрах? Решение: 100 * 0,001 = 0,1 куб. метр. Ответ: 100 литров – это 0,1 метра куб. |
Задача #6: Сколько кубов в 1500 литрах? Решение: 1500 * 0,001 = 1,5 метров кубических.  Ответ: в 1500 литров 1,5 метров кубических. |
| Задача #2: Сколько кубов в 200 литрах? Решение: 200 * 0,001 = 0,2 куб. метра. Ответ: в 200 литров 0,2 м. метра. |
Задача #7: Сколько кубов в 3000 литрах? Решение: 3000 * 0,001 = 3 метров кубических. Ответ: в 3000 литрах — 3 метров кубических. |
| Задача #3: Сколько кубов в 140 литрах? Решение: 140 * 0,001 = 0,14 кубометров. Ответ: в 140 литров 0,14 кубометров. |
Задача #8: Сколько кубов в 5000 литрах? Решение: 5000 * 0,001 = 5 метров кубических. Ответ: в 5 000 литрах — 5 метров кубических. |
| Задача #4: Сколько кубов в 500 литрах? Решение: 500 * 0,001 = 0,5 кубов. Ответ: в 500 литров 0,5 кубов. |
Задача #9: Сколько кубов в 10 000 литрах? Решение: 10 000 * 0,001 = 10 куб. м. Ответ: в 10 000 литрах – 10 куб. м. |
| Задача #5: Сколько кубов в 1000 литрах? Решение: 1000 * 0,001 = 1 метр кубический.  Ответ: в 1000 литрах 1 метр кубический. |
Задача #10: Сколько кубов в 30 000 литрах? Решение: 30 000 * 0,001 = 30 куб. м. Ответ: в 30 000 литров 30 куб. м. |
Для быстроты расчетов предлагаем воспользоваться вам нашими онлайн калькуляторами:
Если остались какие-то вопросы по данной теме оставляйте их здесь внизу в комментариях.
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер плотности потока водяного пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
1 кубический метр [м³] = 1000000 кубический сантиметр [см³]
Исходная величина
Преобразованная величина
кубический метр кубический километр кубический дециметр кубический сантиметр кубический миллиметр литр эксалитр петалитр тералитр гигалитр мегалитр килолитр гектолитр декалитр децилитр сантилитр миллилитр микролитр нанолитр пиколитр фемтолитр аттолитр куб.см капля баррель (нефтяной) баррель американский баррель британский галлон американский галлон британский кварта США кварта британская пинта США пинта британская стакан американский стакан (метрический) стакан британский унция жидкая США унция жидкая британская столовая ложка амер. столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
Общие сведения
Объем — это пространство, занимаемое веществом или предметом. Также объем может обозначать свободное пространство внутри емкости. Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Единицы объема
Кубический метр
Единица измерения объема в системе СИ — кубический метр. Стандартное определение одного кубического метра — это объем куба с ребрами длиной в один метр. Также широко используются производные единицы, например, кубические сантиметры.
Литр
Литр — одна из наиболее часто используемых единиц в метрической системе. Он равен объему куба с ребрами длиной 10 см:
1 литр = 10 см × 10 см × 10 см = 1000 кубических сантиметров
Это все равно, что 0,001 кубических метров. Масса одного литра воды при температуре 4°C примерно равна одному килограмму. Часто используются также миллилитры, равные одному кубическому сантиметру или 1/1000 литра. Миллилитр обычно обозначают как мл.
Джилл
Джиллы — единицы объема, используемые в США для измерения алкогольных напитков. Один джилл — это пять жидких унций в Британской имперской системе или четыре в американской. Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Драм
Драм, или драхма — мера объема, массы, а также монета. В прошлом эта мера использовалась в аптекарском деле и равнялась одной чайной ложке. Позже стандартный объем чайной ложки изменился, и одна ложка стала равна 1 и 1/3 драхмы.
Объемы в кулинарии
Жидкости в кулинарных рецептах обычно измеряют по объему. Сыпучие и сухие продукты в метрической системе, наоборот, измеряют по массе.
Чайная ложка
Объем чайной ложки разный в разных системах измерения. Изначально одна чайная ложка была четвертью столовой, потом — одной третьей. Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Столовая ложка
Объем столовой ложки тоже колеблется в зависимости от географического региона. Так, например, в Америке, одна столовая ложка — это три чайных, пол-унции, примерно 14,7 миллилитра, или 1/16 американской чашки. Столовые ложки в Великобритании, Канаде, Японии, Южной Африке и Новой Зеландии — тоже содержат три чайных ложки. Так, метрическая столовая ложка — 15 миллилитров. Британская столовая ложка — 17.7 миллилитра, если чайная — 5,9, и 15, — если чайная — 5 миллилитров. Австралийская столовая ложка — ⅔ унции, 4 чайных ложки, или 20 миллилитров.
Чашка
Как мера объема, чашка не определяется так строго, как ложки. Объем чашки может варьировать от 200 до 250 миллилитров. Метрическая чашка — 250 миллилитров, а американская немного меньше, примерно 236,6 миллилитра. В американской диетологии объем чашки равен 240 миллилитрам. В Японии чашки еще меньше — всего 200 миллилитров.
Кварты и галлоны
Галлоны и кварты также имеют разную величину, в зависимости от географического региона, где они используются. В имперской системе измерения один галлон равен 4,55 литра, а в американской системе мер — 3,79 литра. В основном в галлонах измеряют топливо. Кварта равна четверти галлона и, соответственно, 1,1 литра в американской системе, и примерно 1,14 литра в имперской системе.
Пинта
В пинтах измеряют пиво даже в странах, где пинту не используют для измерения других жидкостей. В Великобритании в пинтах измеряют молоко и сидр. Пинта равна одной восьмой галлона. В некоторых других странах Содружества Наций и Европы также используют пинты, но, так как они зависят от определения галлона, а галлон имеет разный объем в зависимости от страны, пинты также не везде одинаковы. Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Жидкая унция
Имперская унция примерно равна 0,96 американской унции. Таким образом, в имперской унции содержится приблизительно 28,4 миллилитра, а в американской -29,6 миллилитра. Одна американская унция также приблизительно равна шести чайным ложкам, двум столовым, и одной восьмой чашки.
Вычисление объема
Метод вытеснения жидкости
Объем предмета можно вычислить с помощью метода вытеснения жидкости. Для этого его опускают в жидкость известного объема, геометрически вычисляют или измеряют новый объем, и разница этих двух величин и есть объем измеряемого предмета. Например, если при опускании предмета в чашку с одним литром воды, объем жидкости увеличится до двух литров, значит объем предмета — один литр. Таким способом можно вычислить только объем предметов, которые не впитывают жидкость.
Формулы для вычисления объема
Объем геометрических фигур можно вычислить при помощи следующих формул:
Призма:
произведение площади основания призмы на высоту._5-500x500.jpg)
Прямоугольный параллелепипед: произведение длины, ширины и высоты.
Куб: длина ребра в третьей степени.
Эллипсоид: произведение полуосей и 4/3π.
Пирамида: одна треть произведения площади основания пирамиды и высоты.
Параллелепипед: произведение длины, ширины и высоты. Если высота неизвестна, то ее можно вычислить, используя ребро и угол, который оно образует с основанием. Если мы назовем ребро а , угол А , длину — l , а ширину — w , то объем параллелепипеда V равен:
V = l w a cos(A )
Этот объем также можно вычислить, используя свойства прямоугольных треугольников.
Конус: радиус в квадрате, умноженный на высоту и ⅓π.
Шар: радиус в третьей степени, умноженный на 4/3π.
Цилиндр: произведение площади основания цилиндра, высоты, и π: V=π r² h, где r — радиус цилиндра и h — его высота
Соотношение между объемами цилиндр:шар:конус равно 3:2:1.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Конвертер длины и расстояния Конвертер массы Конвертер мер объема сыпучих продуктов и продуктов питания Конвертер площади Конвертер объема и единиц измерения в кулинарных рецептах Конвертер температуры Конвертер давления, механического напряжения, модуля Юнга Конвертер энергии и работы Конвертер мощности Конвертер силы Конвертер времени Конвертер линейной скорости Плоский угол Конвертер тепловой эффективности и топливной экономичности Конвертер чисел в различных системах счисления Конвертер единиц измерения количества информации Курсы валют Размеры женской одежды и обуви Размеры мужской одежды и обуви Конвертер угловой скорости и частоты вращения Конвертер ускорения Конвертер углового ускорения Конвертер плотности Конвертер удельного объема Конвертер момента инерции Конвертер момента силы Конвертер вращающего момента Конвертер удельной теплоты сгорания (по массе) Конвертер плотности энергии и удельной теплоты сгорания топлива (по объему) Конвертер разности температур Конвертер коэффициента теплового расширения Конвертер термического сопротивления Конвертер удельной теплопроводности Конвертер удельной теплоёмкости Конвертер энергетической экспозиции и мощности теплового излучения Конвертер плотности теплового потока Конвертер коэффициента теплоотдачи Конвертер объёмного расхода Конвертер массового расхода Конвертер молярного расхода Конвертер плотности потока массы Конвертер молярной концентрации Конвертер массовой концентрации в растворе Конвертер динамической (абсолютной) вязкости Конвертер кинематической вязкости Конвертер поверхностного натяжения Конвертер паропроницаемости Конвертер плотности потока водяного пара Конвертер уровня звука Конвертер чувствительности микрофонов Конвертер уровня звукового давления (SPL) Конвертер уровня звукового давления с возможностью выбора опорного давления Конвертер яркости Конвертер силы света Конвертер освещённости Конвертер разрешения в компьютерной графике Конвертер частоты и длины волны Оптическая сила в диоптриях и фокусное расстояние Оптическая сила в диоптриях и увеличение линзы (×) Конвертер электрического заряда Конвертер линейной плотности заряда Конвертер поверхностной плотности заряда Конвертер объемной плотности заряда Конвертер электрического тока Конвертер линейной плотности тока Конвертер поверхностной плотности тока Конвертер напряжённости электрического поля Конвертер электростатического потенциала и напряжения Конвертер электрического сопротивления Конвертер удельного электрического сопротивления Конвертер электрической проводимости Конвертер удельной электрической проводимости Электрическая емкость Конвертер индуктивности Конвертер Американского калибра проводов Уровни в dBm (дБм или дБмВт), dBV (дБВ), ваттах и др. единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
единицах Конвертер магнитодвижущей силы Конвертер напряженности магнитного поля Конвертер магнитного потока Конвертер магнитной индукции Радиация. Конвертер мощности поглощенной дозы ионизирующего излучения Радиоактивность. Конвертер радиоактивного распада Радиация. Конвертер экспозиционной дозы Радиация. Конвертер поглощённой дозы Конвертер десятичных приставок Передача данных Конвертер единиц типографики и обработки изображений Конвертер единиц измерения объема лесоматериалов Вычисление молярной массы Периодическая система химических элементов Д. И. Менделеева
1 кубический метр [м³] = 1000000 куб.см [см³]
Исходная величина
Преобразованная величина
кубический метр кубический километр кубический дециметр кубический сантиметр кубический миллиметр литр эксалитр петалитр тералитр гигалитр мегалитр килолитр гектолитр декалитр децилитр сантилитр миллилитр микролитр нанолитр пиколитр фемтолитр аттолитр куб.см капля баррель (нефтяной) баррель американский баррель британский галлон американский галлон британский кварта США кварта британская пинта США пинта британская стакан американский стакан (метрический) стакан британский унция жидкая США унция жидкая британская столовая ложка амер. столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
столовая ложка (метр.) столовая ложка брит. десертная ложка амер. десертная ложка брит. чайная ложка амер. чайная ложка метрич. чайная ложка брит. джилл, гилл американский джилл, гилл британский миним американский миним британский кубическая миля кубический ярд кубический фут кубический дюйм регистровая тонна 100 кубических футов 100-футовый куб акр-фут акр-фут (США, геодезический) акр-дюйм декастер стер децистер корд тан хогсхед досковый фут драхма кор (библейская единица) хомер (библейская единица) бат (библейская единица) гин (библейская единица) каб (библейская единица) лог (библейская единица) стакан (испанский) объем Земли Планковский объем кубическая астрономическая единица кубический парсек кубический килопарсек кубический мегапарсек кубический гигапарсек бочка ведро штоф четверть винная бутылка водочная бутылка стакан чарка шкалик
Общие сведения
Объем — это пространство, занимаемое веществом или предметом. Также объем может обозначать свободное пространство внутри емкости. Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Объем — трехмерная величина, в отличие от, например, длины, которая является двумерной. Поэтому объем плоских или двумерных объектов равен нулю.
Единицы объема
Кубический метр
Единица измерения объема в системе СИ — кубический метр. Стандартное определение одного кубического метра — это объем куба с ребрами длиной в один метр. Также широко используются производные единицы, например, кубические сантиметры.
Литр
Литр — одна из наиболее часто используемых единиц в метрической системе. Он равен объему куба с ребрами длиной 10 см:
1 литр = 10 см × 10 см × 10 см = 1000 кубических сантиметров
Это все равно, что 0,001 кубических метров. Масса одного литра воды при температуре 4°C примерно равна одному килограмму. Часто используются также миллилитры, равные одному кубическому сантиметру или 1/1000 литра. Миллилитр обычно обозначают как мл.
Джилл
Джиллы — единицы объема, используемые в США для измерения алкогольных напитков. Один джилл — это пять жидких унций в Британской имперской системе или четыре в американской.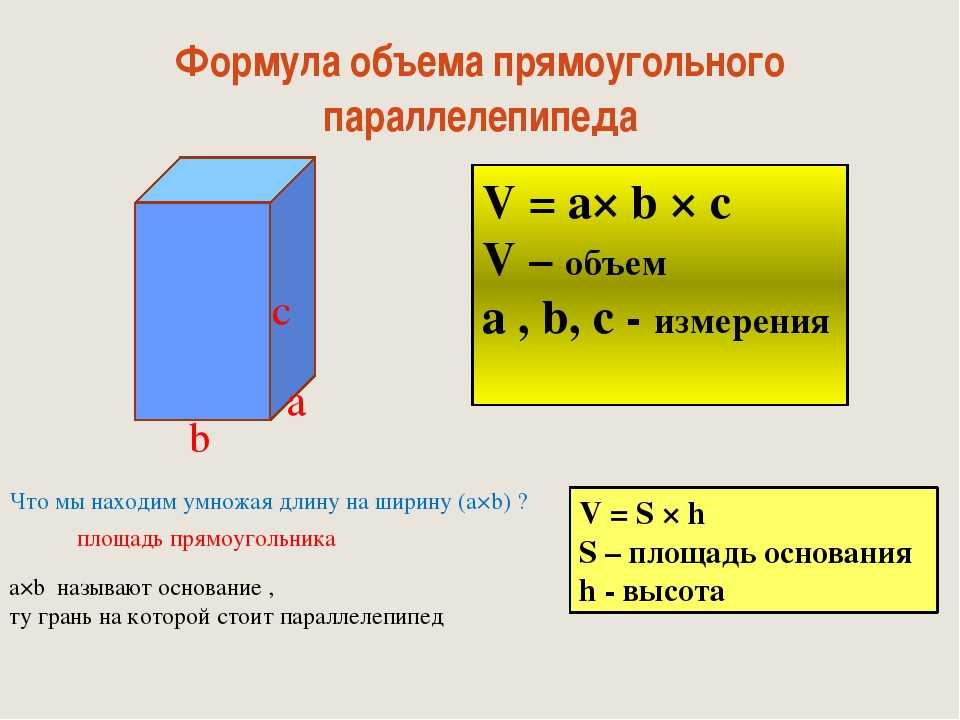 Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Один американский джилл равен четверти пинты или половине чашки. В Ирландских пабах подают горячительные напитки порциями в четверть джилла, или 35,5 миллилитра. В Шотландских порции меньше — одна пятая джилла, или 28,4 миллилитра. В Англии до недавнего времени порции были еще меньше, всего одна шестая джилла или 23,7 миллилитра. Теперь же, это 25 или 35 миллилитров в зависимости от правил заведения. Хозяева могут решать самостоятельно, какую из двух порций им подавать.
Драм
Драм, или драхма — мера объема, массы, а также монета. В прошлом эта мера использовалась в аптекарском деле и равнялась одной чайной ложке. Позже стандартный объем чайной ложки изменился, и одна ложка стала равна 1 и 1/3 драхмы.
Объемы в кулинарии
Жидкости в кулинарных рецептах обычно измеряют по объему. Сыпучие и сухие продукты в метрической системе, наоборот, измеряют по массе.
Чайная ложка
Объем чайной ложки разный в разных системах измерения. Изначально одна чайная ложка была четвертью столовой, потом — одной третьей. Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Именно последний объем сейчас используется в американской системе измерения. Это примерно 4,93 миллилитра. В американской диетологии размер чайной ложки равен 5 миллилитрам. В Великобритании обычно принято использовать 5,9 миллилитра, но в некоторых диетических пособиях и кулинарных книгах — это 5 миллилитров. Объем чайной ложки используемый в кулинарии обычно стандартизирован в каждой стране, но для еды используются ложки разных размеров.
Столовая ложка
Объем столовой ложки тоже колеблется в зависимости от географического региона. Так, например, в Америке, одна столовая ложка — это три чайных, пол-унции, примерно 14,7 миллилитра, или 1/16 американской чашки. Столовые ложки в Великобритании, Канаде, Японии, Южной Африке и Новой Зеландии — тоже содержат три чайных ложки. Так, метрическая столовая ложка — 15 миллилитров. Британская столовая ложка — 17.7 миллилитра, если чайная — 5,9, и 15, — если чайная — 5 миллилитров. Австралийская столовая ложка — ⅔ унции, 4 чайных ложки, или 20 миллилитров.
Чашка
Как мера объема, чашка не определяется так строго, как ложки. Объем чашки может варьировать от 200 до 250 миллилитров. Метрическая чашка — 250 миллилитров, а американская немного меньше, примерно 236,6 миллилитра. В американской диетологии объем чашки равен 240 миллилитрам. В Японии чашки еще меньше — всего 200 миллилитров.
Кварты и галлоны
Галлоны и кварты также имеют разную величину, в зависимости от географического региона, где они используются. В имперской системе измерения один галлон равен 4,55 литра, а в американской системе мер — 3,79 литра. В основном в галлонах измеряют топливо. Кварта равна четверти галлона и, соответственно, 1,1 литра в американской системе, и примерно 1,14 литра в имперской системе.
Пинта
В пинтах измеряют пиво даже в странах, где пинту не используют для измерения других жидкостей. В Великобритании в пинтах измеряют молоко и сидр. Пинта равна одной восьмой галлона. В некоторых других странах Содружества Наций и Европы также используют пинты, но, так как они зависят от определения галлона, а галлон имеет разный объем в зависимости от страны, пинты также не везде одинаковы. Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Имперская пинта равна примерно 568,2 миллилитра, а американская — 473,2 миллилитра.
Жидкая унция
Имперская унция примерно равна 0,96 американской унции. Таким образом, в имперской унции содержится приблизительно 28,4 миллилитра, а в американской -29,6 миллилитра. Одна американская унция также приблизительно равна шести чайным ложкам, двум столовым, и одной восьмой чашки.
Вычисление объема
Метод вытеснения жидкости
Объем предмета можно вычислить с помощью метода вытеснения жидкости. Для этого его опускают в жидкость известного объема, геометрически вычисляют или измеряют новый объем, и разница этих двух величин и есть объем измеряемого предмета. Например, если при опускании предмета в чашку с одним литром воды, объем жидкости увеличится до двух литров, значит объем предмета — один литр. Таким способом можно вычислить только объем предметов, которые не впитывают жидкость.
Формулы для вычисления объема
Объем геометрических фигур можно вычислить при помощи следующих формул:
Призма:
произведение площади основания призмы на высоту.
Прямоугольный параллелепипед: произведение длины, ширины и высоты.
Куб: длина ребра в третьей степени.
Эллипсоид: произведение полуосей и 4/3π.
Пирамида: одна треть произведения площади основания пирамиды и высоты.
Параллелепипед: произведение длины, ширины и высоты. Если высота неизвестна, то ее можно вычислить, используя ребро и угол, который оно образует с основанием. Если мы назовем ребро а , угол А , длину — l , а ширину — w , то объем параллелепипеда V равен:
V = l w a cos(A )
Этот объем также можно вычислить, используя свойства прямоугольных треугольников.
Конус: радиус в квадрате, умноженный на высоту и ⅓π.
Шар: радиус в третьей степени, умноженный на 4/3π.
Цилиндр: произведение площади основания цилиндра, высоты, и π: V=π r² h, где r — радиус цилиндра и h — его высота
Соотношение между объемами цилиндр:шар:конус равно 3:2:1.
Вы затрудняетесь в переводе единицы измерения с одного языка на другой? Коллеги готовы вам помочь. Опубликуйте вопрос в TCTerms и в течение нескольких минут вы получите ответ.
Корень (кубический, квадратный) в степени: решения, таблицы, примеры
Степенью называется выражение вида .
Здесь — основание степени, — показатель степени.
Степень с натуральным показателем
Проще всего определяется степень с натуральным (то есть целым положительным) показателем.
По определению, .
Выражения «возвести в квадрат» и «возвести в куб» нам давно знакомы.
Возвести число в квадрат — значит умножить его само на себя.
.
Возвести число в куб — значит умножить его само на себя три раза.
.
Возвести число в натуральную степень — значит умножить его само на себя раз:
Степень с целым показателем
Показатель степени может быть не только натуральным (то есть целым положительным), но и равным нулю, а также целым отрицательным.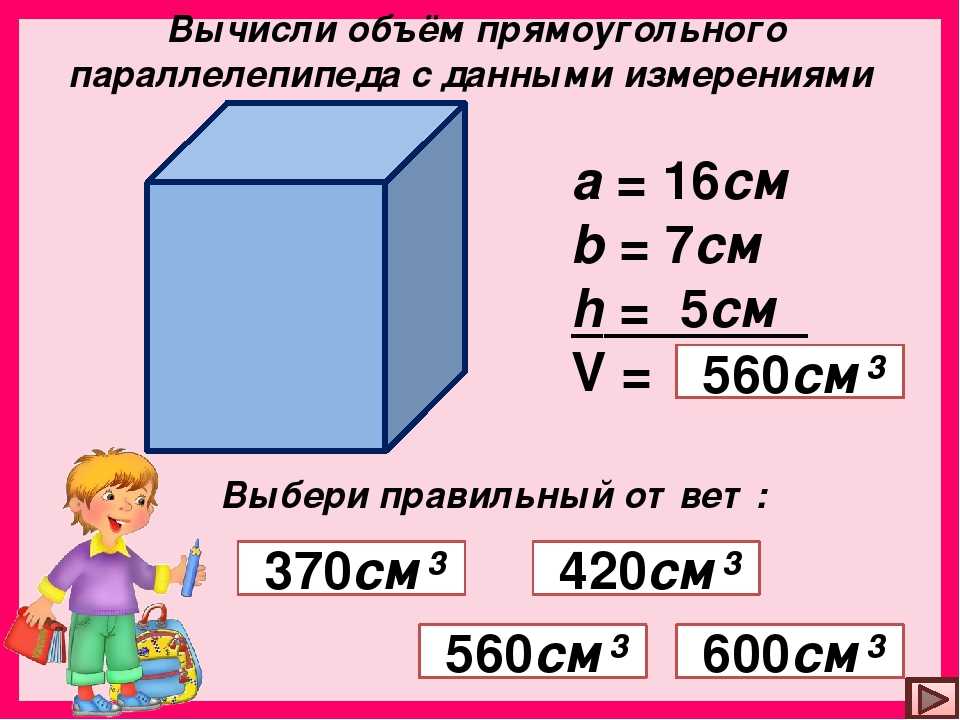
По определению,
.
Это верно для . Выражение 00 не определено.
Определим также, что такое степень с целым отрицательным показателем.
Конечно, все это верно для , поскольку на ноль делить нельзя.
Например,
Заметим, что при возведении в минус первую степень дробь переворачивается.
Показатель степени может быть не только целым, но и дробным, то есть рациональным числом. В статье «Числовые множества» мы говорили, что такое рациональные числа. Это числа, которые можно записать в виде дроби , где — целое, — натуральное.
Здесь нам понадобится новое понятие — корень -степени. Корни и степени — две взаимосвязанные темы. Начнем с уже знакомого вам арифметического квадратного корня.
Определение.
Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .
Согласно определению,
В школьной математике мы извлекаем корень только из неотрицательных чисел. Выражение для нас сейчас имеет смысл только при .
Выражение для нас сейчас имеет смысл только при .
Выражение всегда неотрицательно, т.е. . Например, .
Свойства арифметического квадратного корня:
Запомним важное правило:
По определению, .
Кубический корень
Аналогично, кубический корень из — это такое число, которое при возведении в третью степень дает число .
Например, , так как ;
, так как ;
, так как .
Обратите внимание, что корень третьей степени можно извлекать как из положительных, так и из отрицательных чисел.
Теперь мы можем дать определение корня -ной степени для любого целого .
Корень -ной степени
Корень -ной степени из числа — это такое число, при возведении которого в -ную степень получается число .
Например,
Заметим, что корень третьей, пятой, девятой — словом, любой нечетной степени, — можно извлекать как из положительных, так и из отрицательных чисел.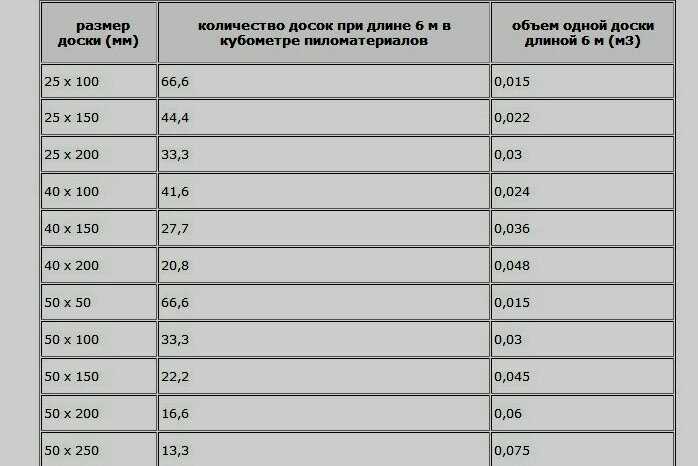
Квадратный корень, а также корень четвертой, десятой, в общем, любой четной степени можно извлекать только из неотрицательных чисел.
Итак, — такое число, что . Оказывается, корни можно записывать в виде степеней с рациональным показателем. Это удобно.
По определению,
в общем случае .
Сразу договоримся, что основание степени больше 0.
Например,
Выражение по определению равно .
При этом также выполняется условие, что больше 0.
Например,
Запомним правила действий со степенями:
— при перемножении степеней показатели складываются;
— при делении степени на степень показатели вычитаются;
— при возведении степени в степень показатели перемножаются;
Покажем, как применяются эти формулы в заданиях ЕГЭ по математике:
1.
Внесли все под общий корень, разложили на множители, сократили дробь и извлекли корень.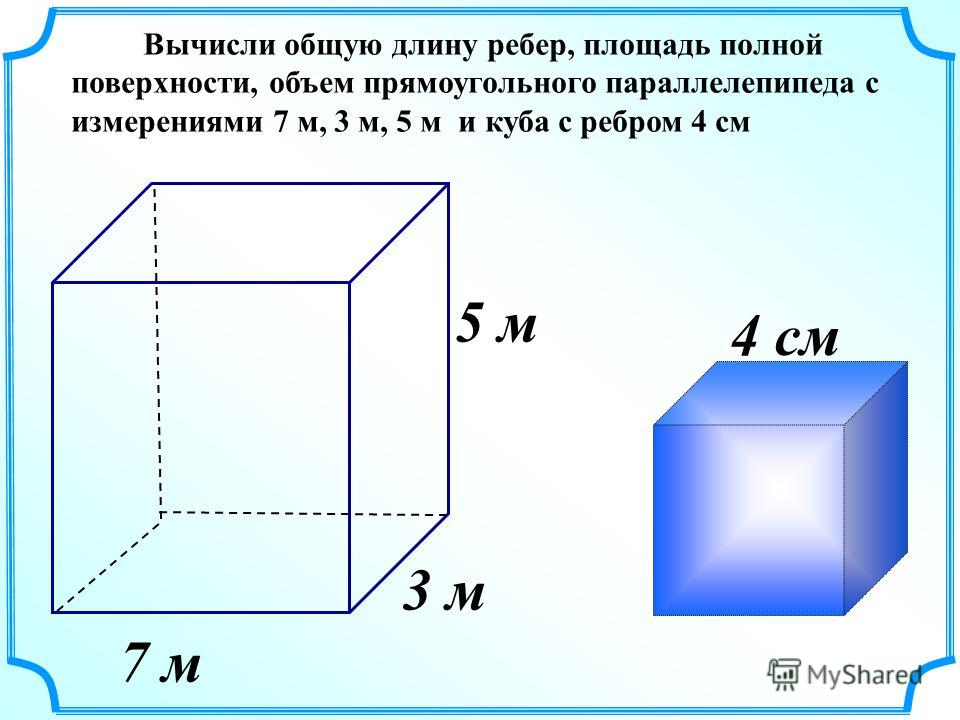
2.
3.
Здесь мы записали корни в виде степеней и использовали формулы действий со степенями.
4. Найдите значение выражения при
Решение:
При получим
Ответ: -0,5.
5. Найдите значение выражения при
Решение:
При a = 12 получим
Мы воспользовались свойствами степеней.
Ответ: 144.
6. Найдите значение выражения при b = — 5.
Решение:
При b = — 5 получим:
Ответ: -125.
7. Расположите в порядке возрастания:
Решение:
Запишем выражения как степени с положительным показателем и сравним.
Так как то
Так как то
Сравним и для этого оценим их разность:
значит
Получим : поэтому
Ответ:
8. Представьте выражение в виде степени:
Решение:
Вынесем за скобку степень с меньшим показателем:
Ответ:
9. Упростите выражение:
Решение:
Приведем основания 6 и 12 к основаниям 2 и 3:
(выполним деление степеней с одинаковыми основаниями)
Ответ: 0,25.
10. Чему равно значение выражения при ?
Решение:
При получим
Ответ: 9.
Сравнение арифметических корней11. Какое из чисел больше: или ?
Решение:
Возведем в квадрат оба числа (числа положительные):
Найдем разность полученных результатов:
так как
Значит, первое число больше второго.
Ответ:
Как избавиться от иррациональности в знаменателеЕсли дана дробь вида то нужно умножить числитель и знаменатель дроби на :
Тогда знаменатель станет рациональным.
Если дана дробь вида или то нужно умножить числитель и знаменатель дроби на сопряженное выражение, чтобы получить в знаменателе разность квадратов.
Сопряженные выражения — это выражения, отличающиеся только знаками. Например,
и и — сопряженные выражения.
Пример:
12. Вот несколько примеров — как избавиться от иррациональности в знаменателе:
Пример 1.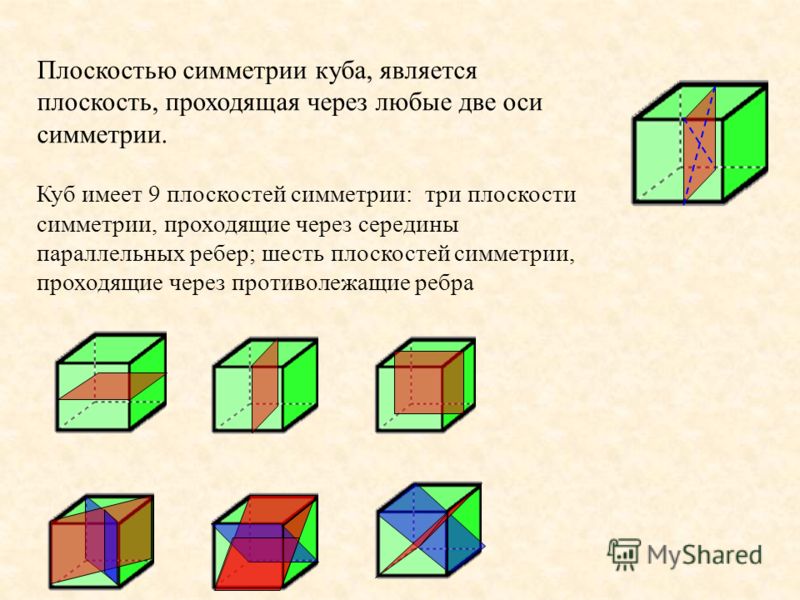
Пример 2.
Пример 3.
Пример 4.
Совет. Если в знаменателе дана сумма двух корней, то в разности первым числом пишите то, которое больше, и тогда разность квадратов корней будет положительным числом.
Пример 5.
13. Сравните и
1)
2) Сравним и 14.
то и а значит,
Ответ: меньше.
Как упрощать иррациональные выражения, пользуясь формулами сокращенного умноженияПокажем несколько примеров.
14. Упростите: выражения:
Пример 5.
т.к.
Пример 6.
Пример 7.
так как
Следующие несколько задач решаются с помощью формулы:
Решение:
Получим уравнение
Ответ:
19. Вычислите значение выражения:
Решение:
Ответ: 1.
20. Вычислите значение выражения:
Решение:
Ответ: 1.
21. Вычислите значение выражения: если
Вычислите значение выражения: если
Решение.
Если то следовательно
Ответ: — 1.
22. Вычислите:
Решение:
Ответ: 1.
Рассмотрим уравнение вида где
Это равенство выполняется, только если
Подробно об таких уравнениях — в статье «Показательные уравнения».
При решении уравнений такого вида мы пользуемся монотонностью показательной функции.
23. Решите уравнение:
а)
б)
в)
Решение.
23. Решите уравнение:
Решение:
тогда
Ответ: -1.
24. Решите уравнение:
Решение:
Ответ: 4.
25. Решите уравнение:
Решение:
Значит,
Ответ: -0,2.
Формулы сокращенного умножения 💣
Формулы сокращенного умножения
Вместо букв a, b могут быть любые числа, переменные или даже целые выражения. Для быстрого решения задач лучше выучить основные 7 формул сокращенного умножения (ФСУ) наизусть.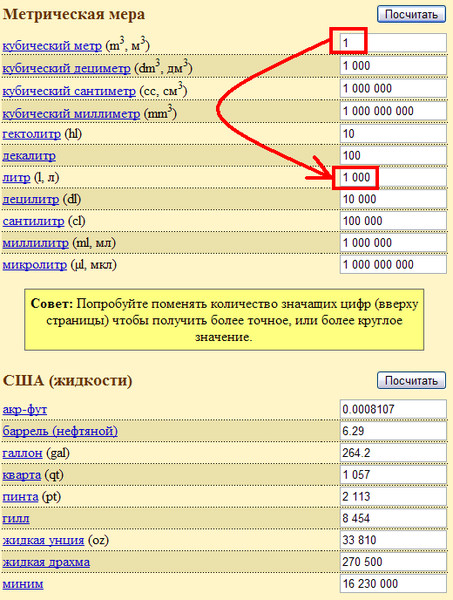 Да, алгебра такая, нужно быть готовым много запоминать.
Да, алгебра такая, нужно быть готовым много запоминать.
Ниже удобная табличка, которую можно распечатать и использовать, как закладку для быстрого запоминания формул.
Практикующий детский психолог Екатерина Мурашова
Бесплатный курс для современных мам и пап от Екатерины Мурашовой. Запишитесь и участвуйте в розыгрыше 8 уроков
Как читать формулы сокращенного умножения
Учимся проговаривать формулы сокращенного выражения:
- Разность квадратов двух выражений равна произведению их разности и их суммы.
- Квадрат суммы двух выражений равен квадрату первого плюс удвоенное произведение первого на второе плюс квадрат второго.
- Квадрат разности двух выражений равен квадрату первого минус удвоенное произведение первого на второе плюс квадрат второго.
- Сумма кубов двух выражений равна произведению суммы первого и второго на неполный квадрат их разности.
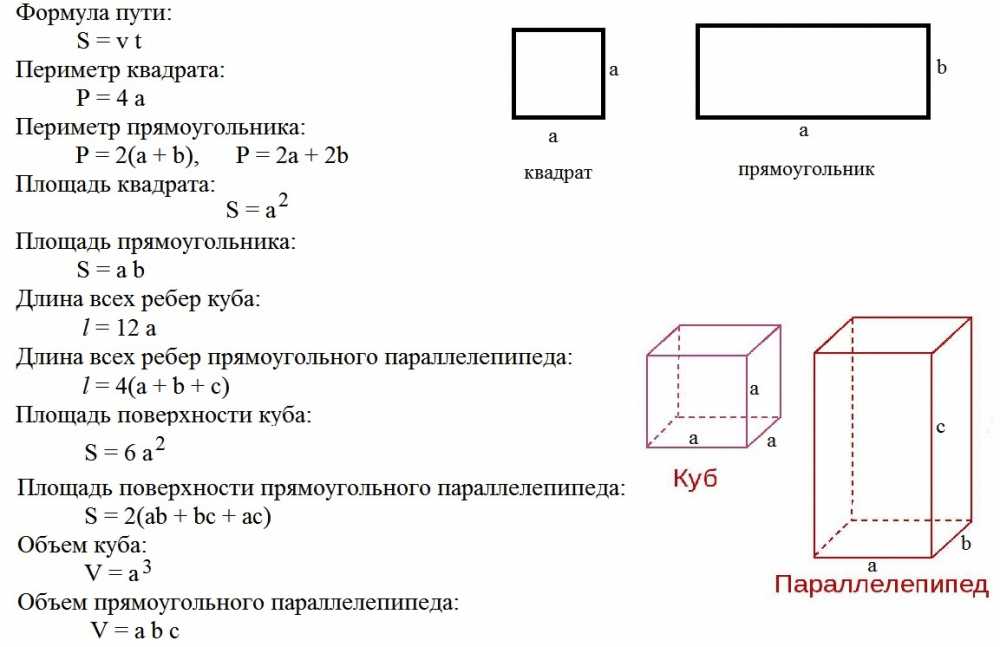
- Разность кубов двух выражений равна произведению разности первого и второго на неполный квадрат их суммы.
- Куб суммы двух выражений равен кубу первого плюс утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго плюс куб второго.
- Куб разности двух выражений равен кубу первого минус утроенное произведение квадрата первого на второе плюс утроенное произведение первого на квадрат второго минус куб второго.
Обучение на курсах по математике — дорога к хорошим оценкам в школе и высокому баллу на экзамене.
Доказательство формул сокращенного умножения
Напомним, что разность квадратов двух чисел a и b равна произведению их разности и их суммы: a2 — b2 = (a — b) * (a + b).
Иначе говоря, произведение суммы a и b на их разность равна разности их квадратов: (a — b) * (a + b) = a2 — b2.
Важно знать, что разность квадратов не равна квадрату разности: a2 — b2 ≠ (a — b)2.
Докажем, что a2 — b2 = (a — b) * (a + b).
Поехали:
- Используя искусственный метод, прибавим и отнимем одно и тоже a * b.
+ a * b — a * b = 0
a2 — b2 = a2 — b2 + ab — ab
- Сгруппируем иначе: a2 — b2 + a * b — a * b = a2 — a * b + a * b — b2
- Продолжим группировать: a2 — a * b — b2 +a * b = (a2 — a * b) + (a * b — b2)
- Вынесем общие множители за скобки:
(a2 — a * b) + (a * b — b2) = a *(a — b) + b *(a — b)
- Вынесем за скобки (a — b). a * (a — b) + b * (a — b) = (a — b) * (a + b)
- Результат доказательства: a2 — b2 = (a — b) * (a + b)
- Для того, чтобы доказать в обратную сторону: (a — b) * (a + b) = a2 — b2, нужно раскрыть скобки: (a — b) * (a + b) = a * a + a * b — b * a — b * b = a2 — b2.

Остальные ФСУ можно доказать аналогичным методом.
Учёба без слёз (бесплатный гайд для родителей)
Пошаговый гайд от Екатерины Мурашовой о том, как перестать делать уроки за ребёнка и выстроить здоровые отношения с учёбой.
Дополнительные формулы сокращенного умножения
К таблице основных ФСУ следует добавить еще несколько важных тождеств, которые пригодятся для решения задач.
Бином Ньютона
Формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных. Записывается вот так:
Пример вычисления биномиальных коэффициентов, которые стоят в строке под номером n в треугольнике Паскаля:
ФСУ для квадрата и куба суммы и разности — являются частными случаями формулы бинома Ньютона при n = 2 и n = 3.
Формула возведения в квадрат суммы трех, четырех и более слагаемых
Пригодится, если слагаемых в сумме, которую нужно возвести в степень, больше, чем два.
(a1+a2+…+an)2 = a12 + a22 + … + an-12 + an2 + 2 * a1 * a2 + 2 * a1 * a3 + 2 * a1 * a4 + … +
+ 2 * a1 * an-1 + 2 * a1 * an + 2 * a2 * a3 + 2 * a2 * a4 + … + 2 * a2 * an-1 + 2 * a2 * an +…+
+ 2 * an-1 * an
Читается так: квадрат суммы n слагаемых равен сумме квадратов всех этих слагаемых и удвоенных произведений всех возможных пар этих слагаемых.
Формула разности n-ых степеней двух слагаемых
an − bn = (a − b) * (an-1 + an-2 * b + an-3 * b2 + … + a * bn-2 + bn-1).
Для четных показателей можно записать так:
a2*m − b2*m = (a2 − b2) *(a2*m−2 + a2*m−4 * b2 + a2*m−6 * b4 + … + b2*m−2).
Для нечетных показателей:
a2*m+1 − b2*·m+1 = (a − b) * (a2*m + a2*m−1 * b + a2*m−2 * b2 + … + b2*m).
Частными случаями являются формулы разности квадратов и кубов при n = 2 и n = 3. Для разности кубов b можно также заменить на −b.
Решение задач
Давайте потренируемся и рассмотрим примеры с дробями.
Задание 1
Что сделать: вычислить квадрат произведения (55 + 10)2.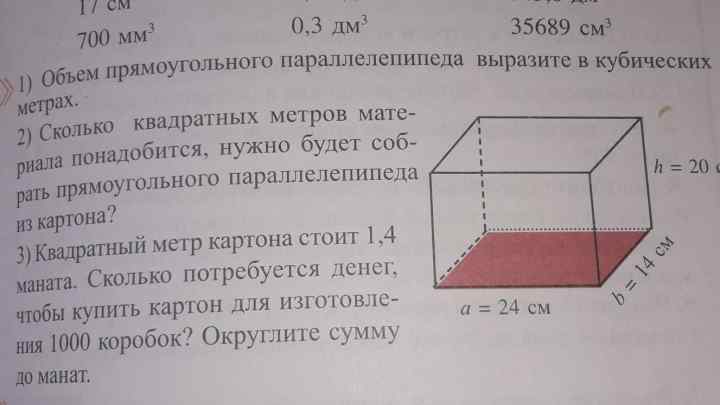
Как решаем: воспользуемся формулой квадрата суммы: (55 + 10)2 = 552 + 2 * 55 * 10 + 102 = 3025 + 1100 + 100 = 4225.
Задание 2
Что сделать: упростить выражение 64 * с3 – 8.
Как решаем: применим разность кубов: 64 * с3 – 8 = (4 * с)3 – 23 = (4 * с – 2)((4 * с)2 + 4 * с * 2 + 22) = (4 * с – 2)(16 * с2 + 8 * с + 4).
Задание 3
Что сделать: раскрыть скобки (7 * y — x) * (7 * y + x).
Как решаем:
- Произведем умножение: (7 * y — x) * (7 * y + x) = 7 * y * 7 * y + 7 * y * x — x * 7 * y — x * x = 49 * y2 + 7 * y * x — 7 * y * x — x2 = 49 * y2 — x2.
- Используем формулу сокращенного умножения: (7 * y — x) * (7 * y + x) = (7 * y)2 — x2 = 49 * y2 — x2.
Многочленов бояться не стоит, просто совершайте последовательно каждое действие. С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
С формулами решать задачки быстрее и удобнее — сохраняйте шпаргалку, запоминайте и радуйте своих учителей 🙂
1.12: Квадратные и кубические единицы
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 213139
Единицы измерения площадей и объемов часто включают показатели степени, поскольку для их определения требуются расчеты. Например, рассмотрим следующий расчет площади. 92\), что читается как «квадратные дюймы» или «дюймы в квадрате». 2\)). 92\)), превращая «квадратные футы» в желаемую единицу измерения.
2\)). 92\)), превращая «квадратные футы» в желаемую единицу измерения.
\( { \text{120} \; \cancel{\rm{in}} \times \cancel{\rm{in}}} \times \dfrac{1 \; \rm{ft}}{12 \; \cancel{\rm{in}}} \times \dfrac{1 \; \rm{ft}}{12 \; \cancel{\rm{in}}}\)
Обратите внимание, что коэффициент пересчета фактически умножается сам на себя, чтобы добиться требуемой отмены единицы. Следовательно, сам коэффициент преобразования можно было бы возвести в степень, как показано ниже.
9{2}\)
Хотя последние два обозначения эквивалентны, правильное использование второго представления требует четкого понимания его смысла. Обратите внимание, что степень должна быть записана вне круглых скобок, так как полный коэффициент преобразования умножается сам на себя. Следовательно, при правильном расчете числа и единицы должны быть возведены в квадрат. Рекомендуется явно записывать несколько коэффициентов преобразования, так как это обычно приводит к меньшему количеству ошибок учащихся по сравнению с использованием второго (сжатого) представления. 9{2}}\)
Следовательно, сам коэффициент преобразования можно было бы возвести в степень, как показано ниже.
9{2}\)
Хотя последние два обозначения эквивалентны, правильное использование второго представления требует четкого понимания его смысла. Обратите внимание, что степень должна быть записана вне круглых скобок, так как полный коэффициент преобразования умножается сам на себя. Следовательно, при правильном расчете числа и единицы должны быть возведены в квадрат. Рекомендуется явно записывать несколько коэффициентов преобразования, так как это обычно приводит к меньшему количеству ошибок учащихся по сравнению с использованием второго (сжатого) представления. 9{2}}\)
 В заданном числе 2 значащие цифры, поэтому в окончательном ответе должно быть 2 значащие цифры. Поскольку количество цифр, которое на самом деле содержит ответ, больше, чем количество цифр, которое должно быть, рассчитанный ответ необходимо округлить до 0,83 в 2 .
В заданном числе 2 значащие цифры, поэтому в окончательном ответе должно быть 2 значащие цифры. Поскольку количество цифр, которое на самом деле содержит ответ, больше, чем количество цифр, которое должно быть, рассчитанный ответ необходимо округлить до 0,83 в 2 . Используя только коэффициенты пересчета, основанные на равенствах из раздела 1.6, переведите 18 900 000 кубических сантиметров в кубические метры.
Раствор
Данная единица измерения — «кубические сантиметры (см 3 )», а желаемая единица — «кубические метры (м 3 )». В разделе 1.6 не упоминается равенство, которое напрямую связывает кубические сантиметры с кубическими метрами. Однако существует равенство модификаторов префикса, связывающее сантиметры и метры: \( { \text{1 м}} = { \text{100 см}}\). Однако, чтобы добиться полной отмены единицы, необходимо применить этот коэффициент преобразования 9{3}}\)
Каждое из чисел, найденных в равенстве модификаторов префикса, является точным. В данном числе 3 значащие цифры, поэтому окончательный ответ должен состоять из 3 значащих цифр. Поскольку количество цифр, которое на самом деле содержит ответ, в точности равно количеству цифр, которое в нем должно быть, никаких корректировок вносить не нужно, и рассчитанный ответ является окончательным ответом.
В данном числе 3 значащие цифры, поэтому окончательный ответ должен состоять из 3 значащих цифр. Поскольку количество цифр, которое на самом деле содержит ответ, в точности равно количеству цифр, которое в нем должно быть, никаких корректировок вносить не нужно, и рассчитанный ответ является окончательным ответом.
Используя только коэффициенты преобразования, основанные на равенствах из раздела 1.6, преобразовать 0,196 квадратных миль в квадратных ярдах.
- Ответить
- Заданная единица измерения — «квадратные мили (ми 2 )», а желаемая единица измерения — «квадратные ярды (ярды 2 )». В разделе 1.6 не упоминается равенство, непосредственно связывающее квадратные мили с квадратными ярдами, и не упоминается равенство, напрямую связывающее мили с ярдами. Следовательно, для достижения требуемого изменения единицы измерения потребуется несколько равенств. В частности, измеренные равенства \( { \text{1 миля}} = { \text{5 280 футов}}\) и \( { \text{1 ярд}} = { \text{3 фута}}\) будут 9{2}}\)
Каждое из чисел, найденных в измеренном равенстве, является точным.
 В данном числе 3 значащие цифры, поэтому окончательный ответ должен состоять из 3 значащих цифр. Поскольку количество цифр, которое на самом деле содержит ответ, больше, чем количество цифр, которое должно быть, рассчитанный ответ необходимо округлить до 607 000 ярдов 2 .
В данном числе 3 значащие цифры, поэтому окончательный ответ должен состоять из 3 значащих цифр. Поскольку количество цифр, которое на самом деле содержит ответ, больше, чем количество цифр, которое должно быть, рассчитанный ответ необходимо округлить до 607 000 ярдов 2 .
1.12: Squared and Cubic Units распространяется по незаявленной лицензии и был создан, изменен и/или курирован LibreTexts.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Показать страницу TOC
- № на стр.
-
- Теги
-

квадратных футов в кубические ярды
Если вы хотите преобразовать между квадратными футами и кубическими ярдами , наш калькулятор квадратных футов в кубические ярды — единственный инструмент, который вам нужен. Просто введите площадь в квадратных футах и высоту /глубину , и вы сможете вычислить объем в кубических ярдах в кратчайшие сроки.
Чтобы рассчитать объем в кубических ярдах по базовым размерам, то есть длине, ширине и высоте, воспользуйтесь нашим калькулятором кубических ярдов. 93yd3 является единицей объема .
Часто нам нужно рассчитать объем строительных или ландшафтных материалов, например, гравия, цемента, почвы, мульчи и т. д., и для выражения этого объема мы используем кубические ярды. Например, если вы готовите клумбу и хотите знать, сколько мульчи и почвы вам потребуется.
Давайте рассмотрим данную цифру, чтобы понять разницу и соотношение между квадратными футами и кубическими ярдами.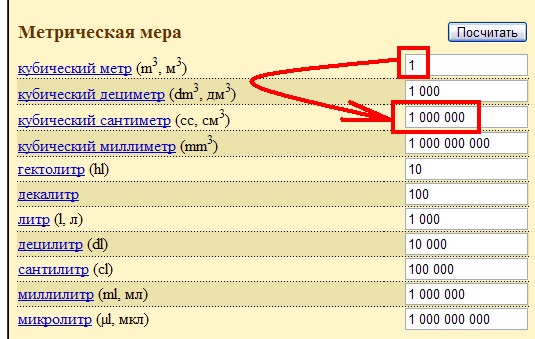 На рисунке показана прямоугольная площадь участка, равная 93
\end {align*}Объем=27 фут3=1 ярд3
На рисунке показана прямоугольная площадь участка, равная 93
\end {align*}Объем=27 фут3=1 ярд3
Вы можете узнать аналогичное преобразование между объемом и площадью в нашем калькуляторе галлонов на квадратный фут, который полезен, если вы строите бассейн во дворе.
Как преобразовать квадратные футы в кубические ярды
Поскольку квадратные футы — это мера площади, а кубические ярды — мера объема, чтобы преобразовать квадратные футы в кубические ярды, нам нужно выполнить следующие шаги:
-
Определите площадь , используя соответствующую формулу и переведя единицы площади в квадратные футы.
-
Измерьте глубину/высоту области и также переведите ее в футы.
-
Умножьте на площадь и глубину/высоту , и вы получите объем в кубических футах.
-
Разделите объем в кубических футах на 27 , чтобы получить объем в кубических ярдах.

-
Вы также можете использовать для этой цели наш калькулятор преобразования квадратных футов в кубические ярды!
Как использовать калькулятор преобразования квадратных футов (кв. футов) в кубические ярды
Теперь давайте посмотрим, как мы можем использовать калькулятор преобразования квадратных футов (кв. футов) в кубические ярды:
-
Введите площадь поверхности в квадратных футах. Вы можете использовать наш калькулятор площади для этой цели.
-
Введите глубину/высоту области. Вы можете выбрать различные единицы измерения, используя раскрывающееся меню.
-
Калькулятор преобразования квадратных футов в кубические ярды даст вам объем в кубических ярдах .
-
Вы также можете использовать этот инструмент как калькулятор кубических ярдов в квадратных футах .
Часто задаваемые вопросы
Что такое кубический ярд?
Кубический ярд — единица объема. Мы можем определить кубический ярд как объем куба с длиной, шириной и высотой в один ярд .
Мы можем определить кубический ярд как объем куба с длиной, шириной и высотой в один ярд .
Как перевести квадратные футы в кубические ярды?
Чтобы преобразовать квадратные футы в кубические ярды, следуйте приведенным инструкциям:
-
Определить длину и ширину интересующей области и вычислить ее площадь в квадратных футах .
-
Узнать глубину или высоту региона в футах.
-
Умножьте результатов шагов 1 и 2 и разделите результат на 27 .
-
Поздравляем! Вы перевели квадратные футы в кубические ярды.
Как перевести кубические ярды в квадратные футы?
Чтобы преобразовать кубические ярды в квадратные футы, выполните следующие действия:
-
Умножьте на объем в кубических ярдах на 27 , чтобы получить объем в кубических футах.

-
Разделите объем на глубину или высоту , измеренную в футах.
-
Вы вычислили площадь в квадратных футах.
Сколько кубических футов в кубическом ярде?
27 футов . Один ярд равен 3 футам. Следовательно, чтобы определить количество кубических футов в кубическом ярде, возьмите куб обеих сторон, и вы получите 1 кубический ярд = 27 кубических футов .
Метрика: кубические единицы
Метрическая система: кубические единицыЕдиницы метрического куба: преобразование одной кубической единицы в другую
Десять примеров
Пробы 1-10
Вернуться в меню показателей
Процесс решения почти такой же, как и при решении задач с квадратными единицами, за исключением того, что вам нужно возвести в куб абсолютное экспоненциальное расстояние между двумя префиксами. Я буду делать те же примеры, что и в учебнике по квадратным единицам, за исключением кубических задач.
Помните, что кубические задачи связаны с объемом.
Пример #1: Преобразование 1,00 м 3 в кубические сантиметры.
Решение:
1) Вот установка для конвертации:
??? см 3 1,00 м 3 х ––––––– = ответ 1 м 3 Обратите внимание, что m 3 отменяется, оставляя cm 3 единицей в ответе.
2) Немного обсуждения:
Абсолютное экспоненциальное расстояние между базовой единицей и сантимами равно 10 2 . Иногда учитель может сказать, что экспоненциальное расстояние равно 2.Имейте в виду, что 2 — это показатель степени, а НЕ то, что вы будете умножать что-то на 2. В кубической ситуации мы должны возвести это в куб, чтобы получить 10 6 . Мы делаем это потому, что есть три измерения в сантиметрах, по одному на каждую из трех сторон куба.
3) Позвольте мне предвидеть проблему:
Вы читаете выше и говорите: «Подождите, куб 2 равен 8, не так ли?» Вы правы, потому что (2) 3 = 2 x 2 x 2 = 8, но мы имеем дело с экспоненциальным значением 2, а не с числом 2. В кубе получается 10 2 , а не 2. Мы бы написали (10 2 ) 3 = 10 2 x 3 = 10 6 .
4) Теперь, чтобы закончить пример:
10 6 см 3 1,00 м 3 х ––––––– = 1,00 x 10 6 см 3 1 м 3 Вы также можете увидеть это так:
(1,00 м 3 ) (10 6 см 3 / м 3 ) = 1,00 x 10 6 см 3
Пример #2: Преобразование 1,00 км 3 в кубические микрометры.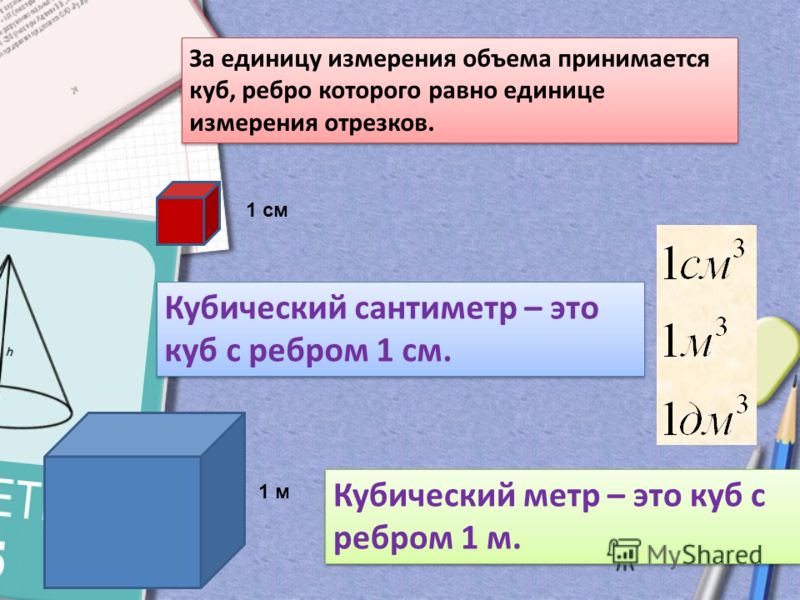
Решение:
1) Вот задача в виде конвертации:
??? мкм 3 1,00 км 3 х ––––––– = ответ 1 км 3 Обратите внимание, что km 3 отменяется, оставляя µm 3 в качестве единицы измерения в ответе.
2) Немного обсуждения:
Между кило- и микро- это абсолютное расстояние 10 9 . Наша методика требует возведения экспоненциального значения в куб, поэтому (10 9 ) 3 = 10 27 . Направление изменения идет от большего префикса к меньшему префиксу, поэтому знак степени в ответе будет положительным.
3) Завершите пример:
10 27 мкм 3 1,00 км 3 х ––––––– = 1,00 x 10 27 мкм 3 1 км 3
Два вышеприведенных примера переходили от большего префикса к меньшему. Это означало, что в одном большом префиксе было много меньших префиксов. Примеры ниже пойдут в противоположном направлении. Спросите себя: сколько более крупных префиксов содержится в одном маленьком префиксе? Ответ = меньше единицы, поэтому знак степени будет отрицательным.
Сказав это, остерегайтесь задачи, в которой показатель степени уже присутствует в задаче, а отрицательное изменение показателя степени не может перевесить показатель степени из задачи. В этом случае в ответе будет положительный показатель степени.
В этом случае в ответе будет положительный показатель степени.
Пример #3: Преобразование 4310 кубических сантиметров в м 3 .
Решение:
1 3 м 3 4310 см 3 х ––––––– = 4,31 x 10¯ 3 м 3 (10 2 ) 3 см 3 Обратите внимание, что 1 в факте преобразования связана с большей (m 3 ) из двух единиц. Больше здесь означает, что 1 м 3 больше, чем 1 см 3 .
Пример #4: Преобразование 86,3 кубических сантиметра в миллиметры 3 .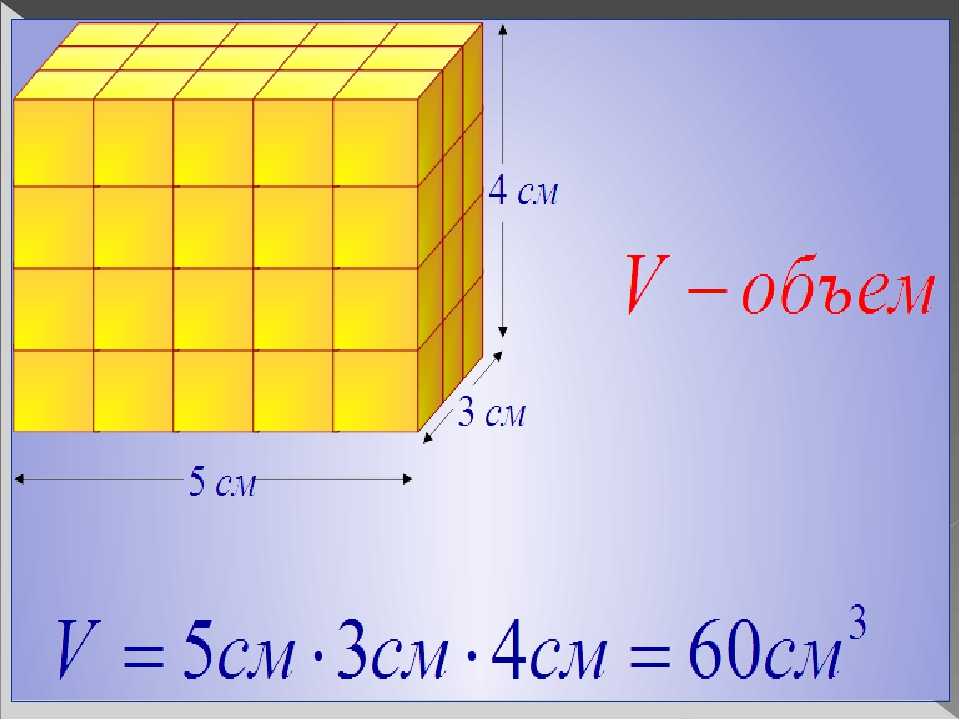
Решение:
86,3 см 3 x (10 3 мм 3 / 1 3 см 3 ) = 8,63 x 10 4 мм 3В одном см 10 мм, поэтому 10 x 10 x 10 дает 10 3 мм 3 .
Пример #5: 5,94 x 10 10 мм 3 . Перевести в дм 3 . Затем переведите в литры.
Решение:
1 дм 3 5,94 x 10 10 мм 3 х ––––––– = 5,94 x 10 4 дм 3 (100 мм) 3 Обратите внимание, как мм 3 входит в знаменатель коэффициента пересчета, чтобы исключить мм 3 из значения, которое нужно преобразовать.

1 дм равен 100 мм, поэтому 1 дм 3 = (100 мм) 3 = 10 6 мм 3
Обратите внимание, что 1 соответствует дм 3 , большей из единиц по сравнению с 1 мм 3 .
5,94 x 10 4 дм 3 = 5,94 x 10 4 л, потому что 1 дм 3 равен 1 л.
Преобразование длин в м
3
Пример #6: Длина стороны металлического куба 2,50 см. Вычислить объем в м 3 .
Решение:
1) Преобразование 2,50 см в метры:
(2,50 см) (1 м/100 см) = 0,0250 м
2) Умножьте, чтобы получить объем куба:
(0,0250 м) (0,0250 м) (0,0250 м) = 1,56 x 10¯ 5 м 3 (до трех знаков)
3) Вот альтернативный путь решения:
(2,50 см) (2,50 см) (2,50 см) = 15,625 см 3(15,625 см 3 ) (1 м / 100 см) 3 = 15,625 x 10¯ 6 м 3
15,625 x 10¯ 6 м 3 = 1,56 x 10¯ 5 м 3 904 fig 0 s 0 9 9 0 81 (до трех)
Пример #7: Перевести 10,6 кг/м 3 в г/см 3
Решение:
1) Сначала выполните некубическое преобразование, конвертируйте кг в г:
10 3 г 10,6 кг/м 3 х ––––– = 1,06 x 10 4 г/м 3 1 кг Обратите внимание на использование экспоненциальной записи в ответе.

2) Затем выполните кубическое преобразование, преобразуйте кубические метры в кубические сантиметры:
(1 м) 3 1,06 х 10 4 г/м 3 х ––––––– = 1,06 x 10¯ 2 г/см 3 (100 см) 3 Обратите внимание, что 100 в кубе равно 10 6 . Вы можете записать 100 в кубе в преобразовании как (10 2 ) 3
Вы также можете записать ответ как 0,0106 г/см 3 .
3) Будьте осторожны, убедитесь, что у вас все на своих местах. Когда я отформатировал эту задачу, я сделал это около 7:30 утра в дождливую субботу.
У меня был обратный коэффициент преобразования для кубического преобразования. Нужен МОАР КОФЕ!!
Пример #8: Преобразуйте плотность алюминия (2,70 г/см 3 ) в кг/м 3 .
Решение:
1) Вот план:
(a) конвертировать г/см 3 в г/м 3 (первый коэффициент пересчета на шаге чуть ниже)(b) перевести г/м 3 в кг/м 3 (второй коэффициент пересчета на шаге чуть ниже)
2) Небольшой размерный анализ:
(10 2 см) 3 1 кг 2,70 г/см 3 x ––––––– х ––––––– = 2,70 x 10 3 кг/м 3 (1 м) 3 1000 г
Пример #9: Преобразуйте 409 кубических дюймов в литры, используя анализ размеров.
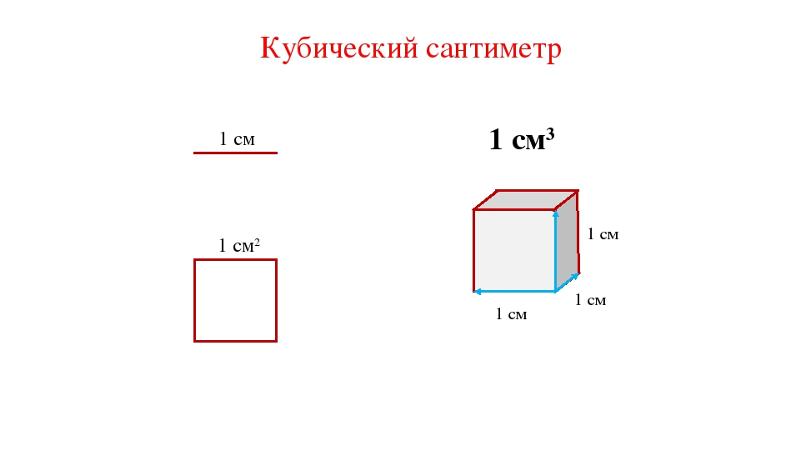
Решение:
1) Вот план:
(a) перевести в 3 в см 3(b) перевести см 3 в мл
(c) перевести мл в л
2) Вот установка:
(2,54 см) 3 1 мл 1 л 409 дюймов 3 х ––––––––– х ––––– х ––––––– = 6,70 л (1 дюйм) 3 1 см 3 1000 мл 3) Комментарии:
(a) представьте, что 1 из 3 представляет собой куб один дюйм на один дюйм на один дюйм.Поскольку 1 дюйм равен 2,54 см, один кубический дюйм равен кубу 2,54 см на 2,54 см на 2,54 см.
(b)1 см 3 = 1 мл — очень удобное преобразование для запоминания.
(c) У Брайана Уилсона есть комментарий по поводу числа 409.
Пример №10: Если сторона куба 25,2 мм, каков его объем в литрах?
Решение:
1) Перевести 25,2 мм в см:
(25,2 мм) (1 см / 10 мм) = 2,52 см2) Определяем объем куба:
(2,52 см) (2,52 см) (2,52 см) = 16,003 см 33) Перевести см 3 в мл:
(16,003 см 3 ) (1 мл / 1 см 3 ) = 16,003 мл4) Преобразование мл в л:
(16,003 мл) (1 л / 1000 мл) = 0,0160 л
Дополнительный пример #1: Моль любого идеального газа при нормальных условиях занимает 22,414 л. Сколько молекул газообразного водорода содержится в 22,414 мм 3 ?
Решение:
1) Я собираюсь построить решение для многомерного анализа, по одному фактору за раз.
Во-первых, давайте изложим информацию из задачи:
1 моль ––––––– х 22,414 л Я намеренно указал это значение, потому что знаю, что окончательным ответом будет некоторое количество молекул на кубический миллиметр. Объем должен идти в знаменателе.
2) Мы должны избавиться от литров и перейти к некоторому типу кубических измерений:
1 моль 1 л ––––––– х ––––– х 22,414 л 1 дм 3 Знание того, что 1 л = 1 дм 3 , является удобным преобразованием для запоминания.
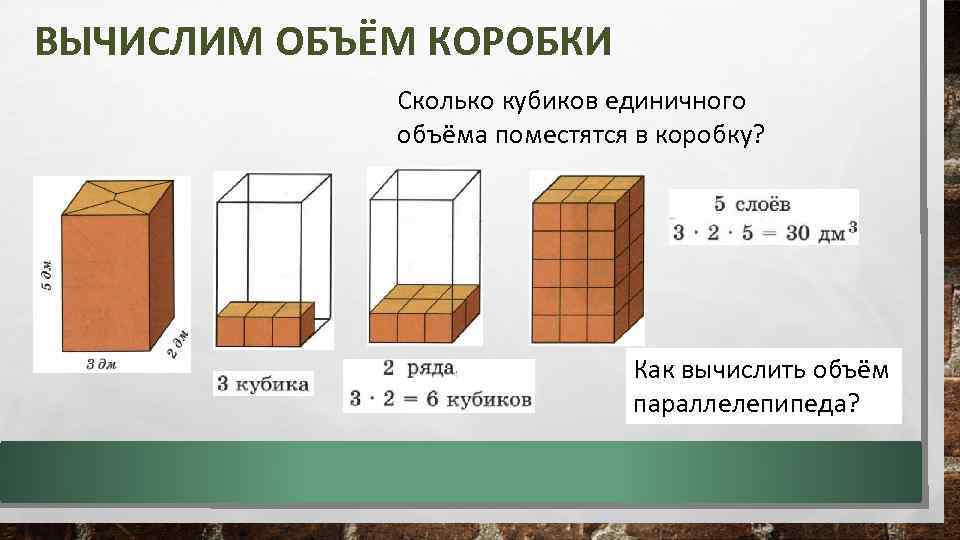
3) Теперь переведем кубические дециметры в кубические миллиметры:
1 моль 1 л 1 дм 3 ––––––– х ––––– х –––––––– х 22,414 л 1 дм 3 100 3 мм 3 для этого:
100 3 мм 3Помните, что в 1 дм 100 мм, значит:
100 мм x 100 мм x 100 мм в одном дм 34) Последнее преобразование из молей в молекулы:
1 моль 1 л 1 дм 3 6,022 x 10 23 молекул ––––––– х ––––– х –––––––– х ––––––––––––––––––– = 2,687 x 10 16 молекул (до 4 цифр) 22,414 л 1 дм 3 100 3 мм 3 1 моль
Бонусный пример #2: Металлический куб имеет следующие размеры: ширина 5,20 дюйма, длина 6,00 см и высота 1,00 фарлонга.
Каков объем куба в кубических метрах? В кубических метрах?
Решение:
1) Переведем каждое измерение в метры. Все, что нам нужно сделать, это перемножить вместе, чтобы получить кубические метры:
(5,20 дюйма) (1 м / 39,3701 дюйма) = 0,13208 м
(6,00 см) (1 м/100 см) = 0,0600 м2) Ферлонг немного более вовлечен:
220 ярдов 3 фута 12 дюймов 2,54 см 1 м 1,00 фарлонг х ––––––– х ––––––– х ––––––– х ––––––– х ––––––– = 201,168 м 1 фарлонг 1 ярд 1 фут 1 дюйм 100 см 3) Просто напоминание об осторожности.
Когда я настроил преобразование фарлонга в метры, я поменял местами 2,54 и 1. Я довольно хорошо разбираюсь в этом, но до сих пор иногда допускаю ошибки. Проверьте свою работу! Вот объем в кубометрах:
(0,13208 м) (0,0600 м) (201,168 м) = 1,59 м 3 (до трех знаков)4) Перевести кубические метры в кубические футы:
(1,594216 м 3 ) (39,3701 дюйм/м) 3 (1 фут / 12 дюймов) 3 = 56,3 фута 3 (до трех цифр)Обратите внимание, что я использовал значение в кубических метрах с несколькими дополнительными цифрами, а не округленное значение 1,59.
Пробы 1-10
Вернуться в меню показателей
Открытые учебники | Сиявула
Загрузите наши открытые учебники в разных форматах, чтобы использовать их так, как вам удобно. Нажмите на обложку каждой книги, чтобы увидеть доступные для загрузки файлы на английском и африкаанс. Лучше, чем просто бесплатные, эти книги также имеют открытую лицензию! См.
различные открытые лицензии для каждой загрузки и пояснения к лицензиям в нижней части страницы.
Математика
- Читать онлайн
Учебники
Английский
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
Африкаанс
- 7A PDF (CC-BY-ND)
- 7B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
Африкаанс
- 8A PDF (CC-BY-ND)
- 8B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
Африкаанс
- 9A PDF (CC-BY-ND)
- 9B PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
Наука
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Английский
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Африкаанс
- PDF (CC-BY-ND)
- ePUB (CC-BY-ND)
- ePUB (CC-BY)
Пособия для учителя
Английский
- PDF (CC-BY-ND)
Африкаанс
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 7А
- PDF (CC-BY-ND)
Класс 7Б
- PDF (CC-BY-ND)
Африкаанс
Граад 7А
- PDF (CC-BY-ND)
Граад 7Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 8А
- PDF (CC-BY-ND)
Класс 8Б
- PDF (CC-BY-ND)
Африкаанс
Граад 8А
- PDF (CC-BY-ND)
Граад 8Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 9А
- PDF (CC-BY-ND)
Класс 9Б
- PDF (CC-BY-ND)
Африкаанс
Граад 9А
- PDF (CC-BY-ND)
Граад 9Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 4А
- PDF (CC-BY-ND)
Класс 4Б
- PDF (CC-BY-ND)
Африкаанс
Граад 4А
- PDF (CC-BY-ND)
Граад 4Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 5А
- PDF (CC-BY-ND)
Класс 5Б
- PDF (CC-BY-ND)
Африкаанс
Граад 5А
- PDF (CC-BY-ND)
Граад 5Б
- PDF (CC-BY-ND)
- Читать онлайн
Учебники
Пособия для учителя
Английский
Класс 6А
- PDF (CC-BY-ND)
Класс 6Б
- PDF (CC-BY-ND)
Африкаанс
Граад 6А
- PDF (CC-BY-ND)
Граад 6Б
- PDF (CC-BY-ND)
Лицензирование наших книг
Эти книги не только бесплатны, но и имеют открытую лицензию! Один и тот же контент, но разные версии (фирменные или нет) имеют разные лицензии, как объяснено:
CC-BY-ND (фирменные версии)
Вам разрешается и поощряется свободное копирование этих версий.
Вы можете копировать, распечатывать и распространять их столько раз, сколько захотите. Вы можете загрузить их на свой мобильный телефон, iPad, ПК или флешку. Вы можете записать их на компакт-диск, отправить по электронной почте или загрузить на свой веб-сайт. Единственное ограничение заключается в том, что вы не можете каким-либо образом адаптировать или изменять эти версии учебников, их содержание или обложки, поскольку они содержат соответствующие бренды Siyavula, логотипы спонсоров и одобрены Департаментом базового образования. Для получения дополнительной информации посетите сайт Creative Commons Attribution-NoDerivs 3.0 Unported.
Узнайте больше о спонсорстве и партнерстве с другими, которые сделали возможным выпуск каждого из открытых учебников.
CC-BY (версии без торговой марки)
Эти версии одного и того же контента без торговой марки доступны для вас, чтобы вы могли делиться ими, адаптировать, преобразовывать, изменять или развивать их любым способом, при этом единственным требованием является предоставление соответствующей ссылки на Siyavula.
Для получения дополнительной информации посетите Creative Commons Attribution 3.0 Unported.
Калькулятор, Ландшафтные материалы, Мульча, Камень, Семена травы, Песок
- Прямоугольник
- Круг
- Треугольник
Прямоугольные расчеты
Длина: футов Ширина: футов Глубина: Дюймы Район: 6 квадратных футов Периметр: 10 футов Объем: кубических ярдов
Круговые вычисления
Радиус: футов Глубина: Дюймы Район: 28,27 квадратных футов Окружность: 18,85 футов Объем: кубических ярдов
Треугольные вычисления
Сколько материала вам нужно?
Для оценки количества, необходимого для неровных поверхностей, разбейте область на более мелкие обрабатываемые формы.
Измерьте каждую из них и присвойте им букву. Рассчитайте квадратные футы для каждого и сложите квадратные метры вместе, чтобы получить общее количество необходимых.
Прямоугольник
- Измерение длины и ширины (в футах)
- Длина x ширина = квадратные футы
- Определите желаемую толщину материала (см. рекомендуемую глубину и таблицу ниже)
- Квадратные футы, разделенные на кв. футы на ярд ( из таблицы) = необходимое количество кубических ярдов
- Пример: прямоугольная площадь 16 футов в длину и 10 футов в ширину, и вам нужен камень толщиной 4 дюйма.
- Вычисления:
- 16 x 10 = 160 квадратных футов
- 160 разделить на 81 = 2 кубических ярда (81 взято из таблицы, 81 — это сколько квадратных футов занимает 1 кубический ярд на глубине 4 дюйма)
Треугольник
- Измерение длины и ширины двух сторон
- Длина x Ширина x 0,5 = квадратные футы
- Квадратные футы, разделенные на кв.
футы на ярд (из таблицы) = необходимые кубические ярды
- треугольника, где одна сторона имеет длину 40 футов, а другая сторона — 10 футов, и вам нужно 4 дюйма глубины мульчи или камня
- Вычисления:
- 40 x 10 x 0,5 = 200 квадратных футов
- 200 разделить на 81 = 2,5 куб. ярдов (81 исходит из таблицы)
Окружность
- Определение радиуса (1/2 диаметра или расстояния в поперечном направлении)
- Формула: Радиус x Радиус x 3,14 = квадратные футы
- Квадратные футы, разделенные на кв. футы на ярд (из таблицы) = куб.
- Пример. Дан круг диаметром 30 футов (радиус 15 футов) и глубиной 3 дюйма
- Вычисления:
- 15 x 15 x 3,14 = 706,5 квадратных футов
- 706,5 разделить на 108 = 6,5 кубических ярдов 101 3 90 90 9
Таблица преобразования – Квадратные футы в Кубические ярды
Преобразует квадратные футы в кубические ярды. 1 кубический ярд покрывает следующее количество квадратных футов на заданной глубине.

- Глубина 1/4 дюйма 1296 кв. футов
- Глубина 1 дюйма 324 кв. фута
- Глубина 2 дюйма 162 кв. фута
- Глубина 3 дюйма 108 кв. футов
- Глубина 4 дюйма 81 кв. футов
- 12 дюймов глубиной 27 квадратных футов
Рекомендуемая глубина засыпки материалов
- Мульча из коры 3 дюйма
- Камень диаметром менее 1 дюйма 3 дюйма
- 1-1 1/2″ Riverstone 4″
- Грунт для пышных газонов 4+»
- Садовый грунт для цветников 6-12″
- Подкормка газона 1/4″
- Дорожки 4″
- 3 Fun Volume 9 Факты
- На кубический ярд приходится 54 50-фунтовых мешка с камнем или песком.
- 27 кубических футов равны 1 кубическому ярду (3’Д x 3’Ш x 3’В).
- Почва весит около 2200 фунтов на кубический ярд.
- Камень весит около 2700 фунтов на кубический ярд.
- Мульча весит 250-750 фунтов на кубический ярд.
- Полноразмерный пикап с 8-футовым кузовом, грузоподъемность которого составляет 3 кубических ярда.

- Грузоподъемность малогабаритного подборщика составляет 1 ½ кубических ярда.
- Обычно полноразмерный грузовик может перевозить ½–1 кубический ярд камня или почвы.
- Обычно небольшой пикап может перевозить от ⅓ до ½ кубических ярдов камня или почвы.
- От 7 до 12 грузов на тачке в 1 кубическом ярде.
- При подкормке ранее мульчированных грядок вам нужно только добавить достаточное количество мульчи на существующую грядку, чтобы получить в общей сложности 3 дюйма. исчезают, и снова появляется земля.
Мешки или навалом
- Попробуйте сделать обоснованное предположение о необходимом количестве, используя формулы. Если вы все еще не уверены, сколько материала в мешках или навалом нужно получить, предоставьте измерения персоналу KLS, и они помогут вам оценить.
- На 1 кубический ярд приходится 54 мешка камня или земли.
- На ярд приходится 27 мешков по 1 куб. футу или 18 мешков по 1,5 куб. фута с мульчей.
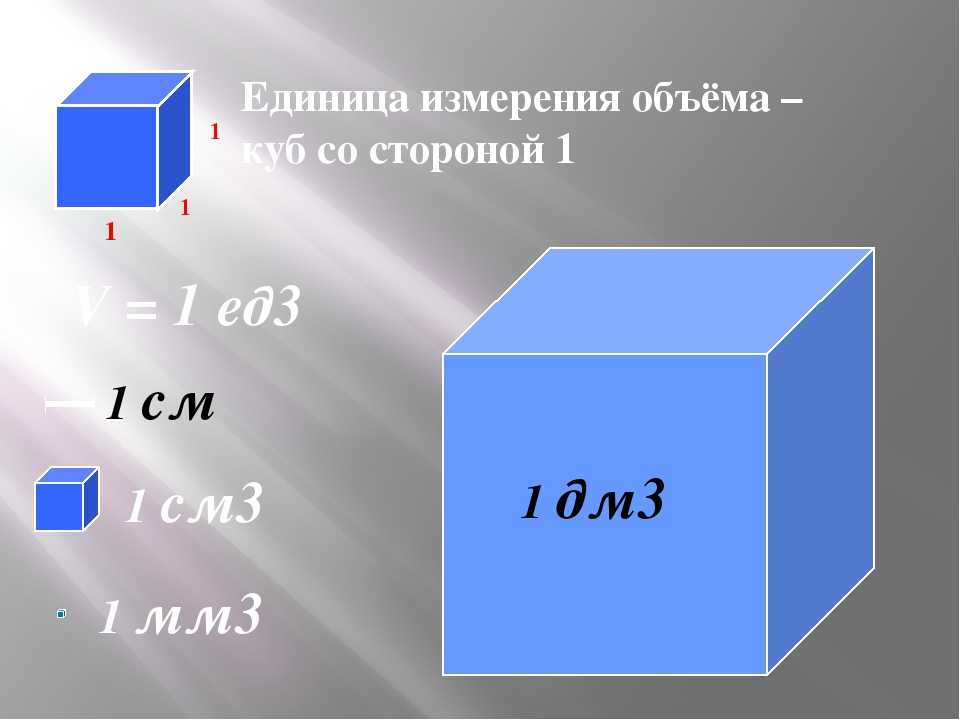
- Предположим, что мешок с камнем или землей объемом ½ куб. фута весит около 50 фунтов и может покрыть 2 квадратных фута при глубине 3 дюйма. Мешок из твердой древесины или кедровой коры содержит около 1 куб. глубиной 3 дюйма. Если у вас есть большие площади, вам, вероятно, нужен объем.
- Более дешевая альтернатива покупке в мешках — привезти и заполнить свои контейнеры сыпучими материалами.
- Если вы обустраиваете небольшой участок, лучше всего подойдут мешки, если у вас нет возможности перевозить сыпучие материалы.
- Мульча, приобретаемая мешками, примерно в 2-3 раза дороже, чем оптом.
- Камень, купленный мешком, примерно в 3-4 раза дороже, чем оптом.
- Грунт, приобретаемый мешками, примерно в 4-5 раз дороже, чем навалом.
Советы по перемещению сыпучих материалов
- При работе с тяжелыми материалами использование большего количества маленьких лопат легче для вашего тела, чем использование меньшего количества, но больших лопат.
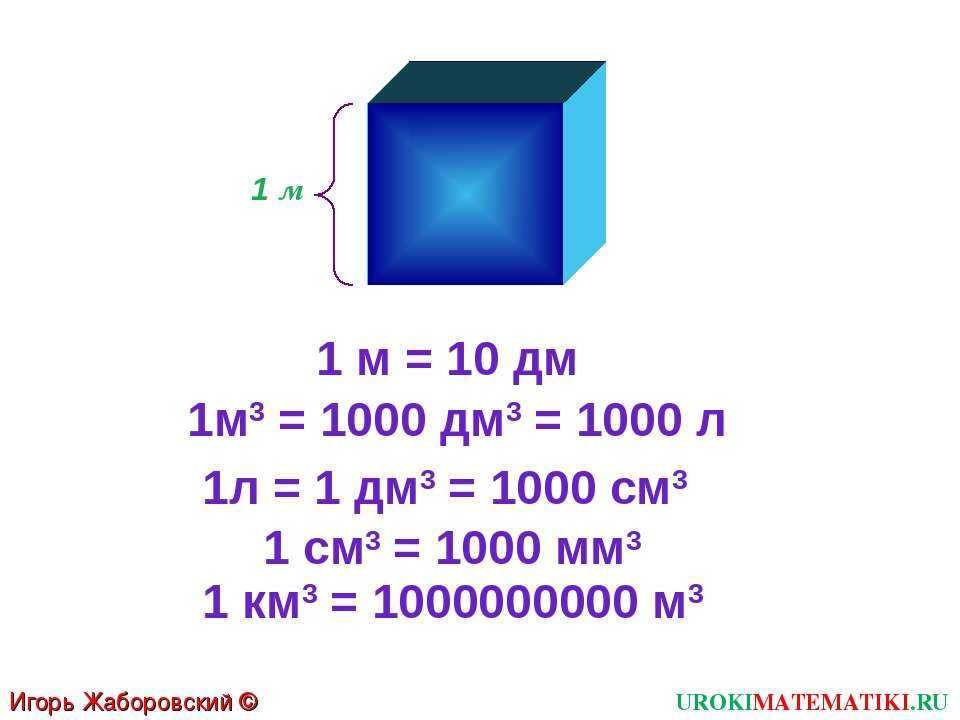
- Подумайте о том, где вы держитесь за лопату: чем ближе ваша рука к весу, тем легче и меньше усилий требуется.
- Следите за тем, чтобы поддерживать хорошую осанку, сведите к минимуму тяжелую работу с наклоном спины, максимально используйте ноги.
- Работайте в хорошем темпе, не зацикливайтесь на том, сколько вам еще нужно двигаться. Постарайтесь сосредоточиться на том, сколько материала вы уже переместили, насколько хорошо он будет выглядеть после того, как вы сделали, и сколько денег вы сэкономите, сделав это самостоятельно.
- Как здорово провести время с друзьями и семьей!
Как выглядит кубический двор?
Ниже приведены несколько образцов свай, чтобы дать вам представление о том, насколько велики сваи для данного количества материала. Объем кучи земли, камня или мульчи будет одинаковым. Однако куча риверстоуна может выглядеть иначе, чем куча кедровой мульчи, потому что она, скорее всего, будет ниже, шире и длиннее кучи, потому что круглые камни разбрасываются дальше при сбросе.
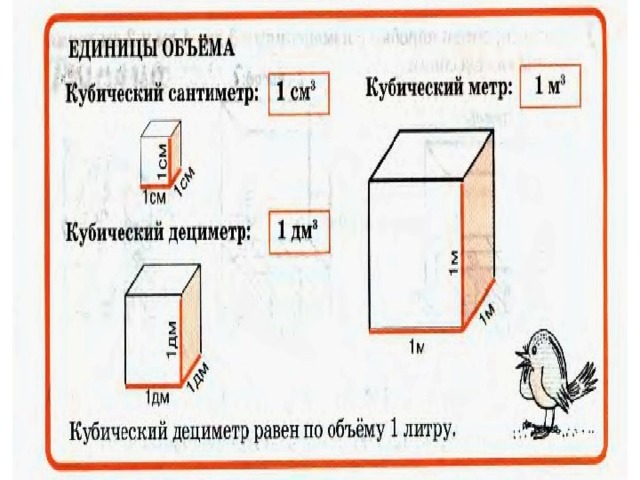
Образцы стопок показывают Тима, рост 6 футов, он держит линейку.
Значение куба 185 (185³)
Дом Инструменты Темы Мобильная версия Дом >> Площадь
Вычислить значение квадратного корня, кубического корня, квадрата, куба и инверсии различных чисел. В математике квадрат — это результат умножения числа самого на себя. Куб числа — это его третья степень, а инверсия — это мультипликативная обратная или обратная величина числа. Квадратный корень из числа «X» — это число «Y», такое что «Квадрат Y» = «X», а кубический корень из числа «X» — это число «Y», такое, что «Куб из Y» = ‘ИКС’.
Куб 185 (185 3 ) = 6 331 625,00
Also find for nearby values … ◄ 145 155 165 175 185 195 205 215 225 ►
Функция Число SquareSquare RootCubeCube RootInverse ( ) = ?
Вместо этого использовать мастер?
Связанные . ..
» Преобразование угла » Преобразование площади » Calculate Area of different objects » Calculate Surface Area of different objects » Trigonometry Calculator » Logarithm Calculator » Surface Current Density Conversion » Surface Преобразование плотности заряда » Преобразование поверхностного натяжения » Преобразование плотности магнитного потока »Преобразование разрешения изображений » Расстояние между городами (или городом) ». » Размеры планет, лун, комет и астероидов » Calendar Creator » Преобразование длины » 9 Преобразование веса0409 »Найдите свой звездный знак » Найдите свой счастливый номер »BMI Calculator (Mass Mass Mass Index) » BMI Calculator (Mass Mass Mass) »BMI Calculator (Mass Mass Mass) » BMI Caldature (Mass Mass) 0418»BMI Callocure (Mass Mass) ». различные занятия
» Рассчитайте свой идеальный вес » Контроль веса » Калькулятор срока родов (беременность) »Когда овуляция (калькулятор овуляции) » Калькулятор безопасного периода (контроль над рождаемостью) ». различные единицы измерения
Интересующая тема … Area Astrology Baby Names Banking Birth Control Chemistry Chinese Astrology City Info Electricity Finance Fluids Geography Health Длина Магнетизм Беременность Радиация Научная Скорость Технология Telephone Temperature Time & Date Train Info Volume Weight World Clock Zodiac Astrology Other
Supported Conversion Types . .
Ускорение Угол Угловое ускорение Угловая скорость Площадь Blood Sugar Clothing Size Computer Storage Unit Cooking Volume Cooking Weight Data Transfer Rate Date Density Dynamic Viscosity Electric Capacitance Electric Charge Электропроводность Электропроводность Электрический ток Напряженность электрического поля Electric Potential Electric Resistance Electric Resistivity Energy Energy Density Energy Mass Euro Currency Fluid Concentration Fluid Flow Rate Fluid Mass Flow Rate Force Частота Экономия топлива Тепловая мощность Плотность тепла Плотность теплового потока Heat Transfer Coefficient Illumination Image Resolution Inductance Kinematic Viscosity Length Luminance (Light) Light Intensity Linear Charge Density Linear Current Density Magnetic Field Strength Магнитный поток Плотность магнитного потока Магнитодвижущая сила Плотность массового потока Molar Concentration Molar Flow Rate Moment of Inertia Number Permeability Power Prefix Pressure Radiation Radiation Absorbed Radiation Exposure Radioactivity Размер обуви Звук Удельный объем Скорость Плотность поверхностного заряда Surface Current Density Surface Tension Temperature Thermal Conductivity Thermal Expansion Thermal Resistance Time Torque Volume Volume Charge Density Water Oil Viscosity Weight