Как перевести квадратные метры в кубические?
В жизни зачастую встречаются ситуации, когда необходимо перевести несхожие единицы измерения, к примеру, квадратные метры в кубические.
В математике, перевод метров квадратных в метры кубические сводится к задаче расчета объема фигуры при заданной площади ее основания. Кубические метры применяют при вычислении объема, тогда как метр квадратный – площади.
Алгоритм перевода квадратов в кубы сводится к выполнению действий умножения длины (Дл), ширины (ШР), высоты (Вс) фигуры, представленных в формуле расчета объема (Об):
Формула расчета объема = Длина * Ширина * Высота
В строительстве и закупках стройматериалов при составлении сметы важным является умение перевода одной величины в другую, так как стоимость изделий и материалов могут выставляться производителями как за м. кв. так и за м. куб.
Также, знание перевода полезно при покупках стройматериалов, которые продаются в м.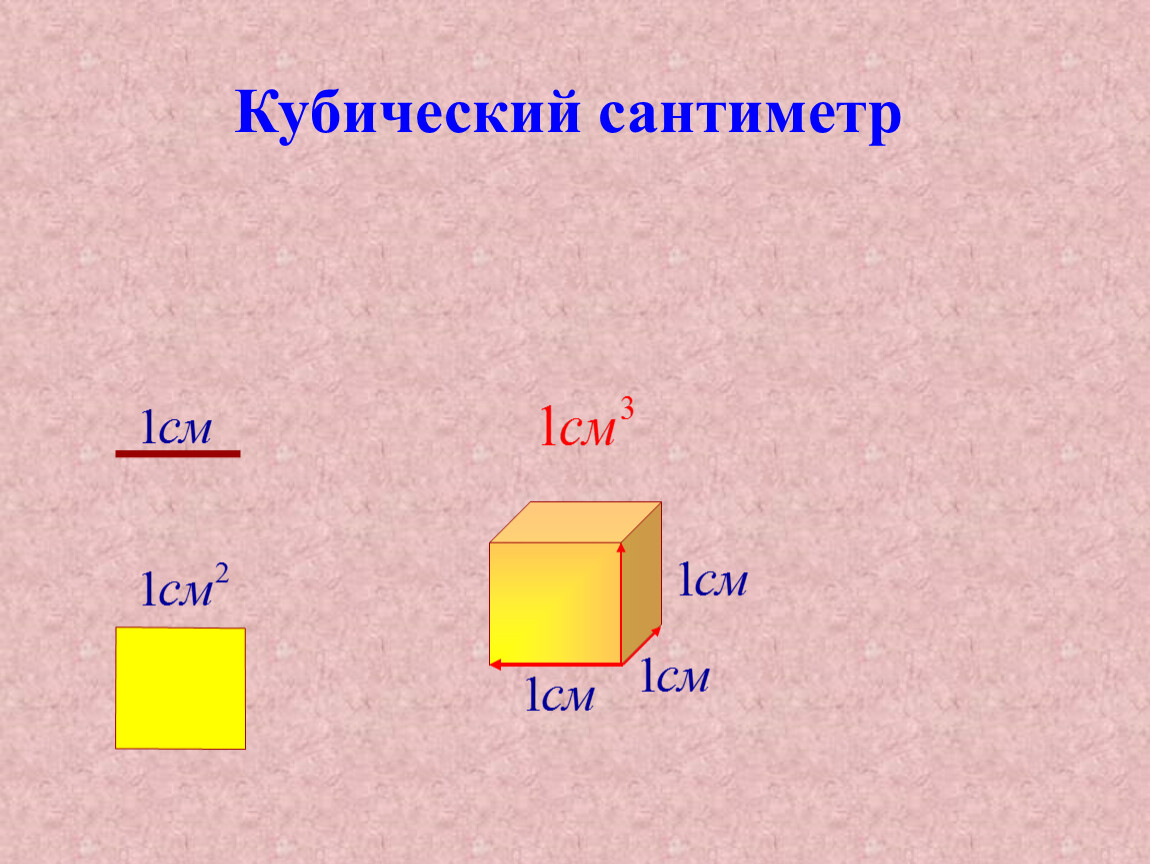
Как быстро перевести без калькулятора?
В качестве примера рассмотрим следующую ситуацию. Для выполнения домашнего ремонта нужно покрыть пол площадью 400 м. кв. доской толщины 5 см. (0,05 м.). Доска реализуется в м. куб. Произведем расчеты потребности доски для выполнения указаного объема работ.
Простая инструкция как перевести — квадратные метры в кубические без калькулятораПлощадь пола множим на толщину доски:
400 м.кв. * 0,05 = 20 м. куб.
Расчеты показывают, что для покрытия пола площадью 400 м. кв. доской толщины 5 см необходимо закупить 20 м. куб. доски.
Автор публикации
01-2 раза в год, веду до результата в блогинге, при наличии мест.
Для связи: ok.ru/denis.povaga
Периметр, площадь и объем
Данный материал содержит геометрические фигуры с измерениями.Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой
P = 9 см + 4 см + 9 см + 4 см = 26 см.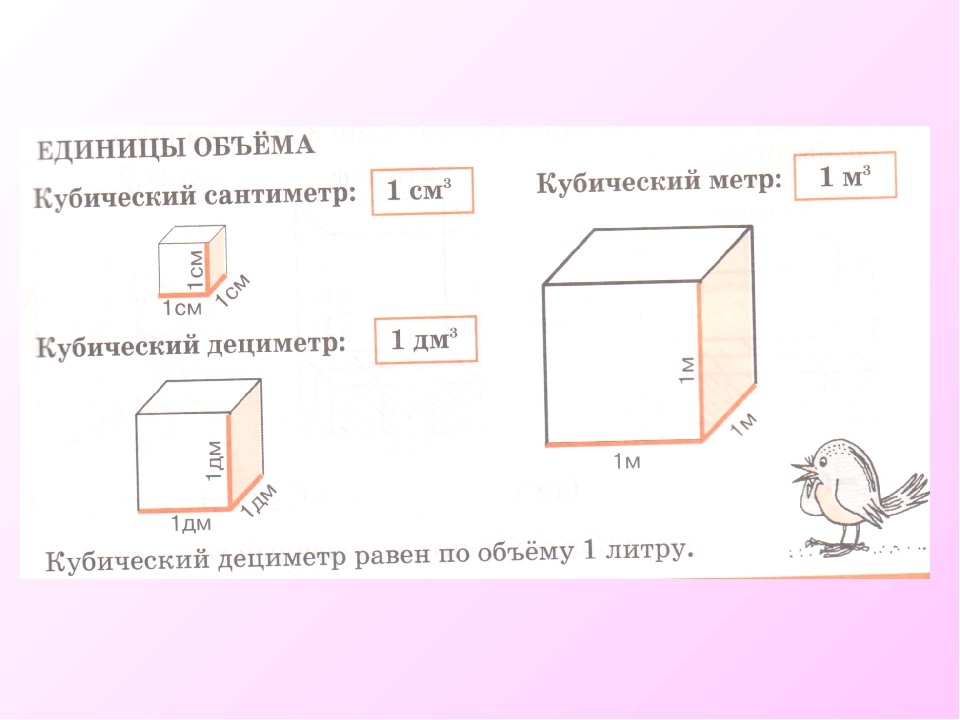
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.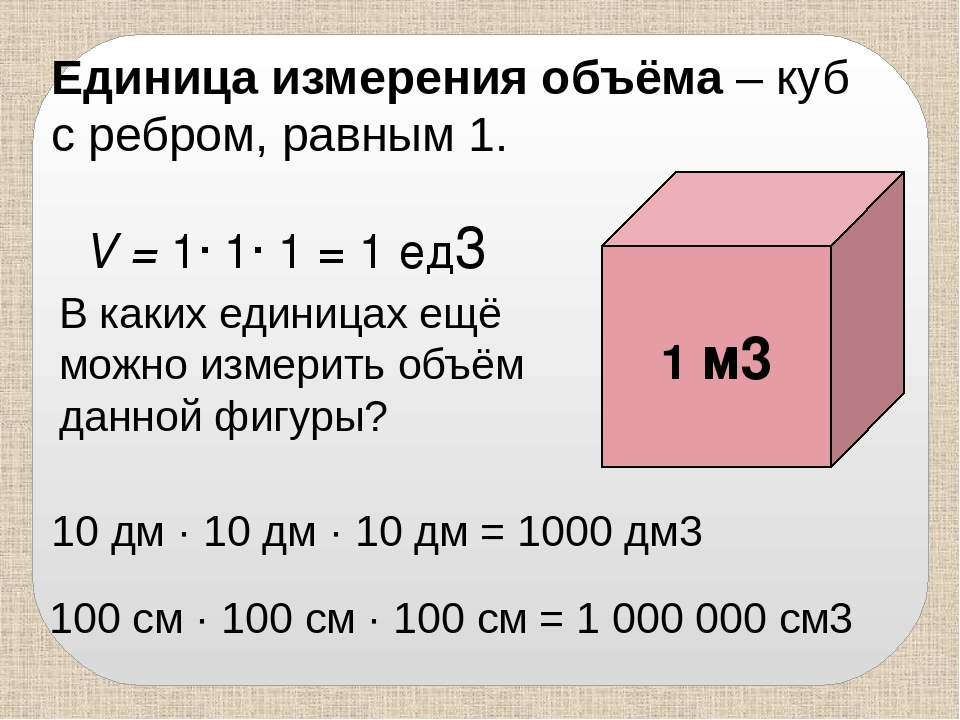
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь.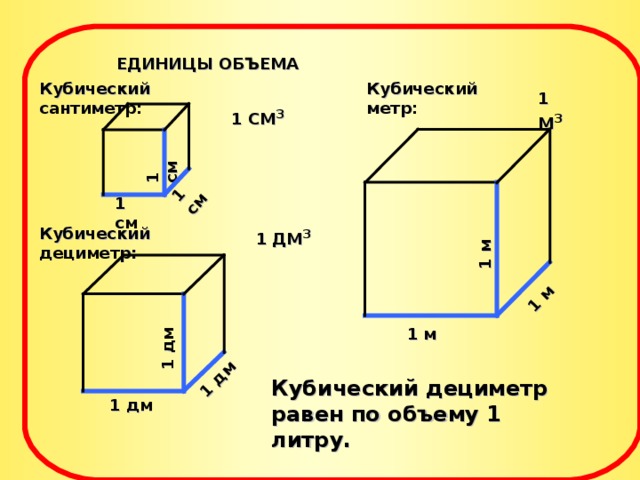 В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).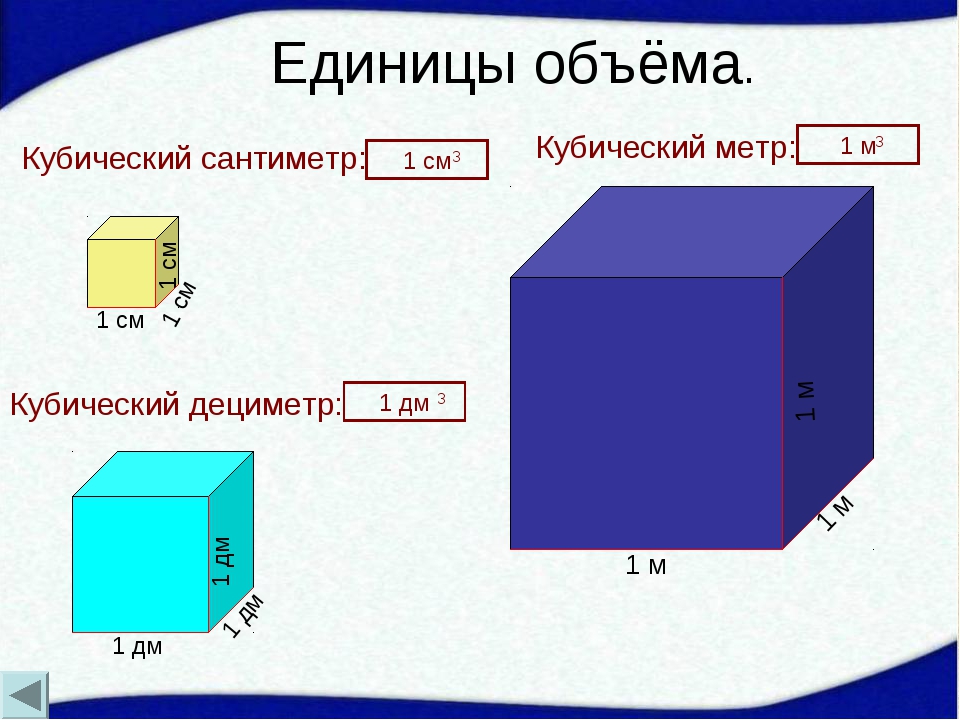
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника. Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.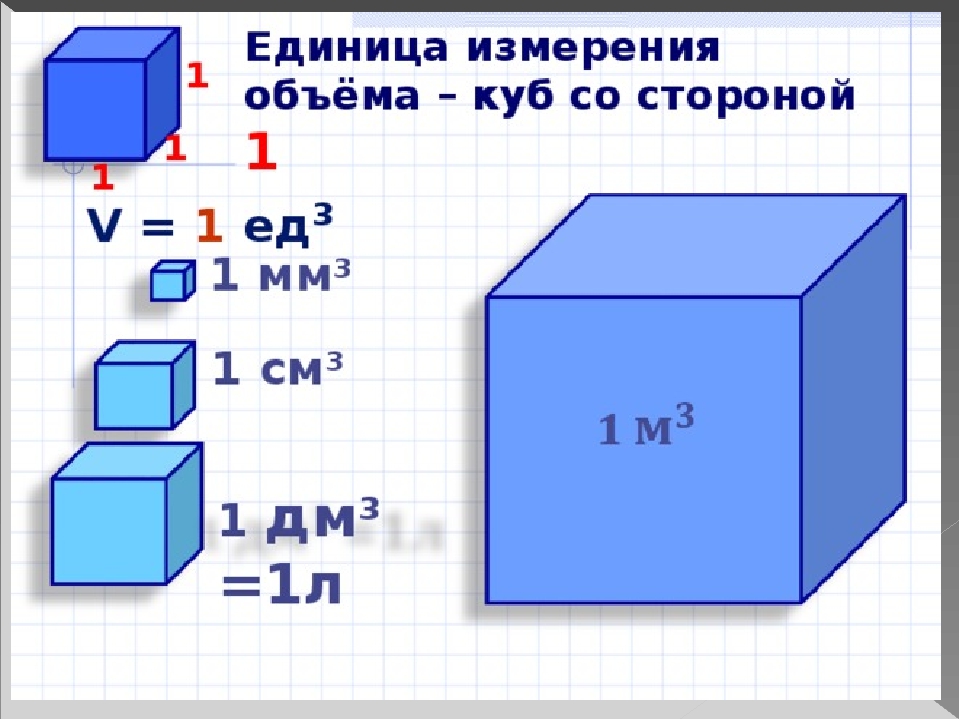
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3.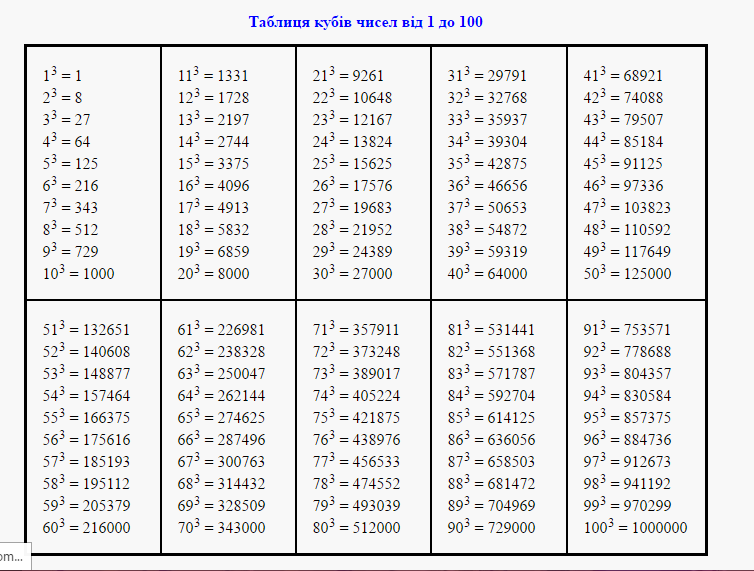 Выразить 5 м2 13 см2 в квадратных сантиметрах.
Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4. Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.
Например, если сказано что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. Например, если сказано что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из грáней, рёбер и вершин.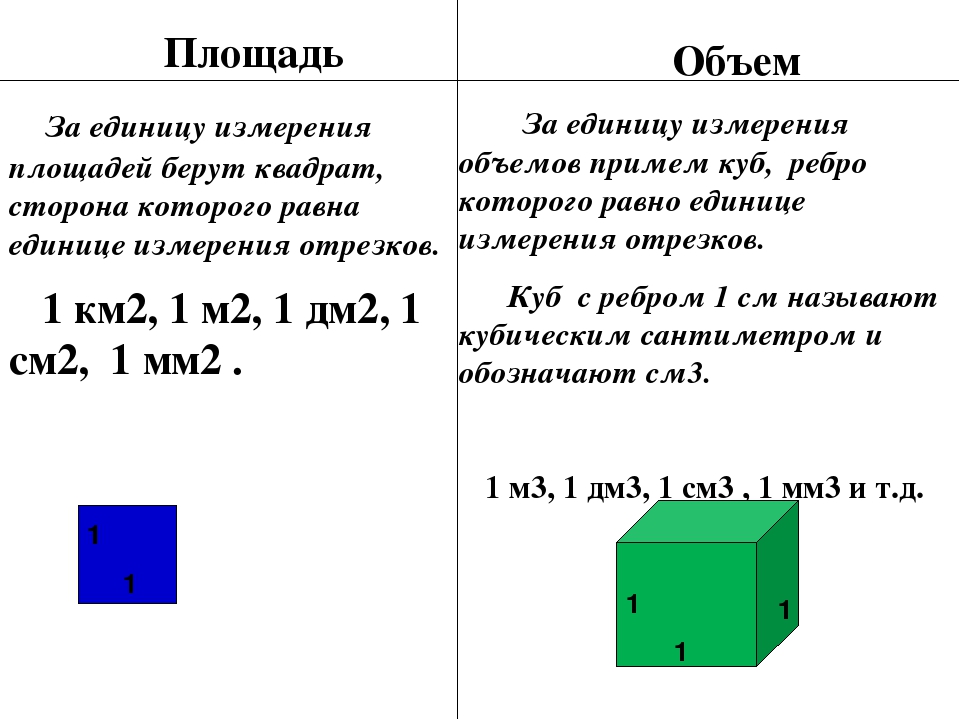 На рисунке показан прямоугольный параллелепипед:
На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грáни параллелепипеда, чёрным цветом — рёбра, красным — вершины.
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.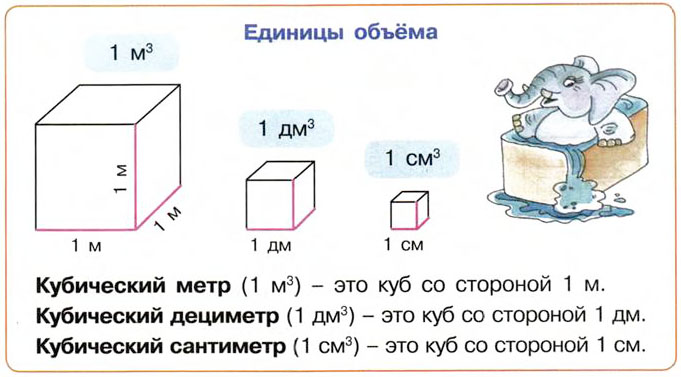
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b = м
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Периметр, площадь и объем — Помощник для школьников Спринт-Олимпик.ру
Данный материал содержит геометрические фигуры с измерениями. Приведённые измерения являются приблизительными и могут не совпадать с измерениями в реальной жизни.
Периметр геометрической фигуры
Периметр геометрической фигуры — это сумма всех её сторон. Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Чтобы вычислить периметр, нужно измерить каждую сторону и сложить результаты измерений.
Вычислим периметр следующей фигуры:
Это прямоугольник. Детальнее мы поговорим об этой фигуре позже. Сейчас просто вычислим периметр этого прямоугольника. Длина его равна 9 см, а ширина 4 см.
У прямоугольника противоположные стороны равны. Это видно на рисунке. Если длина равна 9 см, а ширина равна 4 см, то противоположные стороны будут равны 9 см и 4 см соответственно:
Найдём периметр. Для этого сложим все стороны. Складывать их можно в любом порядке, поскольку от перестановки мест слагаемых сумма не меняется. Периметр часто обозначается заглавной латинской буквой P (англ. perimeters). Тогда получим:
P = 9 см + 4 см + 9 см + 4 см = 26 см.
Поскольку у прямоугольника противоположные стороны равны, нахождение периметра записывают короче — складывают длину и ширину, и умножают её на 2, что будет означать «повторить длину и ширину два раза»
P = 2 × (9 + 4) = 18 + 8 = 26 см.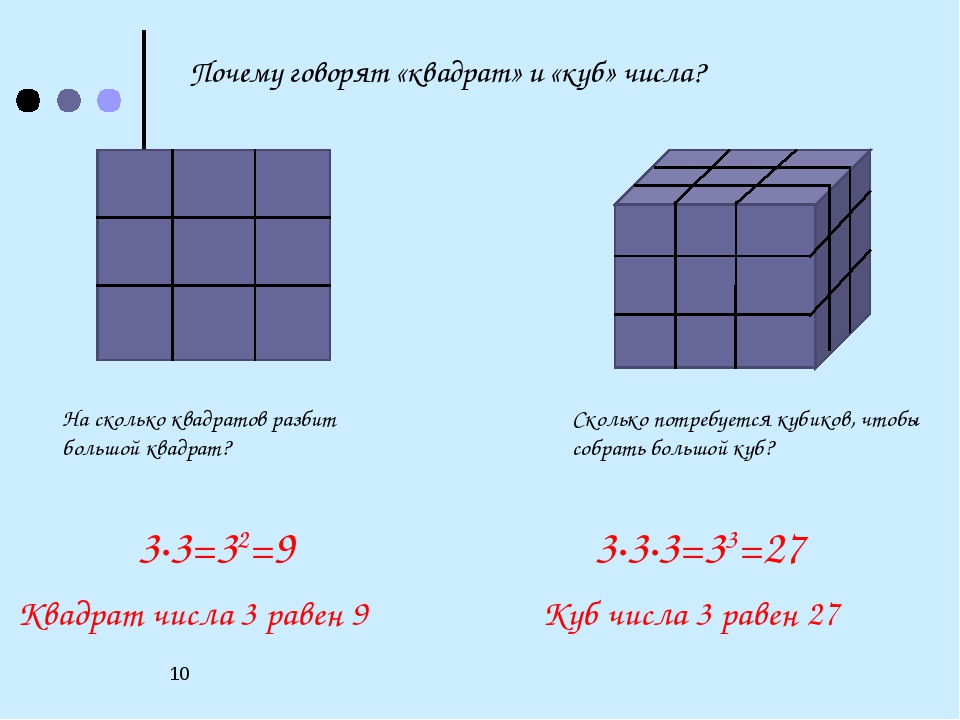
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, найдём периметр квадрата со стороной 5 см. Фразу «со стороной 5 см» нужно понимать как «длина каждой стороны квадрата равна 5 см»
Чтобы вычислить периметр, сложим все стороны:
P = 5 см + 5 см + 5 см + 5 см = 20 см
Но поскольку все стороны равны, вычисление периметра можно записать в виде произведения. Сторона квадрата равна 5 см, и таких сторон 4. Тогда эту сторону, равную 5 см нужно повторить 4 раза
P = 5 см × 4 = 20 см
Площадь геометрической фигуры
Площадь геометрической фигуры — это число, которое характеризует размер данной фигуры.
Следует уточнить, что речь в данном случае идёт о площади на плоскости. Плоскостью в геометрии называют любую плоскую поверхность, например: лист бумаги, земельный участок, поверхность стола.
Площадь измеряется в квадратных единицах. Под квадратными единицами подразумевают квадраты, стороны которых равны единице. Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Например, 1 квадратный сантиметр, 1 квадратный метр или 1 квадратный километр.
Измерить площадь какой-нибудь фигуры означает выяснить сколько квадратных единиц содержится в данной фигуре.
Например, площадь следующего прямоугольника равна трём квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится три квадрата, каждый из которых имеет сторону, равную одному сантиметру:
Справа представлен квадрат со стороной 1 см (он в данном случае является квадратной единицей). Если посмотреть сколько раз этот квадрат входит в прямоугольник, представленный слева, то обнаружим, что он входит в него три раза.
Следующий прямоугольник имеет площадь, равную шести квадратным сантиметрам:
Это потому что в данном прямоугольнике содержится шесть квадратов, каждый из которых имеет сторону, равную одному сантиметру:
Допустим, потребовалось измерить площадь следующей комнаты:
Определимся в каких квадратах будем измерять площадь. В данном случае площадь удобно измерить в квадратных метрах:
В данном случае площадь удобно измерить в квадратных метрах:
Итак, наша задача состоит в том, чтобы определить сколько таких квадратов со стороной 1 м содержится в исходной комнате. Заполним этим квадратом всю комнату:
Видим, что квадратный метр содержится в комнате 12 раз. Значит, площадь комнаты составляет 12 квадратных метров.
Площадь прямоугольника
В предыдущем примере мы вычислили площадь комнаты, последовательно проверив сколько раз в ней содержится квадрат, сторона которого равна одному метру. Площадь составила 12 квадратных метров.
Комната представляла собой прямоугольник. Площадь прямоугольника можно вычислить перемножив его длину и ширину.
Чтобы вычислить площадь прямоугольника, нужно перемножить его длину и ширину.
Вернёмся к предыдущему примеру. Допустим, мы измерили длину комнаты рулеткой и оказалось, что длина составила 4 метра:
Теперь измерим ширину. Пусть она составила 3 метра:
Умножим длину (4 м) на ширину (3 м).
4 × 3 = 12
Как и в прошлый раз получаем двенадцать квадратных метров. Это объясняется тем, что измерив длину, мы тем самым узнаём сколько раз можно уложить в эту длину квадрат со стороной, равной одному метру. Уложим четыре квадрата в эту длину:
Затем мы определяем сколько раз можно повторить эту длину с уложенными квадратами. Это мы узнаём, измерив ширину прямоугольника:
Площадь квадрата
Квадрат это тот же прямоугольник, но у которого все стороны равны. Например, на следующем рисунке представлен квадрат со стороной 3 см. Фраза «квадрат со стороной 3 см» означает, что все стороны равны 3 см
Площадь квадрата вычисляется таким же образом, как и площадь прямоугольника — длину умножают на ширину.
Вычислим площадь квадрата со стороной 3 см. Умножим длину 3 см на ширину 3 см
3 × 3 = 9
В данном случае требовалось узнать сколько квадратов со стороной 1 см содержится в исходном квадрате. В исходном квадрате содержится девять квадратов со стороной 1 см. Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Действительно, так оно и есть. Квадрат со стороной 1 см, входит в исходный квадрат девять раз:
Умножив длину на ширину, мы получили выражение 3 × 3, а это есть произведение двух одинаковых множителей, каждый из которых равен 3. Иными словами выражение 3 × 3 представляет собой вторую степень числа 3. А значит процесс вычисления площади квадрата можно записать в виде степени 32.
Поэтому вторую степень числа называют квадратом числа. При вычислении второй степени числа a, человек тем самым находит площадь квадрата со стороной a. Операцию возведения числа во вторую степень по другому называют возведением в квадрат.
Обозначения
Площадь обозначается заглавной латинской буквой S (англ. Square — квадрат). Тогда площадь квадрата со стороной a см будет вычисляться по следующему правилу
S = a2
где a — длина стороны квадрата. Вторая степень указывает на то, что происходит перемножение двух одинаковых сомножителей, а именно длины и ширины. Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Ранее было сказано, что у квадрата все стороны равны, а значит равны длина и ширина квадрата, выраженные через букву a.
Если задача состоит в том, чтобы определить сколько квадратов стороной 1 см содержится в исходном квадрате, то в качестве единиц измерения площади нужно указывать см2. Это обозначение заменяет словосочетание «квадратный сантиметр».
Например, вычислим площадь квадрат со стороной 2 см.
Значит, квадрат со стороной 2 см, имеет площадь, равную четырём квадратным сантиметрам:
Если задача состоит в том, чтобы определить сколько квадратов со стороной 1 м содержится в исходном квадрате, то в качестве единиц измерения нужно указывать м2. Это обозначение заменяет словосочетание «квадратный метр».
Вычислим площадь квадрата со стороной 3 метра
Значит, квадрат со стороной 3 м, имеет площадь равную девяти квадратным метрам:
Аналогичные обозначения используются при вычислении площади прямоугольника.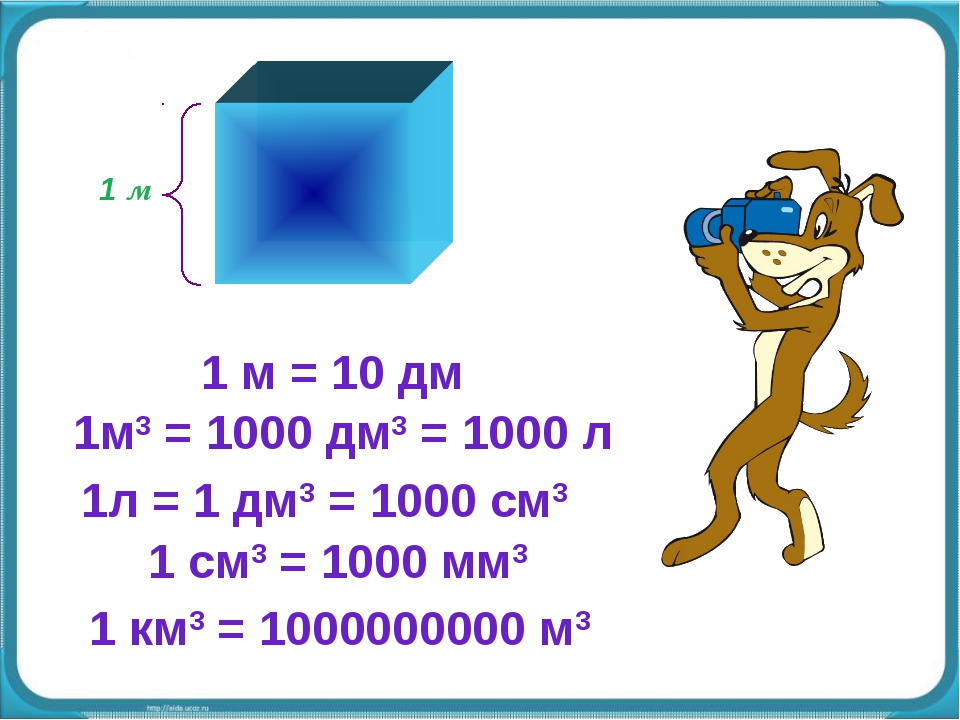 Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
Но длина и ширина прямоугольника могут быть разными, поэтому они обозначаются через разные буквы, например a и b. Тогда площадь прямоугольника, длиной a и шириной b вычисляется по следующему правилу:
S = a × b
Как и в случае с квадратом, единицами измерения площади прямоугольника могут быть см2, м2, км2. Эти обозначения заменяют словосочетания «квадратный сантиметр», «квадратный метр», «квадратный километр» соответственно.
Например, вычислим площадь прямоугольника, длиной 6 см и шириной 3 см
Значит, прямоугольник длиной 6 см и шириной 3 см имеет площадь, равную восемнадцати квадратным сантиметрам:
В качестве единицы измерения допускается использовать словосочетание «квадратных единиц». Например, запись S = 3 кв.ед означает, что площадь квадрата или прямоугольника равна трём квадратам, каждый из которых имеет единичную сторону (1 см, 1 м или 1 км).
Перевод единиц измерения площади
Единицы измерения площади можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Рассмотрим несколько примеров:
Пример 1. Выразить 1 квадратный метр в квадратных сантиметрах.
1 квадратный метр это квадрат со стороной 1 м. То есть все четыре стороны имеют длину, равную одному метру.
Но 1 м = 100 см. Тогда все четыре стороны тоже имеют длину, равную 100 см
Вычислим новую площадь этого квадрата. Умножим длину 100 см на ширину 100 см или возведём в квадрат число 100
S = 1002 = 10 000 см2
Получается, что на один квадратный метр приходится десять тысяч квадратных сантиметров.
1 м2 = 10 000 см2
Это позволяет в будущем умножить любое количество квадратных метров на 10 000 и получить площадь, выраженную в квадратных сантиметрах.
Чтобы перевести квадратные метры в квадратные сантиметры, нужно количество квадратных метров умножить на 10 000.
А чтобы перевести квадратные сантиметры в квадратные метры, нужно наоборот количество квадратных сантиметров разделить на 10 000.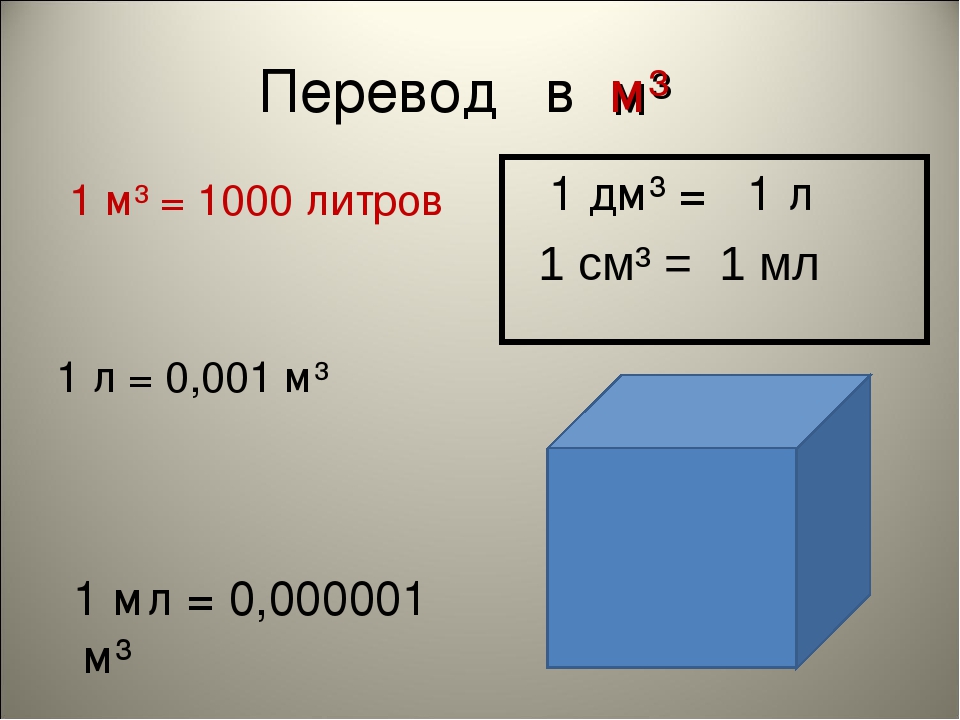
Например, переведём 100 000 см2 в квадратные метры. Рассуждать в этом случае можно так: «если 10 000 см2 это один квадратный метр, то сколько раз 100 000 см2 будут содержать по 10 000 см2»
100 000 см2 : 10 000 см2 = 10 м2
Другие единицы измерения можно переводить таким же образом. Например, переведём 2 км2 в квадратные метры.
Один квадратный километр это квадрат со стороной 1 км. То есть все четыре стороны имеют длину, равную одному километру. Но 1 км = 1000 м. Значит, все четыре стороны квадрата также равны 1000 м. Найдём новую площадь квадрата, выраженную в квадратных метрах. Для этого умножим длину 1000 м на ширину 1000 м или возведём в квадрат число 1000
S = 10002 = 1 000 000 м2
Получается, что на один квадратный километр приходится один миллион квадратных метров:
1 км2 = 1 000 000 м2
Это позволяет в будущем умножить любое количество квадратных километров на 1 000 000 и получить площадь, выраженную в квадратных метрах.
Чтобы перевести квадратные километры в квадратные метры, нужно количество квадратных километров умножить на 1 000 000.
Итак, вернёмся к нашей задаче. Требовалось перевести 2 км2 в квадратные метры. Умножим 2 км2 на 1 000 000
2 км2 × 1 000 000 = 2 000 000 м2
А чтобы перевести квадратные метры в квадратные километры, нужно наоборот количество квадратных метров разделить на 1 000 000.
Например, переведём 3 500 000 м2 в квадратные километры. Рассуждать в этом случае можно так: «если 1 000 000 м2 это один квадратный километр, то сколько раз 3 500 000 м2 будут содержать по 1 000 000 м2»
3 500 000 м2 : 1 000 000 м2 = 3,5 км2
Пример 2. Выразить 7 м2 в квадратных сантиметрах.
Умножим 7 м2 на 10 000
7 м2 = 7 м2 × 10 000 = 70 000 см2
Пример 3. Выразить 5 м2 13 см2 в квадратных сантиметрах.
5 м2 13 см2 = 5 м2 × 10 000 + 13 см2 = 50 013 см2
Пример 4.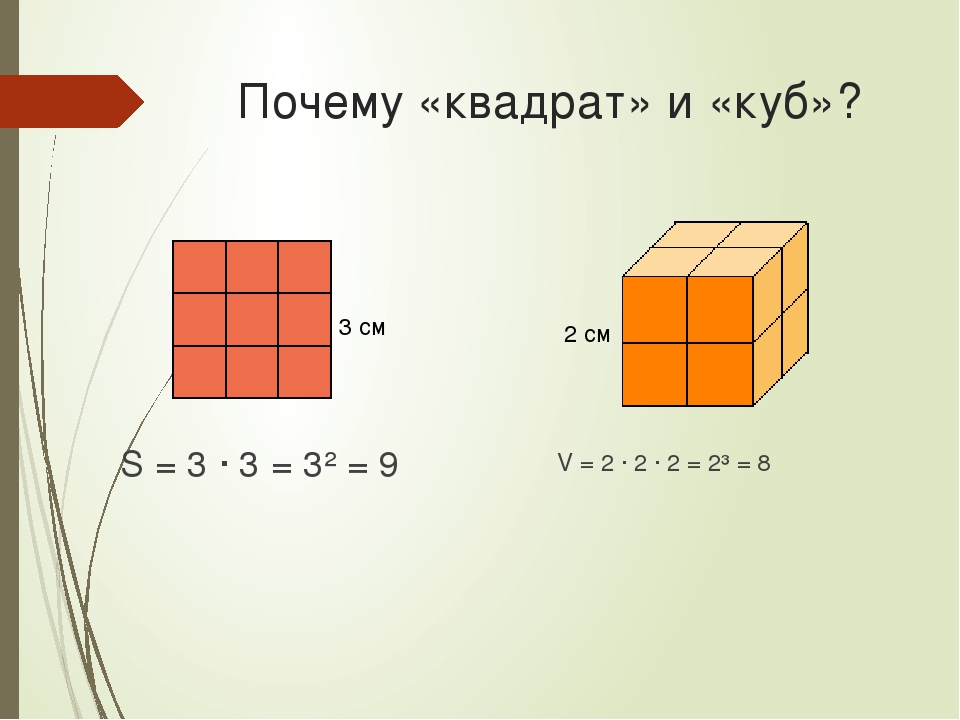 Выразить 550 000 см2 в квадратных метрах.
Выразить 550 000 см2 в квадратных метрах.
Узнаем сколько раз 550 000 см2 содержит по 10 000 см2. Для этого разделим 550 000 см2 на 10 000 см2
550 000 см2 : 10 000 см2 = 55 м2
Пример 5. Выразить 7 км2 в квадратных метрах.
Умножим 7 км2 на 1 000 000
7 км2 × 1 000 000 = 7 000 000 м2
Пример 6. Выразить 8 500 000 м2 в квадратных километрах.
Узнаем сколько раз 8 500 000 м2 содержит по 1 000 000 м2. Для этого разделим 8 500 000 м2 на 1 000 000 м2
8 500 000 м2 × 1 000 000 м2 = 8,5 км2
Единицы измерения площади земельных участков
Площади небольших земельных участков удобно измерять в квадратных метрах.
Площади более крупных земельных участков измеряются в арах и гектарах.
Ар (сокращённо: a) — это площадь равная ста квадратным метрам (100 м2). В виду частого распространения такой площади (100 м2) она стала использоваться, как отдельная единица измерения.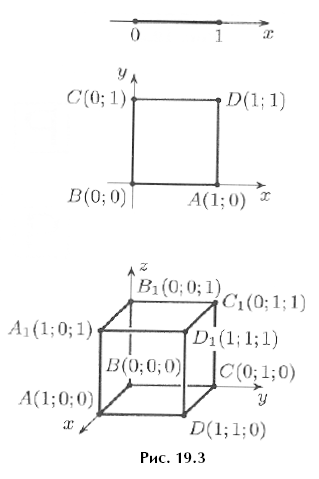
К примеру, если сказано, что площадь какого-нибудь поля составляет 3 а, то нужно понимать, что это три квадрата площадью 100 м2 каждый, то есть:
3 а = 100 м2 × 3 = 300 м2
В народе ар часто называют соткой, поскольку ар равен квадрату, площадью 100 м2. Примеры:
1 сотка = 100 м2
2 сотки = 200 м2
10 соток = 1000 м2
Гектар (сокращенно: га) — это площадь, равная 10 000 м2. К примеру, если сказано, что площадь какого-нибудь леса составляет 20 гектаров, то нужно понимать, что это двадцать квадратов площадью 10 000 м2 каждый, то есть:
20 га = 10 000 м2 × 20 = 200 000 м2
Прямоугольный параллелепипед и куб
Прямоугольный параллелепипед — это геометрическая фигура, состоящая из граней, ребер и вершин. На рисунке показан прямоугольный параллелепипед:
Желтым цветом показаны грани параллелепипеда, чёрным цветом — рёбра, красным — вершины.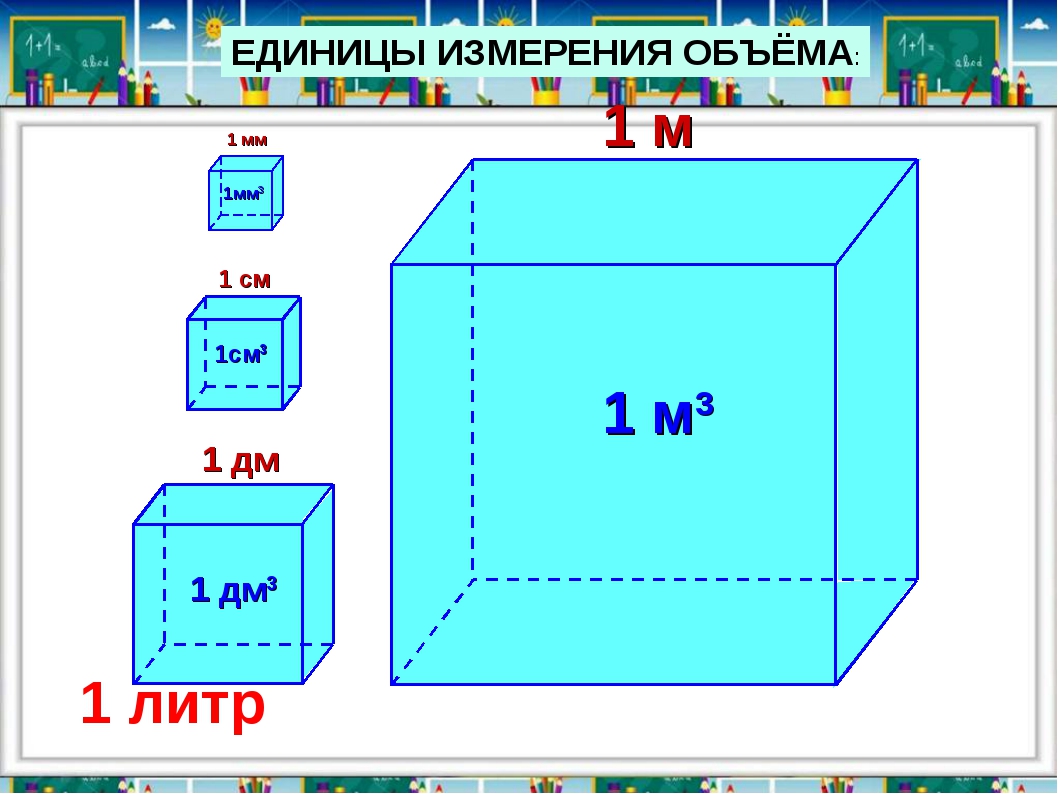
Прямоугольный параллелепипед обладает длиной, шириной и высотой. На рисунке показано где длина, ширина и высота:
Параллелепипед, у которого длина, ширина и высота равны между собой, называется кубом. На рисунке показан куб:
Объём геометрической фигуры
Объём геометрической фигуры — это число, которое характеризует вместимость данной фигуры.
Объём измеряется в кубических единицах. Под кубическими единицами подразумевают кубы длиной 1, шириной 1 и высотой 1. Например, 1 кубический сантиметр или 1 кубический метр.
Измерить объём какой-нибудь фигуры означает выяснить сколько кубических единиц вмещается в данную фигуру.
Например, объём следующего прямоугольного параллелепипеда равен двенадцати кубическим сантиметрам:
Это потому что в данный параллелепипед вмещается двенадцать кубов длиной 1 см, шириной 1 см и высотой 1 см:
Объём обозначается заглавной латинской буквой V. Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
Одна из единиц измерения объема это кубический сантиметр (см3). Тогда объём V рассмотренного нами параллелепипеда равен 12 см3
V = 12 см3
Объём любого параллелепипеда вычисляют следующим образом: перемножают его длину, ширину и высоту .
Объём прямоугольного параллелепипеда равен произведению его длины, ширины и высоты.
V = abc
где, a — длина, b — ширина, c — высота
Так, в предыдущем примере мы визуально определили, что объём параллелепипеда равен 12 см3. Но можно измерить длину, ширину и высоту данного параллелепипеда и перемножить результаты измерений. Мы получим тот же результат
Объём куба вычисляется таким же образом, как и объём прямоугольного параллелепипеда — перемножают длину, ширину и высоту.
Например, вычислим объём куба, длина которого 3 см. У куба длина, ширина и высота равны между собой. Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Если длина равна 3 см, то равны этим же трём сантиметрам ширина и высота куба:
Перемножаем длину, ширину, высоту и получаем объём, равный двадцати семи кубическим сантиметрам:
V = 3 × 3 × 3 = 27 см³
Действительно, в исходный куб вмещается 27 кубиков длиной 1 см
При вычислении объёма данного куба мы перемножили длину, ширину и высоту. Получилось произведение 3 × 3 × 3. Это есть произведение трёх сомножителей, каждый из которых равен 3. Иными словами, произведение 3 × 3 × 3 является третьей степенью числа 3 и может быть записано в виде 33.
V = 33 = 27 см3
Поэтому третью степень числа называют кубом числа. При вычислении третьей степени числа a, человек тем самым находит объём куба, длиной a. Операцию возведения числа в третью степень по другому называют возведением в куб.
Таким образом, объём куба вычисляется по следующему правилу:
V = a3
Где a — длина куба.
Кубический дециметр. Кубический метр
Не все объекты нашего мира удобно измерять в кубических сантиметрах. Например, объём комнаты или дома удобнее измерять в кубических метрах (м3). А объём бака, аквариума или холодильника удобнее измерять в кубических дециметрах (дм3).
Другое название одного кубического дециметра – один литр.
1 дм3 = 1 литр
Перевод единиц измерения объёма
Единицы измерения объёма можно переводить из одной единицы измерения в другую. Рассмотрим несколько примеров:
Пример 1. Выразить 1 кубический метр в кубических сантиметрах.
Один кубический метр это куб со стороной 1 м. Длина, ширина и высота этого куба равны одному метру.
Но 1 м = 100 см. Значит, длина, ширина и высота тоже равны 100 см
Вычислим новый объём куба, выраженный в кубических сантиметрах. Для этого перемножим его длину, ширину и высоту. Либо возведём число 100 в куб:
V = 1003 = 1 000 000 см3
Получается, что на один кубический метр приходится один миллион кубических сантиметров:
1 м3 = 1 000 000 см3
Это позволяет в будущем умножить любое количество кубических метров на 1 000 000 и получить объём, выраженный в кубических сантиметрах.
Чтобы перевести кубические метры в кубические сантиметры, нужно количество кубических метров умножить на 1 000 000.
А чтобы перевести кубические сантиметры в кубические метры, нужно наоборот количество кубических сантиметров разделить на 1 000 000.
Например, переведём 300 000 000 см3 в кубические метры. Рассуждать в этом случае можно так: «если 1 000 000 см3 это один кубический метр, то сколько раз 300 000 000 см3 будут содержать по 1 000 000 см3»
300 000 000 см3 : 1 000 000 см3 = 300 м3
Пример 2. Выразить 3 м3 в кубических сантиметрах.
Умножим 3 м3 на 1 000 000
3 м3 × 1 000 000 = 3 000 000 см3
Пример 3. Выразить 60 000 000 см3 в кубических метрах.
Узнаем сколько раз 60 000 000 см3 содержит по 1 000 000 см3. Для этого разделим 60 000 000 см3 на 1 000 000 см3
60 000 000 см3 : 1 000 000 см3 = 60 м3
Вместимость бака, банки или канистры измеряют в литрах. Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
Литр это тоже единица измерения объема. Один литр равен одному кубическому дециметру.
1 литр = 1 дм3
Например, если вместимость банки составляет 1 литр, это значит что объём этой банки составляет 1 дм3. При решении некоторых задач может быть полезным умение переводить литры в кубические дециметры и наоборот. Рассмотрим несколько примеров.
Пример 1. Перевести 5 литров в кубические дециметры.
Чтобы перевести 5 литров в кубические дециметры, достаточно умножить 5 на 1
5 л × 1 = 5 дм3
Пример 2. Перевести 6000 литров в кубические метры.
Шесть тысяч литров это шесть тысяч кубических дециметров:
6000 л × 1 = 6000 дм3
Теперь переведём эти 6000 дм3 в кубические метры.
Длина, ширина и высота одного кубического метра равны 10 дм
Если вычислить объём этого куба в дециметрах, то получим 1000 дм3
V = 103= 1000 дм3
Получается, что одна тысяча кубических дециметров соответствует одному кубическому метру. А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
А чтобы определить сколько кубических метров соответствуют шести тысячамл кубических дециметров, нужно узнать сколько раз 6 000 дм3 содержит по 1 000 дм3
6 000 дм3 : 1 000 дм3 = 6 м3
Значит, 6000 л = 6 м3.
Таблица квадратов
В жизни часто приходиться находить площади различных квадратов. Для этого каждый раз требуется возводить исходное число во вторую степень.
Квадраты первых 99 натуральных чисел уже вычислены и занесены в специальную таблицу, называемую таблицей квадратов.
Первая строка данной таблицы (цифры от 0 до 9) это единицы исходного числа, а первый столбец (цифры от 1 до 9) это десятки исходного числа.
Например, найдём квадрат числа 24 по данной таблице. Число 24 состоит из цифр 2 и 4. Точнее, число 24 состоит из двух десятков и четырёх единиц.
Итак, выбираем цифру 2 в первом столбце таблицы (столбце десятков), а цифру 4 выбираем в первой строке (строке единиц). Затем, двигаясь вправо от цифры 2 и вниз от цифры 4, найдём точку пересечения. В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
В результате окажемся на позиции, где располагается число 576. Значит, квадрат числа 24 есть число 576
242 = 576
Таблица кубов
Как и в ситуации с квадратами, кубы первых 99 натуральных чисел уже вычислены и занесены в таблицу, называемую таблицей кубов.
Куб числа по таблице определяется таким же образом, как и квадрат числа. Например, найдём куб числа 35. Это число состоит из цифр 3 и 5. Выбираем цифру 3 в первом столбце таблицы (столбце десятков), а цифру 5 выбираем в первой строке (строке единиц). Двигаясь вправо от цифры 3 и вниз от цифры 5, найдём точку пересечения. В результате окажемся на позиции, где располагается число 42875. Значит, куб числа 35 есть число 42875.
353 = 42875
Задания для самостоятельного решения
Задача 1. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите периметр.
Решение
P = 2(a + b)
a = 6, b = 2
P = 2(6 + 2) = 12 + 4 = 16 см
Ответ: периметр прямоугольника равен 16 см.
Задача 2. Длина прямоугольника составляет 6 см, а ширина 2 см. Найдите площадь.
Решение
S = ab
a = 6, b = 2
S = 6 × 2 = 12 см2
Ответ: площадь равна 12 см2.
Задача 3. Площадь прямоугольника составляет 12 см2. Длина составляет 6 см. Найдите ширину прямоугольника.
Решение
S = ab
S = 12, a = 6, b = x
12 = 6 × x
x = 2
Ответ: ширина прямоугольника составляет 2 см.
Задача 4. Вычислите площадь квадрата со стороной 8 см
Решение
S = a2
a = 8
S = 82 = 64 см2
Ответ: площадь квадрата со стороной 8 см равна 64 см2
Задача 5. Вычислите объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см.
Решение
V = abc
a = 6, b = 4, c = 3
V = 6 × 4 × 3 = 72 см3.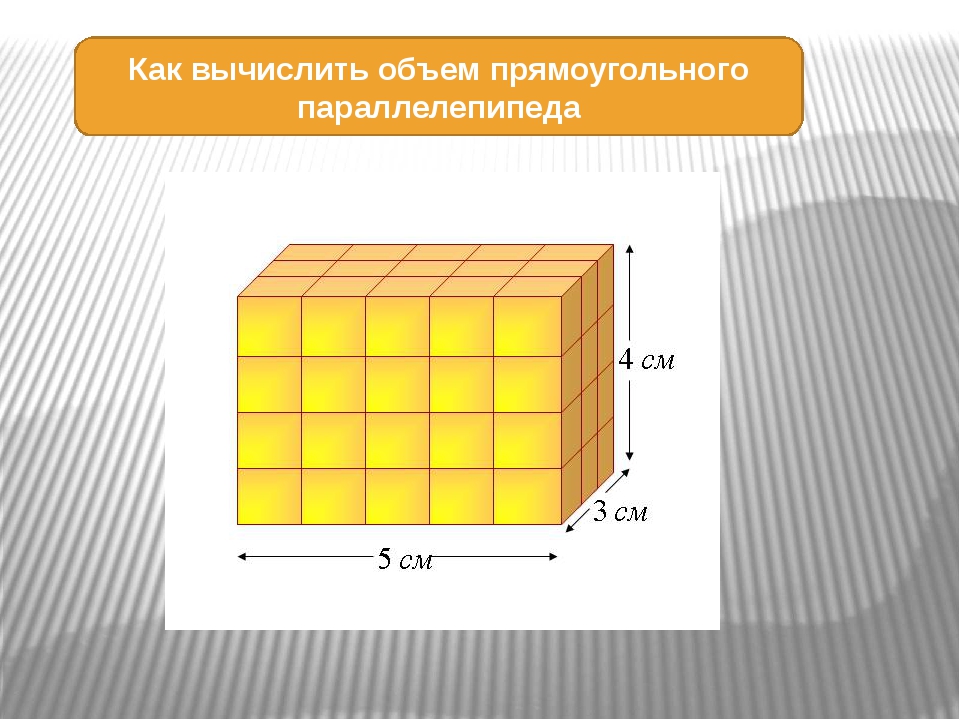
Ответ: объем прямоугольного параллелепипеда, длина которого 6 см, ширина 4 см, высота 3 см равен 72 см3
Задача 6. Объем прямоугольного параллелепипеда составляет 200 см3. Найдите высоту параллелепипеда, если его длина равна 10 см, а ширина 5 см
Решение
V = abc
V = 200, a = 10, b = 5, c = x
200 = 10 × 5 × x
200 = 50x
x = 4
Ответ: высота прямоугольного параллелепипеда равна 4 см.
Задача 7. Площади земельного участка, засеянные пшеницей и льном, пропорциональны числам 4 и 5. На какой площади засеяна пшеница, если под льном засеяно 15 га
Решение
Число 4 отражает площадь, засеянную пшеницей. А число 5 отражает площадь, засеянную льном.
Сказано что площади, засеянные пшеницей и льном пропорциональны этим числам.
Проще говоря, во сколько раз изменяются числа 4 или 5, во сколько же раз изменится и площадь, которая засеяна пшеницей или льном. Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Льном засеяно 15 га. То есть число 5, которое отражает площадь, засеянную льном, изменилось в 3 раза.
Тогда число 4, которое отражает площадь засеянную пшеницей, нужно увеличить в три раза
4 × 3 = 12 га
Ответ: пшеницей засеяно 12 га.
Задача 8. Длина зернохранилища 42 м, ширина составляет
длины, а высота – 0,1 длины. Определите сколько тонн зерна вмещает зернохранилище, если 1 м3 его весит 740 кг.Решение
a — длина
b — ширина
c — высота
a = 42 м
b =
c = 42 × 0,1 = 4,2 м
Определим объем зернохранилища:
V = abc = 42 × 30 × 4,2 = 5292 м3
Определите сколько тонн зерна вмещает зернохранилище:
5292 × 740 = 3916080 кг
Переведём килограммы в тонны:
Ответ: зернохранилище вмещает 3916,08 тонн зерна.
Задача 9. 12. Бассейн имеет форму прямоугольного параллелепипеда, длина которого равна 5,8 м, а ширина – 3,5 м. Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Две трубы наполняют его водой в течение 13 ч 32 мин., причём через одну из них вливается 25 л/мин, а через вторую – 0,75 этого количества. Определите высоту (глубину) бассейна.
Решение
Определим сколько литров в минуту вливается через вторую трубу:
25 л/мин × 0,75 = 18,75 л/мин
Определим сколько литров в минуту вливается в бассейн через обе трубы:
25 л/мин + 18,75 л/мин = 43,75 л/мин
Определим сколько литров воды будет залито в бассейн за 13 ч 32 мин
43,75 × 13 ч 32 мин = 43,75 × 812 мин = 35 525 л
1 л = 1 дм3
35 525 л = 35 525 дм3
Переведём кубические дециметры в кубические метры. Это позволит вычислит объем бассейна:
35 525 дм3 : 1000 дм3 = 35,525 м3
Зная объём бассейна можно вычислить высоту бассейна. Подставим в буквенное уравнение V=abc имеющиеся у нас значения. Тогда получим:
V = 35,525
a = 5.8
b = 3.5
c = x
35,525 = 5,8 × 3,5 × x
35,525 = 20,3 × x
x = 1,75 м
с = 1,75
Ответ: высота (глубина) бассейна составляет 1,75 м.
Предыдущая
Математика с нуляСтепень с целым показателем
СледующаяМатематика с нуляОдночлены
Сколько кирпичей в квадрате кладкиКвадратными метрами измеряется площадь. Для того, чтобы определить сколько кирпичей в 1м2 кладки необходимо произвести простые расчёты: 1. Вычислить площадь одного кирпича. Сколько кубов газа в литре сжиженного пропана?При плотности пропана в жидком состоянии коло 508 г/л и молекулярной массе 44,г/моль,все это при делении получается 11,5192 моль в одном килограмме жидкого газа пропана.Из этого следует что один литр жидкого пропана содержит 11.51 моль газа, который при испарении при нормальных условиях займёт объём 22,4 литра. Из этого получим 11,51 моль х 22,4 л/моль = 257,88 л. Сколько баллонов газа нам необходимо для обогреваВес заполненного на 85% 50-литрового баллона составляет 23,375 кг. Это соответствует 43л жидкого топлива или суммарному объему газа 10 м 3 . При этом пропана в нем не менее 22,4 кг. Наилучшим вариантом является чистый пропан, но по по ГОСТ 15860-84 обязательная пропана в должно быть не менее 60%. Для того, чтобы понять, насколько хватит одного баллона, обратимся к инструкции производителя, где сказано, что котел мощностью 24 кВт потребляет на максимальной мощности примерно 2 кг/ч пропана. Что означает, что при функционировании в полную силу 50 литров хватит на 22,4/2-11,2 часов. Газ сжижается, поступает в баллоны и при таком состоянии газа можно начинать производство. Поэтому при минусовой температуре на улице Пропан-Бутановая смесь при выходе из баллона,превращается в газообразное состояние .И так как у Пропана температура испарения меньше, он испаряется в первую очередь,что и приводит к образованию инея на баллонах и уменьшения давления газа на выходе из испарителя.Поэтому работа котла с одним газовым болонам невозможна,из-за маленькой площади испарения. Но этот основной недостаток можно устранить с помощью газовой гребенки, которая соединит несколько котлов в каскад,что приведет к повышению давления . А для испарения Бутана необходимо обогреть газовые баллоны с помощью воздушной смеси из котельной подавая ее по гофрированной трубе,или с помощью термоодеяла для газовых баллонов.Что позволит Вам сэкономить до 20% газа за счет подогрева бутана и его полного испарения из баллона. Подключаем баллон к отопительному котлу через устройство для понижения давления (редуктор). В то время, когда газ проходит через редуктор он принимает начальное газообразное состояние, а поступая в котел, он сжигается и выделяет достаточно большое количество тепла. Преимущества при отоплении газовыми баллонами:
Как используется 1 куб водыДля наглядности, из 1-го кубического метра воды можно выполнить следующее количество таких процедур:
Для дачников или жителей частных домов необходимо отметить, что указанного объёма воды достаточно для обильного полива одной сотки земли на приусадебном участке. Калькулятор квадратных и кубических метровПеревести Поделитесь информацией с друзьями Другие конвертеры Перевести тонны в кубометры См. такжеПеревод единиц длины Как перевести объем щебня в массуЭтот перевод крайне сложен и часто бывает затруднен. Можно привести следующую таблицу для того, чтобы можно было производить хотя бы приблизительные расчёты. Таблица плотности насыпного щебня в зависимости от марки
Соответственно, закупая определенный объём щебня, можно высчитать его массу по формуле: Масса щебня = Объём щебня * Коэффициент(из таблицы) Например, 2,5 кубометра фракции 5-10 будет весить: 2,5*1,38 = 3,45 тонны. Стоит отметить, что данные показатели действительны только для гранитного щебня из серого гранита высшего качества. А также стоит учитывать, что результат расчётов приблизительный, поскольку на значение коэффициента оказывают влияние вышеперечисленные факторы. Только точное измерение контрольного объёма поможет дать ответы на вопросы. Таблица примерного веса кубометра различных видов щебня
Можно конечно же измерять например с помощью ведра, но это очень трудоёмкий процесс, занимающий много времени. В том случае, если не столь важен именно точный вес 1м3 щебня, то можно взять среднее значение веса 1м3 щебня: 1,4 тонны. Расход грунтовки на 1м2: для чего нужна и нормы расхода ОСБ плиты: технические характеристики, виды, размеры, покраска Каталог пиломатериалов от компании СибЛесГабариты досокКубометр доски – это сколько? Один из самых распространённых вопросов, которые задают мастера-новички. На самом деле на этот вопрос можно дать предельно простой ответ: это, смотря о каком пиломатериале речь! Схема определения линейного размера пиломатериала Как правило, для строительных и ремонтных работ применяют заготовки, произведенные по ГОСТ 8486-86. Этот норматив, регламентирующий основные требования к пиломатериалам хвойных пород (для лиственных есть отдельный документ – ГОСТ 2695-83), определяет, какой размер может иметь изделие. В принципе, подобрать нужную деталь несложно, но все же есть определенные ограничения, которые и лимитируют производство заготовок:
Естественно, встречаются и отступления. Так, при необходимости можно заказать изготовление деталей с другим соотношением толщины и ширины. Их цена, конечно, будет выше, чем стандартных, но при необходимости и наличии подходящего сырья можно выпилить практически любую заготовку. Стандартная длина составляет от 1 до 6 м Что касается длины, то здесь все несколько сложнее. Найти заготовки длиннее 6 м получается далеко не всегда, поскольку эта величина ограничена габаритами товарного вагона. Так что более длинные доски пилятся исключительно под заказ и перевозятся автотранспортом, что удорожает материал. В принципе, этой информации будет вполне достаточно, чтобы мы, зная основные параметры изделий, могли рассчитать, сколько 6 метровых досок в кубе, и какую площадь они займут при обшивке либо укладке на пол. Использование сжиженного газаНесколько сложнее со сжиженным газом. Он широко применяется:
В домашнем хозяйстве сжиженный газ в баллонах выгодно использовать для эксплуатации газопотребляющих приборов бытового назначения при условии отсутствия подвода централизованной магистрали. |
Как переводить площади и объемы в систему СИ
Решая физические задачи, мы сталкиваемся с необходимостью перевода площадей в квадратные метры и объемов в кубические метры. Иногда для этого используют готовые формулы. Но эффективнее запомнить простой принцип, описанный в статье, тогда готовые формулы заучивать не придется.
Примечание: К примеру, площадь в формулу для вычисления давления нужно подставлять, выражая ее в квадратных метрах.
Переводим площадь
Разберем принцип, основанный на определении квадратного метра, для пересчета площадей в систему СИ.
Используем принцип единиц в квадрате
Для начала научимся переводить сантиметры в квадрате в квадратные метры. Алгоритм перевода будет состоять из нескольких простых шагов.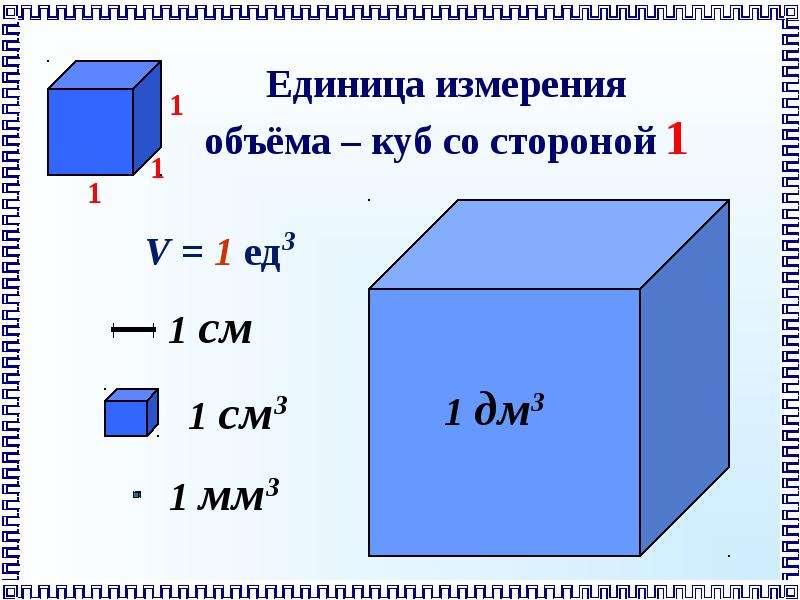 {3} \right) \]
{3} \right) \]
сколько квадратов в листе, как посчитать и перевести, расчет площади
Это будет еще одна небольшая статья из серии «Все обо всем для юных строителей». Материал и правда не очень большой, не очень сложный, но крайне полезный. Сегодня мы поговорим о двух прекрасных вещах: фанере и математике.
Нас очень часто спрашивают «сколько весит фанера? а лист фанеры? а кубометр фанеры? а если квадратный метр фанеры?». Мы конечно же отвечаем на эти вопросы, ведь это наша работа. Но всем нам нужен отдых, хотя бы по ночам, хотя бы в выходные.
|
Итак, сегодня Ант-Снаб научит всех считать. Безусловно, мы не стремимся Теоретическая часть расчета довольна скучная и простая, поэтому пропустим ее Задача: Анатолий перфекционист и поэтому формат фанеры предпочитает 1525х1525 мм, толщина листа 9 мм. |
Решение:
1. Для начала Анатолию нужно определиться с количеством листов, которые вместе составят заветные 350 м2. Для этого делим нужное нам количество квадратных метров на площадь листа (умножая длину листа на его ширину), округляем в бОльшую сторону:
350 / (1,525 х 1,525) = 350 / 2,3256… = 150,4988, округляем и получаем 151 лист
|
2. Далее Анатолию следует узнать количество листов в 1 кубе именно 151 / 47,777 = 3,1605… округляем и получаем 3,161 м3 3. Точный вес материалов из древесины очень сильно зависит от влажности, 3,161 х 700 = 2212,7 кг |
Именно столько будут весить 350 м2 березовой фанеры ФК с форматом листа 1525х1525 мм и толщиной 9 мм. Мы бы посоветовали дачнику Анатолию заказать недорогую доставку и не тратить время в пробках. Но тут уж он сам решит.
|
Разделив общий вес на количество листов, можно узнать вес Подведем итог, 350 квадратных метров фанеры ФК 1525х1525х9 мм это: • 151 лист Хочется отдельно отметить, что вес листа фанеры 9 мм и, |
Как видите все довольно просто, даже если вы решите посчитать все самостоятельно. На этом сегодня все!
Сколько тонн асфальта в кубе для расчета на квадратный метр
При прокладке любой дороги начинать необходимо с того, что рассчитать количество требуемых строительных материалов. В первую очередь это расчет асфальта, как основной статьи расходов, как в финансовом, так и чисто утилитарном плане. Наиболее удобная единица измерений в данном контексте при заказе этого материала — тонна. Чтобы высчитать, количество необходимых кубометров для дороги тоже нужно сделать перевод кубов в тонны, так как расход считается исходя из массы.
В первую очередь это расчет асфальта, как основной статьи расходов, как в финансовом, так и чисто утилитарном плане. Наиболее удобная единица измерений в данном контексте при заказе этого материала — тонна. Чтобы высчитать, количество необходимых кубометров для дороги тоже нужно сделать перевод кубов в тонны, так как расход считается исходя из массы.
Покупка асфальта происходит на основе того, сколько м3 помещается в Камазе. При этом не существует стандартной асфальтовой смеси, то есть при одном объёме получаем разную массу. Чтобы избежать долгого и утомительного поиска коэффициентов перевода асфальта из м3 в тонны, можно обратиться к помощи нашего сайта.
Специально созданный для этих целей онлайн калькулятор поможет вам точно узнать сколько кубов в тонне асфальта и наоборот. Благодаря этому возможно составить смету, соответствующую юридическим и правовым нормам и не допустить перерасхода средств. А зная, сколько весит куб асфальта в тоннах, можно точно подсчитать необходимое количество на требуемую площадь.
Калькулятор расчета
Как рассчитать количество асфальта на 1 м2
Чтобы подсчитать сколько тонн асфальта понадобится на дорожное основание и покрытие нужно знать расход на 1 м2. В среднем на основание или покрытие толщиной в см потребуется примерно 25 килограмм асфальта. Естественно к значению иногда необходимо добавить несколько сот грамм в зависимости от того, мелкозернистый или крупнозернистый асфальт и характеристик минерального сырья для создания. Подробнее подобные характеристики следует уточнять непосредственно у производителя.
Формула же затрат на кв. метр асфальтовой смеси выглядит так – 25*необходимая толщину слоя. Далее потребуется перевести асфальт в тонны в получившемся результате, что сделать ещё проще. Вот простой пример – 25*6=150 килограмм. Как рассчитать асфальт из м2 в тонну теперь? Всё предельно просто, достаточно итог (150), разделить на 1000 и получим 0,15 тонны.
Как рассчитать асфальт из м2 в тонну теперь? Всё предельно просто, достаточно итог (150), разделить на 1000 и получим 0,15 тонны.
Коэффициент асфальта
|
Вид асфальтобетонной смеси |
ТИП |
Плотность т/м3 |
|
Крупнозернистая |
Плотная |
2,4 |
|
Пористая |
2,38 |
|
|
Мелкозернистая |
Тип А |
2,44 |
|
Тип Б |
2,41 |
|
|
Тип В |
2,4 |
|
|
Песчаная |
Тип Г |
2,45 |
|
Тип Д |
2,34 |
Расчет асфальта по площади
Естественно расчет укладки всего на м2 не та площадь, встречающаяся в строительстве на практике.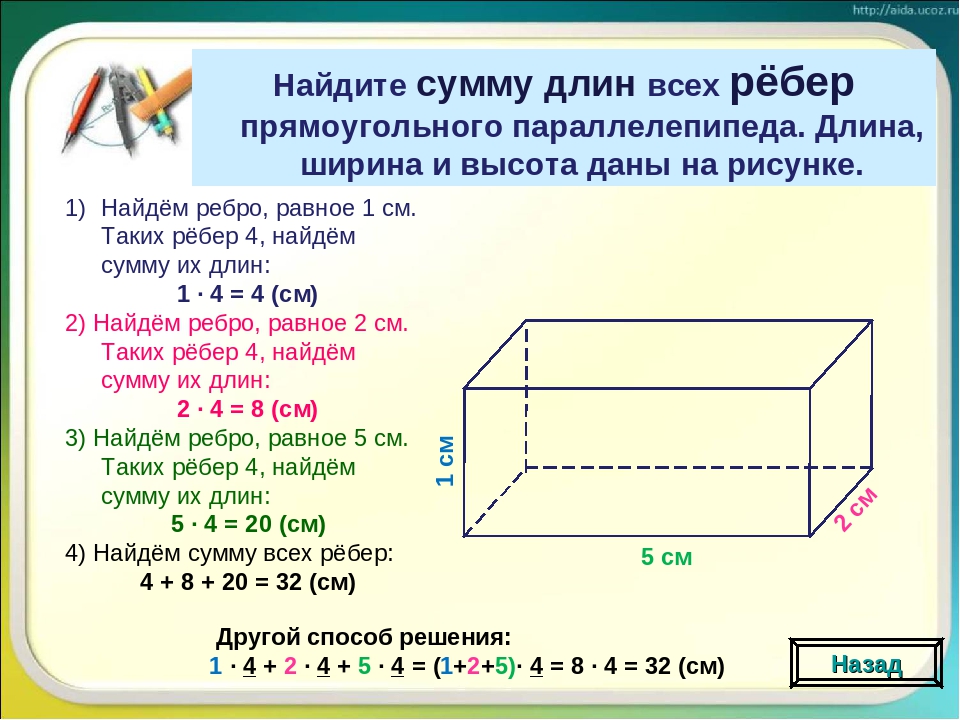 Поэтому продолжаем расчёты дальше. Узнаем сколько тонн асфальта нужно на покрытие дороги с толщиной полотна в 6 см и общей площадью в 2500 м2.Нам уже известно, количество на 1 метр при таком слое. Теперь умножаем 0,15 на 2500 и получаем искомое значение, в случае данного примера это 375 тонн.
Поэтому продолжаем расчёты дальше. Узнаем сколько тонн асфальта нужно на покрытие дороги с толщиной полотна в 6 см и общей площадью в 2500 м2.Нам уже известно, количество на 1 метр при таком слое. Теперь умножаем 0,15 на 2500 и получаем искомое значение, в случае данного примера это 375 тонн.
Правда определённый объём запросов соответствует только чистому расходу на работу. Но при выполнении полного комплекса дорожно-строительных мероприятий существуют и другие частности из-за чего запросы возрастут. Поэтому максимально точное составление сметы может сделать только специалист, оценивающий требуемые объёмы для выполнения работ на определенном объекте.
Квадрат, куб, квадратный корень и кубический корень
Калькулятор квадрата, куба, квадратного корня и кубического корня
Квадрат, куб, квадратный корень и кубический корень для чисел с диапазоном 0-100
| Число x | Квадрат x 2 | Куб x 3 | Квадратный корень x 1/2 | Кубический корень x 1/3 |
|---|---|---|---|---|
| 1 | 1 | 1 | 1. 000 000 | 1.000 |
| 2 | 4 | 8 | 1,414 | 1,260 |
| 3 | 9 | 27 | 1,732 | 1,442 |
| 4 | 16 | 64 | 2.000 | 1,587 |
| 5 | 25 | 125 | 2,236 | 1,710 |
| 6 | 36 | 216 | 2.449 | 1,817 |
| 7 | 49 | 343 | 2,646 | 1,913 |
| 8 | 64 | 512 | 2,828 | 2,000 |
| 81 | 729 900 | 3.000 | 2,080 | |
| 10 | 100 | 1000 | 3,162 | 2,154 |
| 11 | 121 | 1331 | 3.317 | 2,224 |
| 12 | 144 | 1728 | 3,464 | 2,289 |
| 13 | 169 | 2197 | 3,606 | 2,351 |
| 14 | 196 | 3,742 | 2,410 | |
| 15 | 225 | 3375 | 3,873 | 2,466 |
| 16 | 256 | 4096 | 4. 000 000 | 2,520 |
| 17 | 289 | 4913 | 4,123 | 2,571 |
| 18 | 324 | 5832 | 4,243 | 2,621 |
| 19 | 361 | 4,359 | 2,668 | |
| 20 | 400 | 8000 | 4,472 | 2,714 |
| 21 | 441 | 9261 | 4.583 | 2,759 |
| 22 | 484 | 10648 | 4,690 | 2,802 |
| 23 | 529 | 12167 | 4,796 | 2,844 |
| 24 | 576 576 900 | 4,899 | 2,884 | |
| 25 | 625 | 15625 | 5.000 | 2,924 |
| 26 | 676 | 17576 | 5.099 | 2,962 |
| 27 | 729 | 19683 | 5,196 | 3,000 |
| 28 | 784 | 21952 | 5,292 | 3,037 |
| 29 | 841 | |||
| 29 | 841 900 | 5,385 | 3,072 | |
| 30 | 900 | 27000 | 5,477 | 3,107 |
| 31 | 961 | 29791 | 5. 568 568 | 3,141 |
| 32 | 1024 | 32768 | 5,657 | 3,175 |
| 33 | 1089 | 35937 | 5,745 | 3,208 |
| 34 | 1156 3 | |||
| 34 | 1156 3 | |||
| 34 | 5,831 | 3,240 | ||
| 35 | 1225 | 42875 | 5,916 | 3,271 |
| 36 | 1296 | 46656 | 6.000 | 3.302 |
| 37 | 1369 | 50653 | 6.083 | 3.332 |
| 38 | 1444 | 54872 | 6.164 | 152119 |
| 39 | 152119 | 6,245 | 3,391 | |
| 40 | 1600 | 64000 | 6,325 | 3,420 |
| 41 | 1681 | 68921 | 6.403 | 3,448 |
| 42 | 1764 | 74088 | 6,481 | 3,476 |
| 43 | 1849 | 79507 | 6,557 | 3,503 |
| 44 | 1936 900 | 6,633 | 3,530 | |
| 45 | 2025 | 6,708 | 3,557 | |
| 46 | 2116 | 97336 | 6. 782 782 | 3,583 |
| 47 | 2209 | 103823 | 6,856 | 3,609 |
| 48 | 2304 | 110592 | 6,928 | 3,634 |
| 49 | 3,634 | |||
| 49 | 7.000 | 3.659 | ||
| 50 | 2500 | 125000 | 7.071 | 3.684 |
| 51 | 2601 | 132651 | 7.141 | 3,708 |
| 52 | 2704 | 140608 | 7,211 | 3,733 |
| 53 | 2809 | 148877 | 7,280 | 3,756 |
| 54 | 2916 | 7,348 | 3,780 | |
| 55 | 3025 | 166375 | 7,416 | 3,803 |
| 56 | 3136 | 175616 | 7.483 | 3.826 |
| 57 | 3249 | 185193 | 7. 550 550 | 3.849 |
| 58 | 3364 | 195112 | 7.616 | 3.871 |
| 7,681 | 3,893 | |||
| 60 | 3600 | 216000 | 7,746 | 3,915 |
| 61 | 3721 | 226981 | 7.810 | 3,936 |
| 62 | 3844 | 238328 | 7,874 | 3,958 |
| 63 | 3969 | 250047 | 7,937 | 3,979 |
| 8.000 | 4.000 | |||
| 65 | 4225 | 274625 | 8.062 | 4.021 |
| 66 | 4356 | 287496 | 8.124 | 4,041 |
| 67 | 4489 | 300763 | 8,185 | 4,062 |
| 68 | 4624 | 314432 | 8,246 | 4761 |
| 69 | 4761 | 8,307 | 4,102 | |
| 70 | 4900 | 343000 | 8,367 | 4,121 |
| 71 | 5041 | 357911 | 8. 426 426 | 4,141 |
| 72 | 5184 | 373248 | 8,485 | 4,160 |
| 73 | 5329 | 389017 | 8,544 | 4,179 |
| 74 | 544 | 8,602 | 4,198 | |
| 75 | 5625 | 421875 | 8,660 | 4,217 |
| 76 | 5776 | 438976 | 8.718 | 4,236 |
| 77 | 5929 | 456533 | 8,775 | 4,254 |
| 78 | 6084 | 474552 | 8,832 | 4,273 |
| 79 | 493 | 8,888 | 4,291 | |
| 80 | 6400 | 512000 | 8,944 | 4,309 |
| 81 | 6561 | 531441 | 9.000 | 4,327 |
| 82 | 6724 | 551368 | 9,055 | 4,344 |
| 83 | 6889 | 571787 | 9,110 | 4,362 |
| 84 | 59362 | |||
| 84 | 7056 | 9,165 | 4,380 | |
| 85 | 7225 | 614125 | 9,220 | 4,397 |
| 86 | 7396 | 636056 | 9. 274 274 | 4,414 |
| 87 | 7569 | 658503 | 9,327 | 4,431 |
| 88 | 7744 | 681472 | 9,381 | 4,448 |
| 9,434 | 4,465 | |||
| 90 | 8100 | 729000 | 9,487 | 4,481 |
| 91 | 8281 | 753571 | 9.539 | 4,498 |
| 92 | 8464 | 778688 | 9,592 | 4,514 |
| 93 | 8649 | 804357 | 9,644 | 4,531 |
| 9,695 | 4,547 | |||
| 95 | 9025 | 857375 | 9,747 | 4,563 |
| 96 | 9216 | 884736 | 9.798 | 4,579 |
| 97 | 9409 | 3 | 9,849 | 4,595 |
| 98 | 9604 | 941192 | 9,899 | 4,610 |
| 9,899 | 4,610 | |||
| 9,899 | 9,950 | 4,626 | ||
| 100 | 10000 | 1000000 | 10. 000 000 | 4,642 |
Загрузите и распечатайте диаграмму квадратного, кубического, квадратного и кубического корня
Добавьте кубические линии в свой эскиз 3D-модель
Используйте расширение Engineering ToolBox Sketchup — чтобы добавить кубические линии в модели Sketchup.
Закон квадрата-куба — Sketchplanations
В течение многих лет я задавался вопросом, как в детстве я обнаружил, что обезьяньи брусья на детской площадке (часто в тренажерном зале в джунглях в США) намного легче качаться, чем я, как взрослый. И я вижу, что наши дети легко качаются на них, а теперь мне сложно просто висеть на них. Причина этого частично связана с законом квадратного куба.
Закон квадрата-куба — обманчиво простое наблюдение, что по мере увеличения размеров — скажем, когда вы становитесь выше — площадь объекта увеличивается пропорционально квадрату длины, а объем увеличивается пропорционально кубу длины.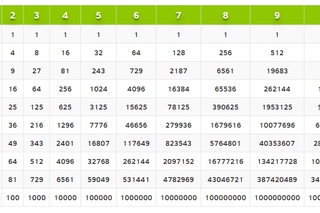 Эта фундаментальная взаимосвязь имеет огромное значение для размеров и форм животных, а также для ограничений того, насколько большими могут быть деревья и насколько большими мы можем строить мосты и здания.
Эта фундаментальная взаимосвязь имеет огромное значение для размеров и форм животных, а также для ограничений того, насколько большими могут быть деревья и насколько большими мы можем строить мосты и здания.
Поскольку сила наших костей, мышц или деревянных балок пропорциональна их площади поперечного сечения, это означает, что, хотя сила большего объекта, принимая те же пропорции, что и меньший, увеличивается пропорционально квадрату длины. , вес (от занимаемого объема) увеличивается пропорционально кубу длины.Таким образом, относительная сила уменьшается с увеличением размера.
Таким образом, некоторые следствия заключаются в том, что небольшой размер детей по сравнению с площадью их мышц и костей делает их относительно более сильными, чем взрослые, и поэтому они могут легче выдерживать свой вес, когда они качаются на брусьях. Точно так же отжиматься сложнее для больших людей, чем для маленьких. И хотя у муравья крошечные тонкие ноги, эти ноги могут легко выдержать 50 других муравьев его размера, в то время как для слона, чтобы выдержать собственный вес, ему нужны короткие ноги, а не тонкие, и нет никаких шансов, что он сможет приблизиться к 50 муравьям. другие слоны на его спине.
другие слоны на его спине.
Это также одна из причин, по которой короткие деревья могут быть тонкими, но большие секвойи имеют относительно более короткие стволы, и нам нужны все более прочные материалы, чтобы строить все большие и большие небоскребы по сравнению с навесом в вашем саду.
Галилей обсуждал это еще в 1638 году, и сегодня это требует некоторого внимания.
Чтобы узнать об этом и других увлекательных идеях масштабирования, см. «Масштаб» Джеффри Уэста.
Еще «набросок пояснений к законам».
Вы можете использовать и передавать это изображение и текст в некоммерческих целях с указанием авторства.Неистовствовать!
См. Лицензию
Экспоненты: квадрат и кубики | Примеры
Начнем с того, что вам известно. Вы можете легко написать 2 x 2 = 4 или даже 3 x 3 x 3 = 27, однако, что вы делаете, когда вам нужно представить 2, умноженные на себя в 10 раз?
Это сложно, правда? Математики уже столкнулись и рассмотрели это конкретное препятствие, и это подводит нас к темам экспонент, квадратов и кубов.
Давайте узнаем больше об экспонентах, квадратах и кубах, прокручивая страницу вниз.
План урока
Что такое экспоненты?
Показатель степени — это число, которое указывает, сколько раз число умножается само на себя.
3 здесь — показатель степени и записывается как индекс.
Показатель степени — это способ представить повторное умножение числа / переменной на себя.
Из приведенного ниже рисунка мы можем понять, что, когда значение показателя степени уменьшается, число, которое он представляет, также становится меньше.
Определение показателей
Показатель степени — это число, которое написано сверху и справа от другого числа или математического выражения (скажем, \ (m + 2 \)), называемого основанием.
Показатель степени указывает, что база возведена в определенную степень.
Показатель степени также называется другими именами, такими как индекс и степень.{n} \) означает, что \ (m \) умножается на себя в \ (n \) раз.
Пример:
Квадраты и Кубы являются предельными случаями экспонент, когда составляющая экспоненты всегда равна 2 и 3 соответственно.
Теперь, когда вы поняли, что такое экспоненты и что они означают, давайте перейдем к интересной теме, связанной с этим.
Примеры экспонент
Вот некоторые примеры экспонент:
- \ (\ begin {align} 3 \ times 3 \ times 3 \ times 3 \ times 3 & = 3 ^ 5 \ end {align} \)
- \ (\ begin {align} -2 \ times -2 \ times -2 & = (-2) ^ 3 \ end {align} \)
- \ (\ begin {align} a \ times a \ times a \ times a \ times a \ times a & = a ^ 6 \ end {align} \)
Вы можете рассчитать показатели, используя следующий «Калькулятор показателей».7 \) вместо записи \ (5 \ times 5 \ times 5 \ times 5 \ times 5 \ times 5 \ times 5 \).
Различные свойства экспонент
Свойства показателей следующие:
Отрицательная экспонента числа определяется как то, сколько раз мы умножаем обратную величину этого числа.
Квадраты и квадратные корни
Точно так же, как квадраты представляют число или переменную, умноженную на себя дважды, квадратный корень означает число, которое нужно умножить само на себя, чтобы получить это конкретное число.
По сути, это операция, обратная квадрату.
Примечание. Числа, которые дают целые числа при вычислении их квадратных корней, называются идеальными квадратами.
Примеры полных квадратов: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100 и т. Д.
Кубики и кубики
Подобно квадратным корням, кубические корни — это операции, обратные кубам.
Итак, если куб представляет собой число, умноженное на себя трижды, кубический корень числа представляет собой число, которое умножается 3 раза, чтобы получить исходное число.х = 27 \)
Я — число от 1 до 100. Я — идеальный квадрат, а также идеальный куб! Я не 1, какой я номер?
Решение
Совершенные квадраты обведены синим цветом , тогда как идеальные кубики выделены красным цветом на рисунке ниже.
64 — единственное число от 1 до 100, которое одновременно является точным квадратом и идеальным кубом, как
\ [8 ^ {2} = 64 \]
\ [4 ^ {3} = 64 \]
| \ (\ следовательно \) Число \ (64.3 \) |
I Интерактивные вопросы
Вот несколько занятий для вас. Выберите / введите свой ответ и нажмите кнопку «Проверить ответ», чтобы увидеть результат.
Подведем итоги
Мини-урок был посвящен увлекательной концепции экспонент, квадратов и кубов. Математическое путешествие по экспонентам, квадратам и кубам начинается с того, что студент уже знает, и переходит к творческому созданию новой концепции в молодых умах.Сделано таким образом, чтобы оно не только было понятным и понятным, но и навсегда осталось с ними. В этом заключается магия Куэмат.
О компании Cuemath
В Cuemath наша команда экспертов по математике стремится сделать обучение интересным для наших любимых читателей, студентов!
Благодаря интерактивному и увлекательному подходу «обучение-обучение-обучение» учителя исследуют тему со всех сторон.
Будь то рабочие листы, онлайн-классы, сеансы сомнений или любые другие формы отношений, это логическое мышление и интеллектуальный подход к обучению, в которые мы, в Cuemath, верим.м} \ конец {выровнено}
4. Как найти квадрат числа?
Чтобы найти квадрат числа, умножьте это число само на себя.
Например, квадрат 2 равен \ (2 \ times 2 = 4 \)
4. Как найти куб числа?
Чтобы найти квадрат числа, умножьте это число на себя дважды.
Например, куб 2 равен \ (2 \ times 2 \ times 2 = 8 \)
5. Как найти квадратный корень и кубический корень?
- Чтобы найти квадратный корень из числа, найдите число, которое при умножении само на себя дает исходное число.
Например: квадратный корень из 4 равен 2, потому что \ (2 \ times 2 = 4 \) - Чтобы найти кубический корень числа, найдите число, которое при трехкратном умножении на себя дает исходное число.
Например: кубический корень из 8 равен 2, потому что \ (2 \ times 2 \ times 2 = 8 \)
Калькулятор кубического корня
Использование калькулятора
Воспользуйтесь этим калькулятором, чтобы найти кубический корень из положительных или отрицательных чисел.Учитывая число
x , кубический корень x — это число a , такое что
a 3 = x . Если x положительный , будет положительным, если
x — отрицательное значение — — отрицательное. Кубические корни — это особая форма нашего общего
Калькулятор радикалов. {\ frac {1} {3}} \).Распространенное определение кубического корня отрицательного числа таково:
(-x) 1/3 = — (x 1/3 ) . [1] Например:
- Кубический корень из -27 записывается как \ (\ sqrt [3] {- 27} = -3 \).
- Кубический корень -8 записывается как \ (\ sqrt [3] {- 8} = -2 \).
- Кубический корень из -64 записывается как \ (\ sqrt [3] {- 64} = -4 \).
Кубические корни (для целочисленных результатов от 1 до 10)
- Кубический корень из 1 1
- Кубический корень из 8 равен 2
- Кубический корень из 27 равен 3
- Кубический корень из 64 равен 4
- Кубический корень из 125 составляет 5
- Кубический корень из 216 равен 6
- Кубический корень из 343 равен 7
- Кубический корень из 512 равен 8
- Кубический корень 729 равен 9
- Кубический корень из 1000 составляет 10
Для вычисления дробных показателей используйте наш калькулятор для Дробные экспоненты.
Список литературы
[1] Вайсштейн, Эрик В. «Кубический корень». Из MathWorld — Интернет-ресурс Wolfram. Кубический корень
Математика — это забавные кубические корни
Головоломка с числами в виде квадратов и кубов
Головоломка с числами в виде квадратов и кубов
Автор Дэвид, 2 мая 2018 г. Головоломка
Когда вы умножаете целое число само на себя, вы получаете квадратное число.Если вы возьмете три копии целого числа и умножите их все вместе, вы получите кубическое число.
Есть только одно двузначное число, которое одновременно является квадратом и кубом. Вы можете определить, какой это номер?
Для тех, кто ищет вызов, можете ли вы найти единственное трехзначное число, которое одновременно является квадратом и кубом?
Прокрутите вниз, чтобы найти ответ!
Ответ на головоломку
Есть много способов решить эту головоломку.Один из способов — перечислить все квадратные числа двумя цифрами: 16, 25, 36, 49, 64, 81.
Затем перечислите все числа куба с двумя цифрами: 27, 64.
Ответ — единственное число в обоих списках: 64.
Есть и более хитрый способ решить эту головоломку, который упрощает решение контрольного вопроса. Он основан на математическом факте: если вы умножите два квадрата вместе, вы получите квадрат! Если вы не уверены в этом факте, попробуйте привести несколько примеров, чтобы понять, что происходит.
Мы начнем с квадрата и используем его, чтобы сделать квадрат, который также является кубом. Начнем с небольшого квадрата: 4.
Мы знаем, что 4 x 4 = 16 — это квадрат из приведенного выше факта, а также из-за того, что означает квадрат. Но мы можем пойти еще дальше. 4 x 16 = 64 — это произведение двух квадратов, поэтому это тоже квадрат. Но вы также можете записать его как 64 = 4 x 4 x 4, превратив его в куб.
Используя этот метод, мы можем вычислить следующий квадрат, который является кубом, повторяя этот процесс.На этот раз начните со следующего наименьшего квадрата: 9. Во-первых, 9 x 9 = 81.
9 x 81 = 729, это произведение двух квадратов, поэтому оно также является квадратом. Вы также можете записать его как 729 = 9 x 9 x 9, превратив его в куб.
Следовательно, ответ на этот вызов — 729.
Чтобы получить больше головоломок и головоломок для детей, подпишитесь на журнал Double Helix!
квадратных и кубических корней | NZ Maths
Назначение
Тот факт, что квадрат и квадратный корень являются обратными, исследуется геометрически и численно.Разработан метод Гаусса для определения квадратных корней, когда доступны только квадраты. Наконец, показан мощный метод вычисления квадратных корней, который быстро дает ответы с любой желаемой точностью.
Конкретные результаты обучения
- Вычислить квадратные и кубические корни.
- Поймите, что возведение в квадрат — это обратное извлечение квадратного корня, а кубическое — обратное извлечение кубического корня.
Описание математики
Этот модуль занимается геометрическим измерением квадратных корней и кубических корней, а также методами их вычисления, когда научный калькулятор не используется.
Возведение целого числа в квадрат дает площадь квадрата с такой длиной стороны. Обратное, нахождение квадратного корня, дает длину стороны квадрата с заданной площадью.
Например, 8 2 = 8 x 8 = 64 — это площадь квадрата со сторонами восемь. √64 = 8 дает длину стороны квадрата площадью 64 квадратных единицы.
Построение куба и нахождение кубического корня — трехмерный эквивалент. Нарезка целого числа дает объем куба с такой длиной ребра.Обратное, нахождение корня куба, дает длину ребра куба с заданным объемом.
Например, 4 3 = 4 x 4 x 4 = 64 — это объем куба с восемью гранями. √64 = 4 дает длину ребра куба объемом 64 кубических единицы.
Необходимые ресурсы
- PowerPoint One
- Copymaster One
- Калькуляторы, но кнопки извлечения квадратного корня и корня n-й степени использовать нельзя.
- Компьютер с программой для работы с электронными таблицами (например, Excel)
- Квадратная бумага
Активность
Сессия 1
- Покажите студентам первый слайд PowerPoint One.
Маленький малиновый квадрат имеет площадь 1 x 1.
Запишите некоторые измерения большого синего квадрата.В следующем обсуждении найдите учащихся, которые определяют длину и площадь сторон.
Как вы думаете, что представляет эта диаграмма?
Что дает возведение в квадрат, если вы знаете длину одной стороны?
Что дает определение квадратного корня, если вы знаете площадь?
- Используйте другие слайды PowerPoint One и попросите учащихся создать диаграмму для каждого квадрата.Например, для третьего слайда напишите:
- Обсудите оценку √6², используя диаграмму. Возведение в квадрат и нахождение квадратного корня замыкает схему диаграммы (по часовой стрелке). Расчет начинается с шести и заканчивается на шести.
- Оценить (√25) 2. Это еще один полный круг по часовой стрелке, но начинается 25 и заканчивается 25.
- Спросите учащихся, знают ли они о каких-либо других парах операций, которые приводят к возврату к начальному числу.Надеюсь, учащиеся познакомятся с такими операциями, как удвоение (2 x) и деление пополам (÷ 2) или добавление n и вычитание n.
- Предоставьте ученикам примеры определения площадей и длин сторон.
Возможно, расширьте некоторых учеников более сложными примерами определения длин сторон.
- На пятом слайде показан кубик Рубика размером 3 x 3 x 3.
Сколько маленьких кубиков составляют этот большой куб?Возможно, вы захотите получить настоящий куб, сделанный из соединяющихся кубиков.Спросите студентов, как они рассчитали ответ. На шестом слайде показана анимация разрыва куба на три слоя 3 x 3. Расчет модели 3 3 на калькуляторе.
Возведение в квадрат дает площадь квадрата от длины стороны.
Куб дает объем куба от длины ребра.
Как вы думаете, какую длину ребра можно определить по объему?
- Используйте кубик Рубика, чтобы представить эту диаграмму:
Слайды шесть, семь, восемь и девять дают другие примеры.Попросите учащихся создать диаграммы для этих рисунков. При необходимости приготовьте настоящие модели.
- упражнения для студентов (независимые примеры см. В Copymaster One).
Найдите объем этих кубиков.
Найдите длины ребер этих кубиков.
Используйте блок-схему для поддержки студентов, если это необходимо.
Сессия 2
Карл Фредрик Гаусс был математическим гением, который нашел способ сложить все числа до 100, когда ему было всего девять лет.Он также создал метод вычисления квадратных корней с использованием итеративного (повторяющегося) приближения.
- Подготовьте квадратный стол следующим образом:
Число
1
2
3
4
5
6
7
8
9
10
Число
1
4
9
16
25
36
49
64
81
100
Как мы можем использовать таблицу для вычисления квадратного корня из 38?
- Обсудите, как эта таблица показывает, что √38 находится между 6 и 7, поскольку 6 2 = 36 и 7 2 = 49.Вы можете написать 6 <√38 <7 и обсудить значение символов «меньше» и «больше».
Какое число находится посередине между 6 и 7?
Давайте посмотрим, приблизит ли квадрат 6,5 нас к 38.
- Разрешение использования только кнопки возведения в квадрат — результат 6,52 = 42,25
- Обсудите, как это показывает 6 <√38 <6.5, потому что 42,25 больше 38.
Попробуйте 6,3 и 6,2, потому что они примерно посередине между 6 и 6.5.
6,3 2 = 39,69 и 6,2 2 = 38,44. Что это говорит нам о √38 ?
- Обсудите, почему 6 <√38 <6.2.
T ry 6,12 = 42,25
Что это говорит нам о √38 ? (√38 между 6,1 и 6,2)
T , возможно, достаточно близко, но что, если вам нужна более высокая точность? Что ты мог сделать?
Учащиеся могут предложить вам попробовать 6,15, чтобы проверить, больше ли √38 или меньше 6.15. Поскольку 6,15 2 = 37,8225, что показывает 6,15 <√38 <6,2. Метод можно использовать многократно, пока не будет достигнуто необходимое количество десятичных знаков.
- Попробуйте 6,18 2 = 38,1924
- Обсудите, почему 6,15 <√38 <6,18
И перейдите к отображению 6,16 <√38 <6,17
- Студенческие упражнения. Найдите эти квадратные корни методом Гаусса с точностью до 0,1 от ответа.
- √53
- √91
- √41
- √77
- √81.4
- √10,6
- Для расширения повторите 2 выше, находя квадратные корни с точностью до 0,01 от ответа.
- Постройте квадраты чисел от нуля до единицы.
- Создайте эту таблицу и нанесите на график упорядоченные пары.
х
0
0,1
0,2
0.3
0,4
0,5
0,6
0,7
0,8
0,9
1
y = x 2
0
0,01
0.04
0,04
0,16
0,25
0,36
0,49
0,64
0,81
1
- Обсудите, как получить квадратные корни из графика. Обсудите, как построить график данных для повышения точности, добавляя дополнительные точки и увеличивая шкалы x и y .)
- Завершите сеанс с помощью этой задачи:
У Хайн есть 24 метра проволочной сетки, чтобы сделать границу своего куриного бега.
Она хочет, чтобы участок был прямоугольной формы.
Какую длину сделать по бокам?
Сессия 3
- Расширьте алгоритм Гаусса на поиск корней куба с желаемой точностью. Обсудите, как эта таблица помогает показать, что 4 <3√110 <5:
Число
1
2
3
4
5
6
7
8
9
10
Номер 3
1
8
27
64
125
216
343
512
729
1000
- Обсудите, почему 3√110 должно быть ближе к 5, чем 4 (поскольку 110 ближе к 125, чем 64).
Какое число мы могли бы попробовать, чтобы приблизиться к кубическому корню?
Студенты могут предложить 4,7 или 4,8.
Как проверить эти числа? (куб их — умножьте каждый на себя, а затем на себя)4,7 3 = 103,823 и 4,8 3 = 110,592
Итак, 4,7 <3√110 <4,8 a
3√110 ближе к 4,7 или 4,8 ? Откуда вы знаете?
- Предложите учащимся продолжить процесс, чтобы найти 3√110 с точностью до двух десятичных знаков.
- Студенческие упражнения. Найдите эти кубические корни с точностью до одного десятичного знака.
- 3√37
- 3√79
- 3√218
- 3√984
- 3√462
- 3√5
- Если 2 3 = 8, что означает 2 4 ?
Если 3√64 = 4, что означает 4√81 ?Невозможно показать физическое представление возведения числа в степень четырех и нахождения корня четвертой степени.Обсудите тот факт, что математики часто создают идеи в своей голове, прежде чем они найдут практическое применение.
- Задача:
Правильно ли 2,59 <4√81 <2,6?2,59 4 = 44,99860561 и 2,6 4 = 45,6976
Таким образом, утверждение верно.
- Студенческие упражнения. Определите, какие утверждения верны:
- 4√625 = 5
- 2,64 <4√625 <2.65
- 7 4 = 49 2
- 5,364 <5√4444 <5,365
- 4√0,0016 = 0,2
- 3√5.0625 = 4√11.3
Сессия 4
- Джесси вычисляет √20. Она угадает 5, зная, что 5 — это слишком много.
Откуда она это знает?Затем она делит 20 на 5 и получает 4. Она знает, что 4 слишком мало.
Откуда она это знает?Джесси считает, что среднее значение 4 и 5, ½ (4 + 5) (четыре плюс пять, разделенные на два) будет ближе к √20, чем 4 или 5.
Откуда она знает, что среднее должно быть ближе?
Усреднение дает ½ (4 + 5) = 4,5, что лучше, чем 4 или 5.Джесси повторяет процесс, используя 4,5. Она вычисляет 20 ÷ 4,5 = 4,4 (четыре и четыре десятых повторяющиеся).
Что она знает из этого расчета?Определение среднего значения 4,5 и 4,4 даст ей еще более точную оценку ½ (4,5 + 4,4) = 4,472 (четыре целых четыре целых семь два повторяющихся).
Примечание учителя: √20 = 2√5.Следовательно, десятичная дробь не будет завершаться.Что могла сделать Джесси сейчас, если ей нужна еще большая точность?
Повторение процесса с использованием 4,472 дает следующее среднее значение:
½ (4,472 + 4,472049…) = 4,4721359…Сравните это число с фактическим √20 = 4,4721359…
- Обсудите, почему этот метод нахождения квадратных корней превосходит метод Гаусса. (Точные результаты получаются намного быстрее). Этот метод обычно приписывают древним вавилонянам или греческому математику Геро.Этому методу более 2000 лет!
- Студенческие упражнения. Найдите следующее, исправьте до 3 десятичных знаков.
- √188
- √69
- √14
- √4,06
- √0,25
- √713
- √0,0811
- √66 000 000
- √0,643
- √7,777
- √2
- Предложите студентам создать электронную таблицу, чтобы быстро находить квадратные корни с помощью вавилонского метода.Помните, что электронная таблица должна быть удобной для пользователя.
Примечание для учителя: упражнение развивает вычислительное мышление, учащиеся разрабатывают итеративный (повторяющийся) алгоритм.
- Пример: в этой таблице показано, как это можно сделать. Моделируется вычисление квадратного корня из 345 с использованием 18 в качестве начального приближения. Если вы предоставляете эту таблицу своим ученикам, убедитесь, что они просматривают формулы в ячейках и обсуждают, что они делают. Обсудите назначение знаков $ в столбце C.
- Студенческое упражнение. Используйте свою электронную таблицу, чтобы найти:
- √555
- √5555
- √1888
- √600 413,8
- √0,0689
- √0.966631
- √400,786,000
- √123 456,789
Глоссарий: Закон квадрата-куба | База данных Marvel
Закон квадрата-куба
Закон квадрата-куба — это принцип, открытый Галилео Галилеем, который гласит, что по мере роста объекта площадь его поверхности увеличивается квадратично, а объем — кубически, т. Е.площадь его поверхности увеличивается на квадрат фактора роста, а объем — на куб фактора роста. Например, если бы человек внезапно стал в 10 раз выше, шире и длиннее, его кости и сухожилия были бы в 10 раз длиннее, его мышцы и кожа покрывали бы в 100 раз большую площадь поверхности, и он был бы в 1000 раз больше и весил бы в 1000 раз. раз больше. Его скелет не сможет выдержать его вес, а его мышцы не смогут перемещать массу его тела. Во вселенной Marvel космические лучи и частицы пима используются для смягчения этого явления.Без них любое животное, ставшее гигантом, сломало бы ноги с первого же шага. [1]
Частицы Пима
Доктор Хэнк Пим обнаружил частицы Пима, которые позволяют ему уменьшаться, сохраняя при этом силу обычного человека, несмотря на его размер, а при росте его размер «пропорционален». [2] Первоначально, однако, когда доктор Пим увеличил свой размер сверх определенного предела и упал, он не мог двигаться и нуждался в помощи Осы, чтобы снова уменьшить его до разумного размера.Он оценивает свой максимальный эффективный размер как двенадцать футов. [ необходима ссылка ] Эрик О’Грэйди попытался воспользоваться своей пропорциональной силой, чтобы ударить парня, но не понимает, что его удар больше похож на пулю, чем на молот. [ необходима ссылка ]
Хэнк Пим написал научную статью под названием « Ха, Ха, я теперь гигантский человек: Да пошли вы, все остальные физики». [1]
Пропорциональная сила паука
Было заявлено, что у Человека-паука пропорциональная сила паука. [3] Позже это было перефразировано, чтобы просто обладать отношением силы к весу паука. [ необходима ссылка ]
Морж (Хьюберт Карпентер) утверждал, что он обладает таким же соотношением силы к весу, что и морж. Это фактически сделало бы его слабее обычного человека. [4]
Другие кейсы
Закон квадрата-куба обсуждался позже, когда Человек-паук использовал свои знания физики, чтобы обнаружить, что Робин Гуд собирается взорваться. [5]
Рид Ричардс из Фантастической четверки столкнулся с инопланетянином, способным поглощать энергию, чтобы вырасти до гигантских размеров, и замечает, что его следы не становятся глубже, поэтому его вес не увеличивается, следовательно, его масса не такая высокая. т, либо. Он просто надувается, как воздушный шар. Таким образом, ему удается «надуть» инопланетянина, подавая ему слишком много энергии. [ необходима ссылка ]
Девушка-белка использовала этот принцип на Enigmo, заставляя его треснуть под собственным весом. [1]
- В Высшей Вселенной: доктор Хэнк Пим может вырасти до шестидесяти футов, поскольку, по словам его жены, 60 футов — это точка, в которой человеческий скелет больше не может поддерживать свою собственную массу. [6] Его способность реконструирована на основе способности Джанет ван Дайн сжиматься, и она упоминает, что не может сжиматься меньше, чем на дюйм, потому что ее тело автоматически знает, каковы его пределы. [ необходимая ссылка ]
- В Что если? Комиксы Советская Фантастическая четверка побеждает Хэнка Пима через удушье, когда Рид заставил его расти, из-за чего его легкие не в состоянии поставлять достаточно кислорода, чтобы поддерживать его.

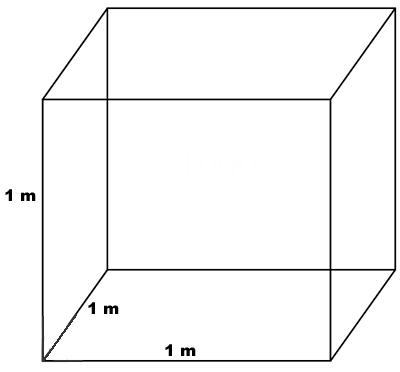 Для этого умножить его ширину на длину. Допустим, 250 мм. на 120 мм. = 30 000 кв.мм.
Для этого умножить его ширину на длину. Допустим, 250 мм. на 120 мм. = 30 000 кв.мм. 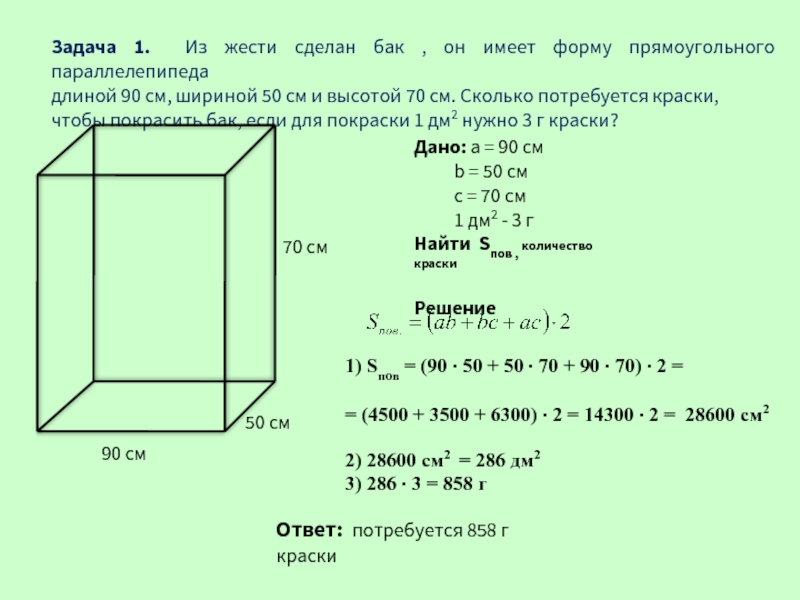 Зная что в одном кубе газа 1000 литров делим на 257,88 литров и получаем 3,877 литров в одном кубометре газа из баллона.Зная сколько килограмм в баллон нам заправили можем приблизительно рассчитать сколько кубов газа нам необходимо для обогрева
Зная что в одном кубе газа 1000 литров делим на 257,88 литров и получаем 3,877 литров в одном кубометре газа из баллона.Зная сколько килограмм в баллон нам заправили можем приблизительно рассчитать сколько кубов газа нам необходимо для обогрева В результате обработки газа давлением он переходит в жидкое состояние, что позволяет закачивать газ большего объема в баллоны.
В результате обработки газа давлением он переходит в жидкое состояние, что позволяет закачивать газ большего объема в баллоны.
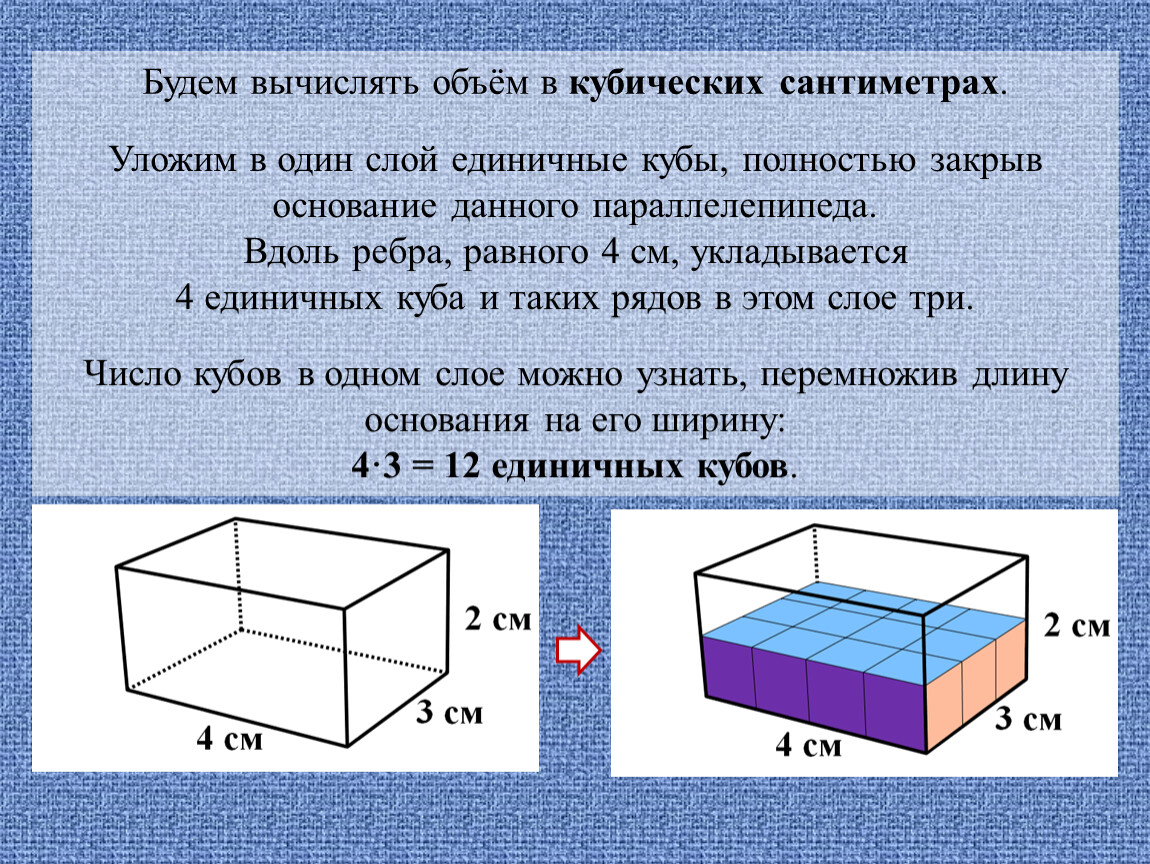
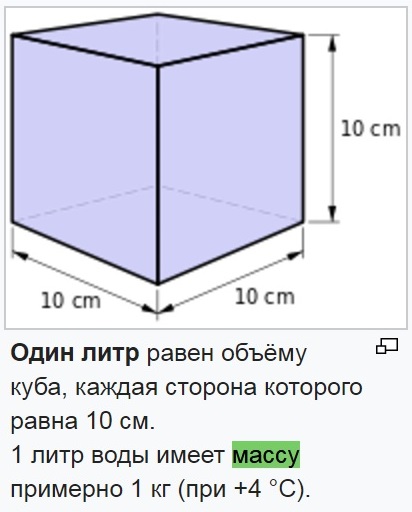
 Каким способом расчёта воспользоваться решает каждый самостоятельно, самое главное, чтобы получить наиболее точный результат, необходимый во время проведения строительных работ.
Каким способом расчёта воспользоваться решает каждый самостоятельно, самое главное, чтобы получить наиболее точный результат, необходимый во время проведения строительных работ.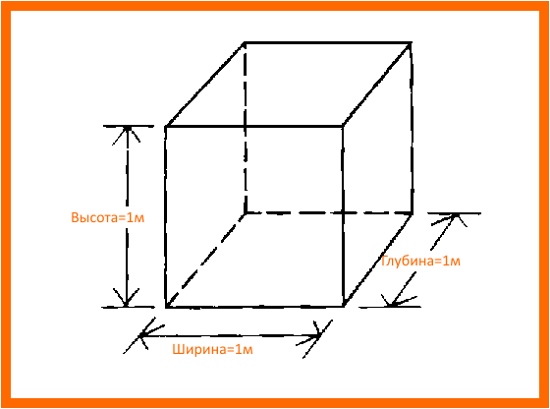
 Возьмем пример из жизни.
Возьмем пример из жизни. Ее в 1 м3 – 47,777 листов.
Ее в 1 м3 – 47,777 листов.