Расчет и нанесение уклона на обмерных чертежах
С необходимостью посчитать уклон постоянно сталкиваются проектировщики, строители, архитекторы, а также люди ряда других профессий, в силу того, что на земной поверхности очень трудно найти идеально ровный участок. Уклон выражается в градусах или в процентах. Обозначение в градусах показывает угол кривизны поверхности. Но уклон может быть представлен и в виде тангенса этого угла, умноженного на 100%.
Как рассчитать уклон поверхности?
Уклон – это отношение превышения (ВС) к заложению (АС) и обозначается в текстовых документах буквой i.
Например, i=1:6
Разделите противолежащий катет (вертикальное расстояние) на прилежащий (расстояние между точками). Если вам нужно получить уклон в процентах, умножьте полученное число на 100%. Чтобы получить уклон в промилле, умножьте результат деления на 1000‰.
Если вам необходимо получить уклон в градусах, воспользуйтесь тем, что полученный при делении катетов результат – тангенс угла наклона.
На видах (фасадах), разрезах, сечениях и схемах перед размерным числом, определяющим величину уклона, наносят знак , острый угол которого должен быть направлен в сторону уклона.
Обозначение уклона наносят непосредственно над линией контура или на полке линии-выноски.
На планах направление уклона плоскостей указывают стрелкой, на которой, при необходимости, проставляют величину уклона (см.рис.).
Построение и обозначение уклона. Пример изображения уклона на планах.
Величину уклона (тангенс угла наклона) указывают в виде простой или десятичной дроби с точностью до третьего знака.
Уклон (в строительстве) — показатель крутизны склона (а также ската кровли).
Укло́н (в геодезии) — показатель крутизны склона; отношение превышения местности к горизонтальному проложению, на котором оно наблюдается. Иными словами, величина уклона равна тангенсу угла между поверхностью склона и горизонталью.
Уклон поверхности равен тангенсу угла α, tgα = h/l — отношение перпендикуляра, опущенного из точки поверхности на прямую поверхность, к длине прямой поверхности от начала склона (при вершине угла α) до перпендикуляра.
Например, подъёму 12 м на 100 м перемещения по горизонтали соответствует уклон, равный 0,12 (12 % или 120 ‰).
При чтении нотации знак «%» произносится «сотых», а «‰» — «тысячных».
Источник:
книга: Единые требования по выполнению строительных чертежей.
М.: Изд-во «Архитектура-С», 2004.
Справочное пособие.
Автор: Георгиевский О.В.
Аннотация:
Справочное пособие по строительному черчению для студентов средних и высших учебных заведений. Пособие выполнено в соответствии с требованиями ГОСТов.
Пособие может быть использовано при выполнении заданий по архитектурно-строительному черчению, а также при выполнении курсовых и дипломных проектов студентами всех строительных специальностей средних и высших учебных заведений.
распечатать
Вконтакте
Одноклассники
Google+
расчёт и таблица соотношений проценты-градусы.
Уклон скатов крыши — от чего зависит и в чём он измеряется.
Такой немаловажный для крыши факт — её уклон. Уклон крыши — это угол наклона кровли относительно горизонтального уровня. По углу наклона скатов крыши бывают малоуклонные (пологие), средней наклонности и крыши с крутыми (сильноуклонными) скатами.
Малоуклонная крыша та крыша, монтаж которой осуществляется из расчёта наименьшего, рекомендованного угла наклона скатов. Так для каждого кровельного покрытия есть свой рекомендуемый минимальный уклон.
От чего зависит уклон кровли
- От способности крыши защищать строение от внешних факторов и воздействий.

- От ветра — чем больше уклон крыши, тем больше значение приходящихся ветровых нагрузок. При крутых уклонах уменьшается сопротивляемость ветру, повышается парусность. В регионах и местах с сильными ветрами рекомендуется применять минимальный уклон крыши, чтоб уменьшить нагрузки на несущие конструкции крыши.
- От кровельного покрытия (материала) — Для каждого кровельного материала существует свой минимальный угол наклона, при котором можно использовать данный материал.
- От архитектурных задумок, решений, местных традиций — так в разных регионах отдаётся предпочтение для той или иной конструкции крыши.
- От атмосферных осадков: снеговых нагрузок и дождей в регионе. На крышах с большим уклоном не будет скапливаться в огромных количествах снег, грязь и листья.
В чем измеряется угол уклона крыши
Обозначение уклона кровли на чертежах может быть как в градусах, так и в процентах. Уклон крыши обозначается латинской буквой i.
Уклон крыши обозначается латинской буквой i.
В СНиПе II-26-76, данная величина указывается в процентах ( % ). В данный момент не существует строгих правил по обозначению размера уклона крыши.
Единицей измерения уклона крыши считают градусы или проценты ( %). Их соотношение указаны ниже в таблице.
Уклон крыши соотношение градусы-проценты
| градусы | % | градусы | % | градусы | % | ||
| 1° | 1,75% | 16° | 28,68% | 31° | 60,09% | ||
| 2° | 3,50% | 17° | 30,58% | 32° | 62,48% | ||
| 3° | 5,24% | 18° | 32,50% | 33° | 64,93% | ||
| 4° | 7,00% | 19° | 34,43% | 34° | 67,45% | ||
| 5° | 8,75% | 20° | 36,39% | 35° | 70,01% | ||
| 6° | 10,51% | 21° | 38,38% | 36° | 72,65% | ||
| 7° | 12,28% | 22° | 40,40% | 37° | 75,35% | ||
| 8° | 14,05% | 23° | 42,45% | 38° | 78,13% | ||
| 9° | 15,84% | 24° | 44,52% | 39° | 80,98% | ||
| 10° | 17,64% | 25° | 46,64% | 40° | 83,90% | ||
| 11° | 19,44% | 26° | 48,78% | 41° | 86,92% | ||
| 12° | 21,25% | 27° | 50,95% | 42° | 90,04% | ||
| 13° | 23,09% | 28° | 53,18% | 43° | 93,25% | ||
| 14° | 24,94% | 29° | 55,42% | 44° | 96,58% | ||
| 15° | 26,80% | 30° | 57,73% | 45° | 100% |
Перевести уклон из процентов в градусы и наоборот из градусов в проценты можно при помощи онлайн конвертера:
Замер уклона крыши
Измеряют угол уклона при помощи уклономера или же математическим способом.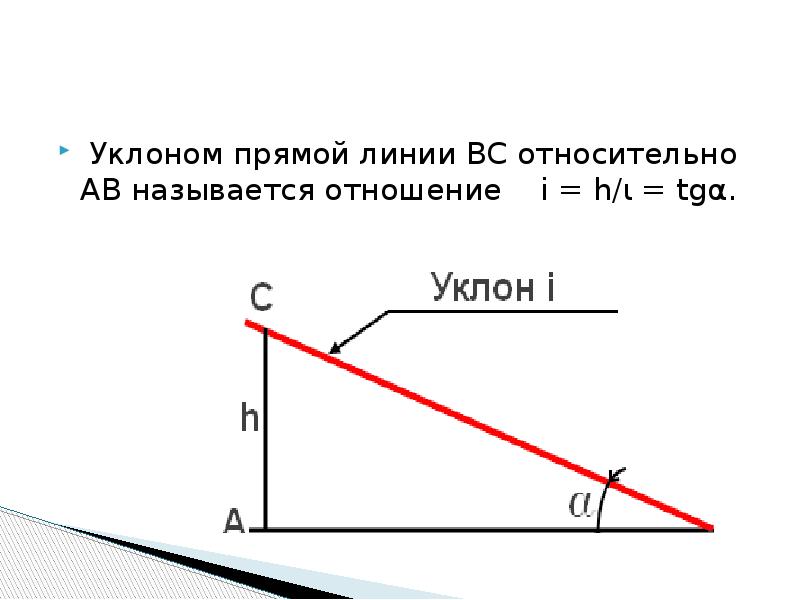
Уклономер — это рейка с рамкой, между планками которой есть ось, шкала деления и к которой закреплён маятник. Когда рейка находится в горизонтальном положении, на шкале показывает ноль градусов. Чтобы произвести замер уклона ската крыши, рейку уклономера держат перпендикулярно коньку, то есть в вертикальном уровне. По шкале уклономера маятник указывает, какой уклон у данного ската крыши в градусах. Такой метод замера уклона стал уже менее актуален, так как сейчас появились разные геодезические приборы для замеров уклонов, а так же капельные и электронные уровни с уклономерами.
Математический расчёт уклона
Можно рассчитать уклон крыши не используя геодезические и другие приборы для замеров уклона. Для этого необходимо знать два размера:
- Вертикальная высота ( H ) от верхней точки ската (как правило конька) до уровня нижней (карниза)
- Заложение ( L ) — горизонтальное расстояние от нижней точки ската до верхней
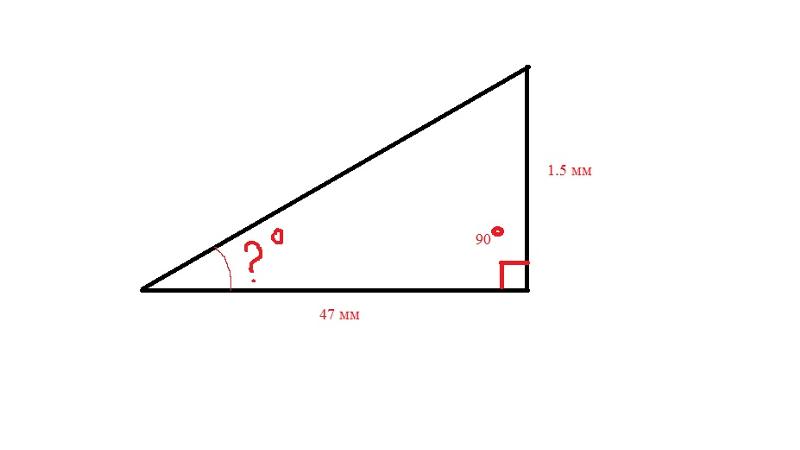
При помощи математического расчёта величину уклона крыши находит следующим образом:
Угол уклона ската i равен отношению высоты кровли Н к заложению L
i = Н : L
Для того, чтобы значение уклона выразить в процентах, это отношение умножают на 100.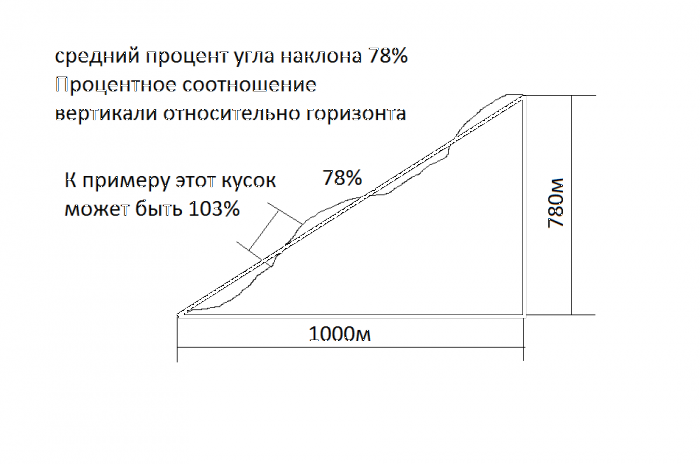 Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Далее,чтобы узнать значение уклона в градусах, переводим по таблице соотношений, расположенной выше.
Чтобы было понятней рассмотрим на примере:
Пусть будет:
Длина заложения 4,5 м, высота крыши 2,0 м.
Уклон равен: i = 2.0 : 4,5 = 0,44 теперь умножим на × 100 = 44 %. Переводим данное значение по таблице в градусы и получаем — 24°.
Минимальный уклон для кровельных материалов (покрытий)
| Вид кровли | Минимальный уклон крыши | ||
|---|---|---|---|
| в градусах | в % | в соотношении высоты ската к заложению | |
| Кровли из рулонных битумных материалов: 3-х и 4-х слойные (наплавляемая кровля) | 0-3° | до 5% | до 1:20 |
| Кровли из рулонных битумных материалов: 2-х слойные (наплавляемая кровля) | от | 15 | |
| Фальцевая кровля | от 4° | ||
| Ондулин | 5° | 1:11 | |
| Волнистые асбоцементные листы (шифер) | 9° | 16 | 1:6 |
| Керамическая черепица | 11° | 1:6 | |
| Битумная черепица | 11° | 1:5 | |
| Металлочерепица | 14° | ||
| Цементно-песчанная черепица | 34° | 67% | |
| Деревянная кровля | 39° | 80% | 1:1. 125 125 |
Как рассчитать угол наклона крыши
Проекты возводимых загородных особняков могут учитывать множество требований, пожеланий и даже причуд или «капризов» их владельцев владельца. Но всегда их «роднит» общая особенность — без надежной крыши никогда не обходится ни одно их зданий. И в этом вопросе на первый план должны выходить не столько архитектурные изыски заказчика, сколько специфические требования к этому элементу строения. Это надежность и устойчивость всей стропильной системы и кровельного покрытия, полноценное выполнение крышей своего прямого предназначения – защиты от проникновения влаги (а в ряде случаев, кроме того, еще и термо- и звукоизоляции), при необходимости – функциональность расположенных непосредственно под кровлей помещений.
Как рассчитать угол наклона крышиПроектирование конструкции крыши – дело чрезвычайно ответственное и достаточно непростое, особенно при сложных ее конфигурациях. Разумнее всего будет доверить это дело профессионалам, которое владеют методикой проведения необходимых расчетов и соответствующим программным обеспечение для этого. Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала.
Однако, владельцу дома тоже могут быть интересны некоторые теоретические моменты. Например, немаловажно знать, как рассчитать угол наклона крыши самостоятельно, хотя бы приблизительно — для начала.
Это даст возможность сразу прикинуть возможность реализации своих «авторских прикидок» — по соответствию задуманного реальным условиям региона, по «архитектуре» самой крыши, по планируемому кровельному материалу, по использованию чердачного помещения. В определенной степени рассчитанный угол ската кровли поможет провести предварительный подсчет параметров и количества пиломатериалов для стропильной системы, общей площади кровельного покрытия.
В каких величинах удобнее измерять угол ската крыши?Казалось бы – совершенно излишний вопрос, так как все со школьной скамьи знают, что угол измеряется в градусах. Но ясность здесь все же нужна, потому что и в технической литературе, и в справочных таблицах, и в привычном обиходе некоторых опытных мастеров нередко встречаются и иные единицы измерения – проценты или же относительные соотношения сторон.
И еще одно необходимое уточнение — что принимается за угол наклона крыши?
Что же понимается под углом наклона крыши?Угол наклона – это угол, образованный пересечением двух плоскостей: горизонтальной и плоскостью ската кровли. На рисунке он показан буквой греческого алфавита α.
Интересующие нас острые углы (тупоугольных скатов не может быть просто по определению), лежит в диапазоне от 0 до 90°. Скаты круче 50 ÷ 60 ° в «чистом» виде встречаются чрезвычайно редко и то, как правило, для декоративного оформления крыш – при строительстве остроконечных башенок в готическом стиле. Однако есть и исключение – такими крутыми могут быть скаты нижнего ряда стропил крыши мансардного типа.
Нижние стропила крыши мансардного типа могут располагаться под очень большим угломИ все же чаще всего приходится иметь дело со скатами, лежащим в диапазоне от 0 до 45°
С градусами понятно – все, наверное, представляют транспортир с его делениями. А ка быть с другими единицами измерения?
Тоже ничего сложного.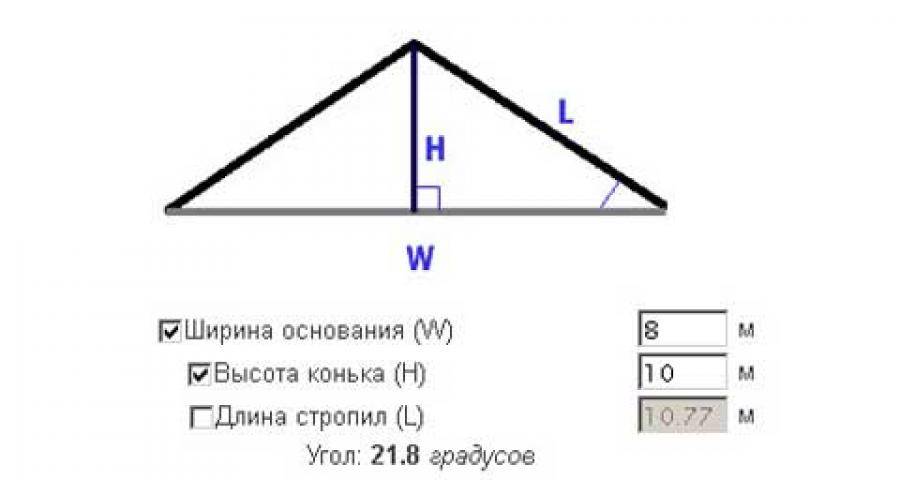
Относительное соотношение сторон – это максимально упрощенная дробь, показывающая отношение высоты подъёма ската (на рисунке выше обозначена латинской Н) к проекции ската крыши на горизонтальную плоскость (на схеме – L).
L – это может быть, в зависимости от конструкции крыши, половина пролета (при симметричной двускатной крыше), пролет полностью (если крыша односкатная), либо, при сложных конфигурациях кровли, действительно линейный участок, определяемый проведенной к горизонтальной плоскости проекцией. Например, на схеме мансардной крыши такой участок хорошо показан – по горизонтальной балке от самого угла до вертикальной стойки, проходящей от верхней точки нижнего стропила.
Угол уклона так и записывается, дробью, например «1 : 3».
Однако, на практике нередко случается так, что использовать величину угла уклона в таком представлении будет чрезвычайно неудобен, если, скажем, числа в дроби получаются некруглые и несокращаемые. Например, мало что скажет неопытному строителю соотношение 3 : 11. На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши – процентами.
Например, мало что скажет неопытному строителю соотношение 3 : 11. На этот случай есть возможность воспользоваться еще одной величиной измерения уклона крыши – процентами.
Находится эта величина чрезвычайно просто – необходимо просто найти результат деления уже упомянутой дроби, а затем умножить его на 100. Например, в приведенном выше примере 3 : 11
3 : 11 = 0,2727 × 100 = 27,27 %
Итак, получена величина уклона ската кровли, выраженная в процентах.
А что делать, если требуется перейти от градусов к процентам или наоборот?
Можно запомнить такое соотношение. 100 % — это угол 45 градусов, когда катеты прямоугольного треугольника равны между собой, то есть в нашем случае высота ската равна длине его горизонтальной проекции.
В таком случае, 45° / 100 = 0,45° = 27´. Один процент уклона равен 27 угловым минутам.
Если подойти с другой стороны, то 100 / 45° = 2,22 %. То есть получаем, что один градус – это 2, 22% уклона.
То есть получаем, что один градус – это 2, 22% уклона.
Для простоты перевода величин из одних в другие можно воспользоваться таблицей:
| Значение в градусах | Значение в % | Значение в градусах | Значение в % | Значение в градусах | Значение в % |
|---|---|---|---|---|---|
| 1° | 2,22% | 16° | 35,55% | 31° | 68,88% |
| 2° | 4,44% | 17° | 37,77% | 32° | 71,11% |
| 3° | 6,66% | 18° | 40,00% | 33° | 73,33% |
| 4° | 8,88% | 19° | 42,22% | 34° | 75,55% |
| 5° | 11,11% | 20° | 44,44% | 35° | 77,77% |
| 6° | 13,33% | 21° | 46,66% | 36° | 80,00% |
| 7° | 15,55% | 22° | 48,88% | 37° | 82,22% |
| 8° | 17,77% | 23° | 51,11% | 38° | 84,44% |
| 9° | 20,00% | 24° | 53,33% | 39° | 86,66% |
| 10° | 22,22% | 25° | 55,55% | 40° | 88,88% |
| 11° | 24,44% | 26° | 57,77% | 41° | 91,11% |
| 12° | 26,66% | 27° | 60,00% | 42° | 93,33% |
| 13° | 28,88% | 28° | 62,22% | 43° | 95,55% |
| 14° | 31,11% | 29° | 64,44% | 44° | 97,77% |
| 15° | 33,33% | 30° | 66,66% | 45° | 100,00% |
Для наглядности будет полезным привести графическую схему, которая очень доступно показывает взаимосвязь всех упомянутых линейных параметров с углом ската и величинами его измерения.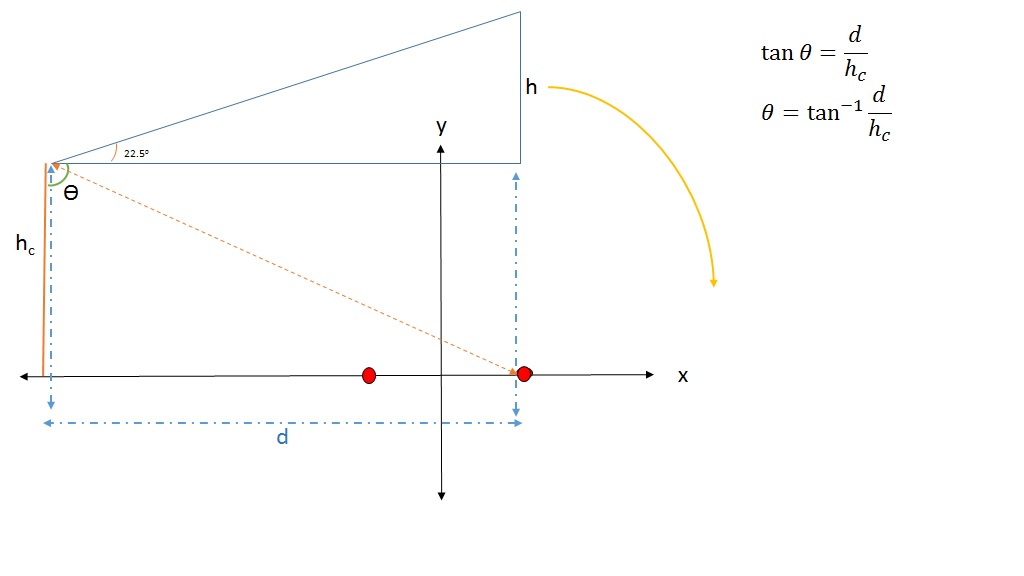
К этому рисунку еще предстоит вернуться, когда будут рассматриваться виды кровельных покрытий.
Еще проще будет рассчитать крутизну и угол наклона ската. если воспользоваться встроенным калькулятором, размещенным ниже:
Калькулятор расчета крутизны ската по известному значению высоты конькаПерейти к расчётамЗависимость типа кровельного покрытия от крутизны скатаПланируя постройку собственного дома, хозяин участка наверняка уже проводит «прикидку» и своей голове, и с членами семьи – как будет выглядеть их будущее жилье. Кровля в этом вопросе, безусловно, занимает одно из первостепенных значений. И вот здесь необходимо учитывать то, что далеко не всякий кровельный материал может использоваться на различных по крутизне скатах крыш. Чтобы не возникало недоразумений позднее, необходим заранее предусматривать эту взаимосвязь.
Диаграмма распределения крыш по крутизне скатаКрыши по углу наклона ската можно условно разделит на плоские (уклон до 5°), с малым уклоном (от 6 до 30°) и крутоуклонные, соответственно, с углом ската более 30°.
У каждого из типов крыш есть свои достоинства и недостатки. Например, плоские крыши имеют минимальную площадь, но потребуют особых мер гидроизоляции. На крутых крышах не задерживаются снежные массы, однако они больше подвержены ветровой нагрузке из-за своей «парусности». Так и кровельный материал – в силу собственных технологических или эксплуатационных особенностей имеет определенные ограничения на применения с разными уклонами скатов.
Обратимся к уже рассматриваемому ранее рисунку (схема A). Черными кружками с дугообразными стрелками и синими цифрами обозначены области применения различных кровельных покрытий (острие стрелки указывает на минимально допустимое значение крутизны ската):
1 – это дранка, щепа, натуральный гонт. В этой же области лежит и применение до сих пор используемых в южных краях камышовых кровель.
2 – натуральное штучное черепичное покрытие, битумно-полимерные плитки, сланцевые плитки.
3 – рулонные материалы на битумной основе, не менее четырёх слоев, с внешней гравийной посыпкой, утопленной в слой расплавленной мастики.
4 – аналогично пункту 3, но для надёжности кровли достаточно трех слоев рулонного материала.
5 – аналогичные вышеописанным рулонные материалы (не менее трех слоев), но без наружной защитной гравийной посыпки.
6 – рулонные кровельные материалы, наклеиваемые на горячую мастику не менее, чем в два слоя. Металлочерепица, профнастил.
7 – волнистые асбестоцементные листы (шифер) унифицированного профиля.
8 – черепичное глиняное покрытие
9 – асбестоцементные листы усиленного профиля.
10 – кровельная листовая сталь с развальцовкой соединений.
11 – шиферное покрытие обычного профиля.
Таким образом, если есть желание покрыть крышу кровельным материалом определенного типа, угол уклона ската должен планироваться в указанных рамках.
Для тех читателей, которые хорошо помнят курс тригонометрии средней школы, этот раздел может показаться неинтересным. Они могут сразу его пропустить и перейти дальше. А вот подзабывшим это нужно освежить знания о взаимозависимости углов и сторон в прямоугольном треугольнике.
Для чего это надо? В рассматриваемом случае возведения крыши всегда в расчетах отталкиваются от прямоугольного треугольника. Два его катета – это длина проекции ската на горизонтальную плоскость (длина пролета, половины пролета и т.п. – в зависимости от типа крыши) и высота ската в высшей точке (на коньке или при переходе на верхние стропила – при расчете нижних стропил мансардной крыши). Понятно, что постоянная величина здесь одна – это длина пролета. А вот высоту можно изменять, варьируя угол наклона крыши.
В таблице приведены две основные зависимости, выраженные через тангенс и синус угла наклона ската. Существуют и иные зависимости (через косинус или котангенс) но в данном случае нам достаточно этих двух тригонометрических функций.
| Графическая схема | Основные тригонометрические соотношения | |
|---|---|---|
| Н — высота конька | ||
| S — длина ската крыши | ||
| L — половина длины пролета (при симметричной двускатной крыше) или длина пролета (при односкатной крыше) | ||
| α — угол ската крыши | ||
| tg α = H / L | Н = L × tg α | |
| sin α = H / S | S = H / sin α | |
Зная эти тригонометрические тождества, можно решить практически все задачи по предварительному проектированию стропильной конструкции.
Для наглядности — треугольник в приложении к крыше домаТак, если необходимо «плясать» от четко установленной высоты подъёма конька, то отношением tg α = H / L несложно будет определить угол.
По полученному делением числу в таблице тангенсов находят угол в градусах. Тригонометрические функции часто бывают заложены в инженерные калькуляторы, они есть в обязательном порядке в таблицах Exel (для тех, кто умеет работать с этим удобным приложением. Правда, там расчет ведется не в градусах, а в радианах). Но чтобы нашему читателю не приходилось отвлекаться на поиски нужных таблиц, приведем значение тангенсов в диапазоне от 1 до 80°.
| Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса | Угол | Значение тангенса |
|---|---|---|---|---|---|---|---|
| tg(1°) | 0.01746 | tg(21°) | 0.38386 | tg(41°) | 0.86929 | tg(61°) | 1.80405 |
| tg(2°) | 0.03492 | tg(22°) | 0.40403 | tg(42°) | 0.9004 | tg(62°) | 1.88073 |
| tg(3°) | 0.05241 | tg(23°) | 0.42447 | tg(43°) | 0. 93252 93252 | tg(63°) | 1.96261 |
| tg(4°) | 0.06993 | tg(24°) | 0.44523 | tg(44°) | 0.96569 | tg(64°) | 2.0503 |
| tg(5°) | 0.08749 | tg(25°) | 0.46631 | tg(45°) | 1 | tg(65°) | 2.14451 |
| tg(6°) | 0.1051 | tg(26°) | 0.48773 | tg(46°) | 1.03553 | tg(66°) | 2.24604 |
| tg(7°) | 0.12278 | tg(27°) | 0.50953 | tg(47°) | 1.07237 | tg(67°) | 2.35585 |
| tg(8°) | 0.14054 | tg(28°) | 0.53171 | tg(48°) | 1.11061 | tg(68°) | 2.47509 |
| tg(9°) | 0.15838 | tg(29°) | 0.55431 | tg(49°) | 1.15037 | tg(69°) | 2.60509 |
| tg(10°) | 0.17633 | tg(30°) | 0.57735 | tg(50°) | 1.19175 | tg(70°) | 2.74748 |
| tg(11°) | 0. 19438 19438 | tg(31°) | 0.60086 | tg(51°) | 1.2349 | tg(71°) | 2.90421 |
| tg(12°) | 0.21256 | tg(32°) | 0.62487 | tg(52°) | 1.27994 | tg(72°) | 3.07768 |
| tg(13°) | 0.23087 | tg(33°) | 0.64941 | tg(53°) | 1.32704 | tg(73°) | 3.27085 |
| tg(14°) | 0.24933 | tg(34°) | 0.67451 | tg(54°) | 1.37638 | tg(74°) | 3.48741 |
| tg(15°) | 0.26795 | tg(35°) | 0.70021 | tg(55°) | 1.42815 | tg(75°) | 3.73205 |
| tg(16°) | 0.28675 | tg(36°) | 0.72654 | tg(56°) | 1.48256 | tg(76°) | 4.01078 |
| tg(17°) | 0.30573 | tg(37°) | 0.75355 | tg(57°) | 1.53986 | tg(77°) | 4.33148 |
| tg(18°) | 0.32492 | tg(38°) | 0.78129 | tg(58°) | 1. 60033 60033 | tg(78°) | 4.70463 |
| tg(19°) | 0.34433 | tg(39°) | 0.80978 | tg(59°) | 1.66428 | tg(79°) | 5.14455 |
| tg(20°) | 0.36397 | tg(40°) | 0.8391 | tg(60°) | 1.73205 | tg(80°) | 5.67128 |
В случае, наоборот, когда за основу берется угол наклона кровли, высота расположения конька определяется по обратной формуле:
H = L × tg α
Теперь, имея значения двух катетов и угла наклона кровли, очень просто вычислить и требуемую длину стропила от конька до карнизного свеса. Можно применить теорему Пифагора
S = √ (L² + H²)
Или же, что, наверное, проще, так как уже известна величина угла, применить тригонометрическую зависимость:
S = H / sin α
Значение синусов углов — в таблице ниже.
| Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса | Угол | Значение синуса |
|---|---|---|---|---|---|---|---|
| sin(1°) | 0.017452 | sin(21°) | 0.358368 | sin(41°) | 0.656059 | sin(61°) | 0.87462 |
| sin(2°) | 0.034899 | sin(22°) | 0.374607 | sin(42°) | 0.669131 | sin(62°) | 0.882948 |
| sin(3°) | 0.052336 | sin(23°) | 0.390731 | sin(43°) | 0.681998 | sin(63°) | 0.891007 |
| sin(4°) | 0.069756 | sin(24°) | 0.406737 | sin(44°) | 0.694658 | sin(64°) | 0.898794 |
| sin(5°) | 0.087156 | sin(25°) | 0.422618 | sin(45°) | 0.707107 | sin(65°) | 0.906308 |
| sin(6°) | 0.104528 | sin(26°) | 0.438371 | sin(46°) | 0.71934 | sin(66°) | 0.913545 |
| sin(7°) | 0.121869 | sin(27°) | 0.45399 | sin(47°) | 0.731354 | sin(67°) | 0.920505 |
| sin(8°) | 0.139173 | sin(28°) | 0.469472 | sin(48°) | 0.743145 | sin(68°) | 0.927184 |
| sin(9°) | 0.156434 | sin(29°) | 0.48481 | sin(49°) | 0.75471 | sin(69°) | 0.93358 |
| sin(10°) | 0.173648 | sin(30°) | 0.5 | sin(50°) | 0.766044 | sin(70°) | 0.939693 |
| sin(11°) | 0.190809 | sin(31°) | 0.515038 | sin(51°) | 0.777146 | sin(71°) | 0.945519 |
| sin(12°) | 0.207912 | sin(32°) | 0.529919 | sin(52°) | 0.788011 | sin(72°) | 0.951057 |
| sin(13°) | 0.224951 | sin(33°) | 0.544639 | sin(53°) | 0.798636 | sin(73°) | 0.956305 |
| sin(14°) | 0.241922 | sin(34°) | 0.559193 | sin(54°) | 0.809017 | sin(74°) | 0.961262 |
| sin(15°) | 0.258819 | sin(35°) | 0.573576 | sin(55°) | 0.819152 | sin(75°) | 0.965926 |
| sin(16°) | 0.275637 | sin(36°) | 0.587785 | sin(56°) | 0.829038 | sin(76°) | 0.970296 |
| sin(17°) | 0.292372 | sin(37°) | 0.601815 | sin(57°) | 0.838671 | sin(77°) | 0.97437 |
| sin(18°) | 0.309017 | sin(38°) | 0.615661 | sin(58°) | 0.848048 | sin(78°) | 0.978148 |
| sin(19°) | 0.325568 | sin(39°) | 0.62932 | sin(59°) | 0.857167 | sin(79°) | 0.981627 |
| sin(20°) | 0.34202 | sin(40°) | 0.642788 | sin(60°) | 0.866025 | sin(80°) | 0.984808 |
Для тех же читателей, кто просто не хочет погружаться в самостоятельные тригонометрические расчеты, рекомендуем встроенный калькулятор, который быстро и точно определит длину ската кровли (без учета карнизного свеса) по имеющимся значениям высоты конька и длины горизонтальной проекции ската.
Калькулятор расчета длины ската кровли по известному значению высоты конькаУмелое использование тригонометрических формул позволяет, при нормальном пространственном воображении и при умении выполнять несложные чертежи, провести расчеты и более сложным по конструкции крыш.
Опираясь на базовые соотношения, несложно разделить на треугольники и рассчитать вальмовую крышуНапример, даже кажущуюся такой «навороченной» вальмовую или мансардную крышу можно разбить на совокупности треугольников, а затем последовательно просчитать все необходимые размеры.
Зависимость размеров помещения мансарды от угла наклона скатов крышиЕсли хозяевами будущего дома планируется использовать чердак в качестве функционального помещения, иначе говоря – сделать мансарду, то определение угла ската крыши приобретает вполне прикладное значение.
Чем больше угол уклона — тем просторнее мансардаМного объяснять здесь ничего не надо – приведённая схема наглядно показывает, что чем меньше угол наклона, тем теснее свободное пространство в чердачном помещении.
Чтобы стало несколько понятнее, лучше выполнить подобную схему в определенном масштабе. Вот, например, как будет выглядеть мансардное помещение в доме с шириной фронтонной части 10 метров. Следует учитывать, что высота потолка никак не может быть ниже 2 метров. (Откровенно говоря, и двух метров маловато для жилого помещения– потолок будет неизбежно «давить» на человека. Обычно исходят из высоты хотя-бы 2.5 метра).
Для образца — масштабированная схема мансардыМожно привести уже подсчитанные средние значения получаемой в мансарде комнаты, в зависимости от угла наклона обычной двускатной крыши. Кроме того, в таблице приведены величины длины стропил и площади кровельного материала с учетом 0,5 метров карнизного свеса кровли.
| Угол ската крыши | Высота конька | Длина ската | Полезная площадь мансардного помещения на 1 метр длины здания (при высоте потолка 2 м) | Площадь кровельного покрытия на 1 метр длины здания |
|---|---|---|---|---|
| 20 | 1.82 | 5.32 | нет | 11.64 |
| 25 | 2.33 | 5.52 | 0.92 | 12.03 |
| 30 | 2.89 | 5.77 | 2.61 | 12.55 |
| 35 | 3.50 | 6.10 | 3.80 | 13.21 |
| 40 | 4.20 | 6.53 | 4.75 | 14.05 |
| 45 | 5.00 | 7.07 | 5.52 | 15.14 |
| 50 | 5.96 | 7.78 | 6.16 | 16.56 |
Итак, чем круче наклон скатов, тем просторнее помещение. Однако, это сразу отзывается резким увеличением высоты стропильной конструкции, возрастанием размеров, а стало быть – и массы деталей для ее монтажа. Гораздо больше потребуется и кровельного материала – площадь покрытия также быстро растет. Плюс к этому, нельзя забывать и о возрастании эффекта «парусности» — большей подверженности ветровой нагрузке. Видам внешних нагрузок будет посвящена последняя глава настоящей публикации.
Для сравнения — крыша мансардного типа дает выигрыш по полезному пространству даже при меньшей высотеЧтобы в определенной степени нивелировать подобные негативные последствия, проектировщики и строители часто применяют особую конструкцию мансардной крыши – о ней уже упоминалось в настоящей статье. Она сложнее в расчетах и изготовлении, но дает существенный выигрыш в получаемой полезной площади мансардного помещения с уменьшением общей высоты здания.
Зависимость величины внешних нагрузок от угла наклона крышиЕще одно важнейшее прикладное применение рассчитанного значения угла наклона кровли – это определение степени его влияния на уровень внешних нагрузок, выпадающих на конструкцию крыши.
Здесь прослеживается интересная взаимосвязь. Можно заранее рассчитать все параметры – углы и линейные размеры, но всегда в итоге приходят к деталировке. То есть необходимо определить, из какого материала будут изготавливаться детали и узлы стропильной системы, какова должна быть их площадь сечения, шаг расположения, максимальная длина между соседними точками опоры, способы крепления элементов между собой и к несущим стенам здания и многое другое.
Вот здесь на первый план выходят нагрузки, которые испытывает конструкция крыши. Помимо собственного веса, огромное значение имеют внешние воздействия. Если не брать в расчет несвойственные для наших краев сейсмические нагрузки, то главным образом надо сосредоточится на снеговой и ветровой. Величина обеих – напрямую связана с углом расположения кровли к горизонту.
Снеговая нагрузкаПонятно, что на огромной территории Российской Федерации среднестатистическое количество выпадаемых в виде снега осадков существенно различается по регионам. По результатам многолетних наблюдений и вычислений, составлена карта территории страны, на которой указаны восемь различных зон по уровню снеговой нагрузки.
Карта распределения зон на территории РФ по снеговой нагрузкеВосьмая, последняя зона – это некоторые малозаселенные районы Дальнего Востока, и ее можно особо не рассматривать. Значения же для других зон – указаны в таблице
| Зональное распределение территории РФ по среднему значению снеговой нагрузки | Значение в кПа | Значение в кг/м² |
|---|---|---|
| I | 0.8 кПа | 80 кг/м² |
| II | 1.2 кПа | 120 кг/м² |
| III | 1.8 кПа | 180 кг/м² |
| IV | 2.4 кПа | 240 кг/м² |
| V | 3.2 кПа | 320 кг/м² |
| VI | 4.0 кПа | 400 кг/м² |
| VII | 4.8 кПа | 480 кг/м² |
Теперь, чтобы рассчитать конкретную нагрузку для планируемого здания, необходимо воспользоваться формулой:
Рсн = Рсн.т × μ
Рсн.т – значение, которое мы нашли с помощью карты и таблицы;
Μ – поправочный коэффициент, который зависит от угла ската α
- при α от 0 до 25° — μ=1
- при α более 25 и до 60° — μ=0,7
- при α более 60° снеговую нагрузку в расчет не принимают, так как снег не должен удерживаться на плоскости скатов кровли.
Например, дом возводится в Башкирии. Планируемая скатов его крыши – 35°.
Находим по таблице – зона V, табличное значение — Рсн.т = 3,2 кПа
Находим итоговое значение Рсн = 3.2 × 0,7 = 2,24 кПа
(если значение нужно в килограммах на квадратный метр, то используется соотношение
1 кПа ≈ 100 кг/м²
В нашем случае получается 224 кг/м².
Ветровая нагрузкаС ветровой нагрузкой все обстоит намного сложнее. Дело в том, что она может быть разнонаправленной – ветер способен оказывать давление на крышу, прижимая ее к основанию, но вместе с тем возникают аэродинамические «подъемные» силы, стремящиеся оторвать кровлю от стен.
Кроме того, ветровая нагрузка воздействует на разные участки крыши неравномерно, поэтому знать только среднестатистический уровень ветровой нагрузки – недостаточно. В расчет принимаются господствующие направления ветров в данной местности («роза ветров»), степень насыщенности участка местности препятствиями для распространения ветра, высота здания и окружающих его строений, другие критерии.
Примерный порядок подсчета ветровой нагрузки выглядит следующим образом.
В первую очередь, по аналогии с ранее проведёнными расчетами, на карте определяется регион РФ и соответствующая ему зона.
Распределение зон на территории РФ по уровню ветрового давленияДалее, по таблице можно определить среднее для конкретного региона значение ветрового давления Рвт
| Региональное распределение территории РФ по уровню средней ветровой нагрузки | Iа | I | II | III | IV | V | VI | VII |
|---|---|---|---|---|---|---|---|---|
| Табличное значение ветрового давления, кг/м ² (Рв) | 24 | 32 | 42 | 53 | 67 | 84 | 100 | 120 |
Далее расчет проводится по следующей формуле:
Рв = Рвт × k × c
Рвт – табличное значение ветрового давления
k – коэффициент, учитывающий высоту здания и характер местности вокруг него. Определяют его по таблице:
| Высота возводимого здания (сооружения) (z) | Зона А | Зона Б | Зона В |
|---|---|---|---|
| не более 5 м | 0.75 | 0.5 | 0.4 |
| от 5 до 10 м | 1.0 | 0.65 | 0.4 |
| от 10 до 20 м | 1.25 | 0.85 | 0.55 |
| от 20 до 40 м | 1.5 | 1.1 | 0.8 |
В таблице указаны три различные зоны:
- Зона «А» — открытая «голая» местность, например, степь, пустыня, тундра или лесотундра, полностью открытые ветровому воздействию побережья морей и океанов, крупных озер, рек, водохранилищ.
- Зона «Б» — территории жилых поселков, небольших городов, лесистые и пересеченные участки местности, с препятствиями для ветра, естественными или искусственными, высотой порядка 10 метров.
- Зона «В» — территории крупных городов с плотной застройкой, со средней высотой зданий 25 метров и выше.
Дом считается соответствующим именно этой зоне, если указанные характерные особенности расположены в радиусе не менее, чем высота здания h, умноженная на 30 (например, для дома 12 м радиус зоны должен быть не мене 360 м). При высоте здания выше 60 м принимается окружность радиусом 2000 м.
c – а вот это – тот самый коэффициент, который и зависит от направления ветра на здание и от угла наклона крыши.
Как уже упоминалось, в зависимости от направления воздействия и особенностей крыши ветер может давать разнонаправленные векторы нагрузки. На схеме ниже приведены зоны ветрового воздействия, на которые обычно делится площадь крыши.
Распределение крыши здания на зоны при подсчете ветровой нагрузкиОбратите внимание – фигурирует промежуточная вспомогательная величина е. Ее принимают равной либо 2 × h, либо b, в зависимости от направления ветра. В любом случае, из двух значений берут то, что будет меньше.
Коэффициент с для каждой из зон берут из таблиц, в который учтен угол уклона кровли. Если для одного участка предусмотрены и положительное и отрицательное значения коэффициента, то проводятся оба вычисления, а затем данные суммируются.
Таблица коэффициента «с» для ветра, направленного в скат кровли
| Угол ската кровли ( α) | F | G | H | I | J |
|---|---|---|---|---|---|
| 15 ° | — 0,9 | -0.8 | — 0.3 | -0.4 | -1.0 |
| 0.2 | 0.2 | 0.2 | |||
| 30 ° | -0.5 | -0.5 | -0.2 | -0.4 | -0.5 |
| 0.7 | 0.7 | 0.4 | |||
| 45 ° | 0.7 | 0.7 | 0.6 | -0.2 | -0.3 |
| 60 ° | 0.7 | 0.7 | 0.7 | -0.2 | -0.3 |
| 75 ° | 0.8 | 0.8 | 0.8 | -0.2 | -0.3 |
Таблица коэффициента «с» для ветра, направленного во фронтонную часть
| Угол ската кровли ( α) | F | G | H | I |
|---|---|---|---|---|
| 0 ° | -1.8 | -1.3 | -0.7 | -0.5 |
| 15 ° | -1.3 | -1.3 | -0.6 | -0.5 |
| 30 ° | -1.1 | -1.4 | -0.8 | -0.5 |
| 45 ° | -1.1 | -1.4 | -0.9 | -0.5 |
| 60 ° | -1.1 | -1.2 | -0.8 | -0.5 |
| 75 ° | -1.1 | -1.2 | -0.8 | -0.5 |
Вот теперь то, подсчитав ветровую нагрузку, можно будет определить суммарное внешнее силовое воздействие для каждого участка крыши.
Рсум = Рсн + Рв
Полученное значение становится исходной величиной для определения параметров стропильной системы. В частности, в таблице, приведенной ниже, можно найти значения допустимой свободной длины стропил между точками опоры, в зависимости от сечения бруса, расстояния между стропилами, сорта материала (древесины хвойных пород) и, соответственно, уровня суммарной ветровой и снежной нагрузки.
| Сорт древесины | Сечение стропил (мм) | Расстояние между соседними стропилами (мм) | |||||
|---|---|---|---|---|---|---|---|
| 300 | 400 | 600 | 300 | 400 | 600 | ||
| суммарная нагрузка (снеговая + ветровая) | 1.0 кПа | 1.5 кПа | |||||
| Древесина высшего сорта | 40×89 | 3.22 | 2.92 | 2.55 | 2.81 | 2.55 | 2.23 |
| 40×140 | 5.06 | 4.60 | 4.02 | 4.42 | 4.02 | 3.54 | |
| 50×184 | 6.65 | 6.05 | 5.28 | 5.81 | 5.28 | 4.61 | |
| 50×235 | 8.50 | 7.72 | 6.74 | 7.42 | 6.74 | 5.89 | |
| 50×286 | 10.34 | 9.40 | 8.21 | 9.03 | 8.21 | 7.17 | |
| I или II сорт | 40×89 | 3.11 | 2.83 | 2.47 | 2.72 | 2.47 | 2.16 |
| 40×140 | 4.90 | 4.45 | 3.89 | 4.28 | 3.89 | 3.40 | |
| 50×184 | 6.44 | 5.85 | 5.11 | 5.62 | 5.11 | 4.41 | |
| 50×235 | 8.22 | 7.47 | 6.50 | 7.18 | 6.52 | 5.39 | |
| 50×286 | 10.00 | 9.06 | 7.40 | 8.74 | 7.66 | 6.25 | |
| III сорт | 40×89 | 3.06 | 2.78 | 2.31 | 2.67 | 2.39 | 1.95 |
| 40×140 | 4.67 | 4.04 | 3.30 | 3.95 | 3.42 | 2.79 | |
| 50×184 | 5.68 | 4.92 | 4.02 | 4.80 | 4.16 | 3.40 | |
| 50×235 | 6.95 | 6.02 | 4.91 | 5.87 | 5.08 | 4.15 | |
| 50×286 | 8.06 | 6.98 | 6.70 | 6.81 | 5.90 | 4.82 | |
| суммарная нагрузка (снеговая + ветровая) | 2.0 кПа | 2.5 кПа | |||||
| Древесина высшего сорта | 40×89 | 4.02 | 3.65 | 3.19 | 3.73 | 3.39 | 2.96 |
| 40×140 | 5.28 | 4.80 | 4.19 | 4.90 | 4.45 | 3.89 | |
| 50×184 | 6.74 | 6.13 | 5.35 | 6.26 | 5.69 | 4.97 | |
| 50×235 | 8.21 | 7.46 | 6.52 | 7.62 | 6.92 | 5.90 | |
| 50×286 | 2.47 | 2.24 | 1.96 | 2.29 | 2.08 | 1.82 | |
| I или II сорт | 40×89 | 3.89 | 3.53 | 3.08 | 3.61 | 3.28 | 2.86 |
| 40×140 | 5.11 | 4.64 | 3.89 | 4.74 | 4.31 | 3.52 | |
| 50×184 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
| 50×235 | 7.80 | 6.76 | 5.52 | 7.06 | 6.11 | 4.99 | |
| 50×286 | 2.43 | 2.11 | 1.72 | 2.21 | 1.91 | 1.56 | |
| III сорт | 40×89 | 3.48 | 3.01 | 2.46 | 3.15 | 2.73 | 2.23 |
| 40×140 | 4.23 | 3.67 | 2.99 | 3.83 | 3.32 | 2.71 | |
| 50×184 | 5.18 | 4.48 | 3.66 | 4.68 | 4.06 | 3.31 | |
| 50×235 | 6.01 | 5.20 | 4.25 | 5.43 | 4.71 | 3.84 | |
| 50×286 | 6.52 | 5.82 | 4.75 | 6.06 | 5.27 | 4.30 | |
Понятно, что при расчете сечения стропил, шага их установки и длины пролета (расстояния межу точками опоры), берутся показатели суммарного внешнего давления для наиболее нагруженных участков кровли. Если посмотреть на схемы и значения коэффициентов таблицы, то это – G и Н.
Чтобы упростить посетителю сайта задачу по вычислению суммарной нагрузки, ниже размещен калькулятор, который рассчитает этот параметр именно для максимально нагруженных участков.
Калькулятор расчета суммарной, снеговой и ветровой нагрузки для определения необходимого сечения стропилПерейти к расчётамУкажите угол ската кровли
Определите по карте и укажите зону своего региона по уровню снеговой нагрузки
IIIIIIIVVVIVII
Определите по карте и укажите зону своего региона по уровню ветрового давления
IaIIIIIIIVVVIVII
Укажите зону расположения здания
•Зона «А» — открытая «голая» местность, например, степь, пустыня, тундра или лесотундра, полностью открытые ветровому воздействию побережья морей и океанов, крупных озер, рек, водохранилищ. •Зона «Б» — территории жилых поселков, небольших городов, лесистые и пересеченные участки местности, с препятствиями для ветра, естественными или искусственными, высотой порядка 10 метров. •Зона «В» — территории крупных городов с плотной застройкой, со средней высотой зданий 25 метров и выше.
Укажите высоту расположения кровли над землей
— не более 5 метров- от 5 до 10 метров- от 11 до 20 метров- свыше 20 метров
Итак, трудно преуменьшить значение правильного расчета угла наклона крыши, влияние этого параметра на целый ряд важнейших характеристик стропильной системы, да и всего здания в целом. Хотя проведение настоящих архитектурных расчетов, конечно, является в большей мере прерогативой специалистов, умение ориентироваться в основных понятиях и проводить несложные базовые вычисления – будет очень полезным для каждого грамотного владельца дома.
И в завершение статьи – видео-урок по расчету стропильной системы обычной двускатной крыши:
Видео: расчёт и монтаж двускатной стропильной системыРасчёт угла наклона крыши | Альфалес
Поскольку от его величины зависит и количество кровельного материала, то выбор угла наклона и его предварительные расчеты производят до начала закупки выбранного кровельного материала.
Что на него влияет
В зависимости от величины уклона скатов крыши зависит особенность ее эксплуатации.
Принято выделять 4 типа крыш: высокие — с углом в 45–60 градусов; скатные — с наклоном от 30 до 45 градусов; пологие — с углом уклона 10–30 градусов; плоские — с углом 10 градусов и меньше.
На выбор величины этого параметра оказывают влияние, в первую очередь, природные факторы, которые характерны для данной местности.
Ветровая нагрузка
Сильный ветер самое большое давление оказывает на кровли высокие. Потому что такие кровли из-за большого угла наклона имеют очень большую площадь. У большой площади поверхности очень высока парусность. Соответственно, очень велика нагрузка на всю конструкцию стропильной системы. И если вы решили устраивать именно высокую кровлю с очень большим уклоном, то следует позаботиться и об очень прочном основании. Однако в районах, где преобладают сильные ветра, небезопасно устраивать и крыши плоские. При таком типе кровли на нижнюю часть ската будет оказываться повышенное давление при сильном ветре. И если крепление кровли будет ослабленным, может произойти срыв всей конструкции. Поэтому в районах, где сильные ветра бывают часто, рекомендуется устраивать скатные кровли с величиной наклона 25–30 градусов. Если же сила ветра невелика, то величина уклона крыши может равняться 30–45 градусов.
Нагрузка снеговая
Если в той местности, где строится дом, в холодное время года снегопад обильный, то следует строить кровлю с большим углом уклона. В этом случае высокая крыша вне конкуренции. На кровлях с большим уклоном снег не задерживается. Именно по этой причине во всех северных странах кровли на зданиях очень высокие (Швеция, Финляндия, Норвегия и пр.). Чем меньше угол уклона кровли, тем дольше выпавший снег будет находиться на скатах. Тем больший вес будет воздействовать на всю конструкцию. Если конструкция стропильной системы сделана с большим запасом прочности, то некоторый слой снега на крыше — это неплохо. Он обеспечивает небольшую дополнительную теплоизоляцию. Однако, если конструкция стропильной системы сооружения на большую нагрузку не рассчитана, то могут быть большие проблемы.
Выбираем уклон в зависимости от используемого кровельного материала
Прошли те времена, когда для покрытия использовали всего два вида кровельных материалов: черепицу и шифер. Каждый материал имеет свои индивидуальные технические характеристики и это при расчете необходимого значения угла наклона обязательно следует учитывать. Ведь может произойти так, что понравившийся вам материал по своим параметрам просто не подойдет.
Минимальный угол наклона
Существует понятие минимального значения этого параметра. Для каждого из материалов этот параметр свой. И если угол наклона, полученный в результате ваших расчетов, окажется меньше, чем минимальная величина для выбранного вами кровельного материала, то использовать его для устройства кровли нельзя.
В дальнейшем может возникнуть очень много проблем, если нарушить это правило:
- для любых штучных наборных кровельных материалов, таких как черепица или шифер, минимальная величина уклона составляет 22 градуса. Именно при таком значении на стыках не скапливается влага и внутрь крыши влага не просачивается;
- угол наклона для рулонных материалов (рубероид, бикрост и пр.) зависит от того, какое вы планируете укладывать количество слоев. Если три слоя, то уклон может составлять 2–5 градусов. Если же два слоя, то его требуется увеличить до 15 градусов;
- производители профнастила рекомендуют при устройстве кровли из этого материала устраивать угол уклона 12 градусов. Профнастил можно использовать и при меньших значениях, но в таком случае необходимо выполнить проклейку стыков листов герметиком;
- для металлической черепицы значение этого параметра равняется 14;
- для ондулина — это величина в 6 градусов;
- минимальный уклон для мягкой черепицы равняется 11 градусам. Но при этом обязательное условие — сплошная обрешетка;
- для мембранных кровельных покрытий не существует жестких требований по минимальному значению этого параметра.
Это о минимальных величинах. Дадим совет — придерживайтесь этих правил, чтобы посреди зимы не пришлось всю кровлю перестилать.
Если в регионе дожди и снега случаются часто, то оптимальной будет крыша, угол наклона скатов у которой будет составлять 45 — 60 градусов. Ведь с кровли необходимо как можно скорее снимать нагрузку от воды и снега. Потому что прочность стропильной системы не беспредельна. А благодаря большому уклону кровли дождь и снег будут сходить максимально быстро.
Если в регионе, где построен дом, постоянно сильные ветра, то с крышей поступают иначе. При меньшем наклоне снижается ее парусность. И не возникает запредельных нагрузок на кровельный материал и стропила. Также не произойдет срывания крыши при резких порывах ветра. При этом оптимальный угол уклона кровли равняется 9–20 градусов.
Очень часто в регионе есть и снега, и ветер. Например, Оренбургская область. В таком случае выбирают среднее значение угла наклона. Как правило, его величина находится в диапазоне 20 — 45 градусов. Если вы обратите внимание, большинство скатных крыш имеют именно такое его значение.
Рассчитываем его величину
Для односкатной
Поскольку односкатная крыша опирается на стены, имеющие разную высоту, то формирование заданного угла наклона производят, просто поднимая одну из стен. Проводим вдоль стены перпендикуляр L сд, берущий свое начало в точке, где оканчивается короткая стена и опирающийся на стену, имеющую максимальную дину. В итоге образуется прямоугольный треугольник.
Для того, чтобы рассчитать длину стороны L bc, надо воспользоваться тригонометрической формулой.
Если длина стены L сд равняется 10 метрам, то, чтобы получить угол наклона 45 градусов, длина стены L bc должна ровняться 14.08 метра.
Для двускатной
Принцип расчета для двускатной крыши похож на предыдущий принцип.
Рассмотрим пример. Катет С — это половина ширины здания. Катет, а — это высота от перекрытия до конька. Гипотенуза является длиной ската. Если нам известны любые два параметра, то величину угла наклона можно легко рассчитать с использованием калькулятора.
Если ширина равна 8, а высота — 10 метров, то следует пользоваться формулой:
cos A = c+b
Ширина с = 8/2 = 4 метра.
В итоге формула выглядит так:
cos A = 4/10 = 0.4
По таблицам Брадиса находим значение угла, которому соответствует данная величина косинуса. Он равняется 66 градусов.
Для четырехскатной
И снова не обойтись без рулетки и таблиц Брадиса. Зная несколько параметров, можно без проблем вычислить другие. В том числе и угол наклона четырехскатной крыши. Следует помнить о том, что все размеры необходимо снимать максимально точно. А измерить уклон уже построенной крыши поможет специальный инструмент — уклономер. Ведь если вы ошибетесь, то углы наклона, длины и площади могут быть не верны. А значит, вы ошибетесь в количестве требуемого материала или прочность кровли окажется ниже запланированной.
Калькулятор уклонов — посчитать онлайн
Чтобы посчитать уклон кровли, крыши, трубопровода, пандуса, лестницы, дороги, реки и т.п. воспользуйтесь нашим очень удобным онлайн калькулятором:
Онлайн калькулятор
Посчитать уклон
Посчитать превышение
Посчитать расстояние
Просто введите значения и выберите единицы измерения уклона.
Теория
Как посчитать уклон
Для того чтобы посчитать уклон вам, для начала, необходимо знать расстояние (L) и превышение (h). Далее следуйте формулам:
В процентах:
Уклон в % = h / L ⋅ 100
В промилле:
Уклон в ‰ = h / L ⋅ 1000
В градусах:
Уклон в ° = arctg(h/L)
Пример
Для примера рассчитаем уклон дороги в процентах: на дистанции в L = 500 м дорога поднимается на h = 30 м:
Уклон дороги = 30/500 ⋅ 100 = 6%
Как посчитать превышение
Чтобы вычислить превышение (h), надо знать расстояние (L) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
h = L ⋅ Уклон в % /100
Если уклон в промилле (‰):
h = L ⋅ Уклон в ‰ /1000
Если уклон в градусах (°):
h = L ⋅ tg(α) , где α — уклон в градусах
Пример
Для примера найдём превышение h, если расстояние L= 5м, а угол уклона α=45°:
h = 5 ⋅ tg(45) = 5 ⋅ 1 = 5 м
Как посчитать расстояние
Для того чтобы посчитать расстояние (L) необходимо знать превышение (h) и уклон (в процентах, в промилле или в градусах).
Если уклон в процентах (%):
L = h / Уклон в % ⋅ 100
Если уклон в промилле (‰):
L = h / Уклон в ‰ ⋅ 1000
Если уклон в градусах (°):
L = h / tg(α), где α — уклон в градусах
Пример
Для примера посчитаем расстояние (L), которое потребуется железной дороге, чтобы подняться на (h =) 6 м при угле подъёма 30‰:
L = 6 / 30 ⋅1000 = 200 м
См. также
как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать
Содержание:
Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.
Определение наклона крыши — от чего зависит
Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:
- Ветровые нагрузки. На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
- Снеговые и дождевые нагрузки. Со снегом все довольно просто – повышение угла наклона упрощает его схождение с поверхности кровли. При наклоне крыши более 45 градусов снег почти не будет задерживаться на ней. При малом угле наклона кровли может появляться снеговой мешок, который увеличивает нагрузку на крышу. С дождевыми осадками такая же ситуация – если угол наклона кровли будет слишком низким, то вода сможет затекать в стыки или вообще застаиваться на поверхности крыши.
Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.
Методика проведения расчетов
При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.
Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:
- Общую массу кровельной конструкции;
- Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.
Упрощенный алгоритм расчетов сводится к следующим действиям:
- Сначала нужно определить вес одного квадратного метра кровельного пирога;
- Полученное значение умножается на общую площадь кровли;
- Масса кровли умножается на коэффициент 1,1.
Пример расчета уклона кровли в градусах
Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.
Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.
Как узнать угол наклона крыши
Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.
Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.
Высота крыши в коньке определяется следующим образом:
- Первым делом нужно рассчитать ширину пролета;
- Полученная величина делится на 2;
- Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.
На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.
Выбор кровельного покрытия в зависимости от наклона крыши
На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.
Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:
- Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
- При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
- Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
- Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.
Заключение
Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода.
Как рассчитать угол наклона крыши
Содержание статьи:
Процесс возведения крыши может остановиться, если заранее не подумать о таких вещах как угол наклона кровли и используемый кровельный материал. Так как эти два показателя имеют прямое влияние друг на друга, то их обязательно стоит учитывать наравне. Напомним, что кровли могут иметь один, два или четыре ската. В зависимости от типа, необходимо правильно подобрать углы скатов и материалы. В данной статье речь будет идти как раз о том, как рассчитать угол наклона крыши.
Что влияет на угол ската крыши?
Точный угол зависит от ряда факторов:
- выбранного материала кровли;
- климатических особенностей региона;
- целевого назначения здания.
В случае двухскатной крыши и более сложной конструкции, на выбор угла влияет не только особенности климата, но также и цели использования чердака. Так, например, если он будет нежилым, то есть используется для хранения различных вещей, то не нужно организовывать большую высоту подкровельного помещения. Ну а если под крышей будет полноценная мансарда, то здесь не обойтись без высокой крыши с большими углами наклонов.
Но на что в итоге следует обратить внимание? На дизайнерское решение, то есть на проект здания, на выбранный материал кровли, на количество осадков и силу ветров.
Очевидно, что для регионов с сильными ветрами необходимо возводить крышу с малыми углами — это позволяет снизить нагрузки на стропильную систему, а также избежать неприятного эффекта «срывания» кровли. Такая же конструкция крыши пригодится и для домов, возведенных в солнечных регионах с высокой температурой воздуха и малым количеством осадков. Для регионов с выраженными атмосферными явлениями (дожди, град, снегопады) угол наклона кровли должен быть большим — вплоть до 60 градусов. Это позволяет разгрузить крышу и стропила от нагрузки снега и воды. Кроме того, благодаря быстрому удалению осадков с поверхности, снижается вероятность протекания кровельного материала в местах стыков.
Для того, чтобы рассчитать угол наклона крыши необходимо принимать во внимание все вышесказанное. Как правило, оптимальными считаются углы наклона скатов в пределах 20-45 градусов. Перед тем, как рассчитать крышу дома, стоит учитывать ширину стены, то есть расстояние от начала скатов, так как при увеличении этого значения можно значительно снизить угол, при этом не ограничив чердак в высоте.Для возведения крыши с уклонами больше 9 градусов можно применять практически все доступные на рынке кровельные материалы — черепицу, профнастил, шифер и т. д. Но здесь важно учитывать индивидуальные требования каждого отдельного материала, а также понимать, как рассчитать уклон кровли правильно.
Кровля из металлочерепицы
Хорошо известно, что металлочерепица гораздо тяжелее других материалов. Именно поэтому стоит очень внимательно проводить расчеты несущей способности системы стропил. Особенно важно учитывать вес материала и угол наклона крыши для металлочерепицы в регионах с сильными ветрами. Динамические нагрузки оказывают крайне негативное влияние на материал и несущую конструкцию, особенно сильно это проявляется при больших углах наклона крыши. Для кровель, возводимых с использованием металлочерепицы, среднее значение угла наклона составляет 22 градуса. Согласно наблюдениям профессионалов именно такой уклон позволяет предотвратить скапливание и проникновение влаги на стыках, хорошо отводить снег и воду, а также противостоять нагрузкам ветра. Минимальный угол наклона крыши при этом должен составлять не менее 14 градусов. Для мягкой черепицы этот показатель равен 11 градусам, при этом такая кровля требует организации сплошной обрешетки.Кровля из профнастила
Данный материал пользуется огромной популярностью. Он отличается малым весом, простотой установки и ремонта. Кроме того, закрепить листы профнастила на обрешетке очень просто. Минимальный угол такой кровли составляет 12 градусов. Именно эта рекомендация указана в инструкции большинства производителей материала.
Кровля из рулонных «мягких» материалов
К таким материалам относят ондулин, рубероид, мембранные покрытия. В зависимости от количества слоев, используемых для покрытия крыши, угол наклона может колебаться от 2 до 15 градусов. Так, для двухслойной кровли уклон составляет 15 градусов, в то время как трехслойная конструкция позволяет покрывать плоскую крышу с углом наклона 2-5 градусов.
Мембранные покрытия могут использоваться для возведения крыш абсолютно любой конфигурации независимо от ее сложности. Так, угол наклона четырехскатной крыши (отдельных ее элементов) может составлять от 2 градусов.
Как можно понять из всего сказанного выше, выбранный угол наклона зависит от решения хозяина. Но при этом во внимание принимаются нагрузки на несущую конструкцию (статические и динамические). Также важно учесть тип обрешетки и ее шаг, так как эти параметры зависят именно от угла наклона. Для малых углов шаг обрешетки составляет в среднем 35-45 см.
Угол наклона крыши напрямую влияет и на расход кровельного материала. Так, чем больший угол, тем больше потребуется материала для покрытия плоскостей.
Во время подбора кровельного материала можно воспользоваться следующими советами:
- при малом уклоне кровли (до 10 градусов), крышу можно покрыть с использованием гравия и крошки камня. При этом берут слой гравия равный 15 мм, а крошки камня — 5 мм;
- при более выраженных углах наклона крыши обязательно применяют гидроизоляцию с помощью битума. Для рулонных материалов, кроме всего прочего, необходимо провести покрытие защитным материалом;
- асбестоцементные листы и профнастил требуют обязательной герметизации швов. Все стыки при этом делаются двойными.
Что нужно знать при выборе крыши — видео урок:
Как рассчитать угол наклона крыши
Данный угол зависит от высоты подъема конька над внешней плоскостью потолка. Этот параметр зависит от цели использования чердачного помещения. Так, если чердак необходим только в хозяйственных целях, то высота конька может быть небольшой. Если же помещение будет использоваться как мансарда, то необходимо поднять его на значительную высоту (подробнее: «Как рассчитать высоту крыши дома»). Расчеты при этом можно провести по простой схеме.Формула расчета угла наклона крыши:
Sin(а)=a/b,
- где a — половина ширины фронтона;
- b — выбранная высота конька.
Предположим, что дом имеет ширину 6 м, а чердак будет использовать для хранения различных хозяйственных вещей, поэтому он будет возвышаться на 1,8 м. Таким образом, синус угла скатов будет равен Sin(а) = 3/1,8 = 1,67. Используя специальные тригонометрические таблицы переведем полученное значение в градусы. В итоге скаты будут иметь угол наклона около 59 градусов. Для большей простоты проведения кровельных работ его можно принять равным 60 градусам.
Угол наклона прямой— Concept
Угол наклона прямой — это угол, образованный пересечением прямой и оси x. Использование горизонтального «пробега» 1 и m для наклона, угла наклона, theta = tan-1 (m) или m = tan (theta). Следовательно, если угол или наклон известны, другое можно найти с помощью одного из уравнений. Если угол наклона отрицательный, то и наклон линии отрицательный.
Какой угол наклона лески? Итак, у меня есть линия, нарисованная здесь уравнением y = mx + b, оно должно быть вам знакомо. Это угол наклона тета, это угол между линией и горизонтом. Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь, если я посмотрю на этот прямоугольный треугольник, и это прямоугольный треугольник, я могу использовать тригонометрию прямоугольного треугольника, чтобы найти связь между тета и m, верно? m — это длина по вертикали этой стороны, поэтому тангенс теты равен m по касательной к 1, тета равен m, так что это соотношение между углом наклона и наклоном, тангенс угла наклона — это наклон, а угол наклона равен арктангенс угла наклона, поэтому вы можете рассчитать наклон по углу наклона, а угол наклона можно рассчитать по углу наклона.
Теперь давайте посмотрим на другой, на несколько частных случаев. Горизонтальные или вертикальные линии. Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет тангенсом 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
А как насчет вертикальной? Что ж, я бы сказал, что угол наклона здесь пи больше 2, поэтому тета равен пи больше 2, каков наклон? Касательная к тэте, прямая касательная к пи более 2, но, конечно, это не определено, и это именно то, что мы хотели бы, чтобы наклон вертикальной линии не был определен, нет наклона, поэтому просто для просмотра, угол наклона линии угол, на который Линия определяет отношение к горизонтали, а наклон — это тангенс теты, угол наклона равен наклону, а угол наклона равен обратному тангенсу наклона.
Наклон лески | Аналитическая геометрия
4.3 Наклон прямой (EMBGD)
На диаграмме показано, что прямая линия составляет угол \ (\ theta \) с положительной осью \ (x \). Это называется углом наклона прямой линии.
Мы замечаем, что если градиент изменяется, то значение \ (\ theta \) также изменяется, поэтому угол наклона линии связан с ее градиентом. Мы знаем, что градиент — это отношение изменения направления \ (y \) к изменению направления \ (x \):
\ [m = \ frac {\ Delta y} {\ Delta x} \]Из тригонометрии мы знаем, что тангенциальная функция определяется как отношение:
\ [\ tan \ theta = \ frac {\ text {противоположная сторона}} {\ text {смежная сторона}} \]
А из схемы видим, что
\ begin {align *} \ tan \ theta & = \ dfrac {\ Delta y} {\ Delta x} \\ \ поэтому m & = \ tan \ theta \ qquad \ text {for} \ text {0} \ text {°} \ leq \ theta <\ text {180} \ text {°} \ end {align *}
Следовательно, градиент прямой линии равен касательной к углу, образованному между прямой и положительным направлением оси \ (x \) -.
Вертикальные линии
- \ (\ theta = \ text {90} \ text {°} \)
- Градиент не определен, поскольку нет изменений в \ (x \) — значениях (\ (\ Delta x = 0 \)).
- Следовательно, \ (\ tan \ theta \) также не определено (график \ (\ tan \ theta \) имеет асимптоту в \ (\ theta = \ text {90} \ text {°} \)).
Горизонтальные линии
- \ (\ theta = \ text {0} \ text {°} \)
- Градиент равен \ (\ text {0} \), поскольку нет изменений в \ (y \) — значениях (\ (\ Delta y = 0 \)).
- Следовательно, \ (\ tan \ theta \) также равно \ (\ text {0} \) (график \ (\ tan \ theta \) проходит через начало координат \ ((\ text {0} \ text { °}; 0)) \).
Линии с отрицательными градиентами
Если прямая линия имеет отрицательный градиент (\ (m <0 \), \ (\ tan \ theta <0 \)), то угол, образованный между линией и положительным направлением оси \ (x \) - тупой. {- 1} (- \ text {0,7}) \\ & = - \ текст {35,0} \ текст {°} \ end {align *}
Этот отрицательный угол лежит в четвертом квадранте.Мы должны добавить \ (\ text {180} \) \ (\ text {°} \), чтобы получить тупой угол во втором квадранте:
\ begin {align *} \ theta & = — \ text {35,0} \ text {°} + \ text {180} \ text {°} \\ & = \ текст {145} \ текст {°} \ end {align *}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \ (\ theta = \ text {145} \ text {°} \) дает градиент \ (m = — \ text {0,7} \).
Вы справитесь! Позвольте нам помочь вам учиться с умом для достижения ваших целей. Siyavula Practice направит вас в удобном для вас темпе, когда вы задаете вопросы в Интернете.
Зарегистрируйтесь, чтобы улучшить свои оценкиУгол наклона
Упражнение 4.5\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {60} \ text {°} \\ \ поэтому m & = \ text {1,7} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {135} \ text {°} \\ \ поэтому m & = — \ text {1} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {0} \ text {°} \\ \ поэтому m & = \ text {0} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {54} \ text {°} \\ \ поэтому m & = \ text {1,4} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {90} \ text {°} \\ \ поэтому m & \ text {не определено} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {45} \ text {°} \\ \ поэтому m & = \ text {1} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {140} \ text {°} \\ \ поэтому m & = — \ text {0,8} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {180} \ text {°} \\ \ поэтому m & = \ text {0} \ end {выровнять *}
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {75} \ text {°} \\ \ поэтому m & = \ text {3,7} \ end {выровнять *}
строка с \ (m = \ dfrac {3} {4} \)
\ begin {align *} \ тан \ тета & = м \\ & = \ frac {3} {4} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,75} \ right) \\ \ поэтому \ theta & = \ text {36,8} \ text {°} \ end {выровнять *}
\ begin {align *} 2у — х & = 6 \\ 2у & = х + 6 \\ y & = \ frac {1} {2} x + 3 \\ \ тан \ тета & = м \\ & = \ frac {1} {2} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,5} \ right) \\ \ поэтому \ theta & = \ text {26,6} \ text {°} \ end {выровнять *}
прямая проходит через точки \ ((- 4; -1) \) и \ ((2; 5) \)
\ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {5 + 1} {2 + 4} \\ & = \ frac {6} {6} \\ \ поэтому m & = 1 \\ \ тан \ тета & = 1 \\ \ theta & = \ tan ^ {- 1} \ left (\ text {1} \ right) \\ \ поэтому \ theta & = \ text {45} \ text {°} \ end {выровнять *}
\ begin {align *} x & = 3y + \ frac {1} {2} \\ x — \ frac {1} {2} & = 3y \\ \ frac {1} {3} x — \ frac {1} {6} & = y \\ \ поэтому m & = \ frac {1} {3} \\ \ theta & = \ tan ^ {- 1} \ left (\ frac {1} {3} \ right) \\ \ поэтому \ theta & = \ text {18,4} \ text {°} \ end {выровнять *}
линия проходит через точки \ ((2; 5) \) и \ ((\ frac {2} {3}; 1) \)
\ begin {align *} m & = \ frac {y_2 — y_1} {x_2 — x_1} \\ & = \ frac {1–5} {\ frac {2} {3} -2} \\ & = \ frac {-4} {- \ frac {4} {3}} \\ \ поэтому m & = 3 \\ \ theta & = \ tan ^ {- 1} \ left (\ text {3} \ right) \\ \ поэтому \ theta & = \ text {71,6} \ text {°} \ end {выровнять *}
линия с градиентом, равным \ (\ text {0,577} \)
\ begin {align *} m & = \ text {0,577} \\ \ theta & = \ tan ^ {- 1} \ left (\ text {0,577} \ right) \\ \ поэтому \ theta & = \ text {30} \ text {°} \ end {выровнять *}
Рабочий пример 8: Наклон прямой
Определите угол наклона (с точностью до десятичного знака \ (\ text {1} \)) прямой, проходящей через точки \ ((2; 1) \) и \ ((- 3; -9) \) . {- 1} 2 \\ & = \ текст {63,4} \ текст {°} \ end {align *}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусов).
Напишите окончательный ответ
Угол наклона прямой равен \ (\ text {63,4} \) \ (\ text {°} \).
Рабочий пример 9: Наклон прямой
Определите уравнение прямой, проходящей через точку \ ((3; 1) \) с углом наклона \ (\ text {135} \ text {°} \).
Используйте угол наклона для определения уклона линии
\ begin {align *} м & = \ загар \ тета \\ & = \ tan \ text {135} \ text {°} \\ \ поэтому m & = -1 \ end {align *}
Запишите градиентно-точечную форму уравнения прямой линии
\ [y — y_1 = m (x — x_1) \]
Заменитель \ (m = -1 \)
\ [y — y_1 = — (x — x_1) \]
Заменить данную точку \ ((3; 1) \)
\ begin {align *} у — 1 & = — (х — 3) \\ у & = -x + 3 +1 \\ & = -x + 4 \ end {align *}
Напишите окончательный ответ
Уравнение прямой: \ (y = -x + 4 \).
Рабочий пример 10: Наклон прямой
Определите острый угол (с точностью до десятичного знака \ (\ text {1} \)) между линией, проходящей через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и прямая \ (y = — \ frac {3} {2} x + 4 \).
Нарисуйте эскиз
Проведите линию через точки \ (M (-1; 1 \ frac {3} {4}) \) и \ (N (4; 3) \) и линию \ (y = — \ frac {3} { 2} x + 4 \) на подходящей системе осей. Метки \ (\ alpha \) и \ (\ beta \), углы наклона двух линий.Обозначьте \ (\ theta \), острый угол между двумя прямыми линиями.
Обратите внимание, что \ (\ alpha \) и \ (\ theta \) — острые углы, а \ (\ beta \) — тупой угол.
\ [\ begin {array} {rll} \ hat {B} _1 & = \ text {180} \ text {°} — \ beta & (\ angle \ text {on str. line}) \\ \ text {and} \ theta & = \ alpha + \ hat {B} _1 \ quad & (\ text {ext.} \ angle \ text {of} \ треугольник = \ text {sum int. opp}) \\ \ поэтому \ theta & = \ alpha + (\ text {180} \ text {°} — \ beta) \\ & = \ text {180} \ text {°} + \ alpha — \ beta \ конец {массив} \]Используйте градиент, чтобы определить угол наклона \ (\ beta \)
Из уравнения \ (y = — \ frac {3} {2} x + 4 \) мы видим, что \ (m <0 \), поэтому \ (\ beta \) - тупой угол такой, что \ (\ text {90} \ text {°} <\ beta <\ text {180} \ text {°} \). {- 1} \ left (\ frac {1} {4} \ right) \\ & = \ текст {14,0} \ текст {°} \ end {align *}
Напишите окончательный ответ
\ begin {align *} \ theta & = \ text {180} \ text {°} + \ alpha — \ beta \\ & = \ text {180} \ text {°} + \ text {14,0} \ text {°} — \ text {123,7} \ text {°} \\ & = \ текст {70,3} \ текст {°} \ end {align *}
Острый угол между двумя прямыми равен \ (\ text {70,3} \) \ (\ text {°} \).{-1} \ left (- \ frac {9} {2} \ right) \\ & = — \ text {77,5} \ text {°} \\ \ поэтому \ theta & = \ text {180} \ text {°} — \ text {77,5} \ text {°} \\ \ поэтому \ theta & = \ text {102,5} \ text {°} \ end {выровнять *}
линия, проходящая через \ ((- 1; -6) \) и \ ((- \ frac {1} {2}; — \ frac {11} {2}) \)
\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {- \ frac {11} {2} + 6} {- \ frac {1} {2} +1} \\ & = \ frac {\ frac {1} {2}} {\ frac {1} {2}} \\ \ поэтому m & = 1 \\ \ theta & = \ tan ^ {- 1} \ left (1 \ right) \\ \ поэтому \ theta & = \ text {45} \ text {°} \ end {выровнять *}
\ begin {align *} 5 & = 10л — 15х \\ 5 + 15x & = 10л \\ \ frac {1} {2} + \ frac {3} {2} x & = y \\ \ поэтому m & = \ frac {3} {2} \\ \ theta & = \ tan ^ {- 1} \ left (\ frac {3} {2} \ right) \\ \ поэтому \ theta & = \ text {56,3} \ text {°} \ end {выровнять *}
\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {3 + 1} {2–0} \\ & = \ frac {4} {2} \\ \ поэтому m & = 2 \\ \ theta & = \ tan ^ {- 1} \ left (2 \ right) \\ \ поэтому \ theta & = \ text {63,4} \ text {°} \ end {выровнять *}
\ begin {align *} m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {2 — 0} {0 — 6} \\ & = \ frac {2} {- 6} \\ \ поэтому m & = — \ frac {1} {3} \\ \ theta & = \ tan ^ {- 1} \ left (- \ frac {1} {3} \ right) \\ \ поэтому \ theta & = — \ text {18,4} \ text {°} \\ \ поэтому \ theta & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\ \ поэтому \ theta & = \ text {161,6} \ text {°} \ end {выровнять *}
Градиент undefined
Определите острый угол между прямой, проходящей через точки \ (A (-2; \ frac {1} {5}) \) и \ (B (0; 1) \), и прямой, проходящей через точки \ ( C (1; 0) \) и \ (D (-2; 6) \).{-1} \ влево (-2 \ вправо) \\ \ поэтому \ alpha & = — \ text {63,4} \ text {°} \\ \ поэтому \ alpha & = \ text {180} \ text {°} — \ text {63,4} \ text {°} \\ \ поэтому \ alpha & = \ text {116,6} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\ \ поэтому \ theta & = \ text {21,8} \ text {°} + (\ text {180} \ text {°} — \ text {116,6} \ text {°}) \\ & = \ текст {85,2} \ текст {°} \ end {выровнять *}
Определите угол между линией \ (y + x = 3 \) и линией \ (x = y + \ frac {1} {2} \).{-1} \ left (1 \ right) \\ \ поэтому \ beta & = \ text {45} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ angle \ треугольник) \\ \ поэтому \ theta & = \ text {45} \ text {°} + (\ text {180} \ text {°} — \ text {135} \ text {°}) \\ & = \ текст {90} \ текст {°} \ end {выровнять *}
Найдите угол между прямой \ (y = 2x \) и прямой, проходящей через точки \ ((- 1; \ frac {7} {3}) \) и \ ((0; 2) \).
Пусть угол наклона линии \ (y = 2x \) равен \ (\ beta \), а угол наклона другой линии равен \ (\ alpha \).{-1} \ left (2 \ right) \\ \ поэтому \ beta & = \ text {63,4} \ text {°} \\ m & = \ frac {y_2 -y_1} {x_2 — x_1} \\ & = \ frac {2 — \ frac {7} {3}} {0 + 1} \\ & = \ frac {- \ frac {1} {3}} {1} \\ \ поэтому m & = — \ frac {1} {3} \\ \ поэтому \ alpha & = — \ text {18,4} \ text {°} \\ \ поэтому \ alpha & = \ text {180} \ text {°} — \ text {18,4} \ text {°} \\ \ поэтому \ alpha & = \ text {161,6} \ text {°} \\ \ text {And} \ theta & = \ beta + (\ text {180} \ text {°} — \ alpha) \ quad (\ text {ext.} \ угол \ треугольник) \\ \ поэтому \ theta & = \ text {63,4} \ text {°} + (\ text {180} \ text {°} — \ text {161,6} \ text {°}) \\ & = \ текст {81,8} \ текст {°} \ end {выровнять *}
Градиент (или наклон) линии и наклон
Приложение: Дорожный знак, обозначающий крутой уклон.
Уклон дороги «15%» эквивалентен «m = 0,15».
Уклон (также известный как уклон ) линии определяется как
`» gradient «= текст (вертикальный подъем) / текст (горизонтальный бег`
На следующей диаграмме градиент линии AB определяется как: `a / b`
Как правило, для линии, соединяющей точки ( x 1 , y 1 ) и ( x 2 , у 2 ) имеем:
Теперь мы можем написать формулу для наклона прямой.
Градиент линии формулы
Из приведенной выше диаграммы видно, что уклон (обычно обозначается м ) определяется как:
`m = (y_2-y_1) / (x_2-x_1`
Интерактивный график — наклон прямой
Вы можете изучить концепцию наклона линии на следующем интерактивном графике (это не фиксированное изображение).
Перетащите либо точку A ( x 1 , y 1 ) или точку B ( x 2 , y 2 градиент), чтобы исследовать, как градиент работает.Числа будут обновляться по мере взаимодействия с графиком.
Обратите внимание, что происходит со знаком (плюс или минус) наклона, когда точка B находится выше или ниже A.
Наклон `= (y_2 — y_1) / (x_2 — x_1)`
`= (BC) / (AC)`
Авторские права © www.intmath.com
Вы можете перемещать график вверх-вниз, влево-вправо, если удерживаете клавишу «Shift», а затем перетаскиваете график.
Если заблудились, всегда можно обновить страницу.
Пример
Найдите наклон прямой, соединяющей точки (−4, −1) и (2, −5).
Ответ
Это задействованные точки:
Итак, уклон:
`m = (y_2-y_1) / (x_2-x_1`
`= (- 5 — (- 1)) / (2 — (- 4)`
`= (- 4) / 6`
`= -2 / 3`
Обратите внимание, что наклон отрицательный . Линия идет «вниз по склону», когда мы движемся слева направо.
Положительные и отрицательные склоны
Как правило, положительный наклон указывает на значение зависимой переменной (обычно y ) увеличивается на при движении слева направо:
Зависимая переменная на приведенном выше графике — это значение y , а независимая переменная — x .
Отрицательный наклон означает, что значение зависимой переменной (обычно y ) равно , уменьшаясь на при движении слева направо:
Наклон
У нас есть линия с уклоном м и углом, который линия составляет с x — ось α.
Из тригонометрии напомним, что тангенс угла α определяется как:
`tan \ alpha = текст (напротив) / текст (рядом)`
Теперь, поскольку наклон также определяется как противоположный / смежный, мы имеем:
Это дает нам результат:
tan α = м
Тогда мы можем найти угол α , используя
α = arctan м
(то есть α = tan -1 м )
Этот угол α называется наклоном линии.@ `
ПРИМЕЧАНИЕ: Размер угла α составляет (по определению) только между `0 °` и `180 °`.
Упражнение 2
Найдите наклон прямой α = 137 °.
Ответ
Ситуация следующая:
Итак, уклон:
м = tan α
= загар 137 °
= -0,933
Обратите внимание, что наклон отрицательный.
|
Уголки
высоты / наклона и Углы подъема или наклона углы выше горизонтали, как если бы вы смотрели с уровня земли в вершина флагштока.Углы депрессии или склонения — это углы ниже горизонтали, как если бы вы смотрели из окна на основание здание на соседнем участке. Всякий раз, когда у вас есть один из этих углов, вы следует сразу начать представлять, как прямоугольный треугольник впишется в описание.
Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса.Итак, я рисую прямоугольный треугольник и помечаю все, что знаю: .
До ближайшей ноги г. Сагуаро — 44 фут в высоту.
Мне нужно выполнить это упражнение по шагам. Я не могу найти высоту башни, AB, пока у меня не будет длины базового компакт-диска.(Представьте, что D перемещается вправо, чтобы встретить продолжение AB, образуя прямоугольный треугольник.) Для этого вычисления я буду использовать высоту холма. Чтобы минимизировать ошибку округления, я буду использовать все цифры из моего калькулятора в моих вычислениях, и пытаюсь «унести» все вычисления в моем калькуляторе .. Теперь, когда у меня есть длина основания, Я могу найти общую высоту, используя угол, который измеряет высоту от уровня моря до вершины башни. Отлично! Сохраняя все цифры и проводя вычисления в своем калькуляторе, я получил точный ответ. Без округления! Но мне нужно вычесть, потому что «300» высота от воды до вершины башни. Первая сотня метров этой общей высоты — холм, итак: Вверх | Вернуться к индексу
|
|
НАЙТИ УРОК Этот урок можно распечатать для личного пользования.
|
Расчет уклона и общего уклона в архитектуре
Архитекторы постоянно предоставляют информацию об уклоне на своих чертежах, используя градиенты, градусы или проценты в зависимости от приложения. Например, крыши обозначаются градиентами, а поперечные уклоны тротуаров обычно обозначаются в градусах. Полезно понять, как рассчитать каждый метод.
Существует три различных способа указать наклон поверхности относительно горизонтальной плоскости: градусы, уклон и процент.
Расчет градиента уклона
Градиенты уклона записываются как Y: X, где Y — это единичная величина подъема, а X — это пробег. Оба числа должны использовать одни и те же единицы измерения. Например, если вы путешествуете на 3 дюйма по вертикали и 3 фута (36 дюймов) по горизонтали, уклон будет 3:36 или 1:12. Это читается как «наклон один из двенадцати».
Расчет процента уклона
Процент уклона рассчитывается так же, как и уклон.Преобразуйте приближение и бег в те же единицы, а затем разделите приближение на разбег. Умножьте это число на 100, и вы получите наклон в процентах. Например, подъем 3 дюйма, разделенный на 36 дюймов = 0,083 x 100 = уклон 8,3%.
Расчет уклона в градусах
Самый сложный способ вычисления наклона — в градусах, и для этого требуется немного математики средней школы. Тангенс данного угла (в градусах) равен подъему, деленному на пробег. Следовательно, величина, обратная тангенсации подъема, деленная на длину пробега, даст угол.
Таблица общих наклонов в архитектуре
В таблице ниже показаны некоторые распространенные уклоны. Полы с уклоном 1:20 не требуют поручней, но все, что круче 1:20, считается пандусом и требует поручней. Пандусы с уклоном 1:12 — это максимальный уклон, разрешенный правилами ADA, и для них требуются поручни. Федеральные коды ADA указывают, что максимальный поперечный уклон доступного маршрута составляет 1:48, что чуть больше 2%. Однако мы видели некоторые юрисдикции, которые разрешают максимальный поперечный уклон 1:50.
| Градусы | Градиент | Процент | |||
|---|---|---|---|---|---|
| 0,6 ° | 1: 95,49 | 1,0% | |||
| 1 ° | 1: 57,2914 | 905% 1: 57,2914 | 905 : 502% | ||
| 1,19 ° | 1: 48 | 2,08% | |||
| 2,86 ° | 1: 20 | 5% | |||
| 4,76 ° | .3% | ||||
| 7,13 ° | 1: 8 | 12,5% | |||
| 10 ° | 1: 5,67 | 17,6% | |||
| 14,04 ° | 15 1: 4 | 15 ° | 1: 3,73 | 26,8% | |
| 26,57 ° | 1: 2 | 50% | |||
| 30 ° | 1: 1,73 | 57,7% | 1: 1 | 100% | |
| 56.31 ° | 1: 0,67 | 150% | |||
| 60 ° | 1: 0,6 | 173,2% | |||
| 63,43 ° | 1: 0,5 | 200% | 78 ° : 0,2 | 500% | |
| 89,43 ° | 1: 0,1 | 1000% | |||
| 90 ° | 1: 0 | инф. |
Скаты крыши
Уклоны крыши идентифицируются с помощью описанного выше градиентного метода, где подъем варьируется, но обычно длина спуска составляет 12.На некоторых очень крутых крышах вы можете увидеть инвертированный градиент, так что длина пролета меняется, но подъем сохраняется как 12.
Кровля с малым уклоном
Кровли с низким уклоном имеют уклон 3:12 или меньше. У них должна быть мембранная кровельная система для обеспечения водонепроницаемости.
| Градиент крыши | Градусы | Процент |
|---|---|---|
| 1/4: 12 | 1,19 ° | 2,08% |
| 1/2: 12 | 2,3915 ° | 17%|
| 1: 12 | 4,76 ° | 8,3% |
| 2: 12 | 9,46 ° | 16,67% |
| 3: 12 | 14,04 ° 905 |
Крутые крыши
Все, что выше 3:12, считается крутой крышей и может быть покрыто металлическими панелями, черепицей или черепицей — эти крыши проливают воду и не считаются водонепроницаемыми.
| Градиент крыши | Градусы | Процент | ||
|---|---|---|---|---|
| 4: 12 | 18.43 ° | 33,33% | ||
| 5: 12 | 22,62 ° | 41,67% | ||
| 6: 12 | 26,57 ° | 50% | ||
| 905 905 905 905 905 305 146 905 905 7: 12 % | ||||
| 8: 12 | 33,69 ° | 66,67% | ||
| 9: 12 | 36,87 ° | 75% | ||
| 10: 12 | 39,8150 | % 11: 12 | 42.51 ° | 91,67% |
| 12:12 | 45 ° | 100% |
Градусов, градиентов и уклонов
Наклон или уклон линии описывает направление и крутизну линия. Уклон может быть выражен в углах, уклонах или ступенях.
Наклон, выраженный как Угол
S угол = tan -1 (y / x) (1)
где
S угол = угол (рад, градусы (°))
x = горизонтальный участок (м, фут..)
y = вертикальный подъем (м, футы …)
Пример — уклон как угол
Уклон как угол для высоты 1 м на расстоянии 2 м можно вычислить как
S угол = tan -1 ((1 м) / (2 м))
= 26,6 °
Наклон, выраженный как Уклон
S уклон (%) = (100%) y / x (2)
где
S уклон (%) = уклон (%)
Пример — уклон как уклон
Уклон как уклон для отметки 1 м на расстоянии 2 м можно рассчитать как
S уклон (%) = (1 м) / (2 м)
= 50 (%)
Наклон и Уклон кровли
Уклон кровли — это уклон, созданный стропилами.Вы можете найти уклон крыши в виде x: 12, например 4/12 или 9/12.
Уклон крыши в форме x: 12 может быть выражен в ступенях как
Степень S (%) = (100%) x / 12 (3)
Пример — Изображение крыши 4/12 как оценка
S уклон (%) = (100%) 4/12
= 33,3%
Угол наклона крыши x: 12 может быть выражен в углах как
S угол = tan -1 (x / 12) (3b)
Пример — Изображение крыши 4/12 как угол
S угол = tan -1 (4/12)
= 18.4 °
Калькулятор наклона или уклона
Расчет угловых градусов, уклона и длины уклона.
y — вертикальный подъем (м, футы, дюймы ….)
x — горизонтальный проход (м, футы, дюймы ….)
(включить всплывающее окно)
Диаграмма наклона или уклона
Используйте эту диаграмму для оценки наклона или уклона. Измерьте горизонтальный пробег и вертикальный подъем и нарисуйте линии на диаграмме, чтобы оценить наклон.
Загрузите и распечатайте диаграмму наклона / уклона
Уклоны в зависимости от уклонов и% уклонов
| Уклон | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Угол (градусы) | |||||||||||||||
Угол 15 | | | ||||||||||||||
| Y | X | ||||||||||||||
| 0,1 | 1 | 573,0 | 0,17 | ||||||||||||
| 0,2 | 1 | 1 | 1 | 5 | 0,35 | ||||||||||
| 0,3 | 1 | 191,0 | 0,52 | ||||||||||||
| 0,4 | 1 | 143,2 | 0,70 | 9015 905 905 905 905 905 0,50 905 0,571 | 100 | 1 | |||||||||
| 0,6 | 1 | 95,49 | 1,05 | ||||||||||||
| 0,7 | 1 | 81.85 | 1,22 | ||||||||||||
| 0,8 | 1 | 71,62 | 1,40 | ||||||||||||
| 0,9 | 1 | 63,66 | 1,57 | 00||||||||||||
| 2 | 1 | 28,64 | 3,49 | ||||||||||||
| 3 | 1 | 19,08 | 5,24 | ||||||||||||
| 4 | 1 | 14.30 | 6,99 | ||||||||||||
| 5 | 1 | 11,43 | 8,75 | ||||||||||||
| 5,74 | 1 | 10 | 10 4 | 905 90510 4 | 905|||||||||||
| 7 | 1 | 8,144 | 12,3 | ||||||||||||
| 8 | 1 | 7,115 | 14,1 | ||||||||||||
| 9 | 1 | 6.314 | 15,8 | ||||||||||||
| 10 | 1 | 5,671 | 17,6 | ||||||||||||
| 11 | 1 | 5,145 | 19,4 | 905 905 905 905 905 905 905 905||||||||||||
| 13 | 1 | 4,331 | 23,1 | ||||||||||||
| 14 | 1 | 4,011 | 24,9 | ||||||||||||
| 15 | 1 | 3.732 | 26,8 | ||||||||||||
| 16 | 1 | 3,487 | 28,7 | ||||||||||||
| 17 | 1 | 3,271 | 30,6 | 905 905 905 905 905 1 905 191 | 2,904 | 34,4 | |||||||||
| 20 | 1 | 2,747 | 36,4 | ||||||||||||
| 21 | 1 | 2.605 | 38,4 | ||||||||||||
| 22 | 1 | 2,475 | 40,4 | ||||||||||||
| 23 | 1 | 2,356 | 42,4 | 1 | 2,145 | 46,6 | |||||||||
| 26 | 1 | 2,050 | 48,8 | ||||||||||||
| 27 | 1 | 1.963 | 51,0 | ||||||||||||
| 28 | 1 | 1.881 | 53,2 | ||||||||||||
| 29 | 1 | 1.804 | 55,4 | 3015 905 905 905 905 905 905 311 | 1,664 | 60,1 | |||||||||
| 32 | 1 | 1,600 | 62,5 | ||||||||||||
| 33 | 1 | 1.540 | 64,9 | ||||||||||||
| 34 | 1 | 1,483 | 67,5 | ||||||||||||
| 35 | 1 | 1,428 | 70,0 | 9015 905 905 905 905 905 905 905 905 905 72 905 905 371 | 1,327 | 75,4 | |||||||||
| 38 | 1 | 1,280 | 78,1 | ||||||||||||
| 39 | 1 | 1.235 | 81,0 | ||||||||||||
| 40 | 1 | 1,192 | 83,9 | ||||||||||||
| 41 | 1 | 1,150 | 86,9 | 905 905 905 1 905 905 1 905 431 | 1,072 | 93,3 | |||||||||
| 44 | 1 | 1,036 | 96,6 | ||||||||||||
| 45 | 1 | 1.000 | 100,0 | ||||||||||||
| 46 | 1 | 0,9657 | 103,6 | ||||||||||||
| 47 | 1 | 0,9325 | 107,2 | 0,9325 905 905107,2 | 905 905 905 491 | 0,8693 | 115,0 | ||||||||
| 50 | 1 | 0,8391 | 119,2 | ||||||||||||
| 51 | 1 | 0.8098 | 123,5 | ||||||||||||
| 52 | 1 | 0,7813 | 128,0 | ||||||||||||
| 53 | 1 | 0,7536 | 132,7 | 905 905 905 905 905 905 905 551 | 0,7002 | 142,8 | |||||||||
| 56 | 1 | 0,6745 | 148,3 | ||||||||||||
| 57 | 1 | 0.6494 | 154,0 | ||||||||||||
| 58 | 1 | 0,6249 | 160,0 | ||||||||||||
| 59 | 1 | 0,6009 | 166,4 | 1 | 0,5543 | 180,4 | |||||||||
| 62 | 1 | 0,5317 | 188,1 | ||||||||||||
| 63 | 1 | 0.5095 | 196,3 | ||||||||||||
| 64 | 1 | 0,4877 | 205,0 | ||||||||||||
| 65 | 1 | 0,4663 | 214,5 | 1 | 0,4245 | 235,6 | |||||||||
| 68 | 1 | 0,4040 | 247,5 | ||||||||||||
| 69 | 1 | 0.3839 | 260,5 | ||||||||||||
| 70 | 1 | 0,3640 | 274,7 | ||||||||||||
| 71 | 1 | 0,3443 | 290,4 | 1 | 0,3057 | 327,1 | |||||||||
| 74 | 1 | 0,2867 | 348,7 | ||||||||||||
| 75 | 1 | 0.2679 | 373,2 | ||||||||||||
| 76 | 1 | 0,2493 | 401,1 | ||||||||||||
| 77 | 1 | 0,2309 | 433,1 | 1 | 0,1944 | 514,5 | |||||||||
| 80 | 1 | 0,1763 | 567,1 | ||||||||||||
| 81 | 1 | 0.1584 | 631,4 | ||||||||||||
| 82 | 1 | 0,1405 | 711,5 | ||||||||||||
| 83 | 1 | 0,1228 | 814,4 | 1 | 0,08749 | 1143 | |||||||||
| 86 | 1 | 0,06993 | 1430 | ||||||||||||
| 87 | 1 | 0.05241 | 1908 | ||||||||||||
| 88 | 1 | 0,03492 | 2864 | ||||||||||||
| 89 | 1 | 0,01746 | 5729 | 905 905 905 905 905 905 905||||||||||||
| Наклон: | 75,00% |
| Длина откоса: |
5,00 м |
| Угол 1: |
36,87 ° |
| Угол 2: |
53,13 ° |
| Периметр треугольника: |
12,00 м |
| Поверхность треугольника: |
6,00 м 2 |
* Гипотенуза: Абсолютно варварский термин, означающий «длину третьей стороны» или «длину склона».
Формула для расчета уклона
Длина откоса рассчитывается по теореме Пифагора. Эта теорема получается путем умножения квадратного корня на сумму квадрата ширины и возведенной в квадрат высоты.
Итак: Квадратный корень ((ширина x ширина) + (высота x высота)) = длина уклона
Наклон 100%
Следует отметить, что уклон в 100% не является вертикальным, но он эквивалентен одинаковой высоте и ширине, что приводит к углу наклона 45 °.Например: горная тропа со 100% уклоном будет подниматься на 100 метров на каждые 100 метров, когда она идет вперед. Расстояние по этому склону составит 141,4 метра.
Пандусы для инвалидов
Уклоны пандуса для инвалидов должны быть:
- максимум 12% при длине менее 50 см
- максимум 8% для длины менее 8 м
- от 4% до 5% для максимальной длины 10 м
Лестницы должны устанавливаться каждые 10 м и иметь минимальную длину 1.40 мес.
Наклон ширины, известный как поперечный уклон, предпочтительно должен быть нулевым и во всех случаях менее 2%. Ширина пандуса должна быть не менее 1,40 м. Его можно уменьшить до 1,20 м, если нет стены с одной или другой стороны.
Наклон ширины, также известный как поперечный уклон, предпочтительно должен быть нулевым и никогда не должен превышать 2%. Ширина пандуса должна быть не менее 1,40 м. Его можно уменьшить до 1,20 м, если одна сторона не прикреплена к стене.
Средний наклон и высота трассы
Вполне возможно рассчитать средний угол наклона пути, используя значения, заданные горизонтальным расстоянием (пробег) и высотой (подъемом), достигнутыми в конце уклона.Если путь ветреный, пройденное расстояние будет больше, чем длина склона.
Рисование под прямым углом
Длина ската соответствует диагонали прямоугольного треугольника. Вы также можете использовать это измерение для вычисления диагонали, чтобы нарисовать прямой угол, метод, широко используемый в строительной отрасли. Обычно используются следующие значения: 3 метра, 4 метра и 5 метров до , чтобы получить прямой угол . К сожалению, использовать такие измерения не всегда возможно.Подставив значения 3 метра и 4 метра на значения, полученные на месте, и результат длины склона (используемый в качестве диагонали), позволит вам правильно нарисовать прямой угол.
