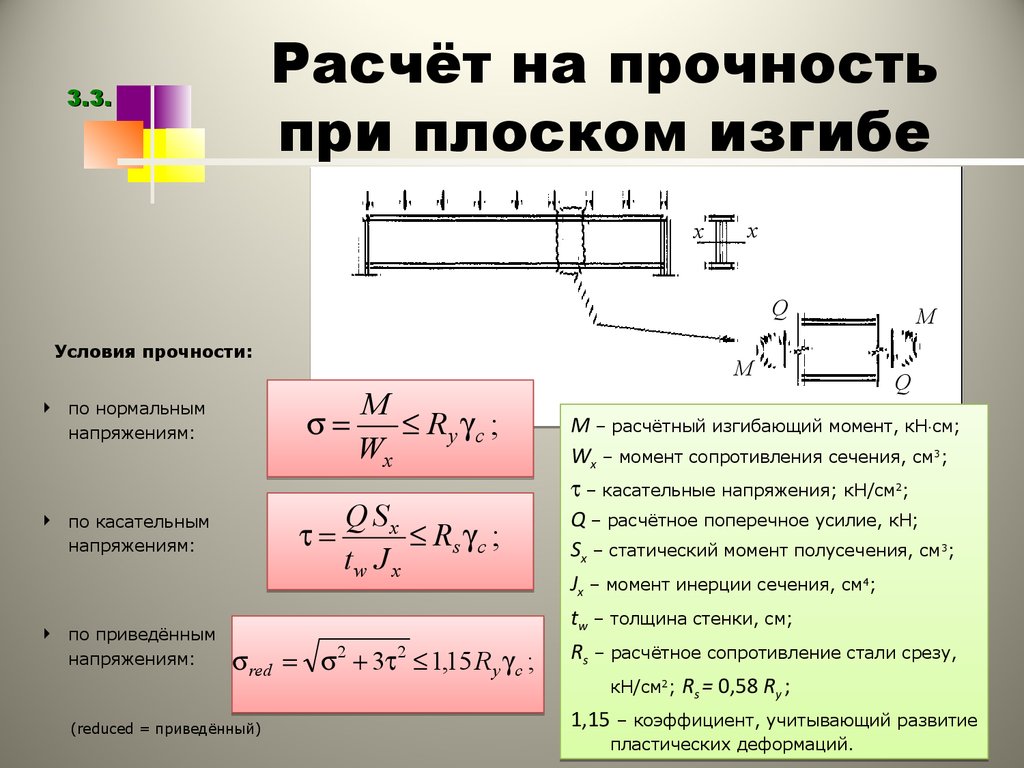
Расчет прогиба балки методом начальных параметров: учимся составлять формулы
В этой статье будем рассматривать универсальный метод расчёта прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера возьмём металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. А также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Кроме того, сечения поворачиваются на определенный угол. Эти две величины, для любого сечения, можно определить с помощью метода начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Расчет прогибов необходим для выполнения расчета на жесткость. Балка может считаться жесткой, только если расчётные значения прогибов не превышают допустимых значений. Если же условие жесткости не выполняется, то принимаются меры по ее повышению. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод, можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине).
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.
Учитывая эти свойства, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой же балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат.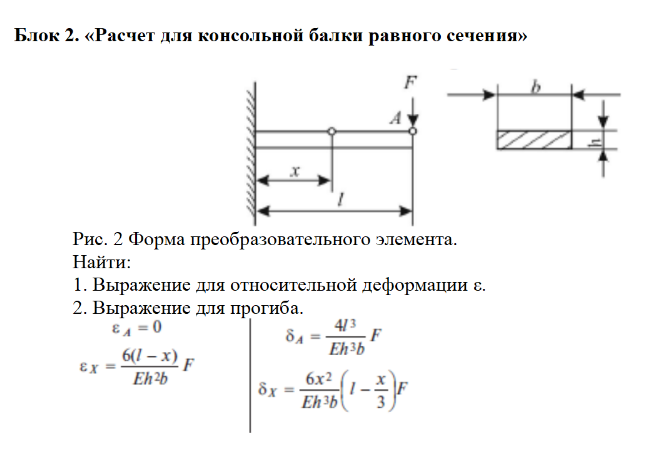
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим сечение в середине пролета – сечение C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала, из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Другие уроки
Основные формулы для расчета прогиба балки
Балка является основным элементом несущей конструкции сооружения. При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.
Балки в доме
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах. Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно. Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Содержание
- 1 Виды балок
- 1.1 Деревянные
- 1.2 Стальные
- 2 Прочность и жесткость балки
- 3 Расчет на жесткость
- 4 Расчет моментов инерции и сопротивления сечения
- 5 Определение максимальной нагрузки и прогиба
- 6 Особенности расчета на прогиб
- 7 Пример подсчета прогиба
Виды балок
Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению. Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Деревянные
Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.
Деревянные перекрытия
Для расчета максимального прогиба следует учитывать:
- Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.
- Форма поперечного сечения и другие геометрические характеристики.
- Различные виды нагрузки на материал.
Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.
Конструкции из древесины хвойных пород
Стальные
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.
При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.
Стальные перекрытия
Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:
- электросварка;
- заклепки;
- болты, винты и другие виды резьбовых соединений.
Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.
Для проведения расчета балки на прогиб может помочь видео:
Прочность и жесткость балки
Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали. Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.
Существует два основных метода расчета прочности и жесткости:
- Простой. При использовании данного метода применяется увеличительный коэффициент.
- Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.
Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.
Расчет балок на прогиб
Расчет на жесткость
Для расчета прочности балки на изгиб применяется формула:
Где:
M – максимальный момент, который возникает в балке;
Wn,min – момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.
Ry является расчетным сопротивлением стали при изгибе. Зависит от вида стали.
γc представляет собой коэффициент условий работы, который является табличной величиной.
Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:
- Составление расчетной схемы объекта.
- Расчет размеров балки и ее сечения.
- Вычисление максимальной нагрузки, которая воздействует на балку.
- Определение точки приложения максимальной нагрузки.
- Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.
- Вычисление значения жесткости или максимально прогиба балки.
Чтобы составить расчетную схему, потребуются такие данные:
- размеры балки, длину консолей и пролет между ними;
- размер и форму поперечного сечения;
- особенности нагрузки на конструкцию и точно ее приложения;
- материал и его свойства.
Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.
Расчет моментов инерции и сопротивления сечения
Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:
Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.
Определение максимальной нагрузки и прогиба
Для точного определения прогиба балки, лучше всего применять данную формулу:
Где:
q является равномерно-распределенной нагрузкой;
E – модуль упругости, который является табличной величиной;
l – длина;
I – момент инерции сечения.
Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.
Особенности расчета на прогиб
Расчет на прогиб проводится обязательно для любых перекрытий. Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:
- Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.

- Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.
- Варианты нагружения консольного стержня, который закреплен жестко.
- Действие на конструкцию сложной нагрузки.
Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.
Пример подсчета прогиба
Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:
- материал изготовления – древесина;
- плотность составляет 600 кг/м3;
- длина составляет 4 м;
- сечение материала составляет 150*200 мм;
- масса перекрывающих элементов составляет 60 кг/м²;
- максимальная нагрузка конструкции составляет 249 кг/м;
- упругость материала составляет 100 000 кгс/ м²;
- J равно 10 кг*м².

Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:
- вес одного метра балки;
- вес м2 перекрытия;
- расстояние, которое оставляется между балками;
- временная нагрузка;
- нагрузка от перегородок на перекрытие.
Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.
Если подставить все эти значения в формулу, то получится:
q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.
Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].
Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.
Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.
Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины. Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид. Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.
Расчет балки на изгиб, прогиб и прочность, включая калькулятор © Геостарт
Рубрика: Строительные материалы
Одной из важнейших задач для строителя считается расчет балки. Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение. В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.
Сегодня придумано немало средств, позволяющих решать данную задачу максимально быстро и точно. Наиболее удобными считаются онлайн-калькуляторы, которые за несколько секунд предоставляют необходимое решение. В данной статье мы разберем расчет балки на изгиб, прогиб, прочность с применением калькулятора.
Как рассчитывать балки на прочность
Расчет балки на прогиб , калькулятор для которого можно найти в интернете, можно произвести следующими методами:
- Рассчитать максимальную нагрузку, которую способна выдержать заданная схема;
- Подобрать сечение;
- Проверочный перерасчет по максимальным значениям напряжения.
Для наглядности следует рассмотреть общий принцип подбора сечения двутавра, расположенной на двух опорах. Загрузка происходит равномерно распределенной нагрузкой или сосредоточенной силой.
Последовательность действий
Для начала расчета балки на прогиб калькулятором необходимо определить точку, в которой будет максимальное значение момента. Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:
Все будет зависеть от того, какая схема представлена в задаче. Наиболее популярны следующие схемы:
- Заделка — шарнир;
- Заделка — заделка;
- Шарнир — шарнир;
- Заделка — свободный конец.
Остальные варианты являются в той или иной степени разновидностями вышеуказанных схем.
Как только вы нашли изгибающий момент, по таблице ищется момент сопротивления Wx указанного сечения по формулам, которые указываются в соответствующих таблицах. При делении максимального момента изгиба на момент сечения можно отыскать максимальное значение напряжения, которое необходимо сравнить с напряжением, которое максимально выдерживает определяемая конструкция.
Сравнение полученных напряжений с напряжением материалов
Онлайн-расчет балки на прочность сопровождается сравнением полученного значения напряжения в сечении с максимально возможным. Здесь необходимо смотреть на таблицу материалов, из которых производятся такие конструкции.
Если материал пластичен, то максимальное напряжение схемы будет равно пределу текучести материала. К таковым относят алюминий, сталь, иные металлы. Хрупкие же материалы по типу чугуна имеют максимальное значение напряжения, равное пределу прочности. Для каждого конкретного материала имеется свое максимальное значение, которое можно найти в таблицах в специальной литературе.
Пример расчета
Предположим, что нам надо проверить на прочность двутавр номер 10. Его длина 2 метра, он жестко заделан в стену, человек массой 90 килограммов решил повиснуть на двутавре. Порядок решения здесь следующий:
- Выбираем расчетную схему, в этом случае заделка — свободный конец;
- Максимальное значение находится в заделке, двутавр имеет на всей длине одинаковое сечение. Тогда P = m*g = 90*10=0,9 кН, M = P*I= 1,8 кН*м;
- Находим по таблице сортаментов для данного двутавра момент сопротивления;
- Затем находим максимальные напряжения в балке б = M/W = 1,8 / 0.
 0000397 = 45,34 Мпа;
0000397 = 45,34 Мпа; - Сравниваем с максимально допустимым напряжением, равным пределу текучести стали, из которой сделан двутавр. Так как 45,34 Мпа меньше 245 Мпа, то такой двутавр выдержит человека массой 90 килограммов.
Можно также решить и вторую задачу, связанной с нахождением максимальной массы человека, которую может выдержать данная балка. Здесь приравнивают значения предела текучести и напряжения в сечении балки, найти максимальный момент и затем наибольшую массу. Для более точного результата следует учитывать различные коэффициенты и брать двойной запас прочности.
Онлайн-калькуляторы
Расчет прогиба балки онлайн-калькулятором достаточно быстрый и точный. Здесь выбирается одна из схем, затем набираются соответствующие числовые значения и происходит расчет по всем необходимым параметрам.
Необходимо указать значения моментов, изгибающих сил, длин участков. Итогом станут эпюры моментов и сил. Решение данными программами достаточно точное и позволяет оперативно посчитать силы и моменты для балок на прочность, изгибы и прогибы.
Преимуществом подобных средств является большой набор схем для расчета, быстрота, точность, простота применения. Однако для уточнения полученного результата надо произвести самостоятельное письменное решение.
В заключение можно сказать следующее: расчет балки на прочность можно произвести как вручную, так и с применением онлайн-калькуляторов. Их можно комбинировать, использовав один из них для проверки другого метода. Рассчитать балку может понадобиться в разных случаях, особенно актуально это становится при строительстве. Только правильно рассчитанная балка позволит построить или реконструировать сооружение с тем условием, что оно прослужит длительное время.
Также данный расчет полезен для всех тех, кто учится или имеет дело с техническими науками, ибо прикладная механика является неотъемлемой частью программы любого технического вуза. Удачных расчетов на прочность!
|
автор Олейников Константин |
Геодезические измерения: виды, классификация и характеристики.
Пример заполнения страницы журнала измерения направлений
Геодезические сети, классификация и способы их развития
Калькулятор расчета
цен на кадастровые
работы
Расчитать
Электропроводка в доме своими руками: пошаговая схема
Подготовка к производству монтажных работ
Проектирование грунтовой заделки трубчатой моноопоры
Расчет уголка на прогиб
Главная » Разное » Расчет уголка на прогиб
Расчет уголка на прогиб и изгиб
Данный онлайн-калькулятор предназначен для того, чтобы Вы могли легко и быстро подобрать размеры уголка в зависимости от приходящейся на него нагрузки. Особенность его в том, что на одной странице возможно сравнение равнополочных (ГОСТ 8509-93) и неравнополочных (ГОСТ 8510-86) уголков. Последние, в свою очередь, можно подбирать в зависимости от расположения его в пространстве, т.е. в зависимости от того, как он будет ориентирован относительно нагрузки.
Содержание:
1. Калькулятор
2. Инструкция к калькулятору
Расчет уголков производится на изгиб и прогиб (по прочности и по деформациям) для следующих расчетных схем:
- Тип 1 — однопролетная шарнирно-опертая балка с равномерно распределенной нагрузкой. Пример: перемычка из уголка, которая несет плиты перекрытия и небольшую высоту кладки. (Подробнее о расчете перемычек из уголка см. этот калькулятор).
- Тип 2 — консольная балка с жесткой заделкой с равномерно распределенной нагрузкой. Пример: железобетонный козырек, выполненный с применением уголка, который жестко (с применением ребер жесткости, ограничивающих любые повороты) приварен к железобетонной стене.
- Тип 3 — однопролетная шарнирно-опертая балка с консолью с равномерно распределенной нагрузкой. Пример: тот же козырек, что и в предыдущей схеме, только здесь уголок с одной стороны заводится в стену, а с другой опирается на раскос (на рисунке синий).

- Тип 4 — однопролетная шарнирно-опертая балка с одной сосредоточенной силой. Пример: перемычка, на которую опирается одна балка перекрытия.
- Тип 5 — однопролетная шарнирно-опертая балка с двумя сосредоточенными силами. Пример: перемычка, на которую опираются две сосредоточенные силы.
- Тип 6 — консольная балка с одной сосредоточенной силой. Пример: козырек дома с кирпичной стенкой на нем, построенного в африканской республике (где никогда не выпадает снег) по фантазии африканского архитектора. Уголки этого козырька жестко заделаны в стену, так как описано во второй схеме.
Примечание: рассчитываемый уголок на рисунках с примерами окрашен в красный цвет.
КалькуляторРасчет прогиба балки онлайн калькулятор. Площадь поперечного сечения профиля. Расчет на прочность.
Описание
При выборе схемы с распределенной нагрузкой, приложенная «Нагрузка Q» указывается как относительная «килограмм на метр». Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Определяется она по формуле Q = [общяя нагрузка, кг]/[общая длина, м].
Использование калькулятора «Расчет прогиба балки онлайн» значительно сократит время и послужит залогом надежных инженерных конструкций.
Калькулятор разработан исключительно по формулам Сопромата и справочным данным для каждого типа материала и сечения балки. Расчет прогиба сечения является теоретическим, следовательно практические значения могут быть отличными от расчетных и зависеть от множества условий.
Однако значения полученные в данном калькуляторе будут невероятно полезными и послужат основой для расчета необходимой конструкции.
Для быстрого доступа к расчетам необходимого профиля добавьте калькулятор в избранное (CTRL+D на ПК или значек «звездочка» справа вверху браузера)
Пример расчета уголка, швеллера и двутавра на прогиб и изгиб
На данной странице представлен пример расчета швеллера. Что касается расчетов уголка и двутавра, то они производится аналогичным образом. Другими словами, данный пример является полезным для следующих калькуляторов:
Другими словами, данный пример является полезным для следующих калькуляторов:
В примере будут описаны несколько действий, которые должны выполняться последовательно.
Дано.
Район строительства — Нижний Новгород.
Расчетная схема — Тип 1.
Необходимо подобрать швеллер, который будет воспринимать нагрузку от снега.
Действие 1. Внесение исходных данных.
Расчетная нагрузка = 240 кг/м2 — так как город Н.Новгород находится в IV снеговом районе (в соответствии с табл. 10.1 и картой 1 СП 20.13330.2011 «Нагрузки и воздействия» [1]).
Fmax = 1/200 — так как пролет балки равен 5 м (пункт 2 табл. E1 [1]).
Расположение — по оси Х (швеллер воспринимает нагрузку вертикально).
Расчетное сопротивление Ry=210 МПа — берется как наихудший вариант для стали.
Действие 2. Выбор предполагающих номеров профилей.
Предположим, что мы рассматриваем два вида профилей: с параллельными гранями и с уклоном полок.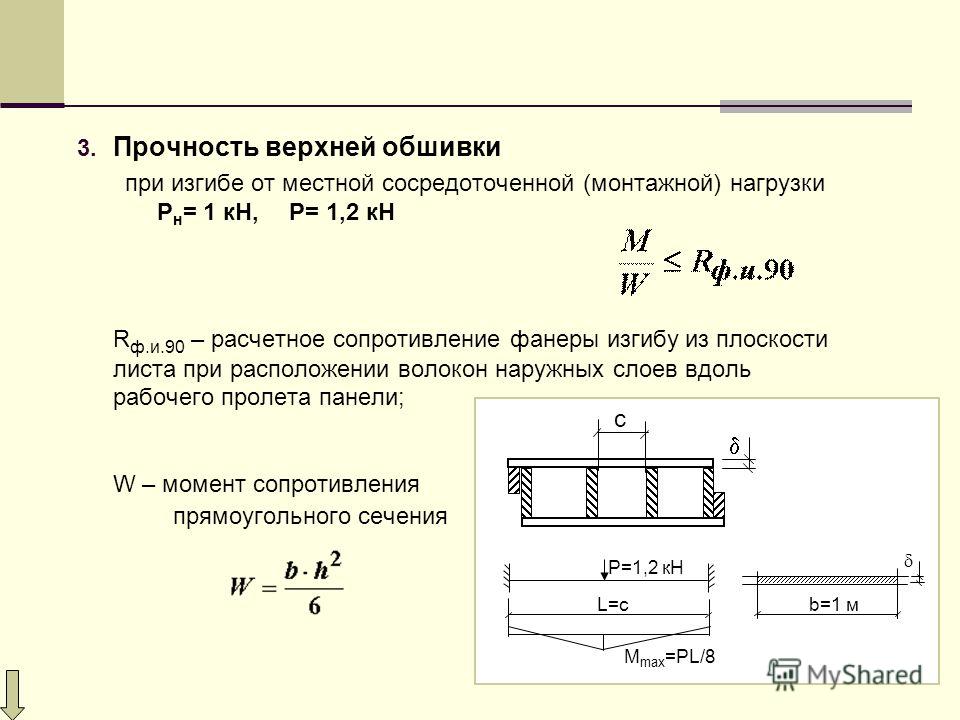 Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
Поэтому для первоначального расчета выбираются швеллеры размером 8П И 8У.
После произведенного расчета видно, что в графе «Запас» в том и другом случае стоят отрицательные значения. Это означает, что выбранные швеллеры не способны воспринимать приложенную на них нагрузку. Следовательно, необходимо выбирать профили большего размера.
Действие 3. Корректирующий расчет.
При увеличении профилей до 10П и 10У ситуация аналогичная. Но после того, как профили были увеличены до 12П и 12У в графах «Запас» появились положительные значения. Следовательно, в качестве балки перекрытия можно принять тот или иной профиль (имеется в виду 12П или 12У).
| Вид проката Уголок равнополочныйУголок неравнополочныйШвеллер с уклоном полокШвеллер с паралельными гранями полокДвутавр с уклоном полокДвутавр с паралел. гранями полок нормальныйДвутавр с паралел. | Вид и назначение стоек (колонн) Стойки и раскосы передаюшие реакции опорОсновные колонныВторостепенные колонны |
| Сталь С235 (Ст3кп2)Сталь С245 (Ст3пс5,Ст3сп5)Сталь С255 (СтГпс,Ст3Гсп)Сталь С285 (Ст3сп,Ст3Гпс,Ст3Гсп)Сталь С345 (12Г2С,09Г2С)Сталь С345К (10ХНДП)Сталь С375 (12Г2С)Сталь С390 (14Г2АФ)Сталь С390Д (14Г2АФД)Сталь С440 (16ГАФ)Сталь С590 (12Г2СМФ) |
| РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ: |
Размеры проката углового профиля оговариваются ГОСТ 8509-93 и ГОСТ 8510-86; швеллеров ГОСТ 8240-97; двутавров ГОСТ 26020-83; тавров – ТУ 14-2-685-86; (получаемых продольной разрезкой пополам горячекатаных двутавров с параллельными гранями полок по ГОСТ 26020-83).
При проектировании строительных конструкций необходимо принимать схемы, обеспечивающие прочность, устойчивость и пространственную неизменяемость сооружения в целом, а также его отдельных элементов при монтаже и эксплуатации.
Поэтому стойку,находящуюся под действием сжимающей её нагрузки необходимо проверять:
- на прочность;
- устойчивость;
- допустимую гибкость.
Согласно Актуализированной редакция СНиП II-23-81 (CП16.13330, 2011) расчет на прочность элементов из стали при центральном растяжении или сжатии силой P следует выполнять по формуле:
P/Fp*Ry*Yc <= 1, где
- P – действующая нагрузка,
- Fp – плошадь поперечного сечения стойки,
- Ry – расчётное сопротивление материала (стали стойки), выбирается по таблице В5 Приложения “В” того же СНиПа;
- Yc – коэффициент условий работы по таблице 1 СНиПа (0.9-1.1). В соответствии с примечанием к этой таблице (пункт 5) в калькуляторе принято Yc=1.

Проверку на устойчивость элементов сплошного сечения при центральном сжатии силой P следует выполнять по формуле:
P / Fi*Fp*Ry*Yc <= 1, где
Fi – коэффициент продольного изгиба центрально-сжатых элементов.
Коэффициент Fi введён в расчёт в качестве компенсации возможности некоторой не прямолинейности стойки, недостаточной жесткости её крепления и неточности в приложении нагрузки относительно оси стойки. Значение Fi зависит от марки стали и гибкости колонны и часто берётся из таблицы 72 СНиП II-23-81 1990г. исходя из гибкости стойки и расчётного сопротивления выбранной стали сжатию, растяжению и изгибу.
Это несколько упрощает и огрубляет расчёт, так как СНиП II-23-81* предусматривает специальные формулы для определения Fi. Гибкость (Lambda) – некоторая величина, характеризующая свойства рассматриваемого стержня в зависимости от его длины и параметров поперечного сечения, в частности радиуса инерции:
Lambda = Lr / i; здесь
- Lr – расчётная длина стержня;
- i – радиус инерции поперечного сечения стержня (стойки,колонны).

Радиус инерции сечения i равен корню квадратному из выражения I / Fp, где
- I – момент инерции сечения,
- Fp – его площадь.
Lr (расчётная длина) определяется как MuL;
здесь L- длина стойки,а Mu – коэфф., зависящий от схемы её крепления:
- “заделка-консоль”(свободный конец) – Mu = 2;
- “заделка-заделка”-Mu = 0.5;
- “заделка-шарнир” -Mu = 0.7;
- “шарнир-шарнир”-Mu=1.
Следует иметь ввиду,что при наличии у формы поперечного сечения 2-ух радиусов инерции (например, у швеллера, двутавра, тавра – относительно осей x-x и y-y), при расчёте Lambda используется меньший.
Уголки (как равнополочные так, и неравнополочные) имеют минимальный радиус инерции относительно оси z-z, который и используется в расчётах. Кроме того,сама Lambda (гибкость стойки), рассчитанная по формуле Lambda=Lr/i не должна превышать 220-ти в соответствии с табл. 19.СНиП II-23-81*; там же содержатся ограничения на предельную гибкость центрально-сжатых стержней.
Для их использования необходимо сделать выбор в таблице калькулятора “Вид, назначение стоек…”. Предельная гибкость стоек, кроме их геометрических параметров, зависит также от коэфф. продольного изгиба (Fi), действующей нагрузки(P), расчётного сопротивления материала стойки (Ry) и условий её работы (Yc).
ПРИМЕЧАНИЕ. Размеры выбранного швеллера, двутавра и тавра указываются в строке “РАЗМЕРЫ ВЫБРАННОГО ПРОФИЛЯ”; размеры полок уголков-в их таблицах; толщина уголков выбирается отдельно после появления возможных толщин выбранного номера уголка в вышеуказанной строке.
Расчет металлической балки на прогиб: учимся составлять формулы
Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.
В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.
Что такое прогиб балки?
Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).
Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.
ν-прогиб сечения C; θ-угол поворота сечения C.
Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.
Метод начальных параметров
Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)
Под начальными параметрами понимаются уже известные перемещения:
- в опорах прогибы равны нулю;
- в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.
Расчет прогибов балки
Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:
Реакции опор
Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.
Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:
Система координат
Далее вводим систему координат, с началом в левой части балки (точка А):
Распределенная нагрузка
Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.
Если бы нагрузка была приложена вот таким способом:
То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:
Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.
Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:
Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:
\[ { V }_{ A }=0\quad при\quad x=0 \]
\[ { V }_{ B }=0\quad при\quad x=8м \]
Записываем уравнение метода начальных параметров для сечения C:
\[ E{ I }_{ z }{ V }_{ C }=… \]
Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:
\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]
Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:
\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]
Учет внешней нагрузки
И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C. { 4 } } =-2см \]
{ 4 } } =-2см \]
Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.
На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).
Расчёт балки, рамы бесплатно онлайн
Лимит расчётов:
|
Добро пожаловать! Данный онлайн-калькулятор предназначен для расчёта балки или рамы и
позволит построить эпюры внутренних силовых факторов (изгибающих моментов, поперечных и
осевых или продольных сил), рассчитать реакции в опорах. В итоге формируется отчёт с
готовым решением. |
|
| КАЛЬКУЛЯТОРЫ КОМПРЕССИОННЫХ ЧЛЕНОВ | |
| Калькулятор | Определение |
| Расчет элементов сжатия (продольного изгиба) | |
| ПРОСТО ОПОРНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Балка с простой опорой и множественными точечными / распределенными нагрузками и моментами | |
| Балка с простой опорой и сосредоточенной нагрузкой в любой точке | |
| Просто поддерживаемая балка с двумя Точечные нагрузки | |
| Балка с простой опорой и частично распределенной промежуточной нагрузкой | |
| Балка с простой опорой и двумя частично распределенными промежуточными нагрузками | |
| Балка с простой опорой и моментом | |
| Балка с простой опорой и двумя моментами | |
| КАНТИЛЬНАЯ БАЛКА КАЛЬКУЛЯТОРЫ ПРОГИБА | |
| Консольная балка с множественными точечными / распределенными нагрузками и моментами | |
| Консольная балка с одинарной нагрузкой | |
| Распределенная нагрузка консольной балки | |
.
% PDF-1.6 % 104 0 объект > endobj xref 104 52 0000000016 00000 н. 0000002216 00000 н. 0000002377 00000 н. 0000002421 00000 н. 0000002547 00000 н. 0000002902 00000 н. 0000003045 00000 н. 0000003182 00000 п. 0000003324 00000 н. 0000003351 00000 п. 0000003418 00000 н. 0000003955 00000 н. 0000004444 00000 н. 0000004471 00000 н. 0000005149 00000 п. 0000005176 00000 п. 0000005771 00000 п. 0000006307 00000 н. 0000006764 00000 н. 0000007200 00000 н. 0000007333 00000 н. 0000007360 00000 п. 0000007733 00000 н. 0000008258 00000 н. 0000008758 00000 н. 0000009241 00000 п. 0000009643 00000 п. 0000009713 00000 н. 0000009908 00000 н. 0000046337 00000 п. 0000046548 00000 п. 0000046941 00000 п. 0000047011 00000 п. 0000047272 00000 п. 0000106092 00000 н. 0000106298 00000 п. 0000106421 00000 н. 0000117145 00000 н. 0000117340 00000 н. 0000117547 00000 н. 0000117617 00000 н. 0000117799 00000 н. 0000156281 00000 н. 0000156483 00000 н. 0000156859 00000 н. 0000156929 00000 н. 0000157517 00000 н. 0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
0000157588 00000 н. 0000157704 00000 н. 0000157824 00000 н. 0000157913 00000 н. 0000001336 00000 н. трейлер ] / Назад 1604346 >> startxref 0 %% EOF 155 0 объект > поток hb«`b«ce`c«`f @
.
Калькулятор для инженеров — момент инерции площади, центр тяжести, модуль упругости углового сечения
Дополнительные ссылки
Викторина по гражданскому строительству
Проверьте свои знания по различным темам гражданского строительства
Статически неопределенные структуры
Определение и методы решения
Решенных примеров
Расчет сил стержня фермы
методом соединений и методом секций
Сила сдвига и изгибающий момент
Иллюстрированные решенные примеры для построения диаграмм силы сдвига и изгибающего момента
Наклон и прогиб балки и фермы
Иллюстрированные решенные примеры для определения наклона и прогиба балки и фермы
Решение неопределенных конструкций
Отклонение откоса, распределение момента и т. Д.
Д.
Балка железобетонная
Решенные примеры для определения прочности и других параметров
Другие полезные ссылки
Небоскребы мира
Высокие здания мира
Профиль инженеров-строителей
Познакомьтесь с выдающимися инженерами-строителями
Профессиональные общества
Международные профессиональные общества инженеров-строителей
Расскажите о нас друзьям
Поищите на нашем сайте больше…
.
Что такое прогиб? | Программное обеспечение SkyCiv Cloud для структурного анализа
перейти к содержанию
Искать:
- Программное обеспечение
- SkyCiv Structural 3D: Программное обеспечение для структурного анализа
- SkyCiv Beam
- SkyCiv Section Builder
- SkyCiv Connection Design
- SkyCiv RC Design
- SkyCiv Foundation Design
- SkyCiv8 Модуль нагрузки на ветер SkyCiv8 Интеграции и надстройки
.
Угол возвышения Солнца (на год) Калькулятор
- Цель использования
- различные солнечные приложения, конечно, но в основном просто для того, чтобы быть проинформированным о моем физическом окружении.
- Комментарий / запрос
- Я мог бы быть более поучительным, если бы время наблюдения имело вариант местного кажущегося полудня, когда солнце находится на самом высоком уровне. Поскольку вы запрашиваете долготу наблюдателя, это должно быть просто.
[1] 2020/12/20 04:17 Мужчина / 60 лет и старше / Пенсионер / Полезно /
- Цель использования
- Расчет максимальной высоты дерева относительно расположения солнечных панелей.
- Комментарий / запрос
- Вычисление корректировки времени от GMT с использованием долготы было бы полезным и простым.
[2] 2020/12/07 03:31 Мужчина / 60 лет и старше / Инженер / Очень /
- Цель использования
- Размещение солнечных панелей
- Комментарий / запрос
- Arigatou gozaimasu!
[3] 2020/12/07 03:25 Мужской / 40-летний уровень / Средняя школа / Университет / аспирант / Очень /
- Цель использования
- Я хочу построить пассивную теплицу на севере ( Северный Квебек), и я хотел знать, под каким углом поставить стену, чтобы максимально эффективно использовать солнце в зимние месяцы
[4] 2020/12/01 22:20 Мужчина / Уровень 50 лет / Офисный работник / Государственный служащий / Полезный /
- Цель использования
- Определение того, в какое время года, в какое время суток и в каком направлении можно видеть радугу в моем местоположении (солнце должно быть ниже 42 градусов над горизонтом).

- Комментарий / запрос
- Я знаю, как узнать мою широту и долготу, поэтому мог бы использовать этот сайт, но если бы была возможность печатать в ближайшем городе, даже если это было бы менее точно, гораздо больше людей уметь его использовать.
[5] 2020/11/16 15:41 Женщина / 60 лет или старше / Пенсионер / Полезно /
- Цель использования
- Анализ выходной мощности солнечной батареи в зависимости от высоты Солнца
- Комментарий / Запрос
- Отличный калькулятор
[6] 2020/11/05 00:16 Мужчина / 60 лет и старше / Учитель / Исследователь / Очень /
- Цель использования
- Проверка тени на крыше для установка PV
- Отчет об ошибке
- По сравнению с диаграммой, углы которой указаны в таблице, азимут и углы возвышения не имеют никакого смысла.Как может полуденное солнце находиться только по азимуту (азимуту) между 39 и 67 градусами? Я мог бы понять эти углы, если бы они были даны от восточной оси.
 Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
Тогда азимут будет в районе 129–157 градусов, то есть примерно в юго-восточном направлении. Кроме того, как солнце может быть выше в зимнее время, чем в летние месяцы? Возможно, если бы эти углы были измерены от вертикальной оси (Зинет), они имели бы больше смысла. Извините, но, на мой взгляд, приведенная здесь информация неверна.
[7] 2020/11/04 20:42 Мужчина / 60 лет и старше / Инженер / Совсем нет /
- Цель использования
- Я фотограф, выясняю положение солнца в определенные дни в месяц, чтобы я мог делать красивые фотографии в «контролируемой» обстановке.
- Комментарий / запрос
- Спасибо. Продолжайте в том же духе!
[8] 2020/11/04 18:11 Женский / 50-летний уровень / Самозанятые / Полезные /
- Цель использования
- ИСПОЛЬЗОВАНИЕ СОЛНЕЧНОЙ ЭНЕРГИИ
- Комментарий / запрос
- ДУМАЯ О СОЛНЦЕ ПАНЕЛИ
[9] 2020/10/20 04:13 Мужчина / 60 лет и старше / Пенсионер / Очень /
- Цель использования
- Самообразование
[10] 2020/10/19 18:32 Мужчина / 60 лет и старше / Пенсионер / Очень /
.
Расчет металлической балки перекрытия на прогиб и на жесткость
/в Плита перекрытия /от adminМеталлические балки двутавровые
Кроме повсеместно ведущегося строительства многоэтажных зданий с большим числом квартир, широкое распространение получило сооружение частных домов, причем не только небольших одноэтажных, но и довольно крупных, с двумя и более этажами, иногда и с мансардой наверху или обитаемым чердаком. Для таких домов уже не подходит каркасный метод; материалом часто служит, вместо дерева, кирпич или железобетон. Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.
Возведение крупных частных домов должно вестись по всем правилам строительной науки, так как ошибки при проектировании или воплощении проекта могут привести к нежелательным последствиям.
Если строящийся дом представляет собой капитальное здание – из бетона, кирпича, шлакоблока, то для потолочных перекрытий, межэтажных и чердачных, целесообразно применить железобетонные плиты. Наиболее подходящий тип каркаса, способный выдержать вес таких перекрытий, – это каркас, элементом которого является металлическая балка двутаврового профиля.
Именно этот вид проката, установленный своей стенкой вертикально, обладает наибольшей несущей способностью. Естественно, фундамент и стены дома при этом должны быть достаточной прочности, чтобы выдерживать дополнительный вес от 0,5 до 1 тонны – столько металла, в зависимости от количества балок и номера профиля может понадобиться для потолочного перекрытия.
Чтобы избежать лишних затрат и лишнего веса каркаса потолка, а также не допустить обрушения или значительного прогиба балок, необходимо заранее рассчитать их параметры и по результатам расчета подобрать нужный прокат. Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.
Расчет сводится к вычислению следующих величин: требуемого момента сопротивления и минимального момента инерции сечения балки, а исходя из последнего – максимального относительного прогиба.
Примечание
Расчет ведется по двум характеристикам – на прочность и на жесткость. По полученным значениям момента сопротивления и момента инерции в таблицах ГОСТ находят требуемый номер проката.
Исходные данные для расчетов
Для каркаса потолочных перекрытий малогабаритных частных домов обычно используется двутавр 10 – 20 номеров. Характеристики этих профилей приводятся в ГОСТ 8239-72 – их линейные размеры, площади сечения, максимальные моменты сопротивления по вертикали Wy и минимальные моменты инерции Jy.
Необходимо знать тип плит, которые будут опираться на балочный каркас, а также размеры несущего периметра дома. Можно применить пустотные железобетонные плиты ПК-12-10-8 (1180 х 990 мм, масса 380 кг), а размеры дома взять 4,5 х 6 м. Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.
Балки укладываются вдоль короткой стены; шаг укладки при таком размере плит равен 1000 мм (стыки плит совпадают с продольными осями балок, при минимальном зазоре 1 см). Это потребуется для расчета распределенной нагрузки, и исходя из нее – линейной нагрузки на балку, вес самой балки по сравнению с распределенной нагрузкой мал, и при вычислении линейной нагрузки им можно пренебречь.
Распределенная нагрузка при таком типе плит будет равна 325 кгс / м2. К этому надо добавить нагрузку возможных перегородок на верхней стороне перекрытия (75 кгс / м2) и возможную временную нагрузку (200 кгс / м2). В итоге нагрузка, распределенная по площади:
Q = 325 + 75 + 200 = 600 кгс / м2,
а линейная нагрузка
q = Q * p = 600 кгс / м = 6 кгс / см.
Эта величина используется в дальнейших расчетах.
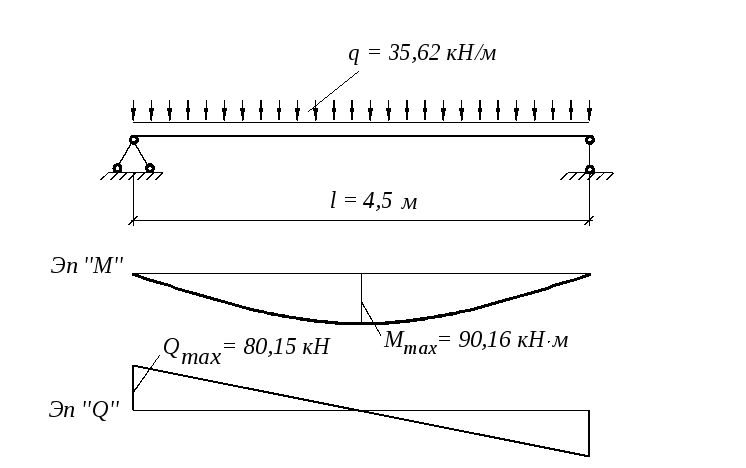
Расчет на прогиб
Изгибающий момент для каждой балки вычисляется, исходя из величины линейной нагрузки q, шага укладки балок p и длины перекрываемого пролета L. Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).
Так как балки укладываются вдоль короткой стороны, то L = 4,5 м = 450 см (конечно, сами балки длиннее – около 5 м, так как опираются на стены, но шарнирными опорами для них служат именно внутренние края стен).
Искомая величина момента, в таком случае:
My = (q * L2) / 8 = 6 * 4502 / 8 = 151875 кгс * см.
Максимальный момент сопротивления сечения балки можно рассчитать, разделив изгибающий момент на расчетное сопротивление стали – например, марки С235, равное 2150 кгс / см2:
Wy = 151875 / 2150 = 70,6 см3.
Это полученное значение надо сравнить с величиной момента сопротивления сечения двутавровой балки. Из таблицы ГОСТ 8239-72 видно, что вычисленный показатель примерно соответствует (с запасом) моменту сопротивления для профиля 14 (81,7 см3). Следовательно, этот номер проката будет удовлетворять требованиям к прочности балок.
Расчет на жесткость
Жесткость балок характеризуется максимальной величиной прогиба при заданных исходных параметрах. В случае распределенной нагрузки прогиб вычисляется по формуле:
В случае распределенной нагрузки прогиб вычисляется по формуле:
f = 5 * q * L4 / (384 * E * Jy), где
- q – линейная нагрузка на балку;
- L – длина пролета;
- E – модуль упругости материала, для стали С235 равный 2,1 * 106 кгс / см2;
- Jy – минимальный момент инерции для данного профиля.
Для принятых ранее исходных данных, с учетом того, что из расчета на прочность наиболее подходящим профилем оказался № 14, для которого Jy, по табличным значениям ГОСТ, равен 572 см4, можно получить:
f = 2,6 см,
а в относительной мере, с учетом того, что длина пролета 450 см – 1 / 172. Это превышает максимально допустимый прогиб, принятый равным 1 / 250.
Поэтому расчет приходится повторить и вычислить прогиб для другого номера проката. Для № 16, у которого момент инерции равен 873 см4, абсолютный прогиб получается 1,74 см, а относительный – 1 / 256, что является приемлемым.
Метод начальных параметров
В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.
Теория по методу начальных параметров
Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым охватим всю теоретическую часть по максимуму.
Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:
Выбор базы и системы координат
Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки.
Базу обозначим буквой O и проведем через нее систему координат:
Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях — упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом использования метода начальных параметров (МНП).
Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях — упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом использования метода начальных параметров (МНП).
Универсальное уравнение МНП
После введения базы, системы координат и обозначения расстояний а, б, в, г записываем универсальное уравнение МНП, с помощью которого, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки):
Теперь поговорим об этой формуле, проанализируем, так сказать:
- E – модуль упругости;
- I – момент инерции;
- VK – прогиб сечения K;
- VO – прогиб сечения O;
- θO – угол поворота сечения О.
Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.
Итак, изучаем эту формулу слева направо. В левой части уравнения обознается искомый прогиб, в нашем случае VK, который дополнительно умножается на жесткость балки — EI:
В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIVO:
Также всегда учитывается угол поворота сечения, которое совпадает с выбранной базой. Причем произведение EIθO всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.
Следующие компоненты этого уравнения учитывают всю нагрузку, которая находится слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.
Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:
В случае с моментами скобка возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен по часовой стрелке и отрицательным, соответственно, если против часовой стрелки:
Знак у момента будет положительный, когда он направлен по часовой стрелке и отрицательным, соответственно, если против часовой стрелки:
Учет распределенной нагрузки
Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки. Но так как, конец распределенной нагрузки совпадает с сечением, прогиб которого мы хотим вычислить, в этом случае, в уравнении учитывается только ее начало.
Причем важно, даже если бы в этом сечении была сила или момент, их бы также не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.
Для распределенной нагрузки скобка возводится в 4 степень и делится на 24. А правило знаков такое же, как и для сосредоточенных сил.
Граничные условия
Чтобы решить уравнение, нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: VK, VO и θO. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и никаких поворотов, то есть VO = 0 и θO = 0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.
Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и никаких поворотов, то есть VO = 0 и θO = 0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.
Если бы балка была закреплена с помощью шарнирно-подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.
Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок, помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.
Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:
Пример расчета прогиба балки
Для закрепления пройденного материала предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок.
Условие задачи
Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·105 МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см4). Рассчитывать будем прогиб свободного торца, находящегося слева.
Подготовительный этап
Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:
В методе начальных параметров есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае рассматриваемый метод будет работать.
Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае рассматриваемый метод будет работать.
В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м от базы и заканчивается на 4 м. В таком случае нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно направленной нагрузкой. Тем самым в расчете прогибов будет уже учитываться 2 распределенные нагрузки:
Расчет прогиба
Записываем граничные условия для заданной расчетной схемы:
VA = 0 при x = 6м
θA = 0 при x = 6м
Напомню, что нас, в этом примере интересует прогиб сечения O (VO). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:
В полученном уравнении у нас содержится две неизвестные величины: искомый прогиб VO и угол поворота этого сечения — θO:
Но чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:
Из второго уравнения найдем угол поворота:
После чего рассчитываем искомый прогиб:
Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.
Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.
Таблицы отклонения балки | МеханиКальк
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
В таблицах ниже приведены уравнения для прогиба, наклона, сдвига и момента вдоль прямых балок для различных условий на концах и нагрузок. Вы можете найти исчерпывающие таблицы в таких справочниках, как Gere, Lindeburg и Shigley. Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Для получения информации об отклонении балки см. наш справочник по напряжениям и отклонениям в балках.
Консольные балки
| Консоль, торцевая нагрузка |
|
|||||||||||||||||||
| Консоль, промежуточная нагрузка |
|
|||||||||||||||||||
| Консоль, равномерно распределенная нагрузка |
|
|||||||||||||||||||
| Консоль, треугольная распределенная нагрузка |
|
|||||||||||||||||||
| Консоль, Конечный момент |
|
Просто поддерживаемые балки
| Просто поддерживаемые, промежуточная нагрузка |
Для a ≥ b:
|
|||||||||||||||||||||
| Простая опора, центральная нагрузка |
|
|||||||||||||||||||||
| Просто поддерживаемый, 2 нагрузки на равном расстоянии от опор |
|
|||||||||||||||||||||
| Простая опора, равномерная распределенная нагрузка |
|
|||||||||||||||||||||
| Простая опора, момент на каждой опоре |
|
|||||||||||||||||||||
| Простая опора, момент в одну опору |
|
|||||||||||||||||||||
| Простая опора, центральный момент |
|
Фиксированные-Фиксированные балки
| Фиксированные-Фиксированные, центральная нагрузка |
|
|||||||||||||||
| Фиксированная-фиксированная, равномерная распределенная нагрузка |
|
Ознакомьтесь с нашим калькулятором луча, основанным на методологии, описанной здесь.
- Расчет напряжений и прогибов в прямых балках
- Построение диаграмм сдвига и моментов
- Можно указать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
- Будинас-Нисбетт, «Машиностроение Шигли», 8-е изд.
- Гир, Джеймс М., «Механика материалов», 6-е изд.
- Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена PE», 13-е изд.
11 Таблицы формул прогиба балки |
11 Таблицы формул прогиба балки
- 1 мая 2021 г.
Формулы прогиба балки
Содержание
Уравнения изгиба и прогиба
При проектировании балок (бетонных, стальных или деревянных) способность к изгибу и сдвигу проверяется в соответствии с применяемой теорией изгиба.
Приложенная сила заставляет элемент изгибаться и подвергаться изгибающим моментам, а концы реагируют на сдвигающие нагрузки.
Профиль изгиба и сдвига балки/элемента зависит от типа опоры балки (т. е. штифтовые, фиксированные и свободные концы).
Формула упругого прогиба балки
\(\frac{M}{I}=\frac{\sigma}{y}=\frac{E}{R}\)
- M — приложенный момент
- I – момент инерции сечения
- \(\sigma\) – напряжение изгиба волокна 92\))
- W — общая нагрузка (ВД х длина)
- w — ВД (усилие на единицу длины, кН/м)
В таблицах ниже приведены формулы прогиба балки для свободно опертой, неподвижной балки и консолей для различных конечных условий и нагрузок.
Таблицы формул прогиба балки
Прогиб балки с простой опорой и формула
Балка с простой опорой при одноточечной нагрузке – (2 штыревых соединения на каждом конце) 93}{48EI}\)
Сила сдвига и реакция:
\(R_A=R_B=\frac{P}{2}\)
Балки с простой опорой под одной точечной нагрузкой, расположенной в любом месте балки – (2 штыревых соединения на каждом конце)
Балка с простой опорой – точечная нагрузка
Момент:
\(M_{C} = \frac {Pab}{L}\)
Уравнение отклонения балки:
, когда a>b,
\(\delta_x = \frac{Pab(L+b)}{27EIL} \sqrt{3a(L+ б)}\)
в \(x=\sqrt{\frac{a(L+b)}{3}}\) from A
Сила сдвига и реакция:
\(R_A= \frac{Pb} {L}\)
\(R_B= \frac{Pa}{L}\)
Простые опорные балки под 2-точечной нагрузкой – (2 штыревых соединения на каждом конце)
Просто поддерживаемая балка – 2-точечная нагрузка
Момент:
\(M_{C} = Pa\)
\ (M = \frac{PL}{3}\)
Уравнение прогиба балки:
, когда a>b, 94}{384EI}\)
Сила сдвига и реакция:
\(R_A = R_B \frac{wL}{2}\)
\(R_A = R_B \frac{wL}{2} \)
Фиксированный конец и штифт с UDL – (1 фиксированный конец и штифтовое соединение на каждом конце).
Примечание – штифтовые опоры не принимают моментов, поэтому изгиб у опоры равен нулю.
Примечание. Неподвижные опоры сопротивляются моменту, поэтому они создают момент
Фиксированная балка и простая опора — UDL93}{8EI}
Сила сдвига и реакция:
\(R_A = W\)
Лучшие сообщения
О НАС
Моя цель состоит в том, чтобы предоставить студентам университетов, изучающим инженерный курс, эффективный инструмент для проверки знаний.
СОЦИАЛЬНАЯ
Инстаграм Facebook-f Linkedin-in
Лучшее руководство по определению прогиба в балках с переменным поперечным сечением — Инженер-наставник
Таблицы балок дают информацию и предполагают, что прогиб Расчет основан на постоянном поперечном сечении. Итак, что мы делаем, если наш луч имеет крест сечение, изменяющееся по длине балки?
Для определения величины отклонения в
балка переменного сечения, необходимо интегрировать формулу прогиба балки
с моментом инерции, являющимся переменной по отношению к длине и
применять граничные условия. Луч
формула отклонения: v’’ = M(x)/[E*I(x)].
Луч
формула отклонения: v’’ = M(x)/[E*I(x)].
Непрерывная или дискретная – Существует два типа секций балки: непрерывная и дискретная. Большинство балок представляют собой непрерывные балки и имеют либо постоянное сечение, либо сечение, которое постепенно изменяется по длине балки. Балки крыши в больших стальных зданиях являются отличным примером непрерывной переменной балки. Балка относительно короткая по высоте на концах и очень высокая в середине.
Дискретные лучи являются лучами которые имеют внезапные разрывы в разрезе. Хотите верьте, хотите нет, иногда это проще для расчета, потому что дискретные сечения обычно постоянны, что приводит к более легкий расчет.
Формула отклонения луча является универсальной
формула, которая позволяет настраивать несколько нагрузок и балок
разделы. Я предупрежу вас, что чем больше
точным должен быть ваш расчет, тем сложнее будет сделать математику. Упрощение здесь сэкономит много времени
и усилие. Как упоминалось перед
формула:
Упрощение здесь сэкономит много времени
и усилие. Как упоминалось перед
формула:
v’’ = M(x)/[E*I(x)]
ускорение отклонения), M — момент, который обычно является функцией положение по длине балки, х. E — модуль упругости, I — момент инерции площади. луч. Все табличные лучи будут считать это константой, и поэтому ни одна из формул отклонения может быть использован.
Теперь, когда мы проинтегрируем приведенное выше уравнение, мы получим выполнение неопределенного интеграла, что означает, что мы должны добавить константу, C n, к многочлену каждый раз, когда мы интегрируем. Поскольку мы будем интегрировать уравнение два раза, мы получим две константы. Если у нас есть дискретный случае у нас будет два или более уравнений.
Граничные условия
требования, которым должна соответствовать формула отклонения луча, когда она
находится в окончательном виде. Окончательная форма
приходит только тогда, когда мы используем граничные условия для решения констант
образован неопределенным интегралом. Общий
случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или
наклон консольной балки должен быть 0 радиан.
Общий
случаи, когда концы свободно опертой балки должны быть 0 (дюймы, мм и т. д.) или
наклон консольной балки должен быть 0 радиан.
В этой статье мы рассмотрим три примера обычных балок переменного сечения.
- Двухсекционная консольная балка с точечной нагрузкой на конце.
- Двухсекционная свободно опертая балка под собственным весом.
- Постоянно меняющаяся неразрезная свободно опертая балка с постоянной распределенной нагрузкой.
https://mentoredengineer.com/the-best-guide-to-solving-statically-indeterminate-beams/
Пример 1: Двухсекционная консольная балка с точечной нагрузкой на конце. 94.
Теперь определим момент и дважды проинтегрируем уравнение прогиба балки, каждый раз добавляя переменную для неопределенного интеграла. Я выбрал, чтобы моя система координат (переменная x) начиналась с основания. Это немного усложняет интегрирование, но переменные C 1 и C 2 взаимно компенсируются из-за граничных условий 1 и 2. Через секунду вы увидите.
Через секунду вы увидите.
Мне нужно только сделать интеграцию для одного из разделов, а затем изменить I 1 до I 2 в уравнениях. Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы положение и наклон на фиксированном конце балки были равны 0 дюймов и 0 радиан. Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом положении должны быть одинаковыми.
Найдем граничные условия 1 и 2
Как упоминалось выше, я предвидел, что переменные C1 и C2 будет равно 0, если я решу, чтобы система координат начиналась с база.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы
чтобы мы могли убедиться, что v 1 = v 2 и s 1 =
s 2 на 50 дюймов. Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Это подтверждает
что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены. Как видите, линии пересекаются и касаются друг друга на расстоянии 50 дюймов. Кроме того, v 1 не имеет отклонения или наклона в основании.
Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как вы можете видеть, отклонение быстро увеличивается после 50 дюймов от основания. Это ясно видно на обоих графиках. 94.
Теперь определим момент и проинтегрируем уравнение отклонения луча дважды каждый раз добавляя переменную. Я выбрал две системы координат. Координата x идет слева направо и координата y идет справа налево. Они связаны:
г = L-x
Я выбрал эту систему координат так, что C 2
и C 4 сократятся, когда мы найдем граничные условия 1 и 2. Это также упрощает математику.
чрезвычайно. Вы увидите через секунду.
Это также упрощает математику.
чрезвычайно. Вы увидите через секунду.
Мне нужно только выполнить интегрирование для одного из разделов, а затем изменить I 1 на I 2 и w 1 на w 2 в уравнениях. В уравнениях правого сечения я также заменю «у» на «х». Я также сохранил переменную «v» как отклонение балки, но изменил первую производную отклонения на переменную «s», чтобы указать наклон. Я также указал переменные.
Теперь, когда проблема определена, давайте настроим граничные условия. Нам нужно, чтобы концы балки имели отклонение 0 дюймов (BC 1 и 2). Также нам потребуются еще два граничных условия на стыке отрезков. Наклон и положение в этом месте должны быть одинаковыми в месте соединения сегментов.
Решим для граничных условий 1 и 2
Как упоминалось выше, я предвидел, что переменные C 2 и C 4 будет равно 0, когда я выберу координату запуск системы на базе.
Далее мы рассмотрим граничные условия 3 и 4. Они немного сложнее.
Они немного сложнее.
Обратите внимание на галочку, которую я поставил в блоке «Найти», чтобы чтобы мы могли убедиться, что v 1 = v 2 и s 1 = с 2 на высоте 200 дюймов. Это подтверждает что положение и наклон будут непрерывными в этой точке.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем четыре граничных условия, которые должны быть выполнены.
О-о, что случилось!?
Линии определенно пересекаются на расстоянии 200 дюймов, и каждый конец имеет 0 дюймов
отклонение, но они не касаются в месте пересечения. Я не только иллюстрирую силу
построение графика решения для точности, а также демонстрация того, что использование двух
различные системы координат представляли собой проблему.
Согласно уравнениям, склоны приближаются к месту
узел на нисходящем склоне равный по величине. Однако сделать эту работу одним из склонов
на самом деле должен подойти. Мы можем
устраните эту проблему, внеся одно небольшое изменение.
Мы можем
устраните эту проблему, внеся одно небольшое изменение.
с 1 = -s 2
Давайте внесем это изменение и приступим к решению.
Да, намного лучше! Наконец, мы объединим два графика вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как и ожидалось, более длинная жесткая секция меньше прогибается.
Как рассчитать данные балки, если вашего случая нет в таблице
Пример 3: постоянно меняющаяся, непрерывная, свободно опертая балка с постоянной распределенной нагрузкой.
Эта задача состоит из свободно опертой стальной балки длиной 300 дюймов с распределенной нагрузкой 1000 фунтов/дюйм поперек балки. Секция начинается с высоты 10 дюймов и линейно увеличивается к центру, где достигает высоты 24 дюймов. Затем он сужается до 10 дюймов.
Чтобы определить, как изменяется момент инерции относительно x, мы будем моделировать в Solidworks и брать сечения через каждые 30 дюймов. Мы сведем эти данные в таблицу и подгоним к ним строку.
Мы сведем эти данные в таблицу и подгоним к ним строку.
Вы, наверное, заметили, что я составил таблицу только для значений от 0 до 150 дюймов. Это потому, что я собираюсь использовать симметрию, чтобы упростить эту сложную задачу. Мы можем использовать симметрию, потому что и нагрузка, и сечение балки симметричны относительно середины балки. Из-за симметрии нам нужно, чтобы конечная точка имела отклонение 0 дюймов, а наклон в середине луча был 0 градусов. Затем мы можем отразить это, чтобы получить непрерывное отклонение луча. В этом случае у нас будет координата x слева направо.
Здесь можно увидеть, что рассчитанные значения I(x) близко соответствуют значениям, указанным в таблице выше. Я назвал вторую производную от положения «а1» (ускорение). Как видите, с верхней и нижней частью, имеющей переменную «x», будет очень весело интегрировать это. Итак, есть одна вещь, которую вам нужно знать обо мне. У меня есть ограничения в том, что я не буду делать. Интеграция — одна из таких вещей. Вот почему у нас есть MathCAD!
Вот почему у нас есть MathCAD!
Как видите, очень кропотливая работа по интеграции был замазан, и мы смогли напрямую решить для нашей границы условия. В уравнениях s(x) и v(x), на самом деле были натуральные бревна и каким-то образом появился арктангенс (не показаны). я до сих пор не жалею позволяя MathCAD делать всю работу.
Следующим шагом является проверка результатов. Это делается в два этапа. Во-первых, построить каждый сегмент по всей длине. Мы ищем, чтобы наши граничные условия были выполнены. Как видите, отклонение при x = 0 дюймов составляет 0 дюймов, а наклон кажется плоским при x = 150 дюймов.
Наконец, мы зеркально отразим графики вместе, сформировав окончательное уравнение для отклонения нашей консольной балки.
Как видите, отклонение составляет 0 дюймов в конечных точках и имеет максимальное отклонение в центре.
Лучшее руководство по расчету статически неопределимых балок
Заключение
В этой статье рассматриваются три популярных варианта нагружения, в которых балка имеет переменное поперечное сечение. Хотя это требует исчисления, часто это очень легко сделать вручную, потому что это многочлены. Если нет, будьте благодарны надежным программам, таким как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа таких лучей. Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
Хотя это требует исчисления, часто это очень легко сделать вручную, потому что это многочлены. Если нет, будьте благодарны надежным программам, таким как MathCAD, которые сделают это за вас. Эта статья должна дать вам хорошее представление о процедуре, используемой для анализа таких лучей. Если ваша балка не загружена именно так, вы всегда можете найти расчет момента в таблице и интегрировать свое сердце.
Определение, типы балок и примеры решений
Прогиб балки
[Нажмите здесь, чтобы просмотреть примеры вопросов]
Балка представляет собой кусок тела длиной , способный выдерживать нагрузку, сопротивляясь изгибу . Отклонение луча в определенном направлении, когда к нему приложена сила , известно как отклонение
луча с. Существуют в основном четыре переменные , которые могут определять величину прогиба балки:- Loading on the structure
- The length of unsupported members
- The material (specifically the Young’s Modulus )
- The cross-section size (specifically the Moment of Inertia (I )
Схема прогиба балки
Расстояние прогиба стержня под нагрузкой можно рассчитать с помощью путем интегрирования функции, которая математически описывает уклон элемента под этой нагрузкой. Как правило, мы вычисляем его, беря двойной интеграл уравнения изгибающего момента, , что означает M(x), деленное на произведение E (модуль Юнга) и I (момент инерции).
Как правило, мы вычисляем его, беря двойной интеграл уравнения изгибающего момента, , что означает M(x), деленное на произведение E (модуль Юнга) и I (момент инерции).
Проверка:
Формула отклонения балки
[Щелкните здесь, чтобы просмотреть примеры вопросов]
Балки могут сильно различаться по своей геометрии и составу . Некоторые простые примеры показаны ниже. Формулы выражены 9Разработано 1000 аппроксимаций для длинных, тонких, однородных, призматических балок
с небольшими отклонениями и линейными упругими свойствами.Консольные балки
Консольные балки — это специальные типы балок, которые ограничены только одной заданной опорой . Эти типы объектов, естественно, будут больше отклоняться из-за поддержки только на одном конце, поэтому наклон и отклонение на этом конце должны быть равны нулю. Консольные балки далее классифицируются как:
- Конечно-загруженная
- Однородно загруженная
Схема консольного луча
Конечная нагрузка.
 луч. Ниже приведена схема, чтобы понять это немного лучше.
луч. Ниже приведена схема, чтобы понять это немного лучше.
Схема консольной балки с торцевой нагрузкой
Для рассчитать прогиб консольной балки 9{3}} {3ei} \)
, где,
Δ B — отклонение луча
F — это сила на одном конце
L — длина луча
E Lough . Модуль
I есть Момент инерции
Если пролет удваивается, прогиб увеличивается в восемь раз . Прогиб в любой точке x вдоль пролета консольной балки с торцевой нагрузкой можно рассчитать, используя: 9{3}}{6EI} \)(3 L-x )
Когда x = L (конец балки), δx идентично δB в приведенном выше уравнении.
Читайте также: Напряжение растяжения
Консольные балки с равномерной нагрузкой
Консольные балки с равномерной нагрузкой имеют силу , действующую равномерно по всей длине балки . Схема выглядит следующим образом:
Схема выглядит следующим образом:
Схема консоли с равномерной нагрузкой
9{2}}{24EI}\)(6L 2 -4Lx + x 2 )
Балки с простой опорой
Балки с простой опорой имеют опору на конце, которая допускает вращение , но не отклонение1 9100 . Простые поддерживаемые балки могут быть дополнительно классифицированы как:
- Центра-загруженные
- OFF-CENTE
- ОБРАТНОГО НАГРУЗКА
9000 9000 1001
9000 9000 01001001
9000 9000 СВЯЗИ СРЕДНЯ СРЕДНОЙ СВЯЗИ.2)\)
Простые балки со смещенной нагрузкой
В этом типе балки сила действует в точке, немного удаленной на от центра. Схема выглядит следующим образом:
Схема нагрузки со смещением от центра
Максимальное упругое отклонение на балке , поддерживаемой двумя простыми опорами, нагруженными на расстоянии a от ближайшей опоры, определяется по формуле:
\ ( \)
Где a — расстояние от груза до ближайшей опоры 92}{3}}\)
Читайте также: Термическое напряжение
Равномерно нагруженные простые балки
В этом типе балок сила действует равномерно по длине балки. Схема представлена следующим образом:
Схема представлена следующим образом:
Схема равномерной нагрузки
Упругое отклонение в средней точке C на балке, поддерживаемой двумя простыми опорами, при равномерной нагрузке, как показано на рисунке, определяется как:
9{}}{384EI}\)Где q равномерная нагрузка на балку (усилие на единицу длины)
См. также: Энергия деформации
Формула отклонения балки Единицы
Примеры вопросов]
Приведенные выше формулы требуют использования последовательного набора единиц измерения. Большинство расчетов производится в единицах СИ.
- Сила: Ньютоны (Н)
- Длина: Метры (м)
- Modulus of elasticity: N/m 2
- Moment of Inertia: m 4
Other units may be used as well, as long as they являются самосогласованными . Например, иногда для измерения нагрузок используется единица измерения килограмм-сил (кгс). В таких случаях модуль упругости необходимо перевести в кгс/м 2 .
Например, иногда для измерения нагрузок используется единица измерения килограмм-сил (кгс). В таких случаях модуль упругости необходимо перевести в кгс/м 2 .
Читайте также: Напряжение и давление
Решенный пример
Вопрос: Консольная балка длиной 2 метра поддерживается только с одного конца. Модуль Юнга металла равен 200 x 10 9 Н·м -2 . Момент инерции 50 кг м 2 . Если к одному концу приложена сила 300 Н, рассчитайте прогиб металлической балки.
Решение: Из вопроса
E= 200 x 10 9 Нм 99*50}\)
=0,08 м
Что следует помнить
[Щелкните здесь, чтобы просмотреть примеры вопросов]
- Прогиб Учет: Максимальный прогиб нагруженной балки должен находиться в определенных пределах, чтобы прочность и эффективность луча не должны быть затронуты.

- Прогиб в балках может быть в целом классифицирован как: Консоли и Просто поддерживаемые балки.
- В зависимости от места приложения силы , консольные и просто поддерживаемые балки могут быть дополнительно классифицированы.
- единиц формулы прогиба балки выражаются через силу, длину, момент инерции или модуль упругости.
- Модуль упругости Юнга балки равен отношению напряжения к деформации в пределах пропорции .
- Модуль Юнга — это свойство материала , которое не зависит от внешних факторов, таких как сила, момент и т. д.
- Три модуля упругости с модулем Юнга , модулем сдвига и модулем объемного сжатия используются для описания упругого поведения объектов , когда они реагируют на деформирующие силы, действующие на них.
- Модуль Юнга и модуль сдвига относятся только к твердым телам.

- Объемный модуль относится к твердым телам, жидкостям и газам.
Вопросы предыдущего года по формуле 9 прогиба балки0989
- Выберите правильное соотношение между параметрами эластичности. [JEE Main 2021]
- Соотношение веса стальной и латунной проволоки при подвешивании. [NEET 2015]
- Какой график является прямой линией. [NEET 2014]
- Коэффициент увеличения длины стальной и медной проволоки. [NEET 2013]
- Рассчитайте усилие, необходимое для растяжения проволоки. [NEET 2018]
- Рассчитайте упругую потенциальную энергию в удлиненном проводе. [НЕТ 2019]
- Рассчитайте соотношение напряжений между двумя удлиненными проводами. [KCET 2018]
- Что такое модуль Юнга. [KCET 2017]
- Какое вещество обладает наибольшей эластичностью? [KCET 2010]
- Отношение гидравлического напряжения к деформации? [KEAM]
- Определите коэффициент e=увеличения длины двух проводов из одного материала.
 [KEAM]
[KEAM] - Определите длину шнура, зная модуль Юнга. [КЕМ]
- Рассчитайте энергию, запасенную в проводе. [KEAM]
- Рассчитать перемещение, когда к кубу приложена сила. [JEE Main 2018]
- Рассчитайте силу, необходимую для того, чтобы втолкнуть пробку в бутылку. [JEE Main 2016]
- Определите модуль Юнга. [JEE Main 2019]
- Выберите неверное утверждение. [KEAM]
- Определите коэффициент изменения напряжения. [Основной JEE 2017]
- Рассчитайте растягивающее напряжение в проводе. [JEE Main 2019]
- Рассчитайте относительное уменьшение радиуса провода. [JEE Main 2013]
Примеры вопросов
Вопросы. Вычислите прогиб консольной балки длиной 2 м, имеющей опору только с одного конца. Модуль Юнга металла 200 × 10 9 и момент инерции 50 кг·м 2 . В конце прилагаемая сила составляет 300 Н. ( 4 знака )
В конце прилагаемая сила составляет 300 Н. ( 4 знака )
Ответ.
Указанные параметры: E = 200 × 109 нм -2
I = 50 кгм 2
L = 2 M
W = 300 N
Сейчас, используя формулу BEAM,
D = WL 3 /3EI
D = 300 × 23/ 3 × 200 × 50
D = 2400/30000
D= 0,08 м
Отсюда величина прогиба балки 8 м или 8 см будет 0,0 .
Вопрос. В случае изгиба балки как зависит депрессия δ от модуля упругости Юнга Y? ( 4 балла )
Отв. Рассмотрим любую балку, но для простоты рассмотрим свободно опертую балку, на которую действует точечная нагрузка в ее центре.
мы знаем, что прогиб свободно опертой балки длиной L, на которую действует точечная нагрузка в ее средней точке, определяется выражением:
D = FL 3 / 48YI
Здесь Y — модуль Юнга для материала балки, а L — момент инерции балки.
Из приведенного выше выражения мы можем сказать, что прогиб обратно пропорционален модулю упругости Юнга.
D ∝ 1 / Y
Это отклонение является депрессией луча, так что мы можем написать:
δ ∝ 1 / Y
Δ ∝
Δ ∝
Δ ∝
Δ ∝
Δ ∝1001 Y -1
Следовательно, при изгибе балки депрессия δ обратно пропорциональна модулю Юнга упругости материала балки.
Вопрос. На свободно опертую балку длиной 6 м действует равномерно распределенная нагрузка 75 кН/м по всему пролету. Определить прогиб балки при закреплении обоих концов при значении EI 5,06 × 10 10 Нмм 2 . ( 4 балла )
( 4 балла )
Отв.
Given parameters are, l = 6 m = 6000 mm
Load, W = 75 kN/m = 75 × 10 3 N/m
= 75 mm
Значение EI = 5,06 × 10 10 Нмм 2
Свободно опертая балка, подверженная равномерно распределенной нагрузке, прогиб определяется как
1000 δ = 5qL 4 /384EI
δ = 5 × 75 × (6000) 4 / 384 × 5.06 × 10 10
δ = 25 mm
Следовательно, величина прогиба балки составляет 25 мм.
Вопрос. В случае изгиба балки как зависит депрессия δ от модуля упругости Юнга Y? ( 4 балла )
Отв. Мы можем найти ответ на этот вопрос, рассмотрев любую балку, но для простоты рассмотрим свободно опертую балку, на которую действует точечная нагрузка в ее центре.
Мы можем найти ответ на этот вопрос, рассмотрев любую балку, но для простоты рассмотрим свободно опертую балку, на которую действует точечная нагрузка в ее центре.
мы знаем, что прогиб свободно опертой балки длиной L, на которую действует точечная нагрузка в ее средней точке, определяется формулой:
D = FL 3 / 48YI
L — момент инерции балки.
Из приведенного выше выражения мы можем сказать, что прогиб обратно пропорционален модулю упругости Юнга.
D ∝ 1 / Y
Это отклонение представляет собой депрессию балки, так что мы можем записать:
δ ∝ 1/ Y
δ ∝ Y -1
Следовательно, при изгибе балки депрессия δ обратно пропорциональна молодому модулю упругости материала балки.
Вопрос. На свободно опертую балку длиной 6 м действует равномерно распределенная нагрузка 75 кН/м по всему пролету. Определить прогиб балки при закреплении обоих концов при значении EI 5,06 × 10 10 Нмм 2 . ( 4 балла )
( 4 балла )
Отв.
Приведены параметры, l = 6 м = 6000 мм
Нагрузка, W = 75 кН/м = 75 × 10 3 Н/м
= 75 мм
Значение EI = 5,061 × 90 10 Нмм 2
Свободно опертая балка с равномерно распределенной нагрузкой, прогиб определяется как0198 10
δ = 25 мм
Следовательно, значение прогиба луча составляет 25 мм.
Вопрос. Каким будет отношение прогибов свободного конца консольной балки от изолированной нагрузки на 1/3 rd и 2/3 rd пролета? ( 3 балла )
Отв.
1-е условие: для консольной балки, находящейся под нагрузкой W на расстоянии L/3 от свободного конца, прогиб определяется по формуле:
Yc 1 = W/3EI × (2L/3) 3 + W/2EI(2L/3) 2 × L/3
Yc 1 = 28WL 90/60194 90/60194 3 90 2-е условие: для консольной балки, находящейся под нагрузкой W на расстоянии 2L/3 от свободного конца:
Yc 2 = W/3EI × (L/3) 3 + W/2EI(L/3)2 × 2L/3
Yc 1 = 8WL3/162EI
Отношение (r) = Y c1 / Y c2 = 28/8 = 7/2
∴ 9006 Yc 64 2 = 7/2
Вопрос. Свободно опертая балка несет равномерно распределенную нагрузку 20 кН/м на длине 5 м. Если жесткость на изгиб 30000 кН·м 2 , каков максимальный прогиб балки? ( 3 балла )
Свободно опертая балка несет равномерно распределенную нагрузку 20 кН/м на длине 5 м. Если жесткость на изгиб 30000 кН·м 2 , каков максимальный прогиб балки? ( 3 балла )
Отв.
Приведенные параметры нагрузки W = 20 кН/м
Длина балки = 5 м
Жесткость на изгиб (EI) = 30000 кН.м 2
Максимальный прогиб в балке δmax = (5/384 )(WL4/EI)
δ макс. = (5/384)(20 × 5 4 / 30000)
δ макс. Свободно опертая балка длиной 5 м нагружена в центре сосредоточенной нагрузкой 1200 Н и прогибается в центре на 12 мм. Определите жесткость на изгиб (EI). ( 3 балла )
Отв.
Указанные параметры: длина L = 5 м = 5000 мм
Нагрузка W = 1200 Н
Прогиб δ = 12 мм
Свободно опертая балка с сосредоточенной нагрузкой в центре, прогиб определяется по формуле ) 3 /48×12
EI = 2,6 × 10 11 Н/мм 2
Запросы. Если на свободно опертую балку с пролетом 4 м действует на обоих концах концевая пара с усилием 4 кН·м, то какова будет величина центрального прогиба? ( 3 балла )
Если на свободно опертую балку с пролетом 4 м действует на обоих концах концевая пара с усилием 4 кН·м, то какова будет величина центрального прогиба? ( 3 балла )
Отв.
Данные параметры: L= 4 м
M = 4 кН-м
Когда свободно опертая балка подвергается воздействию концевых пар на обоих концах, тогда
Максимальное центральное отклонение определяется по формуле: ML 2 /8EI
δ макс. = 4(4) 2 /8EI
δ макс.1000 Также проверьте:
Прогиб стальных балок стал проще
Alasdair’s Engineering Pages © A. N. Beal 2019 70, № 12, 16 июня 1992 г.
Прогибы балок стали проще
Г-н А. Н. Бил из Лидса прислал нам записку, предлагающую простую процедуру приблизительного ручного расчета прогибов стальных балок. Хотя его вклад оказался слишком длинным, чтобы быть включенным в Verulam целиком, сокращенная версия может заинтересовать многих читателей. Г-н Бил отмечает, что, хотя расчет изгибающих напряжений в балке вручную обычно не представляет труда, расчет прогибов может быть гораздо более трудоемким. Поскольку обычно нет необходимости знать отклонения с какой-либо большой степенью точности (в пределах 10%, вероятно, будет достаточно), предлагается следующий подход.
Хотя его вклад оказался слишком длинным, чтобы быть включенным в Verulam целиком, сокращенная версия может заинтересовать многих читателей. Г-н Бил отмечает, что, хотя расчет изгибающих напряжений в балке вручную обычно не представляет труда, расчет прогибов может быть гораздо более трудоемким. Поскольку обычно нет необходимости знать отклонения с какой-либо большой степенью точности (в пределах 10%, вероятно, будет достаточно), предлагается следующий подход.
Случай свободно опертой балки, несущей равномерную нагрузку, иллюстрирует этот подход.
Если взять формулу прогиба (Δ = 5WL³/384EI) и выразить ее через изгибающий момент (M = WL/8), получится Δ = 5ML³/48EI.
Теперь для стальной балки напряжение упругого изгиба fbt = M/Z, где Z = 2I/D, что дает fbt = MD/2I.
(Z — модуль упругости, I — момент инерции, а D — общая глубина сечения.)
Подстановка этого значения в формулу прогиба дает Δ = 5 fbtL³/24ED. При E 210 кН/мм² получается:
Δ (мм) = 0,992 fbtL²/D . . . (1)
. . (1)
Здесь fbt, L и D выражены в их обычных единицах Н/мм², м и мм соответственно.
Для всех практических целей формула
Δ = fbtL²/D . . . (2)
удобен в использовании, легко запоминается и точен с точностью до 1%.
Г-н Бил затем переходит к рассмотрению других распределений нагрузки, аналогичным образом связывая центральный прогиб Δ с экстремальным напряжением волокна fbt, что дает результаты, показанные в первом столбце результатов в таблице 1. Во втором столбце приведены значения для фиксированной нагрузки.2618 оконечных балок, которые, по мнению г-на Била, могут применяться для оценки прогибов неразрезных балок.
Наконец, г-н Бил иллюстрирует, как его процедура может быть использована для сложных нагрузок, путем расчета прогиба свободно опертой балки, нагруженной, как показано на рис. 1:
рис. 1
Центральный изгибающий момент, рассчитанный как 444,3 кНм.
Для сечения балки Z = 2474 см³, D = 539,5 мм, что дает
fbt = 179,6 Н/мм².
Простое приближенное отклонение с использованием ур. (2) равно
ΔAPP = 179,6 x 7²/539,5 = 16,3 мм = L/429 OK.
Для более точной оценки, учитывая, что большая часть момента создается центральной точечной нагрузкой, мы можем взять коэффициент ближе к значению точечной нагрузки 0,8 (скажем, 0,85), что дает
Δ = 0,85 fbt x L² /D = 13,9 мм
Для сравнения, точный компьютерный анализ той же балки дал отклонение 13,8 мм.
Поэтому для большинства практических целей нам нужно запомнить только четыре простые формулы для прогибов свободно опертых или неразрезных стальных балок, как показано в таблице 2.
Эти формулы не только облегчают жизнь для простых равномерных и точечных нагрузок —
Есть берущие?
Оригинал этого документа можно получить по телефону
www. istructe.org/thestructuralengineer
istructe.org/thestructuralengineer
|
Таблица 2 |
Прогиб |
|
|
Распределенная нагрузка |
Точечная нагрузка |
|
|
Просто- |
фбтL²/D |
0,8fbtL²/D |
|
Фиксированный — |
0,6fbtL²/D |
0,4fbtL²/D |
Δ = прогиб (мм)
fbt = напряжение при максимальном прогибающем моменте (Н/мм²)
L = пролет (м)
D = глубина (мм)
|
Таблица 1 |
Прогиб (мм) |
|
|
Загрузка |
Просто поддерживается |
Фиксированный — |
|
0,99fbtL²/D |
0,60fbtL²/D |
|
|
0,95fbtL²/D |
0,56fbtL²/D |
|
|
0,89fbtL²/D |
0,51fbtL²/D |
|
|
1,01fbtL²/D |
0,66fbtL²/D |
|
|
0,94fbtL²/D |
0,53fbtL²/D |
|
|
0,79fbtL²/D |
0,40fbtL²/D |
|
|
0,74fbtL²/D |
0,38fbtL²/D |
(Отклонение — TotalConstructionHelp)
(Отклонение — TotalConstructionHelp)(Здесь мы будем обращаться к конструкционным балкам, лагам и перемычкам, а не к искусственным Балки)
Балки и перемычки на самом деле просто балки.
Балка – конструктивный элемент, который обычно располагается горизонтально и способен выдерживать нагрузки, в первую очередь за счет сопротивления изгибу. Изгибающая сила индуцированных в материале балки в результате нагрузок, включающих ее собственный вес (вес балки) и дополнительные нагрузки (другие нагрузки, называемые динамическими нагрузками). и мертвые грузы, такие как люди и мебель). Эти нагрузки производят то, что называются изгибающими моментами в балке, а также могут иметь изгибающие моменты в каждой поддерживаемый конец, когда концы закреплены на торцевых опорах. Фиксированный означает, что они прикреплены таким образом, что часть нагрузки на балку приходится на переносятся на торцевые соединения (такие как стены или колонны). Балки бывают разных размеров и форм. Они, как правило, либо однородны
или композитный. Однородный пучок — это пучок из одного материала, например,
дерево или сталь. Композит – это материал, изготовленный из разных материалов, таких как
как, бетонная балка со стальной арматурой. Некоторые типы балок:
|
| |
|
|
Все это может показаться чрезмерным, но это не так. Некоторые эксперты говорят, что инженерия состоит на 80% из логики и на 20% из приложений. Некоторые могут обсудить это. но здесь мы предоставим вам основную инженерную информацию и приложения, которые вы не всегда можете найти доступными. Пока балки нагружены по-разному. Ниже вам будет показано, как все это работает и как выбрать балку (деревянную или стали). Мы также коснемся выбора бетонной балки в разделе Балка. Простая опорная равномерно распределенная балка с уравнениями и решениями:В приведенном выше примере есть шаги, необходимые для выбора и проектирования дерева. Луч. Если вы хотите выбрать и спроектировать стальную балку, шаги будут такими: такой же. Есть несколько вещей, которые меняются, например, напряжение на изгиб в Материал, момент инерции, модуль упругости и сечение Модуль. Все остальные уравнения были бы такими же, если бы у вас было то же самое. нагрузка (W) и пролет (L). Обычные этапы проектирования балки:
|

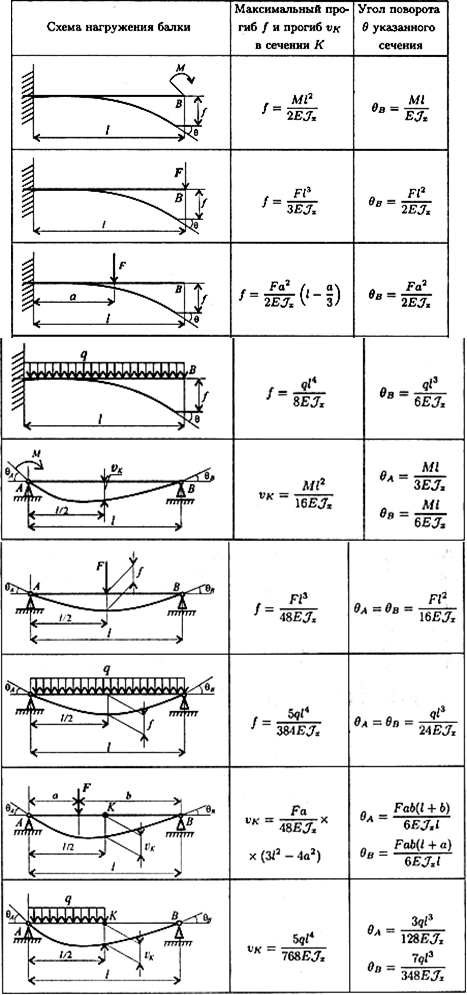 гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный
гранями полок широкопол.Двутавр с паралел. гранями полок колнныйДвутавр с паралел. гранями полок доп.сери(Д)Тавр с паралелными гранями полок нормальныйТавр с паралел. гранями полок широкополочныйТавр с паралелными гранями полок колнный