Формула расчет прогиба балки: Расчет балки на прогиб: формулы и пример расчета

Содержание

Основы сопромата, расчет прогиба балки

Cодержание:

Основы сопромата кратко.

1. Виды опор.

1.1. Шарнирные опоры.

Расчетная длина (пролет) балки.

1.2. Опорные связи шарнирно закрепленной балки.

1.3 Жесткое защемление на опорах.

1.4. Скользящие заделки.

2. Нагрузки (внешние силы).

3. Напряжения (внутренние силы).

4. Реакции опор.

5. Уравнения статического равновесия.

4.1. Определение опорных реакций.

6. Уравнения изгибающего момента.

7. Балка на двух шарнирных опорах.

8. Консольная балка.

9. Метод сечений.

10. Определение момента сопротивления.

11. Определение угла поворота.

12. Определение прогиба.

13. Определение угла поворота через прогиб.

14. Список использованной литературы.

Расчет прогиба балки не то, чтобы такой уж сложный, но для того, чтобы каждый раз не повторять одни и те же операции при расчете и этим максимально сократить время расчета, специалисты по сопромату уже давно вывели формулы для наиболее вероятных вариантов опор балок и нагрузок, действующих на балки.

Достаточно только определиться с расчетной моделью балки и формула для расчета прогиба к Вашим услугам. Но аксиомы: «если хочешь, чтобы работа была сделана хорошо, сделай это сам» пока никто не отменял. Дело в том, что в разного рода справочниках и пособиях иногда бывают опечатки или ошибки, поэтому использовать готовые формулы не всегда есть хорошо.

11. Определение угла поворота.

(вернуться к основному содержанию)

Прогиб строительной конструкции, а в нашем случае балки — единственная величина, которую проще всего определить опытным путем и сложнее всего теоретическим. Когда мы прикладывали к линейке нагрузку (давили на нее пальцем или мощью своего интеллекта), то невооруженным глазом видели, что линейка прогибалась:

Рисунок 11.1. Перемещение центра тяжести поперечного сечения балки в центре балки и угол поворота продольной оси, проходящей через центр тяжести поперечного сечения, на одной из опор.

Если бы мы хотели определить величину прогиба опытным путем, то достаточно было бы измерить расстояние от стола, на котором лежат книги (на рисунке не показан) до верха или низа линейки, затем приложить нагрузку и измерить расстояние от стола до верха или низа линейки. Разница в расстояниях — это и есть искомый прогиб (на фотографии величина прогиба обозначена оранжевой линией):

Фотография 1.

Но попробуем прийти к тому же результату, следуя по тернистому пути теории сопромата.

Так как балка прогнулась (в хорошем значении этого слова), получается, что и продольная ось, проходящая через центры тяжести поперечных сечений всех точек балки, и до приложения нагрузки совпадавшая с осью х, сместилась. Это смещение центра тяжести поперечного сечения по оси у называется прогибом балки f. Кроме того, очевидно, что на опоре эта самая продольная ось теперь находится под некоторым углом θ к оси х, а в точке действия сосредоточенной нагрузки угол поворота = 0, так как нагрузка у нас приложена посредине и балка прогнулась симметрично. Угол поворота принято обозначать «θ«, а прогиб «f» (во многих справочниках по сопромату прогиб обозначается как «ν«, «w» или любыми другими литерами, но нам, как практикам, удобнее использовать обозначение «

f«, принятое в СНиПах).

Как определить этот самый прогиб мы пока не знаем, но зато мы знаем, что нагрузка, действуя на балку, создает изгибающий момент. А изгибающий момент создает внутренние нормальные сжимающие и растягивающие напряжения в поперечных сечениях балки. Эти самые внутренние напряжения приводят к тому, что в верхней части балка сжимается, а в нижней растягивается, при этом длина балки по оси, проходящей через центры тяжести поперечных сечений остается такой же, в верхней части длина балки уменьшается, а в нижней части увеличивается, причем чем дальше расположены точки поперечных сечений от продольной оси, тем больше будет деформация. Определить эту самую деформацию мы можем используя еще одну характеристику материала — модуль упругости.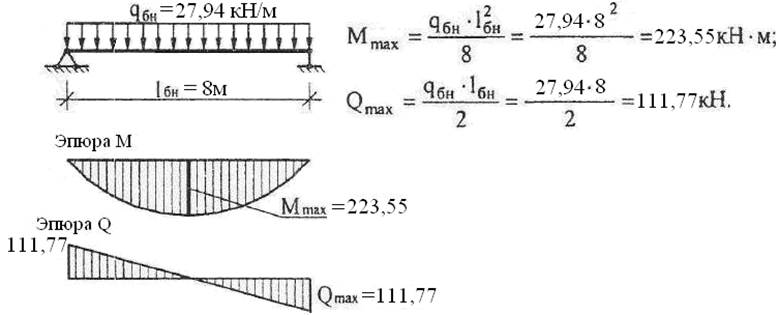

Если мы возьмем кусок бинтовой резины и попробуем его растянуть, то обнаружим, что резина растягивается очень легко, а выражаясь по научному деформируется на значительную величину при воздействии даже небольшой нагрузки. Если мы попробуем проделать то же самое с нашей линейкой, то растянуть ее даже на десятые доли миллиметра руками вряд ли получится, даже если прилагать к линейке нагрузку в десятки раз большую, чем к бинтовой резине. Это свойство любого материала описывается модулем Юнга, который часто называется просто модулем упругости. Физический смысл модуля Юнга при максимально допустимом загружении рассчитываемой конструкции примерно следующий: модуль Юнга показывает отношение нормальных напряжений, (которые при максимально допустимом загружении равны расчетному сопротивлению материала к относительной деформации при таком загружении:

E = R/Δ (11.1.1)

а это значит, что для работы материала в области упругих деформаций значение внутренних нормальных напряжений, действующих не абстрактно, а на вполне определенную площадь сечения, с учетом относительной деформации не должно превышать значения модуля упругости:

E ≥ N/ΔS (11. 1.2)

в нашем случае балка имеет прямоугольное сечение, поэтому S = b·h, где b — ширина балки, h — высота балки.

Измеряется модуль Юнга в Паскалях или кгс/м². Для абсолютного большинства строительных материалов модули упругости определены эмпирическим путем, узнать значение модуля для того или иного материала можно по справочнику или сводной таблице.

Определить величину деформации для поперечного сечения, к которому приложена равномерно распределенная нагрузка или сосредоточенная сила в центре тяжести поперечного сечения, очень просто. В таком сечении возникают нормальные сжимающие или растягивающие напряжения, равные по значению действующей силе, направленные противоположно и постоянные по всей высоте балки (согласно одной из аксиом теоретической механики):

Рисунок 507.10.1

и тогда определить относительную деформацию, если известны геометрические параметры балки (длина, ширина и высота) несложно, простейшие математические преобразования формулы (11. 1.2) дают следующий результат:

Δ = Q/(S·Е) (11.2.1) или Δ = q·h/(S·Е) (11.2.2)

Так как расчетное сопротивление показывает какую максимальную нагрузку можно приложить к определенной площади, то в данном случае мы можем рассматривать действие сосредоточенной нагрузки на всю площадь сечения нашей конструкции. В некоторых случаях важно определить деформации именно в точке приложения сосредоточенной нагрузки, но сейчас мы эти случаи не рассматриваем. Чтобы определить суммарную деформацию, нужно обе части уравнения умножить на длину балки:

Δl = Q·l/(b·h·Е) (11.2.3) или Δl = q·h·l/(b·h·Е) (11.2.4)

Но в рассматриваемом нами случае на поперечные сечения балки действует не сосредоточенная сила, приложенная к центру тяжести поперечного сечения, а изгибающий момент, который можно представить в виде следующей нагрузки:

Рисунок 149. 8.3

При такой нагрузке максимальные внутренние напряжения и соответственно максимальные деформации будут происходить в самой верхней и в самой нижней части балки, а посредине никаких деформаций не будет. Равнодействующую для такой распределенной нагрузки и плечо действия сосредоточенной силы мы находили в предыдущей части (2), когда определяли момент сопротивления балки. Поэтому теперь без особого труда можем определить суммарную деформацию в самой верхней и в самой нижней части балки:

Δх = M·х/((h/3)·b·(h/2)·Е) (11.3.1)

или

Δх = M·х/(W·Е) (11.3.2)

так как W = b·h²/6 (10.6)

Эту же формулу мы можем получить и другим способом. Как мы знаем, момент сопротивления поперечного сечения балки должен удовлетворять следующему условию:

W ≥ М / R (10.3)

Если мы будем рассматривать эту зависимость как уравнение и заменим в этом уравнении значение R на ΔЕ, получим следующее уравнение:

W = М / ΔЕ (11. 4.1)

И тогда:

М = WΔЕ (11.4.2) a

Δ = M/(W·Е) (11.4.5) и соответственно Δх = M·х/(W·Е) (11.3.2)

В результате деформации, которую мы только что определили, наша балка могла была бы выглядеть так:

Рисунок 11.2. Предполагаемая (для наглядности) деформация балки

то есть в результате деформаций самая верхняя и самая нижняя точки поперечного сечения сместятся на величину Δх. А это значит, что зная величину деформации и высоту балки, мы можем определить угол поворота θ поперечного сечения на опоре балки. Из школьного курса геометрии мы знаем, что отношение катетов прямоугольного треугольника (в нашем случае катеты Δх и h/2) равно тангенсу угла θ:

tgφ = Δх/(h/2) (11.5.1)

и тогда

tgφ = 2 M·х/(h·W·Е) (11.5.3)

Если вспомнить, что момент инерции — это момент сопротивления поперечного сечения, умноженный на расстояние от центра тяжести до крайней точки сечения или наоборот, момент сопротивления — это момент инерции, разделенный на расстояние от центра тяжести до крайней точки сечения:

W = I/(h/2) (10. 7) или I = W·h/2 (10.7.2)

то мы можем заменить момент сопротивления на момент инерции:

tgφ = M·х/(I·Е) (11.5.4)

хотя делать это было не обязательно, но таким образом мы получили формулу угла поворота почти такой, как она дается во всех учебниках и справочниках по сопромату. Главное отличие в том, что обычно речь идет о угле поворота, а не о тангенсе угла. И хотя при малых деформациях значения тангенса угла и угол сопоставимы, но тем не менее угол и тангенс угла — это разные вещи (впрочем в некоторых справочниках, например: Фесик С.П. «Справочник по сопротивлению материалов» Киев: Будiвельник. — 1982 переход от тангенса к углу упоминается, хотя и без достаточных на мой взгляд объяснений). Более того, если быть совсем уж точным, то таким способом мы определяем отношение продольной деформации к высоте балки

Рассчитываемые элементы далеко не всегда имеют прямоугольное сечение, как наша рассматриваемая линейка. В качестве балок и перемычек могут использоваться различные горячекатаные профили, тесанные и не тесанные бревна и вообще все, что угодно. Тем не менее понимание принципов расчета момента инерции позволяет определить момент инерции для поперечного сечения любой, даже очень сложной геометрической формы. В абсолютном большинстве случаев вычислять самому момент инерции нет необходимости, для металлических профилей сложного сечения (уголки, швеллера, двутавры и др.) момент инерции, как впрочем и момент сопротивления определяется по сортаменту. Для элементов круглого овального, треугольного сечения и некоторых других видов сечения определить момент инерции можно по соответствующей таблице.

Если рассматривать суммарную деформацию всей балки, т.е. по всей длине l, то очевидно, что суммарная деформация при наших нагрузках не может быть только с одной стороны балки, как показано на рисунке 11.3.а:

Рисунок 11. 3.

Так как к нашей балке нагрузка приложена посредине, в результате чего реакции на опорах, возникающие в результате действия нагрузки равны между собой и каждая равна половине приложенной нагрузки, то скорее при этих условиях суммарная деформация будет выглядеть так, как показано на рисунке 11.3.b и тогда в нашем конкретном случае угол наклона поперечного сечения на каждой из опор будет:

tgθ = M·х/(2IЕ) (11.5.5)

Пока мы определяли тангенс угла поворота простым графоаналитическим методом и в случае, когда нагрузка к балке приложена посредине, это у нас неплохо получилось. Но варианты приложения нагрузок к балке бывают всякие и хотя суммарная деформация всегда будет равна Δl, но угол наклона поперечных сечений на опорах может быть разным. Если мы присмотримся к формулам (11.5.4) и (11.5.5) повнимательнее, то увидим, что мы умножаем значение момента в некоторой точке на величину х, которая с точки зрения теоретической механики ни чем не отличается от понятия — «плечо действия силы». Получается, что для определения тангенса угла поворота мы должны умножить значение момента на плечо действия момента, и значит, понятие «плечо» можно применить не только к силе, но и к моменту. Когда мы использовали понятие плеча действия силы, открытое еще Архимедом, то мы и предполагали как далеко это может нас завести. Метод, показанный на рисунке 5.3, дал нам значение плеча момента = х/2. Теперь попробуем определить плечо момента другим способом (графоаналитический метод). Тут нам пригодятся эпюры, построенные для балки на шарнирных опорах:

Рисунок 149.7.1 Рисунок 149.7.2

Теория сопротивления материалов позволяет рассматривать внутренние нормальные напряжения, характеризуемые эпюрой «М» рисунка 149.7.1 для балки с постоянной жесткостью, как некую внешнюю фиктивную нагрузку. Тогда площадь эпюры «М» от начала балки до середины пролета — это фиктивная опорная реакция материала балки на равномерно изменяющуюся нагрузку.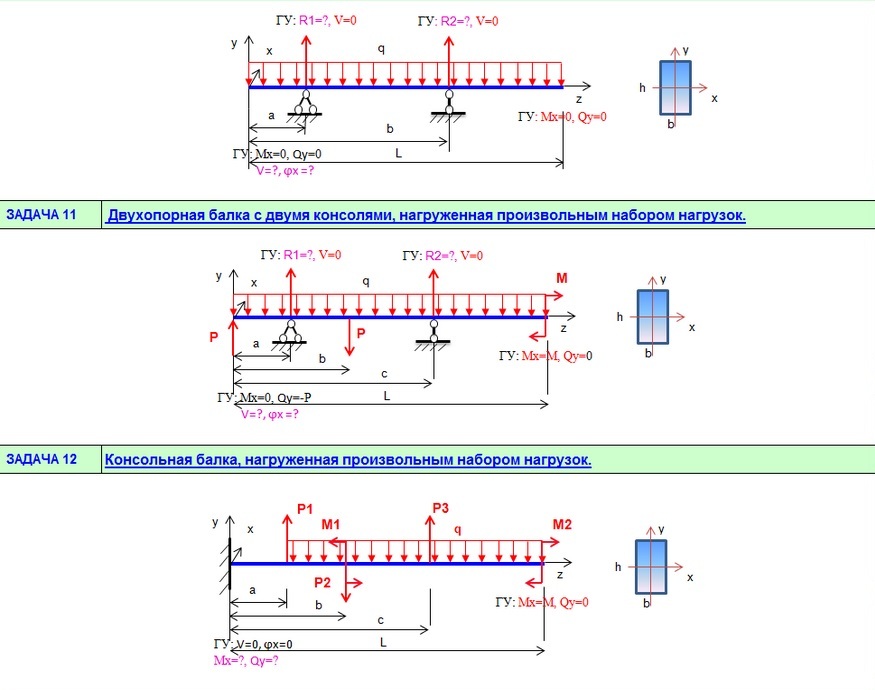 А фиктивный изгибающий момент — это площадь эпюры «М», умноженная на расстояние от центра тяжести эпюры «М» до рассматриваемой точки. Так как значение изгибающего момента посредине пролета составляет Ql/4, то площадь такой фигуры составит Ql/4(l/2)(1/2) = Ql²/16. А если это значение разделить на жесткость ЕI, то мы получим значение тангенса угла поворота.

Забегая наперед, определим значение прогиба. Расстояние от центра тяжести треугольной эпюры «М» до середины пролета равно l/6, тогда фиктивный изгибающий момент составит (Ql²/16)l/2 — (Ql²/16)l/6 = Ql³/48. Тогда прогиб f = Ql³/48EI. А так как эпюра моментов у нас расположена снизу балки, то такая фиктивная нагрузка будет в итоге давать отрицательное значение угла поворота и прогиба, что в общем-то логично, так как при таком действии нагрузки прогиб — смещение центра тяжести поперечного сечения будет происходить вниз по оси у.

Характерная особенность графоаналитического метода состоит в том, что количество вычислений можно еще сократить. Для этого нужно умножить площадь эпюры фиктивной нагрузки на расстояние от центра тяжести эпюры до начала координат, а не до рассматриваемой точки на оси. Например, для вышеприведенного случая (Ql²/16)l/3 = Ql³/48

При равномерно распределенной нагрузке эпюра моментов описывается квадратичной параболой, определить площадь такой фигуры и расстояние до центра тяжести сложнее, но для того нам и нужны знания по геометрии, чтобы можно было определить площадь любой фигуры и положение центра тяжести такой фигуры.

Таким образом получается, что для балки, на которую действует сосредоточенная нагрузка в середине балки при х=l/2:

tgθ = М·(x/2)/(ЕI) = ((Ql/4)·(l/4))/(ЕI) = Ql²/(16EI) (11.6.1)

То, что мы только что делали называется интегрированием, ведь если умножить значение значение эпюры «Q» (рисунок 149.7.1) на длину действия нагрузки, мы тем самым определим площадь прямоугольника со сторонами «Q» и х, при этом площадь данного прямоугольника равняется значению эпюры «М» в точке х.

Теоретически получается, что мы можем определить значение тангенса угла поворота, интегрируя одно из уравнений моментов, составленных для нашей балки. Максимальное значение тангенса угла поворота для балки на двух шарнирных опорах, на которую действует сосредоточенная нагрузка посредине (рисунок 149.7.1), будет при х=l/2

tgθ = ∫Mdx/(EI) = ∫Axdx/(EI)= Ax²/(2EI) = (Q/2)·(l/2)²/(2ЕI) = Ql²/(16EI) (11.6.2)

где А — это реакция опоры = Q/2

При распределенной нагрузке интегрирование уравнения моментов: q(l/2)·x — qx²/2 для левой части балки дает следующий результат:

tgθ = ∫Mdx/(EI) = q·(l/2)·(l/2)²/(2ЕI) -q·(l/2)³/(6ЕI) = ql³/(24EI) (11.6.3)

Тот же результат мы получим и при использовании графо-аналитического метода.

Когда мы определяли угол поворота, то для наглядности предположили, что балка деформировалась так, как показано на рисунке 5.2, потом так, как показано на рисунке 11.3.b, потом мы выяснили, что если бы второй опоры не было, то балка повернулась вокруг первой опоры, но в действительности вторая опора есть и потому так балка деформироваться (при нашей нагрузке на балку) не может. Так как на опоре нет никакого вращающего момента и соответственно никаких внутренних напряжений, способных изменить геометрическую форму балки, то геометрическая форма балки на опоре остается неизменной, а внутренние напряжения, увеличивающиеся по ходу балки, деформируют балку все сильнее и это приводит к тому, что балка поворачивается вокруг шарнирных опор и этот угол поворота равен углу наклона поперечного сечения θ (так как мы рассматриваем балку-параллелепипед):

Рисунок 11.4. Реальная деформация балки.

Если мы просто постоим эпюру углов поворота для балки со сосредоточенной нагрузкой посредине по уравнениям для левой и для правой части балки, то эпюра будет выглядеть так:

Рисунок 11.5.

Данная эпюра была бы правильной только для балки, изображенной на рисунке 5.3.а. Очевидно, что в нашем случае эпюра так выглядеть не может и для построения правильной эпюры нужно учесть, что поперечные сечения балки имеют наклон на обоих опорах, причем наклон этот одинаковый по значению, но разный по направлению а наклон поперечного сечения балки посредине =0. Если мы опустим эпюру на Ql²/16EI, которое мы получаем при интегрировании уравнения моментов для левой части балки и которое показывает угол наклона поперечного сечения именно на опоре, то получим эпюру следующего вида:

Рисунок 11.6.

Данная эпюра абсолютно точно показывает, изменение угла поворота поперечных сечений, вдоль всей балки, а значение тангенса угла поворота на левой опоре балки не что иное, как некая постоянная С₁, которую мы получаем, если интегрирование выполнять корректно. И тогда уравнение угла поворота для балки при данной нагрузке на участке 0<x<0.5l будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) (11.6.5)

Эпюра углов поворота для балки с распределенной нагрузкой визуально ни чем не отличается от эпюры углов поворота для балки со сосредоточенной нагрузкой, разница только в том, что эпюра углов поворота для балки с распределенной нагрузкой — это кубическая парабола. Уравнение угла поворота для балки с равномерно распределенной нагрузкой будет выглядеть так:

tgθ_х = — tgθ_A + Ax²/(2EI) — qx³/(6ЕI) (11.6.6)

По поводу знаков в данном уравнении. «-» означает, что рассматриваемый член уравнения как бы пытается повернуть балку против часовой стрелки относительно рассматриваемого поперечного сечения, а «+» — по часовой стрелке. Впрочем и по эпюре углов поворота видно, что значение tgθ_А должно быть отрицательным. Таким образом, если сечение имеет наклон по часовой стрелке относительно оси х, то оно будет отрицательным, а если против часовой стрелки — то положительным.

Ну и теперь самое главное, все эти разборки с углом поворота поперечного сечения нужны нам были для того, чтобы определить прогиб балки.

12. Определение прогиба.

(вернуться к основному содержанию)

Как мы видим из рисунка 11.4, треугольник с катетами h/2 и Δх является подобным треугольнику с катетом Х и вторым катетом, равным f+у, а это значит, что теперь мы можем определить значение прогиба:

tgθ = (f + y)/Х (12.1)

тогда

f + y = tgθ·X (12.2.1) или f + y = М·x·Х/(2ЕI) (12.2)

при малых значениях х значение у близко к 0, но в более дальних точках сечения значение у увеличивается. Значение у — это и есть влияние на величину прогиба наличия второй опоры. Отметим, что это значение у показывает разницу между реальным наклоном продольной оси балки и наклоном продольной оси балки, если бы балка просто поворачивалась вокруг опоры, и получается, что значение у зависит от изменения угла поворота. Кроме того, мы опять получили уравнение, в котором значение прогиба в некоторой точке зависит от тангенса угла поворота (12.2.1) и таким образом получается, что у угла поворота тоже есть «плечо действия». Например при у=f/2 (если присмотреться к левой части фотографии 1, то посредине балки это где-то так и будет) мы бы получили следующую формулу для определения прогиба:

f = М·x²/(3ЕI) (12.3.1)

Но мы не будем ничего предполагать, а воспользуемся интегрированием. Если мы проинтегрируем уравнение моментов для левой части балки, то получим значение у (эпюра для у показана бирюзовым цветом на фотографии 1):

у =∫∫∫(Q/2)dх = (Q/2)·(l/2)³/6EI = Ql³/(96EI) (12.3.2)

или площадь фиолетовой эпюры для левой части балки(рисунок 5.5), но нам нужна площадь голубой эпюры на левом участке балки (рисунок 5.6), которая в 2 раза больше площади фиолетовой эпюры. Таким образом:

f =2∫∫∫(Q/2)dх =2 (Q/2)·(l/2)³/6EI = Ql³/(48EI) (12.3.3)

Почему площадь голубой эпюры в 2 раза больше площади фиолетовой эпюры, объяснить очень легко. Площадь треугольника равна 1/2 от площади прямоугольника с теми же сторонами, площадь фигуры, описанной квадратной параболой, составляет 1/3 от площади прямоугольника с теми же сторонами. Если бы мы развернули фиолетовую эпюру, то получили бы прямоугольник, образованный голубой и фиолетовой эпюрами. Соответственно, если из площади прямоугольника вычесть 1/3, то мы получим 2/3. У этого логического ряда есть продолжение — площадь фигуры, описанной кубической параболой, составляет 1/4 от площади прямоугольника с теми же сторонами и так далее.

Мы можем найти значение прогиба и другим способом. Из рисунка 11.4 и формул (12.2) следует, что:

f_х = — tgθx + ∫tgθdx (12.3.4)

f_l/2 = — (Ql²/16EI) l/2 + (Ql³/96EI) = -(Ql³/48EI) (12.3.5)

В данном случае знак «-» показывает, что центр поперечного сечения балки переместится вниз по оси у относительно оси х. А теперь вернемся к фотографии 1. Под продольной осью балки изображена эпюра у, именно это значение в точке l/2 мы и вычли, решая уравнение (12.3.3). Кроме того получается, что соотношение между f и у зависит от коэффициента предыдущего интегрирования, т.е. у = kf или f = y/k. Когда мы интегрировали уравнение сил, то получили коэффициент 1/2. Впрочем, такое же значение мы получили и тогда, когда определяли плечо действия момента. Если продолжить этот логический ряд, то получается, что при определении прогиба от распределенной нагрузки мы должны использовать коэффициент 1/3, то есть прогиб в середине балки мы можем вычислить по следующей формуле:

f= 2∫∫∫(ql/2)dx — 3∫∫∫∫qdх = (2(qlx³/6) — 3(qx⁴/24))/EI = 5ql⁴/(384EI) (12.4.4)

или

f_х= — ∫tgθdx + ∫∫∫(ql/2)dx -∫∫∫∫qdх (12.4.5)

f_l/2 = (- ql³x/24 + (qlx³/6) — (qx⁴/24))/EI = — 5ql⁴/(384EI) (12.4.6)

В данном случае знак «-» означает, что центр тяжести поперечного сечения перемещается вниз по оси у.

Примечание: Предложенный метод определения прогиба несколько отличается от общепринятых, так как я старался сделать основной упор на наглядность.

Если определять прогиб графоаналитическим методом, то площадь фиктивной нагрузки — эпюры моментов, описываемой квадратной параболой, будет составлять (согласно таблице 378.1) (2ql²/(8·3))l/2 = ql³/24. А расстояние от центра тяжести эпюры до начала координат составляет 5/8, Тогда фиктивный момент равен (ql3/24)(5l/(8·2)) = 5ql⁴/384.

Конечно же, сосредоточенная нагрузка к балке может быть приложена и не посредине, распределенная нагрузка может быть не только равномерно распределенной и действовать не по всей длине балки, да и варианты крепления балки на опорах бывают разные. Но для того и существуют готовые формулы, чтобы ими пользоваться.

-Позвольте! — Скажете вы, — Все это хорошо, но как быть с касательными напряжениями? Ведь они действуют вдоль оси у и потому должны как-то влиять на прогиб!

Все верно. Касательные напряжения действительно влияют на прогиб, однако для балок с соотношением l/h > 10 это влияние очень незначительно и потому допустимо для определения прогиба пользоваться изложенным в данной статье методом.

Но это еще не все, как мы уже говорили, определить значение прогиба опытным путем достаточно просто по методу, описанному в самом начале статьи. Так так ничего лучшего под рукой не было, то я взял деревянную линейку, прообраз которой я так долго описывал (см. фотографию 1). Деревянная линейка имела размеры около 91.5 см, ширину b=4.96 см и высоту h=0.32 cм (высоту и ширину определял штангенциркулем). Затем я положил линейку на опоры, при этом расстояние между опорами составило около 90 см и таким образом получил балку с пролетом l=90 см. Под воздействием собственного веса линейка конечно же немного прогнулась, но столь малый прогиб меня не интересовал. Я измерил рулеткой (точность до 1 мм) расстояние от пола до низа линейки (77.65 см), затем приложил посредине условно сосредоточенную нагрузку (поместил посредине мерный стакан весом около 52 грамм с 250 граммами воды) и измерил расстояние от пола до низа линейки при нагрузке (75.5 см). Разница этих двух измерений и составила искомый прогиб. Таким образом величина прогиба определенного опытным путем составила 77.65 — 75.5 = 2.15 см. Осталось только найти модуль упругости для древесины, определить момент инерции для данного сечения и точно посчитать нагрузку. Модуль упругости Е для древесины = 10⁵ кгс/см², момент инерции прямоугольного сечения I_z = bh³/12 = 4.98·0.32³/12 = 0.01359872 см⁴, полная нагрузка — 0.302 кг.

Расчет прогиба по формуле дал: f = Ql³/(48EI) = 0.302·90³/(48·10⁵·0.0136) = 3.37 см. Напомню, что прогиб, определенный опытным путем, составил: f = 2.15 см. Возможно следовало учесть влияние на прогиб первой производной функции — тангенса угла поворота? Ведь угол наклона, судя по фотографии, достаточно большой.

Проверяем: tgθ = Ql²/(16EI) = 0.302·90²/(16·10⁵·0.0136) = 0.11233. Тогда согласно формулы (542.12) f = 3.37/((1 + 0.112²)^3/2) = 3.307 см. Т.е. влияние конечно есть, но оно не превышает 2% или 0.63 мм.

Результат меня сначала удивил, но потом объяснений для такого расхождения нашлось несколько, в частности в середине поперечное сечение линейки было не прямоугольным, так как линейка была деформирована от времени и воздействия воды, соответственно момент инерции для такого сечения больше чем, для прямоугольного, кроме того, линейка изготовлена не из сосны, а из более твердой породы древесины, для которой и модуль упругости следует принимать больше. Да и с научной точки зрения одного результата совершенно недостаточно, чтобы говорить о каких-либо закономерностях. После этого я проверил величину прогиба для деревянного бруска с моментом инерции I=2.02 см⁴, длиной более 2 м при пролете 2 м под нагрузкой 2 кг, приложенной посредине бруска и тогда значение прогиба, определенного теоретическим путем и опытным путем, совпало до десятых долей миллиметра. Конечно, можно было бы и дальше продолжать эксперименты, но так уж получилось, что до меня это уже сделали сотни других людей и получили на практике результаты, очень близкие к теоретическим. А если еще учесть, что идеально изотропные материалы бывают только в теории, то это очень хорошие результаты.

13. Определение угла поворота через прогиб.

(вернуться к основному содержанию)

Определить значение угла поворота для шарнирно опертой балки, на которую действует только изгибающий момент M на одной из опор, например на опоре А, казалось бы, проще простого:

tgθ_х = — tgθ_A + Мx/(EI) — Аx²/(2ЕI) (13.1.1)

где А = М/l, (B = — M/l), но для этого нужно знать угол поворота на опоре А, а мы его не знаем, однако вычислить его помогает понимание того, что прогиб на опорах будет равен нулю и тогда:

f_A = tgθ_Bl — Bl³/(6EI) = 0; tgθ_B = — Ml³/(6l²EI) = — Ml/(6EI) (13.1.2)

f_B = tgθ_Al + Ml²/(2EI)- Al³/(6EI) = 0; tgθ_A = — Ml/(3EI) (13.1.3)

Как видим, угол поворота на опоре к которой приложен изгибающий момент, в два раза больше угла поворота на противоположной опоре, это очень важная закономерность, которая в дальнейшем нам очень пригодится.

Когда сосредоточенная нагрузка к балке приложена не по центру тяжести или распределенная нагрузка является неравномерной, то углы поворота на опорах определяются через прогиб, как в вышеприведенном примере. Другими словами — значения начальных параметров определяются в ходе решения дифференциальных уравнений.

формула, механизм и примеры вычисления прогиба по стандартам

Для строительства прочного, надежного и долговечного здания, нужно знать такой показатель, как прогиб балки (формула), то есть величину жесткости.

Данное направление изучается в таких науках (дисциплинах), как “Сопротивление материалов”, “Теория прочности”, “Механика строительная” и прочее.

Прочность и жесткость балки

Балки в доме

Современные строительные технологии, применяемые для просчета стройконструкций, называемых также стержневыми, по качествам прочности и жесткости дают уникальную возможность на первом же этапе проектировки вычислить величину прогиба.

Кроме этого, можно, опираясь на рассчитанные данные, составить заключение о вероятности использования строительной конструкции.

Какой вопрос позволяет решать указанная далее формула для расчета жесткости? Данные, полученные таким путем, говорят о самых больших изменениях в геометрии детали, что могут возникнуть в строительной конструкции.

Несмотря на некоторую бюрократизацию методик для вычисления прогиба, используются опытные формулы, а если воздействие реальных нагрузок отличается от идеальных или усредненных, вопрос решается введением дополнительных коэффициентов для запаса прочности. Понятия «жесткость» и «прочность» связаны и абсолютно неразделимы.

Хотя некоторые различия все-таки есть. Но только в том случае, если рассматривать данные показатели в автомашинах. В стройконструкциях главное нарушение конструкции объектов случается потому, что снижаются или нивелируются полностью вопросы, связанные с запасом прочности, вследствие чего здания нельзя эксплуатировать.

Деревянные балки из древесины хвойных пород

На сегодня в таких предметах изучения, как «Сопромат» и другие, приняты 2 метода для расчета прочности и жесткости:

Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
W _{n, m}_і_n – момент сопротивления сечения (его значение находят по таблице).
R_y – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
У_c – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

М / (W _{n, min}* R_y* У_c) ≤1

Чтобы правильно применить формулу, нужно действовать так:

Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
Записать ее точные размеры.
Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Зная значение параметров рассматриваемой балки и сил, действующих на нее, сделав нехитрые вычисления, можно быстро справится с задачей вычисления допустимого прогиба балки дома.

Как вычислить вспомогательные величины

Для получения полной информации о значениях, необходимых для достижения конечной цели вычислений, нужно узнать, каков момент сопротивление сечения (формула № 2):

W_n_{(требуемое)} = М _мах/ (R_y* У_c)

Необходимо обязательно уитывать ориентирование рассматриваемого балочного сечения, так как с уменьшением моментов инерций жесткость балок снижается, чего допускать нельзя. Для выяснения максимального значения нагрузки f, которое может выдержать балка, надо вычислить его по такой формуле № 3:

f = (5 / 384) * [(q_n * L⁴) / (E * J)] £ [¦], где

L – продольный размер, в метрах
E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
J – момент инерции по сечению
q_n – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

J = b * h³/ 12

Обозначения:

b – диаметр сечений
h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2)³/ 12 = 10 000 см⁴или 0,0001 м⁴

Кроме указанных расчетных или табличных величин, среди важных факторов, которые нужно учитывать при определении максимальных нагрузок, выделяют такие: статические (которые действуют постоянно, независимо от переменных внешних факторов), периодические (действие ветра, вибрации, ударов).

Пример подсчета прогиба

Прогиб балки (формула, пример расчета) вычисляется так. Допустим, есть балка, для которой нужно рассчитать прогиб, с такими параметрами:

Материал изготовления – дерево.
Плотность 600 кг/м³.
Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
Масса перекрывающих элементов – 60 кг/м².
Максимальная нагрузка q равна 249 кг/м.
E (насколько упруго дерево) – 100 000 кгс/ м².
J балок – 10 кг*м².

Максимально допустимая нагрузка вычисляется с учетом веса не только балочной конструкции, но и перекрытия, а также опор.

Расчет на поперечный прогиб

Не лишним будет учесть тяжесть, которую будут оказывать люди или приборы, механизмы и другие тяжелые вещи, если вычисляется прогиб балок этажа дома. Нужны такие данные, как:

Сколько весит один пог. метр рассматриваемой балки.
Сколько весит каждый м² перекрытия.
Какова временная нагрузка на перекрытие.
Сколько составляет нагрузка от перегородок на 1 м² перекрытия.
Каков коэфф. k (это промежуток, оставляемый между балками).

Чтобы упростить пример расчетов, принимают масс перекрытия за 60 кг/м², нормальную непостоянную нагрузку на каждое перекрытие – 250 кг/м², нагрузки от перегородок равными 75 кг/м², тяжесть части деревянных балок – 18 кг/погонный метр. Когда расстояние между перекрытиями равно составляет 600 мм, тогда коэффициент k равен 0,6. Подставляем в формулу все эти значения:

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

f = (5 / 384) * [(q_n * L⁴) / (E * J)] = (5 / 384) * [(249 * 4⁴) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Это – показатель уровня прогиба во время воздействия максимальной нагрузки. Что именно он обозначает? Получается, что менее, чем на один сантиметр прогнется балка при указанной максимальной нагрузке. После этого нужно сравнить полученный результат с единицей: 0,83 меньше 1.

При расчетах деформации важных строящегося здания используют указанные выше простые формулы. Прогиб балки по формуле СНиП является универсальным способом вычисления жесткости балок и величины их прогибания.

Как посчитать балку на изгиб — на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Расчет балки на прогиб

Однопролетные балки на двух шарнирных опорах
1	Расчет балки на двух шарнирных опорах при одной сосредоточенной нагрузке	Смотреть расчет
2	Расчет балки на двух шарнирных опорах при двух сосредоточенных нагрузках	Смотреть расчет
3	Расчет балки на двух шарнирных опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
4	Расчет балки на двух шарнирных опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
5	Расчет балки на двух шарнирных опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на двух опорах
6	Расчет балки с жестким защемлением на опорах при одной сосредоточенной нагрузке	Смотреть расчет
7	Расчет балки с жестким защемлением на опорах при двух сосредоточенных нагрузках	Смотреть расчет
8	Расчет балки с жестким защемлением на опорах при одной равномерно-распределенной нагрузке	Смотреть расчет
9	Расчет балки с жестким защемлением на опорах при одной неравномерно-распределенной нагрузке	Смотреть расчет
10	Расчет балки с жестким защемлением на опорах при действии изгибающего момента	Смотреть расчет
Балки с жестким защемлением на одной опоре (консольные)
11	Расчет однопролетной балки с жестким защемлением на одной опоре при одной сосредоточенной нагрузке	Смотреть расчет
12	Расчет однопролетной балки с жестким защемлением на одной опоре при одной равномерно-распределенной нагрузке	Смотреть расчет
13	Расчет однопролетной балки с жестким защемлением на одной опоре при одной неравномерно-распределенной нагрузке	Смотреть расчет
14	Расчет однопролетной балки с жестким защемлением на одной опоре при действии изгибающего момента	Смотреть расчет
Балки двухпролетные
15	Расчет двухпролетной с шарнирными опорами при одной сосредоточенной нагрузке	Смотреть
16	Расчет двухпролетной с шарнирными опорами при двух сосредоточенных нагрузках	Смотреть
17	Расчет двухпролетной с шарнирными опорами при одной равномерно-распределенной нагрузке	Смотреть
18	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть
19	Расчет двухпролетной с шарнирными опорами при одной неравномерно-распределенной нагрузке	Смотреть

Расчет металлической балки на прогиб: учимся составлять формулы

Приветствую тебя, читатель экспресс-курса — «сопромат для чайников» на сайте – SoproMats.ru. Меня зовут Константин Вавилов, я являюсь автором статей по сопромату и других материалов данного ресурса. В этой статье, будем рассматривать универсальную методику расчета прогибов балки — метод начальных параметров. Как и любая другая статья для чайников, на нашем проекте, этот материал будет изложен максимально просто, лаконично и без лишних заумных терминов.

В качестве примера, возьмем металлическую балку на двух опорах. Запишем для нее формулу для вычисления прогиба, посчитаем его численное значение. И также в конце этой статьи дам ссылки на другие полезные статьи с примерами определения прогибов для различных расчетных схем.

Что такое прогиб балки?

Под действием внешней нагрузки, поперечные сечения балки перемещаются вертикально (вверх или вниз), эти перемещения называются прогибами. Сопромат позволяет нам определить прогиб балки, зная ее геометрические параметры: длину, размеры поперечного сечения. И также нужно знать материал, из которого изготовлена балка (модуль упругости).

Кстати! Помимо вертикальных перемещений, поперечные сечения балки, поворачиваются на определенный угол. И эти величины также можно определить методом начальных параметров.

ν-прогиб сечения C; θ-угол поворота сечения C.

Прогибы балки необходимо рассчитывать, при расчете на жесткость. Расчётные значения прогибов не должны превышать допустимых значений. Если расчетное значение меньше, чем допустимое, то считают, что условие жесткости элемента конструкции соблюдается. Если же нет, то принимаются меры по повышению жесткости. Например, задаются другим материалом, у которого модуль упругости БОЛЬШЕ. Либо же меняют геометрические параметры балки, чаще всего, поперечное сечение. Например, если балка двутаврового профиля №12, не подходит по жесткости, принимают двутавр №14 и делают перерасчет. Если потребуется, повторяют подбор, до того момента пока не найдут тот самый – двутавр.

Метод начальных параметров

Метод начальных параметров, является довольно универсальным и простым методом. Используя этот метод можно записывать формулу для вычисления прогиба и угла поворота любого сечения балки постоянной жесткости (с одинаковым поперечным сечением по длине.)

Под начальными параметрами понимаются уже известные перемещения:

в опорах прогибы равны нулю;
в жесткой заделке прогиб и угол поворота сечения равен нулю.

Учитывая эти хитрости, их называют еще граничными условиями, определяются перемещения в других частях балки.

Расчет прогибов балки

Посмотрим, как пользоваться методом начальных параметров на примере простой балки, которая загружена всевозможными типами нагрузок, чтобы максимально охватить все тонкости этого метода:

Реакции опор

Для расчета нужно знать все внешние нагрузки, действующие на балку, в том числе и реакции, возникающие в опорах.

Если ты не знаешь, как определять реакции, то рекомендую изучить данный материал, где я как раз рассказываю, как они определяются на примере этой балки:

Система координат

Далее вводим систему координат, с началом в левой части балки (точка А):

Распределенная нагрузка

Метод начальных параметров, который будем использовать чуть позднее, работает только в том случае, когда распределенная нагрузка доходит до крайнего правого сечения, наиболее удаленного от начала системы координат. Конкретно, в нашем случае, нагрузка обрывается и такая расчетная схема неприемлема для дальнейшего расчета.

Если бы нагрузка была приложена вот таким способом:

То можно было бы сразу приступать к расчету перемещений. Нам же потребуется использовать один хитрый прием – ввести дополнительные нагрузки, одна из которых будет продолжать действующую нагрузку q, другая будет компенсировать это искусственное продолжение. Таким образом, получим эквивалентную расчетную схему, которую уже можно использовать в расчете методом начальных параметров:

Вот, собственно, и все подготовительные этапы, которые нужно сделать перед расчетом.

Приступим непосредственно к самому расчету прогиба балки. Рассмотрим наиболее интересное сечение в середине пролета, очевидно, что это сечение прогнется больше всех и при расчете на жесткость такой балки, рассчитывалось бы именно это сечение. Обзовем его буквой – C:

Относительно системы координат записываем граничные условия. Учитывая способ закрепления балки, фиксируем, что прогибы в точках А и В равны нулю, причем важны расстояния от начала координат до опор:

\[ { V }_{ A }=0\quad при\quad x=0 \]

\[ { V }_{ B }=0\quad при\quad x=8м \]

Записываем уравнение метода начальных параметров для сечения C:

\[ E{ I }_{ z }{ V }_{ C }=… \]

Произведение жесткости балки EI и прогиба сечения C будет складываться из произведения EI и прогиба сечения в начале системы координат, то есть сечения A:

\[ E{ I }_{ z }{ V }_{ C }=E{ I }_{ z }{ V }_{ A }+ … \]

Напомню, E – это модуль упругости первого рода, зависящий от материала из которого изготовлена балка, I – это момент инерции, который зависит от формы и размеров поперечного сечения балки. Также учитывается угол поворота поперечного сечения в начале системы координат, причем угол поворота дополнительно умножается на расстояние от рассматриваемого сечения до начала координат:

\[ E{ I }_{ z }{ V }_{C }=E{ I }_{ z }{ V }_{ A }+E{ I }_{ z }{ \theta }_{ A }\cdot 4+… \]

Учет внешней нагрузки

И, наконец, нужно учесть внешнюю нагрузку, но только ту, которая находится левее рассматриваемого сечения C.{ 4 } } =-2см \]

Таким образом, такая балка прогнется максимально на 2 см. Знак «минус» указывает на то, что сечение переместится вниз.

На этом, пожалуй, закончу данный урок. Если у вас возникли какие-либо вопросы по представленным материалам, задавайте вопросы в комментариях к этой статье. А также рекомендую вам посмотреть другие примеры определение прогибов этим методом. Там вы найдете более сложные задачи, определение углов поворотов, примеры расчета консольных балок (с жесткой заделкой).

Пример расчета прогиба балки — Яхт клуб Ост-Вест

Прочность и жесткость балки

Деревянные балки из древесины хвойных пород

Простой. При просчитывании показателей на основе этого метода используют увеличенный коэффициент.
Точный. Тут используются не только коэффициенты, показывающие запас прочности, но также осуществляется вычисление пограничного состояния (какую нагрузку может выдержать балка).

Как рассчитывать прогиб для балки дома

Чтобы просчитать, подходит ли конкретная балка для строительства дома, нужно знать такие показатели:

M – это тот максимальный момент, который возникает в балке, находящийся по эпюру моментов. Эпюр – это специальный чертеж с изображением пространственная фигура изображается на плоскости.
W _{n, m}_і_n – момент сопротивления сечения (его значение находят по таблице).
R_y – сопротивление, что оказывает материал, из которого изготовлен элемент конструкции дома, изгибаясь от нагрузки.
У_c – дополнительный показатель (его можно найти в одной из многочисленных таблиц строительных нормативов).

Формула для расчета прогиба представляет из себя неравенство следующего вида (формула № 1):

Чтобы правильно применить формулу, нужно действовать так:

Нарисовать схематично балку и ее будущее расположение под крышей дома. Чтобы верно изобразить на чертеже все части исследуемого объекта, нужно знать форму и линейные размеры балки, поперечного сечения, характер будущих нагрузок, материал, из которого балка изготовлена.
Записать ее точные размеры.
Рассчитать по указанной формуле, чему равно частное максимального момента балки к произведению остальных трех величин.
Сравнить полученный результат с единицей: если он меньше или равен 1, то вычисления дают положительный ответ.

Как вычислить вспомогательные величины

f = (5 / 384) * [(q_n * L 4 ) / (E * J)] £ [¦], где

L – продольный размер, в метрах
E – коэффициент, показывающий упругость (для каждого материала или сплава он будет разным)
J – момент инерции по сечению
q_n – это нагрузка, равномерно-распространенная, выражается в кг/м или в Н/м

Показатель J рассчитывается так:

b – диаметр сечений
h – вертикальный размер сечения

Примером для сечений, величиной 15 на 20 сантиметров:

J = 0,15 * (0,2) 3 / 12 = 10 000 см 4 или 0,0001 м 4

Пример подсчета прогиба

Материал изготовления – дерево.
Плотность 600 кг/м 3 .
Длина балки L – 4 м, остальные размеры: 15 см х 20 см.
Масса перекрывающих элементов – 60 кг/м².
Максимальная нагрузка q равна 249 кг/м.
E (насколько упруго дерево) – 100 000 кгс/ м².
J балок – 10 кг*м².

Расчет на поперечный прогиб

Сколько весит один пог. метр рассматриваемой балки.
Сколько весит каждый м 2 перекрытия.
Какова временная нагрузка на перекрытие.
Сколько составляет нагрузка от перегородок на 1 м 2 перекрытия.
Каков коэфф. k (это промежуток, оставляемый между балками).

q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.

Изгибающий момент нужно вычислить по формуле №3, учитывая все указанные выше данные. Получается:

f = (5 / 384) * [(q_n * L 4 ) / (E * J)] = (5 / 384) * [(249 * 4 4 ) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.

Как посчитать балку на изгиб — на видео:

Заметили ошибку? Выделите ее и нажмите Ctrl+Enter, чтобы сообщить нам.

Для заданной балки двутаврового сечения ( = 210 МПа, Е = 2 х 10 5 МПа) и нагрузок требуется;

1. Построить эпюры поперечных сил и изгибающих моментов;

2. Определить нормальные и касательные напряжения в сечениях с наибольшим моментом и поперечной силой на расстоянии h/4 от нейтральной оси;

3. Определить прогиб конца балки точки В.

При построении эпюр Q и М необходимо соблюдать правило знаков. Положительное направление сил показано на схеме.

1. Определяем опорные реакции

2. Методом сечений определяем ординаты поперечной силы в характерных сечениях. Для этого балку разбиваем на два участка. Границы участков – места изменения нагрузки. Построение эпюры начинаем с правого свободного конца балки.

Максимум изгибавшего момента находится в сечении, где поперечная сила равна нулю. Положение этого сечения определяем из условия:

3. Методом сечений определяем изгибающие моменты в характерных сечениях и строим эпюру моментов. Экстремум в т. х = 2 м.

Наиболее нагруженным сечением в балке является сечение А у заделки, где М_max = 120 кН м, Q_mах = – 80 кН.

4. Из условий прочности по нормальным напряжениям определяем требуемый момент сопротивления сечения.

По сортаменту ГОСТ 8509-72 принимаем двутавр № 33.

Максимальные напряжения в опасном сечении будут равны

5. Определяем нормальное напряжение в точке Е сечения на расстоянии h/4 = 8,25 см от нейтральной оси (рис. 4.9.).

Для определения касательного напряжения в точке Е вычислим статический момент отсеченной выше точки Е площади относительно центральной оси Х.

6. Определяем прогиб балки в точке В, используя универсальное уравнение прогибов

Для заданной консольной балки граничные условия будут: угол поворота сечения А ; прогиб сечения А

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Для студента самое главное не сдать экзамен, а вовремя вспомнить про него. 9825 – | 7406 – или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Процесс проектирования современных строений и построек регулируется огромным количеством различных строительных норм и правил. В большинстве случаев нормы требуют обеспечения определенных характеристик, например, деформации или прогиба балок плит перекрытия под статической или динамической нагрузкой. Например, СНиП № 2.09.03-85 определяет для опор и эстакад прогиб балки не более чем в 1/150 длины пролета. Для чердачных перекрытий этот показатель составляет уже 1/200, а для межэтажных балок и того меньше – 1/250. Поэтому одним из обязательных этапов проектирования является выполнение расчета балки на прогиб.

Способы выполнить расчет и проверку на прогиб

Причина, по которой СНиПы устанавливают столь драконовские ограничения, проста и очевидна. Чем меньше деформация, тем больше запас прочности и гибкости конструкции. Для прогиба менее 0,5% несущий элемент, балка или плита все еще сохраняет упругие свойства, что гарантирует нормальное перераспределение усилий и сохранение целостности всей конструкции. С увеличением прогиба каркас здания прогибается, сопротивляется, но стоит, с выходом за пределы допустимой величины происходит разрыв связей, и конструкция лавинообразно теряет жесткость и несущую способность.

Просчитать прогиб конструкции можно несколькими способами:

Воспользоваться программным онлайн-калькулятором, в котором «зашиты» стандартные условия, и не более того;
Использовать готовые справочные данные для различных типов и видов балок, для различных опор схем нагрузок. Нужно только правильно идентифицировать тип и размер балки и определить искомый прогиб;
Посчитать допустимый прогиб руками и своей головой, большинство проектировщиков так и делают, в то время как контролирующие архитектурные и строительные инспекции предпочитают второй способ расчета.

Измерив, насколько просела балка потолочного перекрытия, можно с 99% уверенностью определить, находится ли конструкция в аварийном состоянии или нет.

Методика выполнения расчета на прогиб

Прежде чем приступать к расчету, нужно будет вспомнить некоторые зависимости из теории сопротивления материалов и составить расчетную схему. В зависимости от того, насколько правильно выполнена схема и учтены условия нагружения, будет зависеть точность и правильность расчета.

Используем простейшую модель нагруженной балки, изображенной на схеме. Простейшей аналогией балки может быть деревянная линейка, фото.

В нашем случае балка:

Имеет прямоугольное сечение S=b*h , длина опирающейся части составляет L ;
Линейка нагружена силой Q , проходящей через центр тяжести изгибаемой плоскости, в результате чего концы поворачиваются на небольшой угол θ , с прогибом относительно начального горизонтального положения, равным f ;
Концы балки опираются шарнирно и свободно на неподвижных опорах, соответственно, не возникает горизонтальной составляющей реакции, и концы линейки могут перемещаться в произвольном направлении.

Для определения деформации тела под нагрузкой используют формулу модуля упругости, который определяется по соотношению Е=R/Δ , где Е – справочная величина, R — усилие, Δ — величина деформации тела.

Вычисляем моменты инерции и сил

Для нашего случая зависимость будет выглядеть так: Δ = Q/(S·Е) . Для распределенной вдоль балки нагрузки q формула будет выглядеть так: Δ = q·h/(S·Е) .

Далее следует наиболее принципиальный момент. Приведенная схема Юнга показывает прогиб балки или деформацию линейки так, если бы ее раздавливали под мощным прессом. В нашем случае балку изгибают, а значит, на концах линейки, относительно центра тяжести, приложены два изгибающих момента с разным знаком. Эпюра нагружения такой балки приведена ниже.

Чтобы преобразовать зависимость Юнга для изгибающего момента, необходимо обе части равенства умножить на плечо L. Получаем Δ*L = Q·L/(b·h·Е) .

Если представить, что одна из опор жестко закреплена, а на второй будет приложен эквивалентный уравновешивающий момент сил M_max = q*L*2/8 , соответственно, величина деформации балки будет выражаться зависимостью Δх = M·х/((h/3)·b·(h/2)·Е) . Величину b·h 2 /6 называют моментом инерции и обозначают W . В итоге получается Δх = M·х/(W·Е) основополагающая формула расчета балки на изгиб W=M/E через момент инерции и изгибающий момент.

Чтобы точно выполнить расчет прогиба, потребуется знать изгибающий момент и момент инерции. Величину первого можно посчитать, но конкретная формула для расчета балки на прогиб будет зависеть от условий контакта с опорами, на которых находится балка, и способа нагружения, соответственно для распределенной или концентрированной нагрузки. Изгибающий момент от распределенной нагрузки считается по формуле Mmax = q*L 2 /8. Приведенные формулы справедливы только для распределенной нагрузки. Для случая, когда давление на балку сконцентрировано в определенной точке и зачастую не совпадает с осью симметрии, формулу для расчета прогиба приходится выводить с помощью интегрального исчисления.

Момент инерции можно представить, как эквивалент сопротивления балки изгибающей нагрузке. Величину момента инерции для простой прямоугольной балки можно посчитать по несложной формуле W=b*h 3 /12, где b и h – размеры сечения балки.

Из формулы видно, что одна и та же линейка или доска прямоугольного сечения может иметь совершенно разный момент инерции и величину прогиба, если положить ее на опоры традиционным способом или поставить на ребро. Недаром практически все элементы стропильной системы крыши изготавливаются не из бруса 100х150, а из доски 50х150.

Реальные сечения строительных конструкций могут иметь самые разные профили, от квадрата, круга до сложных двутавровых или швеллерных форм. При этом определение момента инерции и величины прогиба вручную, «на бумажке», для таких случаев становится нетривиальной задачей для непрофессионального строителя.

Формулы для практического использования

На практике чаще всего стоит обратная задача – определить запас прочности перекрытий или стен для конкретного случая по известной величине прогиба. В строительном деле очень сложно дать оценку запасу прочности иными, неразрушающими методами. Нередко по величине прогиба требуется выполнить расчет, оценить запас прочности здания и общее состояние несущих конструкций. Мало того, по выполненным измерениям определяют, является деформация допустимой, согласно расчету, или здание находится в аварийном состоянии.

Например, если вы намерены покупать готовое здание, простоявшее достаточно долго на проблемном грунте, нелишним будет проверить состояние перекрытия по имеющемуся прогибу. Зная предельно допустимую норму прогиба и длину балки, можно безо всякого расчета оценить, насколько критическим является состояние строения.

Строительная инспекция при оценке прогиба и оценке несущей способности перекрытия идет более сложным путем:

Первоначально измеряется геометрия плиты или балки, фиксируется величина прогиба;
По измеренным параметрам определяется сортамент балки, далее по справочнику выбирается формула момента инерции;
По прогибу и моменту инерции определяют момент силы, после чего, зная материал, можно выполнить расчет реальных напряжений в металлической, бетонной или деревянной балке.

Вопрос – почему так сложно, если прогиб можно получить, используя для расчета формулу для простой балки на шарнирных опорах f=5/24*R*L 2 /(E*h) под распределенным усилием. Достаточно знать длину пролета L, высоту профиля, расчетное сопротивление R и модуль упругости Е для конкретного материала перекрытия.

Ответ прост — необходимо непросто рассчитать, но и сохранить на бумаге ход выполнения проверочного расчета, чтобы сделанные выводы о состоянии перекрытия можно было проверить и перепроверить по всем этапам проверки.

Заключение

Аналогичным образом поступает большинство разработчиков и проектантов серьезных построек. Программа – это хорошо, она помогает очень быстро выполнить расчет прогиба и основных параметров нагружения перекрытия, но важно также предоставить заказчику документальное подтверждение полученных результатов в виде конкретных последовательных расчетов на бумаге.

Расчет прогиба балки методом начальных параметров

В этой статье будут рассмотрены основные нюансы расчета прогибов, методом начальных параметров, на примере консольной балки, работающей на изгиб. А также рассмотрим пример, где с помощью универсального уравнения, определим прогиб балки и угол поворота.

Теория по методу начальных параметров

Возьмем консольную балку, нагруженную сосредоточенной силой, моментом, а также распределенной нагрузкой. Таким образом, зададимся такой расчетной схемой, где присутствуют все виды нагрузок, тем самым, охватим всю теоретическую часть по максимуму. Обозначим опорные реакции в жесткой заделке, возникающие под действием внешней нагрузки:

Выбор базы и обозначение системы координат

Для балки выберем базу с левой стороны, от которой будем отсчитывать расстояния до приложения сил, моментов, начала и конца распределенной нагрузки. Базу обозначим буквой O и проведем через нее систему координат:

Базу традиционно выбирают с левого краю балки, но можно выбрать ее и справа. Тогда в уравнении будут противоположные знаки, это может пригодиться в некоторых случаях, упростит немного решение. Понимание, когда принимать базу слева или справа, придет с опытом решения задач на метод начальных параметров.

Универсальное уравнение прогибов для балки

После введения базы, системы координат и обозначении расстояний а, б, в, г записываем универсальную формулу, с помощью которой, будем рассчитывать прогиб балки (вертикальное перемещение сечения K, находящегося на свободном торце балки): Теперь поговорим об этой формуле, проанализируем так сказать:

E – модуль упругости;
I – момент инерции;
V_k – прогиб сечения K;
V_O – прогиб сечения O;
θ_O – угол поворота сечения О.

Не буду приводить вывод этой формулы, не хочу отпугивать читателей, продвинутые студенты могут ознакомиться с выводом самостоятельно в учебнике по сопромату. Я только расскажу об основных закономерностях этого уравнения и как записать его для любой балки постоянного сечения.

Итак, изучаем эту формулу с лева направо. В левой части уравнения обознается искомый прогиб, в нашем случае V_k, который дополнительно умножается на жесткость балки — EI:В уравнении всегда учитывается прогиб сечения балки, совпадающего с нашей базой EIV_O:

Также всегда учитывается угол поворота сечения совпадающего с выбранной базой. Причем, произведение EIθ_O всегда умножается на расстояние от базы до сечения, прогиб которого рассчитывается, в нашем примере — это расстояние г.

Следующие компоненты этого уравнения учитывают всю нагрузку находящуюся слева от рассматриваемого сечения. В скобках расстояния от базы до сечения отнимаются расстояния от базы до соответствующей силы или момента, начала или конца распределенной нагрузки.

Скобка, в случае с сосредоточенными силами, возводится в 3 степень и делится на 6. Если сила смотрит вверх, то считаем ее положительной, если вниз, то в уравнении она записывается с минусом:

В случае с моментами, скоба возводится во 2 степень и делится на 2. Знак у момента будет положительный, когда он направлен почасовой стрелке и отрицательным, соответственно, когда против часовой стрелки.

Учет распределенной нагрузки

Теперь поговорим о распределенной нагрузке. Как уже говорилось, в уравнении метода начальных параметров должно учитываться начало и конец распределенной нагрузки, но конец ее совпадает с сечением, прогиб которого мы хотим вычислить, поэтому в уравнение попадает только ее начало.

Причем важно, даже если бы в этом сечении была бы сила или момент, их бы так же не учитывали. Нас интересует все, что находится слева от рассматриваемого сечения.

Для распределенной нагрузки скобочка возводится в 4 степень и делится на 24. Правило знаков такое же, как и для сосредоточенных сил:

Граничные условия

Чтобы решить уравнение нам понадобятся еще кое-какие данные. С первого взгляда в уравнении у нас наблюдается три неизвестных: V_K, VO и θ_O. Но кое-что мы можем почерпнуть из самой схемы. Мы знаем, в жесткой заделке не может быть никаких прогибов, и ни каких поворотов, то есть V_O=0 и θ_O=0, это и есть так называемые начальные параметры или их еще называют граничными условиями. Теперь, если бы у нас была реальная задача, мы бы подставили все численные данные и нашли перемещение сечения K.

Если бы балка была закреплена с помощью шарнирно подвижной и неподвижной опоры, тогда мы бы приняли прогибы в опорах равными нулю, но угол поворота в опорах был бы уже отличен от нуля. Более подробно об этом рассказано в другой моей статье, посвященной методу начальных параметров на примере балки на двух опорах.

Чуть не забыл про еще одну величину, которую часто требуется определять методом начальных параметров. Как известно, при изгибе, поперечные сечения балок помимо того, что перемещаются вертикально (прогибаются) так еще и поворачиваются на какой-то угол. Углы поворота и прогибы поперечных сечений связаны дифференциальной зависимостью.

Если продифференцировать уравнение, которое мы получили для прогиба поперечного сечения K, то получим уравнение угла поворота этого сечения:

Пример расчета прогиба балки

Для закрепления пройденного материала, предлагаю рассмотреть пример с заданными численными значениями всех параметров балки и нагрузок. Возьмем также консольную балку, которая жестко закреплена с правого торца. Будем считать, что балка изготовлена из стали (модуль упругости E = 2·10⁵ МПа), в сечении у нее двутавр №16 (момент инерции по сортаменту I = 873 см⁴). Рассчитывать будем прогиб свободного торца, находящегося слева.

Подготовительный этап

Проводим подготовительные действия, перед расчетом прогиба: помечаем базу O, с левого торца балки, проводим координатные оси и показываем реакции, возникающие в заделке, под действием заданной нагрузки:

В методе начальных параметров, есть еще одна особенность, которая касается распределенной нагрузки. Если на балку действует распределенная нагрузка, то ее конец, обязательно должен находиться на краю балки (в точке наиболее удаленной от заданной базы). Только в таком случае, рассматриваемый метод будет работать. В нашем примере, нагрузка, как видно, начинается на расстоянии 2 м. от базы и заканчивается на 4 м. В таком случае, нагрузка продлевается до конца балки, а искусственное продление компенсируется дополнительной, противоположно-направленной нагрузкой. Тем самым, в расчете прогибов будет уже учитываться 2 распределенные нагрузки:

Расчет прогиба

Записываем граничные условия для заданной расчетной схемы:

V_A = 0 при x = 6м

θ_A = 0 при x = 6м

Напомню, что нас, в этом примере, интересует прогиб сечения O (V_O). Для его нахождения составим уравнение, для сечения A, в которое будет входить искомая величина:

В полученном уравнении, у нас содержится две неизвестные величины: искомый прогиб V_Oи угол поворота этого сечения — θ_O:

Таким образом, чтобы решить поставленную задачу, составим дополнительное уравнение, но только теперь, не прогибов, а углов поворотов, для сечения A:Из второго уравнения, найдем угол поворота:После чего, рассчитываем искомый прогиб:

Таким образом, свободный торец такой балки, прогнется практически на 6 см. Данную задачу, можно решить несколько проще, если ввести базу с правого торца. В таком случае, для решения потребовалось бы лишь одно уравнение, однако, оно было бы немного объемнее, т.к. включало реакции в заделке.

Выполнение расчета прогиба деревянной балки

При действии нагрузки деревянные балки могут получать довольно большие прогибы, в результате которых нарушается их нормальная эксплуатация. Поэтому кроме расчетов по первой группе предельных состояний (прочность), необходимо выполнить расчет деревянных балок и по второй группе т. е.

по прогибам. Расчет деревянных балок на прогиб выполняется на действие нормативных нагрузок. Нормативную нагрузку получаем разделением расчетной нагрузки на коэффициент надежности по нагрузке.

Вычесление нормативной нагрузки выполнятся в сервисе расчет деревянных балокавтоматически. Нормальная эксплуатация балок возможна, в случае если расчетный прогиб деревянной балки не превышает прогиб, установленный нормами. Нормативными документами установлены конструктивные и эстетико-психологические требования.

1. Конструктивные требования к прогибам деревянных балок.

Представлены в СП64.13330.2011 “ДЕРЕВЯННЫЕ КОНСТРУКЦИИ” Таблица 19Элементы конструкцийПредельные прогибы в долях пролета, не более1 Балки междуэтажных перекрытий 2 Балки чердачных перекрытий 3 Покрытия (кроме ендов): а) прогоны, стропильные ноги б) балки консольные в) фермы, клееные балки (кроме консольных) г) плиты д) обрешетки, настилы 4 Несущие элементы ендов 5 Панели и элементы фахверха1/2501/2001/2001/1501/3001/250 1/1501/4001/250

1. Эстетическо-психологические требования к прогибам деревянных балок.

Представлены в СП20.13330.2011 “НАГРУЗКИ И ВОЗДЕЙСТВИЯ” Приложение Е.2

Элементы конструкцийВертикальные предельные прогибы 2 Балки, фермы, ригели, прогоны, плиты, настилы (включая поперечные ребра плит и настилов):а) покрытий и перекрытий, открытых для обзора, при пролете l, м: l<1 l<3 l<6 l<12 l<24 1/1201/150 1/2001/2501/300В случае если балка скрыта (к примеру, под подшивным потолком) то соблюдение эстетико-психологических требований не является обязательным. В данном случае необходимо выполнить расчет прогибов балкина соблюдение только конструктивных требований по прогибам.

Чтобы построить деревянный дом необходимо провести расчёт несущей способности деревянной балки. Также особое значение в строительной терминологии имеет определение прогиба.

Без качественного математического анализа всех параметров просто невозможно построить дом из бруса. Именно поэтому перед тем как начать строительство крайне важно правильно рассчитать прогиб деревянных балок. Данные расчёты послужат залогом вашей уверенности в качестве и надёжности постройки.

Что нужно для того чтобы сделать правильный расчёт

Расчёт несущей способности и прогиба деревянных балок не такая простая задача, как может показаться на первый взгляд. Чтобы определить, сколько досок вам нужно, а также, какой у них должен быть размер необходимо потратить немало времени, или же вы просто можете воспользоваться нашим калькулятором.

Во-первых, нужно замерить пролёт, который вы собираетесь перекрыть деревянными балками.

Во-вторых, уделите повышенное внимание методу крепления. Крайне важно, насколько глубоко фиксирующие элементы будут заходить в стену. Только после этого вы сможете сделать расчёт несущей способности вместе с прогибом и ряда других не менее важных параметров.

Длина

Перед тем как рассчитать несущую способность и прогиб, нужно узнать длину каждой деревянной доски.

Данный параметр определяется длиной пролёта. Тем не менее это не всё. Вы должны провести расчёт с некоторым запасом.

Важно! Если деревянные балки заделываться в стены — это напрямую влияет на их длину и все дальнейшие расчёты.

При подсчёте особое значение имеет материал, из которого сделан дом. Если это кирпич, доски будут монтироваться внутрь гнёзд. Приблизительная глубина около 100—150 мм.

Когда речь идёт о деревянных постройках параметры согласно СНиПам сильно меняются. Теперь достаточно глубины в 70—90 мм. Естественно, что из-за этого также изменится конечная несущая способность.

Если в процессе монтажа применяются хомуты или кронштейны, то длина брёвен или досок соответствует проёму. Проще говоря, высчитайте расстояние от стены до стены и в итоге сможете узнать несущую способность всей конструкции.

Важно! При формировании ската крыши брёвна выносятся за стены на 30—50 сантиметров. Это нужно учесть при подсчёте способности конструкции противостоять нагрузкам.

К сожалению, далеко не всё зависит от фантазии архитектора, когда дело касается исключительно математики. Для обрезной доски максимальная длина шесть метров. В противном случае несущая способность уменьшается, а прогиб становится больше.

Само собой, что сейчас не редкость дома, у которых пролёт достигает 10—12 метров. В таком случае используется клееный брус.

Он может быть двутавровым или же прямоугольным. Также для большей надёжности можно использовать опоры. В их качестве идеально подходят дополнительные стены или колоны.

Совет! Многие строители при необходимости перекрыть длинный пролёт используют фермы.

Общая информация по методологии расчёта

В большинстве случаев в малоэтажном строительстве применяются однопролётные балки.

Они могут быть в виде брёвен, досок или брусьев. Длина элементов может варьироваться в большом диапазоне. В большинстве случаев она напрямую зависит от параметров строения, которые вы собираетесь возвести.

Внимание! Представленный в конце странички калькулятор расчета балок на прогиб позволит вам просчитать все значения с минимальными затратами времени. Чтобы воспользоваться программой, достаточно ввести базовые данные.

Роль несущих элементов в конструкции выполняют деревянные бруски, высота сечения которых составляет от 140 до 250 мм, толщина лежит в диапазоне 55—155 мм. Это наиболее часто используемые параметры при расчёте несущей способности деревянных балок.

Очень часто профессиональные строители для того чтобы усилить конструкцию используют перекрёстную схему монтажа балок. Именно эта методика даёт наилучший результат при минимальных затратах времени и материалов.

Если рассматривать длину оптимального пролёта при расчёте несущей способности деревянных балок, то лучше всего ограничить фантазию архитектора в диапазоне от двух с половиной до четырёх метров.

Внимание! Лучшим сечением для деревянных балок считается площадь, у которой высота и ширина соотносятся как 1,5 к 1.

Как рассчитать несущую способность и прогиб

Стоит признать, что за множество лет практики в строительном ремесле был выработан некий канон, который чаще всего используют для того, чтобы провести расчёт несущей способности:

M/W<=Rд

Расшифруем значение каждой переменной в формуле:

Буква Мвначале формулы указывает на изгибающий момент. Он исчисляется в кгс*м.Wобозначает момент сопротивления. Единицы измерения см3.

Расчёт прогиба деревянной балки является частью, представленной выше формулы. Буква Муказывает нам на данный показатель. Чтобы узнать параметр применяется следующая формула:

M=(ql2)/8

В формуле расчёта прогиба есть всего две переменных, но именно они в наибольшей степени определяют, какой в конечном итоге будет несущая способность деревянной балки:

Символ q показывает нагрузку, которую способна выдержать доска.В свою очередь буква l— это длина одной деревянной балки.

Внимание! Результат расчёт несущей способности и прогиба зависит от материала из которого сделана балка, а также от способа его обработки.

Насколько важно правильно рассчитать прогиб

Этот параметр крайне важен для прочности всей конструкции. Дело в том, что одной стойкости бруса недостаточно для долгой и надёжной службы, ведь со временем его прогиб под нагрузкой может увеличиваться.

Прогиб не просто портит эстетичный вид перекрытия. Если данный параметр превысит показатель в 1/250 от общей длины элемента перекрытия, то вероятность возникновения аварийной ситуации возрастёт в десятки раз.

Так зачем нужен калькулятор

Представленный ниже калькулятор позволит вам моментально просчитать прогиб, несущую способность и многие другие параметры без использования формул и подсчётов. Всего несколько секунд и данные по вашему будущему дому будут готовы.

В современном индивидуальном строительстве деревянные балки используются почти в каждом проекте. Найти постройку, в которой не используются деревянные перекрытия, практически невозможно. Деревянные балки применяются и для устройства полов, и в качестве несущих элементов, как опоры для межэтажных и чердачных перекрытий.

Формула расчета прогиба балки.

Известно, что деревянные балки, как и любые другие, могут прогибаться под воздействием различных нагрузок.

Эта величина — стрелка прогиба — зависит от материала, характера нагрузки и геометрических характеристик конструкции. Небольшой прогиб вполне допустим. Когда мы ходим, например, по деревянному настилу, то чувствуем, как пол слегка пружинит, однако если такие деформации незначительны, то нас это мало беспокоит.

Насколько можно допустить прогиб, определяется двумя факторами:

Прогиб не должен превышать расчетных допустимых значений.Прогиб не должен мешать эксплуатации здания.

Чтобы узнать, насколько будут деформироваться деревянные элементы в конкретном случае, нужно произвести расчеты на прочность и жесткость. Подробные и детальные расчеты такого рода — это работа инженеров-строителей, однако, имея навык математических вычислений и зная несколько формул из курса сопротивления материалов, вполне можно самостоятельно рассчитать деревянную балку.

Вспомогательная таблица для расчета количества балок.

Любая постройка должна быть прочной.

Именно поэтому балки перекрытия проверяют в первую очередь на прочность, чтобы конструкция могла выдерживать все необходимые нагрузки, не разрушаясь. Кроме прочности конструкция должна обладать жесткостью и устойчивостью. Величина прогиба является элементом расчета на жесткость.

Прочность и жесткость неразрывно связаны между собой. Вначале делают расчеты на прочность, а затем, используя полученные результаты, можно сделать расчет прогиба.

Чтобы правильно спроектировать собственный загородный дом, необязательно знать полный курс сопротивления материалов. Но углубляться в слишком подробные вычисления не стоит, как и просчитывать различные варианты конструкций.

Чтобы не ошибиться, лучше воспользоваться укрупненными расчетами, применяя простые схемы, а высчитывая нагрузки на несущие элементы, всегда делать небольшой запас в большую сторону.

Алгоритм вычисления прогиба

Рассмотрим упрощенную схему расчета, опуская некоторые специальные термины, и формулы для расчета двух основных случаев нагружения, принятых в строительстве.

Нужно выполнить следующие действия:

Составить расчетную схему и определить геометрические характеристики балки.Определить максимальную нагрузку на этот несущий элемент.При необходимости проверить брус на прочность по изгибающему моменту.Вычислить максимальный прогиб.

Расчетная схема балки и момент инерции

Расчетную схему сделать довольно просто. Нужно знать размеры и форму поперечного сечения элемента конструкции, способ опирания, а также пролет, то есть расстояние между опорами. Например, если вы укладываете опорные брусья перекрытия на несущие стены дома, а расстояние между стенами 4 м, то пролет будет l=4 м.

Деревянные балки рассчитывают как свободно опертые. Если это балка перекрытия, то принимается схема с равномерно распределенной нагрузкой q. В случае если нужно определить изгиб от сосредоточенной нагрузки (например, от небольшой печки, выложенной прямо на перекрытии), принимается схема с сосредоточенной нагрузкой F, равной весу, который будет давить на конструкцию.

Для определения величины прогиба f необходима такая геометрическая характеристика, как момент инерции сечения J.4.
Здесь нужно обратить внимание на то, что момент инерции прямоугольного сечения зависит от того, как оно сориентировано в пространстве. Если брус положить широкой стороной на опоры, то момент инерции будет значительно меньше, а прогиб — больше.
Этот эффект каждый может прочувствовать на практике. Все знают, что доска, положенная обычным способом, прогибается гораздо сильнее, чем та же доска, положенная на ребро. Это свойство очень хорошо отражается в самой формуле для вычисления момента инерции.
Определение максимальной нагрузки
Для определения максимальной нагрузки на балку нужно сложить все ее составляющие: вес самого бруса, вес перекрытия, вес обстановки вместе с находящимися там людьми, вес перегородок.
Все это нужно сделать в пересчете на 1 пог. м балки. Таким образом, нагрузка q будет состоять из следующих показателей:
Расчет на смятие опорных участков балки.
вес 1 пог.
м балки;вес 1 кв. м перекрытия;временная нагрузка на перекрытие;нагрузка от перегородок на 1 кв.3/48*E*J, где:
F — сила давления на брус, например, вес печи или другого тяжелого оборудования.
Модуль упругости Е для разных видов древесины различен, эта характеристика зависит не только от породы дерева, но и от вида бруса — цельные балки, клееный брус или оцилиндрованное бревно имеют различные модули упругости.
Подобные вычисления могут производиться с различными целями. Если вам нужно просто узнать, в каких пределах будут находиться деформации элементов конструкции, то после определения стрелки прогиба дело можно считать завершенным. Но если вас интересует, насколько полученные результаты соответствуют строительным нормам, то необходимо выполнить сравнение полученных результатов с цифрами, приведенными в соответствующих нормативных документах.
Балка является основным элементом несущей конструкции сооружения.
При строительстве важно провести расчет прогиба балки. В реальном строительстве на данный элемент действует сила ветра, нагружение и вибрации. Однако при выполнении расчетов принято принимать во внимание только поперечную нагрузку или проведенную нагрузку, которая эквивалентна поперечной.
При расчете балка воспринимается как жесткозакрепленный стержень, который устанавливается на двух опорах.
Если она устанавливается на трех и более опорах, расчет ее прогиба является более сложным, и провести его самостоятельно практически невозможно.Основное нагружение рассчитывается как сумма сил, которые действуют в направлении перпендикулярного сечения конструкции. Расчетная схема требуется для определения максимальной деформации, которая не должна быть выше предельных значений. Это позволит определить оптимальный материал необходимого размера, сечения, гибкости и других показателей.
Виды балок
Для строительства различных сооружений применяются балки из прочных и долговечных материалов. Такие конструкции могут отличаться по длине, форме и сечению.
Чаще всего используются деревянные и металлические конструкции. Для расчетной схемы прогиба большое значение имеет материал элемента. Особенность расчета прогиба балки в данном случае будет зависеть от однородности и структуры ее материала.
Деревянные
Для постройки частных домов, дач и другого индивидуального строительства чаще всего используются деревянные балки. Деревянные конструкции, работающие на изгиб, могут использоваться для потолочных и напольных перекрытий.
Для расчета максимального прогиба следует учитывать:
Материал. Различные породы дерева обладают разным показателем прочности, твердости и гибкости.Форма поперечного сечения и другие геометрические характеристики.Различные виды нагрузки на материал.
Допустимый прогиб балки учитывает максимальный реальный прогиб, а также возможные дополнительные эксплуатационные нагрузки.
Конструкции из древесины хвойных пород
Стальные
Металлические балки отличаются сложным или даже составным сечением и чаще всего изготавливаются из нескольких видов металла. При расчете таких конструкций требуется учитывать не только их жесткость, но и прочность соединений.
Металлические конструкции изготавливаются путем соединения нескольких видов металлопроката, используя при этом такие виды соединений:
электросварка;заклепки;болты, винты и другие виды резьбовых соединений.
Стальные балки чаще всего применяются для многоэтажных домов и других видов строительства, где требуется высокая прочность конструкции. В данном случае при использовании качественных соединений гарантируется равномерно распределенная нагрузка на балку.
Для проведения расчета балки на прогиб может помочь видео:
Прочность и жесткость балки
Чтобы обеспечить прочность, долговечность и безопасность конструкции, необходимо выполнять вычисление величины прогиба балок еще на этапе проектирования сооружения. Поэтому крайне важно знать максимальный прогиб балки, формула которого поможет составить заключение о вероятности применения определенной строительной конструкции.
Использование расчетной схемы жесткости позволяет определить максимальные изменения геометрия детали.
Расчет конструкции по опытным формулам не всегда эффективен. Рекомендуется использовать дополнительные коэффициенты, позволяющие добавить необходимый запас прочности. Не оставлять дополнительный запас прочности – одна из основных ошибок строительства, которая приводит к невозможности эксплуатации здания или даже тяжелым последствиям.
Существует два основных метода расчета прочности и жесткости:
Простой. При использовании данного метода применяется увеличительный коэффициент.Точный. Данный метод включает в себя использование не только коэффициентов для запаса прочности, но и дополнительные вычисления пограничного состояния.
Последний метод является наиболее точным и достоверным, ведь именно он помогает определить, какую именно нагрузку сможет выдержать балка.
Расчет на жесткость
Для расчета прочности балки на изгиб применяется формула:
Где:
M – максимальный момент, который возникает в балке;
Wn,min– момент сопротивления сечения, который является табличной величиной или определяется отдельно для каждого вида профиля.
Ryявляется расчетным сопротивлением стали при изгибе. Зависит от вида стали.
γcпредставляет собой коэффициент условий работы, который является табличной величиной.
Расчет жесткости или величины прогиба балки является достаточно простым, поэтому расчеты может выполнить даже неопытный строитель. Однако для точного определения максимального прогиба необходимо выполнить следующие действия:
Составление расчетной схемы объекта.Расчет размеров балки и ее сечения.Вычисление максимальной нагрузки, которая воздействует на балку.Определение точки приложения максимальной нагрузки.Дополнительно балка может быть проверена на прочность по максимальному изгибающему моменту.Вычисление значения жесткости или максимально прогиба балки.
Чтобы составить расчетную схему, потребуются такие данные:
размеры балки, длину консолей и пролет между ними;размер и форму поперечного сечения;особенности нагрузки на конструкцию и точно ее приложения;материал и его свойства.
Если производится расчет двухопорной балки, то одна опора считается жесткой, а вторая – шарнирной.
Расчет моментов инерции и сопротивления сечения
Для выполнения расчетов жесткости потребуется значение момент инерции сечения (J) и момента сопротивления (W). Для расчета момента сопротивления сечения лучше всего воспользоваться формулой:
Важной характеристикой при определении момента инерции и сопротивления сечения является ориентация сечения в плоскости разреза. При увеличении момента инерции увеличивается и показатель жесткости.
Определение максимальной нагрузки и прогиба
Для точного определения прогиба балки, лучше всего применять данную формулу:
Где:
q является равномерно-распределенной нагрузкой;
E – модуль упругости, который является табличной величиной;
l – длина;
I – момент инерции сечения.
Чтобы рассчитать максимальную нагрузку, следует учитывать статические и периодические нагрузки. К примеру, если речь идет о двухэтажном сооружении, то на деревянную балку будет постоянно действовать нагрузка от ее веса, техники, людей.
Особенности расчета на прогиб
Расчет на прогиб проводится обязательно для любых перекрытий.
Крайне важен точный расчет данного показателя при значительных внешних нагрузках. Сложные формулы в данном случае использовать необязательно. Если использовать соответствующие коэффициенты, то вычисления можно свести к простым схемам:
Стержень, который опирается на одну жесткую и одну шарнирную опору, и воспринимает сосредоточенную нагрузку.Стержень, который опирается на жесткую и шарнирную опору, и при этом на него действует распределенное нагружение.Варианты нагружения консольного стержня, который закреплен жестко.Действие на конструкцию сложной нагрузки.
Применение этого метода вычисления прогиба позволяет не учитывать материал. Поэтому на расчеты не влияют значения его основных характеристик.
Пример подсчета прогиба
Чтобы понять процесс расчета жесткости балки и ее максимального прогиба, можно использовать простой пример проведения расчетов. Данный расчет проводится для балки с такими характеристиками:
материал изготовления – древесина;плотность составляет 600 кг/м3;длина составляет 4 м;сечение материала составляет 150*200 мм;масса перекрывающих элементов составляет 60 кг/м²;максимальная нагрузка конструкции составляет 249 кг/м;упругость материала составляет 100 000 кгс/ м²;J равно 10 кг*м².
Для вычисления максимальной допустимой нагрузки учитывается вес балки, перекрытий и опор. Рекомендуется также учесть вес мебели, приборов, отделки, людей и других тяжелых вещей, который также будут оказывать воздействие на конструкцию. Для расчета потребуются такие данные:
вес одного метра балки;вес м2 перекрытия;расстояние, которое оставляется между балками;временная нагрузка;нагрузка от перегородок на перекрытие.
Чтобы упросить расчет данного примера, можно принять массу перекрытия за 60 кг/м², нагрузку на каждое перекрытие за 250 кг/м², нагрузки на перегородки 75 кг/м², а вес метра балки равным 18 кг. При расстоянии между балками в 60 см, коэффициент k будет равен 0,6.
Если подставить все эти значения в формулу, то получится:
q = ( 60 + 250 + 75 ) * 0,6 + 18 = 249 кг/м.
Для расчета изгибающего момента следует воспользоваться формулой f = (5 / 384) * [(qn * L4) / (E * J)] £ [¦].
Подставив в нее данные, получается f = (5 / 384) * [(qn * L4) / (E * J)] = (5 / 384) * [(249 * 44) / (100 000 * 10)] = 0,13020833 * [(249 * 256) / (100 000 * 10)] = 0,13020833 * (6 3744 / 10 000 000) = 0,13020833 * 0,0000063744 = 0,00083 м = 0,83 см.
Именно это и является показателем прогиба при воздействии на балку максимальной нагрузки. Данные расчеты показывают, что при действии на нее максимальной нагрузки, она прогнется на 0,83 см. Если данный показатель меньше 1, то ее использование при указанных нагрузках допускается.
Использование таких вычислений является универсальным способом вычисления жесткости конструкции и величины их прогибания. Самостоятельно вычислить данные величины достаточно легко. Достаточно знать необходимые формулы, а также высчитать величины.
Некоторые данные необходимо взять в таблице. При проведении вычислений крайне важно уделять внимание единицам измерения. Если в формуле величина стоит в метрах, то ее нужно перевести в такой вид.
Такие простые ошибки могут сделать расчеты бесполезными. Для вычисления жесткости и максимального прогиба балки достаточно знать основные характеристики и размеры материала. Эти данные следует подставить в несколько простых формул.
Источники:
rascheta.net
bouw.ru
1poderevu.ru
viascio.ru
Отклонение луча: что это такое?
Отклонение луча: что это такое? (Определение отклонения)
Прогиб, в терминологии проектирования конструкций, относится к перемещению балки или узла из исходного положения из-за сил и нагрузок, приложенных к элементу. Это также известно как смещение и может происходить из-за приложенных извне нагрузок или из-за веса самой конструкции и силы тяжести, к которой это относится.
Прогиб может возникать в балках, ферм, каркасах и в основном в любой другой конструкции.Чтобы определить отклонение, возьмем простое отклонение консольной балки, в конце которой стоит человек с весом (W):
Сила человека, стоящего в конце, заставит балку изгибаться и отклоняться от своего естественного положения. На приведенной ниже диаграмме синяя балка соответствует исходному положению, а пунктирная линия имитирует отклонение консольной балки:
Как видите, балка изогнулась или отошла от исходного положения. Это расстояние в каждой точке стержня является значением или определением отклонения.
Как правило, существует 4 основные переменные, которые определяют величину прогиба балки. К ним относятся:
Какая нагрузка на конструкцию
Длина неподдерживаемого стержня
Материал, в частности модуль Юнга
Размер поперечного сечения, а именно момент инерции (I)
Уравнения отклонения балки
Прогиб балки (прогиб балки) рассчитывается на основе множества факторов, включая материалы, момент инерции секции, приложенную силу и расстояние от опоры.Существует ряд формул и уравнений прогиба балки, которые можно использовать для расчета базового значения прогиба в различных типах балок.
Как правило, прогиб можно рассчитать путем деления двойного интеграла уравнения изгибающего момента M (x) на EI (модуль Юнга x момент инерции).
Какая единица измерения отклонения?
Единица отклонения или смещения — это единица длины и обычно принимается в миллиметрах (для метрических единиц) и дюймах (для британских).Это число определяет расстояние, на которое луч отклонился от исходного положения.
Отклонение консольной балки
Консольные балки — это балки особого типа, которые ограничены только одной опорой, как показано в приведенном выше примере. Эти элементы, естественно, будут отклоняться больше, поскольку они поддерживаются только с одного конца.
Для расчета прогиба консольной балки вы можете использовать приведенное ниже уравнение, где W — сила в конечной точке, L — длина консольной балки, E = модуль Юнга и I = момент инерции.
Просто поддерживаемое отклонение луча
Другой пример отклонения — отклонение балки с простой опорой. Эти балки поддерживаются на обоих концах, поэтому отклонение балки обычно левое и имеет форму, сильно отличающуюся от формы консоли. Под действием равномерно распределенной нагрузки (например, собственного веса) балка будет плавно отклоняться к средней точке:
Мы надеемся, что вы нашли эту короткую статью, чтобы определить прогиб балки в проектировании конструкций.Пожалуйста, не стесняйтесь оставлять комментарии ниже или попробуйте воспользоваться нашим калькулятором пролета балки, чтобы попробовать на себе и применить эту теоретическую концепцию на практике с помощью программного обеспечения для расчета конструкций.
Напряжение и отклонение балки | MechaniCalc
ПРИМЕЧАНИЕ. Эта страница использует JavaScript для форматирования уравнений для правильного отображения. Пожалуйста, включите JavaScript.
Многие конструкции можно представить как прямую балку или как набор прямых балок. По этой причине анализ напряжений и прогибов в балке является важной и полезной темой.
В этом разделе рассматриваются поперечная сила и изгибающий момент в балках, диаграммы сдвига и момента, напряжения в балках и таблица общих формул прогиба балок.
Содержание
Ограничения и граничные условия
Чтобы балка оставалась в статическом равновесии при приложении к ней внешних нагрузок, балка должна быть закреплена. Ограничения определяются в отдельных точках вдоль балки, а граничное условие в этой точке определяет характер ограничения.Граничное условие указывает, является ли балка фиксированной (удерживаемой от движения) или свободной для движения в каждом направлении. Для двумерного луча интересующими направлениями являются направление x (осевое направление), направление y (поперечное направление) и вращение. Чтобы ограничение существовало в точке, граничное условие должно указывать, что в этой точке зафиксировано хотя бы одно направление.
Общие граничные условия показаны в таблице ниже. Для каждого граничного условия в таблице указано, является ли балка фиксированной или свободной в каждом направлении в точке, где определено граничное условие.
Граничное условие Направление
Осевое (X) Поперечное (Y) Вращение
Свободно Свободно Свободно Свободно
Фиксированное Фиксированное Фиксированное Фиксированное
Штифтовое Фиксированный Фиксированный Свободный
Направляемый по X Свободный Фиксированный Фиксированный
Направляемый по Y Фиксированный Свободно Фиксированный
Ролик по X Свободный Фиксированный Свободный
Ролик по оси Y Фиксированный Свободный Свободный
Если граничное условие указывает, что балка зафиксирована в определенном направлении, тогда в месте граничного условия может существовать внешняя реакция в этом направлении.Например, если балка закреплена в направлении y в определенной точке, тогда в этой точке может развиться внешняя поперечная сила реакции (y). Аналогичным образом, если балка зафиксирована от вращения в определенной точке, то в этой точке может возникнуть внешний реакционный момент.
Основываясь на приведенном выше обсуждении, мы можем видеть, что фиксированное граничное условие может создавать осевые и поперечные силы реакции, а также момент. Точно так же мы видим, что закрепленное граничное условие может развивать осевые и поперечные силы реакции, но не может развивать момент реакции.
Обратите внимание на граничное условие Free в таблице выше. Это граничное условие указывает, что луч может свободно перемещаться во всех направлениях в этой точке (т. Е. Он не зафиксирован и не ограничен в каком-либо направлении). Следовательно, на данный момент ограничения не существует. Это подчеркивает тонкую разницу между ограничением и граничным условием. Граничное условие указывает фиксированное / свободное состояние в каждом направлении в определенной точке, а ограничение — это граничное условие, в котором фиксируется по крайней мере одно направление.
Сила сдвига и изгибающий момент
Чтобы найти поперечную силу и изгибающий момент по длине балки, сначала решите внешние реакции при каждом ограничении. Например, консольная балка ниже имеет приложенную силу, показанную красной стрелкой, а реакции показаны синими стрелками при фиксированном граничном условии.
Внешние реакции должны уравновешивать приложенные нагрузки таким образом, чтобы балка находилась в статическом равновесии.После того, как внешние реакции решены, сделайте разрезы по длине балки и решите внутренние реакции на каждом разрезе. (Силы реакции и моменты в разрезах секции называются внутренними реакциями, поскольку они являются внутренними по отношению к балке.) Пример разреза разреза показан на рисунке ниже:
Когда балка разрезается по сечению, при решении внутренних реакций можно учитывать любую сторону балки. Выбранная сторона не влияет на результаты, поэтому выберите наиболее легкую.На рисунке выше выбрана сторона балки справа от разреза. Выбранная сторона отображается как синяя секция балки, а секция, показанная серым, игнорируется. Внутренние реакции на разрезе показаны синими стрелками. Реакции рассчитываются таким образом, чтобы рассматриваемое сечение балки находилось в статическом равновесии.
Конвенция о знаках
Знаки сдвига и момента важны. Знак определяется после того, как сделан разрез и решены реакции для части балки на одной стороне разреза.Сила сдвига в разрезе секции считается положительной, если она вызывает вращение выбранной секции балки по часовой стрелке, и считается отрицательной, если вызывает вращение против часовой стрелки. Изгибающий момент в разрезе секции считается положительным, если он сжимает верхнюю часть балки и удлиняет ее нижнюю часть (т. Е. Если он заставляет балку «улыбаться»).
Исходя из этого соглашения о знаках, поперечная сила в разрезе секции для примера консольной балки на рисунке выше является положительной, поскольку она вызывает вращение выбранной секции по часовой стрелке.Момент отрицательный, поскольку он сжимает нижнюю часть балки и удлиняет верхнюю часть (т. Е. Заставляет балку «хмуриться»).
На рисунке ниже показаны стандартные условные обозначения для силы сдвига и изгибающего момента. Силы и моменты слева положительны, а справа — отрицательны.
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
Расчет напряжений и прогибов в прямых балках
Строит диаграммы сдвига и момента
Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Диаграммы сдвига и момента
Сила сдвига и изгибающий момент в балке обычно выражаются диаграммами.Диаграмма сдвига показывает поперечную силу по длине балки, а диаграмма моментов показывает изгибающий момент по длине балки. Эти диаграммы обычно показаны сложенными друг на друга, и комбинация этих двух диаграмм представляет собой диаграмму момента сдвига. Диаграммы момента сдвига для некоторых общих конечных условий и конфигураций нагрузки показаны в таблицах прогиба балок в конце этой страницы. Пример диаграммы момента сдвига показан на следующем рисунке:
Общие правила построения диаграмм момента сдвига приведены в таблице ниже.Все правила в этой таблице показаны на рисунке выше.
Диаграмма сдвига Схема моментов
Точечные нагрузки вызывают вертикальный скачок на диаграмме сдвига. Направление прыжка совпадает со знаком точечной нагрузки.
Равномерно распределенные нагрузки дают прямую наклонную линию на диаграмме сдвига. Наклон линии равен величине распределенной нагрузки.
Диаграмма сдвига горизонтальна для расстояний вдоль балки без приложенной нагрузки.
Сдвиг в любой точке балки равен наклону момента в этой же точке:
Диаграмма моментов представляет собой прямую наклонную линию для расстояний вдоль балки без приложенной нагрузки. Наклон линии равен величине сдвига.
Равномерно распределенные нагрузки приводят к параболической кривой на диаграмме моментов.
Максимальные / минимальные значения момента возникают там, где линия сдвига пересекает ноль.
Момент в любой точке балки равен площади под диаграммой сдвига до этой точки:
M = ∫ V dx
Напряжения изгиба в балках
Изгибающий момент M по длине балки можно определить по диаграмме моментов.Изгибающий момент в любом месте балки затем можно использовать для расчета изгибающего напряжения по поперечному сечению балки в этом месте. Изгибающий момент изменяется по высоте поперечного сечения в соответствии с приведенной ниже формулой для изгиба :
где M — изгибающий момент в интересующем месте по длине балки, I _c — центроидный момент инерции поперечного сечения балки, а y — расстояние от нейтральной оси балки до интересующей точки по высоте. поперечного сечения.Отрицательный знак указывает, что положительный момент приведет к сжимающему напряжению выше нейтральной оси.
Напряжение изгиба равно нулю на нейтральной оси балки, которая совпадает с центром тяжести поперечного сечения балки. Напряжение изгиба линейно увеличивается от нейтральной оси до максимальных значений на крайних волокнах вверху и внизу балки.
Максимальное напряжение изгиба возникает в крайнем волокне балки и рассчитывается как:
где c — центроидное расстояние поперечного сечения (расстояние от центроида до крайнего волокна).
Если балка асимметрична относительно нейтральной оси, так что расстояния от нейтральной оси до верха и низа балки не равны, максимальное напряжение будет возникать в самом дальнем от нейтральной оси месте. На рисунке ниже растягивающее напряжение в верхней части балки больше, чем сжимающее напряжение в нижней части.
Модуль упругости поперечного сечения объединяет центроидный момент инерции I _c и центральное расстояние c:
Преимущество модуля сечения состоит в том, что он характеризует сопротивление сечения изгибу одним членом.Модуль сечения можно подставить в формулу изгиба для расчета максимального напряжения изгиба в поперечном сечении:
Ознакомьтесь с нашим калькулятором балок, основанным на методике, описанной здесь.
Расчет напряжений и прогибов в прямых балках
Строит диаграммы сдвига и момента
Может указывать любую конфигурацию ограничений, сосредоточенных сил и распределенных сил
Напряжения сдвига в балках
Сила сдвига V по длине балки может быть определена из диаграммы сдвига.Сила сдвига в любом месте вдоль балки затем может использоваться для расчета напряжения сдвига по поперечному сечению балки в этом месте. Среднее напряжение сдвига по поперечному сечению определяется как:
Напряжение сдвига меняется по высоте поперечного сечения, как показано на рисунке ниже:
Напряжение сдвига равно нулю на свободных поверхностях (вверху и внизу балки) и максимально в центре тяжести. Уравнение для касательного напряжения в любой точке, расположенной на расстоянии y ₁ от центра тяжести поперечного сечения, определяется следующим образом:
где V — поперечная сила, действующая в месте поперечного сечения, I _c — центроидный момент инерции поперечного сечения, а b — ширина поперечного сечения.Все эти термины являются константами. Член Q — это первый момент области, ограниченной интересующей точкой и крайним волокном поперечного сечения:
Напряжения сдвига для нескольких общих поперечных сечений обсуждаются в следующих разделах.
Напряжения сдвига в прямоугольном сечении
Распределение касательного напряжения по высоте прямоугольного поперечного сечения показано на рисунке ниже:
Первый момент площади в любой заданной точке y ₁ по высоте поперечного сечения вычисляется по формуле:
Максимальное значение Q приходится на нейтральную ось балки (где y ₁ = 0):
Напряжение сдвига в любой заданной точке y ₁ по высоте поперечного сечения рассчитывается по формуле:
где I _c = b · h ³/12 — центроидный момент инерции поперечного сечения.Максимальное напряжение сдвига возникает на нейтральной оси балки и рассчитывается по формуле:
где A = b · h — площадь поперечного сечения.
Из предыдущего уравнения видно, что максимальное напряжение сдвига в поперечном сечении на 50% превышает среднее напряжение V / A.
Напряжения сдвига в круглых сечениях
Круглое поперечное сечение показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что касательное напряжение по ширине балки является постоянным.Это предположение справедливо в центре тяжести кругового поперечного сечения, хотя нигде больше не действует. Следовательно, хотя распределение напряжения сдвига по высоте поперечного сечения не может быть легко определено, максимальное напряжение сдвига в сечении (возникающее в центре тяжести) все же может быть вычислено. Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2r — диаметр (ширина) поперечного сечения, I _c = πr ⁴/4 — центроидный момент инерции, а A = πr ² — площадь поперечного сечения.
Напряжения сдвига в круглых сечениях трубы
Круглое поперечное сечение трубы показано на рисунке ниже:
Максимальное значение первого момента Q, возникающего в центроиде, определяется как:
Затем максимальное напряжение сдвига рассчитывается по формуле:
где b = 2 (r _o — r _i) — эффективная ширина поперечного сечения, I _c = π (r _o ⁴ — r _i ⁴) / 4 — центроидный момент инерции, а A = π (r _o ² — r _i ²) — площадь поперечного сечения.
Напряжения сдвига в двутавровых балках
Распределение напряжения сдвига вдоль стенки двутавровой балки показано на рисунке ниже:
Уравнения для касательного напряжения в балке были получены с использованием предположения, что касательное напряжение по ширине балки является постоянным. Это предположение справедливо для стенки двутавровой балки, но неверно для полок (особенно там, где стенка пересекает полки). Однако стенка двутавровой балки принимает на себя подавляющую часть усилия сдвига (примерно 90% — 98%, согласно Гиру), и поэтому можно консервативно предположить, что стенка несет всю силу сдвига.
Первый момент площади перемычки двутавровой балки определяется как:
Напряжение сдвига вдоль стенки двутавровой балки определяется по формуле:
где t _w — толщина стенки, а I _c — центроидный момент инерции двутавровой балки:
Максимальное значение напряжения сдвига возникает на нейтральной оси (y ₁ & равно; 0), а минимальное значение напряжения сдвига в полотне возникает на внешних волокнах полотна, где оно пересекает фланцы y ₁ & equals; & pm; h _w/2):
PDH Classroom предлагает курс повышения квалификации на основе этой справочной страницы по анализу пучка.Этот курс можно использовать для выполнения требований к кредитам PDH для поддержания вашей лицензии PE.
Теперь, когда вы прочитали эту справочную страницу, получите за нее кредит!
Таблицы прогиба балки
В таблицах ниже приведены уравнения прогиба, наклона, сдвига и момента вдоль прямых балок для различных конечных условий и нагрузок. Вы можете найти исчерпывающие таблицы в таких источниках, как Гир, Линдебург и Шигли.Однако приведенные ниже таблицы охватывают большинство распространенных случаев.
Консольные балки
Балки с простой опорой
Фиксированные фиксированные балки
Подпишитесь, чтобы получать обновления о последних улучшениях:
Список литературы
Будинас-Нисбетт, «Машиностроительный проект Шигли», 8-е изд.
Гир, Джеймс М., «Механика материалов», 6-е изд.
Линдебург, Майкл Р., «Справочное руководство по машиностроению для экзамена на физическую форму», 13-е изд.
«Руководство по анализу напряжений», Лаборатория динамики полета ВВС, октябрь 1986 г.
Как рассчитать прогиб балки
В этом руководстве мы собираемся изучить отклонение балки и посмотрим, как мы можем рассчитать отклонение любой балки из первых принципов, используя дифференциальное уравнение кривой отклонения. Мы рассмотрим числовой пример, прежде чем обсуждать, как мы можем использовать суперпозицию вместе с табличными формулами для ускорения процесса. Когда вы закончите это руководство, вы захотите взглянуть на это, где мы расширяем то, что мы здесь узнаем, и представляем способ ускорения вычислений под названием Macauley’s Method . Но давайте сначала рассмотрим основы.
Содержание ниже даст вам представление о том, что мы будем обсуждать.
1.0 Дифференциальное уравнение кривой прогиба
Дифференциальное уравнение кривой прогиба используется для описания поведения при изгибе, поэтому оно возникает при изучении поведения изгиба балки и продольного изгиба колонны. Уравнение просто описывает форму кривой прогиба элемента конструкции, подвергающегося изгибу. Итак, если
измеряет расстояние вдоль балки и представляет отклонение балки, уравнение говорит:
(1)
, где
— жесткость балки при изгибе и описывает изгибающий момент балки как функцию от.В этом руководстве мы не будем вдаваться в вывод уравнения, а сосредоточимся на его применении.
Наша цель — использовать это уравнение для расчета прогиба балки,
, поэтому нам нужно дважды интегрировать уравнение, чтобы получить выражение для. Лучший способ разобраться с этим — рассмотреть пример.
1.1 Допущение «малого прогиба»
Прежде чем мы рассмотрим приведенный ниже пример, мы должны сформулировать предположения, на которых основан наш анализ.Первый — это так называемое допущение о «малом прогибе». Чтобы получить уравнение 1, мы сделали предположение, что прогиб нашей балки (или любой отклоняющей конструкции, к которой мы применяем это уравнение) невелик. Другими словами, если мы рассмотрим короткую изогнутую длину нашей балки, претерпевающую прогиб, изогнутая длина,
, должна быть приблизительно равна ее проекции на горизонтальную плоскость,.
Мы также должны предположить, что в любой точке нашего луча вращение луча
достаточно мало, чтобы мы могли сказать, т.е.е. угол поворота в точке примерно равен наклону кривой прогиба. Для большинства практических случаев прогиб — это проблема, связанная с эксплуатацией, и мы ожидаем, что он будет относительно небольшим и в значительной степени незаметным невооруженным глазом. Таким образом, это предположение о небольшом отклонении выполняется в большинстве случаев, но вы должны знать о его существовании.
1.2 Допущение линейной упругости
Для вывода уравнения 1 также предполагалось, что материал, из которого сделана балка, был линейно упругим и, следовательно, подчинялся закону Гука.Это должно быть так, потому что мы полагаемся на тот факт, что кривизна балки пропорциональна соответствующему изгибающему моменту. Это важно помнить, потому что наши уравнения прогиба станут неточными для пластических деформаций, что, вероятно, также опровергнет наше предположение о малом прогибе. Теперь, когда мы знаем границы, в которых мы работаем, мы можем перейти к следующему примеру.
2.0 Определение уравнений изгибающего момента
Рассмотрим свободно опертую балку на рис.1 ниже. Балка подвергается двум точечным нагрузкам и равномерно распределенной нагрузке. Наша задача — определить прогиб в середине и максимальный прогиб. Обратите внимание: поскольку балка не нагружена симметрично, максимальный прогиб не должен происходить в середине пролета. Статический анализ балки показывает опорные реакции на
и,
Рис. 1. Одноопорная балка.
Снова посмотрев на дифференциальное уравнение кривой прогиба, мы увидим, что нам нужны выражения, которые описывают изгибающий момент как функцию
.Рассматривая здесь нагрузку, отметим, что диаграмма изгибающего момента не будет описываться одной непрерывной функцией. Наличие двух точечных нагрузок означает, что нам фактически потребуются три уравнения, чтобы полностью описать, как изгибающий момент изменяется вдоль балки; с этой целью мы рассмотрим луч как три различных области:
, где
измеряется слева направо с началом координат в позиции. Уравнения для получены путем выполнения разрезов в конструкции, чтобы выявить внутренний изгибающий момент, а затем оценки внутреннего изгибающего момента как функции с учетом моментного равновесия подконструкции.Если вы не уверены в чем-либо из этого, перейдите к этой статье о диаграммах сдвига и моментов, чтобы освежить свои знания.
2.1 Внутренний изгибающий момент в области 1
Чтобы оценить внутренний изгибающий момент в области 1, мы разрезаем конструкцию в этой области, чтобы выявить изгибающий момент
. Наш разрез делается на расстоянии справа от опоры, рис.2. Рис. 2. Субструктура, созданная воображаемым разрезом, сделанным в области 1. Разрез показывает внутренний изгибающий момент в этой области,.
Теперь мы знаем, что подконструкция находится в равновесии под действием внутреннего сдвига (не показано) и внутреннего изгибающего момента.Таким образом, мы можем оценить моментное равновесие, чтобы определить выражение для
.
(2)
Помните, что это уравнение действительно для значений
.
2.2 Внутренний изгибающий момент в области 2
Теперь мы можем повторить процесс, чтобы определить соответствующее уравнение для области 2. Рис. 3. показывает субструктуру, созданную разрезом, чтобы выявить внутренний изгибающий момент.
Рис 3. Субструктура, созданная воображаемым разрезом, сделанным в области 2.На разрезе виден внутренний изгибающий момент в этой области.
Оценка суммы моментов разреза, как указано выше,
(3)
Снова отметим, что это уравнение справедливо для
.
2.3 Внутренний изгибающий момент в области 3
Наконец, мы можем установить соответствующее уравнение для области 3, рис. 4 ниже.
Рис. 4. Субструктура, созданная воображаемым разрезом, сделанным в области 3. Разрез показывает внутренний изгибающий момент в этой области,.
Оценка равновесия моментов выхода опорной конструкции,
(4)
И снова для полноты заметим, что это уравнение справедливо только для
.
3.0 Интегрирование дифференциального уравнения кривой прогиба
Теперь, когда мы установили, как изменяется изгибающий момент, мы можем подставить соответствующие выражения для
в дифференциальное уравнение и выполнить интегрирование. После подстановки наших выражений для в уравнение 1 мы имеем
(5)
(6)
(7)
Интегрирование каждого выражения дает
(8)
(9)
(10)
Здесь мы отмечаем, что наша интеграция сгенерировала три неизвестных константы интеграции,
и.Мы также отмечаем, что теперь у нас есть член в наших уравнениях, который соответствует наклону кривой прогиба. Нам нужно выполнить еще одно интегрирование, чтобы свести это обратно к самому смещению,. Эта интеграция дает,
(11)
(12)
(13)
Мы снова видим, что эта интеграция дала нам еще 3 константы интеграции:
и. Всего у нас есть шесть неизвестных констант, которые нам нужно идентифицировать. Хорошая новость заключается в том, что теперь у нас есть уравнение для отклонения в каждой области.
3.1 Нахождение констант интегрирования
Чтобы найти постоянные интегрирования, нам нужны некоторые условия или ограничения, которые мы можем представить в форме уравнения. Поскольку нам нужно решить шесть неизвестных, нам понадобится шесть уравнений ограничений. Это следующие:
в, уклоны на участках 1 и 2 одинаковые.
ат, прогибы на участках 1 и 2 одинаковы.
ат, уклоны на участках 2 и 3 совпадают.
at, прогибы в областях 2 и 3 одинаковы.
в (опора A) прогиб равен нулю.
в (опора D) прогиб равен нулю.
Первые четыре условия называются условиями непрерывности и являются прямым результатом того факта, что балка и, следовательно, отклонения и уклоны являются непрерывными. Последние два — классические граничные условия. Теперь мы можем использовать эти утверждения для построения шести уравнений, из которых можно определить постоянные интегрирования.
Состояние (1)
На
наклоны в областях 1 и 2 одинаковые.Поэтому мы можем приравнять уравнения 8 и 9 и подставить в.
(14)
Состояние (2)
На
прогибы в областях 1 и 2 одинаковы. Итак, приравнивание уравнений 11 и 12 к дает нам,
(15)
Состояние (3)
На
наклоны в областях 2 и 3 одинаковы, поэтому, используя уравнения 9 и 10 с,
(16)
Состояние (4)
На
прогибы в областях 2 и 3 одинаковы.Приравнивая уравнения 12 и 13 к,
(17)
Состояние (5)
Пятое условие — стандартное граничное условие; на
прогиб равен нулю. Таким образом, мы можем позволить уравнению 11 равняться нулю с,
(18)
Состояние (6)
Последнее условие относится к другой границе; на
прогиб также равен нулю. Таким образом, применяя это к уравнению 13 с, дает,
(19)
Теперь, когда у нас есть шесть уравнений, нам нужно использовать их для решения неизвестных констант.Безусловно, самый простой способ сделать это — расположить их в матричной форме и решить систему, инвертируя матрицу коэффициентов. Матричное представление системы:
(20)
Вектор неизвестных констант получается как,
(21)
На данный момент нам нужен способ инвертировать матрицу, и поскольку это матрица
, мы не будем делать это вручную! Я буду использовать следующий код Python для выполнения операции в уравнении 21.
import numpy as np #Numpy для работы с массивами
# Определить каждую строку матрицы коэффициентов
row1 = [1, -1, 0, 0, 0, 0]
row2 = [3 , -3, 0, 1, -1, 0]
row3 = [0, 1, -1, 0, 0, 0,]
row4 = [0, 6, -6, 0, 1, -1 ]
row5 = [0, 0, 0, 1, 0, 0]
row6 = [0, 0, 8, 0, 0, 1]
A = np.mat ([row1, row2, row3, row4, row5, row6]) # Определить матрицу коэффициентов
B = np.array ([[337.5], [675], [900], [3600], [0], [-14613.334]])
C = AI * B # Неизвестные константы
Если вы хотите установить Python на вашем компьютере, вы можете прочитать эту лекцию. Это позволит вам настроить удобную среду программирования Python. Предполагая, что вы это сделали или у вас есть собственный способ инвертирования матриц, константы оцениваются как
4.0 Расчет прогиба балки
На этом этапе мы можем суммировать три уравнения, которые описывают прогиб в трех областях нашей балки:
(22)
(23)
(24)
4.1 Прогиб в средней части
Чтобы рассчитать прогиб в середине пролета, мы подставляем
в уравнение 23, что дает нам,
Теперь, когда у нас есть полное определение отклонения балки, мы можем построить его график, чтобы лучше понять форму отклонения.На рис. 5 ниже показан график внутреннего изгибающего момента и отклоненной формы. Обратите внимание, что по оси Y отклонение является функцией
. Рис. 5. Балка без опоры, график изгибающего момента и график формы отклонения.
4.2 Местоположение максимального прогиба
Из рис. 5 выше видно, что, несмотря на несимметричную нагрузку, максимальный прогиб происходит очень близко к середине пролета. Мы можем подтвердить точное местоположение максимального отклонения, распознав, что в этом месте наклон кривой отклонения равен нулю.Другими словами, касательная к кривой отклонения в точке максимального отклонения будет горизонтальной и, следовательно, иметь нулевой наклон.
Путем осмотра мы знаем, что максимальное отклонение происходит в области 2. Но предположим, что мы этого не знали. Мы можем позволить каждому уравнению для наклона кривой прогиба,
, уравнениям 8, 9 и 10, равняться нулю, и решить для корней каждого уравнения, то есть значений x, при которых наклон равен нулю. Я позволю Python делать здесь ручную работу …
# Определить многочлены
p1 = np.poly1d ([- 10/3, 139.375 / 2, 0, -856.354]) #Region 1
p2 = np.poly1d ([- 10/3, 64.375 / 2, 225, -1193.854]) #Region 2
p3 = np.poly1d ([- 10/3, 14.375 / 2, 525, -2093.854]) #Region 3
# Извлечь корни
rootRegion1 = p1.r #Region 1
rootRegion2 = p2.r # Регион 2
rootRegion3 = p3.r # Регион 3
Корни,
Значения, выходящие за границы соответствующего региона, могут быть немедленно отброшены.Остается только
в области 2. Как мы и подозревали, это очень близко к средней точке пролета. Теперь мы могли бы подставить это значение обратно в уравнение 12, чтобы подтвердить значение максимального отклонения, но, поскольку мы уже вычислили отклонение при, мы не будем этого делать.
5.0 Использование суперпозиции для расчета прогиба балки
Выше мы видели, как определить отклонение балки из первых принципов. Это дало нам полную картину отклонения, но это был относительно долгий процесс, чтобы добраться сюда.Мы можем использовать принцип суперпозиции, чтобы получить ответ для отклонения в середине пролета намного быстрее, используя табличные формулы для отклонения балки. Эти формулы уже определены и сведены в таблицы для общих случаев нагружения с использованием только что продемонстрированной нами техники. Оценивая прогиб в середине пролета для каждой нагрузки отдельно и суммируя вызванные прогибы, мы получаем тот же результат, что и выше.
5.1 Равномерно распределенная нагрузка
Рассмотрим формулу прогиба балки при равномерно распределенной нагрузке, рис.6,
(25)
На
эта формула оценивается как. Рис. 6. Балка с простой опорой, подверженная равномерно распределенной нагрузке.
5.2 Точечная нагрузка # 1
Формула прогиба балки, подверженной одиночной точечной нагрузке, рис. 7, где расстояние
меньше расстояния до положения, в котором оценивается прогиб, имеет вид
(26)
Это оценивается как
5.3 Точечная нагрузка # 2
Наконец, оценивая формулу для прогиба, где
, рис.8,
(27)
Это оценивается как
.
Суммируя результаты трех средних прогибов,
Конечно, это то же самое значение, которое мы получили выше. Построив эти уравнения, мы можем дополнительно визуализировать вклад каждой нагрузки в общую форму отклонения, рис. 9.
Рис. 9. Общая отклоненная форма, полученная как наложение отдельных прогибов от каждой нагрузки, рассматриваемой отдельно.
На этом мы завершаем обсуждение отклонения балки.В конце концов, вам решать, какой подход вы решите использовать для расчета прогибов. Конечно, есть и другие методы, которые вы можете использовать для оценки прогиба, но в любом случае хорошо иметь представление о том, как это можно сделать, исходя из первых принципов. Помните, что, как и любой вывод, у этого есть свои ограничивающие допущения, о которых говорилось выше. Все, что мы обсуждали выше, действительно только в том случае, если мы удовлетворяем этим ограничивающим предположениям.
Теперь, когда мы рассмотрели фундаментальный метод решения дифференциального уравнения кривой прогиба, самое время познакомиться с методом Macauley’s Method .Проверьте это в этом посте.
На этом пока все, увидимся в следующем.
Консольные балки — моменты и прогиб
Консольные балки — одиночная нагрузка на конце
Максимальная сила реакции
на неподвижном конце может быть выражена как:
R _A = F (1a)

, где
R _A = сила реакции в A (Н, фунт)
F = сила одностороннего действия в B (Н, фунт)
Максимальный момент
на неподвижном конце может быть выражается как
M _max = M _A
= — FL (1b)
где
M _A = максимальный момент в A (Нм, Нмм, фунт-дюйм)
L = длина балки (м, мм, дюйм)
Максимальный прогиб
на конце консольной балки можно выразить как
δ _B = FL ³ / (3 EI) (1c)
где
δ _B = максимальный прогиб в B (м, мм, дюйм)
E = модуль упругости эластичность (Н / м ² (Па), Н / мм ², фунт / дюйм ² (psi))
I = момент инерции (м ⁴, мм ⁴, дюйм ⁴)
b = длина между B и C (м, мм, дюйм)
Напряжение
Напряжение в изгибающейся балке может быть выражено как
σ = y M / I ( 1d)
где
σ = напряжение (Па (Н / м ²), Н / мм ², psi)
y = расстояние до точки от нейтральной оси (м, мм , дюйм)
M = изгибающий момент (Нм, фунт дюйм)
I = момент инерции (м ⁴, мм ⁴, в ⁴)
Максимальный момент консольной балки находится в фиксированной точке, а максимальное напряжение можно рассчитать, комбинируя 1b и 1d to
σ _max = y _max FL / I (1e)

Пример — консольная балка с одинарной нагрузкой на конце, метрические единицы
Максимальный момент на неподвижном конце UB 305 x 127 x 42 балка стальная полка консольная балка 5000 мм длинная, с моментом инерции 8196 см ⁴ (81960000 мм ⁴) , модуль упругости 200 ГПа (200000 Н / мм ² ) и с одинарной нагрузкой 3000 Н в конце можно рассчитать как
M _max = (3000 Н) (5000 мм)
= 1.5 10 ⁷ Нмм
= 1,5 10 ⁴ Нм
Максимальный прогиб на свободном конце можно рассчитать как
δ _B = (3000 Н) (5000 мм) ³ / (3 (2 10 ⁵ Н / мм ²) (8.196 10 ⁷ мм ⁴))

= 7,6 мм
Высота балки 300 мм и расстояние от крайней точки до нейтральной оси 150 мм .Максимальное напряжение в балке можно рассчитать как
σ _max = (150 мм) (3000 Н) (5000 мм) / ( 8,196 10 ⁷ мм ⁴ )
= 27,4 (Н / мм ²)
= 27,4 10 ⁶ (Н / м ², Па)
= 27,4 МПа
Максимальное напряжение намного ниже предела прочности при растяжении прочность для большинства сталей.
Консольная балка — одинарная нагрузка
Максимальная сила реакции
на неподвижном конце может быть выражена как:
R _A = F (2a)

где
46 90 A771 R
= сила реакции в A (Н, фунт)
F = сила одностороннего действия в B (Н, фунт)
Максимальный момент
на неподвижном конце может быть выражен как
M _max = M _A
= — F a (2b)
где
M _A = максимальный момент в A (Н.m, N.mm, lb.in)
a = длина между A и B (м, мм, дюйм)
Максимальный прогиб
на конце консольной балки можно выразить как
δ _C = (F a ³ / (3 EI)) (1 + 3 b / 2 a) (2c)
где
δ _C = максимальное отклонение в C (м, мм , дюйм)
E = модуль упругости (Н / м ² (Па), Н / мм ², фунт / дюйм ² (psi))
I = момент инерции ( м ⁴, мм ⁴, дюйм ⁴)
b = длина между B и C (м, мм, дюйм)
Максимальный прогиб
под действием единого усилия быть выраженным как
δ _B = F a ³ / (3 EI) (2d)
где e
δ _B = максимальный прогиб в B (м, мм, дюйм)

Максимальное напряжение
Максимальное напряжение может быть рассчитано путем объединения 1d и 2b до
σ _max = y _max F a / I (2e)

Консольная балка — калькулятор одиночной нагрузки
Универсальный калькулятор — будьте последовательны и используйте метрические значения на основе м или мм или британские значения на основе дюймов.Стандартные типовые значения указаны в миллиметрах.
F — Нагрузка (Н, фунт)
a — Длина балки между A и B (м, мм, дюйм)
b — Длина балки между B и C (м, мм, дюйм)
I — момент инерции (м ⁴, мм ⁴, дюйм ⁴)
E — модуль упругости (Н / м ², Н / мм ² , psi)
y — Расстояние от нейтральной оси (м, мм, дюйм)
Консольная балка — равномерно распределенная нагрузка
Максимальная реакция
на неподвижном конце может быть выражена как:
R _A = q L (3a)

, где
R _A = сила реакции в A (Н, фунт)
q = равномерно распределенная нагрузка (Н / м, Н / м) мм, фунт / дюйм)
L = длина консольной балки (м, мм, дюйм)
9 0775
Максимальный момент
на фиксированном конце можно выразить как
M _A = — q L ²/2 (3b)
Максимальный прогиб
в конце можно выразить как
δ _B = q L ⁴ / (8 EI) (3c)
где
δ _B = максимальное отклонение в B (м, мм, дюйм)
Консольная балка — Калькулятор равномерной нагрузки
Универсальный калькулятор — используйте метрические значения на основе м или мм или имперские значения на основе дюймов.Стандартные типовые значения указаны в миллиметрах.
q — Равномерная нагрузка (Н / м, Н / мм, фунт / дюйм)
L — Длина балки (м, мм, дюйм)
I — Момент инерции (м ⁴, мм ⁴, дюйм ⁴)
E — Модуль упругости (Па, Н / мм ², psi)
y — Расстояние от нейтральной оси (м, мм, дюйм)
Более одной точечной нагрузки и / или равномерной нагрузки, действующей на консольную балку
Если на консольную балку действует более одной точечной нагрузки и / или равномерная нагрузка — результирующий максимальный момент на фиксированном конце A и результирующий максимальный прогиб на конце B может быть рассчитан путем суммирования максимального момента в A и максимального прогиба в B для каждой точки и / или равномерной нагрузки.
Консольная балка — уменьшающаяся распределенная нагрузка
Максимальная сила реакции
на неподвижном конце может быть выражена как:
R _A = q L / 2 (4a)

75
где
R _A = сила реакции в A (Н, фунт)
q = уменьшающаяся распределенная нагрузка — максимальное значение при A — ноль при B (Н / м, фунт / фут)
Максимальный момент
при фиксированный конец может быть выражен как
M _max = M _A
= — q L ²/6 (4b)
где
M _A = максимум момент в A (N.m, N.mm, lb.in)
L = длина балки (м, мм, дюйм)
Максимальный прогиб
на конце консольной балки можно выразить как
δ _B = q L ⁴ / (30 EI) (4c)
где
δ _B = максимальный прогиб в B (м, мм, дюйм)
E = модуль упругости ( Н / м ² (Па), Н / мм ², фунт / дюйм ² (psi))
I = момент инерции (м ⁴, мм ⁴, дюйм ⁴)
Вставьте балки в свою модель Sketchup с помощью Engineering ToolBox Sketchup Extension
Расчет профиля полного прогиба и оптимизация модуля Юнга для инженерных материалов с высокими эксплуатационными характеристиками
Расчет профиля полного прогиба
Образцы были подготовлены и испытаны, как описано ниже. ребристая в разделах «Методы».Поле смещения балки (рис. 2) дискретизируется в регулярной сетке, и для каждого кадра программное обеспечение DIC вычисляет вертикальное (d _v) и горизонтальное (d _h) смещение каждой ячейки сетки. Среднее вертикальное смещение стержня по горизонтальной оси w ’(x) вычисляется для каждого кадра путем усреднения смещения соответствующих ячеек по высоте балки, как показано в уравнении (1). Среднее вертикальное смещение балки затем корректируется путем фиксации вертикального смещения левой опоры w (x _l) и правой w (x _r) на ноль.Это достигается путем применения к усредненному вертикальному смещению жесткого переноса C и поворота φ , как определено в уравнениях (2) и схематически показано на рис. 3. Влияние вращения на горизонтальную ось можно не учитывать, поскольку они намного меньше, чем дискретизация клеток. Скорректированный профиль отклонения может быть рассчитан для каждого кадра записанного эксперимента с помощью уравнения (3), и пример показан на рис. 4.
Рисунок 2
( a ) Пример кадров, используемых для экстраполяции смещения поле балки во время испытания на трехточечный изгиб, ( b ) поле вертикального смещения d _v и ( c ) поле горизонтального смещения d _h до разрушения.
Рисунок 3
( a ) Пример конфигурации до (черный) и во время теста (красный). Схематическое изображение средней коррекции вертикального смещения путем применения ( b ) жесткого вертикального перемещения и ( c ) вращения для получения ( d ) скорректированного профиля полного отклонения каждой рамы.
Рис. 4: Типичная последовательность профилей прогиба до отказа (серый).
В частности, показан профиль при 20% (черный штрих), 60% (черный) и 100% (красный штрих) пиковой нагрузки.
Расчет модуля Юнга
Последовательности профилей отклонения балки были синхронизированы с историей нагрузки, зарегистрированной датчиком испытательного стенда, что привело к значению приложенной нагрузки для каждого профиля. Предполагая, что поперечные сечения балки остаются плоскими и перпендикулярными деформированной оси балки, теоретический профиль вертикального смещения (w _EB), связанный с приложенной нагрузкой, можно выразить как функцию модуля Юнга (E) эквивалентной линейно-упругая изотропная и однородная балка с заданной геометрией.В уравнении (4) теоретическое вертикальное смещение определяется как функция местоположения (x) и E, тогда как момент инерции (I) и промежуток между двумя опорами (опорами) являются двумя константами, которые фиксируются геометрией исследуемой балки. Затем для каждого кадра может быть определено одно значение модуля Юнга, индекс = —, путем минимизации суммы квадратов разностей между теоретическим и соответствующим экспериментальным отклонением (наименьшие квадраты) по всей длине балки между опоры.Повторяя минимизацию, показанную в уравнении (5) для каждого кадра, можно определить ряд промежуточных модулей Юнга ( E _i), которые наилучшим образом представляют отклонение балки для каждой приложенной нагрузки в каждом кадре. . Эти промежуточные модули затем можно использовать для определения единственного значения модуля Юнга, которое наилучшим образом представляет линейную зависимость напряжения от деформации для испытуемого материала в любом выбранном диапазоне приложенной нагрузки. Диапазон от 20% до 80% пиковой нагрузки был выбран для определения единственного значения модуля Юнга для каждого образца.Поэтому промежуточные модули были преобразованы в соответствующие им значения прогиба в середине пролета, и линейная регрессия методом наименьших квадратов была проведена для переменной прогиба для приложенной нагрузки в определенном диапазоне. Затем для каждого образца определяли значение модуля Юнга с помощью уравнения (6), где H — высота образца, а м — наклон соответствующей линии наилучшего соответствия.
Неопределенность и оптические искажения
Предлагаемый подход основан на предположении, что плоскость цели не смещается значительно в направлении, перпендикулярном этой плоскости, то есть к камере или от нее, что может ложно указывать на расширение или сжатие соответственно.Для этих экспериментов это можно считать правдой, поскольку максимальные смещения в плоскости в направлении нагрузки, которые были бы доминирующими, составляли всего лишь 1 или 2 пикселя. Для оценки ошибки возможного оптического искажения был рассмотрен независимый эксперимент. Постоянное вертикальное смещение было применено к идентичной спекл-панели, соединенной с верхним штампом установки для трехточечной гибки, как показано на рис. 5 (а). Эксперимент проводился в режиме управления вытеснением, со скоростью ползуна 0.4 мм / сек, что в среднем соответствует вертикальному смещению 0,8 мкм м на кадр. Поскольку максимальное вертикальное смещение до исправления, которое испытывали стержни в среднем до разрушения, обычно составляло 30-40 мкм м, в зависимости от испытуемого образца, например на рис. 2 ошибка была консервативно оценена на 100 кадрах, что соответствует общему вертикальному смещению 80 мкм м, что в два раза больше типичного диапазона смещения испытанного образца. Та же процедура, что и для образцов пучка, была использована для расчета горизонтального профиля вертикального смещения спекл-панели.На рис. 5 (б) показано исправленное отклонение луча для каждого рассматриваемого кадра. Поскольку панель подвергается жесткому вертикальному перемещению без отклонения, погрешность оценки для каждого местоположения профиля отклонения, рассчитанного с помощью предлагаемой методики, может быть определена как максимальное абсолютное значение профиля отклонения в каждом кадре. Расчетная ошибка, как показано на рис. 5 (c) (пунктирная линия), стремится к значению от 0,1 до 0,2 мкм м. Эта ошибка слишком консервативна, когда профиль прогиба используется для расчета модуля Юнга.В этом случае все местоположения профиля отклонения вместо этого сравниваются с теоретическим отклонением в процессе оптимизации. Оценка ошибки отклонения в этом случае может быть затем определена как максимальное отклонение (на полпути между двумя опорами) наилучшей интерполяционной кривой, заданной теоретическим профилем отклонения Эйлера-Бернулли. В этом случае расчетная ошибка, показанная на рис. 5 (c) (сплошная линия), ниже, чем предыдущая. Максимальное значение этой оценочной ошибки стремится к 0.1 μ м и соответствует вертикальному смещению, аналогичному максимальному до отказа в реальных испытаниях. Поскольку модуль Юнга для любой приложенной нагрузки является линейной функцией максимального (среднего) значения профиля отклонения балки, и это значение варьируется от 15 до 20 мкм м, в зависимости от испытуемого образца, относительная погрешность, вызванная Оптические искажения по последним оценкам модуля Юнга, рассчитанного до разрушения, составляют от 0,5% до 0,7%.
Рис. 5
( a ) Конфигурация балки до и после применения движения твердого тела.( b ) Оптическое искажение горизонтального профиля вертикального смещения спекл-панели во время эксперимента. ( c ) Тенденция расчетных максимальных ошибок для каждого кадра.
Прецизионность и точность
Ниже приводится сравнение предложенной методологии и стандартных подходов, предложенных в EN 843-2: 2006, с использованием данных смещения и деформации, извлеченных в дискретных точках из данных деформации ДИК с полным полем поля. Как показано на рис.6 (а) сравниваем:
Предлагаемая методика;
Три виртуальных смещения (средний пролет и на обеих опорах, три набора, размещенные на разной высоте на видимой поверхности балки;
Два виртуальных тензодатчика, расположенные близко к нижней поверхности балки (с поправкой на указывают значение деформации на нижней поверхности).
Рисунок 6
( a ) Представление точек, из которых вертикальные смещения рассчитываются стандартным методом с использованием трех различных наборов виртуальных датчиков смещения (оранжевые квадраты , синие треугольники и красные кресты) и площадь, использованная в предлагаемой методике (черная пунктирная линия).Две стрелки (зеленая и пурпурная) показывают расположение двух виртуальных тензодатчиков. ( b ) Схематическое изображение различных определений вертикальных смещений стандартным методом по трем точкам данных в двух разных местах (желтый, синий и красный) и с помощью предлагаемой методологии на основе наилучшей интерполяции полного профиля отклонения (черный ).
Для этого сравнения использовались наборы данных из одного репрезентативного испытания на изгиб.Алгоритм, предложенный в EN 843-2: 2006 для датчиков смещения, эквивалентен вычислению модуля Юнга по теории изгиба Эйлера-Бернулли, но с использованием только максимального вертикального смещения в середине пролета относительно среднего вертикального смещения на двух опорах, так как показано на рис. 6 (б).
В предлагаемом методе используется весь набор данных о вертикальном смещении, охватывающий всю наблюдаемую поверхность балки, чтобы получить полный профиль отклонения для образца.Этот профиль отклонения корректируется, чтобы исключить смещение и вращение твердого тела, затем анализируется для определения кривой отклонения Эйлера-Бернулли наилучшего соответствия, как показано на рис. 6 (b). Повторяя этот процесс для каждого кадра, можно определить серию промежуточных модулей Юнга, которые наилучшим образом представляют отклонение балки для каждой приложенной нагрузки в каждом кадре. Эти промежуточные модули могут впоследствии использоваться для определения единственного значения модуля Юнга, которое наилучшим образом представляет линейную зависимость напряжения от деформации для испытуемого материала.Использование большего набора данных смещения для определения изгиба балки и более сложного метода учета перемещений и вращения твердого тела являются ключевыми особенностями, которые позволяют предлагаемому методу иметь более высокий уровень точности по сравнению с стандартный метод с тремя датчиками перемещения.
Чтобы сравнить уровни точности двух методологий, промежуточные модули Юнга, определенные с использованием предложенной методологии, были преобразованы обратно в соответствующие им значения прогиба в середине пролета для каждой приложенной нагрузки.Таким образом, можно сравнивать кривую сила-отклонение, полученную по предложенной методологии (то есть в полном поле), с кривыми, полученными с помощью стандартного метода, эквивалентного DIC, на основе наборов виртуальных датчиков смещения, размещенных на разной высоте балки. Значения силы и прогиба при 20% и 80% пиковой нагрузки затем использовались для оценки модуля Юнга по трем кривым в соответствии с процедурой, предложенной в EN 843-2: 2006, Раздел 4.
Кривые сила-прогиб изображенный на рис.7 (а) предполагают, что стандартный метод может быть чувствительным к выбору расположения виртуальных датчиков на поверхности луча, в частности, к тому, расположены ли виртуальные датчики рядом с внутренней или внешней дугой отклоняющего луча. Эта вариабельность результатов стандартного метода указывает на более низкую точность, поскольку в наших примерах он генерирует три значения модуля Юнга, которые отличаются более чем на 3%, с более низким значением, полученным в самых нижних положениях, которые аналогичны положения преобразователя указаны в стандарте EN 843-2: 2006, раздел 4.В вспомогательной ссылке на EN 843-2: 2006 ²² отмечается, что стандартный метод квазистатического изгиба обычно дает более низкие значения, чем другие стандартные методы для керамических материалов. Вместо этого в предлагаемой методологии используются данные со всей поверхности луча, от внутренней до внешней дуги, что устраняет изменчивость из-за выбора местоположения виртуального преобразователя. Предлагаемая методология генерирует более высокий модуль упругости, чем те, которые определены виртуальными датчиками смещения (с использованием данных DIC) и применением стандартных методов расчета.Это говорит о том, что предлагаемая методология обеспечивает более высокую точность и может устранить потенциальное отклонение в сторону более низких значений, которое может быть наложено стандартным методом квазистатического изгиба.
Рисунок 7
( a ) Сравнение кривых сила-прогиб, рассчитанных стандартным методом из трех наборов трех точек данных (оранжевого, синего и красного) и с предложенной методологией на основе наилучшей интерполяции полной прогиб профиль (черный). ( b ) Подмножество данных, показанных в ( a ), с усилием в процентах от пиковой нагрузки и ограниченным диапазоном от 20% до 80%.Соответствующие линейные тренды (серые пунктирные линии), полученные из модуля Юнга, экстраполированного из двух кривых при 20% и 80% пиковой нагрузки, также нанесены на график для каждого набора. ( c ) Сравнение кривых «сила-деформация» двух виртуальных тензодатчиков и предложенной методологии. Соответствующие линейные тренды (серые пунктирные линии), полученные из модуля Юнга, экстраполированного из трех кривых при 20% и 80% пиковой нагрузки, также представлены на графике.
На рис.7 (b) сила была нормализована с пиковой нагрузкой, а диапазон данных был ограничен до 20–80% от пиковой нагрузки (в пределах диапазона 10–90%, указанного в EN 843-2: 2006). Также нанесены линии тренда, определенные стандартным методом анализа, который учитывает значения только в двух выбранных оператором оценочных точках (например, 20% и 80% пиковой нагрузки). Количественная оценка уровня точности может быть получена путем вычисления суммы квадратов остатков (SSR) между значениями, указанными линейным трендом, и фактическими данными отклонения, которые представляют собой отклонение измерения от значения, указанного этим трендом.Предлагаемая методология полного поля имеет более низкую SSR (таблица на рис. 7 (b), 4,28 против 5,51, 7,60 и 8,10 мкм ²) и, следовательно, более высокий уровень точности. Промежуточные модули Юнга из предложенной методологии также использовались для обратного расчета соответствующих значений горизонтальной деформации на нижней поверхности образца в середине пролета для каждого значения приложенной нагрузки. Сопоставимые значения горизонтальной деформации также были извлечены непосредственно из данных деформации ДИК в полном поле в двух дискретных точках чуть выше нижнего края наблюдаемой поверхности.Каждый из них был скорректирован до эквивалентного значения на нижней поверхности. Результирующие данные по силе-деформации (от 20% до 80% пиковой нагрузки) представлены на рис. 7 (с). Значения силы и деформации при 20% и 80% пиковой нагрузки затем использовались для оценки модуля Юнга, как предложено в EN 843-2: 2006, Раздел 4. Опять же, количественная оценка уровня точности также может быть получена из расчет SSR между значениями, указанными линейным трендом, и фактическими данными деформации. Предлагаемая методика, основанная на полнополевом ДИК, имеет SSR на два порядка меньше, чем те, которые получены стандартным методом (таблица на рис.7 (c) 2,07 10 ⁻⁸ против 1,44 10 ⁻⁶ и 2,08 10 ⁻⁶), и, следовательно, гораздо более высокий уровень точности.
Это сравнение было проведено для эксперимента, который был записан с использованием современного оборудования, и поэтому только изображения с высоким разрешением были проанализированы с использованием DIC. Разумно предположить, что повышение точности предлагаемой методологии будет более значительным для изображений с более низким разрешением, потому что был использован весь набор данных о деформации (поддержка для поддержки и по всей высоте), а не гораздо меньшие подмножества этих данных, представляющих всего несколько отдельных локаций.
Легкий прогиб стальной балки
Верулам, инженер-строитель Том. 70, No. 12, 16 июня 1992 г.
Легкое отклонение луча
Г-н А. Н. Бил из Лидса прислал нам записку с предложением простой процедуры приблизительного ручного расчета прогибов стальных балок. Хотя его вклад оказался слишком длинным, чтобы его можно было полностью включить в Verulam, его сокращенная версия может заинтересовать многих читателей. Г-н Бил отмечает, что, хотя расчет вручную изгибающих напряжений в балке обычно не является трудным, расчет прогибов может быть гораздо более трудоемким.Поскольку обычно нет необходимости знать прогиб с какой-либо большой степенью точности (в пределах 10%, вероятно, будет адекватным), предлагается следующий подход.
Случай с балкой с простой опорой, поддерживающей равномерную нагрузку, иллюстрирует подход.
Если мы возьмем формулу прогиба (Δ = 5WL³ / 384EI) и выразим ее через изгибающий момент (M = WL / 8), то получится Δ = 5ML³ / 48EI.
Теперь для стальной балки напряжение упругого изгиба fbt = M / Z, где Z = 2I / D, что дает fbt = MD / 2I.
(Z — модуль упругости, I — момент инерции, D — общая глубина сечения.)
Подставив это в формулу прогиба, мы получим Δ = 5 fbtL³ / 24ED. При E 210 кН / мм² это становится:
Δ (мм) = 0,992 фбтL² / д. . . (1)
Здесь fbt, L и D выражены в их обычных единицах измерения: Н / мм², м и мм соответственно.
Для всех практических целей формула
Δ = fbtL² / D. . . (2)
удобен в использовании, легко запоминается и отличается точностью до 1%.
Мистер Бил затем переходит к рассмотрению других распределений нагрузки, аналогичным образом связывая центральный прогиб Δ с экстремальным напряжением волокна fbt, давая результаты, показанные в первом столбце результатов таблицы 1. Во втором столбце приведены значения для балок с фиксированными концами — , которые Г-н Бил предлагает использовать его для оценки прогибов непрерывных балок.
Наконец, г-н Бил показывает, как его методика может использоваться для сложных нагрузок, вычисляя отклонение нагруженной балки с простой опорой, как показано на рис. 1:
Фиг.1
Центральный изгибающий момент, рассчитанный как 444,3 кНм.
Для сечения балки, Z = 2474 см³, D = 539,5 мм, что дает
фут = 179,6 Н / мм².
Простое приблизительное отклонение с использованием ур. (2) это
ΔAPP = 179,6 x 7² / 539,5 = 16,3 мм = L / 429 OK.
Для более точной оценки, учитывая, что большая часть момента создается центральной точечной нагрузкой, мы могли бы взять коэффициент, более близкий к значению точечной нагрузки, равному 0.8 (скажем, 0,85), что дает
Δ = 0,85 футов x L² / D = 13,9 мм
Для сравнения, точный компьютерный анализ той же балки дал отклонение 13,8 мм.
Следовательно, для большинства практических целей нам нужно запомнить только четыре простых формулы для прогиба прямопертой или непрерывной стальной балки, как показано в Таблице 2.
Эти формулы не только упрощают жизнь для простых равномерных и точечных нагрузок — они означают, что прогиб при более сложных схемах нагружения может быть рассчитан без труда.Они также особенно подходят для проверки компьютерных рисунков «обратной стороной конверта». Лучше всего то, что их легко запомнить.
Есть желающие?
Отклонение луча
Балка — конструктивный элемент, способный выдерживать большие нагрузки при изгибе. В случае небольших прогибов форму балки можно описать линейным дифференциальным уравнением четвертого порядка.
Рассмотрим вывод этого уравнения. Для изгибающейся балки угол \ (d \ theta \) появляется между двумя соседними секциями, расположенными на расстоянии \ (dx \) (рисунок \ (1 \)).
Рис. 1.
Деформация \ (\ varepsilon \) в каждой точке пропорциональна координате \ (y, \), которая отсчитывается от нейтральной линии. Длина нейтральной линии не изменилась.
Из геометрии рисунка \ (1 \) следует, что
\ [\ varepsilon = \ frac {y} {R}, \]
где \ (R \) — радиус кривизны балки.
Величина нормального напряжения \ (\ sigma \) в поперечном сечении также будет зависеть от координаты \ (y. \). Его можно оценить по закону Гука:
\ [\ sigma = \ varepsilon E = \ frac {E} {R} y, \]
где \ (E \) — модуль упругости балки.2}}} = \ frac {{M \ left (x \ right)}} {{EI}}.} \]
Изгибающий момент \ ({M \ left (x \ right)} \) можно выразить через известную внешнюю нагрузку \ ({q \ left (x \ right)} \), действующую на балку. Действительно, мы выбираем малый элемент \ (dx \) и рассматриваем условия его равновесия (рисунок \ (3 \)).
Рис. 3.
Сумма проекций всех сил на ось \ (z \) равна нулю:
\ [{- Q — qdx} + {Q + dQ} = {0.} \]
Сумма моментов всех сил вокруг, например, правого края элемента \ (dx \) (точка \ (B \) на рисунке \ (3 \)) также равна нулю:
\ [{- M + M + dM} — {Qdx — q \ frac {{{{\ left ({dx} \ right)} ^ 2}}} {2}} = {0.4}}} = q. \]
Это уравнение при соответствующих граничных условиях определяет прогиб нагруженной балки.
Решенные проблемы
Щелкните или коснитесь проблемы, чтобы увидеть решение.
Пример 1
Определите прогиб балки, жестко зажатой с обоих концов и нагруженной равномерно распределенной силой (рисунок \ (4 \)).
Пример 2
Тонкий цилиндрический вал длиной \ (L \) вращается с угловой скоростью \ (\ omega.\) На какой скорости \ (\ omega \) вал разрушается? Модуль упругости материала \ (E, \), масса вала \ (M, \) и радиус секции \ (a. \)
.

Граничное условие	Направление
Граничное условие	Осевое (X)	Поперечное (Y)	Вращение
Свободно	Свободно	Свободно	Свободно
Фиксированное	Фиксированное	Фиксированное	Фиксированное
Штифтовое	Фиксированный	Фиксированный	Свободный
Направляемый по X	Свободный	Фиксированный	Фиксированный
Направляемый по Y	Фиксированный	Свободно	Фиксированный
Ролик по X	Свободный	Фиксированный	Свободный
Ролик по оси Y	Фиксированный	Свободный	Свободный