Балки онлайн: Балка-онлайн SOPROMATu.NET

Содержание

Онлайн калькулятор: Опорные реакции простой балки

Данный онлайн калькулятор предназначен для нахождения опорных реакций в простейшей балке, находящейся под воздействием поперечных сил. Простая балка — прямолинейный брус, закрепленная на двух опорах: одной — шарнирно-неподвижной (опора А), другой — шарнирно-подвижной (опора В). Калькулятор выводит опорные реакции V_A и V_B, уравнения равновесия в символьном виде и показывает модель нагрузок. Обратите внимание, что если требуется задать нагрузку действующую левее опоры A, то расстояние от опоры нужно задать со знаком минус. Теорию и формулы расчета можно найти ниже под калькулятором.

Опорные реакции простой балки

Расстояние между опорами, м

Нагрузка

	Расстояние от опоры A	Нагрузка	Значение	Направление	Направление момента	Протяженность	Изменение

Записей:

51020501001000

Нагрузка

Расстояние от опоры A

Отрицательное, если нагрузка приложена к точке, лежащей левее опоры.

НагрузкаСосредоточенная нагрузка, кНРавномерно распределенная, кН/мЛинейно распределенная, кН/мМомент, кН*М

Значение

Направление↓ вниз↑ вверх

Направление момента↻ По часовой стрелке↺ Против часовой стрелки

Протяженность

Изменение\ Убывание/ Возрастание

Импортировать данныеОшибка импорта

Данные

Для разделения полей можно использовать один из этих символов: Tab, «;» или «,» Пример: -50.5;L;50.5;up;anticlockwise;50.5;increase

Загрузить данные из csv файла

Детали

Точность вычисления

Знаков после запятой: 2

Реакция опоры А, кН

Реакция опоры B, кН

Положительное направление момента сил

↻ По часовой стрелке

↺ Против часовой стрелки

Уравнения моментов сил

Файл очень большой, при загрузке и создании может наблюдаться торможение браузера.

Реакции опор

Под воздействием нагрузок в опорах балки возникают уравновешивающие силы, называемые реакциями опор. Эти силы зависят от вида нагрузки и типа самих опор.

Шарнирно подвижная опора

Шарнирно подвижная опора ( в нашей модели обозначена как «B») позволяет балке свободно перемещаться в горизонтальной плоскости и препятствует вертикальному перемещению, поэтому при любой нагрузке она имеет только вертикальную реакцию V_B.

Шарнирно неподвижная опора

Шарнирно неподвижная опора крепится к балке, что препятствует её горизонтальному и вертикальному перемещению. При наличии сил, действующих на балку в горизонтальной плоскости, эта опора дает еще и горизонтальную реакцию. Однако в нашей модели все силы действуют поперечно балке, поэтому горизонтальная реакция опоры A всегда будет равна нулю.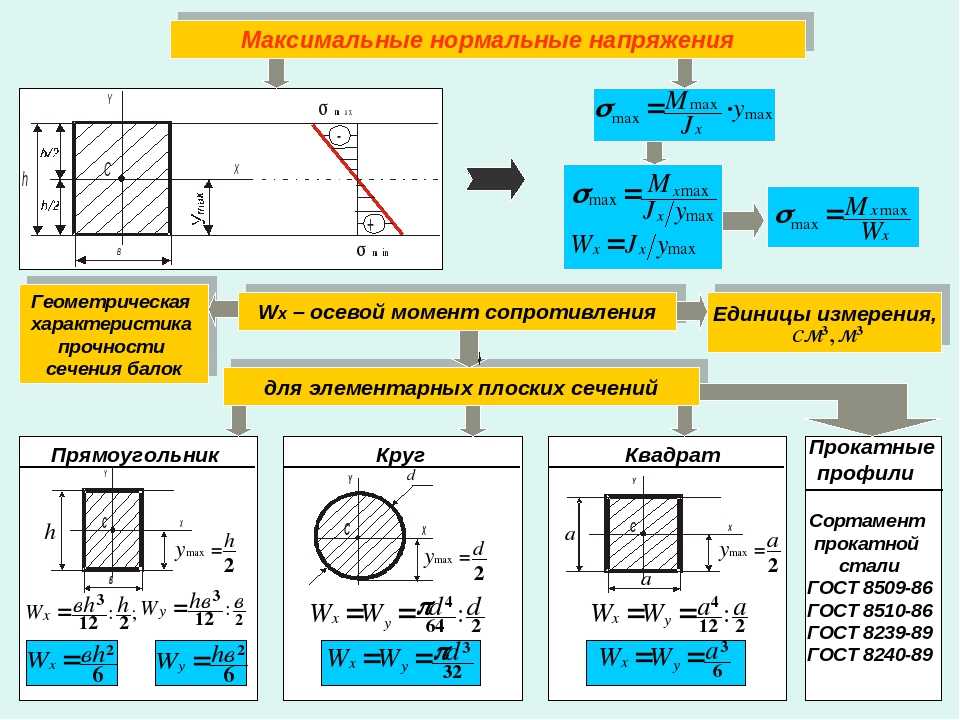 Вертикальную реакцию опоры A обозначим V_A.

Уравнения равновесия

Как мы знаем из статики, все силы и моменты сил в неподвижной системе, уравновешены. Поэтому суммы сил и моментов в любой точке этой системы равны нулю.
Все силы при поперечной нагрузке на простую балку действуют параллельно оси Y, поэтому можно составить только два независимых уравнения равновесия для проекции сил и моментов на ось Y. Этого вполне достаточно для нахождения двух неизвестных реакций опор V

A и V_B.
При составлении уравнений у нас есть выбор:

составить одно уравнение равновесия проекции сил и одно уравнение равновесия моментов в некоторой точке
составить два уравнения равновесия моментов в двух точках.

Воспользуемся вторым способом, а первый оставим для проверки полученного результата.
Удобнее всего составлять уравнения для точек А и B, в которых находятся опоры:

Напомним, что моментом силы в определенной точке называется произведение силы F на кратчайшее расстояние от этой точки до линии действия силы (плечо) l:

Исходя из этого, уравнения равновесия моментов в точках А и B для системы поперечных сил F₁. ..F_n, действующих на балку приобретают вид:

Где F_i

— модуль приложенной силы или реакции опоры в Ньютонах. l_{i_A} и l_{i_B} — длина рычага в метрах (кратчайшее расстояние от точки приложения силы i до опоры A и B соответственно). s_{i_A} и s_{i_B} — знак момента силы i в точке A и B соответственно.
Правило выбора знаков момента сил: знак положительный (+1) для момента, закручивающего балку вокруг выбранной точки по часовой стрелке ↻ и отрицательный (-1) для противоположного направления ↺. Можно выбрать и противоположные значения. Уравнения примут немного другой вид, но результат от этого не изменится.

Система сосредоточенных сил, действующих на простую балку

Например, для системы сил, показанной на рисунке выше, уравнения равновесия можно записать следующим образом:

Вычисляя, получаем значения реакций опор: V_A = 15.42 и V_B = 14.58. Проверим, что сумма всех сил равна нулю (для сил действующих вниз — знак положительный, для действующих вверх — отрицательный):

Составляя уравнения, мы исходили из того, что реакции обеих опор направлены вверх.

При расчетах может получиться так, что реакция опоры окажется отрицательной. Это означает, что реакция такой опоры направлена вниз (сумма моментов сил, действующих на балку, пытается оторвать её от опоры).

Распределенная нагрузка

В расчетах, иногда требуется задать нагрузку, которая распределена определенным образом по участку длины a. Для вычисления реакций опор такую нагрузку можно заменить её равнодействующей силой. Точкой приложения такой силы считается центр масс распределенной нагрузки, а модуль вычисляется как интеграл от функции распределения нагрузки на заданном участке. Для простых функций модуль легко выразить через заданную интенсивность нагрузки.

Пример системы распределенных нагрузок, действующих на простую балку

В таблице ниже представлены формулы для модуля сосредоточенной равнодействующей силы и точек её приложения для всех видов распределенных нагрузок, поддерживаемых калькулятором:

Нагрузка	Модуль	Точка приложения
Равномерная		1/2 a
Линейно убывающая		1/3 a
Линейно возрастающая		2/3 a

В формулах q — это интенсивность нагрузки в Н/м, a — диапазон действия распределенной нагрузки, точка приложения силы отсчитывается от начала диапазона действия распределенной нагрузки. Интенсивность для линейно распределенной нагрузки задается для участка максимума нагрузки ( полагаем, что в точке минимума, интенсивность = 0).
После вычисления модуля и плеча равнодействующей распределенной нагрузки их можно подставить в уравнения моментов, точно так же, как мы это делали с сосредоточенными силами.

Сосредоточенный момент

Еще один способ задания нагрузки в калькуляторе — при помощи момента в Нм, приложенного к некоторой точке. Значение сосредоточенного момента добавляется к уравнениям равновесия со знаком, определяемым направлением момента в соответствии с правилом знаков. Точка приложения сосредоточенного момента для вычисления реакций опор в простой балке значения не имеет.

Прокатная балка онлайн

Інструкція.

Программа позволяет определить опорные реакции, построить эпюры внутренних усилий (поперечных сил, изгибающих моментов) и эпюры перемещений (угла поворота, прогиб балки) для двухопорном и консольной балки.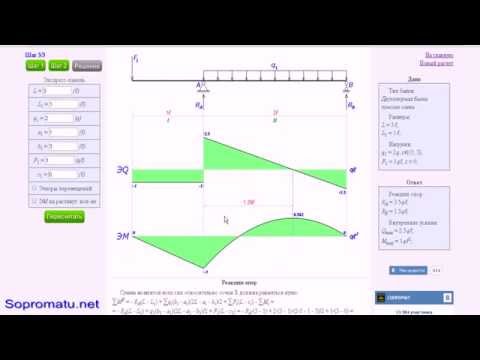

Дальнейшие инструкции будут приведены на примере балки на двух опорах.

1. Выберите условия крепления концов балки. Возможны варианты — свободный, шарнир и жесткое. В нашем примере левый — «шарнир», а правый — «свободный».

Если по ошибке был выбран другой вариант, нажимаем на кнопку «Новая схема».

2. Указываем длину балки, координаты опор и допускаемые напряжения. Длина балки равна «16» (м), а координаты опор от левого конца балки, соответственно к опоре A — «0» (не нужно указывать) и к опоре B — «11» (м). Допустимые нормальные напряжения σ_adm = 160 МПа, допустимые касательные напряжения τ_adm = 100 МПа.

3.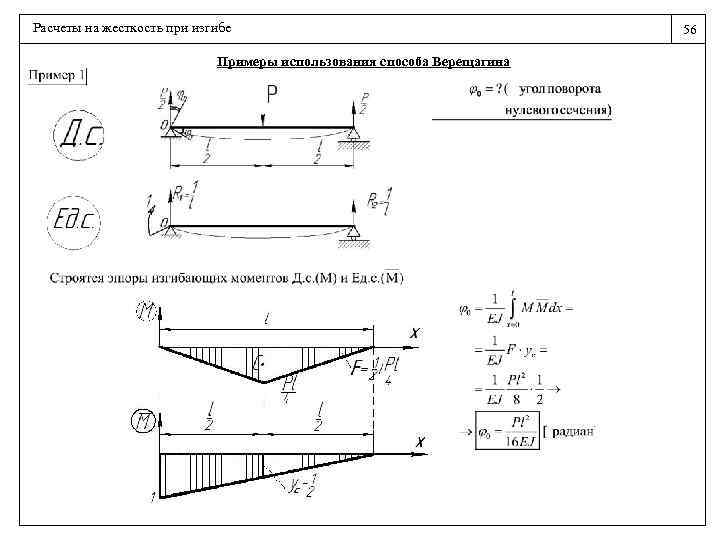 Указываем нагрузки.
Выбираем количество сосредоточенных моментов — «1». В таблице вводим значения моментов и их координаты от левого конца балки. M₁=18 (кН·м), a

1=9 (м)(момент который вращается против часовой стрелки — положительный, по — отрицательный).
Выбираем количество сосредоточенных сил — «1». В таблице вводим значение сил и их координаты. F₁=-20 (кН), b₁=4 (м) (сила направленная вниз — положительная, вверх — отрицательная).
Выбираем количество равномерно распределенной нагрузки — «1». В таблице вводим значение РРН, координаты начала и конца РРН. q₁=4 (кН/м), c₁=11 (м) та d₁=16 (м) (РРН направлено вниз — положительное, вверх — отрицательное).

4. Нажимаем на кнопку «Посчитать прокатную балку». После нажатия определяются опорные реакции, строятся эпюры усилий, перемещений и подбирается двутавровое сечение. Если нужно определить усилия и перемещения в произвольном сечении, введите координату в форму. Если нужно, задайте точность расчета и выберите правое или левое сечение.

Скриншот к примеру:

Скриншот к примеру (эпюра поперечных сил):

Скриншот к примеру (эпюра изгибающих моментов):

Скриншот к примеру (эпюра углов поворота):

Скриншот к примеру (эпюра прогибов):

Задайте длину и условия крепления балки:

Длина балки:

Левый: Выберитесвободныйшарниржесткое

Правый: Выберитесвободныйшарниржесткое

Координата опоры A (от левого конца балки): (м)

Координата опоры B (от левого конца балки): (м)

Допустимые нормальные напряжения (МПа)

Допустимые касательные напряжения (МПа)

Задайте нагрузки на балку:

Количество моментов (M):Выберите (0)12345678910

Момент оборачивается против часовой стрелки — положительный, за — отрицательный.

№

Количество сил (F):Выберите (0)12345678910

Сила направлена вниз — положительная, вверх — отрицательная.

№

Количество РРН (q):Выберите (0)12345678910

Равномерно распределенная нагрузка направлено вниз — положительное, вверх — отрицательное.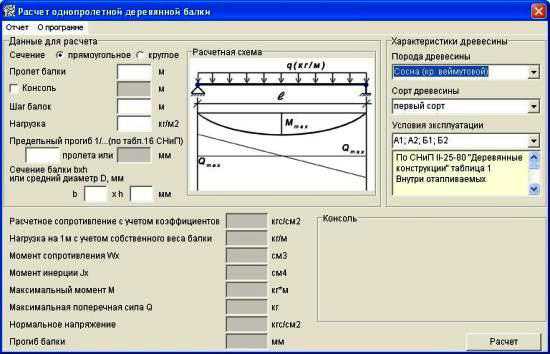

Момент сопротивления слишком большой, возможны большие перенапряжения! Перенапряжение должны быть не более 5%! Скорее всего нужного профиля в сортаменте (ГОСТ 8239-72) нет, попробуйте найти ГОСТ 26020-83.

Значение опорных реакций (положительная — направлена вниз, отрицательная — вверх):

R_A= кН

R_B= кН

Значение усилий в произвольном сечении:

Координата x= 2345678910СправаСлева

Значение эпюры Q при x= м: кН

Значение эпюры M при x= м: кН·м

Значение эпюры при x= м: кН·м²·рад

Значение эпюры при x= м: кН·м³

Начальные параметры:

кН

кН·м

кН·м²·рад

кН·м³

Максимальные значения усилий:

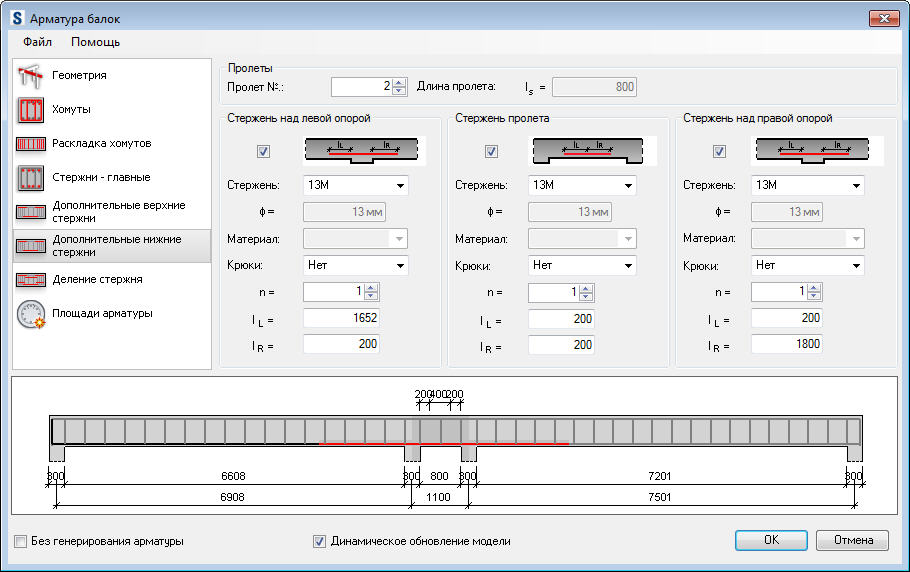
Подбор поперечного сечения.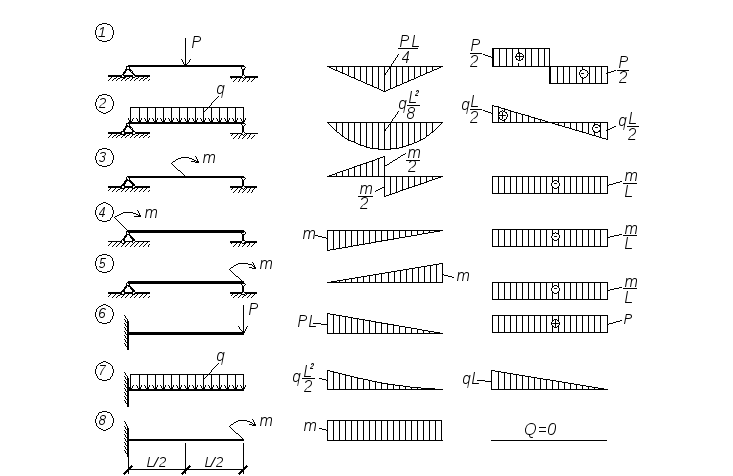

Нужный момент сопротивления:

_тр см ³

Из таблицы сортамента (ГОСТ 8239-72) принимаем двутавр №, с такими геометрическими характеристиками:

см⁴; см³; см³.

Размеры сечения:

мм; мм; мм; мм.

Полная проверка прочности балки.

а) По максимальным нормальным напряжением (сечение при м).

МПа

% — недонапряжение. перенапряжение.

б) По максимальным касательным напряжением (сечение при м).

МПа

% — недонапряжение. перенапряжение.

Вычисляем статический момент полки двутавра относительно центральной оси :

см³,

касательное напряжение в точке стыка полки и стенки:

МПа.

в) Главные напряжения проверяем в (сечение при м, СправаСлева).

Усилия в сечении: кН·м, кН.

Определяем нормальное и касательное напряжение в точке стыка полки и стенки двутавра:

МПа;

МПа.

По четвертой теории прочности:

МПа

% — недонапряжение. перенапряжение.

Определяем касательное напряжение на нейтральной оси:

МПа.

Эпюра поперечных сил:

Эпюра изгибающих моментов:

Эпюра углов поворота:

Эпюра прогибов:

МАГАЗИНОВ | БАЛКИ

main-area", "category": ".tab-japan"}»> Япония
Остальные страны Азии
Международный
Магазины

Харадзюку
- BEAMS HARAJUKU
  1F/2F, 3-24-7 Jingumae, Shibuya-ku, Tokyo
  03 3470 3947
- BEAMS F / Международная галерея BEAMS
  1F-2F, 3-25-15 Jingumae, Shibuya-ku, Tokyo
  03-3470-3946 (BEAMS F) / 03-3470-3948 (Международная галерея BEAMS)
- BEAMS WOMEN HARAJUKU
  B1F Jingumae Terrace, 3-25-15 Jingumae, Shibuya-ku Tokyo
  03 5413 6415 / 03-5771-5745 (Vermeerist BEAMS)
- BEAMS BOY HARAJUKU
  1F, 3-24-5 Jingumae, Shibuya-ku, Tokyo
  03 5770 5550
- BEAMS PLUS HARAJUKU
  1F, 3-25-12 Jingumae, Shibuya-ku, Tokyo
  03 3746 5851
- BEAMS RECORDS
  1F, 3-25-15 Jingumae, Shibuya-ku, Tokyo
  03 3746 0789
- BEAMS T HARAJUKU
  1F, 3-25-15 Jingumae, Shibuya-ku, Tokyo
  03 3470 8601
- Uniform Circus BEAMS
  3F, 1-5-8 Jingumae, Shibuya-ku, Tokyo
  03-3470-9393
- BEAMS KOUBOU
  2F, 3-25-15 jingumae shibuya-ku Tokyo
  080 9703 9379
- BEAMS GOLF POP UP STORE HARAJUKU
  1F, 3-25-14 Jingumae Shibuya-ku Tokyo
  03-6438-9826
Сибуя
- Pilgrim Surf+Supply
  1F, 1-14-7 Jinnan, Shibuya-ku, Tokyo
  03 5459 1690
- BEAMS MEN SHIBUYA
  1F/2F, 1-15-1 Jinnan, Shibuya-ku, Tokyo
  03 3780 5500
- BEAMS JAPAN SHIBUYA
  TOKYU PLAZA SHIBUYA 2F, 1-2-3 Dogenzaka, Shibuya-ku, Tokyo
  03 5422 3974
Эбису
- BEAMS EBISU
  Atre Ebisu 4F, 1-5-5 Ebisu-Minami, Shibuya-ku, Tokyo
  03 5447 7061
Дайканьяма
- Kodomo BEAMS
  1F, 19-7 Sarugakucho, Shibuya-ku, Tokyo
  03 5428 4844
Гинза
- BEAMS GINZA
  2F/3F, 4-4-1 Ginza, Chuo-ku, Tokyo
  03 3567 2223（2F Casual）／ 03 3567 2224（3F Formal）
Маруноути
- БАЛОЧНЫЙ ДОМ MARUNOUCHI
  МАРУНОУЧИ корп. 1F, 2-4-1 Marunouchi, Chiyoda-ku, Tokyo
  03 5220 8686
- BEAMS SHIN-MARUNOUCHI
  SHIN-MARUNOUCHI корп. 3F, 1-5-1 Marunouchi, Тиёда-ку, Токио
  03 5288 7670
- BEAMS GOLF DAIMARU TOKYO
  DAIMARU TOKYO 11F, 1-9-1 Marunouchi, Chiyoda-ku, Tokyo
  03 5218 2210
Юракучо
- BEAMS PLUS YURAKUCHO
  Shin-Yurakucho Bldg. 1F, 1-12-1 Юракучо, Тиёда-ку Токио
  03 5220 3151
- BEAMS GOLF YURAKUCHO
  Yurakucho Denki Bldg. 1F, 1-7-1 Юракучо, Тиёда-ку, Токио
  03 5221 6001
- СТАНЦИЯ BEAMS & WINDS
  Shin-Yurakucho Bld. B2F, 1-12-1 Юракучо, Тиёда-ку, Токио
  03 3214 0800
Роппонги
- BEAMS HOUSE ROPPONGI
  TOKYO MIDTOWN·Galleria 1F, 9-7-3 Akasaka, Minato-ku, Tokyo
  03 5413 7690
- BEAMS ROPPONGI HILLS
  2F-3F Roppongi Hills West Walk, 6-10-1 Роппонги, Минато-ку Токио
  03 5775 1620（2F）／03 5775 1623（3F）
Синдзюку
- BEAMS F SHINJUKU
  6/7F, 3-32-6 Shinjuku, Shinjuku-ku, Tokyo
  03 5368 7305
- BEAMS JAPAN
  B1F — 5F, 3-32-6 Синдзюку, Синдзюку-ку, Токио
  03 5368 7300
- Demi-Luxe BEAMS SHINJUKU
  LUMINE Shinjuku 1 2F , 1-1-5 Nishi-Shinjuku, Shinjuku-ku, Tokyo
  03 5339 9070
- BEAMS SHINJUKU
  LUMINE EST Shinjuku B2F, 3-38-1 Shinjuku, Shinjuku-ku, Tokyo
  03 5369 2140
- Ray BEAMS SHINJUKU
  LUMINE EST Синдзюку 1F, 3-38-1 Синдзюку, Синдзюку-ку Токио
  03 5368 2191
- BEAMS NEWS
  EKINAKA NEWoMan 2F, 5-24-55 Сендагая, Сибуя-ку, Токио
  03 3351 3090
- BEAMS GOLF ODAKYU DEPARTMENT SHINJUKU
  M2F, Odakyu Department Shinjuku Maine Store, 1-5-1 Nishishinjuku, Shinjuku-ku Tokyo
  03 5325 1090
Футакотамагава
- BEAMS FUTAKOTAMAGAWA
  Tamagawa Takashimaya Торговый центр South Bldg. 2F, 3-17-1 Тамагава, Сетагая-ку, Токио
  03 3707 8998
- BEAMS GOLF Tamagawa Takashimaya
  Тамагава Takashimaya Торговый центр South Bldg. 5F, 3-17-1, Тамагава, Сетагая-ку, Токио
  03 5491 5741
Икебукуро
- BEAMS IKEBUKURO
  LUMINE Ikebukuro1F, 1-11-1 Nishi-Ikebukuro, Toshima-ku, Tokyo
  03 5956 1590
- Demi-Luxe BEAMS IKEBUKURO
  LUMINE Ikebukuro B1F, 1-11-1 Nishi-Ikebukuro, Toshima-ku Tokyo
  03 5957 5791
Китасенью
- BEAMS KITASENJU
  LUMINE Kitasenju 3F, 42-2 Senjuasahicho, Adachi-ku, Tokyo
  03 5284 2211
Осиаге
- BEAMS TOKYO SKYTREE TOWN
  TOKYO SKY TREE TOWN Solamachi 2F, 1-1-2 Oshiage Sumida-ku, Tokyo
  03 5819 4011
Тойосу
- B:MING LIFE STORE by BEAMS Городской причал LaLaport Toyosu
  Городской причал LaLaport Toyosu 1F, 2-4-9 Toyosu, Кото-ку, Токио
  03 3532 3100
Китидзёдзи
- BEAMS KICHIJOJI
  kirarina Kichijoji 3F, 2-1-25 Kichijojiminamicho, Musashino-shi, Tokyo
  0422 70 2571
Тачикава
- BEAMS TACHIKAWA
  LUMINE Tachikawa 2F, 2-1-1 Akebonocho, Tachikawa-shi, Tokyo
  042 548 1070 （мужские） / 042 548 1071 （женские）
- 0
Мачида
- BEAMS MACHIDA
  LUMINE Machida 2F, 6-1-11 Haramachida, Machida-shi, Tokyo
  042 732 5101
Минамиосава
- BEAMS OUTLET TAMA MINAMI OSAWA
  MITSUI OUTLET PARK TAMA MINAMI OSAWA, 1-600 Minami-Osawa, Hachioji-shi, Tokyo
  042 678 7600
Минамимачида
- BEAMS OUTLET MINAMIMACHIDA
  1F Grandberry Park, 3-4-1 Tsuruma, Machida-shi Tokyo
  042 850 7061

я; я++) {%>

tab-asia-btn", "group": ".asia-area", "category": ".tab-beijing"}»> Пекин
Тайвань
Гонконг
Бангкок

BEAMS BEIJING Sanlitun Village
Sanlitun Village South Area, Sanlitun Road, 11, район Чаоян, Пекин, Китай
+86 10 6416 2087

BEAMS TAIPEI
No.340, Fujin Street, Taipei City, Taiwan
+886 2 2767 2716
BEAMS OUTLET LINKOU
No. 356, Section 1, Wenhua 3rd Rd, Linkou District, New Taipei City, Taiwan
+886 2 2600 3783
BEAMS Breeze NAN SHAN atre
3F, No. 17, Songzhi Rd., Xinyi District, Taipei City 110, Тайвань
+886 2 2723 6584
BEAMS TAICHUNG MITSUKOSHI
№ 301, секция 3, бульвар Тайвань, район Ситунь, город Тайчжун
+886 4 2251 6010
BEAMS OUTLET ТАЙЧУНГ
№ 168, секция 10, бульвар Тайвань, район Уци, город Тайчжун
+886 4 2656 4138

Ray BEAMS HONG KONG FESTIVAL WALK
LG1-31, Festival Walk, Kowloon Tong, Kowloon, Hong Kong, China
＋852 2265 7659
ЛУЧИ ГОНКОНГ ОДИН
Магазин UG207, The ONE, Цим Ша Цуй, Коулун, Гонконг, Китай
+852 2677 0230
BEAMS HONG KONG HYSAN PLACE
Магазин 626-627, 6F, Hysan Place, Козуэй Бэй, Гонконг, Китай
+852-2759-3282

BEAMS BANGKOK
1A 09-10, торговый комплекс EmQuartier, 693 Sukhumvit Road, Klongton Nua, Wattana, Bangkok 10110 Таиланд
+662 003 6067
BEAMS BANGKOK PARAGON
2F Paragon Department Store, 991/1 Rama I Rd.

Балки онлайн: Балка-онлайн SOPROMATu.NET