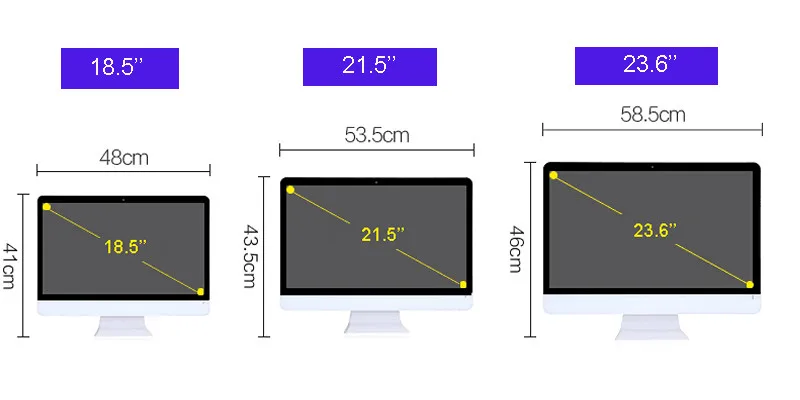
Как узнать диагональ монитора: 3 способа
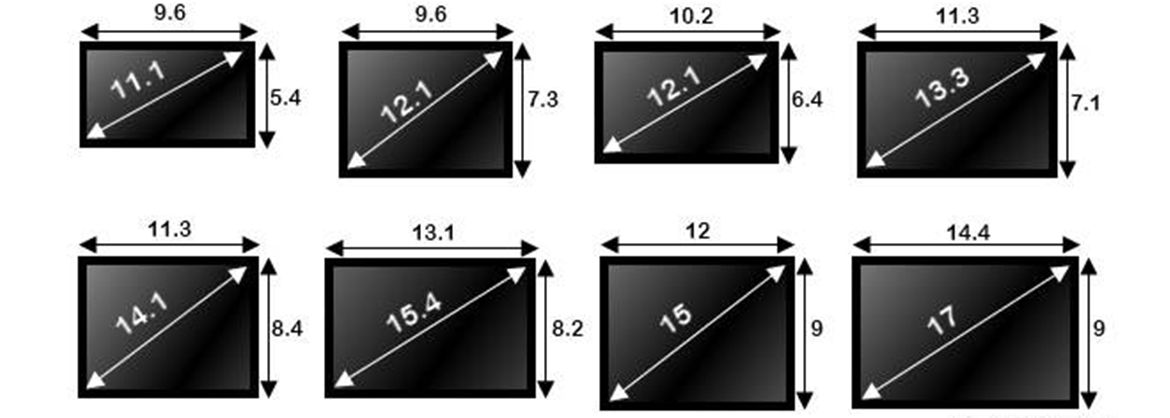
Всех приветствую на нашем ламповом портале WiFiGiD.RU. Сегодня я расскажу вам, как узнать диагональ монитора компьютера или экрана ноутбука. Я распишу несколько простых способов, которые вам должны помочь. Как вы знаете, для измерения используются дюймы. Чтобы примерно представлять себе размер, их лучше всего перемножить на наши любимые и родные сантиметры:
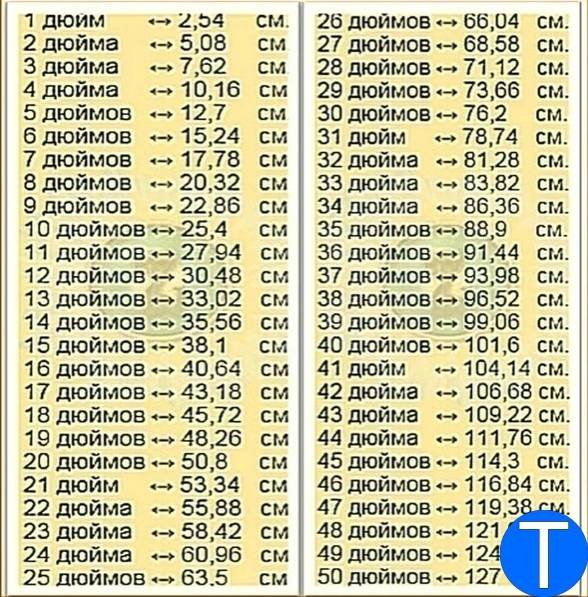
1 дюйм = 2,54 см
Содержание
- Способ 1: Поиск информации
- Способ 2: Измерение
- Способ 3: С помощью программы
- Задать вопрос автору статьи
Очень часто производитель указывает дюймы в названии самой модели монитора, или ноутбука. Например, модель AOC Q27G2S/EU – имеет диагональ 27 дюйма. Или LG 27MP400-B – имеет ту же самую диагональ. Чтобы посмотреть название, можно глянуть на специальную этикетку. Она обычно наклеена на задней части монитора. Если у вас более старая модель, то наклейка может быть наклеена спереди.
Если у вас монитор от китайской фирмы Xiaomi или Huawei, то подобной цифры скорее всего не будет. Еще одна особенность именно по мониторам – цифра в названии всегда округляется. Например, модель AOC 24B2XDM – на самом деле имеет диагональ 23,8 дюйма. А экран LG UltraGear 32GN600-B – имеет диагональ 31,5.
У ноутбуков все немного по-другому. Да, в названии частенько можно встретить размер диагонали, но округления там нет. Так ноутбук Lenovo IdeaPad Gaming 3 15IMH05 – имеет диагональ 15,6. А модель HP OMEN 16-c0007ur – 16,1. Название ноутбука можно посмотреть на той же самой этикетке – её обычно лепят на дно аппарата или на переднюю часть рядом с клавиатурой. Там же можно увидеть и размер диагонали.
У ноутбуков можно встретиться с той же самой проблемой – не всегда в названии модели есть размер диагонали. В любом случае название нам еще может пригодиться – мы можем просто взять и загуглить эту информацию. Просто откройте любой поисковик и вбейте полное наименование модели в строку поиска. После этого перейдите в любой магазин, на официальную страницу или посмотрите обзор – там по любому будет информация о диагонали.
После этого перейдите в любой магазин, на официальную страницу или посмотрите обзор – там по любому будет информация о диагонали.
ПОМОЩЬ! Если вы не можете самостоятельно найти диагональ – просто напишите в комментариях точную модель вашего монитора или ноутбука, и я вам сразу же отвечу.
Способ 2: Измерение
Еще один простой вариант – это просто измерить диагональ монитора или экрана. Даже если у вас и будет какая-то погрешность при этом, она все равно будет минимальной. Для этого подойдет любая линейка или даже мягкий «сантиметр». Для измерения мы будем использовать два противоположных угла, которые находятся по диагонали. После этого вам нужно поделить получившееся число на 2,54. Напомню, что диагональ может иметь не точную цифру – например, диагонали 17,3 или 16,1 дюйма.
Способ 3: С помощью программы
Узнать сколько дюймов монитор на компьютере или ноутбуке можно с помощью стороннего программного обеспечения. Лучше всего использовать утилиту – AIDA64. Она позволяет просмотреть почти все характеристики, которыми обладает ваш ПК. Программа хоть и платная, но у неё есть бесплатный пробный период. Скачиваем, устанавливаем и запускаем её. Далее открываем раздел «Дисплей», переходим в подраздел «Монитор» и в правом блоке находим «Тип монитора» – эти цифры и будут вашей диагональю. Здесь же вы можете посмотреть и модель самого экрана.
Лучше всего использовать утилиту – AIDA64. Она позволяет просмотреть почти все характеристики, которыми обладает ваш ПК. Программа хоть и платная, но у неё есть бесплатный пробный период. Скачиваем, устанавливаем и запускаем её. Далее открываем раздел «Дисплей», переходим в подраздел «Монитор» и в правом блоке находим «Тип монитора» – эти цифры и будут вашей диагональю. Здесь же вы можете посмотреть и модель самого экрана.
Площадь прямоугольника размером 23 x 13 и геометрические свойства, такие как симметрия, периметр прямоугольника, диагонали
|
Нам дано, что длина прямоугольника = 23,0 единицы, а ширина = 13,0 единицы. AD = BC = 23,0 ед. А АВ = CD = 13,0 ед. Единицами могут быть любые единицы длины: дюймы, см, футы, мили, км и т. д. Геометрические свойства, которые мы вычислим Вычислим площадь, периметр, длину диагонали, радиус описанной окружности, площадь описанной окружности и углы, образуемые диагональю со сторонами. Вычисление площади прямоугольника Площадь этого прямоугольника = длина х ширина (длина х ширина) = 23,0 х 13,0 = 299,0 квадратных единиц
Вычисление периметра прямоугольникаПериметр этого прямоугольника = 2 * (длина + ширина) = 2 * (23,0 + 13,0) = 72,0 шт. Диагональ этого прямоугольника может быть вычислена с помощью теоремы Пифагора (или теоремы Пифагора). Треугольники ADC (или BDC) являются прямоугольными треугольниками. Итак, диагональ(и) можно рассматривать как гипотенузу прямоугольного треугольника. Таким образом, квадрат длины диагонали равен сумме квадратов длины и ширины. Длина диагоналей AC и BD = (23,0 2 + 13,0 2 ) (1/2) Итак, длина диагонали = 26,42 единицы Вычисление радиуса и площади описанной окружности На самом деле у прямоугольника нет вписанной окружности, которая касается каждой стороны. Однако действительно возможно нарисовать окружность, проходящую через все 4 вершины прямоугольника. Обе диагонали являются диаметрами окружности. Угол в полуокружности является прямым углом: каждый из 4 углов прямоугольника становится углом полукруга, когда мы рисуем описанную окружность. Радиус описанной окружности = половина длины диагонали = 26,42/2 единицы = 13,21 единицы Площадь описанной окружности = PI x радиус окружности2 = PI * 13,21 * 13,21 = 548,21 квадратных единиц Симметрия и оси симметрии Прямоугольник имеет 2 оси симметрии: прямую, проходящую через середины сторон AB и CD, и другую прямую, проходящую через середины сторон AD и BC. Оба проходят через точку E. Прямоугольник также является «изогональным» по своей природе, хотя это понятие вы, возможно, изучите или столкнетесь с ним позже. Вычисление угла, образованного диагональю со сторонами Мы можем использовать немного тригонометрии, чтобы вычислить это. Тангенс угла CAD = Тангенс угла ACB = ширина прямоугольника / длина прямоугольника = 13,0/23,0 = 0,57 Угол CAD = Угол ACB = tan -1 и угол BAC = угол ACD = 90 градусов — угол CAD = 1,06 радиана = 60,52 градуса Примеры конгруэнтности и конгруэнтных треугольников Каждая диагональ делит прямоугольник на пару конгруэнтных треугольников. ДиагональBD делит прямоугольник на равные треугольники BAD и BCD. Доказательство: (a) Угол BAD = угол BCD = 90 градусов (прямой угол) (b) BD общая сторона обоих (гипотенуза) (c) BA = CD = 13,0 единиц (противоположные стороны прямоугольника равны) (d) AD = BC = 23,0 единицы (противоположные стороны прямоугольника равны) Используя (a) (b) и (c), два треугольника конгруэнтны, используя конгруэнтность RHS или HL (гипотенуза-каттер). Или, используя (c), (a) и (d), два треугольника конгруэнтны, используя конгруэнтность SAS (сторона-угол-сторона) Аналогично можно доказать, что AC делит прямоугольник на два равных треугольника. Две диагонали делят прямоугольник на две пары конгруэнтных треугольников (Треугольник AEB и треугольник CED равны, треугольник BEC и треугольник AED равны) Чтобы доказать, что треугольник AEB и треугольник CED конгруэнтны: (a) AB = CD = 13,0 единиц (Противоположные стороны прямоугольника равны) (б) Угол ABD = Угол CDB (AB параллелен CD, а BD — их секущая, это противоположные углы, значит равные) (c) Угол BAC = угол DCA (по той же причине, что и выше) (d) Угол BEA = угол CED (противоположные углы или вертикальные углы равны) Итак, мы можем доказать конгруэнтность двух треугольников с помощью ASA Congruence (используя (c) (a) (b)) Или мы можем доказать конгруэнтность двух треугольников с помощью Конгруэнтности AAS Аналогичным образом мы можем доказать, что треугольники BEC и AED равны. Геометрические свойства прямоугольниковПомните: прямоугольник — это четырехугольник с 4 прямыми углами. Противоположные стороны равны. Все свойства, применимые к параллелограммам, применимы и к прямоугольникам. Квадрат можно рассматривать как частный случай прямоугольника, у которого все стороны равны. Каждый прямоугольник представляет собой выпуклый многоугольник и вписанный четырехугольник, диагональ которого представляет собой диаметр описанной окружности. Еще несколько примеров: Геометрические свойства прямоугольника размером 24 х 13, Геометрические свойства прямоугольника размером 24 x 14. Чтобы больше узнать о геометрических особенностях и свойствах прямоугольников, формулах, связанных с измерением и т. д., вам может быть полезно прочитать свойства учебника по прямоугольникам здесь. Многие из этих концепций являются частью программы по математике для 9 и 10 классов программы GCSE в Великобритании, Common Core Standards в США, программы ICSE/CBSE/SSC в Индии. |
Как найти длину диагонали прямоугольника
Все математические ресурсы SAT
16 Диагностических тестов 660 практических тестов Вопрос дня Карточки Learn by Concept
SAT Math Help » Геометрия » Плоская геометрия » Четырехугольники » Прямоугольники » Как найти длину диагонали прямоугольника
Какова длина диагонали прямоугольника, длина которого 3 фута, а ширина 4 фута?
Правильный ответ:
Объяснение:
Диагональ прямоугольника эквивалентна нахождению длины гипотенузы прямоугольного треугольника со сторонами 3 и 4. Используя теорему Пифагора:
Следовательно, диагональ прямоугольника равна 5 футам.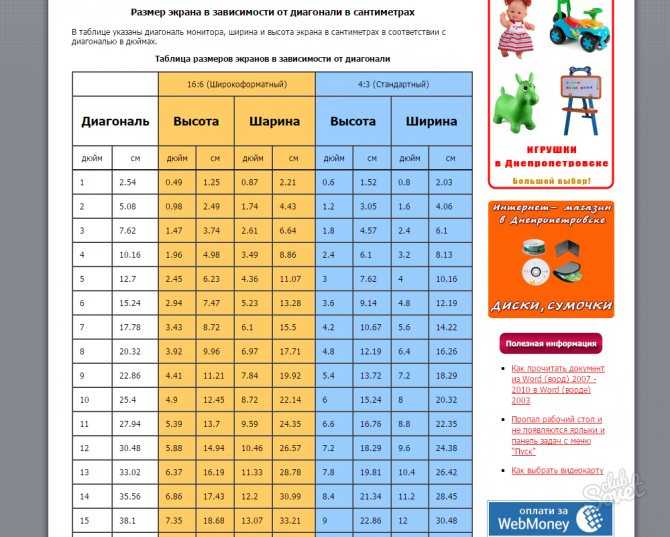 .
.
Сообщить об ошибке
Длина и ширина прямоугольника относятся как 3:4. Если площадь прямоугольника 108 квадратных сантиметров, какова длина диагонали?
Possible Answers:
24 centimeters
15 centimeters
9 centimeters
12 centimeters
18 centimeters
Correct answer:
15 centimeters
Объяснение:
Длина и ширина прямоугольника относятся к 3:4, поэтому стороны можно записать как 3 x и 4 x .
Мы также знаем площадь, поэтому пишем уравнение и решим для x:
(3 x ) (4 x ) = 12 x 2 = 108.
x 2 =
x = 3
Теперь мы можем Recalcul и The Glencul и The Glencul and The Glencum ширина:
длина = 3x = 3(3) = 9 сантиметров
ширина = 4x = 4(3) = 12 сантиметров
Используя теорему Пифагора, мы можем найти диагональ, c :
длина 2 + ширина 2 = c 2
9 2 + 12 2 = C 2
81 + 144 = C 2
225 = C 2
C = 15 санту диагональ прямоугольника со сторонами 8 и 15.
Возможные ответы:
Правильный ответ:
Объяснение:
Решить. просто используйте теорему Пифагора, где и .
Таким образом,
Сообщить об ошибке
На приведенном выше рисунке изображен куб, каждое ребро которого имеет длину 18. Укажите длину кратчайшего пути из точки A в точку B, полностью пролегающего по поверхности куба. куб.
Возможные ответы:
Правильный ответ:
Пояснение:
Кратчайший путь проходит по двум поверхностям призмы. Есть три возможных варианта — сверху и спереди, справа и спереди, сзади и снизу — но, как оказалось, поскольку все грани — (конгруэнтные) квадраты, все три пути имеют одинаковую длину.

 Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.
Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.