Уклон 2 1: Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности ChertimVam.Ru

Уклон и Конусность — Определение, обозначение на чертеже, формула расчёта уклона и конусности ChertimVam.Ru

Иногда, в задачах по начертательной геометрии или работах по инженерной графике, или при выполнении других чертежей, требуется построить уклон и конус. В этой статье Вы узнаете о том, что такое уклон и конусность, как их построить, как правильно обозначить на чертеже.

Что такое уклон? Как определить уклон? Как построить уклон? Обозначение уклона на чертежах по ГОСТ.

Уклон. Уклон это отклонение прямой линии от вертикального или горизонтального положения.
Определение уклона. Уклон определяется как отношение противолежащего катета угла прямоугольного треугольника к прилежащему катету, то есть он выражается тангенсом угла а. Уклон можно посчитать по формуле i=AC/AB=tga.

Построение уклона. На примере (рисунок ) наглядно продемонстрировано построение уклона. Для построения уклона 1:1, например, нужно на сторонах прямого угла отложить произвольные, но равные отрезки. Такой уклон, будет соответствовать углу в 45 градусов. Для того чтобы построить уклон 1:2, нужно по горизонтали отложить отрезок равный по значению двум отрезкам отложенным по вертикали. Как видно из чертежа, уклон есть отношение катета противолежащего к катету прилежащему, т. е. он выражается тангенсом угла а.

Обозначение уклона на чертежах. Обозначение уклонов на чертеже выполняется в соответствии с ГОСТ 2.307—68. На чертеже указывают величину уклона с помощью линии-выноски. На полке линии-выноски наносят знак и величину уклона. Знак уклона должен соответствовать уклону определяемой линии, то есть одна из прямых знака уклона должна быть горизонтальна, а другая должна быть наклонена в ту же сторону, что и определяемая линия уклона. Угол уклона линии знака примерно 30°.

Что такое конусность? Формула для расчёта конусности. Обозначение конусности на чертежах.

Конусность. Конусностью называется отношение диаметра основания конуса к высоте.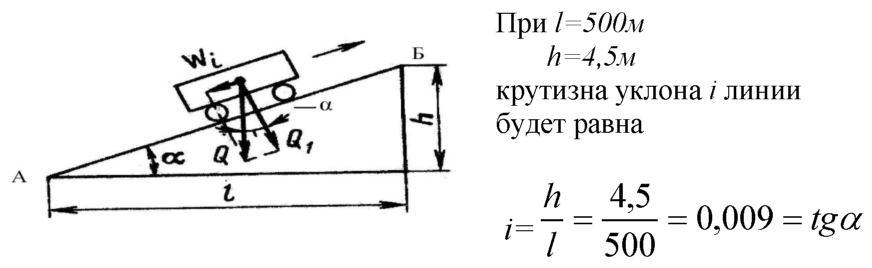 Конусность рассчитывается по формуле К=D/h, где D – диаметр основания конуса, h – высота. Если конус усеченный, то конусность рассчитывается как отношение разности диаметров усеченного конуса к его высоте. В случае усечённого конуса, формула конусности будет иметь вид: К = (D-d)/h.

Обозначение конусности на чертежах. Форму и величину конуса определяют нанесением трех из перечисленных размеров: 1) диаметр большого основания D; 2) диаметр малого основания d; 3) диаметр в заданном поперечном сечении Ds , имеющем заданное осевое положение Ls; 4) длина конуса L; 5) угол конуса а; 6) конусность с . Также на чертеже допускается указывать и дополнительные размеры, как справочные.

Размеры стандартизованных конусов не нужно указывать на чертеже. Достаточно на чертеже привести условное обозначение конусности по соответствующему стандарту.

Конусность, как и уклон, может быть указана в градусах, дробью (простой, в виде отношения двух чисел или десятичной), в процентах.

Например, конусность 1:5 может быть также обозначена как отношение 1:5, 11°25’16», десятичной дробью 0,2 и в процентах 20.
Для конусов, которые применяются в машиностроении, OCT/BKC 7652 устанавливает ряд нормальных конусностей. Нормальные конусности — 1:3; 1:5; 1:8; 1:10; 1:15; 1:20; 1:30; 1:50; 1:100; 1:200. Также в могут быть использованы — 30, 45, 60, 75, 90 и 120°.

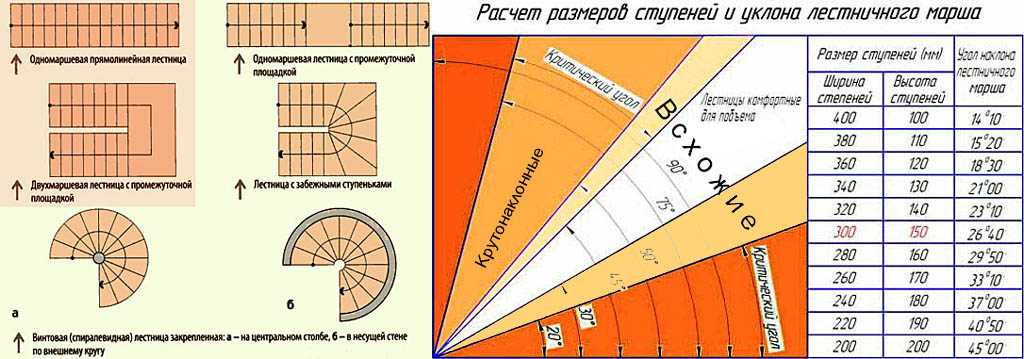
Угол наклона лестницы – Оптимальные значения и как рассчитать

С каждым годом при строительстве частных домов предъявляются все более жесткие требования к качеству, эргономичности и практичности отдельных конструкций. Лестница является наиболее используемым элементом в любом многоэтажном доме и в этой статье мы постараемся ответить на вопрос, как подобрать наиболее оптимальный угол наклона марша, для того чтобы эксплуатация изделия была наиболее комфортной и не сопровождалась трудностями при перемещении между ярусами.

Попробуйте наши калькуляторы расчета лестниц – у нас вы найдете качественную графику, подробные расчеты и готовую смету по материалам.

 

Содержание

• Что такое угол наклона лестницы
• Оптимальный угол наклона лестницы
• Какие показатели влияют на уклон лестницы
• Как рассчитать угол наклона лестницы
• Расчет угла наклона лестницы – Онлайн калькулятор
• Расчет наклона лестницы вручную

 

Что такое угол наклона лестницы?

Угол наклона лестницы – это угол наклона лестничного марша по отношению к поверхности пола. Соответственно, чем меньше числовое значение угла, тем более пологая конструкция получается.

Небольшой угол подъема позволяет подобрать наиболее оптимальную ширину проступи и высоту ступени, что в свою очередь обеспечивает более высокий уровень безопасности при эксплуатации пожилыми, детьми и людьми с ограниченными возможностями.

Главным недостатком такого типа конструкции является чрезвычайная массивность и громоздкость – не в каждом доме найдется свободное пространство под такое сооружение, а если и найдется, то без необходимости, редко кто готов так неэффективно использовать жилую площадь.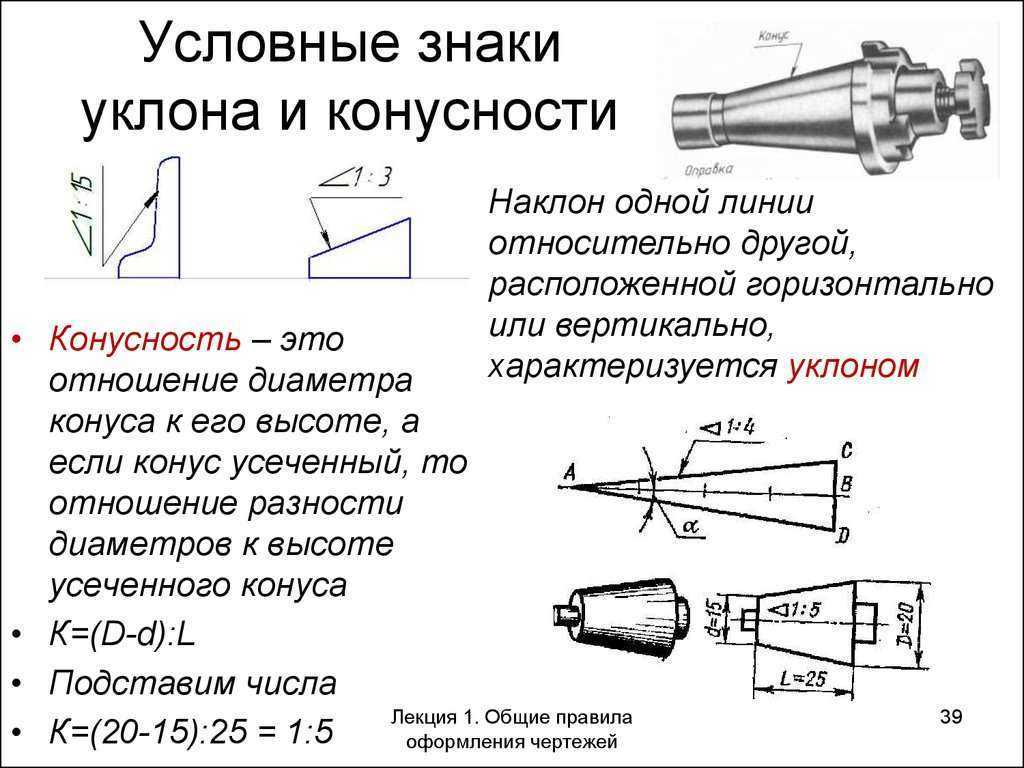

Также не рекомендуется устанавливать слишком крутую конструкцию, так как она накладывает определенные физические ограничения на жильцов. Из-за высоких ступеней перемещаться по такой лестнице будет проблематично, утомительно и зачастую небезопасно.

Нас часто спрашивают: уклон лестницы 1:1 – что это значит и сколько это ? Ответ крайне прост – уклон 1:1 равен углу в 45 градусов, т.е. глубина ступени фактически равна ее высоте. Уклон 1:2 – это угол в 27,5 градусов, т.е. глубина ступени в два раза больше ее высоты.

 

Оптимальный угол наклона лестницы

Для определения оптимального угла наклона лестничного марша ориентируются на строительные нормативы, технические особенности помещения и конечно же, личные предпочтения.

Считается, что в частном домостроении для повседневного использования наиболее приемлемым является уклон в 45 градусов, оптимальным 35-45 градусов, а идеальным – 30-35. В этих случаях, при использовании лестницы человек будет прилагать наименьшие усилия при перемещении и у него не возникнет чувство дискомфорта.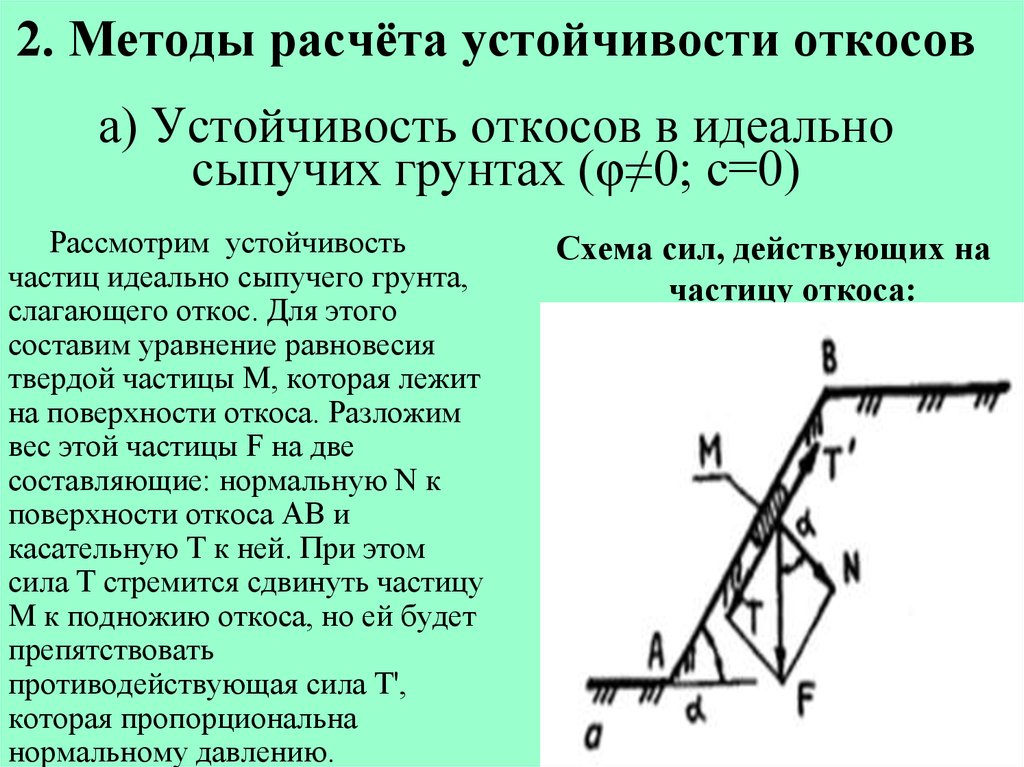

Тем не менее не всегда рационально использовать именно такие уклоны. В зависимости от назначения и места установки, ориентироваться стоит на другие рекомендованные значения.

Например, разбив все конструкции на несколько групп можно определить оптимальные углы наклона:

• Пандусы . Используются при наличии людей с ограниченными возможностями. Обязательно должны быть пологими с углами не более 15 градусов.
• Уличные и садовые лестницы. Применяются в общественных пространствах, парках, садах. Должны обеспечивать комфортный подъем для широкого круга людей, поэтому наклон не должен быть значительным – до 30 градусов.
• Внутренние лестницы. Используются в многоквартирных и частных домах. Считается что лестница с уклоном от 30 до 45 градусов является наиболее оптимальной, так обеспечивает комфортное перемещение для среднестатистического человека и не занимает большую площадь.
• Чердачные лестницы. В случаях, когда невозможно и/или нецелесообразно установить классическую лестничную конструкцию, применяются крутые, но компактные чердачные лестницы с углом до 60 градусов.
• Стремянки, трапы, пожарные лестницы. Приставные лестницы являются временным решением и используются крайне редко, они устанавливаются с минимальным уклоном, т.е. практически вертикально.

Не забывайте, что главным критерием при выборе угла наклона лестницы должны быть потребности проживающих в доме людей, так как именно им придется использовать конструкцию в наибольшей степени.

 

Какие показатели влияют на уклон лестницы?

Как уже было не раз отмечено, что на показатель уклона лестницы влияют ширина и высота ступеней. Низкие ступени и широкая проступь обеспечивают более пологую, но в то же время более громоздкую конструкцию, соответственно, более высокие и узкие ступени позволяют использовать меньшее пространство, так как увеличивается максимальный угол подъема лестницы.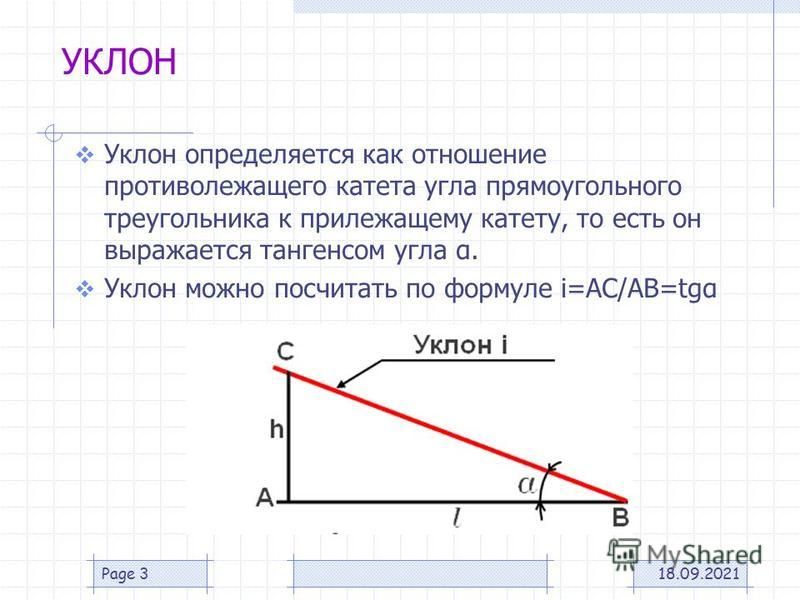

Считается, что оптимальным показателем высоты ступени является 15-18 см. Более высокое значение приводит к возникновению трудностей при перемещении, а меньшее к нецелесообразному укрупнению сооружения.

Ширина проступи определяет непосредственно эффективную глубину ступенек. Подбирается на основании средней длины шага пользователей и технических возможностей помещения. Рекомендованная ширина 27-30 см.

Почти все конструктивные особенности изделия определяет ГОСТ 23120-78 «Лестницы маршевые, площадки и ограждения».

 

Как рассчитать угол наклона лестницы?

Расчет угла наклона лестничного марша является одной из самых важных задач при проектировании конструкции, так как именно этот параметр предопределяет характеристики остальных элементов сооружения. Мы предлагаем вам ознакомиться с двумя методами расчета – автоматизированный с помощью онлайн-калькулятора и классический ручной.

 

Расчет угла наклона лестницы – Онлайн калькулятор

Если вы боитесь ошибиться и у вас нет лишнего времени, лучшим решением для того чтобы рассчитать угол наклона лестницы на второй этаж станут наши надежные онлайн-калькуляторы. У нас доступен расчет следующих типов конструкций:

• прямая лестница на тетивах;
• прямая лестница на косоурах;
• прямая лестница с ломаным косоуром;
• лестница на косоурах с забежными ступенями с поворотом на 90;
• лестница на косоурах с забежными ступенями с поворотом на 180;
• одномаршевая лестница на косоурах с площадкой с поворотом на 90;
• двухмаршевая лестница на косоурах с площадкой с поворотом на 180;
• трехмаршевая лестница на косоурах с площадкой с поворотом на 180.

Перейдите на страницу интересующей лестницы, введите необходимые параметры проема и нажмите кнопку «Рассчитать».

Вам будет доступен блок с результатами расчета, в котором вы можете подчерпнуть большое количество полезной информации – практически готовую смету. В отдельном окне выводятся чертежи, схемы и 3D-модель конструкции.

 

Расчет наклона лестницы вручную

Классическим, но не всегда рациональным методом является расчет угла лестницы вручную. Мы покажем, как применяя простые геометрические правила можно определить искомое значение и разберем пример.

Существует два основных способа расчета:

• Способ #1 – наиболее простой. Зная параметры глубины и высоты ступени, вы можете сразу определить угол наклона лестницы, так как фактически он будет совпадать с углом наклона гипотенузы прямоугольного треугольника, образованного ступенями. Для того чтобы его определить нужно знать тангенс угла А.

Формула расчета угла наклона лестницы: tg(A) = h / s

• Способ #2. Суть расчета сводится к тому же, только здесь в качестве катетов прямоугольного треугольника выступает высота и длина проема. Рассмотрим второй случай, как наиболее подробный.

Считается, что максимально комфортными и удобными лестницами являются те, при ходьбе на которых не приходится искусственно изменять привычную длину шага. У каждого человека свой стандарт, однако среднее значение находится в пределах 60-65 см. Вы можете измерить свой, а мы продолжим пример с размером равным 63 см.

Рекомендованные значения ширины проступи и высоты ступеней мы уже обсуждали, но как понять какое именно значение подобрать из этих интервалов.

Опытным путем специалисты выяснили, что длина шага равна сумме глубины проступи и двойной высоте ступеней. То же самое можно записать в виде формулы:

Формула расчета ступеней: 2 × h + s = 60/65 см

Т.е. зная длину шага человека и допустимые интервалы, можно подобрать наиболее комфортные параметры ступеней. Перебрав все возможные варианты, у нас получились найти две пары теоретических значений: s = 27 см и h = 18 см или s = 29 см и h = 17 см. Возьмем первую.

Для тех, кто не хочет углубляться в подробности, можно остановиться на формуле tg(A) = h / s и закончить расчет прямо сейчас.

Далее нам необходимо определить высоту этажа. Мы возьмем стандартный потолок для частного дома – 270 см и прибавим толщину перекрытия с конструкцией пола верхнего этажа, в среднем, это составляет 30 см.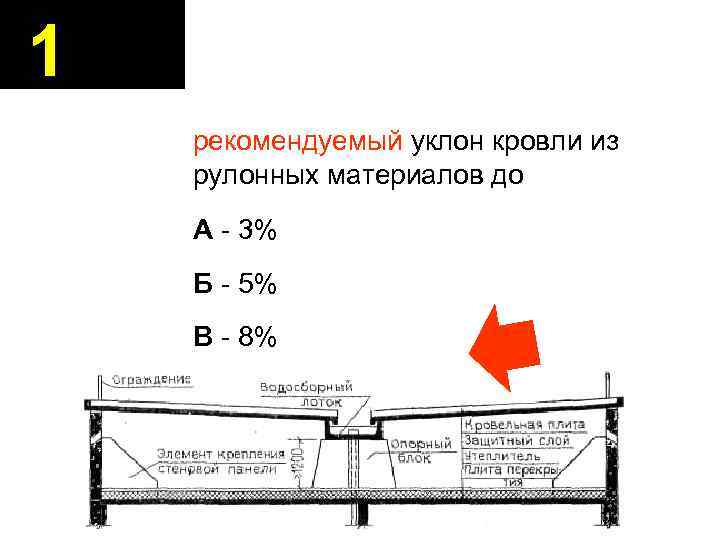 Вам же необходимо измерить рулеткой фактическое значение и в дальнейших расчетах использовать именно его.

Зная высоту этажа и высоту ступеней, мы можем определить их количество:

300 см / 18 см = 16,7 ступеней.

Так как число получилось не целое, округлим в большую сторону (до 17) и произведем обратный расчет, для определения точной высоты ступеней.

300 см / 17 = 17,6 см.

Теперь вернемся к первоначальной формуле и рассчитаем реальную ширину проступи по известной высоте ступеней.

63 см – 17,6 см × 2 = 27,8 см.

У нас получилось, что h = 17,6 см, s = 27,8 см – оба значение соответствуют рекомендуемым, значит можно продолжить расчет.

Так как мы рассчитываем пример для наглядности – для упрощения расчетов мы округляем сотые доли полученных значений. В реальной ситуации, так делать не рекомендуется .

Дальше определим длину лестницы в горизонтальной проекции на основании данных по количеству ступеней и их длине.

17 × 27,8 см = 472,6 см.

После проведения вычислений вам необходимо убедиться в наличии необходимого пространства для монтажа лестницы. Если такового нет (что часто случается), необходимо выполнить расчет в обратную сторону, отталкиваясь не от оптимального угла наклона лестницы, а от возможностей помещения.

Также следует рассмотреть многомаршевые конструкции. Для них расчет проводится аналогично, только для каждого марша в отдельности.

Но предположим, что у вас имеется необходимая площадь, тогда заключительный этап работ сводится к определению тангенса угла, образованного длиной и высотой проема.

В этом случае, оптимальный угол наклона лестницы будет равен:

tg(α) = 300 / 472,6 = 0,63

α = arctg(0,63) = 32.2°

У нас получилась идеальная лестница , так как мы заранее взяли идеальные размеры ступеней, но из-за ограниченных размеров помещения, чаще всего так не получается и приходится увеличивать угол.

Например, если мы возьмем максимальный угол наклона лестницы в 40 градусов, то длину проема можно уменьшить до 357 см.

tg(40°) ≈ 0,84

0,84 = 300 см / x см

x ≈ 357 см

Манипуляции с длиной проема и углом наклона лестницы непременно приведут к изменению параметров ступеней и скорее всего они выйдут из диапазона комфортных, но если помещение технически не может вместить лестницу – другого выбора нет.

Помните, что грамотно выполненный расчет угла наклона лестницы – это единственно верный путь к удобству и безопасности при эксплуатации. Доверьте свои расчеты нашим надежным калькуляторам лестниц и будьте уверены в своей конструкции!

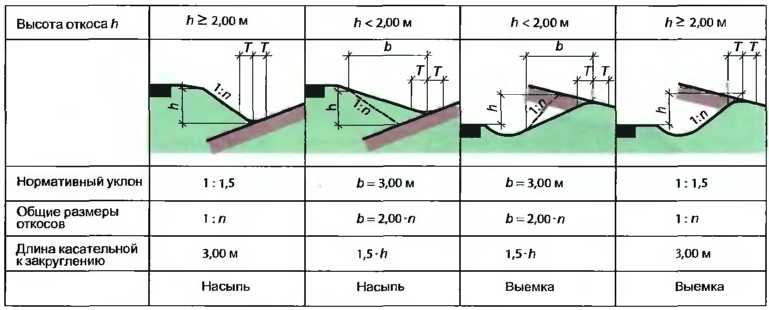
Соотношение между градусами, процентным уклоном и отношением к выраженному градиенту уклона

Соотношение между градусами, процентным уклоном и отношением к выраженному градиенту уклона

Экологический менеджмент, оценка, смягчение последствий, восстановление, образование и разъяснительная работа

Эллиотт Менаше, Greenbelt Consulting

Градиент склона является ключевым фактором, влияющим на относительную устойчивость склона.

Он определяет степень, в которой сила тяжести действует на массу почвы. Склоны часто бывают неровными и сложными, а уклоны сильно различаются по всему профилю данной береговой линии. Каждый участок профиля склона следует рассматривать как отдельную единицу участка управления и восстановления. Градиент уклона может быть выражен несколькими способами. Формулы определения уклона (Рисунок 1) и общая таблица градиентов уклона (Рисунок 2) иллюстрируют три часто используемых обозначения (отношение, процент и угол).

Рисунок 1. Формулы определения уклона

HD = горизонтальное расстояние, VD = вертикальное расстояние.

	Формула	Пример	Результат
Коэффициент наклона (Г:В)	HD : ВД	100:50	2:1
Наклон в процентах (%)	( ВД ÷ HD ) × 100	(50 ÷ 100) × 100	50%
Угол наклона (°)	ArcTan ( VD ÷ HD )	АркТан (50 ÷ 100)	26,6°

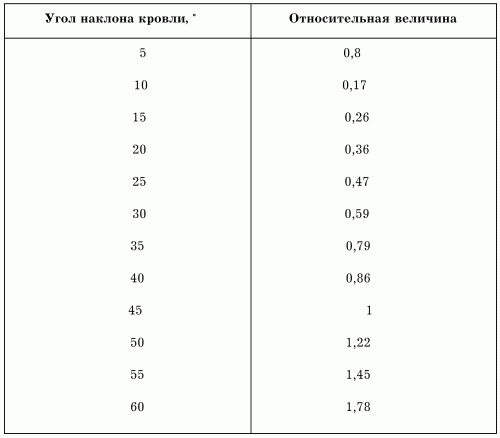Рис. 2. Общие уклоны

Угол (°)	Процент (%)	Соотношение (Г:В)
2,5	5,0
5,7	10,0	10:1
10,0	17,6
14,0	25,0	4:1
18,0	33,5	3:1
19,3	35,0
20,0	36,4
24,2	45,0
26,1	49,0
26,6	50,0	2:1
30,0	57,7
33,0	66,7	1,5:1
35,0	70,0
38,6	80,0
42,0	90,0
45,0	100,0	1:1
55,0	142,8
60,0	173,2

Подготовлено Эллиотом Менаше для программы прибрежной подготовки (www. greenbeltconsulting.com), 2004 г.

Доступно для скачивания в формате PDF.

Материалы на этом сайте доступны для использования некоммерческими организациями и общественным образованием. Любое другое использование или перепрофилирование требует разрешения автора. Эта информация защищена Законом об авторских правах © 2004–2017.

Калькулятор уклона

Создано Матеушем Мухой и Юлией Жулавиньской

Отредактировано Богной Шик и Джеком Боуотером

Последнее обновление: 21 декабря 2022 г.

Содержание:

• Как найти уклон
• Формула уклона
• Другие связанные темы
• Часто задаваемые вопросы

Калькулятор уклона определяет уклон или градиент между двумя точками в декартовой системе координат. Наклон — это в основном величина наклона линии, которая может иметь положительное, отрицательное, нулевое или неопределенное значение. Прежде чем пользоваться калькулятором, наверное, стоит научиться находить уклон по формуле уклона. Чтобы найти уравнение прямой для любых двух точек, через которые проходит эта линия, используйте наш калькулятор формы пересечения наклона.

Как найти уклон

1. Определите координаты (x1,y1)(x_1, y_1)(x1​,y1​) и (x2,y2)(x_2, y_2)(x2​,y2​). Мы будем использовать формулу для расчета наклона линии, проходящей через точки (3,8)(3, 8)(3,8) и (−2,10)(-2, 10)(−2,10) .
2. Введите значения в формулу. Это дает нам (10-8)/(-2-3)(10-8)/(-2-3)(10-8)/(-2-3).
3. Вычтите значения в скобках, чтобы получить 2/(-5)2/(-5)2/(-5).
4. Упростите дробь, чтобы получить наклон −2/5–2/5–2/5.
5. Проверьте результат с помощью калькулятора уклона.

Чтобы найти наклон линии, нам нужны две координаты на линии. Достаточно любых двух координат. В основном мы измеряем величину изменения координаты y, часто известную как рост , деленную на изменение координаты x, известную как

run . Вычисления по нахождению наклона просты и включают в себя не что иное, как базовое вычитание и деление.

🙋 Чтобы найти градиент нелинейных функций, вы можете использовать калькулятор средней скорости изменения.

Формула наклона

наклон=y2−y1x2−x1\mathrm{slope} = \frac{y_2 — y_1}{x_2 — x_1}slope=x2​−x1​y2​−y1​​

Обратите внимание, что наклон линии легко вычисляется вручную с использованием небольших целых чисел координат. Формула становится все более полезной по мере того, как координаты принимают большие значения или десятичные значения.

Стоит отметить, что любая горизонтальная линия имеет нулевой градиент, потому что горизонтальная линия имеет те же координаты y. Это приведет к нулю в числителе формулы наклона. С другой стороны, вертикальная линия будет иметь неопределенный наклон, поскольку координаты x всегда будут одинаковыми. Это приведет к ошибке деления на ноль при использовании формулы.

Точно так же, как наклон можно вычислить, используя конечные точки сегмента, можно вычислить и среднюю точку. Середина — важное понятие в геометрии, особенно при вписании многоугольника внутрь другого многоугольника, когда его вершины касаются середины сторон большего многоугольника. Это можно получить с помощью калькулятора средней точки или просто взяв среднее значение каждой координаты x и среднее значение координаты y, чтобы сформировать новую координату.

Наклон линий важен для определения того, является ли треугольник прямоугольным. Если любые две стороны треугольника имеют наклоны, которые умножаются на -1, то треугольник является прямоугольным. Вычисления для этого можно выполнить вручную или с помощью калькулятора прямоугольного треугольника. Вы также можете использовать калькулятор расстояний, чтобы вычислить, какая сторона треугольника является самой длинной, что поможет определить, какие стороны должны образовывать прямой угол, если треугольник прямоугольный.

Знак перед градиентом, предоставленным калькулятором наклона, указывает, является ли линия возрастающей, убывающей, постоянной или неопределенной. Если график линии перемещается из нижнего левого угла в верхний правый, он увеличивается и, следовательно, является положительным. Если он уменьшается при движении из левого верхнего угла в правый нижний, то градиент отрицательный.

Часто задаваемые вопросы

Как найти наклон по уравнению?

Метод для определения наклона по уравнению зависит от формы уравнения перед вами. Если форма уравнения y = mx + c, то наклон (или градиент) просто m . Если уравнение не в этой форме, попробуйте изменить уравнение. Чтобы найти градиент других полиномов, вам нужно будет продифференцировать функцию по x .

Как рассчитать уклон холма?

1. Используйте карту, чтобы определить расстояние между вершиной и основанием холма по прямой.
2. Использование той же карты или GPS, найти высоту между вершиной и подошвой холма . Убедитесь, что точки, от которых вы измеряете, такие же, как и в шаге 1.
3. Преобразуйте оба измерения в одни и те же единицы.
4. Разделите разницу высот на расстояние между двумя точками.
5. Это число представляет собой уклон холма, если он увеличивается линейно. Если это не так, повторите шаги, но там, где есть заметное изменение наклона.

Как рассчитать длину склона?

1. Измерьте разницу между верхней и нижней частью уклона по осям x и y.
2. Если вы можете измерить только изменение по оси x, умножьте это значение на градиент, чтобы найти изменение по оси y.
3. Убедитесь, что единицы измерения для обоих значений одинаковы.
4. Используйте теорему Пифагора, чтобы найти длину склона . Возведите в квадрат как изменение x, так и изменение y.
5. Сложите два значения вместе.
6. Найдите квадратный корень из суммы.
7. Это новое значение представляет собой длину склона.

Что такое наклон 1 из 20?

Уклон 1/20 — это уклон, который увеличивается на 1 единицу за каждые 20 единиц, пройденных по горизонтали . Так, например, пандус длиной 200 футов и высотой 10 футов будет иметь уклон 1/20. Наклон 1/20 эквивалентен градиенту 1/20 (как ни странно) и образует угол 2,86° между собой и осью x.

Как найти наклон кривой?

Поскольку наклон кривой меняется в каждой точке, вы можете найти наклон кривой, продифференцировав уравнение по x и в полученном уравнении подставив x вместо точки, в которой вы хотите найти градиент.

Скорость изменения равна наклону?

Скорость изменения графика также является его наклоном , который также совпадает с градиентом. Скорость изменения можно найти, разделив изменение в направлении y (по вертикали) на изменение в направлении по оси x (горизонтально), если, конечно, оба числа выражены в одних и тех же единицах. Скорость изменения особенно полезна, если вы хотите предсказать будущее предыдущего значения чего-либо , поскольку при изменении переменной x будет присутствовать соответствующее значение y (и наоборот).

Где вы используете уклон в повседневной жизни?

Уклоны (или уклоны) имеют множество применений в повседневной жизни . Есть несколько очевидных физических примеров — у каждого холма есть склон, и чем круче холм, тем больше его уклон . Это может быть полезно, если вы смотрите на карту и хотите найти лучший холм для спуска на велосипеде. Вы тоже, наверное, спите под скатом, под крышей . Наклон крыши будет меняться в зависимости от стиля и места вашего проживания. Но, что более важно, если вы когда-нибудь захотите узнать, как что-то меняется со временем, вы в конечном итоге построите график с наклоном .

Что такое уклон 10%?

Уклон 10 % — это наклон, который увеличивается на 1 единицу за каждые 10 единиц, пройденных по горизонтали (10 %). Например, крыша с уклоном 10% и шириной 20 м будет иметь высоту 2 м. Это то же самое, что и градиент 1/10 , а между линией и осью x формируется угол 5,71°.

Как найти площадь под уклоном?

Чтобы найти площадь под уклоном, необходимо проинтегрировать уравнение и вычесть нижнюю границу площади из верхней границы.

Для линейных уравнений:

1. Запишите уравнение в виде y = mx + c .
2. Напишите новую строку, в которой вы добавляете 1 к порядку x (например, x становится x ² , х ^2,5 становится х ^3,5 ).
3. Разделите m на новый номер заказа и поставьте его перед новым x.
4. Умножьте c на x и добавьте это в новую строку.
5. Решите эту новую строку дважды, где x — верхняя граница области, которую вы хотите найти, и где x — нижняя граница.
6. Вычтите нижнюю границу из верхней.
7. Поздравьте себя с достижением.

Какой градус наклона 5 к 1?

Наклон 5 к 1 — это уклон, который при каждом увеличении на 5 единиц по горизонтали увеличивается на 1 единицу . Число градусов между наклоном 5 к 1 и осью x составляет 11,3°. Это можно найти, сначала вычислив наклон, разделив изменение в направлении y на изменение в направлении x, а затем найдя арктангенс наклона.