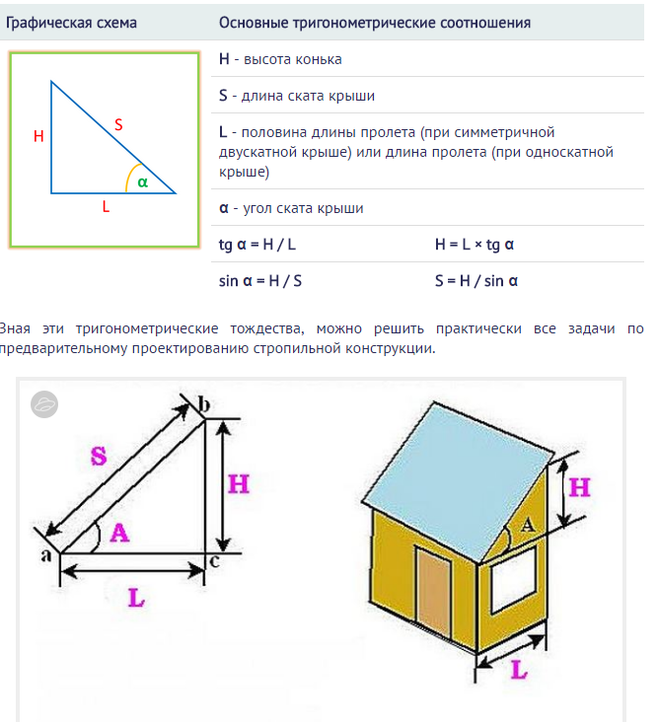
Как определить угол наклона уже готовой кровли
Расчет уклона кровли — обязательный этап проектирования дома. От угла наклона скатов зависят снеговая и ветровая нагрузки на крышу, которые через стены передаются на фундамент.
Но есть ситуации, когда необходимо узнать фактический уклон уже готовой кровли. Например, при реконструкции крыши с заменой кровельного материала более тяжелым или при установке солнечных панелей на скатах. Ниже — два способа, как определить угол наклона в этом случае.
Определить уклон ската можно либо с помощью специальных инструментов, либо воспользовавшись базовыми законами геометрии. Первый способ проще и точнее, второй доступен всегда — главное, чтобы была рулетка, а остальные инструменты не важны.
Инструментальный метод
Чтобы определить угол наклона кровли просто и быстро, используйте специальные измерительные инструменты:
- угломеры, которые измеряют угол между двумя «плечами» инструмента;
- уклономеры, которые показывают уклон кровли относительно гравитационного поля Земли.

Угломеры для расчета уклона кровли
Угломер — чрезвычайно простой, но эффективный инструмент. Он бывает механическим и электронным.
Механический угломер состоит из планок, которые соединены друг с другом с одного края, и шкалы между ними. Со второй стороны концы планок свободные и могут вращаться вокруг места соединения. Шкала показывает, на какой угол две части угломера повернуты друг относительно друга. Конструкция настолько простая, что, при необходимости, механический угломер можно даже сконструировать самостоятельно из двух линеек и транспортира.
Электронные угломеры по принципу работы точно такие же. Есть только одно отличие: шкала для определения угла между плечами инструмента заменена специальным датчиком, который считывает положение планок. Результат отображается на небольшом экране.
Механические угломеры — более надежный инструмент: нет риска, что откажет датчик или экран. Но с точки зрения удобства электронные устройства выигрывают.
Как определить угол наклона кровли с помощью угломера:
- одну из планок плотно прижмите к стойке, подпирающей коньковую балку, или к самому коньку;
- вторую планку прижмите к нижней кромке стропильной ноги;
- запишите результат измерений и повторите их для разных стропил 8-10 раз;
- отбросьте результаты, которые сильно выбиваются из ряда измерений — слишком большие или слишком маленькие;
- для остальных вычислите среднее арифметическое — это и будет угол наклона кровли.
Учитывайте, что для расчета уклона кровли нужно обязательно делать не одно измерение, а несколько, иначе вы рискуете получить некорректные результаты. Приведем пример.
Допустим, вы сделали 10 измерений угломером и получили следующие результаты.
| Номер измерения | Угол, градусы |
| 1 | 25,3 |
| 2 | 28,1 |
| 3 | 25,8 |
| 4 | 25,4 |
| 5 | 27,5 |
| 6 | 25,1 |
| 7 | 25,3 |
| 8 | 30 |
| 9 | 25,5 |
| 10 | 25,2 |
Второе, пятое и восьмое измерение явно выбиваются из ряда, поэтому их нужно отбросить. Выполняем расчет уклона кровли только по семи измерениям: складываем их и делим на количество. В результате получаем среднее арифметическое — 25,37°. Если бы мы не отфильтровали измерения, то угол бы получился почти на градус больше — 26,32°. И это еще небольшая разница: измерение угла между разными парами стропил и стоек может дать результаты, отличающиеся на 5-7°, иногда даже больше.
Выполняем расчет уклона кровли только по семи измерениям: складываем их и делим на количество. В результате получаем среднее арифметическое — 25,37°. Если бы мы не отфильтровали измерения, то угол бы получился почти на градус больше — 26,32°. И это еще небольшая разница: измерение угла между разными парами стропил и стоек может дать результаты, отличающиеся на 5-7°, иногда даже больше.
Такая разница связана с качеством пиломатериалов, которые обычно используют для стропильной системы. Ее рекомендуют делать из калиброванного леса, то есть из досок, сечение которых примерно одинаковое по всей длине и равно эталонному. Для этого их пропускают через специальный станок — рейсмус, который срезает лишнее и доводит размеры досок до необходимых.
Но калибровка сильно повышает стоимость пиломатериалов, поэтому для большинства стропильных систем с целью экономии берут обычные, некалиброванные доски. Еще и часто недостаточно просушенные. А их ширина даже в сыром виде может отличаться на десятки миллиметров. Причем не у разных досок, а просто по длине одной.
Причем не у разных досок, а просто по длине одной.
В верхней части стропила выводят в плоскость — нужно же уложить кровельное покрытие, — а в нижней эта разница остается. Она и дает такую погрешность, из-за которой перед тем, как определить угол наклона кровли, нужно сделать множество измерений, чтобы получить более-менее точный результат.
Уклономеры для определения угла наклона ската
Уклономерами пользоваться еще проще, чем угломерами. В основе таких приборов специальные магнитные датчики — инклинометры. Они измеряют угол наклона поверхности, на которой установлены, относительно гравитационного поля Земли. Поэтому это более точный инструмент для расчета уклона кровли.
Чтобы определить угол наклона ската, достаточно просто поставить уклономер на кровельное покрытие или верхнюю кромку стропильной ноги. Независимо от качества пиломатериалов, сверху стропила с обрешеткой выводят в плоскость. Поэтому погрешность будет меньше — для получения точного результата нужно будет повторить измерения 3-4 раза.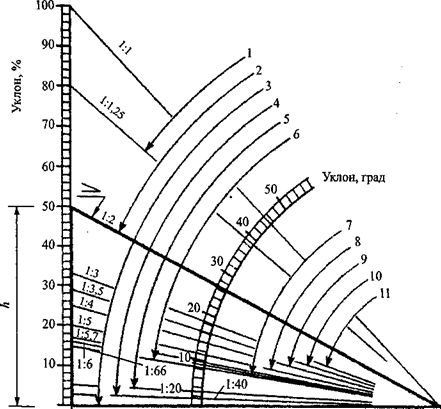
Если установить уклономер на кровельное покрытие нет возможности, его можно прижать к низу стропил. Но тогда измерения нужно будет делать по той же схеме, что и с угломером: 8-10 штук с отбрасыванием крайних значений и расчетом среднего.
Расчет уклона кровли по длине стропил
Угломер или уклономер — это специализированный инструмент, который не всегда есть под рукой, да и покупать его ради одного измерения нет смысла. Поэтому для расчета уклона кровли чаще пользуются базовыми законами геометрии.
Дело в том, что стропило, опорная стойка и перекрытие — это, по сути, стороны прямоугольного треугольника, где стропильная нога — гипотенуза. Следовательно, рассчитать уклон кровли можно по формуле:
α = (h/l)·100%
Здесь:
- α — угол наклона ската, %;
- h — высота крыши, включая коньковую балку, м;
- l — расстояние от середины опорной стойки до карнизного свеса ската, м.
Этот метод дает довольно точный результат, поскольку на него никак не влияют характеристики пиломатериалов. Но угол получается не в привычных градусах, а в процентах. Поэтому для дальнейших расчетов полученное значение нужно перевести.
Но угол получается не в привычных градусах, а в процентах. Поэтому для дальнейших расчетов полученное значение нужно перевести.
Как вычислить угол наклона в градусах? Сделать это можно двумя способами.
Первый способ подходит тем, у кого есть инженерный калькулятор и кто умеет с ним обращаться. Нужно посчитать арктангенс при делении высоты крыши на длину ската:
α = arctg(h/l)
Второй способ проще — нужно вычислить уклон в процентах с помощью следующей схемы.
Просто приложите линейку к схеме: один конец — к крайней точке справа, другой — к тому значению на вертикальной шкале, которое соответствует полученному вами углу наклона в процентах. Тогда место пересечения линейки со скругленной шкалой (транспортиром) покажет уклон в градусах.
Чтобы узнать уклон кровли, можно воспользоваться одним из двух методов:
- инструментальным — измерить его напрямую с помощью уклономера или угломера;
- расчетным — стропила, перекрытие и стойки образуют прямоугольный треугольник, поэтому угол можно рассчитать, разделив высоту крыши до конька на расстояние по полу от карнизного свеса до опор.
Расчетный метод даст уклон в процентах. Как рассчитать угол наклона в градусах? Взять арктангенс от соотношения или воспользоваться специальной схемой для перевода процентов в градусы.
Будьте в курсе!
Подпишитесь на новостную рассылку
Как рассчитать угол наклона крыши
Содержание статьи:
- 1 Как величина уклона зависит от используемого материала
- 2 Что влияет на наклон
- 3 Зависимость угла от места строительства
- 4 Пример расчёта
Многие хозяева загородной недвижимости говорят о том, что крыша собственного дома должна быть не только надёжной, но и красивой. Добиться максимальной функциональности и красивого внешнего вида рассматриваемой конструкции можно при правильном подборе материалов, а также вычислении необходимого уклона. В нашей статье опишем, как рассчитать угол наклона крыши. Для этого необходимо владеть данными о ветровой и снеговой нагрузке, месте строительства и свойствах покрытия.
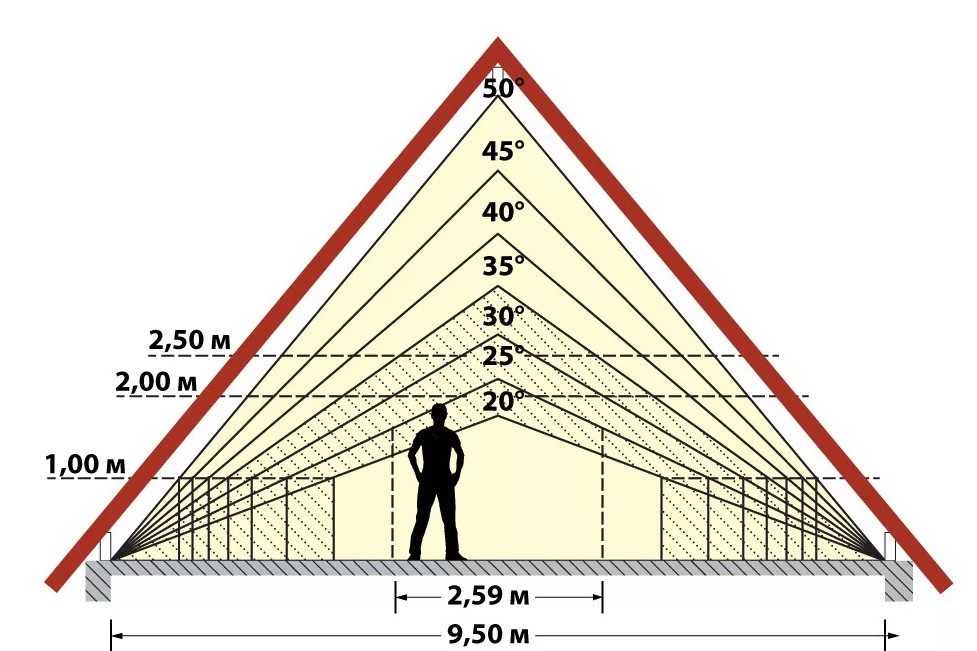
Перед тем как определить угол наклона крыши в градусах нужно узнать для каких целей будет использоваться чердак. Если эта часть дома будет жилой наклон нужно делать максимальным, что позволит увеличить высоту потолков и сделает помещения просторнее. Вторым вариантом выхода со сложившейся ситуации будет устройство ломаной мансардной кровли. В большинстве случаев подобную конструкцию делают двускатной, но некоторые могут иметь и четыре ската. Здесь нужно всё тщательно высчитать, ведь при увеличении высоты конька увеличивается полезный объём мансарды. Вместе с тем повышается площадь покрытия и финансовые вложения на устройство кровли.
До того как рассчитать угол наклона кровли ознакомьтесь со следующей полезной информацией:
- При увеличении высоты конька возрастают финансовые вложения на используемые для покрытия материалы;
- На скаты со значительной площадью сильнее воздействует ветер. Если взять два здания с одинаковыми габаритными размерами, но имеющие разный угол наклона в градусах (например, 11 и 45), то нагрузка от одинаковых по силе потоков ветра на второй дом будет почти в 5 раз выше.

- Если вы не знаете, как найти угол наклона, возьмите его большим от 60 градусов. На таких кровлях не задерживаются атмосферные осадки и снег.
- Не каждое изделие для кровли может применяться на больших по углу наклона скатах. Под углом наклона подразумевается соотношение высоты ската к половине ширины дома.
Крыши с небольшим углом уклона имеют уменьшенную площадь по сравнению с крутыми кровлями, они гораздо дешевле, но при монтаже такого покрытия тоже нужно учитывать определённые нюансы:
- Устройство специальных снегозадержателей для предотвращения схода лавин. Одним из вариантов отвода снеговых масс считается устройство специального обогрева для ускорения таянья снегов.
- При незначительных перепадах высот покрытия существует высокая вероятность проникновения влаги в конструкцию кровли через стыки. Чтоб крыша не дала течь необходимо использовать усиленную гидроизоляцию.
Как можно понять, конструкции с небольшим уклоном имеют больше недостатков, чем положительных качеств. В связи с этим каждый строитель должен знать, как определить угол наклона крыши в градусах.
В связи с этим каждый строитель должен знать, как определить угол наклона крыши в градусах.
Как величина уклона зависит от используемого материала
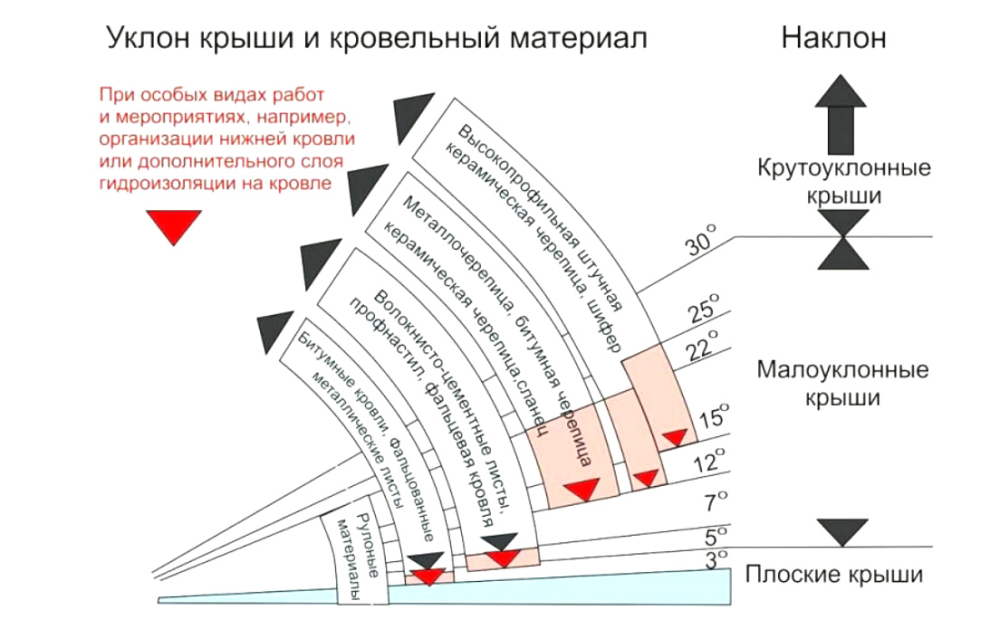
Кровля загородного дома или хозяйской постройки может иметь низкие или отвесные скаты. Во время проектирования этой конструкции необходимо рассчитать сечение стропил и расстояние между ними. Как определить угол наклона для разных кровельных материалов, пытаются понять многие, но эти значения давно уже вычислены.
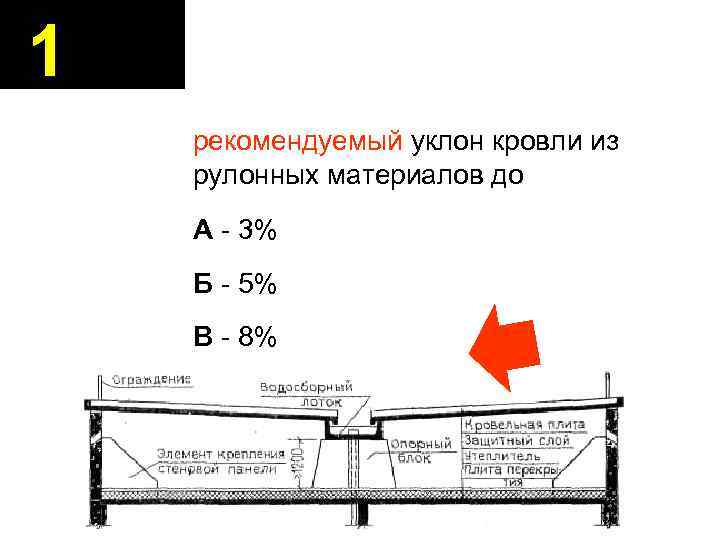
Во время монтажа рулонных гидроизоляционных материалов, когда рубероид укладывается в два слоя, наклон покрытия не должен превышать 15 градусов. Многие хотели бы знать, как определить угол наклона крыши в градусах если она покрыта тремя слоями гибкой черепицы. В данном случае описываемый показатель может меняться от 2 до 5 градусов.
Обратите внимание на следующие нюансы устройства:
- Наплавляемый рубероид рекомендован к использованию при величине уклона до 25˚ в два слоя, от 0 до 10˚ – в три слоя.

- Асбестоцементные листы используются на кровлях, имеющих уклон до 26˚.
- Минимальный уклон для натуральной черепицы составляет 33 градуса;
- Профлист или металлочерепица – 29 градусов и больше.
Расход кровельных изделий тоже зависит от рассматриваемого параметра. так конструкции с небольшими уклонами стоят гораздо дешевле аналогов, имеющих угол больше 45 градусов.
Что влияет на наклон
Все используемые кровли могут иметь различную форму и количество скатов. Например, у гаражей или других хозяйских построек может присутствовать всего один скат, у сараев таких плоскостей две, а вот кровли гражданских зданий состоят из двух или четырёх скатов. Как определить угол наклона крыши в градусах недоумевают многие строители. По мнению экспертов, подобные расчеты можно проводить при помощи специальных матриц или графиков. Кроме этого, узнать угол наклона крыши можно из курса геометрии при помощи треугольника. Чаще всего описываемый конструкционный элемент напоминает именно эту фигуру.
Кроме этого, узнать угол наклона крыши можно из курса геометрии при помощи треугольника. Чаще всего описываемый конструкционный элемент напоминает именно эту фигуру.
На этапе проектирования кровли нужно выбрать необходимые изделия и провести необходимые расчёты. Замечено, что тип покрытия берётся во внимание при расчёте угла любой скатной конструкции. Если хозяин постройки не знает, как посчитать наклон правильно, то эта величина находится в пределах 9-20 градусов. При проектировании кровли здания учитывайте следующие нюансы:
- предназначение постройки;
- материал, из которого изготовлено покрытие;
- климатические особенности региона строительства.
Если планируется монтаж крыши с двумя или большим количеством скатов нужно обратить внимание не только на перечисленные требования, но и на район строительства. Также необходимо брать во внимание предназначение чердачного помещения. Если мансарда будет использоваться для хранения ненужных вещей, то делать ее высокую и повышать расход кровельного материала нет смысла. При использовании жилого чердачного помещения необходимо выбирать стропила с максимальным сечением и размещать их на небольшом расстоянии друг от друга.
При использовании жилого чердачного помещения необходимо выбирать стропила с максимальным сечением и размещать их на небольшом расстоянии друг от друга.
Зависимость угла от места строительства
В регионах с постоянными сильными ветрами необходимо делать уклон минимальным. В связи с этим нагрузка от потоков воздуха на кровлю будет небольшой. Высокие крыши страдают от ветра гораздо больше, чем низкие. Нельзя сказать, что ветер не срывает покрытие с крыш, имеющих небольшой уклон. Далее узнаем, как найти угол наклона кровли для зданий, построенных в регионах с постоянными ветрами:
- При небольшой интенсивности воздушных потоков уклон имеет значение 34-40 градусов;
- При наличии сильных ветров этот показатель уменьшают до 15…25 градусов.
В местности с большим количеством атмосферных осадков наклон желательно увеличивать до параметров в 60˚. Такой уклон позволит быстро выводить снег и воду за пределы покрытия. Уклон крыши обычно меняется в диапазоне 9…60˚, но самыми распространёнными вариантами уклона считается диапазон 19…44 градуса.
Пример расчёта
А теперь ознакомимся, как рассчитать угол наклона крыши на конкретном примере. Для начала необходимо узнать высоту конька по отношению к основанию. Этот параметр зависит от предназначения чердака. Если это помещение будет использоваться в качестве мансарды, то нам понадобится ещё одна величина – длина фронтона или основания.
Как измерить угол наклона, если высота от основания кровли до конька составляет 1,8 метра, а длина фронтона принимается кратной 6 метрам. Для начала необходимо разделить «подошву треугольника» на две части, а затем вычисляют синус угла по теореме Пифагора.
В нашем случае, это значение синуса угла, который находится из соотношения прилежащей стороны к противолежащей. Сначала делим треугольник на две равные части 6/2=3. Теперь вычисляем синус нужного угла 3/1,8= 1,6. Заглядываем в таблицу Брадиса и видим, что это значение соответствует углу в 59 градусов.
Как найти угол наклона крыши
Главная » Разное » Как найти угол наклона крыши
как узнать угол наклона ската в градусах, как рассчитать угол стропил двухскатной крыши, узнать и высчитать
Содержание:
Чтобы крыша здания могла в полной мере выполнять все возложенные на нее функции, необходимо при ее создании учесть ряд параметров. Одним из самых важных параметров крыши является ее уклон, который обеспечивает отвод атмосферных осадков с ее поверхности и влияет на способность выдерживать внешние нагрузки. О том, как посчитать наклон крыши, и пойдет речь в данной статье.
Определение наклона крыши — от чего зависит
Чтобы провести правильный расчет уклона крыши, необходимо учитывать несколько факторов, среди которых сильнее всего выделяются следующие:
- Ветровые нагрузки
.
 На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать.
На уклон скатов очень сильно влияет ветер. Чтобы крыша могла нормально сопротивляться его воздействию, нужно правильно подобрать ее угол. При слишком больших углах нагрузка на них будет высокой, но чрезмерное уменьшение угла тоже может быть опасным – пологую кровлю сильным порывом ветра может попросту сорвать. - Снеговые и дождевые нагрузки. Со снегом все довольно просто – повышение угла наклона упрощает его схождение с поверхности кровли. При наклоне крыши более 45 градусов снег почти не будет задерживаться на ней. При малом угле наклона кровли может появляться снеговой мешок, который увеличивает нагрузку на крышу. С дождевыми осадками такая же ситуация – если угол наклона кровли будет слишком низким, то вода сможет затекать в стыки или вообще застаиваться на поверхности крыши.
Отталкиваясь от этих факторов, можно рассчитывать угол наклона скатов. Кроме того, перед тем, как рассчитать угол двухскатной крыши, стоит обратить внимание на рекомендуемые показатели: для местности с сильными ветрами подойдет уклон в 15-20 градусов, а в остальных случаях оптимальная величина уклона составляет 35-40 градусов. Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.
Разумеется, нужно понимать, что расчет двухскатной крыши индивидуален, и выбирать усредненные показатели просто так нежелательно.
Методика проведения расчетов
При проектировании крыши нужно в обязательном порядке проводить ряд расчетов, среди которых всегда должен присутствовать расчет угла наклона скатов. Данный параметр напрямую влияет на конструкцию крыши: при увеличении наклона снижается снеговая нагрузка, но увеличивается воздействие ветра, поэтому стропильную систему приходится дополнительно усиливать. Для обустройства скатов под большим углом требуется еще и большее количество материалов, что негативно сказывается на стоимости строительства.
Перед тем, как узнать градус наклона крыши, нужно рассчитать эксплуатационную нагрузку на крышу, для чего требуется два параметра:
- Общую массу кровельной конструкции;
- Пиковые уровни снежных осадков, свойственные региону, где проходит строительство.
Упрощенный алгоритм расчетов сводится к следующим действиям:
- Сначала нужно определить вес одного квадратного метра кровельного пирога;
- Полученное значение умножается на общую площадь кровли;
- Масса кровли умножается на коэффициент 1,1.
Пример расчета уклона кровли в градусах
Чтобы понять, как высчитать угол крыши, стоит рассмотреть процесс расчетов на конкретном примере. Для примера будут взяты следующие данные: обрешетка имеет толщину 2,5 см, один квадратный метр кровли весит 15 кг, в качестве теплоизоляционного материала используется утеплитель толщиной 10 см, квадратный метр которого имеет вес 10 кг, а для покрытия используется ондулин с весом 3 кг на квадратный метр.
Расчет ската крыши проводится в соответствии с описанной выше методикой. Подстановка имеющихся данных приводит к следующему выражению: (15+10+3)х1,1 = 30,8 кг/кв.м. Полученная величина вполне допустима – среднестатистическая нагрузка на крышу жилых зданий составляет немногим меньше 50 кг/кв.м. Кроме того, в формуле присутствует коэффициент 1,1, который немного увеличивает фактический вес кровельной конструкции и позволяет в дальнейшем заменить кровельное покрытие на более тяжелое.
Как узнать угол наклона крыши
Между уклоном кровельных скатов и снежной нагрузкой имеется прямая зависимость. Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.
Если угол наклона крыши меньше 25 градусов, то коэффициент снежной нагрузки равен 1, а при углах, варьирующихся в пределах от 25 до 60 градусов, то этот коэффициент увеличивается до 1,25. Крыша с большим углом наклона не будет подвергаться снежным нагрузкам вообще, поэтому они не учитываются при расчетах.
Чтобы определить угол наклона крыши, нужно воспользоваться таблицей Брадиса и простой методикой: высота кровельной конструкции делится на длину фронтона, разделенную на два, после чего остается найти таблице угол, который соответствует полученному результату.
Высота крыши в коньке определяется следующим образом:
- Первым делом нужно рассчитать ширину пролета;
- Полученная величина делится на 2;
- Чтобы сделать расчет высоты конька, результат предыдущего расчета умножается на коэффициент, соответствующий определенному углу наклона.
На примере реализация такой методики расчета выглядит так: при ширине здания, равной 8 метрам, и 25-градусном уклоне кровли, расчетный коэффициент составляет 0,47. В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.
В итоге подстановки значений получается выражение следующего вида: 4х0,47 = 1,88 м. Полученная величина – это высота крыши, соответствующая имеющимся исходным данным.
Выбор кровельного покрытия в зависимости от наклона крыши
На рынке материалы для крыши присутствуют в большом ассортименте, поэтому с выбором подходящего варианта особых проблем не будет. Кровельные покрытия отличаются по характеристикам и возможностям применения, и все их параметры необходимо изучить перед тем, как измерить угол крыши – только в этом случае удастся создать надежную и эффективную конструкцию.
Выбирая материал для кровли, стоит отталкиваться от следующих рекомендаций:
- Если угол наклона стропил составляет от 2,5 до 10 градусов, то лучше всего подойдут покрытия из каменной крошки или гравия. В первом случае верхний слой покрытия имеет толщину 3-5 мм, а во втором – 10-15 мм.
- При наклоне более 10 градусов оптимальным вариантом будут крупнозернистые или рулонные материалы, дополненные битумной гидроизоляцией.
- Для обустройства скатных крыш с углом наклона не более 20 градусов обычно используется профнастил или листовой асбестоцемент. Все швы и стыки между кровельными материалами должны быть обработаны герметиком.
- Если угол наклона крыши находится в пределах 20-60 градусов, то она чаще всего накрывается металлическими листами. Стыки материалов в данном случае нужно в обязательном порядке герметизировать.
Заключение
Знание того, как узнать угол наклона крыши в градусах, существенно упростит процесс ее проектирования и позволит создать максимально надежную конструкцию, которая сможет хорошо защищать коробку здания от атмосферных осадков, ветра и холода.
Угол наклона и уклон прямой
Пусть прямая l пересекает ось x в точке A. Угол между положительной осью x и прямой l, измеренный против часовой стрелки, называется углом наклона прямой l.
На приведенном выше рисунке, если θ — угол прямой l, то мы имеем следующие важные моменты.
(i) 0 ° ≤ θ ≤ 180 °
(ii) Для горизонтальных линий θ = 0 ° или 180 ° и для вертикальных линий θ = 90 °
(iii) Если прямая линия изначально проходит вдоль оси x и начинает вращаться вокруг фиксированной точки A на оси x против часовой стрелки и, наконец, совпадает с осью x, тогда угол наклона прямой в исходном положении равен 0 °, а угол наклона прямой линии линия в конечном положении — 0 °.
(iv) Линии, перпендикулярные оси x, называются вертикальными линиями.
(v) Линии, перпендикулярные оси Y, называются горизонтальными линиями.
(vi) Другие линии, не перпендикулярные ни оси x, ни оси y, называются наклонными линиями.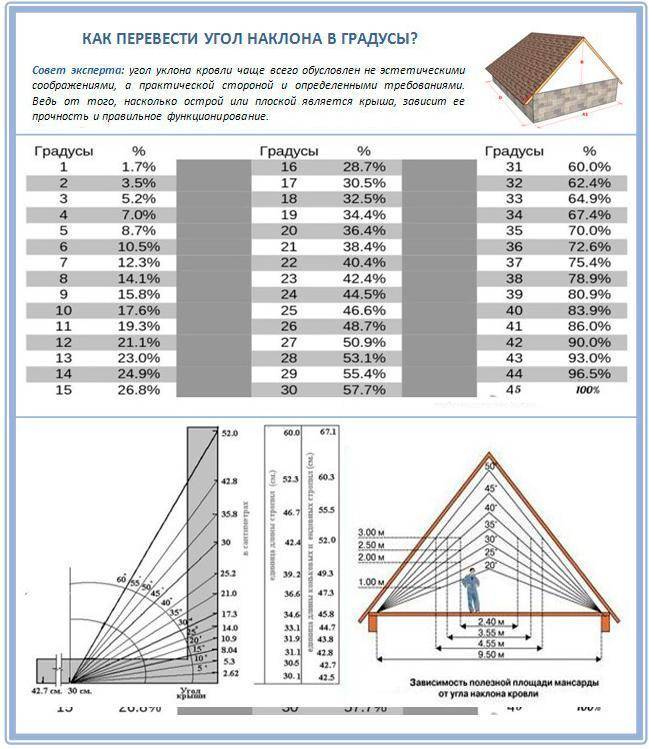
Угол наклона и уклон линии — Применение
Основное применение угла наклона прямой — это определение уклона.
Если θ — это угол наклона прямой l, то tgθ называется крутизной наклона линии и обозначается буквой «m».
Следовательно, наклон прямой составляет
m = tan θ
для 0 ° ≤ θ ≤ 180 °
Найдем наклон прямой, используя приведенную выше формулу
(i) Для горизонтального линий угол наклона 0 ° или 180 °.
То есть
θ = 0 ° или 180 °
Следовательно, наклон прямой составляет
m = tan0 ° или tan 180 ° = 0
(ii) Для вертикальных линий угол наклона равен 90 °.
То есть
θ = 90 °
Следовательно, наклон прямой линии равен
m = tan90 ° = Не определено
(iii) Для наклонных линий, если θ острый, то наклон положительный. Если же θ тупой, то наклон отрицательный.
Наклон линии — положительный или отрицательный, ноль или неопределенный
Когда мы визуально смотрим на прямую линию, мы можем легко узнать знак наклона.
Чтобы узнать знак наклона прямой, мы всегда должны смотреть на прямую слева направо.
Это иллюстрируют приведенные ниже цифры.
Практические задачи
Задача 1:
Найдите угол наклона прямой, уклон которой равен 1 / √3.
Решение:
Пусть θ будет углом наклона прямой.
Тогда наклон линии равен
m = tanθ
Дано: Наклон = 1 / √3
Тогда
1 / √3 = tanθ
θ = 30 °
Итак, угол наклона 30 °.
Задача 2:
Если угол наклона прямой составляет 45 °, найдите ее наклон.
Решение:
Пусть θ будет углом наклона прямой.
Тогда наклон прямой
m = tanθ
Дано: θ = 45 °
Тогда
m = tan 45 °
m = 1
Итак, наклон равен 1.
Задача 3:
Если угол наклона прямой составляет 30 °, найдите ее наклон.
Решение:
Пусть θ будет углом наклона прямой.
Тогда наклон линии
m = tanθ
Дано: θ = 30 °
Тогда
m = tan30 °
m = 1 / √3
Итак, наклон равен 1 / √3.
Задача 4:
Найдите угол наклона прямой, имеющей наклон √3.
Решение:
Пусть θ будет углом наклона прямой.
Тогда наклон линии,
m = tanθ
Дано: Наклон = √3
Тогда
√3 = tanθ
θ = 60 °
Итак, угол наклона равен 60 °.
Задача 5:
Найдите угол наклона прямой линии, уравнение которой y = x + 32.
Решение:
Пусть θ будет углом наклона прямой.
Данное уравнение имеет форму пересечения наклона.
То есть
y = mx + b
Сравнивая
y = x + 32
и
y = mx + b,
получаем наклон m = 1.
Мы знаем, что наклон линии
m = tanθ
Тогда
1 = tanθ
θ = 45 °
Итак, угол наклона равен 45 °.
Кроме того, что описано в этом разделе, если вам нужны другие математические данные, воспользуйтесь нашим пользовательским поиском Google здесь.
Вы также можете посетить следующие веб-страницы, посвященные различным вопросам математики.
ЗАДАЧИ СО СЛОВАМИ
Задачи со словами HCF и LCM
Задачи со словами на простых уравнениях
Задачи со словами на линейных уравнениях
Задачи со словами на квадратных уравнениях
Алгебраные задачи со словами
Проблемы со словами в поездах
Проблемы со словами по площади и периметру
Проблемы со словами по прямой и обратной вариациям
Проблемы со словами по цене за единицу
Проблемы со словами по цене за единицу
Word задачи по сравнению ставок
Преобразование обычных единиц в текстовые задачи
Преобразование метрических единиц в текстовые задачи
Word задачи по простому проценту
Word по сложным процентам
Word задачи по типам ngles
Проблемы с дополнительными и дополнительными углами в словах
Проблемы со словами с двойными фактами
Проблемы со словами в тригонометрии
Проблемы со словами в процентах
Проблемы со словами о прибылях и убытках
Разметка и разметка Задачи со словами
Задачи с десятичными словами
Задачи со словами о дробях
Задачи со словами о смешанных фракциях
Одношаговые задачи с уравнениями со словами
Проблемы со словами о линейных неравенствах
Слово соотношения и пропорции Задачи со словами
Проблемы со временем и рабочими словами
Задачи со словами на множествах и диаграммах Венна
Задачи со словами на возрастах
Проблемы со словами в теореме Пифагора
Процент числового слова pr проблемы
Проблемы со словами при постоянной скорости
Проблемы со словами при средней скорости
Проблемы со словами на сумме углов треугольника 180 градусов
ДРУГИЕ ТЕМЫ
Сокращения прибылей и убытков
Сокращения в процентах
Сокращения в таблице времен
Сокращения времени, скорости и расстояния
Сокращения соотношения и пропорции
Домен и диапазон рациональных функций
Область и диапазон рациональных функций функции с отверстиями
Графики рациональных функций
Графики рациональных функций с отверстиями
Преобразование повторяющихся десятичных дробей в дроби
Десятичное представление рациональных чисел
Нахождение квадратного корня с использованием long di зрение
Л. Метод CM для решения временных и рабочих задач
Метод CM для решения временных и рабочих задач
Преобразование задач со словами в алгебраические выражения
Остаток, когда 2 степени 256 делится на 17
Остаток при делении 17 степени 23 на 16
Сумма всех трехзначных чисел, делимых на 6
Сумма всех трехзначных чисел, делимых на 7
Сумма всех трехзначных чисел, делимых на 8
Сумма всех трехзначных чисел, образованных с использованием 1, 3 , 4
Сумма всех трех четырехзначных чисел, образованных ненулевыми цифрами
Сумма всех трех четырехзначных чисел, образованных с использованием 0, 1, 2, 3
Сумма всех трех четырехзначных чисел числа, образованные с использованием 1, 2, 5, 6
.
| Уголки высоты / наклона и Углы подъема или наклона углов над горизонтом, как если бы вы смотрели с уровня земли в вершина флагштока.
Две десятых мили составляют 0,2 × 5280 футов = 1056 футов, так что это мое горизонтальное расстояние. Мне нужно найти высоту х кактуса.Итак, я рисую прямоугольный треугольник и маркирую все, что знаю: .
Мне нужно выполнить это упражнение по шагам. Я не могу найти высоту башни, AB, пока у меня не будет длины базового компакт-диска. Чтобы минимизировать ошибку округления, я буду использовать все цифры из моего калькулятора в моих вычислениях, и пытаюсь «унести» все вычисления в моем калькуляторе .. Теперь, когда у меня есть длина основания, Я могу найти общую высоту, используя угол, который измеряет высоту от уровня моря до вершины башни. Отлично! Сохраняя все цифры и проводя вычисления в своем калькуляторе, я получил точный ответ. Без округления! Но мне нужно вычесть, потому что «300» высота от воды до вершины башни. Первая сотня метров этой общей высоты — холм, итак: Вверх | Вернуться к индексу
| НАЙТИ УРОК Этот урок можно распечатать для личного пользования. | |
.
Угол наклона прямой — Concept
Угол наклона прямой — это угол, образованный пересечением прямой и оси x. Использование горизонтального «пробега» 1 и m для наклона, угла наклона, theta = tan-1 (м) или m = tan (theta). Следовательно, если угол или наклон известен, другой можно найти с помощью одного из уравнений. Если угол наклона отрицательный, то и наклон линии отрицательный.
Какой угол наклона лески? Итак, у меня есть линия, нарисованная здесь уравнением y = mx + b, оно должно быть вам знакомо. Это угол наклона тета, это угол между линией и горизонталью.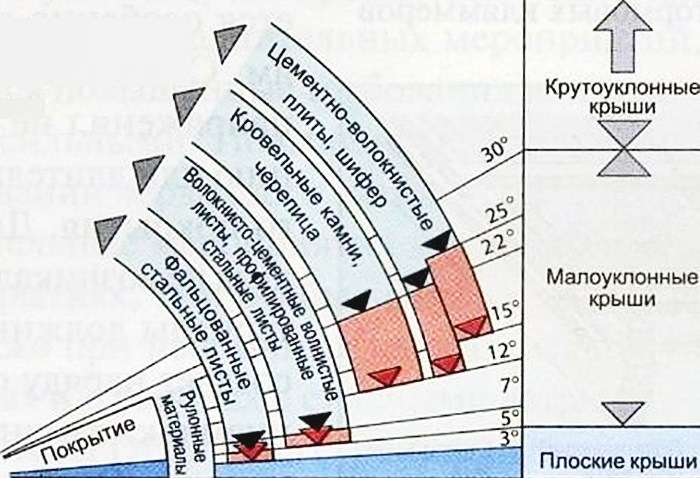 Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь я хочу выяснить, как я могу вычислить эту линию, как она соотносится с уравнением линии, поэтому я нарисовал здесь маленький треугольник, а затем я обозначу стороны, скажем, я обозначу это 1, что будет с этой стороны быть? Теперь я знаю, что наклон, наклон линии равен подъему над пробегом, поэтому наклон будет равен вопросительному знаку над 1, так что это будет наклон.
Теперь, если я посмотрю на этот прямоугольный треугольник, и это прямоугольный треугольник, я могу использовать тригонометрию прямоугольного треугольника, чтобы найти взаимосвязь между тета и m, верно? m — это длина по вертикали этой стороны, поэтому тангенс теты равен m по касательной к 1, тета равен m, так что это соотношение между углом наклона и наклоном, тангенс угла наклона — это наклон, а угол наклона равен арктангенс угла наклона, поэтому вы можете рассчитать наклон по углу наклона, а угол наклона можно рассчитать по углу наклона.
Теперь давайте посмотрим на другой, на несколько частных случаев. Горизонтальные или вертикальные линии. Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет тангенсом 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
Теперь горизонтальная линия не обязательно будет пересекать ось x, конечно, для линии до y = 0 это ось x, но мы определяем ее угол наклона равным 0, и, конечно же, тангенс 0 равен 0, поэтому наклон будет тангенсом 0, который равен 0, и это то, что мы, как мы определяем наклон горизонтальной линии, это 0.
А как насчет вертикальной? Что ж, я бы сказал, что здесь угол наклона пи больше 2, поэтому тета больше пи больше 2, каков наклон? Касательная к тэте, прямая касательная к пи более 2, но, конечно, это не определено, и это именно то, что мы хотели бы, чтобы наклон вертикальной линии не был определен, нет наклона, поэтому просто для просмотра, угол наклона линии угол, на который Линия определяет отношение к горизонтали, а наклон — это тангенс теты, угол наклона равен наклону, а угол наклона равен обратной тангенсе наклона.
.
Нахождение угла в прямоугольном треугольнике
Угол с любых двух сторон
Мы можем найти неизвестный угол в прямоугольном треугольнике, если нам известны длины двух его сторон .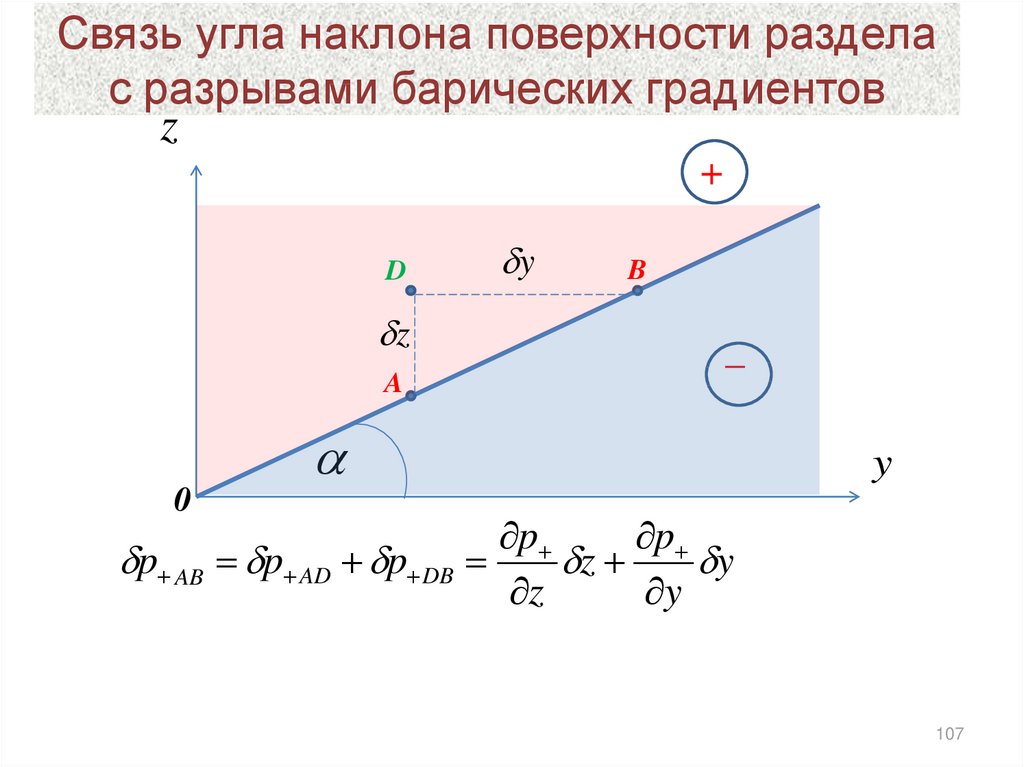
Пример
Лестница прислонена к стене, как показано.
Какой угол между лестницей и стеной?
Ответ — использовать синус, косинус или тангенс!
Но какой использовать? У нас есть специальная фраза «SOHCAHTOA», чтобы помочь нам, и мы используем ее так:
Шаг 1 : найдите имен двух известных нам сторон
- Соседний примыкает к углу,
- Напротив напротив угла
- , а самая длинная сторона — Гипотенуза .
Пример: в нашем примере лестницы нам известна длина:
- сторона Напротив угол «х», который равен 2,5
- самая длинная сторона, называемая Гипотенуза , что составляет 5
Шаг 2 : теперь используйте первые буквы этих двух сторон ( O pposite и H ypotenuse) и фразу «SOHCAHTOA», чтобы найти, какой из синуса, косинуса или тангенса использовать:
| SOH. | S ine: sin (θ) = O pposite / H ypotenuse |
| … CAH … | C осин: cos (θ) = A djacent / H ypotenuse |
| … TOA | T Угол: tan (θ) = O pposite / A djacent |
В нашем примере это O pposite и H ypotenuse, что дает нам « SOH cahtoa», что говорит нам, что нам нужно использовать Sine .
Шаг 3 : Поместите наши значения в уравнение синуса:
S дюйм (x) = O pposite / H ypotenuse = 2,5 / 5 = 0,5
Шаг 4 : Теперь решите это уравнение!
грех (х) = 0,5
Далее (поверьте мне на данный момент) мы можем преобразовать это в это:
х = грех -1 (0,5)
Затем возьмите наш калькулятор, введите 0,5 и используйте кнопку sin -1 , чтобы получить ответ:
х = 30 °
И у нас есть ответ!
Но что означает
sin -1 …?Итак, функция синуса «sin» принимает угол и дает нам соотношение «противоположность / гипотенуза»,
Но sin -1 (так называемый «обратный синус») идет другим путем.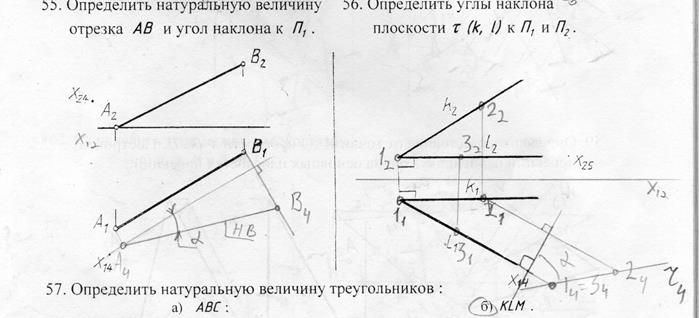 ..
..
… это принимает соотношение «противоположная сторона / гипотенуза» и дает нам угол.
Пример:
- Синус Функция: sin ( 30 ° ) = 0,5
- Функция обратной синусоиды: sin -1 ( 0,5 ) = 30 °
| На калькуляторе нажмите одну из следующих кнопок (в зависимости от от вашей марки калькулятора): либо «2ndF sin», либо «shift sin». |
На вашем калькуляторе попробуйте использовать sin и sin -1 , чтобы увидеть, какие результаты вы получите!
Также попробуйте cos и cos -1 . И tan и tan -1 .
Давай, попробуй.
Шаг за шагом
Вот четыре шага, которые нам нужно выполнить:
- Шаг 1 Найдите две известные нам стороны — противоположную, смежную и гипотенузу.
- Шаг 2 Используйте SOHCAHTOA, чтобы решить, какой из Sine, Cosine или Tangent использовать в этом вопросе.

- Шаг 3 Для синуса вычислить противоположное / гипотенузу, для косинуса вычислить смежное / гипотенузу или для касательного вычислить противоположное / смежное.
- Шаг 4 Найдите угол на своем калькуляторе, используя один из следующих значений: sin -1 , cos -1 или tan -1
Примеры
Давайте рассмотрим еще пару примеров:
Пример
Найдите угол подъема плоскости из точки А на земле.
- Step 1 Две известные нам стороны — это O pposite (300) и A djacent (400).
- Шаг 2 SOHCAH TOA сообщает нам, что мы должны использовать T angent.
- Шаг 3 Вычислить Противоположный / Соседний = 300/400 = 0,75
- Шаг 4 Найдите угол с помощью калькулятора, используя tan -1
Tan x ° = напротив / рядом = 300/400 = 0.75
tan -1 из 0,75 = 36,9 ° (с точностью до 1 знака после запятой)
Если не указано иное, углы обычно округляются до одного десятичного знака.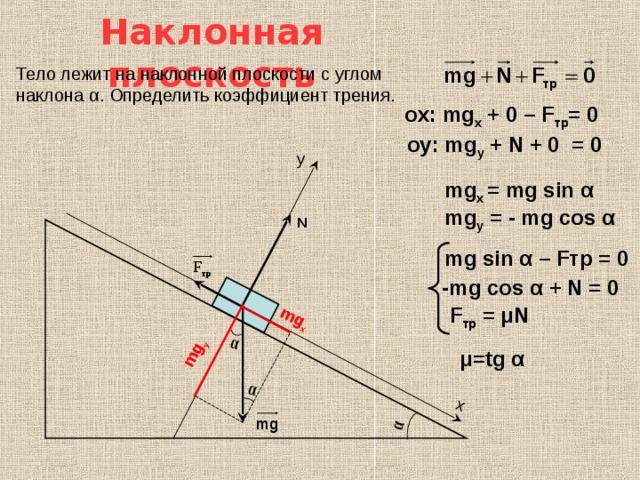
Пример
Найдите величину угла a °
- Step 1 Две известные нам стороны: A djacent (6750) и H ypotenuse (8100).
- Step 2 SOH CAH TOA сообщает нам, что мы должны использовать осин C .
- Шаг 3 Вычислить прилегающее / гипотенузу = 6,750 / 8,100 = 0,8333
- Шаг 4 Найдите угол с помощью калькулятора, используя cos -1 из 0,8333:
cos a ° = 6,750 / 8,100 = 0,8333
cos -1 из 0,8333 = 33,6 ° (с точностью до 1 знака после запятой)
.
теория, примеры, решение задач, угол наклона прямой к оси х
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Угол наклона прямой и угловой коэффициент прямой
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси Ох с их угловым коэффициентом. Допустим, что задана декартова система координат Ох на плоскости.
Определение 1Угол наклона прямой к оси Ох, расположенный в декартовой системе координат Оху на плоскости, это угол, который отсчитывается от положительного направления Ох к прямой против часовой стрелки.
Когда прямая параллельна Ох или происходит совпадение в ней, угол наклона равен 0. Тогда угол наклона заданной прямой α определен на промежутке [0, π).
Определение 2Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k. Из определения получим, что k=tg α.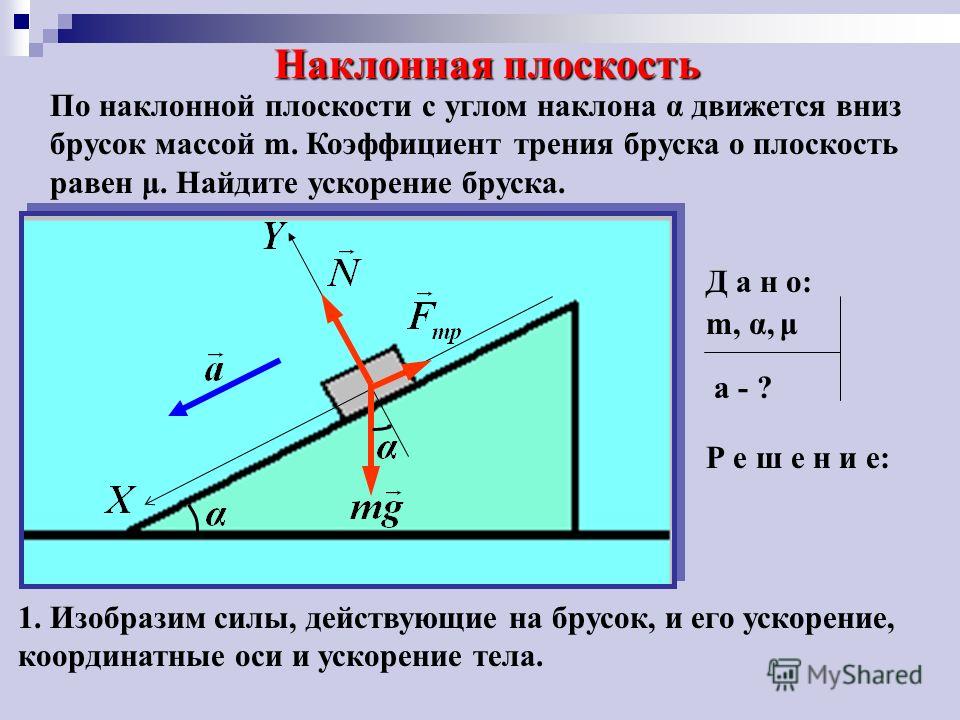 Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Пример 1Посчитать угловой коэффициент прямой при угле наклона равном 120°.
Решение
Из условия имеем, что α=120°. По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k=tg α=120=-3.
Ответ: k=-3.
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k>0, тогда угол прямой острый и находится по формуле α=arctg k. Если k<0, тогда угол тупой, что дает право определить его по формуле α=π-arctgk.
Определить угол наклона заданной прямой к Ох при угловом коэффициенте равном 3.
Решение
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к Ох меньше 90 градусов. Вычисления производятся по формуле α=arctg k=arctg 3.
Ответ: α=arctg 3.
Пример 3Найти угол наклона прямой к оси Ох, если угловой коэффициент = -13.
Решение
Если принять за обозначение углового коэффициента букву k, тогда α является углом наклона к заданной прямой по положительному направлению Ох. Отсюда k=-13<0, тогда необходимо применить формулу α=π-arctgkПри подстановке получим выражение:
α=π-arctg-13=π-arctg 13=π-π6=5π6.
Ответ: 5π6.
Уравнение с угловым коэффициентом
Уравнение вида y=k·x+b, где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом. Уравнение характерно для любой прямой, непараллельной оси Оу.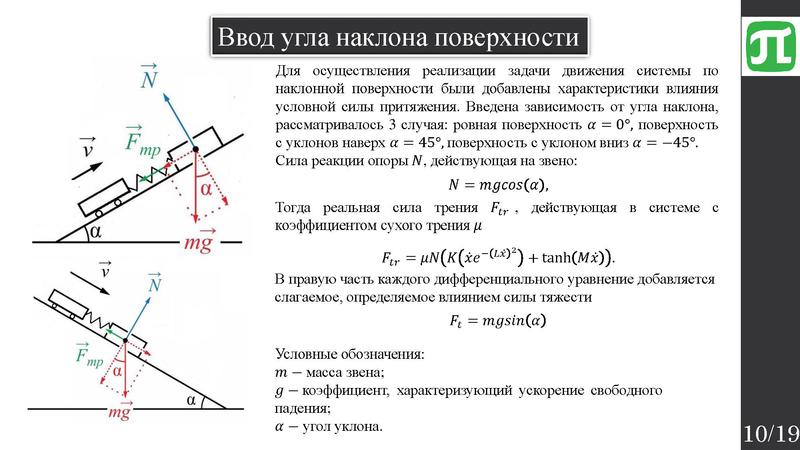
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y=k·x+b. В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М, M1(x1, y1), в уравнениеy=k·x+b, тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Пример 4Задана прямая с угловым коэффициентом y=13x-1. Вычислить, принадлежат ли точки M1(3, 0) и M2(2, -2) заданной прямой.
Решение
Необходимо подставить координаты точки M1(3, 0) в заданное уравнение, тогда получим 0=13·3-1⇔0=0. Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M2(2, -2), тогда получим неверное равенство вида -2=13·2-1⇔-2=-13. Можно сделать вывод, что точка М2 не принадлежит прямой.
Ответ: М1 принадлежит прямой, а М2 нет.
Известно, что прямая определена уравнением y=k·x+b, проходящим через M1(0, b), при подстановке получили равенство вида b=k·0+b⇔b=b.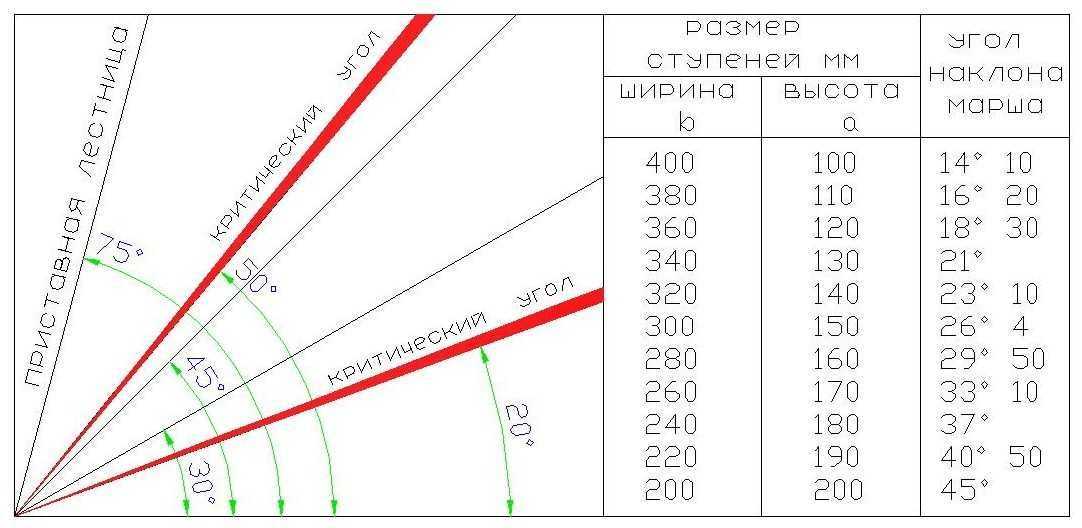 Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y=k·x+b на плоскости определяет прямую, которая проходит через точку 0, b. Она образует угол αс положительным направлением оси Ох, где k=tg α.
Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y=k·x+b на плоскости определяет прямую, которая проходит через точку 0, b. Она образует угол αс положительным направлением оси Ох, где k=tg α.
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y=3·x-1. Получим, что прямая пройдет через точку с координатой 0, -1 с наклоном в α=arctg3=π3 радиан по положительному направлению оси Ох. Отсюда видно, что коэффициент равен 3.
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M1(x1, y1).
Равенство y1=k·x+b можно считать справедливым, так как прямая проходит через точку M1(x1, y1). Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y-y1=k·(x-x1). Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M1(x1, y1).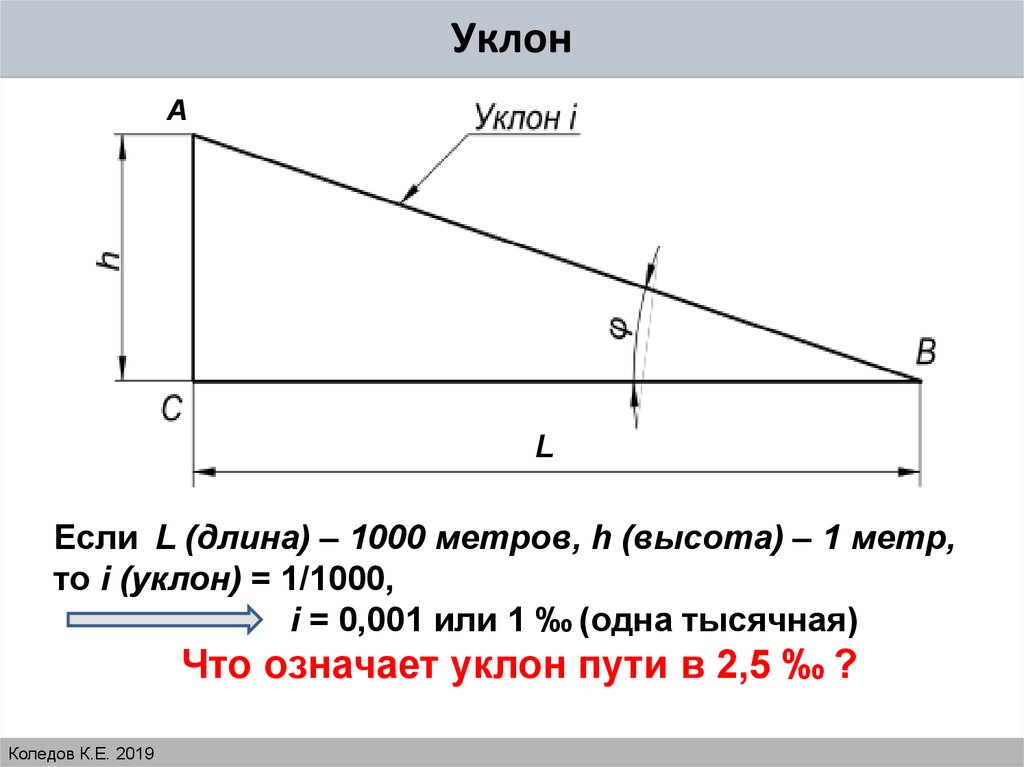
Составьте уравнение прямой, проходящей через точку М1 с координатами (4,-1), с угловым коэффициентом равным -2.
Решение
По условию имеем, что x1=4, y1=-1, k=-2. Отсюда уравнение прямой запишется таким образом y-y1=k·(x-x1)⇔y-(-1)=-2·(x-4)⇔y=-2x+7.
Ответ: y=-2x+7.
Пример 6Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М1 с координатами (3,5), параллельную прямой y=2x-2.
Решение
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y=2x-2, отсюда следует, что k=2. Составляем уравнение с угловым коэффициентом и получаем:
y-y1=k·(x-x1)⇔y-5=2·(x-3)⇔y=2x-1
Ответ: y=2x-1.
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись.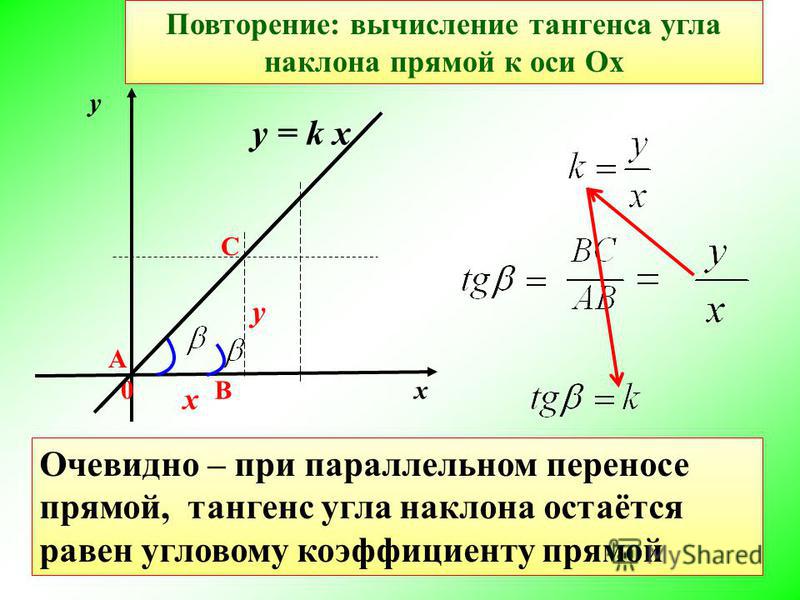 Для этого необходимо представлять в другом виде. Например, уравнение вида y=k·x+b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Для этого необходимо представлять в другом виде. Например, уравнение вида y=k·x+b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x-x1ax=y-y1ay. Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y=k·x+b⇔y-b=k·x⇔k·xk=y-bk⇔x1=y-bk.
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Пример 7Привести уравнение прямой с угловым коэффициентом y=-3x+12к каноническому виду.
Решение
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y=-3x+12⇔-3x=y-12⇔-3x-3=y-12-3⇔x1=y-12-3
Ответ: x1=y-12-3.
Общее уравнение прямой проще всего получить из y=k·x+b, но для этого необходимо произвести преобразования: y=k·x+b⇔k·x-y+b=0.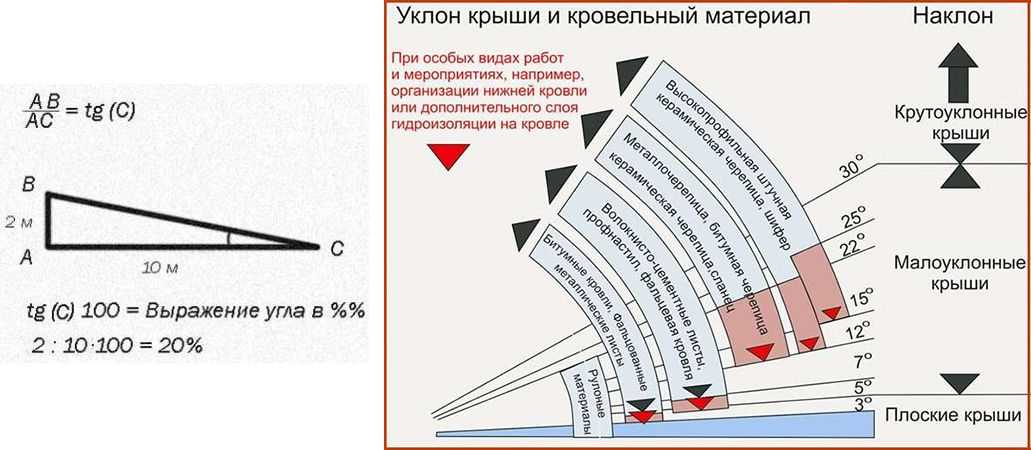 Производится переход из общего уравнения прямой к уравнениям другого вида.
Производится переход из общего уравнения прямой к уравнениям другого вида.
Дано уравнение прямой видаy=17x-2. Выяснить, является ли вектор с координатами a→=(-1, 7) нормальным вектором прямой?
Решение
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y=17x-2⇔17x-y-2=0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n→=17, -1, отсюда 17x-y-2=0. Понятно, что вектор a→=(-1, 7) коллинеарен вектору n→=17, -1, так как имеем справедливое соотношение a→=-7·n→. Отсюда следует, что исходный вектор a→=-1, 7 — нормальный вектор прямой 17x-y-2=0, значит, считается нормальным вектором для прямой y=17x-2.
Ответ: Является
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения Ax+By+C=0, где B≠0, к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим Ax+By+C=0⇔-AB·x-CB.
Результат и является уравннием с угловым коэффициентом, который равняется -AB.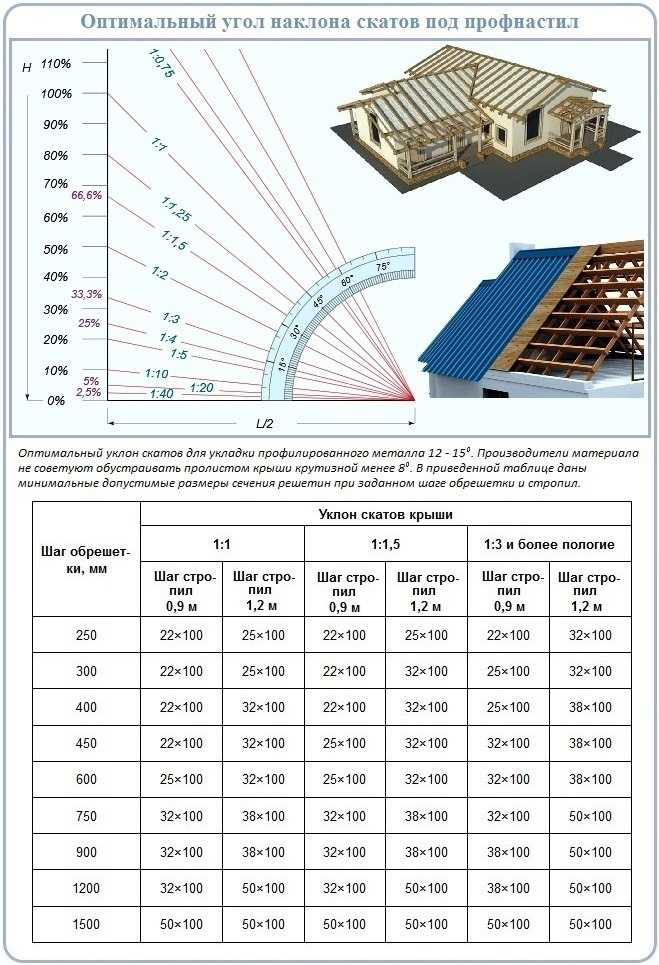
Задано уравнение прямой вида 23x-4y+1=0 . Получить уравнение данной прямой с угловым коэффициентом.
Решение
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
23x-4y+1=0⇔4y=23x+1⇔y=14·23x+1⇔y=16x+14.
Ответ: y=16x+14.
Аналогичным образом решается уравнение вида xa+yb=1, которое называют уравнение прямой в отрезках, или каноническое вида x-x1ax=y-y1ay. Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
xa+yb=1⇔yb=1-xa⇔y=-ba·x+b.
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x-x1ax=y-y1ay⇔ay·(x-x1)=ax·(y-y1)⇔⇔ax·y=ay·x-ay·x1+ax·y1⇔y=ayax·x-ayax·x1+y1
Пример 10Имеется прямая, заданная уравнением x2+y-3=1. Привести к виду уравнения с угловым коэффициентом.
Решение.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на -3 для того, чтобы получить необходимо уравнение с угловым коэффициентом.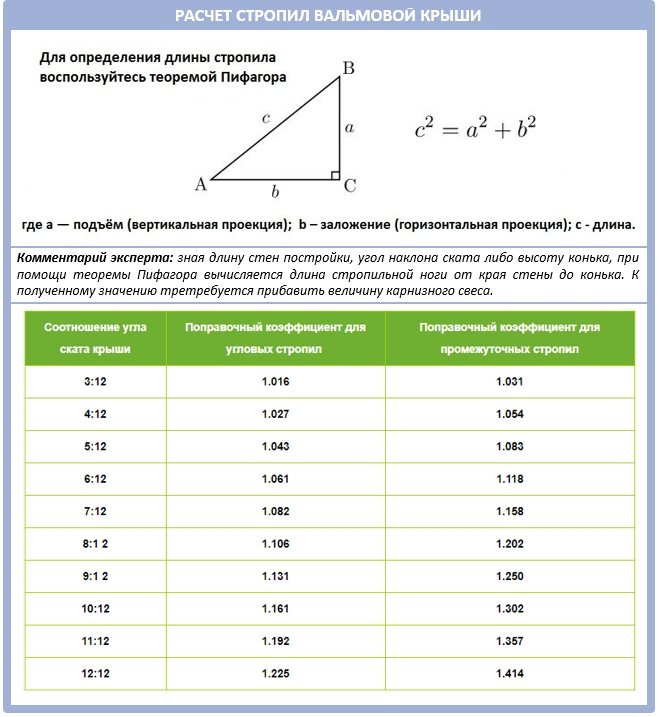 Преобразуя, получим:
Преобразуя, получим:
y-3=1-x2⇔-3·y-3=-3·1-x2⇔y=32x-3.
Ответ: y=32x-3.
Пример 11Уравнение прямой вида x-22=y+15 привести к виду с угловым коэффициентом.
Решение
Необходимо выражение x-22=y+15 вычислить как пропорцию. Получим, что 5·(x-2)=2·(y+1). Теперь необходимо полностью его разрешить, для этого:
5·(x-2)=2·(y+1)⇔5x-10=2y+2⇔2y=5x-12⇔y=52x
Ответ: y=52x-6.
Для решения таких заданий следует приводит параметрические уравнения прямой вида x=x1+ax·λy=y1+ay·λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Пример 12Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x=λy=-1+2·λ.
Решение
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x=λy=-1+2·λ⇔λ=xλ=y+12⇔x1=y+12.
Теперь необходимо разрешить данное равенство относительно y, чтобы получить уравнение прямой с угловым коэффициентом.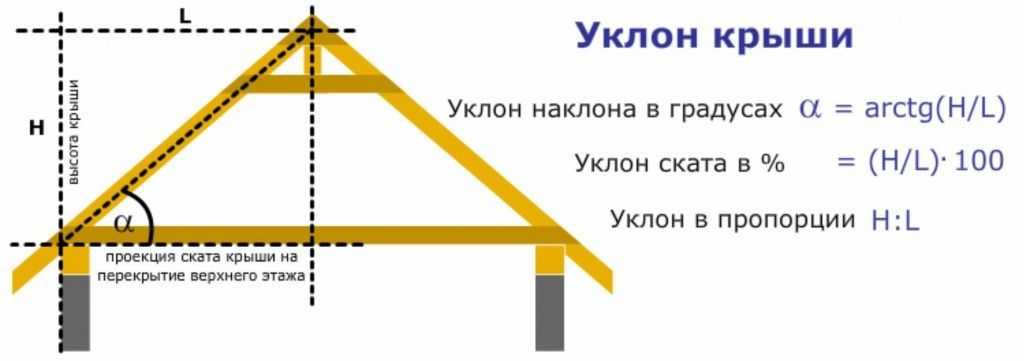 для этого запишем таким образом:
для этого запишем таким образом:
x1=y+12⇔2·x=1·(y+1)⇔y=2x-1
Отсюда следует, что угловой коэффициент прямой равен 2. Это записывается как k=2.
Ответ: k=2.
Решение задач
от 1 дня / от 150 р.
Курсовая работа
от 5 дней / от 1800 р.
Реферат
от 1 дня / от 700 р.
Найти угловой коэффициент и угол наклона прямых. Уравнение прямой с угловым коэффициентом: теория, примеры, решение задач
Прямая y=f(x) будет касательной к изображенному на рисунке графику в точке х0 в том случае, если она проходит через точку с координатами (х0; f(x0)) и обладает угловым коэффициентом f»(x0). Найти такой коэффициент, зная особенности касательной, несложно.
Вам понадобится
- — математический справочник;
- — простой карандаш;
- — тетрадь;
- — транспортир;
- — циркуль;
- — ручка.
Инструкция
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0).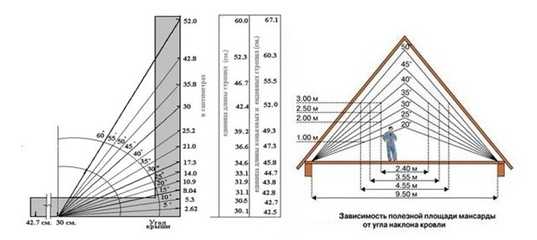 Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Изобразите на дополнительные касательные, которые бы соприкасались с графиком функции в точках x1, х2 и х3, а также отметьте углы, образуемые этими касательными с осью абсцисс (такой угол отсчитывают в положительном направлении от оси до касательной прямой). К примеру, угол, то есть, α1, будет острым, второй (α2) – тупой, а третий (α3) равен нулю, поскольку касательная прямая параллельна оси ОХ. В таком случае тангенс тупого угла – отрицательное , тангенс острого угла – положительное, а при tg0 результат равен нулю.
Обратите внимание
Правильно определите угол, образуемый касательной. Для этого используйте транспортир.
Полезный совет
Две наклонные прямые будут параллельными в том случае, если их угловые коэффициенты равны между собой; перпендикулярными, если произведение угловых коэффициентов этих касательных равно -1.
Источники:
- Касательная к графику функции
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного по известному значению косинуса от этой же величины.
Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного по известному значению косинуса от этой же величины.
Инструкция
Вычтите частное от единицы на возведенное в значение косинуса заданного угла, а из результата извлеките квадратный корень — это и будет значение тангенса от угла, выраженное его косинус: tg(α)=√(1-1/(cos(α))²). При этом обратите внимание на то, что в формуле косинус стоит в знаменателе дроби. Невозможность деления на ноль исключает использование этого выражения для углов, равных 90°, а также отличающихся от этой величины на числа, кратные 180° (270°, 450°, -90° и т.д.).
Существует и альтернативный способ вычисления тангенса по известному значению косинуса. Его можно применять, если не установлено ограничение на использование других . Для реализации этого способа сначала определите величину угла по известному значению косинуса — это можно сделать с помощью функции арккосинус. Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Есть и еще экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное вы получите с любыми значениями, имеющими же . Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.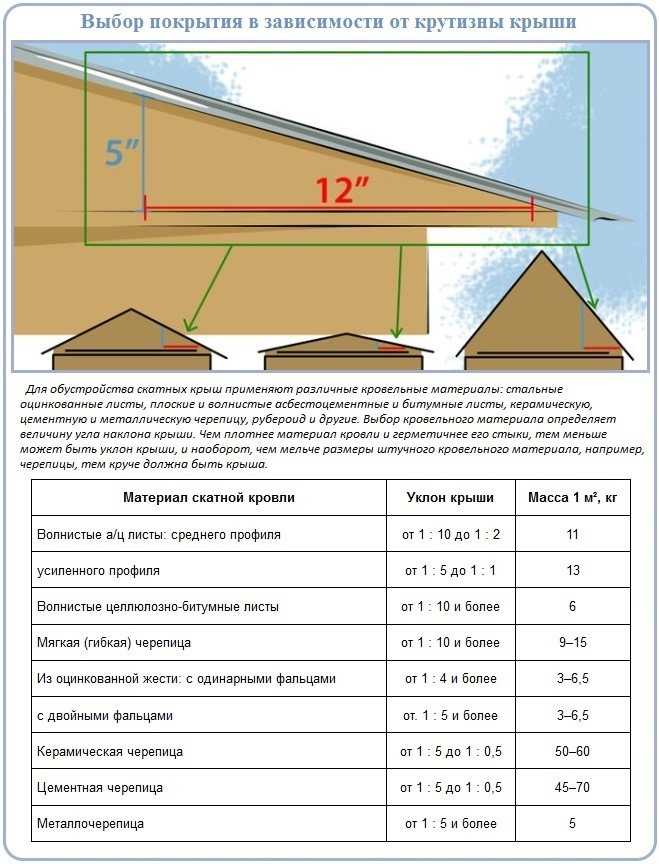
Источники:
- косинус через тангенс формула
Одна из тригонометрических функций, чаще всего обозначаемая буквами tg, хотя встречаются и обозначения tan. Проще всего представить тангенс как отношение синуса угла к его косинусу. Это нечетная периодическая и не непрерывная функция, каждый цикл которой равен числу Пи, а точка разрыва соответствует отметке в половину этого числа.
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела» , мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью .
- Как брать простейшие производные, например, производную показательного уравнения, описано . Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции.
В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у).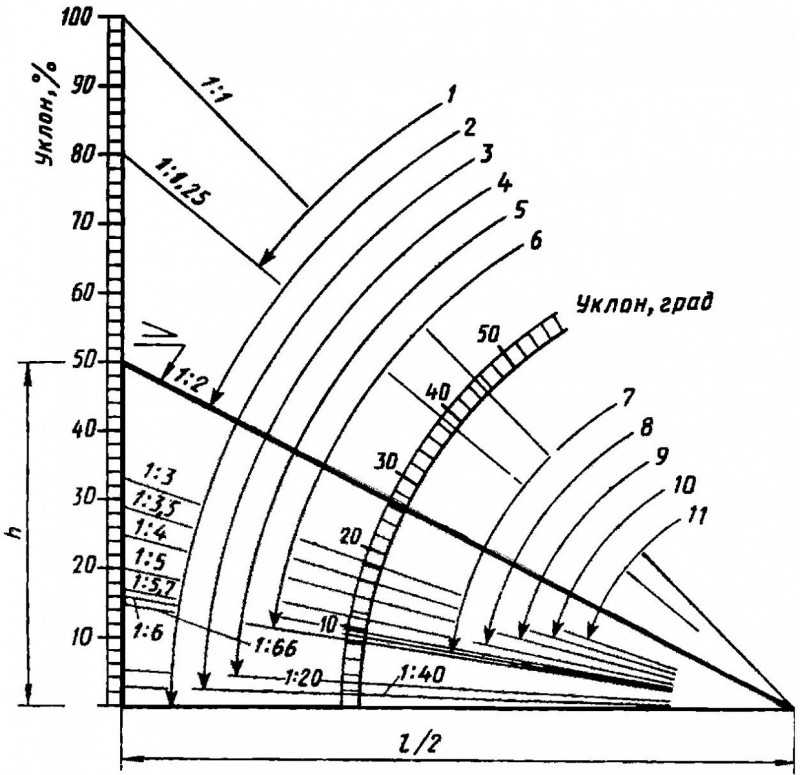 {2}+6x}
в точке А(4,2) равен 22.
{2}+6x}
в точке А(4,2) равен 22.
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой.
 В нашем примере соедините точки с координатами (4,2) и (26,3).
В нашем примере соедините точки с координатами (4,2) и (26,3).
Продолжение темы уравнение прямой на плоскости основывается на изучении прямой линии из уроков алгебры. Данная статья дает обобщенную информацию по теме уравнения прямой с угловым коэффициентом. Рассмотрим определения, получим само уравнение, выявим связь с другими видами уравнений. Все будет рассмотрено на примерах решений задач.
Yandex.RTB R-A-339285-1
Перед записью такого уравнения необходимо дать определение угла наклона прямой к оси О х с их угловым коэффициентом. Допустим, что задана декартова система координат О х на плоскости.
Определение 1
Угол наклона прямой к оси О х, расположенный в декартовой системе координат О х у на плоскости, это угол, который отсчитывается от положительного направления О х к прямой против часовой стрелки.
Когда прямая параллельна О х или происходит совпадение в ней, угол наклона равен 0 . Тогда угол наклона заданной прямой α определен на промежутке [ 0 , π) .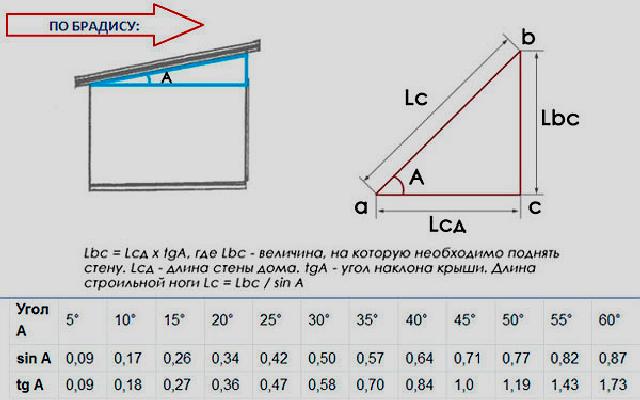
Определение 2
Угловой коэффициент прямой – это тангенс угла наклона заданной прямой.
Стандартное обозначение буквой k . Из определения получим, что k = t g α . Когда прямая параллельна Ох, говорят, что угловой коэффициент не существует, так как он обращается в бесконечность.
Угловой коэффициент положительный, когда график функции возрастает и наоборот. На рисунке показаны различные вариации расположения прямого угла относительно системы координат со значением коэффициента.
Для нахождения данного угла необходимо применить определение об угловом коэффициенте и произвести вычисление тангенса угла наклона в плоскости.
Решение
Из условия имеем, что α = 120 ° . По определению необходимо вычислить угловой коэффициент. Найдем его из формулы k = t g α = 120 = — 3 .
Ответ: k = — 3 .
Если известен угловой коэффициент, а необходимо найти угол наклона к оси абсцисс, тогда следует учитывать значение углового коэффициента. Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k
Если k > 0 , тогда угол прямой острый и находится по формуле α = a r c t g k . Если k
Пример 2
Определить угол наклона заданной прямой к О х при угловом коэффициенте равном 3 .
Решение
Из условия имеем, что угловой коэффициент положительный, а это значит, что угол наклона к О х меньше 90 градусов. Вычисления производятся по формуле α = a r c t g k = a r c t g 3 .
Ответ: α = a r c t g 3 .
Пример 3
Найти угол наклона прямой к оси О х, если угловой коэффициент = — 1 3 .
Решение
Если принять за обозначение углового коэффициента букву k , тогда α является углом наклона к заданной прямой по положительному направлению О х. Отсюда k = — 1 3
α = π — a r c t g — 1 3 = π — a r c t g 1 3 = π — π 6 = 5 π 6 .
Ответ: 5 π 6 .
Уравнение вида y = k · x + b , где k является угловым коэффициентом, а b некоторым действительным числом, называют уравнением прямой с угловым коэффициентом.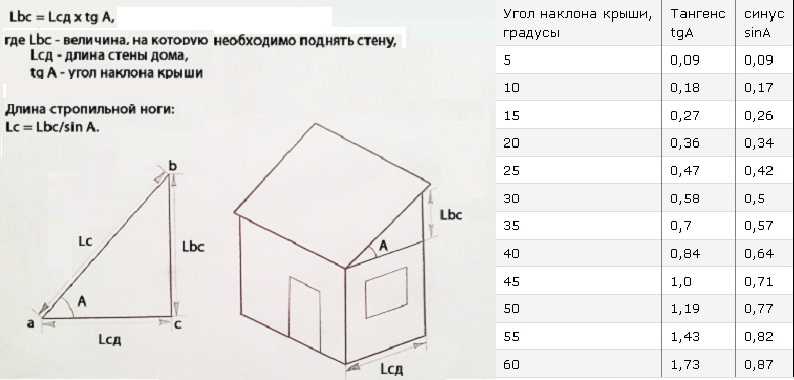 Уравнение характерно для любой прямой, непараллельной оси О у.
Уравнение характерно для любой прямой, непараллельной оси О у.
Если подробно рассмотреть прямую на плоскости в фиксированной системе координат, которая задана уравнением с угловым коэффициентом, который имеет вид y = k · x + b . В данном случае значит, что уравнению соответствуют координаты любой точки прямой. Если подставить координаты точки М, M 1 (x 1 , y 1) , в уравнение y = k · x + b , тогда в этом случае прямая будет проходить через эту точку, иначе точка не принадлежит прямой.
Пример 4
Задана прямая с угловым коэффициентом y = 1 3 x — 1 . Вычислить, принадлежат ли точки M 1 (3 , 0) и M 2 (2 , — 2) заданной прямой.
Решение
Необходимо подставить координаты точки M 1 (3 , 0) в заданное уравнение, тогда получим 0 = 1 3 · 3 — 1 ⇔ 0 = 0 . Равенство верно, значит точка принадлежит прямой.
Если подставим координаты точки M 2 (2 , — 2) , тогда получим неверное равенство вида — 2 = 1 3 · 2 — 1 ⇔ — 2 = — 1 3 . Можно сделать вывод, что точка М 2 не принадлежит прямой.
Ответ: М 1 принадлежит прямой, а М 2 нет.
Известно, что прямая определена уравнением y = k · x + b , проходящим через M 1 (0 , b) , при подстановке получили равенство вида b = k · 0 + b ⇔ b = b . Отсюда можно сделать вывод, что уравнение прямой с угловым коэффициентом y = k · x + b на плоскости определяет прямую, которая проходит через точку 0 , b . Она образует угол α с положительным направлением оси О х, где k = t g α .
Рассмотрим на примере прямую, определенную при помощи углового коэффициента, заданного по виду y = 3 · x — 1 . Получим, что прямая пройдет через точку с координатой 0 , — 1 с наклоном в α = a r c t g 3 = π 3 радиан по положительному направлению оси О х. Отсюда видно, что коэффициент равен 3 .
Уравнение прямой с угловым коэффициентом, проходящей через заданную точку
Необходимо решить задачу, где необходимо получить уравнение прямой с заданным угловым коэффициентом, проходящим через точку M 1 (x 1 , y 1) .
Равенство y 1 = k · x + b можно считать справедливым, так как прямая проходит через точку M 1 (x 1 , y 1) . Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · (x — x 1) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 (x 1 , y 1) .
Чтобы убрать число b, необходимо из левой и правой частей вычесть уравнение с угловым коэффициентом. Из этого следует, что y — y 1 = k · (x — x 1) . Данное равенство называют уравнением прямой с заданным угловым коэффициентом k, проходящая через координаты точки M 1 (x 1 , y 1) .
Пример 5
Составьте уравнение прямой, проходящей через точку М 1 с координатами (4 , — 1) , с угловым коэффициентом равным — 2 .
Решение
По условию имеем, что x 1 = 4 , y 1 = — 1 , k = — 2 . Отсюда уравнение прямой запишется таким образом y — y 1 = k · (x — x 1) ⇔ y — (- 1) = — 2 · (x — 4) ⇔ y = — 2 x + 7 .
Ответ: y = — 2 x + 7 .
Пример 6
Написать уравнение прямой с угловым коэффициентом, которое проходит через точку М 1 с координатами (3 , 5) , параллельную прямой y = 2 x — 2 .
Решение
По условию имеем, что параллельные прямые имеют совпадающие углы наклона, отсюда значит, что угловые коэффициенты являются равными. Чтобы найти угловой коэффициент из данного уравнения, необходимо вспомнить его основную формулу y = 2 x — 2 , отсюда следует, что k = 2 .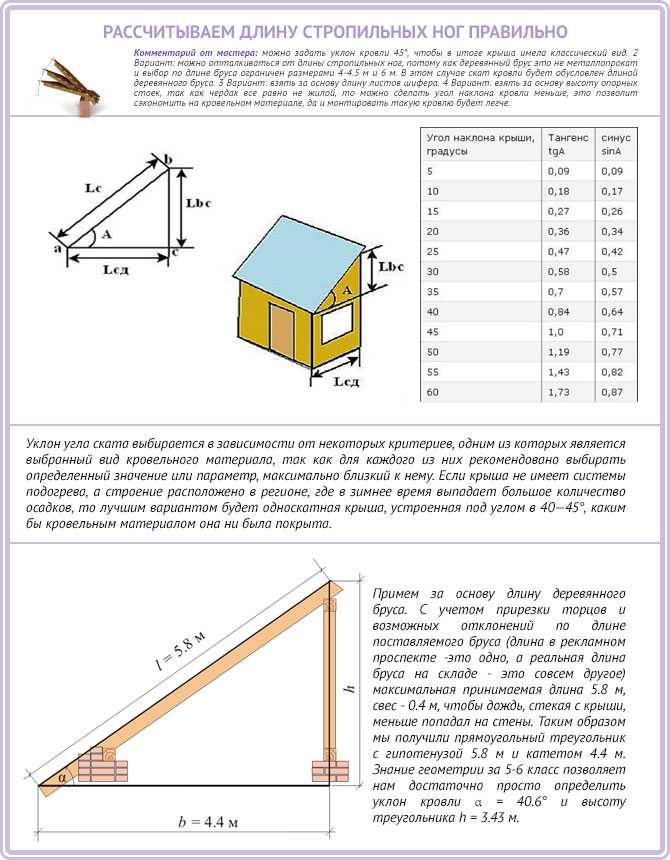 Составляем уравнение с угловым коэффициентом и получаем:
Составляем уравнение с угловым коэффициентом и получаем:
y — y 1 = k · (x — x 1) ⇔ y — 5 = 2 · (x — 3) ⇔ y = 2 x — 1
Ответ: y = 2 x — 1 .
Переход от уравнения прямой с угловым коэффициентом к другим видам уравнений прямой и обратно
Такое уравнение не всегда применимо для решения задач, так как имеет не совсем удобную запись. Для этого необходимо представлять в другом виде. Например, уравнение вида y = k · x + b не позволяет записать координаты направляющего вектора прямой или координаты нормального вектора. Для этого нужно научиться представлять уравнениями другого вида.
Можем получить каноническое уравнение прямой на плоскости, используя уравнение прямой с угловым коэффициентом. Получаем x — x 1 a x = y — y 1 a y . Необходимо слагаемое b перенести в левую часть и поделить на выражение полученного неравенства. Тогда получим уравнение вида y = k · x + b ⇔ y — b = k · x ⇔ k · x k = y — b k ⇔ x 1 = y — b k .
Уравнение прямой с угловым коэффициентом стало каноническим уравнением данной прямой.
Пример 7
Привести уравнение прямой с угловым коэффициентом y = — 3 x + 12 к каноническому виду.
Решение
Вычислим и представим в виде канонического уравнения прямой. Получим уравнение вида:
y = — 3 x + 12 ⇔ — 3 x = y — 12 ⇔ — 3 x — 3 = y — 12 — 3 ⇔ x 1 = y — 12 — 3
Ответ: x 1 = y — 12 — 3 .
Общее уравнение прямой проще всего получить из y = k · x + b , но для этого необходимо произвести преобразования: y = k · x + b ⇔ k · x — y + b = 0 . Производится переход из общего уравнения прямой к уравнениям другого вида.
Пример 8
Дано уравнение прямой вида y = 1 7 x — 2 . Выяснить, является ли вектор с координатами a → = (- 1 , 7) нормальным вектором прямой?
Решение
Для решения необходимо перейти к другому виду данного уравнения, для этого запишем:
y = 1 7 x — 2 ⇔ 1 7 x — y — 2 = 0
Коэффициенты перед переменными являются координатами нормального вектора прямой. Запишем это так n → = 1 7 , — 1 , отсюда 1 7 x — y — 2 = 0 . Понятно, что вектор a → = (- 1 , 7) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Понятно, что вектор a → = (- 1 , 7) коллинеарен вектору n → = 1 7 , — 1 , так как имеем справедливое соотношение a → = — 7 · n → . Отсюда следует, что исходный вектор a → = — 1 , 7 — нормальный вектор прямой 1 7 x — y — 2 = 0 , значит, считается нормальным вектором для прямой y = 1 7 x — 2 .
Ответ: Является
Решим задачу обратную данной.
Необходимо перейти от общего вида уравнения A x + B y + C = 0 , где B ≠ 0 , к уравнению с угловым коэффициентом. для этого решаем уравнение относительно у. Получим A x + B y + C = 0 ⇔ — A B · x — C B .
Результат и является уравннием с угловым коэффициентом, который равняется — A B .
Пример 9
Задано уравнение прямой вида 2 3 x — 4 y + 1 = 0 . Получить уравнение данной прямой с угловым коэффициентом.
Решение
Исходя из условия, необходимо решить относительно у, тогда получим уравнение вида:
2 3 x — 4 y + 1 = 0 ⇔ 4 y = 2 3 x + 1 ⇔ y = 1 4 · 2 3 x + 1 ⇔ y = 1 6 x + 1 4 .
Ответ: y = 1 6 x + 1 4 .
Аналогичным образом решается уравнение вида x a + y b = 1 , которое называют уравнение прямой в отрезках, или каноническое вида x — x 1 a x = y — y 1 a y . Нужно решить его относительно у, только тогда получим уравнение с угловым коэффициентом:
x a + y b = 1 ⇔ y b = 1 — x a ⇔ y = — b a · x + b .
Каноническое уравнение можно привести к виду с угловым коэффициентом. Для этого:
x — x 1 a x = y — y 1 a y ⇔ a y · (x — x 1) = a x · (y — y 1) ⇔ ⇔ a x · y = a y · x — a y · x 1 + a x · y 1 ⇔ y = a y a x · x — a y a x · x 1 + y 1
Пример 10
Имеется прямая, заданная уравнением x 2 + y — 3 = 1 . Привести к виду уравнения с угловым коэффициентом.
Решение.
Исходя из условия, необходимо преобразовать, тогда получим уравнение вида _formula_. Обе части уравнения следует умножить на — 3 для того, чтобы получить необходимо уравнение с угловым коэффициентом. Преобразуя, получим:
y — 3 = 1 — x 2 ⇔ — 3 · y — 3 = — 3 · 1 — x 2 ⇔ y = 3 2 x — 3 .
Ответ: y = 3 2 x — 3 .
Пример 11
Уравнение прямой вида x — 2 2 = y + 1 5 привести к виду с угловым коэффициентом.
Решение
Необходимо выражение x — 2 2 = y + 1 5 вычислить как пропорцию. Получим, что 5 · (x — 2) = 2 · (y + 1) . Теперь необходимо полностью его разрешить, для этого:
5 · (x — 2) = 2 · (y + 1) ⇔ 5 x — 10 = 2 y + 2 ⇔ 2 y = 5 x — 12 ⇔ y = 5 2 x
Ответ: y = 5 2 x — 6 .
Для решения таких заданий следует приводит параметрические уравнения прямой вида x = x 1 + a x · λ y = y 1 + a y · λ к каноническому уравнению прямой, только после этого можно переходить к уравнению с угловым коэффициентом.
Пример 12
Найти угловой коэффициент прямой, если она задана параметрическими уравнениями x = λ y = — 1 + 2 · λ .
Решение
Необходимо выполнить переход от параметрического вида к угловому коэффициенту. Для этого найдем каноническое уравнение из заданного параметрического:
x = λ y = — 1 + 2 · λ ⇔ λ = x λ = y + 1 2 ⇔ x 1 = y + 1 2 .
Теперь необходимо разрешить данное равенство относительно y , чтобы получить уравнение прямой с угловым коэффициентом. для этого запишем таким образом:
x 1 = y + 1 2 ⇔ 2 · x = 1 · (y + 1) ⇔ y = 2 x — 1
Отсюда следует, что угловой коэффициент прямой равен 2 . Это записывается как k = 2 .
Ответ: k = 2 .
Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter
Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где
k
–
это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y = kx + b , то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент! Уравнение прямой походящей через две данные точки. Формула имеет вид:
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:
*Оба катета равны шести (это их длины).
Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Ответ: 1
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Наши точки имеют координаты (5;0) и (0;5). Значит,
Приведём формулу к виду y = kx + b
Получили, что угловой коэффициент k = – 1.
Ответ: –1
Прямая a проходит через точки с координатами (0;6) и (8;0). Прямая b проходит через точку с координатами (0;10) и параллельна прямой a b с осью оx.
В данной задаче можно найти уравнение прямой a
, определить угловой коэффициент для неё. У прямой b
угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b
. А затем, подставив в него значение y = 0, найти абсциссу. НО!
НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Ответ: 40/3
Прямая a проходит через точки с координатами (0;8) и (–12;0). Прямая b проходит через точку с координатами (0; –12) и параллельна прямой a . Найдите абсциссу точки пересечения прямой b с осью оx .
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а . Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Приведём к виду y = kx + b :
Получили, что угловой k
= 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Ответ: 18
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Приведём к виду y = kx + b
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу нужно подставить в найденное уравнение х = 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу в точке (0;–12).
Искомая ордината равна –12.
Ответ: –12
Найдите ординату точки пересечения прямой, заданной уравнением
3х + 2у = 6 , с осью Oy .
Координата точки пересечения заданной прямой с осью оу имеет вид (0;у ). Подставим в уравнение абсциссу х = 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу
равна 3.
*Решается система:
Ответ: 3
Найдите ординату точки пересечения прямых, заданных уравнениями
3х + 2у = 6 и у = – х .
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х вместо у :
Ордината равна минус шести.
Ответ: – 6
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.
Найдите ординату точки пересечения оси оy и прямой, проходящей через точку B (6;4) и параллельной прямой, проходящей через начало координат и точку A (6;8).
1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
>> Угол наклона прямой от 0 до 90 градусов
>> Угол наклона прямой от 90 до 180 градусов
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Как высчитать угол наклона крыши — какой он должен быть?
Дата последнего изменения:
23 января 2017
Время на чтение:
7 минут
582
Монтаж кровли имеет множество нюансов. К примеру, угол наклона кровли. На первый взгляд, можно выбрать любой подходящий тип кровли с желаемым наклоном. Но это не так. От него зависит конструкция стропильной системы, выбор кровельного материала и т. д.
Как определить угол наклона крыши в градусах? Многие интересуются этим вопросом. Для плоских кровель этот показатель минимальный, и практически не имеет никаких особенностей. А вот конструкции с использованием стропильных систем, имеют множество особенностей, на которые следует обратить внимание. В противном случае эксплуатация сооружения доставит множество хлопот.
В противном случае эксплуатация сооружения доставит множество хлопот.
Важным фактором для сооружения скатной крыши является правильный расчет уклона кровли, от которого зависит степень отвода осадков. Его выражают в процентах, градусах и соотношении катетов. Как определить угол наклона крыши в градусах правильно?
Крыши, с большим уклоном принято называть крутыми, а с маленьким – пологими.
В этой статье
- Угол наклона
- Материал и уклон
- Климат местности
- Назначение строения
- Как рассчитать угол спуска?
- Итог
Угол наклона
Прежде чем приступить к выбору угла наклона, следует выбрать кровельное покрытие. Чаще всего используют металлочерепицу, профнастил, шифер, рулонные материалы, черепицу.
Представим треугольник с прямым углом. Известно, что гипотенуза будет больше любого катета. В таком случае наименьший допустимый показатель и будет оптимальным углом наклона. Как узнать его?
Он зависит от герметичности конструкции в целом и финишного кровельного материала, а точнее, его плотности. Известно, чем больше угол наклона, тем больше показатель парусности. Кровли с небольшим наклоном часто задерживают осадки. В итоге создается повышенная нагрузка на поверхность конструкции.
Известно, чем больше угол наклона, тем больше показатель парусности. Кровли с небольшим наклоном часто задерживают осадки. В итоге создается повышенная нагрузка на поверхность конструкции.
Для точного определения оптимального наклона крыши можно воспользоваться специальными программами и таблицами. Они помогают узнать уклон в соотношении катетов и процентах, которые можно в дальнейшем связать с градусным определением. Как измерить этот показатель?
Материал и уклон
Выбирая кровельный материал, обратите внимание на его характеристики. Здесь должны быть указаны нижние и верхние допустимые пределы угла наклона кровли. К примеру, нижний предел для шифера – 120, а верхний – 450.
Помните, чем меньше угол наклона, тем меньше расходуется материал. Известно, что сооружение плоской кровли намного выгоднее сооружения скатной практически вдвое. При сооружении такой конструкции экономятся средства не только на кровельном материале, но и на древесине.
Климат местности
Угол наклона кровли также зависит от климатических условий, в которых сооружено здание. Почему? В местности, где крыши дома в большинстве случаев имеют минимальный угол наклона, часто дуют сильные ветра. Таким образом, конструкция уменьшает неблагоприятное воздействие ветра на крышу в целом. Кровли, которые имеют меньше 10 градусов уклона, практически не подвержены такому влиянию. Но здесь возникает вероятность срыва ветряным потоком кровельного материала.
[wpsm_box type=»info» float=»none» text_align=»left»]
Как посчитать оптимальный вариант? Специалисты рекомендуют возводить кровли в 35 градусов в местностях с небольшими ветряными нагрузками. При сильном ветре крыша должна быть 15-25 градусов.[/wpsm_box]
Какой должен быть угол для мансард? Для его расчета необходимо длину торца разделить вдвое. А высота ската в торце стандартна (1,8 м).
В местностях, где часто выпадают большие осадки, угол наклона может быть равен 60 градусам.
Назначение строения
Наклон кровли зависит и от назначения чердака, если сооружается кровля с минимум 2 скатами. Если это пространство будет использоваться в дальнейшем не для проживания, то делают невысокое помещение. Большое пространство ни к чему, ведь здесь будет скапливаться прохладный воздух. Хранение ненужных вещей не требует особых условий. Главное, чтоб не попадала влага на них.
Если же чердак будет использоваться для проживания, то следует побеспокоиться о сооружении просторного помещения. А соответственно и угол наклона будет иметь значительную величину.
Как рассчитать угол спуска?
Для расчета используют специальные программы. Для того, чтобы нею воспользоваться, необходимо знать ширину основания, длину стропил, высоту конька.
[wpsm_box type=»info» float=»none» text_align=»left»]
Воспользоваться специальными программами сможет не каждый. Если вы неуверены в своих силах, то обратитесь к специалистам. Они смогут не только рассчитать определенный уклон крыши, но и приготовят проект, по которому можно быстро и правильно возвести надежную кровлю. [/wpsm_box]
[/wpsm_box]
Можно и самостоятельно рассчитать этот показатель. Для этого необходимо знать значение высоты объема конька. Этот показательно и определяет назначение будущего чердачного пространства.
Если будущее чердачное помещение вы будете использовать как мансарду, то расчет необходимо провести по примеру. Допустим, что ширина фронта 6 м. Эту величину необходимо разделить пополам. 6/2 = 3 Высота ската в коньке часто равна 1,8 м. Зная эти значения, вы можете самостоятельно найти угол наклона крыши.
После узнаем синус угла, который определяет отношение катета прилежащего к противоположному. По формуле видно, что Sin A=3/1, 8=1,67. Теперь воспользуемся таблицей Брадиса. Нужно найти приближенное значение к 1,67 равняется 59 градусам. Значит, для такой кровли идеальным является 60 градусов наклона.
Итог
Прежде чем приступить к сооружению кровли, тщательно спланируйте все. Подготовьте расчеты, план, схемы. Здесь вы можете выбрать заранее оптимальный угол наклона, учитывая все вышеупомянутые факторы. К тому же они помогут высчитать необходимое количество кровельного материала, так у вас не будет избытка по завершении строительства. Помните, что от этого зависит дальнейшая эксплуатация сооружения. И насколько длительной она будет, зависит только от правильной технологии и качества ее сооружения.
К тому же они помогут высчитать необходимое количество кровельного материала, так у вас не будет избытка по завершении строительства. Помните, что от этого зависит дальнейшая эксплуатация сооружения. И насколько длительной она будет, зависит только от правильной технологии и качества ее сооружения.
Понравилась статья?
Поставьте лайк автору и поделитесь в соц. сетях
4.3 Наклон линии | Аналитическая геометрия
4.3 Наклон линии (EMBGD)
На диаграмме показано, что прямая образует угол \(\theta\) с положительной осью \(x\). Это называется угол наклона прямой.
Мы замечаем, что если градиент изменяется, то значение \(\theta\) также изменяется, поэтому угол
наклон линии связан с ее градиентом. Мы знаем, что градиент – это отношение изменения
\(y\)-направление на изменение \(x\)-направления:
Мы знаем, что градиент – это отношение изменения
\(y\)-направление на изменение \(x\)-направления:
Из тригонометрии мы знаем, что функция тангенса определяется как отношение:
\[\tan \theta = \frac{\text{противоположная сторона}}{\text{прилегающая сторона}}\]
А из схемы мы видим, что
\начать{выровнять*} \tan \theta &= \dfrac{\Delta y}{\Delta x} \\ \поэтому m &= \tan \theta \qquad \text{ for } \text{0}\text{°} \leq \theta < \текст{180}\текст{°} \end{выравнивание*}
Следовательно, градиент прямой линии равен тангенсу угла, образованного между прямой и положительное направление оси \(х\).
Вертикальные линии
- \(\тета = \текст{90}\текст{°}\)
- Градиент не определен, поскольку значения \(x\) не изменились (\(\Delta x = 0\)).

- Следовательно, \(\tan \theta\) также не определено (график \(\tan \theta\) имеет асимптоту в \(\theta = \текст{90}\текст{°}\)).
Горизонтальные линии
- \(\тета = \текст{0}\текст{°}\)
- Градиент равен \(\text{0}\), поскольку значения \(y\) не изменяются (\(\Delta y = 0\)).
- Следовательно, \(\tan \theta\) также равно \(\text{0}\) (график \(\tan \theta\) проходит через происхождение \((\text{0}\text{°};0))\).
Линии с отрицательным уклоном
Если прямая имеет отрицательный наклон (\(m < 0\), \(\tan \theta < 0\)), то угол, образованный между прямой и положительным направлением оси \(х\) тупая.
Из диаграммы CAST в тригонометрии мы знаем, что функция тангенса отрицательна во втором и четвертом квадрант. Если мы вычисляем угол наклона для линии с отрицательным градиентом, мы должны добавить \(\text{180}\text{°}\), чтобы изменить отрицательный угол в четвертом квадранте на тупой угол в второй квадрант: 9{-1}(-\текст{0,7}) \\ &= -\текст{35,0}\текст{°} \конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой
угол во втором квадранте:
Мы должны добавить \(\text{180}\)\(\text{°}\) чтобы получить тупой
угол во втором квадранте:
\начать{выровнять*} \тета &= -\текст{35,0}\текст{°} + \текст{180}\текст{°} \\ &= \текст{145}\текст{°} \конец{выравнивание*}
И мы всегда можем использовать наш калькулятор, чтобы проверить, что тупой угол \(\theta = \text{145}\text{°}\) дает градиент \(m = -\text{0,7}\).
Угол наклона
Учебник Упражнение 4.5
\(\text{60}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{60}\text{°} \\ \поэтому m &= \text{1,7} \end{align*}
\(\text{135}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -\text{1} \end{выравнивание*}
\(\text{0}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{0}\text{°} \\ \поэтому m &= \text{0} \end{align*}
\(\text{54}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{54}\текст{°} \\ \поэтому m &= \text{1,4} \end{выравнивание*}
\(\text{90}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \загар \текст{90}\текст{°} \\ \поэтому m & \text{ не определено} \end{align*}
\(\text{45}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{45}\text{°} \\ \поэтому m &= \text{1} \end{выравнивание*}
\(\text{140}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{140}\text{°} \\ \поэтому m &= -\text{0,8} \end{align*}
\(\text{180}\text{°}\)
\begin{align*} м &= \загар \тета\\ &= \tan \text{180}\text{°} \\ \поэтому m &= \text{0} \end{выравнивание*} 9{-1} \влево( \text{0,75} \вправо) \\ \поэтому \тета &= \text{36,8}\text{°} \end{align*}
\(2y — x = 6\)
\begin{align*} 2у — х&=6\ 2у &= х + 6 \\ y &= \frac{1}{2}x + 3 \\ \загар \тета &= м \\ &= \фракция{1}{2} \\ \theta &= \tan^{-1} \left( \text{0,5} \right) \\ \поэтому \тета &= \текст{26,6}\текст{°} \end{выравнивание*} 9{-1} \влево( \текст{1} \вправо) \\ \поэтому \тета &= \text{45}\text{°} \end{align*}
\(y=4\)
Горизонтальная линия
\(x = 3y + \frac{1}{2}\)
\begin{align*} х &= 3y + \frac{1}{2} \\ x — \frac{1}{2} &= 3y \\ \frac{1}{3}x — \frac{1}{6} &= y \\ \поэтому m &= \frac{1}{3} \\ \theta &= \tan^{-1} \left( \frac{1}{3} \right) \\ \поэтому \тета &= \text{18,4}\text{°} \end{выравнивание*} 9{-1} \влево( \текст{0,577} \вправо) \\ \поэтому \тета &= \text{30}\text{°} \конец{выравнивание*}
Рабочий пример 8: Наклон прямой линии
Определить угол наклона (с точностью до \(\text{1}\) десятичного знака) прямой линии
проходящей через точки \((2;1)\) и \((-3;-9)\). {-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
{-1}2\\
&= \текст{63,4}\текст{°}
\end{выравнивание*}
Важно: убедитесь, что ваш калькулятор находится в режиме DEG (градусы).
Напишите окончательный ответ
Угол наклона прямой равен \(\text{63,4}\)\(\text{°}\).
temp textРабочий пример 9: Наклон прямой линии
Определите уравнение прямой, проходящей через точку \((3;1)\) и с углом наклон \(\text{135}\text{°}\).
Используйте угол наклона для определения градиента линии
\begin{align*} м &= \загар \тета\\ &= \tan \text{135}\text{°} \\ \поэтому m &= -1 \конец{выравнивание*}
Запишите уравнение прямой линии в форме точки градиента. x — x_1)\]
Подставить заданную точку \((3;1)\)
\begin{выравнивание*} у — 1 & = -(х — 3) \\ у&=-х+3+1\ &= -х + 4 \конец{выравнивание*}
Напишите окончательный ответ
Уравнение прямой линии \(y = -x + 4\).
Рабочий пример 10: Наклон прямой линии
Определить острый угол (с точностью до \(\text{1}\) десятичного разряда) между прямой, проходящей через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямая \(y = — \frac{3}{2}x + 4\).
Начертить эскиз
Начертить прямую через точки \(M(-1;1\frac{3}{4})\) и \(N(4;3)\) и прямую \(y = — \ дробь{3}{2}x + 4\) в подходящей системе координат. Обозначьте \(\alpha\) и \(\beta\) углы наклона две линии. Обозначьте \(\theta\) острый угол между двумя прямыми.
Обратите внимание, что \(\alpha\) и \(\theta\) — острые углы, а \(\beta\) — тупой угол.
\[\begin{массив}{rll}
\hat{B}_1 &= \text{180}\text{°} — \beta & (\angle \text{на строке}) \\
\text{and} \theta &= \alpha + \hat{B}_1 \quad & (\text{ext.} \angle \text{ of } \triangle =
\text{ сумма внутр. опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
опп}) \\
\поэтому \тета &= \альфа + (\текст{180}\текст{°} — \бета) \\
&= \text{180}\text{°} + \alpha — \beta
\конец{массив}\]
9{-1} \left(-\frac{3}{2}\right) &= -\text{56,3}\text{°}
\конец{выравнивание*}
Этот отрицательный угол лежит в четвертом квадранте. Мы знаем, что угол наклона \(\beta\) равен тупой угол, лежащий во второй четверти, поэтому
\начать{выравнивать*} \beta &= -\text{56,3}\text{°} + \text{180}\text{°}\\ &= \текст{123,7}\текст{°} \конец{выравнивание*}
Определить градиент и угол наклона линии через \(M\) и \(N\)
Определение градиента \начать{выравнивать*} m & = \frac{y_2 — y_1}{x_2 — x_1} \\ & = \dfrac{3 — \frac{7}{4}}{4-(-1)} \\ & = \dfrac{\frac{5}{4}}{5} \\ &= \фракция{1}{4} \end{align*}
Определить угол наклона \начать{выравнивать*} \загар \альфа & = м\\ & = \фракция{1}{4} \\ \поэтому \alpha & = \tan^{-1} \left( \frac{1}{4} \right) \\ &= \текст{14,0}\текст{°} \end{выравнивание*}
Напишите окончательный ответ
\begin{align*} \тета & = \текст{180}\текст{°} + \альфа — \бета\\ & = \text{180}\text{°} + \text{14,0}\text{°} — \text{123,7}\text{°} \\ & = \текст{70,3}\текст{°} \end{align*}
Острый угол между двумя прямыми равен \(\text{70,3}\)\(\text{°}\). {-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
{-1} \left( -\text{2} \right) \\
&= -\текст{63,4}\текст{°} \\
\поэтому \theta &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \тета &= \text{80}\text{°}
\end{выравнивание*} 9{-1} \влево(-\frac{9}{2} \вправо) \\
&= -\текст{77,5}\текст{°} \\
\поэтому \тета &= \text{180}\text{°} — \text{77,5}\text{°} \\
\поэтому \тета &= \текст{102,5}\текст{°}
\end{align*}
линия, проходящая через \((-1;-6)\) и \((-\frac{1}{2};-\frac{11}{2})\)
\begin{выравнивание*} m &= \frac{y_2 -y_1}{x_2 — x_1} \\ &= \frac{-\frac{11}{2}+ 6}{-\frac{1}{2}+1} \\ &= \ гидроразрыва {\ гидроразрыва {1} {2}} {\ гидроразрыва {1} {2}} \\ \поэтому m &= 1 \\ \theta &= \tan^{-1} \left( 1 \right) \\ \поэтому \тета &= \text{45}\text{°} \end{выравнивание*} 9{-1} \влево(-\frac{1}{3} \вправо) \\ \поэтому \тета &= -\текст{18,4}\текст{°} \\ \поэтому \тета &= \text{180}\text{°} — \text{18,4}\text{°} \\ \поэтому \тета &= \текст{161,6}\текст{°} \end{align*}
Градиент undefined
Определить острый угол между линией, проходящей через точки \(A(-2;\frac{1}{5})\)
и \(B(0;1)\) и прямой, проходящей через точки \(C(1;0)\) и \(D(-2;6)\). {-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
{-1} \left(-2 \right) \\
\поэтому \alpha &= -\text{63,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{63,4}\text{°} \\
\поэтому \alpha &= \text{116,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{21,8}\text{°} + (\text{180}\text{°} —
\text{116,6}\text{°} ) \\
&= \текст{85,2}\текст{°}
\конец{выравнивание*}
Определить угол между прямой \(y + x = 3\) и прямой \(x = y + \frac{1}{2}\).
Пусть угол наклона линии \(y + x = 3\) равен \(\alpha\), а угол наклона наклон линии \(x = y + \frac{1}{2}\) равен \(\beta\). Пусть угол между двумя строки будут \(\тета\):
\начать{выравнивать*}
у &= — х + 3 \\
\поэтому m &= — 1 \\
\alpha &= \tan^{-1} \left(-1\right) \\
\поэтому \alpha &= -\text{45}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{45}\text{°} \\
\поэтому \alpha &= \text{135}\text{°} \\
х &= у + \ гидроразрыва {1} {2} \\
х — \фракция{1}{2} &= у \\
\поэтому m &= 1 \\
\beta &= \tan^{-1} \left(1 \right) \\
\поэтому \бета &= \text{45}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. {-1} \left( 2 \right) \\
\поэтому \бета &= \text{63,4}\text{°} \\
m &= \frac{y_2 -y_1}{x_2 — x_1} \\
&= \frac{2 — \frac{7}{3}}{0 + 1} \\
&= \frac{-\frac{1}{3}}{1} \\
\поэтому m &= -\frac{1}{3} \\
\поэтому \alpha &= -\text{18,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{18,4}\text{°} \\
\поэтому \alpha &= \text{161,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{63,4}\text{°} + (\text{180}\text{°} —
\текст{161,6}\текст{°} ) \\
&= \текст{81,8}\текст{°}
\конец{выравнивание*}
{-1} \left( 2 \right) \\
\поэтому \бета &= \text{63,4}\text{°} \\
m &= \frac{y_2 -y_1}{x_2 — x_1} \\
&= \frac{2 — \frac{7}{3}}{0 + 1} \\
&= \frac{-\frac{1}{3}}{1} \\
\поэтому m &= -\frac{1}{3} \\
\поэтому \alpha &= -\text{18,4}\text{°} \\
\поэтому \alpha &= \text{180}\text{°} — \text{18,4}\text{°} \\
\поэтому \alpha &= \text{161,6}\text{°} \\
\text{And } \theta &= \beta + (\text{180}\text{°} — \alpha) \quad (\text{ext. } \angle
\треугольник)\\
\поэтому \theta &= \text{63,4}\text{°} + (\text{180}\text{°} —
\текст{161,6}\текст{°} ) \\
&= \текст{81,8}\текст{°}
\конец{выравнивание*}
Как пользоваться калькулятором угла наклона
Калькулятор угла наклона , также называемый калькулятором угла наклона, можно использовать для определения угла наклона любого наклона, будь то взлетно-посадочная полоса самолета или подвесное произведение искусства. на стене. Калькулятор требует, чтобы вы вводили высоту склона и расстояние от того места, где вы стоите, до его нижней точки, а затем выводит угол между вашим положением и нижней точкой.
на стене. Калькулятор требует, чтобы вы вводили высоту склона и расстояние от того места, где вы стоите, до его нижней точки, а затем выводит угол между вашим положением и нижней точкой.
Что такое тангенс?
Касательная — это линия, которая только касается кривой в одной точке, но не пересекает ее и не пересекает ее. Угол наклона — это угол между касательной и осью x. Вы можете использовать калькулятор угла наклона , чтобы найти этот угол. Чтобы использовать его, вам понадобятся координаты точки, где касательная касается кривой. Обычно они задаются в виде (x, y). Тангенс имеет наклон, который можно найти, разделив y на x. Угол наклона 90 градусов минус угол, образованный этим наклоном с осью x.
Самый простой способ запомнить, как пользоваться калькулятором угла наклона , — запомнить аббревиатуру AOI. Это означает угол наклона, поэтому, если вы не уверены, что это значит, вы можете найти дополнительную информацию об этом в свободное время. Просто убедитесь, что вы всегда можете вычислить углы быстро и точно, когда это необходимо!
Просто убедитесь, что вы всегда можете вычислить углы быстро и точно, когда это необходимо!
Что такое угол наклона?
Угол наклона — это угол между линией и плоскостью или между двумя пересекающимися линиями. Он также известен как угол возвышения или угол депрессии. Вы можете использовать калькулятор угла наклона, чтобы найти угол между двумя линиями или между линией и плоскостью. Если вы используете его для нахождения угла между двумя линиями, вам необходимо знать расстояния от обеих точек на одной линии до другой точки на другой линии. Формула для нахождения этого:
Дифракция света создает радугу, когда солнечный свет падает на капли воды в атмосфере Земли. Радуга всегда появляется с красными снаружи и синими внутри из-за преломления на разных длинах волн каплями воды на разной высоте в атмосфере Земли. Когда мы смотрим на радугу снизу, ее цвета меняются местами, потому что мы видим их через большее количество воздуха, чем если бы мы смотрели на них вверх.
Также проверьте: Таблица преобразования триггеров
Три различных типа касательных
Существует три различных типа касательных, которые можно использовать при расчете калькулятора угла наклона . Первая — это секущая, то есть линия, пересекающая окружность в двух точках. Вторая — хорда, представляющая собой линию, пересекающую окружность в двух точках и проходящую через центр окружности. Третий — касательная, представляющая собой прямую, пересекающую окружность только в одной точке. Один из способов рассчитать угол наклона с помощью касательной — использовать так называемый метод «точка за точкой». При использовании этого метода найдите длину желаемого радиуса (r) с одной стороны и измерьте ее в градусах от заданной начальной точки (P). Затем разделите r на 360°; это даст вам ответ в градусах на градус. Теперь возьмите это число и умножьте его на пи/180°, чтобы преобразовать его в радианы на радиан. Наконец, вычтите pi/2 из вашего окончательного ответа, чтобы получить окончательный ответ для градусов на градус.
Поиск правильного значения тангенса
Калькулятор угла наклона — это инструмент, который позволяет найти правильное значение тангенса заданного угла. Это важно, потому что тангенс используется во многих математических формулах. Чтобы использовать калькулятор, просто введите угол, тангенс которого вы хотите найти, и нажмите «Вычислить». Ответ будет отображаться как в градусах, так и в радианах. Затем вы можете использовать это значение в любой формуле, требующей тангенса. Например, если вы хотите найти площадь треугольника, используя значения синуса и косинуса, ваше уравнение будет выглядеть так: A = sin(x) x cos(x). Просто подставьте соответствующие значения sin(a) и cos(a), чтобы найти x. Ключ к решению этих типов уравнений заключается в нахождении подходящего значения тангенса для каждой части уравнения.
Воспользуйтесь нашим калькулятором угла наклона уже сегодня!
Тангенс — это тригонометрическое отношение, которое говорит вам, насколько конкретная сторона прямого угла наклона калькулятора (или любого треугольника, если уж на то пошло) выше или ниже другой. Например, если у вас есть треугольник 30-60-90, то сторона 1 на 30 градусов выше стороны 2, а сторона 2 на 60 градусов выше стороны 3. Поскольку нахождение различных триггерных соотношений может сбивать с толку (и, честно говоря, не все это полезны в повседневной жизни), существует множество простых способов их вычисления. Вы можете использовать любой онлайн-калькулятор триггеров или просто посмотреть значения триггеров самостоятельно.
Например, если у вас есть треугольник 30-60-90, то сторона 1 на 30 градусов выше стороны 2, а сторона 2 на 60 градусов выше стороны 3. Поскольку нахождение различных триггерных соотношений может сбивать с толку (и, честно говоря, не все это полезны в повседневной жизни), существует множество простых способов их вычисления. Вы можете использовать любой онлайн-калькулятор триггеров или просто посмотреть значения триггеров самостоятельно.
Узнайте о некоторых отличных приложениях для расчета углов наклона
Когда дело доходит до приложений, которые могут вычислять углы наклона, существует несколько различных отличных вариантов. Первый называется Тангенс. Это приложение разработано для устройств Android и iOS, и им довольно просто пользоваться. Просто введите длину одной стороны треугольника и угол, который вы хотите вычислить, а Тангенс сделает все остальное. Еще один отличный вариант — Angle Finder. Это приложение также доступно для устройств Android и iOS, и им так же легко пользоваться, как и Tangent. Просто введите длину одной стороны треугольника и угол, который вы хотите рассчитать, и Angle Finder даст вам ответ. Эти два приложения действительно удобны в использовании, и они делают калькулятор угла наклона проще, чем когда-либо прежде. Если вы ищете что-то более продвинутое или у вас есть устройства Windows Phone или Blackberry, попробуйте Calculus Pro. Все, что вам нужно сделать, это ввести три измерения вашего треугольника, и это приложение сделает всю работу за вас. Вы получите точные расчеты как для остроугольных, так и для тупоугольных треугольников, поэтому он идеально подходит, если вам нужно измерить любой тип угла.
Просто введите длину одной стороны треугольника и угол, который вы хотите рассчитать, и Angle Finder даст вам ответ. Эти два приложения действительно удобны в использовании, и они делают калькулятор угла наклона проще, чем когда-либо прежде. Если вы ищете что-то более продвинутое или у вас есть устройства Windows Phone или Blackberry, попробуйте Calculus Pro. Все, что вам нужно сделать, это ввести три измерения вашего треугольника, и это приложение сделает всю работу за вас. Вы получите точные расчеты как для остроугольных, так и для тупоугольных треугольников, поэтому он идеально подходит, если вам нужно измерить любой тип угла.
Угол наклона линии
Математические слова: Угол наклона линии
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Угол между двумя линиями — Формула, примеры
Угол между двумя линиями помогает узнать взаимосвязь между двумя линиями. Это мера наклона между двумя линиями. Для двух пересекающихся прямых существует два угла между прямыми: острый угол и тупой угол. Здесь мы рассматриваем острый угол между прямыми, для угла между двумя прямыми .
Угол между двумя линиями полезен для нахождения меры угла между двумя сторонами замкнутого многоугольника. Проверим формулы и примеры для угла между двумя прямыми в координатной плоскости и трехмерном пространстве..
| 1. | Как найти угол между двумя линиями? |
| 2. | Формулы для угла между двумя линиями |
| 3. | Угол между двумя линиями в трехмерном пространстве |
4. |
Примеры угла между двумя линиями |
| 5. | Практические вопросы |
| 6. | Часто задаваемые вопросы об угле между двумя линиями |
Как найти угол между двумя линиями?
Угол между двумя линиями можно рассчитать, зная наклон двух линий или зная уравнение двух линий. Угол между двумя линиями обычно дает острый угол между двумя линиями.
Угол между двумя линиями можно вычислить по наклону двух линий и с помощью функции тригонометрического тангенса. Рассмотрим две линии с наклонами \(m_1\) и \(m_2\) соответственно. Острый угол θ между прямыми можно вычислить по формуле функции тангенса. Острый угол между двумя прямыми находится по следующей формуле.
Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\)
Далее, мы можем найти угол между двумя прямыми, если заданы уравнения двух прямых. Пусть уравнения двух линий будут \(l_1 = a_1x + b_1y + c_1 = 0\) и \(l_2 = a_2x + b_2y + c_2 = 0\). Угол между двумя прямыми можно вычислить по тангенсу угла между двумя прямыми.
Угол между двумя прямыми можно вычислить по тангенсу угла между двумя прямыми.
Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\)
Формулы для угла между двумя линиями
Следующие различные формулы помогают легко найти угол между двумя линиями.
- Угол между двумя линиями, одна из которых представляет собой ax + by + c = 0, а другая линия является осью x, равен θ = Tan -1 (-a/b).
- Угол между двумя линиями, одна из которых представляет собой линию y = mx + c, а другая линия является осью x, равен θ = Tan -1 м .
- Угол между двумя прямыми, параллельными друг другу и имеющими одинаковый наклон (\(m_1 = m_2\)) равен 0º. 92}{2bc}\)
Угол между двумя линиями в трехмерном пространстве
Угол между двумя линиями в трехмерном пространстве можно вычислить аналогично углу между двумя линиями в координатной плоскости. Для двух линий с уравнениями \(r = a_1 + λb_1\) и \(r = a_2 + λb_2\) угол между линиями определяется следующей формулой.
Cosθ = \(\dfrac{b_1.b_2}{|b_1|.|b_2|}\)
Далее для двух линий, имеющих отношение направлений как \((a_1, b_1, c_1)\), и \( (a_2, b_2, c_2)\), угол между линиями можно вычислить по приведенной ниже формуле. 92}}\)
Также для двух прямых, имеющих направляющие косинусы \(l_1, m_1, n_1\) и \(l_2, m_2, n_2\), угол между двумя прямыми можно вычислить по следующей формуле .
Cosθ = \(|l_1.l_2 + m_1.m_2 + n_1.n_2|\)
Связанные темы
Следующие темы помогут лучше понять понятие угла между двумя линиями.
- Координатная геометрия
- Уравнение прямой
- Параллельные линии
- Типы углов
Примеры угла между двумя линиями
-
Пример 1: Найдите угол между двумя линиями, имеющими наклон 1 и 1/2 соответственно.
Решение:
Наклоны двух прямых равны \(m_1\) = 1 и \(m_2\) = 1/2.
Формула для нахождения угла между двумя линиями: Tanθ = \(\frac{m_1 — m_2}{1 + m_1.
 m_2}\).
m_2}\). Tanθ = \(\frac{1 — 1/2}{1 + 1/2.1}\) 9{-1} \frac{1}{3}\).
-
Пример 2: Найдите угол между двумя прямыми, используя уравнения 3x + 4y — 10 = 0 и 4x -5y + 2 = 0. + 4y — 10 = 0 и 4x -5y + 2 = 0.
Здесь мы имеем \(a_1 = 3, b_1 = 4, a_2 = 4, b_2 = -5\)
Угол между двумя линиями может рассчитать по формуле Tanθ =\(\dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\). 9{-1}-\frac{31}{8}\).
перейти к слайдуперейти к слайду
Есть вопросы по основным математическим понятиям?
Станьте чемпионом по решению проблем, используя логику, а не правила. Узнайте, почему стоит математика, с нашими сертифицированными экспертами
Запишитесь на бесплатный пробный урок
Практические вопросы по углу между двумя линиями
перейти к слайдуперейти к слайду
Часто задаваемые вопросы об угле между двумя линиями
Как найти угол между двумя линиями?
Угол между двумя линиями можно рассчитать по наклону линий или по уравнению двух линий. Самая простая формула для нахождения угла между двумя линиями — это наклон двух линий. Угол между двумя линиями с наклоном \(m_1\) и \(m_2\) соответственно равен Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\).
Самая простая формула для нахождения угла между двумя линиями — это наклон двух линий. Угол между двумя линиями с наклоном \(m_1\) и \(m_2\) соответственно равен Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\).
По какой формуле найти угол между двумя прямыми?
Это две важные формулы для нахождения угла между двумя линиями в координатной плоскости. Для двух линий, имеющих наклоны \(m_1\) и \(m_2\) соответственно, угол между двумя линиями равен Tanθ = \(\dfrac{m_1 — m_2}{1 + m_1.m_2}\). И вторая формула для нахождения угла между двумя линиями, имеющими уравнения \(l_1 = a_1x + b_1y + c_1 = 0\) и \(l_2 = a_2x + b_2y + c_2 = 0\), это Tanθ =\(\ dfrac{a_2b_1 — a_1b_2}{a_1a_2 + b_1b_2}\).
Как найти угол между двумя линиями в трехмерной геометрии?
Угол между двумя линиями в трехмерной геометрии, имеющей уравнения линий \(r = a_1 + λb_1\) и \(r = a_2 + λb_2\), равен Cosθ = \(\dfrac{b_1. b_2}{|b_1|.|b_2|}\).
Угол наклона при наличии компонента напряжения сдвига
| ✖Напряжение сдвига — это сила, стремящаяся вызвать деформацию материала путем проскальзывания вдоль плоскости или плоскостей, параллельных приложенному напряжению. | Дина на квадратный сантиметрГигапаскальКилограмм-сила на квадратный сантиметрКилограмм-сила на квадратный дюймКилограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный сантиметрКилоньютон на квадратный метрКилоньютон на квадратный миллиметрКилопаскальМегапаскальНьютон на квадратный сантиметрНьютон на квадратный метрНьютон на квадратный миллиметрПаскальФунт-сила на единицу площади на квадратный дюйм | +10% -10% | |
| ✖Вертикальное напряжение в точке – это напряжение, действующее перпендикулярно поверхности.ⓘ Вертикальное напряжение в точке [σ z ] | Атмосфера Техническая на квадратный сантиметрЭксапаскальФемтопаскальФутовая вода (15°C)Футовая вода (4°C)Футовая вода (60°F)ГигапаскальГрамм-сила на кв. СантиметрГектопаскальДюйм ртутного столба (32°F)Дюйм ртутного столба (60°F)Дюйм водяного столба (4°C)Дюйм водяного столба (60°F)Килограмм-сила на квадратный сантиметрКилограмм-сила на квадратный метрКилограмм-сила на квадратный миллиметрКилоньютон на квадратный метрКилопаскальКилофунт на квадратный дюймKip -сила на квадратный дюйммегапаскальметр морской водыметр воды (4°C)микробармикропаскальмиллибармиллиметр ртутного столба (0°C)миллиметр воды (4°C)миллипаскальнанопаскальньютон на квадратный сантиметрньютон на квадратный метрньютон на квадратный миллиметрпаскальпетапаскальпикопаскальпьезфунт на квадратный дюймфунт на квадратный футфунт на квадратный футфунт на квадратный футфунт-сила на квадрат Фут-фунт-сила на квадратный дюймФунт-фунт на квадратный футСтандартная атмосфераТерапаскальТон-сила (длинная) на кв. | +10% -10% |
|
✖Угол наклона к горизонтальной поверхности.ⓘ Угол наклона при наличии компонента напряжения сдвига [i] |
кругциклградусгонградадмиллирадианминутугловые минутыточкаквадрантчетвертькруградианреволюцияпрямой уголсекундаполукругсекстантазнакповорот |
⎘ Копировать |
👎
Формула
Перезагрузить
👍
Угол наклона при наличии компонента напряжения сдвига Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Напряжение сдвига: 50 Па —> 50 Па Преобразование не требуется
Вертикальное напряжение в точке: 10 Мегапаскаль —> 10000000 Паскаль (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу измерения
5. 00000000002083E-06 Радиан —> 0.000286478897566027 9000
00000000002083E-06 Радиан —> 0.000286478897566027 9000
< 8 Калькуляторы компонентов напряжения сдвига
Угол наклона при заданной составляющей касательного напряжения Формула
Угол наклона = asin(напряжение сдвига/вертикальное напряжение в точке)
я = asin(𝜏/σ z )
Что такое угол наклона?
Угол наклона линии — это угол, образованный пересечением линии и оси x. Используя горизонтальный «прогон» 1 и м для наклона, угол наклона, тета = тангенс-1 (м) или м = тангенс (тета).
Как рассчитать угол наклона, если указан компонент напряжения сдвига?
Угол наклона при наличии компонента напряжения сдвига Калькулятор использует Угол наклона = asin(напряжение сдвига/вертикальное напряжение в точке) для расчета угла наклона. Угол наклона при наличии компонента напряжения сдвига вычисляет значение угла наклона, когда у нас есть предварительная информация о других используемых параметрах. Угол наклона обозначается цифрой 9Символ 0594 и .
Угол наклона при наличии компонента напряжения сдвига вычисляет значение угла наклона, когда у нас есть предварительная информация о других используемых параметрах. Угол наклона обозначается цифрой 9Символ 0594 и .
Как рассчитать угол наклона при наличии компонента напряжения сдвига с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для угла наклона при наличии компонента напряжения сдвига, введите напряжение сдвига (𝜏) и вертикальное напряжение в точке (σ z ) и нажмите кнопку расчета. Вот как можно объяснить расчет угла наклона при расчете компонента напряжения сдвига с заданными входными значениями -> 0,000286 = asin(50/10000000) .
Часто задаваемые вопросы
Что такое угол наклона, если предоставляется компонент напряжения сдвига?
Угол наклона при наличии компонента напряжения сдвига вычисляет значение угла наклона, когда у нас есть предварительная информация о других используемых параметрах, и представляется как i = asin(𝜏/σ z ) или Угол наклона = asin(напряжение сдвига/вертикальное напряжение в точке) . Напряжение сдвига — это сила, стремящаяся вызвать деформацию материала путем проскальзывания вдоль плоскости или плоскостей, параллельных приложенному напряжению, а вертикальное напряжение в точке — это напряжение, действующее перпендикулярно поверхности.
Напряжение сдвига — это сила, стремящаяся вызвать деформацию материала путем проскальзывания вдоль плоскости или плоскостей, параллельных приложенному напряжению, а вертикальное напряжение в точке — это напряжение, действующее перпендикулярно поверхности.
Как рассчитать угол наклона при наличии компонента напряжения сдвига?
Угол наклона при предоставлении компонента напряжения сдвига вычисляет значение угла наклона, когда у нас есть предварительная информация о других используемых параметрах, рассчитывается с использованием Угол наклона = asin(Напряжение сдвига/Вертикальное напряжение в точке) . Чтобы рассчитать угол наклона при наличии компонента напряжения сдвига, вам потребуется напряжение сдвига (𝜏) и вертикальное напряжение в точке (σ z ) . С помощью нашего инструмента вам нужно ввести соответствующее значение напряжения сдвига и вертикального напряжения в точке и нажать кнопку расчета. Вы также можете выбрать единицы измерения (если есть) для ввода (ов) и вывода.
Доля
Скопировано!
4,5 Наклон | NWCG
Уклон относится к углу или уклону склона. Наклон может быть восходящим или нисходящим. Уклон обычно выражается в процентах и соответствует величине подъема или вертикальному расстоянию, деленному на пробег или горизонтальное расстояние. Процентное значение на 100. Наклон также может быть выражен как угол, который дает величину отклонения от плоскости в виде числа градусов. Преобразование между процентом уклона и углом наклона можно выполнить с помощью научного калькулятора и функции арктангенса (арктангенса). По сути, угол наклона представляет собой арктангенс процента наклона (с процентом наклона, выраженным в десятичной дроби).
Пример 1 — Процент уклона составляет 60 процентов. Какой угол наклона?
Шаг 1. Измените 60 процентов на десятичную форму. Шестьдесят процентов означает 60 из 100. Можно записать 60/100 = 0,60. См. главу 1.
См. главу 1.
Угол наклона = обратный тангенс угла наклона в процентах (в десятичном выражении)
Угол наклона = обратный тангенс угла наклона 0,60
Шаг 2. Введите 0,6 в калькулятор и нажмите кнопку обратного, обратного или «второго» , затем кнопку загара, чтобы получить арктангенс. Калькулятор покажет угол наклона.
Уклон 60% соответствует углу наклона 31°.
ИЗМЕРЕНИЕ ПРОЦЕНТА УКЛОНА
Процент уклона можно измерить с помощью клинометра или измерителя уклона или путем деления подъема на прогон, как описано в этом мультимедийном руководстве. Нажмите на изображение ниже, чтобы просмотреть урок, который включает аудио.
Нажмите на рисунок выше, чтобы просмотреть руководство по измерению уклона.
Если у вас есть клинометр или другое цифровое устройство для измерения уклона в полевых условиях, наведите клинометр, как описано ниже:
1. Откройте оба глаза, чтобы увидеть объект и прочесть шкалу.
2. Проверьте, какая шкала считывается. В видоискателе есть две шкалы: процентная шкала наклона на правом поле и шкала угла наклона на левом поле. Вертикальный угол в градусах.
3. Наведите клинометр с уровня глаз на объект или на удаленную точку, которая также находится примерно на уровне глаз.
4. Прочтите показания весов в процентах или градусах наклона.
Обратите внимание, что на неровной местности клинометр следует размещать на шесте на уровне глаз и считывать показания до удаленной точки на другом шесте той же высоты, чтобы получить более точные показания.
Пример 2. Используйте измерения подъема и пробега, показанные на рисунке ниже, для оценки процента уклона.
Процент уклона = (8 футов / 40 футов) × 100 = 0,20 × 100 = 20%
Процент уклона составляет 20 процентов.
РАСЧЕТ ГОРИЗОНТАЛЬНОГО РАССТОЯНИЯ
Если наклон и вертикальное расстояние (подъем) известны, то можно рассчитать горизонтальное расстояние (пробег). Уравнение процента наклона можно изменить, чтобы получить уравнение для горизонтального расстояния.
Уравнение процента наклона можно изменить, чтобы получить уравнение для горизонтального расстояния.
Наклон в процентах = (подъем/пробег) × 100
Переставьте члены уравнения: умножьте обе части на прогон.
пробег × уклон % = подъем/пробег × 100 × пробег
Разделите обе стороны на процент уклона.
(угол × уклон %) / (уклон %) = (подъем × 100) / (уклон %)
пробег = (подъем × 100) / уклон % — это мера горизонтального расстояния.
Пример 3. Холм имеет уклон 8 процентов. Высота холма 15 футов. Что такое горизонтальное расстояние?
горизонтальное расстояние = пробег = (подъем × 100) / наклон %
Шаг 1. Введите заданные значения в уравнение.
Шаг 2. Решить.
пробег = ((15 футов × 100) / 8) = (1500 футов / 8) = 188 футов
Холм имеет горизонтальное расстояние 188 футов.
РАСЧЕТ НАКЛОННОГО РАССТОЯНИЯ
Наклонное расстояние (h) — это длина склона от нижней до вершины склона, которая больше, чем вертикальное и горизонтальное расстояние.
Наклонное расстояние можно рассчитать, если известны вертикальная высота (подъем) и горизонтальное расстояние (пробег) прямого угла. Существует прямой угол, если вертикальное и горизонтальное расстояния «истинны» по отношению к вертикали и горизонтали соответственно. См. следующий рисунок, на котором x обозначен как бег, а y — подъем. Чтобы рассчитать наклонное расстояние, вам понадобится простой научный калькулятор с функцией извлечения квадратного корня (√z).
Пример 4 — Найдите наклонное расстояние для вертикального и горизонтального расстояний, показанных на рисунке ниже.
Шаг 1. Используйте уравнение h = √ (x 2 + y 2 )
Расстояние наклона =
√ [(горизонтальное расстояние) 2 + (версическое расстояние) 8 2 2 + (версическое расстояние) 8 2 2 + (версическое расстояние) 8 2 2 + (версическое расстояние) 8888888888888888888888 гг.

 Углы депрессии или склонения — это углы ниже горизонтали, как если бы вы смотрели из окна вниз на основание здание на соседнем участке. Всякий раз, когда у вас есть один из этих углов, вы следует сразу начать представлять, как прямоугольный треугольник впишется в описание.
Углы депрессии или склонения — это углы ниже горизонтали, как если бы вы смотрели из окна вниз на основание здание на соседнем участке. Всякий раз, когда у вас есть один из этих углов, вы следует сразу начать представлять, как прямоугольный треугольник впишется в описание.  Я использую рисование как способ отслеживать информацию; конкретный размер не имеет значения.
Я использую рисование как способ отслеживать информацию; конкретный размер не имеет значения. 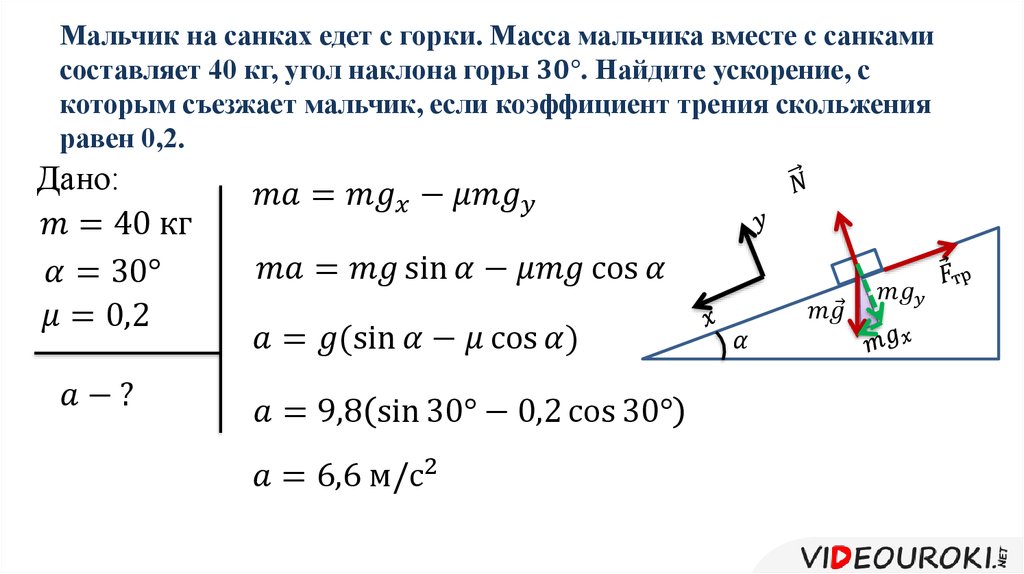 Так Я буду использовать эту часть рисунка.
Так Я буду использовать эту часть рисунка.  (Представьте, что D перемещается вправо, чтобы встретить продолжение AB, образуя прямоугольный треугольник.) Для этого вычисления я буду использовать высоту холма.
(Представьте, что D перемещается вправо, чтобы встретить продолжение AB, образуя прямоугольный треугольник.) Для этого вычисления я буду использовать высоту холма.  «Углы наклона и склонения». Purplemath . Доступна с
«Углы наклона и склонения». Purplemath . Доступна с 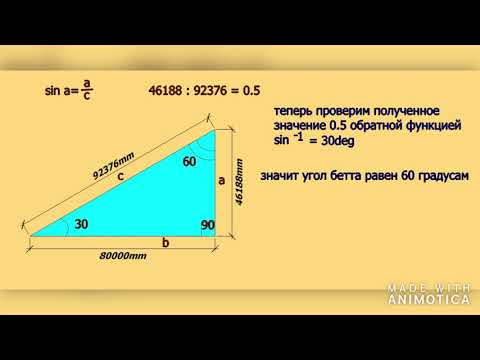 ..
..