Таблица расчета мощности: Расчет мощности по току и напряжению

Таблица расчета мощности гидростанции — НПП «ГидроКуб»

Р(бар)	N(кВт)	N(кВт) Двигатели
		0,12	0,18	0,25	0,37	0,55	0,75	1,1	1,5	2,2	3	4	5,5	7,5	11	15	18,5	22	30	37	45
		Q(л/мин)
10	Q(л-мин)	6,12	9,18	12,75	18,87	28,05	38,25	56,1	76,5	112,2	153	204	280,5	382,5	561	765	943,5	1122	1530	1887	2295
50	Q(л-мин)	1,22	1,84	2,55	3,77	5,61	7,65	11,22	15,3	22,44	30,6	40,8	56,1	76,5	112,2	153	188,7	224,4	306	377,4	459
100	Q(л-мин)	0,61	0,92	1,28	1,89	2,81	3,83	5,61	7,65	11,22	15,3	20,4	28,05	38,25	56,1	76,5	94,35	112,2	153	188,7	229,5
150	Q(л-мин)	0,41	0,61	0,85	1,26	1,87	2,55	3,74	5,1	7,48	10,2	13,6	18,7	25,5	37,4	51	62,9	74,8	102	125,8	153
200	Q(л-мин)	0,31	0,46	0,64	0,94	1,4	1,91	2,81	3,83	5,61	7,65	10,2	14,03	19,13	28,05	38,25	47,18	56,1	76,5	94,35	114,75
250	Q(л-мин)	0,24	0,37	0,51	0,75	1,12	1,53	2,24	3,06	4,49	6,12	8,16	11,22	15,3	22,44	30,6	37,74	44,88	61,2	75,48	91,8
300	Q(л-мин)	0,2	0,31	0,43	0,63	0,94	1,28	1,87	2,55	3,74	5,1	6,8	9,35	12,75	18,7	25,5	31,45	37,4	51	62,9	76,5
350	Q(л-мин)	0,17	0,26	0,36	0,54	0,8	1,09	1,6	2,19	3,21	4,37	5,83	8,01	10,93	16,03	21,86	26,96	32,06	43,71	53,91	65,57
700	Q(л-мин)	0,09	0,13	0,18	0,27	0,4	0,55	0,8	1,09	1,6	2,19	2,91	4,01	5,46	8,01	10,93	13,48	16,03	21,86	26,96	32,79

Калькулятор расчета мощности конвектора по площади помещения

Калькулятор Расчет мощности конвекторов по площади Расчет мощности конвекторов по объему

Подобрать конвектор по параметрам

Расчет мощности конвектора: полезные таблицы и формулы

При проектировании системы отопления в квартире или доме важно определить необходимую мощность теплового оборудования. Для этого нужно знать площадь помещения, высоту потолков, количество внешних стен и окон для применения повышающего коэффициента. Если высота потолков в доме – около 2,7 м, вы легко произведете расчет мощности конвекторов по площади. Согласно нормам СНиП 41-01-2003, 1 кВт тепловой энергии достаточно для обогрева 10 кв. м помещения.

Как рассчитать мощность конвекторов по площади?

В соответствии со строительными нормами номинальная мощность конвектора для комнаты 25 кв. м составит:

(25 кв. м : 10 кв. м) * 1 кВт = 2,5 кВт

или

25 кв. м * 0,1 кВт = 2,5 кВт

Полученный результат приведен без учета особенностей помещения. Для повышения точности вычислений учтите следующие факторы:

• расположение конвектора под окном снижает теплоотдачу, поэтому для компенсации тепловых потерь выбирайте оборудование на 5 – 10 % мощнее;
• если окна занимают большую площадь стены (панорамные, французские), а также выходят на север и северо-восток, при расчетах увеличьте результат на 15 %;
• угловое расположение помещения требует увеличения мощности на 20 %, а при наличии в такой комнате 2 окон полученный результат повышают на 30 %.

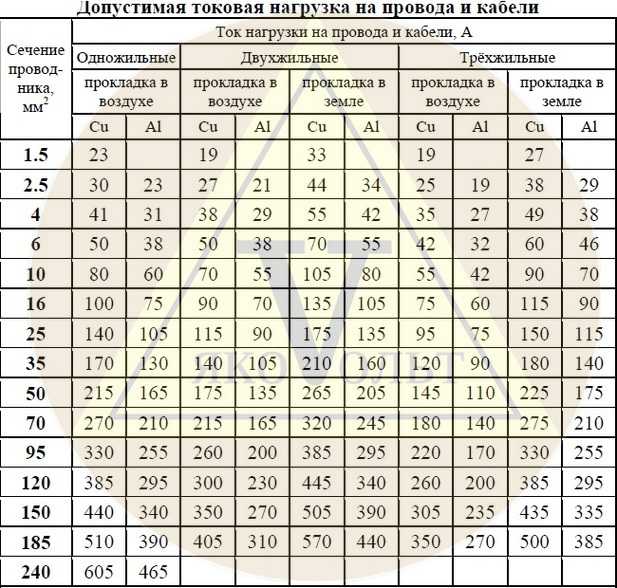
Сделать расчеты наиболее точными вам поможет таблица повышающих коэффициентов:

Особенность помещения	Коэффициент
Отсутствие утепления стен	1,1
Установка конвектора под окном	1,05
Монтаж конвектора в угловом помещении с 1 окном	1,2
Монтаж конвектора в угловом помещении с 2 окнами	1,3
Наличие однослойных стеклопакетов	0,9
Высота потолков от 2,8 до 3 м	1,05

Произведем расчет мощности электрического конвектора отопления для угловой комнаты с двумя внешними стенами и площадью 18 кв. м:

(18 кв. м * 0,1 кВт) * 1,2 = 2,16 кВт

В некоторых регионах при расчете учитывают климатические особенности, но в средней полосе России погодный коэффициент равен 1,0.

Расчет мощности конвектора по объему помещения

Согласно положениям СП 60.13330.2012, для обогрева помещений с очень высокими и низкими потолками необходимо 41 Вт на 1 куб. м объема. Зная длину, ширину комнаты и высоту потолка, вы сможете рассчитать мощность отопления на калькуляторе по формуле:

abc * 0,041 кВт,

где abc – формула расчета объема;

0,041 кВт – норматив тепловой энергии.

Рассчитаем мощность конвектора для комнаты 3х4 м с потолками 2 м:

(3*4*2) * 0,041 = 0,984 кВт

Для обогрева такой комнаты потребуется конвектор мощностью 1 кВт (без учета повышающих коэффициентов).

Введение в оценку мощности и размера выборки

• план исследования
• размер выборки
• статистика

ЦЕЛИ

1. Понимание оценки мощности и размера выборки.

2. Поймите, почему мощность является важной частью как дизайна исследования, так и анализа.

3. Понимать различия между расчетами размера выборки в сравнительных и диагностических исследованиях.

4. Узнайте, как выполнить расчет объема выборки.

   • – (а) Для непрерывных данных

   • – (b) Для прерывистых данных

   • – (в) Для диагностических тестов

ОЦЕНКА МОЩНОСТИ И РАЗМЕРА ВЫБОРКИ

Оценка мощности и размера выборки является мерой того, сколько пациентов необходимо для исследования. Почти все клинические исследования подразумевают изучение выборки пациентов с определенной характеристикой, а не всей популяции. Затем мы используем эту выборку, чтобы сделать выводы обо всей совокупности.

В предыдущих статьях из серии статей о статистике, опубликованных в этом журнале, статистический вывод использовался для определения того, верны ли найденные результаты или, возможно, они обусловлены только случайностью. Ясно, что мы можем уменьшить вероятность того, что наши результаты будут случайными, устранив предвзятость в дизайне исследования с помощью таких методов, как рандомизация, ослепление и т. д. Однако на вероятность того, что наши результаты могут быть неверными, влияет еще один фактор — количество обследованных пациентов. Интуитивно мы предполагаем, что чем больше доля всего изучаемого населения, тем ближе мы подойдем к истинному ответу для этого населения. Но сколько нам нужно изучить, чтобы подобраться как можно ближе к правильному ответу?

ЧТО ТАКОЕ МОЩНОСТЬ И ПОЧЕМУ ОНА ВАЖНА

Оценки мощности и размера выборки используются исследователями для определения количества субъектов, необходимых для ответа на исследовательский вопрос (или нулевой гипотезы).

Примером может служить случай тромболизиса при остром инфаркте миокарда (ОИМ). В течение многих лет клиницисты считали, что это лечение принесет пользу, учитывая предполагаемую этиологию ОИМ, однако последовательные исследования не смогли доказать это. Лишь после завершения достаточно мощных «мега-испытаний» была доказана небольшая, но важная польза от тромболизиса.

Как правило, в этих исследованиях тромболизис сравнивали с плацебо, и часто в качестве первичного критерия исхода использовали смертность через определенное количество дней. Основная гипотеза исследований могла заключаться в сравнении, например, смертности на 21-й день тромболизиса по сравнению с плацебо. Тогда есть две гипотезы, которые нам нужно рассмотреть:

1. Нулевая гипотеза состоит в том, что нет никакой разницы между методами лечения с точки зрения смертности.

2. Альтернативная гипотеза заключается в том, что существует разница между методами лечения с точки зрения смертности.

Пытаясь определить, являются ли две группы одинаковыми (принимая нулевую гипотезу) или они различаются (принимая альтернативную гипотезу), мы потенциально можем совершить два вида ошибок. Они называются ошибкой первого рода и ошибкой второго рода.

Говорят, что ошибка I рода возникает, когда мы неправильно отвергаем нулевую гипотезу (то есть, она верна и между двумя группами нет различий) и сообщаем о различиях между двумя изучаемыми группами.

Говорят, что ошибка типа II возникает, когда мы неправильно принимаем нулевую гипотезу (то есть она ложна и существует различие между двумя группами, которая является альтернативной гипотезой) и сообщаем, что между двумя группами нет различий .

Их можно представить в виде таблицы два на два (таблица 1).

Таблица 1

Таблица «два на два»

Расчет мощности говорит нам, сколько пациентов требуется, чтобы избежать ошибки типа I или типа II.

Термин «мощность» обычно используется в отношении всех оценок размера выборки в исследованиях. Строго говоря, «мощность» означает количество пациентов, необходимое для того, чтобы избежать ошибки II типа в сравнительном исследовании. Оценка размера выборки — это более широкий термин, который рассматривает не только ошибку типа II и применим ко всем типам исследований. В просторечии эти термины используются взаимозаменяемо.

ЧТО ВЛИЯЕТ НА СИЛУ ИССЛЕДОВАНИЯ?

Существует несколько факторов, которые могут повлиять на эффективность исследования. Их следует учитывать на ранних этапах разработки исследования. Некоторые факторы мы можем контролировать, другие нет.

Точность и дисперсия измерений в любой выборке

Почему исследование может не обнаружить различий, если они действительно есть? Для любого заданного результата выборки пациентов мы можем только определить распределение вероятностей вокруг этого значения, которое подскажет, где находится истинное значение популяции. Наиболее известным примером этого являются 95% доверительные интервалы. Размер доверительного интервала обратно пропорционален количеству исследуемых субъектов. Таким образом, чем больше людей мы изучаем, тем точнее мы можем определить, где находится истинная ценность населения.

На рис. 1 показано, что для одного измерения чем больше изучаемых субъектов, тем уже становится распределение вероятностей. В группе 1 среднее значение равно 5 с широкими доверительными интервалами (3–7). При удвоении числа обследованных пациентов (но в нашем примере значения остались прежними) доверительные интервалы сузились (3,5–6,5), что дает более точную оценку истинного среднего значения для популяции.

Рисунок 1

Изменение ширины доверительного интервала с увеличением числа субъектов.

Распределение вероятности того, где находится истинное значение, является неотъемлемой частью большинства статистических тестов для сравнений между группами (например, тесты t ). Исследование с небольшим размером выборки будет иметь большие доверительные интервалы и будет отображаться как статистически ненормальное только в том случае, если между двумя группами существует большая разница. Рисунок 2 демонстрирует, как увеличение числа субъектов может дать более точную оценку различий.

Рисунок 2

Эффект уменьшения доверительного интервала для демонстрации истинной разницы в средних значениях. Этот пример показывает, что первоначальное сравнение между группами 1 и 3 не показало статистической разницы, поскольку доверительные интервалы перекрывались. В группах 3 и 4 число больных удваивается (хотя среднее значение остается прежним). Мы видим, что доверительные интервалы больше не перекрываются, что указывает на то, что разница в средних значениях вряд ли возникла случайно.

Величина клинически значимой разницы

Если мы пытаемся выявить очень небольшие различия между методами лечения, требуются очень точные оценки истинного значения популяции. Это связано с тем, что нам нужно очень точно найти истинное значение популяции для каждой группы лечения. И наоборот, если мы находим или ищем большое различие, может быть приемлемым довольно широкое распределение вероятностей.

Другими словами, если мы ищем большую разницу между методами лечения, мы могли бы принять широкое распределение вероятности, если мы хотим обнаружить небольшую разницу, нам потребуется большая точность и небольшое распределение вероятности. Поскольку ширина распределения вероятностей в значительной степени определяется тем, сколько субъектов мы изучаем, ясно, что искомая разница влияет на расчеты размера выборки.

Факторы, влияющие на расчет мощности

• Прецизионность и дисперсия измерений в любом образце

• Величина клинически значимой разницы

• Насколько уверены мы, чтобы избежать ошибки 1-го типа

• Тип статистического теста, который мы проводим

При сравнении двух или более образцов мы обычно мало контролируем размер эффекта. Тем не менее, мы должны убедиться, что разница стоит обнаружения. Например, можно разработать исследование, которое продемонстрирует сокращение времени начала местной анестезии с 60 до 59 секунд, но такая небольшая разница не будет иметь клинического значения. И наоборот, исследование, демонстрирующее разницу от 60 секунд до 10 минут, явно будет. Указание того, что является «клинически важным отличием», является ключевым компонентом расчета размера выборки.

Насколько важна ошибка типа I или типа II для рассматриваемого исследования?

Мы можем указать, насколько мы были бы обеспокоены тем, чтобы избежать ошибки типа I или типа II. Говорят, что ошибка первого рода возникает, когда мы неправильно отвергаем нулевую гипотезу. Обычно мы выбираем вероятность <0,05 для ошибки I рода. Это означает, что если мы найдем положительный результат, шансы найти это (или большую разницу) будут менее чем в 5% случаев. Этот показатель, или уровень значимости, обозначается как pα и обычно предварительно устанавливается нами на ранней стадии планирования исследования при расчете размера выборки. По соглашению, а не по дизайну, мы чаще всего выбираем 0,05. Чем ниже уровень значимости, тем ниже мощность, поэтому использование 0,01 соответственно уменьшит нашу мощность.

(Чтобы избежать ошибки типа I, т. е. если мы найдем положительный результат, шансы найти это или большую разницу будут иметь место менее чем в α% случаев)

Говорят, что происходит ошибка типа II когда мы неверно принимаем нулевую гипотезу и сообщаем, что между двумя группами нет разницы. Если действительно есть разница между вмешательствами, мы выражаем вероятность получения ошибки второго рода и вероятность того, что мы ее обнаружим. Эта цифра обозначается как pβ. В отношении допустимого уровня pβ существует меньше условностей, но цифры 0,8–0,9являются общими (то есть, если разница между вмешательствами действительно существует, мы обнаружим ее в 80–90% случаев). Мощность исследования, pβ, представляет собой вероятность того, что исследование обнаружит заданную разницу в измерениях между двумя группами, если она действительно существует, при заданном значении pα и размере выборки, N.

Тип статистического теста, который мы выполняем

Расчеты размера выборки показывают, как статистические тесты, использованные в исследовании, могут работать. Поэтому неудивительно, что тип используемого теста влияет на то, как рассчитывается размер выборки. Например, параметрические тесты лучше находят различия между группами, чем непараметрические тесты (именно поэтому мы часто пытаемся преобразовать базовые данные в нормальные распределения). Следовательно, для анализа, основанного на непараметрическом тесте (например, U Манна-Уитни), потребуется больше пациентов, чем для анализа, основанного на параметрическом тесте (например, 9 баллов Стьюдента).0103 т тест).

СЛЕДУЕТ ЛИ РАСЧЕТ ОБЪЕМА ВЫБОРКИ ДО ИЛИ ПОСЛЕ ИССЛЕДОВАНИЯ?

Ответ определенно до, иногда во время, а иногда и после.

При разработке исследования мы хотим убедиться, что проделанная нами работа стоит того, чтобы мы получили правильный ответ и получили его наиболее эффективным способом. Это делается для того, чтобы мы могли набрать достаточное количество пациентов, чтобы придать нашим результатам адекватную силу, но не слишком много, чтобы тратить время на получение большего количества данных, чем нам нужно. К сожалению, при разработке исследования нам, возможно, придется сделать предположения о желаемом размере эффекта и дисперсии данных.

Промежуточные расчеты мощности иногда используются, когда известно, что данные, использованные в первоначальном расчете, сомнительны. Их следует использовать с осторожностью, поскольку повторный анализ может привести к тому, что исследователь прекратит исследование, как только будет получена статистическая значимость (что может произойти случайно несколько раз во время набора участников). После начала исследования анализ промежуточных результатов может быть использован для выполнения дальнейших расчетов мощности и соответствующих корректировок размера выборки. Это может быть сделано, чтобы избежать преждевременного прекращения исследования или, в случае спасения жизни или опасных методов лечения, чтобы избежать продления исследования. Расчеты промежуточного размера выборки следует использовать только в том случае, если это указано в методе априорного исследования.

Когда мы оцениваем результаты испытаний с отрицательными результатами, особенно важно задаться вопросом о размере выборки исследования. Вполне может быть, что исследование было недостаточно мощным и что мы неправильно приняли нулевую гипотезу, что является ошибкой второго рода. Если бы в исследовании участвовало больше субъектов, то разница вполне могла бы быть обнаружена. В идеальном мире этого никогда не должно происходить, потому что расчет размера выборки должен появляться в разделе методов всех статей, реальность показывает нам, что это не так. Как потребители исследований, мы должны иметь возможность оценить силу исследования на основании полученных результатов.

Ретроспективный расчет размера выборки не рассматривается в этой статье. Несколько калькуляторов для ретроспективного размера выборки доступны в Интернете (калькуляторы мощности UCLA (http://calculators. stat.ucla.edu/powercalc/), интерактивные статистические страницы (http://www.statistics.com/content/javastat. html). для обоснования расчетов (хотя это можно решить, проведя предварительное исследование и используя полученные данные)9.0015

Ясно, что расчет размера выборки является ключевым компонентом клинических испытаний, поскольку в большинстве этих исследований упор делается на выявление величины различий между методами лечения. Все клинические испытания должны иметь оценку размера выборки.

В исследованиях других типов необходимо проводить оценку размера выборки, чтобы повысить точность наших окончательных результатов. Например, основными показателями результатов для многих диагностических исследований будут чувствительность и специфичность конкретного теста, обычно сообщаемые с доверительными интервалами для этих значений. Как и в случае со сравнительными исследованиями, чем больше изучаемых пациентов, тем больше вероятность того, что результаты выборки будут отражать истинную ценность популяции. Выполняя расчет размера выборки для диагностического исследования, мы можем указать точность, с которой мы хотели бы сообщить доверительные интервалы для чувствительности и специфичности.

Поскольку клинические испытания и диагностические исследования, вероятно, составляют основу исследовательской работы в области медицины неотложных состояний, мы сосредоточились на них в этой статье.

МОЩНОСТЬ СРАВНИТЕЛЬНЫХ ИСПЫТАНИЙ

Исследования, сообщающие непрерывные данные с нормальным распределением

Предположим, что Эгберт Эверард стал участником клинического исследования с участием пациентов с гипертонией. Новый антигипертензивный препарат Jabba Juice сравнивали с бендрофлуазидом в качестве нового препарата первой линии для лечения гипертонии (таблица 2).

Таблица 2

Эгберт записывает некоторые вещи, которые, по его мнению, важны для расчетов

Как видите, значения pα и pβ несколько типичны. Обычно они устанавливаются по соглашению, а не меняются от одного исследования к другому, хотя, как мы увидим ниже, они могут меняться.

Ключевым требованием является «клинически важное различие», которое мы хотим обнаружить между группами лечения. Как обсуждалось выше, это различие должно быть клинически важным, поскольку, если оно очень мало, о нем, возможно, не стоит знать.

Еще одна цифра, которую нам необходимо знать, — это стандартное отклонение переменной в исследуемой популяции. Измерения артериального давления представляют собой форму нормально распределенных непрерывных данных и, как таковые, будут иметь стандартное отклонение, которое Эгберт обнаружил в других исследованиях, посвященных аналогичным группам людей.

Как только мы узнаем эти две последние цифры, мы можем вычислить стандартизированную разницу, а затем использовать таблицу, чтобы получить представление о необходимом количестве пациентов.

Разница между средними значениями является клинически важной разницей, т. е. представляет собой разницу между средним артериальным давлением в группе бендрофлуазида и средним артериальным давлением в группе нового лечения.

Из записей Эгберта:

Используя таблицу 3, мы видим, что при стандартизированной разнице 0,5 и уровне мощности (pβ) 0,8 необходимое количество пациентов составляет 64. Эта таблица предназначена для односторонней гипотезы, (?) Нулевая гипотеза требует исследования чтобы быть достаточно мощным, чтобы обнаружить, что одно лечение лучше или хуже другого, поэтому нам потребуется как минимум 64 × 2 = 128 пациентов. Это делается для того, чтобы мы получали пациентов, попадающих в обе стороны от средней разницы, которую мы установили. 9Таблица 3 Номограмма для расчета объема выборки.

Исходя из этого, мы можем использовать линейку, чтобы соединить стандартизированную разность с мощностью, необходимой для исследования. Там, где край пересекает среднюю переменную, указывается требуемое число N.

Номограмму также можно использовать для расчета мощности для сравнения двусторонней гипотезы непрерывного измерения с одинаковым количеством пациентов в каждой группе.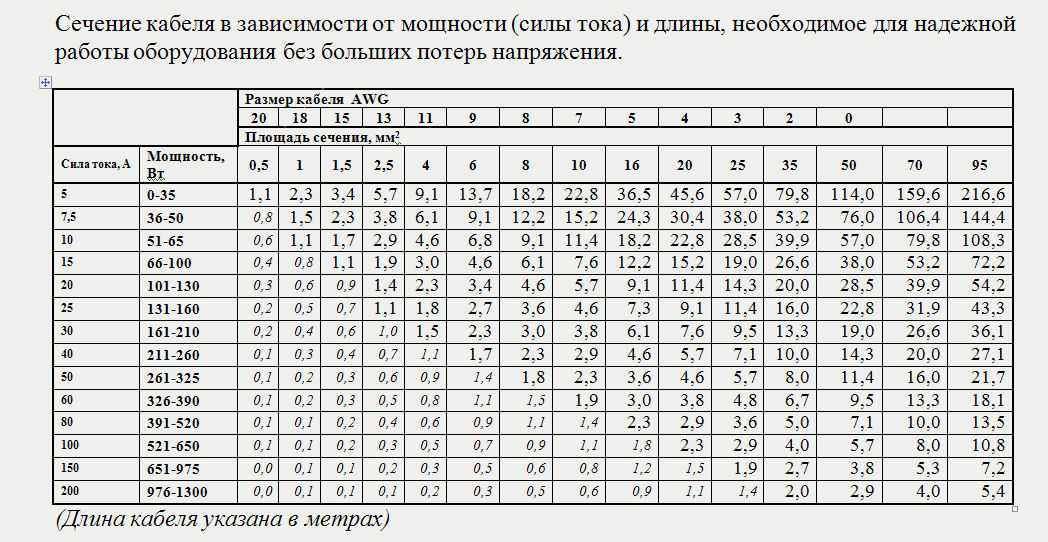

Если данные не распределены нормально, номограмма ненадежна, и следует обратиться за официальной статистической помощью.

Исследования, сообщающие категориальные данные

Предположим, что Эгберт Эверард в своем постоянном стремлении улучшить уход за своими пациентами, страдающими инфарктом миокарда, был убежден представителем фармацевтической компании помочь в проведении исследования нового посттромболизисного препарата Jedi Flow. . Из предыдущих исследований он знал, что потребуются большие числа, поэтому провел расчет размера выборки, чтобы определить, насколько сложной будет задача (таблица 4).

Таблица 4

Расчет размера выборки

И снова значения pα и pβ являются стандартными, и мы установили уровень для клинически важной разницы.

В отличие от непрерывных данных расчет размера выборки для категорийных данных основан на пропорциях. Однако, как и в случае с непрерывными данными, нам все еще необходимо рассчитать стандартизованную разницу.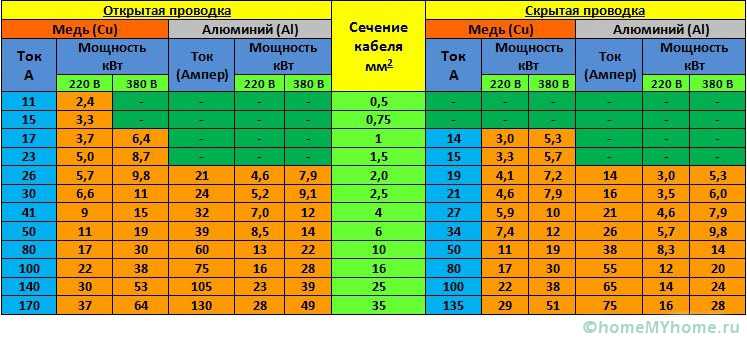 Это позволяет нам использовать номограмму для расчета необходимого количества пациентов.

р ₁ = пропорциональная смертность в группе тромболизиса = 12% или 0,12

p ₂ = пропорциональная смертность в группе Jedi Flow = 9% или 0,09 (это 3% клинически важная разница в смертности, которую мы хотим показать).

P=(p ₁₊ p ₂ )/2=

Стандартизированная разница составляет 0,1. Если мы воспользуемся номограммой и проведем линию от 0,1 до оси мощности на уровне 0,8, мы увидим пересечение с центральной осью на уровне 0,05 pα, нам потребуется 3000 пациентов в исследовании. Это означает, что нам нужно 1500 пациентов в группе Jedi Flow и 1500 в группе тромболизиса.

МОЩНОСТЬ В ДИАГНОСТИЧЕСКИХ ИСПЫТАНИЯХ

Расчеты мощности редко используются в диагностических исследованиях, и, по нашему опыту, немногие знают о них. Они имеют особое значение для практики неотложной медицинской помощи из-за характера нашей работы. Описанные здесь методы взяты из работы Будерера. ³

Доктор Эгберт Эверард решает, что диагностика переломов лодыжки может быть улучшена за счет использования нового ручного ультразвукового устройства в отделении неотложной помощи на Звезде Смерти. Устройство DefRay используется для осмотра лодыжки и позволяет определить, сломана лодыжка или нет. Доктор Эверард считает, что это новое устройство может снизить потребность пациентов в часах ожидания в рентгенологическом отделении, тем самым избегая боли в ушах у пациентов, когда они возвращаются. Он считает, что DefRay можно использовать в качестве инструмента скрининга, только те пациенты с положительным тестом DefRay будут отправлены в рентгенологическое отделение для демонстрации точного характера травмы.

Он разрабатывает диагностическое исследование, в котором все пациенты с подозрением на перелом лодыжки обследуются в отделении неотложной помощи с помощью DefRay. Этот результат записывается, а затем пациентов отправляют на рентгенограмму независимо от результата теста DefRay.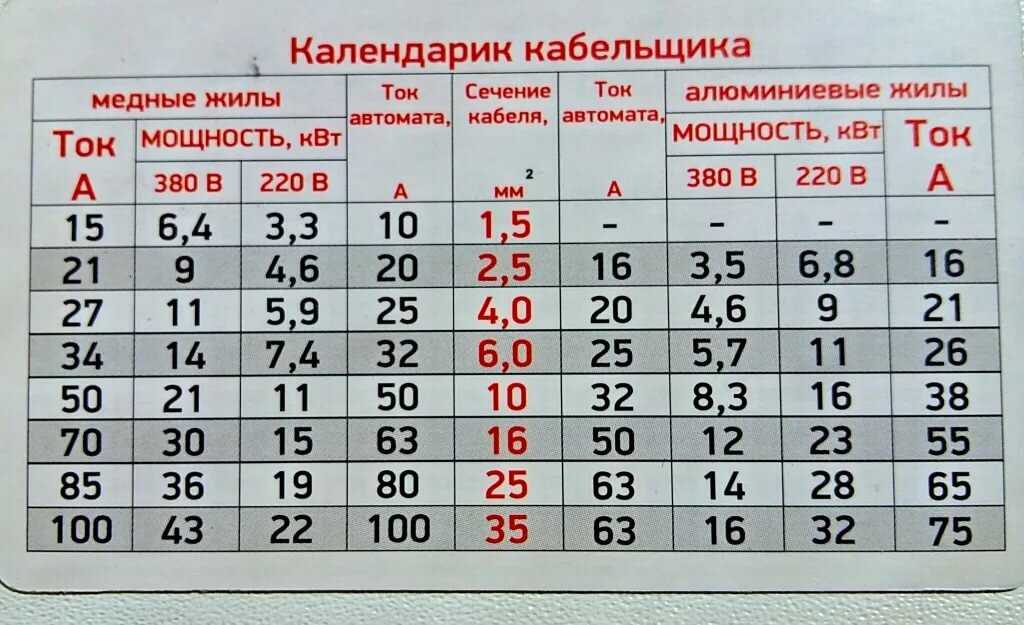 Затем доктор Эверард и его коллега сравнивают результаты DefRay со стандартной рентгенограммой.

Пропущенные переломы лодыжек стоили отделению доктора Эверарда больших денег в прошлом году, и поэтому очень важно, чтобы DefRay показал хорошие результаты, если он будет принят в качестве скринингового теста. Эгберту интересно, сколько пациентов ему понадобится. Он делает записи (таблица 5).

Таблица 5

Расчеты Эверарда

Для диагностического исследования мы рассчитываем мощность, необходимую для достижения адекватной чувствительности или адекватной специфичности. Расчеты основаны на стандартном способе представления диагностических данных «два на два», как показано в таблице 6.

Таблица 6

Таблица отчета «два на два» для диагностических тестов

Для расчета потребности в адекватной чувствительности

Для расчета потребности в адекватной специфичности

Если бы Эгберт был в равной степени заинтересован в тесте со специфичностью и чувствительностью, мы бы взяли большее из двух, но он этого не делает.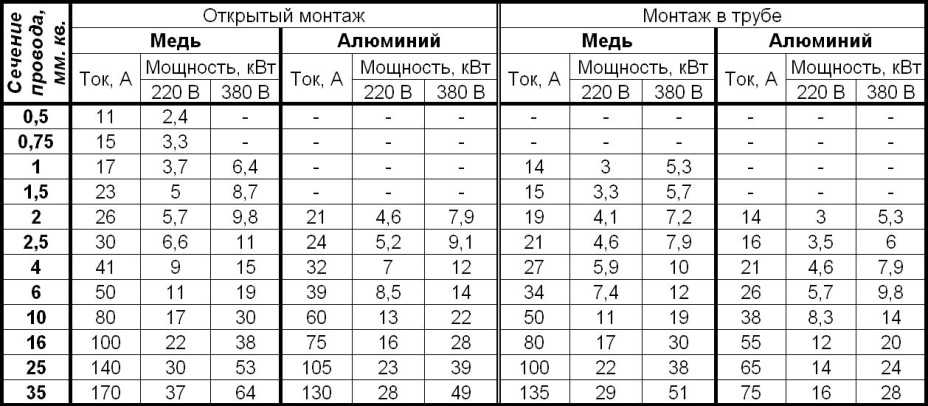 Он больше всего заинтересован в том, чтобы убедиться, что тест имеет высокую чувствительность, чтобы исключить переломы лодыжки. Поэтому он берет для чувствительности цифру 243 пациента.

ЗАКЛЮЧЕНИЕ

Оценка размера выборки является ключом к проведению эффективных сравнительных исследований. Понимание концепций мощности, размера выборки и ошибок первого и второго рода поможет исследователю и критическому читателю медицинской литературы.

ВИКТОРИНА

1. Какие факторы влияют на расчет мощности для пробной терапии?

2. Доктор Эгберт Эверард хочет протестировать новый анализ крови (Sithtastic) для диагностики гена темной стороны. Он хочет, чтобы тест имел чувствительность не менее 70 % и специфичность 90 % с уровнем достоверности 5 %. Распространенность заболевания в этой популяции составляет 10%.

3. Если доктор Эверард испытает новый метод лечения ожогов световым мечом, который, как надеялись, снизит смертность с 55% до 45%. Он устанавливает pα равным 0,05 и pβ равным 0,9.9, но обнаруживает, что ему нужно много пациентов, поэтому, чтобы облегчить себе жизнь, он изменяет мощность на 0,80.

   1. Сколько пациентов в каждой группе ему потребовалось с pα до 0,05 и pβ до 0,80?

   2. Сколько пациентов ему понадобилось при более высокой (первоначальной) мощности?

Ответы на викторину

1. См. рамку.

2. (i) 2881 пациент; (ii) 81 пациент

3. (i) около 400 пациентов в каждой группе; (ii) около 900 пациентов в каждой группе

Благодарности

Мы хотели бы поблагодарить Фиону Леки, почетного старшего лектора по неотложной медицине больницы Хоуп, Салфорд, за ее помощь в подготовке этой статьи.

ССЫЛКИ

1. Дрисколл П. , Уордроп Дж. Введение в статистику. J Accid Emerg Med2000;17:205.

2. ↵

   Гор С.М. , Альтман Д.Г. Насколько велика выборка. В: Статистика на практике . Лондон: Издательство BMJ, 2001: 6–8.

3. ↵

   Будерер Н.М. . Статистическая методология: I. Включение распространенности заболевания в расчет размера выборки для чувствительности и специфичности. Академия скорой медицинской помощи1996;3:895–900.

Расчет мощности и размера выборки

Пропустить навигацию

• МЕТОДЫ ИССЛЕДОВАНИЯ И СТАТИСТИКА
• ВВЕДЕНИЕ
  • 0 Об этих материалах
  • 1 Введение и обзор
• ФУНДАМЕНТ
  • 2 Понимание, описание и изучение данных
    • Определение данных
    • Проверь себя
    • Числовые сводки и дисплей
    • Проверь себя
    • Категориальные сводки и отображение
    • Проверь себя
    • Две числовые переменные
    • Проверь себя
    • Преобразования: Z-счета
    • Проверь себя
    • Преобразования: регистрируемые переменные
    • Проверь себя
    • Описание бинарных переменных (распространенность и заболеваемость)
    • Проверь себя
  • 3 Основные принципы дизайна исследования
    • От популяции до выборки
    • Введение в наблюдательный и экспериментальный дизайн
    • Проверь себя
  • 4 Идеи статистического вывода
    • Точечные оценки и параметры генеральной совокупности
    • Варианты выборки и распределения выборки
    • Проверь себя
    • Смещение и точность
    • Проверь себя
    • Что такое доверительный интервал?
    • Проверь себя
    • Что такое проверка гипотез?
    • Проверь себя
  • 5 Базовая вероятность
    • Понимание вероятности и связи с выводом
    • Проверь себя
• СТАТИСТИЧЕСКИЙ ВЫВОД
  • 6 Оценка и проверка гипотез
    • Центральная предельная теорема и нормальное распределение
    • Проверь себя
    • Центральная предельная теорема на практике: единичные средние и пропорции
    • Проверь себя
    • Связь между проверкой гипотезы и КИ
    • Проверь себя
• ПРОСТЫЕ СРАВНЕНИЯ
  • 7 простых сравнений
    • Средства сравнения
    • Проверь себя
    • Сравнение пропорций
    • Критерий независимости хи-квадрат
    • Проверь себя
    • Отчет о результатах и ​​выводы
  • 8 Непараметрические тесты
    • Ранговые непараметрические тесты
  • Какой тест?
• ДИЗАЙН И ПРОВЕДЕНИЕ ИССЛЕДОВАНИЯ
  • 9 Клинические испытания
    • Лекция
    • Проверь себя
  • 10 Наблюдательные исследования
    • Введение в обсервационные исследования
    • Построение доказательств — пример
    • Поперечные исследования
    • Когортные исследования
    • Исследования случай-контроль
    • Проверь себя
    • Интерпретация обсервационных исследований
  • 11 Лабораторные навыки
    • Лекция
  • 12 Размер образца и мощность
    • Расчет мощности и объема выборки
    • Проверь себя
  • 13 Этика
    • Лекция
• СТАТИСТИЧЕСКОЕ МОДЕЛИРОВАНИЕ
  • 14 Введение в регрессионные модели
    • Модели и статистические модели
    • Электронная лекция: Введение в статистическое моделирование
• СИНТЕЗ ДОКАЗАТЕЛЬСТВ
  • 15 систематических обзоров
  • 16 Метаанализ
• ГЛОССАРИЙ
• КРЕДИТЫ

При просмотре этого видео студент должен уметь:

1. Определить статистическую мощность
2. Перечислите потенциальные последствия проведения исследования с малой мощностью, а также исследования со слишком большой мощностью.
3. Объясните, что такое ошибка типа 1 и типа 2, и приведите типичные значения частот ошибок типа 1 и типа 2, которые используются при анализе и планировании исследования.
4. Укажите факторы, влияющие на мощность, и факторы, которые необходимо указать для расчета объема выборки.

Некоторые примечания о поведении вычислений размера выборки и мощности для неравных размеров групп

Эта информация была исключена из видео и поэтому включена здесь в виде текста.

Во многих сценариях соотношение участников в контрольной и лечебной группах или в группе, подвергшейся воздействию, к группе, не подвергшейся воздействию, неодинаково. В таких условиях нам нужен ОБЩИЙ размер выборки большего размера, чтобы получить ОДИНАКОВУЮ статистическую мощность для данного размера эффекта (δ) и уровня значимости (α).

Есть много причин, по которым у нас могут быть группы неравного размера. Например, в обсервационном исследовании это может просто отражать долю людей, подвергшихся и не подвергшихся воздействию интересующего фактора; в исследовании «случай-контроль» результат может быть редким, поэтому мы выбираем больше контрольных групп, чтобы повысить эффективность исследования, поскольку их легче и дешевле набирать; в рандомизированном контролируемом исследовании лечение может быть дорогостоящим и поэтому назначается только меньшей части пациентов.

Чтобы проиллюстрировать влияние неравных групп на силу, давайте предположим, что мы хотим определить разницу в 250 г в весе при рождении между двумя группами детей, рожденных матерями с избыточным весом. Одна группа матерей прошла интенсивную программу обучения и консультаций, чтобы помочь им правильно питаться и заниматься спортом во время беременности. Мы предполагаем, что SD населения в каждой группе составляет 400 г, а общий размер выборки равен 100.

Таблица 1 ниже показывает, что если группы имеют одинаковый размер (соотношение 1:1), то мощность равна 0,87. Исследование имеет 87% шанс обнаружить истинную разницу в массе тела при рождении в 250 г. Сила уменьшается по мере того, как размеры групп становятся все более и более неравными. Таким образом, мы получаем максимальную мощность для заданного общего размера выборки, когда группы имеют одинаковый размер.

Таблица 1.

Размер образца		Соотношение (вмешательство:контроль)	Мощность	N элементов управления, необходимых для получения той же мощности, что и при соотношении 1:1
Вмешательство	Управление
50	50	1:1	0,88
33	77	1:2	0,84 906:40	106
25	75	1:3	0,77	>5000
20	80	1:4	0,71

 

Еще один важный момент, касающийся мощности, взят из таблицы 1. В столбце последней строки показано количество контролей, необходимых для достижения той же мощности, что и для соотношения 1:1 в исследовании 100 мам (0,88). Вы можете видеть, что если у нас было 33 мамы в группе вмешательства, то нам нужно 106 мам в контрольной группе, чтобы получить мощность 88%. Однако, если бы у нас было 25 мам в группе вмешательства, то даже если бы мы смогли набрать более 25000 контрольных, мы все равно не достигли бы такой же мощности, как исследование 1:1 100 пациенток. Таким образом, есть предел тому, сколько власти мы можем получить, привлекая больше элементов управления. Поведение этого сложное, поскольку оно зависит от размера меньшей группы и SD.

Как упоминалось выше, в исследовании «случай-контроль» часто проще набрать больше контролей, поскольку мы часто используем схему «случай-контроль» для изучения редких исходов. Непосредственно следуя предыдущему абзацу, мы также можем вычислить дополнительное увеличение мощности за счет увеличения соотношения контролей и случаев в исследовании случай-контроль.