|
СКОЛЬКО БЛОКОВ СТОУНЛАЙТ В ОДНОМ КУБЕ? Очень частый, но к сожалению смешной первый вопрос, который приходится слышать это: — СКОЛЬКО В КУБЕ ГАЗОБЛОКА? Клиент сразу получает встречный вопрос: — КАКОГО? *** И это абсолютно нормальный встречный вопрос, учитывая все разнообразие размеров газобетона Стоунлайт. Чтобы долго не водить Вас за нос приведу таблицу размеров и пересчета в кубы, а после таблицы научу Вас делать рассчет самостоятельно. Итак таблица:
Почему ни один нормальный человек не в состоянии сразу ответить на вопрос: «Сколько блоков в одном кубе?» Да все потому, что все блоки разные и разных размеров и в кубе каждого блока вмещается разное количество. Вот тут вы найдете превосходную статью, которая поможет Вам рассчитать сколько блоков любых размеров содержится в одном кубическом метре.
СКОЛЬКО БЛОКОВ
|
Узнаем как рассчитать, сколько в одном кубе квадратных метров строительного материала
Во время строительства нередко возникает вопрос о том, сколько в одном кубе квадратных метров. Это касается множества материалов, которые по своим параметрам имеют три показателя: длину, ширину, высоту. Чтобы получить кубический показатель, исходя из размеров, необходимо выяснить метрические данные единицы материала. Для этого измеряется длина, ширина, высота, а для удобства расчетов показатели переводятся в метры. Например, если размер стороны составляет 25 см, то при переводе будет 0,25 м.
Данный расчет поможет решить, сколько в одном кубе квадратных метров. Для определения площади используются кв. м, т. к. достаточно двух показателей, ширины и высоты. Кубический метраж нужен для определения объема помещений, емкостей, а также для расчета потребности материала для строительства большого строения.
Вычисляем, сколько литров в 1 кубе воды
Запасы пресной воды составляют на сегодняшний день около 80 000 кубических километров. Это много…
Общий принцип расчета
Соответственно, чтобы рассчитать, сколько в одном кубе квадратных метров, нужно площадь основания умножить на показатель высоты, толщины или глубины, используя при этом метровую единицу измерения. Если необходимо произвести расчет количества материала, чтобы узнать, сколько в кубе квадратных единиц, то нужно знать толщину того изделия, которое берется для вычисления. А далее, исходя из общей площади, рассчитывается необходимое количество на 1 кв. м. Более подробно можно рассмотреть на конкретных примерах.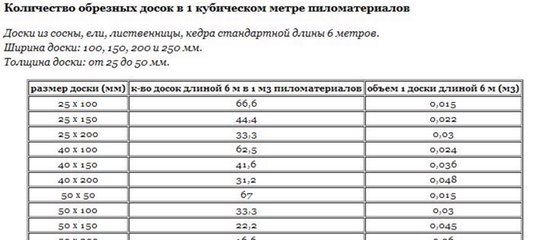
Кирпич
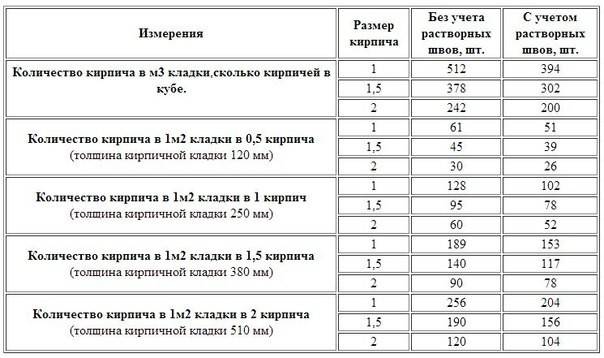
Чтобы рассчитать потребность материала на возведение стен, необходимо посчитать, сколько в одном кубе квадратных метров кирпича. Для начала вычисляют площадь кирпича, умножив его ширину на длину. Размеры материала составляют 250х120 мм. Переводим в метры, получается 0,25х0,12. Умножаем, и выходит, что площадь одного кирпича составляет 0,03 кв. м. После 1 кв. м делим на 0,03 кв. м и получаем, что в 1 кв. м помещается 33,3 кирпича. Теперь, чтобы вычислить, сколько входит кирпичей в один кубический метр, необходимо использовать высоту площади кирпича, которая составляет 65 мм или 0,065 м. Последующие действия позволят высчитать количество на 1 куб. м, для чего куб делится на высоту кирпича и умножается на количество кирпичей одного рядя, т. е. 1/0,065х33,3. с округлением получается 512 кирпичей, вмещающихся в 1 куб. м. Строительные объемы кирпича вычисляются не только для возведения стен, поэтому, чтобы посчитать необходимо количество материала на заполнение 1 кв.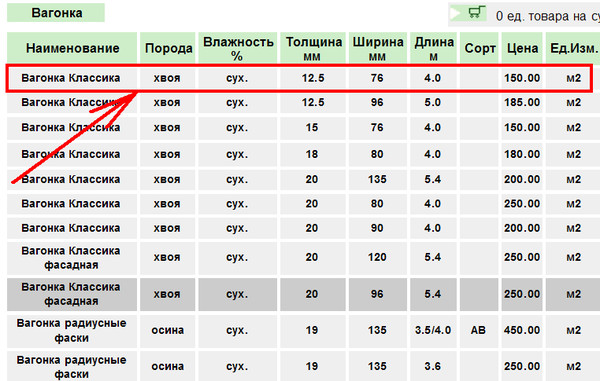 м, следует учитывать, каким образом будет укладываться кирпич. Если он ставится на ребро, то соответственно расход на 1 кв. м снижается, следовательно, и потребность уменьшается.
м, следует учитывать, каким образом будет укладываться кирпич. Если он ставится на ребро, то соответственно расход на 1 кв. м снижается, следовательно, и потребность уменьшается.
Узнаем как рассчитать количество кирпича на дом? Попробуем…
Учимся рассчитывать, какое количество кирпича необходимо для строительства дома. В статье приведено…
Пеноблок
Чтобы определить, сколько в одном кубе квадратных метров пеноблоков, можно использовать технику расчета количества кирпичей. Но пеноблок по своим размерам намного больше и считать его рядами проблематичней. Поэтому лучше использовать другой расчет, который будет не менее точным, чем при вычислении кирпича. Для строительства используются разные размеры блока, поэтому приводить пример на каждом изделии нецелесообразно. Для удобства будет учитываться стандартный стеновой блок размерами 600х200х300 мм. Переводить в метры не обязательно, удобнее будет считать кубическими сантиметрами. Исходя из того, что куб представляет собой фигуру с равными сторонами, то его показатели составляют 100х100х100 см. Таким образом, перемножив стороны, получаем 1000000 куб. см. Такой же методикой считается объем единицы пеноблока 60х20х30, и получается результат 36000 куб. см. Далее объемы между собой делятся, 1000000/36000, и получается 27,7 штук пеноблока в кубическом метре.
Таким образом, перемножив стороны, получаем 1000000 куб. см. Такой же методикой считается объем единицы пеноблока 60х20х30, и получается результат 36000 куб. см. Далее объемы между собой делятся, 1000000/36000, и получается 27,7 штук пеноблока в кубическом метре.
Узнаем как много в кубе шлакоблока: примеры вычисления
Тонкости расчета шлакоблоков на 1 куб. м. В чем преимущества шлакоблока как строительного…
Брус
Пиломатериал для стен имеет большие по значению показатели, поэтому, чтобы рассчитать, сколько в одном кубе квадратных метров бруса, будет использоваться показатель квадратного сантиметра. Брус, как и пеноблок, имеет разную длину, ширину и высоту, но для примера используется один из широко используемых параметров древесины 6000х200х150 мм. Перемножив стороны одного бруса, переведя их в сантиметры, 600х20х15, получаем результат 180000 кв. см. Далее по отработанной схеме, 1000000 куб. см. делятся на 180000 и получается, что в 1 кубе 5,55 штук бруса. При определении необходимого объема, чтобы расчеты были максимально правильными, нужно учитывать соединение материала, угловые стыки, вырезы под проемы окон и дверей, а также усадку, которая происходит в результате усушки строения и может сократить высоту потолка вплоть до 15 см, а значит, и материала потребуется для строительства больше.
При определении необходимого объема, чтобы расчеты были максимально правильными, нужно учитывать соединение материала, угловые стыки, вырезы под проемы окон и дверей, а также усадку, которая происходит в результате усушки строения и может сократить высоту потолка вплоть до 15 см, а значит, и материала потребуется для строительства больше.
Бетон
Эти расчеты необходимы, чтобы, к примеру, залить площадь пола или некой площадки. Перевозка и учет раствора осуществляется в куб. см, а площадь кв. см. Чтобы вычислить, сколько в одном кубе квадратных метров бетона, необходимо посчитать площадь планируемого участка заливки и умножить ее на глубину заложения. Например, необходимо залить монолитную плиту под будущий дом размером 8х10 метров с глубиной 0,8 метра. Для определения объема показатели перемножаются, 8х10х0,8, и получается 64 куб. м, которые понадобятся для заполнения данного объема. Следует учитывать небольшой запас, чтобы на этапе заливки не оказалось, что по некоторым причинам раствора не хватило.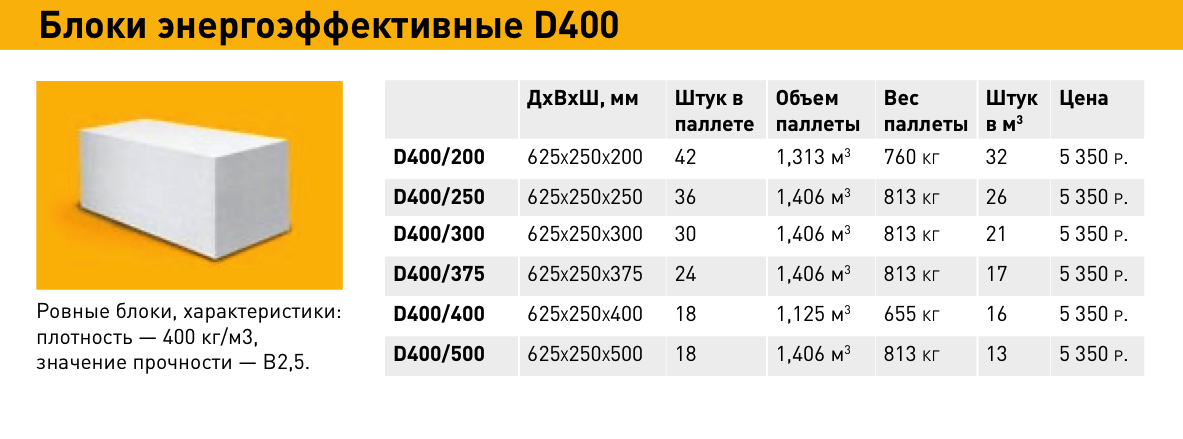
Заключение
Чтобы вычислить количество необходимого материала и осуществить его доставку в нужном объеме, можно использовать на первый взгляд простые вышеуказанные расчеты. Также необходимо брать во внимание некоторые особенности, такие как стыковка бруса, толщина джута, использование раствора при кладке кирпича и блока, что существенно может изменить исходный показатель. Не следует забывать о распиле строительного материала, а значит, наличии обрезков, которые входят в общий расчет, но остаются без применения. Кроме того, схема расчетов является универсальной, ее можно применять для вычисления требуемого материала любой формы и размеров.
комбинаторика — Затемнение квадратов кубика Рубика
Отказ от ответственности: Это старый неполный ответ, которому уже несколько лет. Я начал это еще до того, как получил формальное математическое образование, и так и не вернулся, чтобы закончить это.
Чтобы сделать нашу жизнь проще, мы можем разделить детали на 3 типа:
Кромки (3 наклейки)
Стороны (2 наклейки)
Центры (1 наклейка)
Также обратите внимание, что я наблюдаю за кубом с желтым и черным (позже я назову его белым) цветами для верхней и нижней сторон в качестве цветовой схемы по умолчанию.
(Другие части следуют за красной, синей, оранжевой, зеленой)
Для кубика Рубика $3\times3\times3$ сначала мы можем решить средние части.
Можно сделать вывод, что если цветовая схема известна, то все затемненные центры можно определить, если у нас есть хотя бы 2 соседних.
Это означает, что мы можем очистить 4 центра, если сохраним 2 соседних. Это можно проверить, играя с собственным кубиком или просто следуя законам правильных позиций и используя что-то вроде решателя. (Это потому, что центры не могут быть действительно переключены, но части вокруг них могут, так что это выглядит так)
Тогда давайте посмотрим, сколько наклеек с краев можно скрыть или отклеить, поскольку любая конфигурация $n\times n\times n$ всегда имеет ровно 8 ребер.
Мы можем перечислить их по цветам, которые они содержат:
(красный, синий, зеленый, оранжевый, желтый, белый)
$$ Р,З,У $$
$$ Р,З,Ш $$
$$ Р,Б,У $$
$$ Р,Б,Ш $$
$$ О,Г,Г $$
$$ О,Г,В $$
$$ О,Б,У $$
$$ O,B,W $$
Если вы хотите знать, сколько наклеек можно отклеить и при этом идентифицировать каждый угол, вы можете спросить себя; Сколько наклеек вы можете взять, чтобы при складывании их обратно у вас был только один возможный способ?
Я нашел максимальное количество 12 из 24 наклеек; взяв все R или O, затем все B или G и, наконец, все Y или W.
Вот пример:
$$ -,-,- $$ $$ -,-,W $$ $$ -,В,- $$ $$ -,В,В $$ $$ О,-,- $$ $$ О,-,В $$ $$ О,В,- $$ $$ O,B,W $$
Теперь, перетасовав порядок и вращение всех 8 ребер всеми возможными способами, будет только один способ наклеить удаленные наклейки, таким образом, вы все равно сможете идентифицировать части.
Теперь боковые части, которые могут быть немного сложными.
На кубике Рубика $3\times3\times3$ 12 ребер:
$$ G,R $$ $$ Р,Б $$ $$ В, О $$ $$ О,G $$ $$ Y,G $$ $$ Г, Вт $$ $$ В,Б $$ $$ Б, Г $$ $$ Р,В $$ $$ В,О $$ $$ О,Г $$ $$ Y,R $$
Теперь вы можете попробовать сделать то же самое.
Сначала я попытался удалить все белые наклейки, затем это позволяет мне взять один цвет из $Y,?$ штук, кроме желтого, и после этого больше ничего нельзя взять, не предоставляя несколько решений для краев; так что было 5 наклеек.
Затем, после других неудачных попыток, я обнаружил, что можно удалить 6 наклеек; по одной каждого цвета, чтобы не было нескольких наклеек одного цвета без второго цвета, и я почти уверен, что здесь нельзя сделать более 6.
Если кто-то может сделать здесь лучше, дайте мне знать.
Итак, если я не ошибся, для кубика Рубика $3\times3\times3$ можно удалить всего $12+6+4 = 22$ из 54 наклеек сверху (следуя тому, что я указал) без потеря любой информации о состояниях куба.
Кубик Рубика $2\times2\times2$ состоит всего из 8 ребер, поэтому здесь можно удалить 12 из 24 наклеек.
Теперь мы можем попытаться обобщить это на другие $n\times n\times n$ кубы.
Теперь мы знаем, что можем для;
$n=2$ возьми 12 из 24
$n=3$ возьми 22 из 54
Для любого $n\times n\times n$ куба у нас всегда есть 8 ребер, так что это $+12$ закрытых наклеек.
Для боковых частей у нас есть $n$ каждой части (отсортированный набор частей):
$$ W,R $$ $$ В,Б $$ $$ В,Г $$ $$ В,О $$ $$ Г, Р $$ $$ Д,Б $$ $$ Y,G $$ $$ Д,О $$ $$ Р,Б $$ $$ Р,Г $$ $$ О,Б $$ $$ O,G $$
Здесь нечего делать, кроме как применить то же самое, что я сделал в кубе $3\times 3\times 3$;
Удалите 6 наклеек, по одной каждого цвета, чтобы не осталось нескольких наклеек одного цвета без второго цвета, и делайте это для каждого нового набора боковых частей.
Это дает нам еще $6\times(n-2)$ фрагментов, которые нужно скрыть.
Опять же, если вы можете сделать лучше с отсортированным набором, который я предоставил, пожалуйста, дайте мне знать.
Пока количество наклеек, которые мы можем скрыть, составляет: $$12+6\times(n-2)+C$$
Где $C$ — количество «подвижных» и «неподвижных» центров, которые мы могут скрывать, которые появляются после $n>3$ и еще предстоит выяснить.
(когда $n=3$, тогда $c=4$ )
Итак, теперь центральные части куба $4\times 4\times 4$ и все остальные со сторонами $2k$ ($k>1$) отличны от любых $2k+1$ гранных кубов;
$2k+1$ как и наш стандартный кубик $3\times3\times3$ имеет 6 «реальных центров», которые неподвижны и $4$ из $6$ могут быть скрыты, остальные одностикерные центры здесь «подвижные» и ведут себя по-разному при вращении.
То же самое касается всех центров, которые являются «мобильными» в кубах по $2k$. 92$$
Завтра рано утром у меня занятия, так что спокойной ночи.
Редактировать: Это должно быть вычислено и проверено, чтобы убедиться, что я не сделал где-то ошибка.
Сколько квадратов на кубике Рубика?
ОТВЕТЫ: 26
-
ДжуДжуби одет в ПАЛЬТО из шоколада
м руды, чем я могу сосчитать на пальцах рук и ног!!!
-
LuckyLefty доставили вам письмами WTF
или ч это МНОГО 😐 я думал, что у меня это было впервые в 54… тогда я подумал, нет, ты должен считать каждый лист, а потом я понял, что должен считать КАЖДЫЙ КУБИК на КАЖДОМ ЛИСТЕ, и я просто не хочу заниматься этой математикой 🙂
-
любовные шимпанзе
Я угадаю 60
-
техниос
9 умножить на 6 54
-
ануча123
T слишком много для меня .
 … лол
Хорошо, теперь серьезно:
Вы сказали квадраты, а не кубы, так что… На каждой грани куба есть девять маленьких квадратов и 4 средних квадрата (2 х 2), а затем один большой квадрат (3 х 3), так что всего 14 на каждую грань куба. куб. Тогда есть 6 граней, так что 6 X 14 = 84. Это мой ответ.
… лол
Хорошо, теперь серьезно:
Вы сказали квадраты, а не кубы, так что… На каждой грани куба есть девять маленьких квадратов и 4 средних квадрата (2 х 2), а затем один большой квадрат (3 х 3), так что всего 14 на каждую грань куба. куб. Тогда есть 6 граней, так что 6 X 14 = 84. Это мой ответ. -
Джеалса
W Размер шапки Кубик Рубика? Там есть что-то вроде суперкубов… {улыбается}
-
техниос
o оооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооо…
-
Austinius SillyVilles Resident Lothario
2 9 куб.
 54 лица.
54 лица. -
техниос
w это 3х3 или 4х4 ооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооооо
-
Изменчивость
T шляпа зависит от нескольких вещей. Если вы используете кубик Рубика 3x3x3, то: Если считать только отдельные ящики, то их пятьдесят четыре. Если вы включаете коробки 2×2, которых по четыре на каждой грани, то их девяносто. Если вы считаете каждую грань 3×3 как еще один квадрат, то их девяносто девять.
-
Счет закрыт
T здесь 60 квадратов 54 цветных квадрата + сам куб имеет шесть квадратных граней.

-
Тальман
6 Х 9 + 54
-
самми08
лот 🙂
-
Анонимный
i t имеет 6 сторон/цветов и девять одного цвета
-
лучший
-
Твитчипантс
4 2.
 .. ответ на все вопросы!
.. ответ на все вопросы! -
Скобби Ду
-
ТМС
6 0 там по 9 с каждой стороны = 54×6 тогда посчитаем стороны куба =6 + 54= 60 тк
-
Кимми
I ts 54. 6 сторон и 9 квадратов =54
-
Анонимный
1 2 3 4 5 6 7 8 9 У куба 6 сторон 6 х 9 = 54
-
BigDaddyBS
9 1×1 квадрат с каждой стороны * 6 сторон = 54 4 квадрата 2×2 с каждой стороны * 6 сторон = 24 1 квадрат 3х3 с каждой стороны * 6 сторон = 06 Общее количество квадратов на кубике Рубика = 84.
 ТЕПЕРЬ, если это кубик Рубика 16×16 (кажется, я помню, что где-то видел их), есть НАМНОГО больше. 😉
ТЕПЕРЬ, если это кубик Рубика 16×16 (кажется, я помню, что где-то видел их), есть НАМНОГО больше. 😉 -
НоМорф
T здесь, вероятно, тысячи Квадратов работают над кубиками Рубика, пока мы говорим.
-
ТЕРРИТУКЕР
-
-Проблемы свободы- Миннесота Ницца
5 4. 6 сторон, по 9 квадратов на каждой стороне.
-
Чистый Отец
5 4 цвета.

 11
11 78
78 Необходимо четко отдавать себе отчет в том, что завод не
Необходимо четко отдавать себе отчет в том, что завод не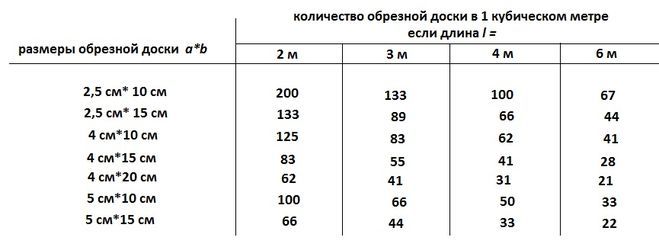 16
16 92
92 кубических
кубических куб+2 подд. по 1,92 = 34,56 м.куб + 3,84 = 38,4 м.куб.
куб+2 подд. по 1,92 = 34,56 м.куб + 3,84 = 38,4 м.куб. 5 из
5
.
Всего
151 голос.
5 из
5
.
Всего
151 голос. Мы изготав-ливаем перегородки следующих размеров:
Мы изготав-ливаем перегородки следующих размеров: