Сколько квадратов доски в кубе: Сколько досок 6 метров в кубе? (таблица, формула, пример расчёта)

Содержание

Сколько квадратных метров доски в кубе? | DZEN BLOGGER.

Сколько квадратных метров доски в кубе: габариты изделий, количество деталей, расчет объема и площади?

Сколько квадратных метров доски в кубе: габариты изделий, количество деталей, расчет объема и площади

Все фото из статьи

Содержание

Разбираться, сколько досок в квадратном метре, сколько кубов материала нужно для реализации того или иного проекта, сколько квадратов можно обшить одним кубометром материала и т.д., должен любой, кто планирует стройку или ремонт. И хоть сегодня несложно найти табличные значения практически для любой ситуации, желательно все же понимать, как осуществляются расчеты, и при необходимости уметь провести вычисления своими руками.

Чтобы понять, сколько здесь материала, придется провести нехитрые расчеты

Габариты досок

Кубометр доски — это сколько? Один из самых распространённых вопросов, которые задают мастера-новички. На самом деле на этот вопрос можно дать предельно простой ответ: это, смотря о каком пиломатериале речь!

Схема определения линейного размера пиломатериала

Как правило, для строительных и ремонтных работ применяют заготовки, произведенные по ГОСТ 8486-86.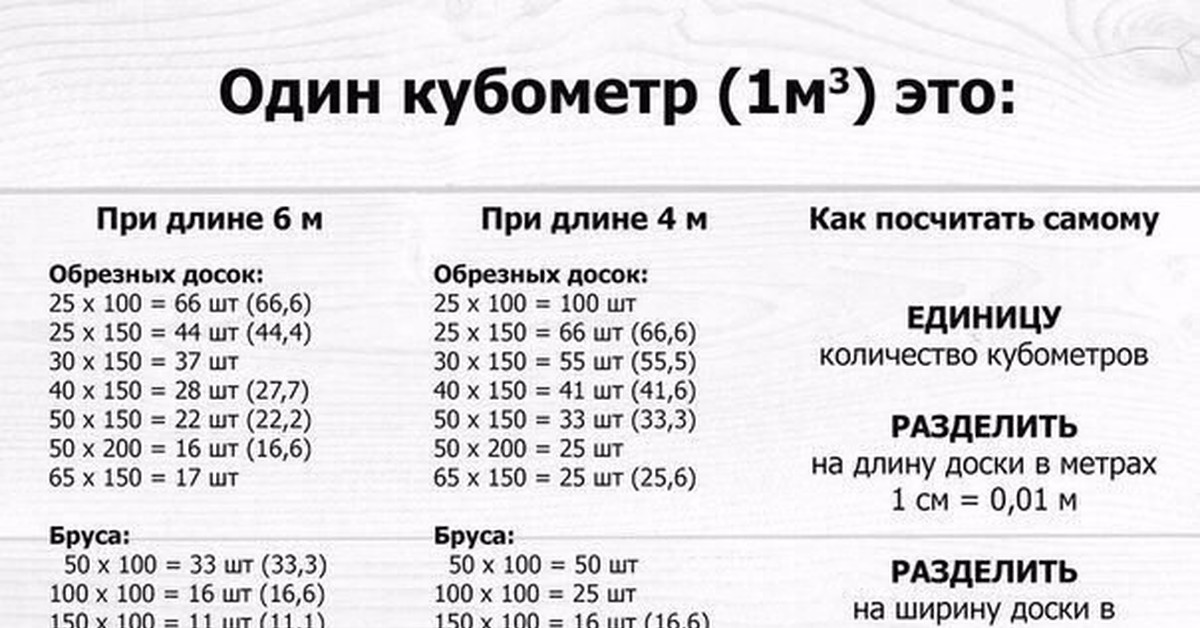 Этот норматив, регламентирующий основные требования к пиломатериалам хвойных пород (для лиственных есть отдельный документ — ГОСТ 2695-83), определяет, какой размер может иметь изделие.

В принципе, подобрать нужную деталь несложно, но все же есть определенные ограничения, которые и лимитируют производство заготовок:

толщина – от 16 до 75 мм;
ширина – от 75 до 275 мм;
длина — от 1 до 6 м.

Естественно, встречаются и отступления. Так, при необходимости можно заказать изготовление деталей с другим соотношением толщины и ширины. Их цена, конечно, будет выше, чем стандартных, но при необходимости и наличии подходящего сырья можно выпилить практически любую заготовку.

Стандартная длина составляет от 1 до 6 м

Что касается длины, то здесь все несколько сложнее. Найти заготовки длиннее 6 м получается далеко не всегда, поскольку эта величина ограничена габаритами товарного вагона. Так что более длинные доски пилятся исключительно под заказ и перевозятся автотранспортом, что удорожает материал.

В принципе, этой информации будет вполне достаточно, чтобы мы, зная основные параметры изделий, могли рассчитать, сколько 6 метровых досок в кубе, и какую площадь они займут при обшивке либо укладке на пол.

Примеры расчетов

Количество деталей в кубе

Пиломатериалы обычно реализуются по объему

Итак, первую часть этого раздела мы посвятим определению того, сколько досок в кубометре. Задача эта достаточно проста, поскольку нам достаточно 1 м3 поделить на объем одной детали.

Единичный объём вычисляем по формуле Д х Ш х Т, где:

Д – длина;
Ш – ширина;
Т – толщина.

Обратите внимание!

Рассчитывая, сколько досок в одном кубометре, нужно не забывать о переводе единиц, так как обычно параметры поперечного сечения указываются в миллиметрах, а длина – в метрах.

Фото калькулятора, используемого для вычислений

В качестве примера вычислим, сколько в кубе 4 метровых досок шириной 150 мм и толщиной 25 мм:

Вычисляем объем одной заготовки: 4 х 0,150 х 0,025 = 0,015 м3.
Определяем количество деталей: 1 / 0,015 = 66,7.
Округляем до целого значения, получая 66 штук.

Обратите внимание!

Обычно округляют до последней целой цифры.

Это, конечно, несколько противоречит правилам математики, но в данном случае стоит ориентироваться на сложившуюся практику.

Чтобы вам было проще рассчитывать количество досок в кубе — таблица 4 метра / 6 метров приводится ниже:

Длина, м

Толщина, мм

Ширина, мм

Объем единицы, м3

Количество, штук

100

0, 016

150

0,024

100

0,020

150

0,030

100

0,024

150

0,036

100

0,030

150

0,045

Естественно, имея под рукой такую таблицу, посчитать, сколько метров доски в кубе (погонных, о квадратных мы поговорим ниже), будет очень легко: берем количество досок и умножаем на их длину.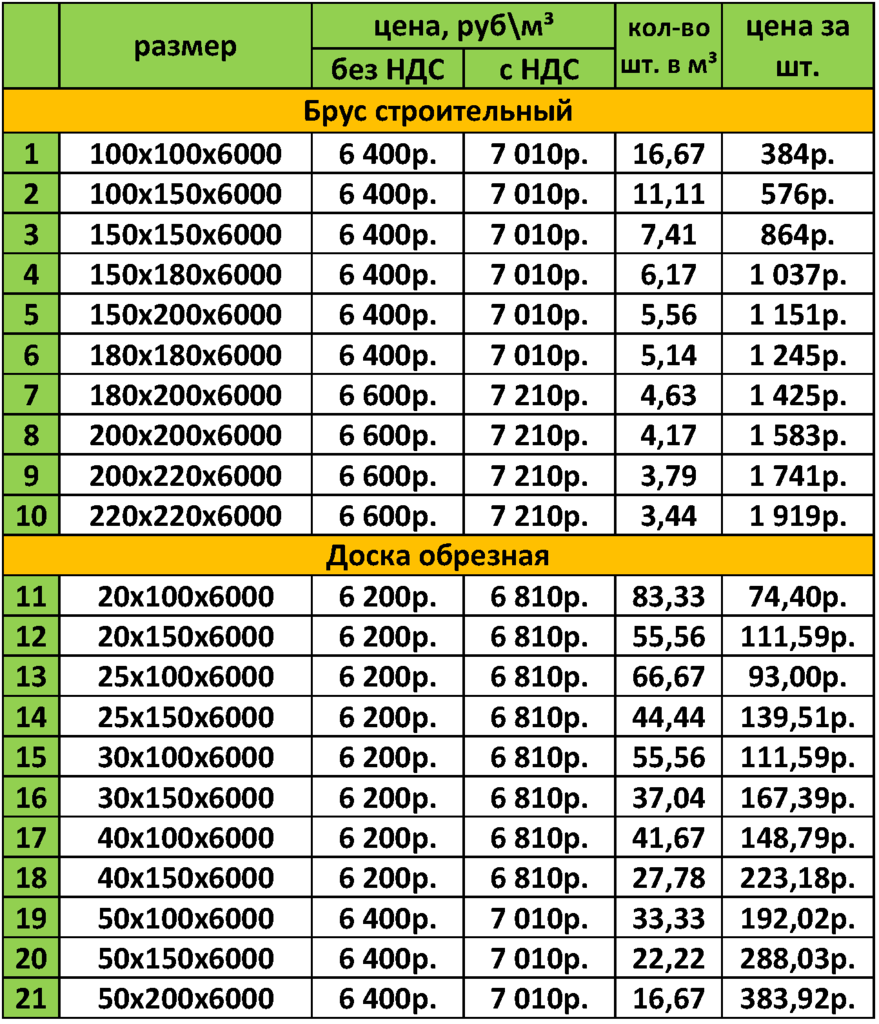

Так, для деталей 4000х50х100 этот показатель будет равен: 50 х 4 = 200 м. пог.

Еще один вариант таблицы соотношения объема и количества

Объем и площадь

Следующая инструкция посвящена определению площади, которую можно обшить/покрыть, израсходовав одни кубометр пиломатериала.

Чтобы обустроить напольное покрытие, как на этом фото, нужно заранее вычислить объем материала для отделки требуемой площади

Здесь в первую очередь необходимо определить площадь одного элемента, просто умножив его длину на ширину. Так, если мы планируем обшивать стену деревянной вагонкой 3 м с шириной 220 мм и толщиной 20 мм, то площадь одной доски будет равна 3 х 0,22 = 0,66 м2.
Затем определяем количество таких изделий в кубометре. Объем одной доски будет равен 3 х 0,22 х 0, 02 = 0,0132 м3. Следовательно, в кубе у нас будет 1 / 0,0132 = 75 деталей заданного размера.
Далее полученное количество умножаем на площадь одной доски: 75 х 0,66 = 49,5 м2.

Обратите внимание!

Высчитывая, сколько квадратных метров в 1 кубе доски – вагонки, нужно принимать во внимание не фактические размеры панелей, а размеры «видимой части».

Связано это с тем, что при монтаже шипы замковых элементов скрываются в пазах, и ширина уменьшается, так что расхождение теоретического расчета с фактическим может доходить до 8 -10%.

При расчетах с вагонкой длина шипа не учитывается

Также при переводе кубатуры в объем нужно помнить, что иногда возникает необходимость укладки досок без стыков. При этом следует подбирать детали с такой длиной, которая обеспечит появление минимального количества отходов, иначе наши затраты на покупку материала существенно (и неоправданно!) возрастут.

Советы при работе с необрезными деталями

Все рекомендации, приведенные выше, касались работы с обрезной доской, ровным деревянным брусом, вагонкой и т.д. Однако для решения различных задач иногда задействуются необрезная доска и горбыль, которые имеют неправильную форму.

В этом случае для вычисления хотя бы приблизительного объема материала поступаем следующим образом:

Объем необрезной заготовки или горбыля вычислить куда сложнее

Сначала определяем среднюю толщину заготовки. Для этого выполняем несколько промеров в самой толстой и самой тонкой части, суммируем полученные результаты и делим на количество измерений.
Затем рассчитываем среднюю ширину по тому же алгоритму.

Обратите внимание!

Чем ближе форма изделия к правильному параллелепипеду, тем меньше промеров нужно сделать для получения сколько-нибудь точного значения.

Полученные средние величины перемножаем, затем умножаем на длину необрезной планки/горбыля, и получаем объем единицы пиломатериала.

Можно поступить и несколько проще. Зная, что выход полноценной доски из необрезных заготовок составляет около 70 – 80% по объему, мы просто приобретаем сырье с запасом, умножая требуемую величину на коэффициент 1,25 — 1,3. Впрочем, так мы тоже получим только приблизительный результат, потому вероятность избытка/недостатка материала все же будет присутствовать.

Заключение

Мы надеемся, что следуя приведенным советам, вы разберетесь, как посчитать квадратный метр доски, как определить количество деталей в кубометре и т. д. Более подробную информацию можно найти на видео в этой статье, а если у вас в ходе изучения методик возникнут вопросы, вы сможете задать их в комментариях ниже!

https://rubankom.com/materialy/pilomaterialy/doski/1583-skolko-kvadratnyh-metrov-doski-v-kube

инструкция, фото- и видео-уроки, цена

Если вы задумали сделать ремонт или приступили к строительству загородного дома, то вполне вероятно, что у вас возникнет необходимость в приобретении пиломатериала. При осуществлении такой покупки очень часто встает вопрос о том, какое количестве досок соответствует одному кубическому метру пиломатериала, или какую площадь поверхности можно облицевать одним кубометром.

Панели из дерева для внутренних работ.

КОЛИЧЕСТВО ЕДИНИЦ В КУБИЧЕСКОМ МЕТРЕ.

Для наглядности выполним расчёт и определим, сколько штук обрезной доски (габариты 150х25х6000 в миллиметрах или 0,15х0,025х6 в метрах) находится в одном кубометре.

Находим объём одной доски: 0,15х0,025х6 = 0,0225 м3
Определяем количество досок в одном кубическом метре и округляем до целого числа (именно так идет подсчет в торговой сети): 1:0,0225 = 44,44 шт. =44 шт.

КОЛИЧЕСТВО КВАДРАТОВ В КУБОМЕТРЕ

Чтобы выполнить отделку стен каким-либо облицовочным материалом, необходимо узнать какую площадь можно облицевать из одного кубического метра при определенной толщине этого материала.

Вид после облицовки вагонкой

Расчёт выполняется в следующей последовательности:

Определяемся с необходимой толщиной обрезной доски. Для примера принимаем 0,025 м (25 мм).
Рассчитываем площадь, которую можно облицевать одним кубическим метром материала: 1 : 0,025 = 40 м2.
Делаем замеры и считаем площадь стены. Например, стена 4х2,5 м имеет площадь 10 м2.
Определяем необходимый объём досок для покупки: 10:40=0,25 м3.
Из предыдущего примера мы знаем, что объём одной доски составляет 0,0225 м3.
Определяем необходимое количество досок: 0,25:0,0225=11,11шт.
Покупаем с запасом 12 штук, общим объёмом: 0,0225х12=0,27 м3.

Вывод: Придерживаясь этого алгоритма расчета можно, подставляя свои значения, найти необходимый для облицовки объём пиломатериала.

РАСЧЁТ МАТЕРИАЛА ДЛЯ ОТДЕЛКИ

Материалы для облицовки стен нашли широкое применение, как для внутренних, так и для наружных отделочных работ. Их особенностью является простота монтажа, минимум подготовительных работ и большие межремонтные сроки эксплуатации.

Монтаж в вертикальном направлении

ВО ВНУТРЕННЕМ ПРОСТРАНСТВЕ

Для расчета материала необходимо выполнить ряд операций:

Составить список помещений, в которых планируются отделочные работы.
В каждом помещении определиться, что подлежит отделке (стены, пол, потолок).
Рисуем и нумеруем планы (прямоугольники), куда в дальнейшем будем наносить размеры:

План пола;
План потолка;
План каждой стены подлежащей отделке. Если на стене имеются окно или дверь, то эти проёмы наносим на план.

Измеряем и записываем полученные размеры (в метрах, с точностью до второго знака после запятой) в ранее заготовленные планы:

Для пола замеряем длину и ширину помещения. Замеры делать от стен, а не от плинтуса. Эти размеры проставить и на план потолка.
Для каждой стены замеряем её длину и высоту. Если есть дверь, то измеряем её высоту и ширину, а также замеряем размер от двери до любой примыкающей стены. Также поступаем и с оконным проёмом, но дополнительно измеряем расстояние от пола до низа окна.

Подсчитываем площади стен, пола, потолка по каждому помещению. Площади окон и дверей вычитаем из площади стен.
Суммируем полученные результаты. Как правило, к общей сумме добавляется десять процентов на непредвиденные обстоятельства.

НА ФАСАДЕ СТРОЕНИЯ

Для наружных и внутренних облицовочных работ порядок выполнения замеров и подсчета площадей не имеет принципиальных отличий. Площадь чердачного фронтона имеющая, как правило, форму близкую к треугольнику будем считать в запас, как площадь треугольника (умножаем длину на высоту и делим на два).

Фото 4. Фасад здания после окончания отделочных работ

Порядок операций при выполнении замеров и подсчета площадей для наружных облицовочных работ:

Схематично рисуем планы фасадов с нанесением оконных и дверных проёмов. (Не забываем нанести чердачный фронтон и входную группу).
Измеряем и записываем полученные размеры в заготовленные планы.
Выполняем подсчет площадей по каждому фасаду.
Из общей площади вычитаем площадь оконных и дверных проёмов.

ДОПОЛНИТЕЛЬНЫЕ СВЕДЕНИЯ

Чтобы определить объём облицовочного материала, необходимо расчётную площадь фасада, за вычетом оконных и дверных проёмов, умножить на толщину отделочного материала. Единица измерения метр.
Для определения облицовочного материала в штуках необходимо расчётную площадь фасада разделить на площадь одной доски.
Определяя площадь доски при соединении досок способом «паз-шип», необходимо из размера доски по ширине исключить выступающую часть шипа.

Различные размеры у пиломатериалов

МАССА ТОВАРА В ЗАВИСИМОСТИ ОТ ФАКТОРОВ

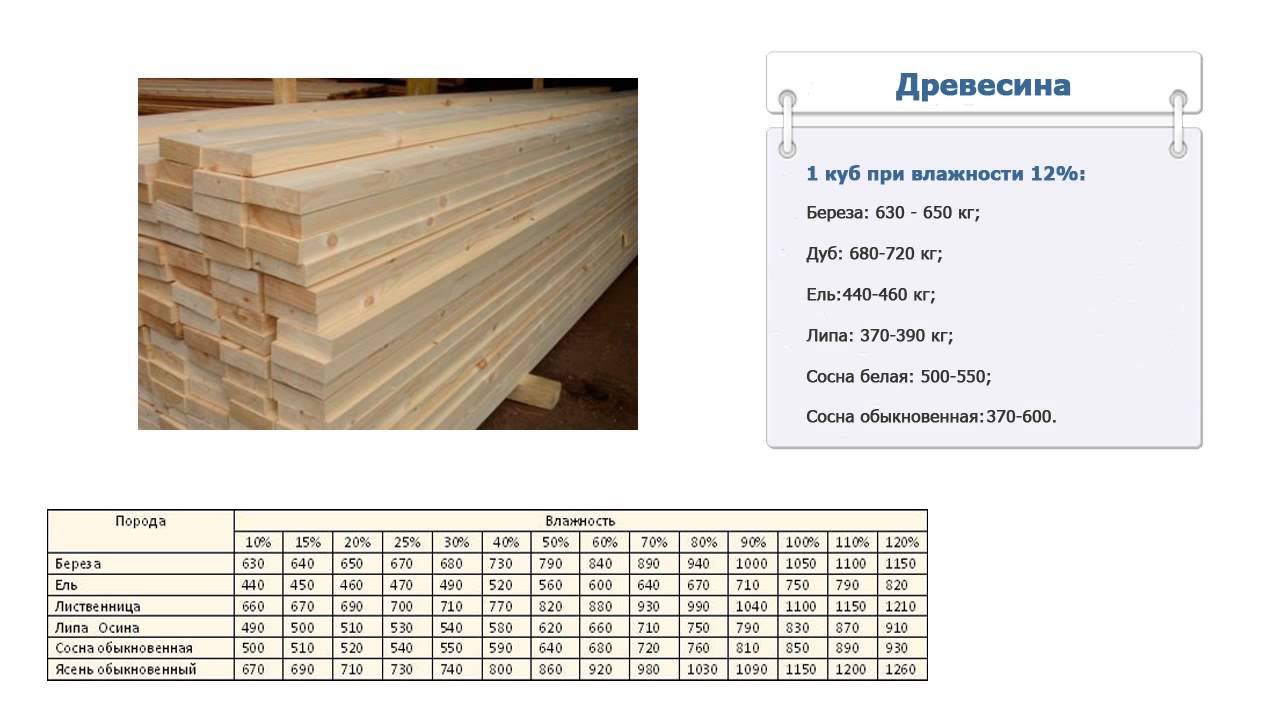
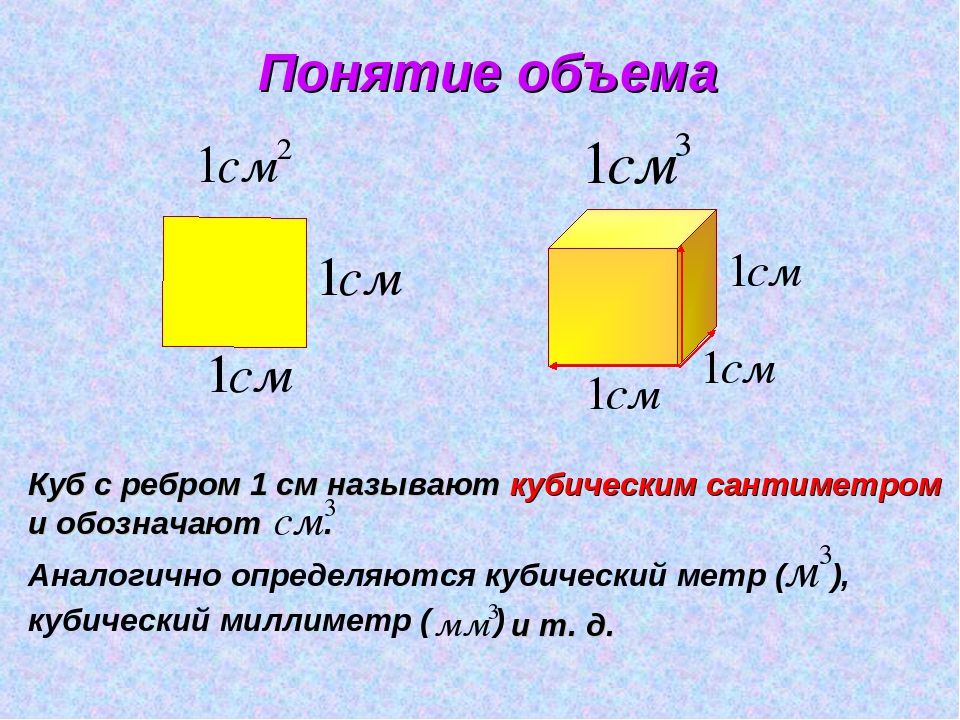
Чтобы определиться с массой отделочного материала, необходимо знать его объёмный вес. Объёмный вес облицовочного материала из древесины зависит от таких факторов при изготовлении, как порода древесины и её влажность.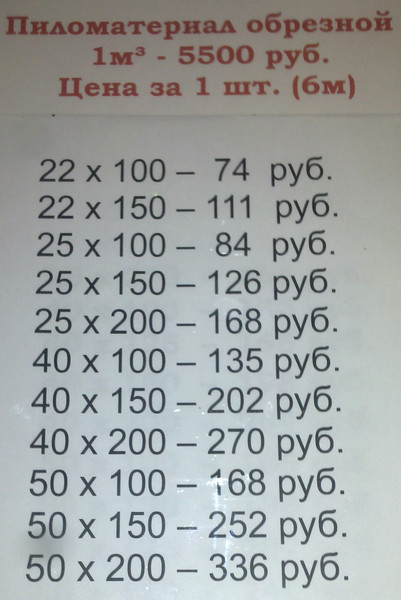 В таблице 1 даны сравнительные показатели объемного веса в кг/м3, в зависимости от породы и влажности древесины.

Древесина Влажность	Бук, граб, дуб	Лиственница	Сосна, ольха	Кедр, липа, ель
10-18%	700	600	500	450
19-23%	750	650	550	500
24-45%	800	700	600	550
Более 45%	1000	900	800	800

В ЗАКЛЮЧЕНИЕ

Шесть шагов для определения объёма облицовочных материалов:

Выполнить замеры.
Посчитать площади подлежащие облицовке.
Сходить в магазин и определить понравившуюся марку товара и записать основные размеры доски (длину, ширину, толщину), а также стоимость.
В зависимости от расчётной площади и толщины доски определить объём облицовочного материала, который необходимо приобрести. Полученные значения увеличиваем на 10%.
Для контроля при покупке определяем, какое количество досок будет соответствовать объёму закупаемого материала, рассчитанному в кубических метрах.
Определяем общую стоимость материала и идем покупать.

Примечание

При покупке необходимо оценить качество товара и его внешний вид.

Особое внимание обратить на возможное отклонение от геометрических размеров и прямолинейности. Материал с обнаруженными дефектами нужно заменить.

Сколько вагонки в кубе? Расчет количества квадратных метров досок, как рассчитать, сколько штук и квадратов в кубе

Касательно приобретения материалов существуют некоторые правила, однако покупатели обычно их не используют, в результате чего допускают большую ошибку. Проблема заключается в том, что многие покупатели не способны сами грамотно посчитать количество требуемого материала для отделки дома, например, в 20 кв. м. Они не пользуются существующими таблицами, с помощью которых можно сделать точные расчеты.

Такие покупатели приобретают примерное количество отделочного материала, которого потом либо не хватает, либо остается достаточно много. В результате человек теряет либо свое время на покупку новой партии, либо изначально переплачивает за материал.

Что такое вагонка?

Под вагонкой понимается тонкая доска, которая изготавливается из натурального дерева.

Данная доска оснащена особыми боковыми пазами для выполнения фиксации. Название данного вида досок произошло от того, что из них ранее строили. Раннее из данного материала возводили жилые вагонки, которые выступали в качестве непостоянного жилья. На сегодняшний день качество вагонки находится на достаточно высоком уровне, поэтому ее активно используют для возведения элитного жилья.

Вагонка является одним из лучших материалов для осуществления внутренней облицовки помещения. Также она демонстрирует отличные свойства при фасадной отделке.

Главными достоинствами вагонки являются:

привлекательный внешний вид;
способность утеплять помещения;
прекрасные звукоизоляционные свойства;
возможность спрятать имеющуюся коммуникацию;
длительный срок эксплуатации.

Сегодня на рынке можно встретить вагонку не только из натурального дерева, но и из пластика.

Пластиковая вагонка ориентирована преимущественно на декоративную внутреннюю отделку. Достоинством данного материала является высокое качество, прочность, простота установки и красивый внешний вид.

Деревянная вагонка изготавливается из натурального материала – древесины. Помещение, которое будет отделано с помощью данных досок, будет характеризоваться естественным микроклиматом. Важно отметить, что при повышенном количестве влаги дерево способно впитать её, а при нехватке, напротив, выделять. При этом в помещении будет сосредоточен приятный аромат, а атмосфера будет максимально уютной.

Вагонка лиственных пород

Наиболее распространенными лиственными породами, которые используются для изготовления вагонки, являются липа, ольха и дуб. Рассмотрим их подробнее.

Липа характеризуется отличной прочностью. Она имеет привлекательный цвет, который, к сожалению, темнеет при эксплуатации. Необходимо использовать специальные пропитки для сохранения изначального цвета. Вагонка из данного материала отлично зарекомендовала себя в помещениях с повышенной влажностью.

Ольха при нагревании будет выделять соединения, которые помогают восстановить здоровье. Подобный материал активно используется для отделки бани. Ольха характеризуется экологической чистотой, привлекательной текстурой и низким коэффициентом теплопроводности. Подобная вагонка выступает в качестве отличного звукоизолятора. Единственным недостатком является необходимость в защите для продления эксплуатационного срока.
Дуб представляет собой элитный материал, который преимущественно используется для внутренней отделки.

Вагонка хвойных пород

Вагонка также изготавливается и из хвойных пород.

Ель. Вагонка из данного материала легко обрабатывается и соединяется между собой.
Данный материал отличается низким показателем шероховатости.
Сосна. Вагонка в данном случае характеризуется красивым рисунком и привлекательным золотистым цветом. Это качественный и сравнительно недорогой материал.

Лиственница. Характеризуется отличной прочностью, способна удерживать тепло.
Кедр. Отличается долгим эксплуатационным сроком, особенно если вагонка защищена от прямого попадания влаги. Данный отделочный материал способен отлично удерживать тепло.

Сколько материала содержится в одном кубическом метре?

Чтобы правильно рассчитать требуемый объём определённой продукции, важно знать некоторые особенности осуществления подсчетов.

Если материал изготовлен из дерева, методика вычисления кубатуры сравнительно одинаковая. В данном случае неважно, из какого материала выполнены доски.

Для того чтобы сделать верные и максимально точные вычисления, необходимо воспользоваться следующей инструкцией.

Изначально требуется измерить основные параметры материала. За основу берем одну панель и вычисляем ее длину, ширину и толщину. Рассмотрим на практике один из примеров. Представим, что параметры нашего изделия следующие: 16х14х5000. Показатели указаны в миллиметрах.

Далее необходимо вычислить объем 1-го изделия. Для этого нужно перевести рассматриваемые единицы в метры. Для этого делаем следующее: 0,016*0,14*5=0,0112 м3.
Далее 1 м3 требуется поделить на то число, которое было получено во втором шаге. В результате у нас получается 89,29.

Таким образом вычисляется, сколько квадратов как в 6 кубах, так и 60.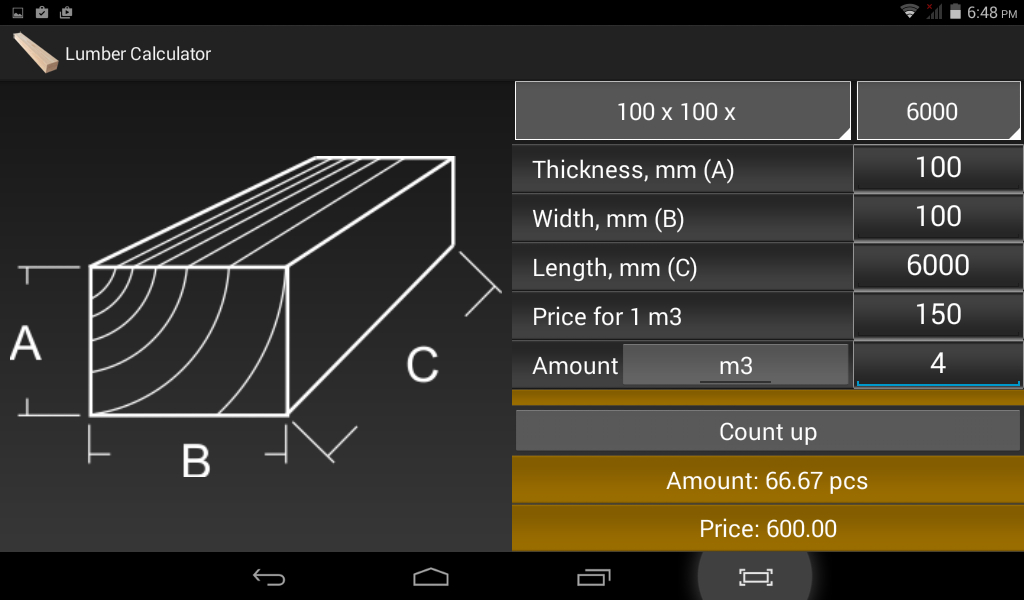 Также можно определить, сколько там штук.

Крайне важно четко следовать инструкции. Это требуется для того, чтобы расчеты были максимально точными.

Обратите внимание, что некоторые продавцы могут обманывать, выполняя неправильное округление. Делают они это с целью увеличения величины покупки.

Как рассчитать количество площади в одном кубическом метре

Для того чтобы избежать переплаты и не приобретать дополнительно панели, вам нужно знать, сколько в одном кубическом метре имеется площади, которая планируется быть облицованной. В этом случае огромную роль играет толщина изделия, которая может быть совершенно разной в зависимости от выбранного материала.

Многие задаются вопросом, зачем вообще нужна кубатура.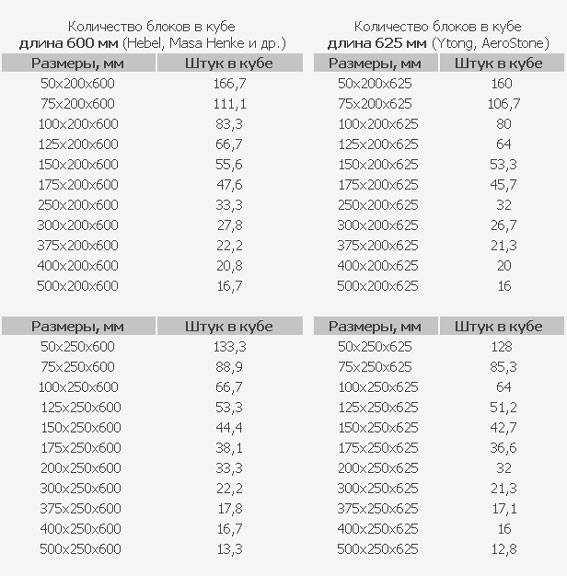 Это требуется для того, чтобы вы могли рассчитать площадь, которая может быть покрыта отделочными материалами. Исходя из этого, вам потребуется определить, сколько в одном кубе вагонки содержится квадратных метров.

Произвести расчёт несложно – достаточно воспользоваться инструкцией.

Изначально нужно измерить толщину одной приобретенной отделочной панели. Если мы имеем дело с деревянным материалом, то параметр будет находиться в диапазоне 13-26 мм.
Далее необходимо перевести данный результат в метры, поскольку объемные критерии должны измеряться именно в этой единице измерения. Рассмотрим ситуацию, когда толщина одной панели равна 17 мм. Переведя данное значение в метры, мы получим 0,017 м.
Завершающим этапом является деление куба на число, полученное ранее. У вас должно получиться следующее: 1/0,017=58,82 м2.

Обратите внимание, что расчеты можно произвести даже в уме, если это позволяют математические способности. Тем не менее с помощью калькулятора вы сможете добиться максимально точных результатов.

Рассчитываем объём материала для осуществления отделки

Сегодня наибольшим спросом пользуются деревянные панели, с помощью которых можно выполнять отделку различных помещений. Чтобы приступить к данному процессу, изначально важно произвести расчеты для определения количества нужного материала. Важно, чтобы данные расчеты были максимально точными – это поможет вам избежать покупки лишнего материала и переплаты за него.

Важно отметить, что количество выбранного материала во многом зависит от того, будет ли это внешняя отделка или внутренняя.

Рассмотрим подробно оба варианта.

Внутренняя обшивка

Для определения объема требуемой вагонки при внутренней облицовке помещения нужно разделить квадратуру на несколько отдельных площадей. Это позволяет рассчитать плоскость в качестве обычной геометрической фигуры. Как правило, помещение представляется в качестве прямоугольника, однако встречаются исключения. Длина досок в данном случае играет важную роль, поскольку она может быть разной, поэтому необходимо измерять длину всех отрезков.

Для определения количества требуемого материала необходимо следовать инструкции.

Изначально нужно определить ширину и длину помещения, которое необходимо отделать. Если планируется осуществить облицовку и потолочной поверхности, то её площадь также нужно вычислить.
Важно определить высоту и протяжённость стены для определения общей площади. Как правило, в одном помещении имеются две стены, расположенные параллельно и идентичные друг другу. Поэтому достаточно просчитать всего лишь одну из стен для того, чтобы определить протяженность и высоту двух.

В дальнейшем необходимо сложить все полученные значения. Не стоит забывать о том, что необходимо отнимать квадратуру проемов, которые есть в комнате. Рекомендуем прибавлять к полученному результату 10%, поскольку при отделке помещения нельзя обойтись без отходов. Даже если вы точно определили длину изделия, отходы всегда будут присутствовать.

Внешняя облицовка вагонкой

Если вы решили выполнить внешнюю обшивку здания, к примеру, фронтона, то расчеты будут производиться аналогично. Единственная трудность в данном случае заключается в вычислении площади фронтона.

Разберем процесс расчета пошагово.

Необходимо определить обшиваемую площадь точно так же, как и в случае с внутренней отделкой помещения.
Для определения площади фронтона необходимо взять длину основания и умножить его на высоту. Полученный результат в дальнейшем нужно разделить пополам.
Складываем все цифры. При этом не забываем отнимать от полученного результата площадь имеющихся проемов.

В следующем видео смотрите, сколько вагонки в кубе.

как рассчитать количество? Калькуляторы, советы

Автор: Олег Мальцев

Краткое содержание статьи:

Столкнуться с необходимостью определить, сколько квадратных метров в кубе можно не только на уроках математики, но и в жизни. Чаще всего такие расчеты производятся при строительстве. Для того, чтобы не допустить ошибок в расчете объема и стоимости стройматериала, нужно знать и уметь определить эти величины самостоятельно.

Для чего измерять кубометры?

Необходимость вычислить кубометры может возникнут в первую очередь при ремонтно-строительных работах. Кубический метр – это мера объема, которой измеряется множество строительных материалов, таких как:

Лес;
Кирпич;
Газоблок;
Бетон.

Квадратные метры – мера площади. Разница между этими двумя показателями в том, что для вычисления первой надо знать три величины исследуемого объекта:

Высоту;
Ширину;
Длину.

А для вычисления площади достаточно всего двух:

Длины;
Ширины.

Таким образом понятно, что для вычисления кубометра нужна площадь изделия. Надо отметить, что все расчеты в данном случае производятся исключительно в метрах. То есть все величины, которые измерены в сантиметрах до начала расчетов необходимо перевести в метры.

Если есть такие данные, как длина, ширина и высота, можно посчитать с помощью этого или этого онлайн-калькулятора.

Сколько в кубическом метре квадратных метров?

При расчете кубометра имейте в виду, что стандартом является куб, каждая грань которого равна одному квадратному метру. Таким образом, высота, длина и ширина такого куба одинакова.

Для того чтобы измерить кубометр квадратными метрами необходимо:

Измерить высоту требуемого предмета;
Перевести ее в метры;
Разделить один квадрат на получившее значение высоты.

Таким образом, измерить кубометр материала совсем не сложно. Для этого нужно знать всего три метрические единицы. Принимая во внимание, что в данном случае две из них равны одному, то нам остается всего лишь разделить единицу на высоту изделия.

Как измерить количество предметов в кубе?

Если вам нужно рассчитать объем материала в штуках, помещающихся в куб, можно сделать следующие расчеты:

Рассчитать площадь одного предмета, то есть умножить длину на ширину;
Перевести получившееся значение в квадратные метры;
После один квадрат разделить на площадь одного предмета. Так вы получите число предметов, входящих в один квадратный метр;
Измерить высоту объекта;
Перевести ее в метры;
Разделить один квадрат высоты на высоту объекта. Таким образом вы узнаете число квадратных метров материала в кубе;
Умножить число предметов на количество квадратных метров.

Таким образом вы получите объем строительных материалов в штуках. Такие расчеты используются для выяснения числа кирпичей или газоблоков.

Также, таким образом при необходимости можно посчитать требуемое количество любого стройматериала, у которого есть длина, ширина и высота. Например, ламината или напольной плитки.

Определение количества досок в одном кубометре леса

Для строительства лес, как правило, продают в строительных магазинах кубами. Свои подсчеты хозяева обычно ведут в штуках. Для того, чтобы понимать:

Сколько кубов леса заказывать;
Или наоборот, сколько досок получится в одном кубе, надо предварительно сделать некоторые расчеты.

Перед тем, как начинать их, уточните у продавца длину одной доски. Разные поставщики предлагают разный лес. У кого-то это шестиметровый брус, у кого-то трехметровый, а у кого-то могут быть и 1 метр 20 сантиметров. А также узнайте стандартную высоту и ширину. Обычно она около 2 – 2,5 сантиметров.

Зная исходную длину, считаем сколько таких досок в кубическом метре:

Умножаем длину бруса на необходимую вам и согласованную заранее с магазином ширину. При этом помним, что расчеты производятся в метрах. Так мы узнаем площадь одной доски;
Делим один квадрат на площадь одного бруса. Получаем количество досок в одном квадрате;
Делим один квадрат на высоту бруска, переведенную в метры. В нашем случае 2,5 см = 0,025 м. Получаем число квадратов в кубе;
Умножаем количество досок в одном квадрате на число квадратных метров в кубе.

Таким образом, определив количество необходимых досок в кубе вы сможете заказать нужное вам число кубометров для строительства.

Количество бетона в кубометрах

В бетонных работах также используются величины квадратного и кубического метража. Секрет заключается в том, что перед вызовом специальной машины с бетоном:

Вам потребуется измерить площадь участка, который вы планируете бетонировать;
Определиться с глубиной заливки;
Перевести все величины в метры;
Перемножить их между собой.

Так вы получите количество бетона, которое необходимо залить на ваш участок, для получения желаемой высоты бетонной подушки. Однако, при заказе раствора не следует указывать точную цифру. Лучше заказать немного больше, так как могут быть погрешности в ровности сторон участка и глубины заливки.

Таким образом, для того, чтобы узнать сколько квадратных метров в кубе, надо всего лишь знать высоту предмета, который вам необходимо измерить. Путем простого деления одного куба на этот показатель, вы уже получите требуемую величину. А в дальнейшем она поможет вам рассчитать более детально количество требуемого материала.

Видео: подсчет количества досок в кубе

В данном ролике математик Михаил Бураков расскажет о простом методе подсчета количества досок в одном кубе материала:

Кубатура доски. Сколько доски в кубе. Сколько квадратов в кубе

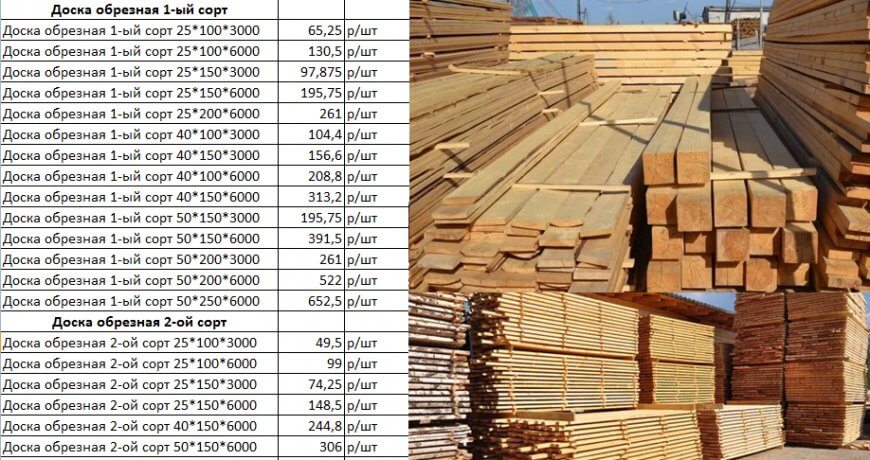
С помощью этой таблицы можно определить кубатуру 1 доски / бруса, а так же узнать, сколько досок / брусьев содержится в кубе.

Обрезной пиломатериал
Размер, мм	Кубатура 1 шт, куб.м.	Сколько штук в кубе, шт.	Сколько м2 в кубе, кв.м.
251006000	0,015	66,67	40
251256000	0,01875	53,33	40
251506000	0,0225	44,44	40
401006000	0,024	41,67	25
401256000	0,03	33,33	25
401506000	0,036	27,78	25
50506000	0,015	66,67	20
501006000	0,03	33,33	20
501256000	0,0375	26,67	20
501506000	0,045	22,22	20
502006000	0,06	16,67	20
1001006000	0,06	16,67	10
1001506000	0,09	11,11	10
1002006000	0,12	8,33	10
1501506000	0,135	7,41	6,67
1502006000	0,18	5,55	6,67
2002006000	0,24	4,17	5
Вагонка
12,5906000	0,00675	148,15	80
16906000	0,00864	115,74	62,5
Имитация бруса
161356000	0,01296	77,16	62,5
211356000	0,01701	58,79	47,62
211856000	0,02331	42,9	47,62
Половая доска
28906000	0,01512	66,14	35,71
281356000	0,02268	44,09	35,71
361356000	0,02916	34,29	27,77
Блок-хаус
281356000	0,02268	44,09	35,71
361856000	0,03996	25,02	27,77

Если вы задаетесь вопросом: сколько доски в кубе, сколько бруса в кубе, сколько квадратов в кубе, какая кубатура пиломатериала — Вам точно поможет эта таблица. В таблице указаны 3 основных расчетных показателя: кубатура 1 доски / бруса, количество досок / бруса в кубе и количество квадратных метров в кубе.

Таблица соответствия площади пиломатериалов и их объема

В данной таблице представлено соответствие площади и объема пиломатериалов производства СеверЛес. С её помощью можно определить какое количество упаковок содержится в одном кубическом метре пиломатериала или сколько квадратных метров покрывает пиломатериал одной упаковки.

Продукция	В 1 упаковке М²	В 1м³ упаковок	М2 в 1м³
Евровагонка 12,5×96(88)x1500	1,32	55,6	73,39
1800	1,58	46,3	73,39
2000	1,76	41,7	73,39
2100	1,85	39,7	73,39
2200	1,94	37,9	73,39
2400	2,11	34,7	73,39
2500	2,2	33,3	73,39
2700	2,38	30,9	73,39
3000	2,64	27,8	73,39
3300	2,9	25,3	73,39
3500	3,08	23,8	73,39
3600	3,17	23,1	73,39
3900	3,43	21,4	73,39
4000	3,52	20,8	73,39
5000	4,4	16,7	73,39
6000	5,28	13,9	73,39
«Штиль» 14х121х6000 (5 шт)	3,45	19,68	67,9
«Штиль» 14х145х6000 (5 шт)	4,11	16,42	67,49
«Штиль» 17х96х6000 (7 шт)	3,78	14,58	55,1
Блок-хаус 21х96х3000 (6 шт)	1,62	27,6	44,7
Блок-хаус 29х145х6000(3шт)	2,52	13,2	33,3
Блок-хаус 36х195х6000(2шт)	2,27	11,9	27
Блок-хаус 46х195х6000(2шт)	2,27	9,29	21
Доска пола 21х96х3000(6шт)	1,62	27,6	44,7
Доска пола 29х96х3000(4шт)	1,08	29,93	32,3
Доска пола 38х96х3000(3шт)	0,81	30,5	24,7
Доска пола 36х145х6000(2шт	1,68	16	26,9
Имитация бруса 18х145х6000(5шт)	4,11	12,77	52,5
Имитация бруса 21х145х6000 (4 шт)	3,28	13,68	44,9
Имитация бруса 21х195х6000 (4 шт)	4,53	10,17	46
Доска строг. 21х96х3000 (6 шт)	1,73	27,56	47,68
Доска строг. 21х145х3000 (4 шт)	1,74	27,37	47,62
Доска строг. 21х115х3000 (4 шт)	1,38	34,51	47,62
Доска строг. 50х150х3000 (1 шт)	0,9	22,22	20
Брусок 40х40х3000 (6шт)		34,72
Брусок 40х50х3000 (6 шт)		27,8
Брусок 50х50х3000 (6 шт)		22,2
Рейка 18х45х3000 (12шт)		34,3
Рейка 20х45х3000 (12 шт)		30,9

Расчет количества досок, бруса, вагонки

Как рассчитать количество досок

Допустим, вы рассчитали, что для постройки вам требуется 40 досок длиной 6 м, шириной 150 мм, толщиной 40 мм. Переведите все эти величины в метры и перемножьте между собой:

40х6х0,15х0,04=1,44, где 40 – количество досок; 6 – длина доски; 0,15 – ширина доски; 0,04 – толщина доски.

В итоге получили 1,44 кубических метра, без малого полтора кубических метра.

Таким же методом подсчитайте, сколько досок окажется в одном кубическом метре: разделите кубометр на объем одной доски. Для нашего примера, в котором доска толщиной 40 мм, шириной 150 мм и длиной 6 м, расчет будет таким:

1/0,04/0,15/6=27,7777.

Это означает, что в одном кубическом метре уместятся примерно 28 необходимых вам досок.

Приведенный выше расчет подходит для бруса и обрезной доски. Рассчитывать количество необходимой вагонки, необрезной доски и прочих пиломатериалов придется несколько иначе – понадобится таблица расчета кубатуры пиломатериала. Например, для подсчета необрезной доски очень часто используют переводной коэффициент 1.2, т.к. при получении куба обрезной доски около 0,2 м³ идет в отходы.

Как рассчитать количество вагонки

Для расчета количества вагонки необходимо знать только размеры поверхности, которую надо отделать.

Например, ваше помещение имеет размеры 3,2м х 4,6м, высота потолков 2,5м. Вы хотите, чтобы доски располагались вертикально. Значит вам нужна вагонка длиной 2,5м.

Учитывая, что рабочая ширина вагонки — 88мм, а у вас две стены длиной 3,2м и две стены длиной 4,6м значит на стену длиной 3,2м вам надо 3,2/0,088=36,36=37 досок, на стену длиной 4,6м вам надо 4,6/0,088=52,27=53 доски.

Итого 37х2+53х2=180 досок, т.е. 18 пачек вагонки по 2,5м длиной.

Но у вас в комнате имеются двери и окна — это уменьшает количество необходимой вагонки.

Допустим в вашей комнате есть одна дверь размером 0,8х2м и одно окно размером 1,2х1,5м на расстоянии 0,8м от пола.

Тогда вычитаем из общего количества (0,8+1,5)х0,088=26,13=26 досок, т.е. вам надо 180-26=154 доски=16 пачек вагонки 2,5м.

У вас остались неиспользованные 6 досок длиной 2,5 метра. Их вы можете использовать для заделки проема над дверью и окном, а также под окном. Если этих 6 досок не хватит, то можно еще купить вагонку другой длины, например, 0,5 или 0,6 метра (по высоте над дверью, окном и под окном).

Как рассчитать количество бруса на дом

Расчет бруса, совершенно точно произвести невозможно. Все будет зависеть от монтажа строения и от качества бруса. Случается, что брус, который отличный на вид, при распиливании оказывается абсолютно не годным для установки, поэтому его нужно покупать с запасом.

Формула: V = суммарная длина стен × высота стен × на толщину бруса. После чего мы получим количество кубометров бруса, необходимых для постройки дома.

Пример: нужно построить дом 6×9 м, с пятой стеной. Его высота составит 3 метра. Брус возьмем размером 150×150 мм.

Чтобы рассчитать брус на такой дом, необходимо узнать периметр стен включительно с пятой стеной: 6+6+6+9+9=36 метров погонных. После чего умножаем эту суммарную длину на высоту этажа, которая равна 3 метра, и получаем: 36 м пог. × 3 м = 108 квадратных метров. Далее получившуюся площадь умножаем на толщину бруса: 108 кв. м × 0,15 м = 16,2 куб. м.

Таким образом, на наш дом размером 6×9 метров нам понадобится 16,2 кубических метров бруса.

Также существует другой способ расчета бруса.

1	Просчитываем длину стен по всему периметру планируемого строения и разделяем на длину бруса. Так узнаем количество бруса, что потребуется на установку одного венца. Затем измеряем высоту строения и разделяем ее на толщину бруса. Цифра, что получится будет количеством бруса, необходимым для возведения высоты. Ее нужно умножить на количество несущих стен и на количество, которое перед этим определили для установки одного венца. Число, полученное в итоге, будет количеством бруса, выраженное в штуках.
2	Если в воздвигаемом строении предусмотрена установка несущих стен не лишь по всему периметру, но и дополнительных, то при проведении подсчетов, необходимо учитывать длину и высоту всех несущих стен.
3	Во всех расчетах не производится из рассчитанного бруса вычитание площади окон и дверей. Но к количеству бруса, даже не исключая из расчета площадь окон и дверей, следует сверх рассчитанного количества прибавить 20-25%.

Количество квадратов на шахматной доске

Можете ли вы расширить свою технику для вычисления количества прямоугольников на шахматной доске?

Еще одна головоломка, которую мне прислали по электронной почте через этот веб-сайт. Моим инстинктом было то, что ответ был просто большим, но я подумал об этом, и решение на самом деле довольно простое …

Во-первых, почему ответ — не просто 64…
Все красные квадраты на картинке выше будут считаться действительными квадратами, поэтому мы спрашиваем, сколько квадратов любого размера от 1×1 до 8×8 есть на шахматной доске.

Ключ в том, чтобы подумать, сколько позиций может быть расположено в квадрате каждого размера … Квадрат 2×2, например, в силу своего размера может быть расположен в 7 местах по горизонтали и 7 по вертикали. т.е. в 49 различных позициях. Квадрат 7×7 может поместиться только в 2 положениях по вертикали и 2 по горизонтали.Рассмотрим, что ниже …

размер	горизонтальных позиций	вертикальных позиций	позиций
1х1	8	8	64
2х2	7	7	49
3×3	6	6	36
4×4	5	5	25
5×5	4	4	16
6×6	3	3	9
7×7	2	2	4
8×8	1	1	1
		всего	204

Всего на шахматной доске 204 клетки.Это сумма количества возможных позиций для всех квадратов размером от 1×1 до 8×8.

Формула для шахматной доски n x n?

Математически это записывается следующим образом:

Доказательство явного решения выходит за рамки этого сайта, но если вы хотите найти его, математик назовет его «суммой квадратов первых n натуральных чисел».’Окончательный ответ дает

n ³/3 + n ²/2 + n / 6

Можете ли вы расширить свою технику для вычисления количества прямоугольников на шахматной доске?

Все приведенные выше примеры будут допустимыми прямоугольниками …

Есть несколько способов решить эту проблему. Но имеет смысл сначала расширить нашу технику от задачи о квадратах. Ключ к этому — думать о каждом прямоугольнике индивидуально и учитывать количество позиций, в которых он может быть расположен.Например, прямоугольник 3×7 может располагаться в 6 положениях по горизонтали и 2 по вертикали. Из этого мы можем построить матрицу всех возможных прямоугольников и суммы.

Размеры		1	2	3	4	5	6	7	8
	позиций	8	7	6	5	4	3	2	1
1	8	64	56	48	40	32	24	16	8
2	7	56	49	42	35	28	21	14	7
3	6	48	42	36	30	24	18	12	6
4	5	40	35	30	25	20	15	10	5
5	4	32	28	24	20	16	12	8	4
6	3	24	21	18	15	12	9	6	3
7	2	16	14	12	10	8	6	4	2
8	1	8	7	6	5	4	3	2	1
										1296

Всего существует 1296 возможных прямоугольников.

Элегантный подход к прямоугольникам, учтите вершины и диагонали.

Вершины — это пересечения. Для нашей доски их 81 (9 х 9). Диагональ, начинающаяся в одной вершине и заканчивающаяся в другой, однозначно описывает прямоугольник.Чтобы быть диагональной, а не вертикальной или горизонтальной линией, мы можем начинать где угодно, но конечная точка не должна иметь одинаковые вертикальные или горизонтальные координаты. Таким образом, существует 64 (8 x 8) возможных конечных точек.

Таким образом, допустимые диагонали 81 x 64 = 5184.

Однако, хотя каждая диагональ описывает уникальный прямоугольник, каждый прямоугольник не описывает уникальную диагональ.

Мы тривиально видим, что каждый прямоугольник может быть представлен четырьмя диагоналями.

Итак, наше количество прямоугольников равно 81 x 64/4 = 1296 .

n x n или n x m?

n x n: (n + 1) ² x n ²/4
n x m: (n + 1) x (m + 1) x (n x m) / 4

Что, очевидно, можно превратить во что-то более сложное.

Прямоугольники в математической номенклатуре

⁹ C ₂ • ⁹ C ₂ = 36 ² = 1296

© Найджел Колдвелл, 2004 г. — — вопросов на этом сайте могут быть воспроизведены без дополнительного разрешения, я не претендую на авторские права на них.Ответы принадлежат мне и не могут быть воспроизведены без моего явного предварительного согласия. Пожалуйста, задавайте вопросы, используя ссылку вверху страницы. Безопасная версия этой страницы.

Скрытые прямоугольники

Получено аккуратное решение первой части задачи от Саны, Дженни, Криса и Розион из Мадрасского колледжа, Сент-Эндрюс. Мне нравится использовать линии, а не думать о прямоугольники точно так же, как и квадраты (что я и сделал). Эту идею довольно легко обобщить на шахматы размером n x n. доска.

Остальные верные решения были получены от Андрея из школы 205. Бухарест, средняя школа общины Мэри Берчвуд и Чен из Китайская средняя школа, Сингапур.

Молодец.

На шахматной доске 1296 различных прямоугольников.

204 из этих прямоугольников — квадраты.

Первый взгляд на квадраты:

Рассмотрите возможность размещения квадрата размером 1 x 1 вдоль левого края. шахматной доски. Этот квадрат может находиться в любой из 8 позиций (как на шахматной доске 8 на 8 квадратов).Аналогично квадрат может быть размещен в любом из восьми положений по верхнему краю. Так общее количество

1 x 1 квадрат = 8 x 8 = 64.

Квадрат 2 x 2 может занимать 7 позиций вдоль левого края. и 7 позиций по верхнему краю 7, что дает 7 x 7 = 49 квадратов размер 2 x 2.

Продолжая таким образом, мы получаем квадраты размером 3 x 3, 4 x 4 и скоро.

Размер квадрата	Кол-во квадратов
1 х 1	8 х 8 = 64
2 х 2	7 x 7 = 49
3 x 3	6 х 6 = 36
4 х 4	5 х 5 = 25
5 x5	4 х 4 = 16
6 х 6	3 х 3 = 9
7 x 7	2 х 2 = 4
8 х 8	1 х 1 = 1

Итак, квадратов 204.

Затем, глядя на прямоугольники:

Чтобы сформировать прямоугольник, вы должны выбрать 2 из 9 вертикальных линий. и 2 из 9 горизонтальных линий.

Для двух горизонтальных линий: первую строку можно выбрать в 9 способов второй — восемь способов. Это означало бы, что вы могли сказать разница между строками 1 и 3, скажем, и 3 и 1, что не случай, поэтому вам нужно разделить 9 x8 8 на 2, получив 36.

Аналогичным образом вы можете выбрать две вертикальные линии 36 способами.

Итак, количество прямоугольников равно 362

362 = 1296

В следующем подходе используются несколько других решений. отправлено.

Прямоугольник (или квадрат) будет иметь высоту от 1 до 8 единиц. и шириной от 1 до 8 единиц. Это можно представить в виде таблица с каждой возможной шириной, представленной столбцом, и каждый восемь подряд.

Записи в таблице ниже указывают количество каждого прямоугольник на шахматной доске (используя аргументы, аналогичные первым часть проблемы выше).

В последнем столбце таблицы указано общее количество прямоугольники в каждой строке.

Высота / ширина	1	2	3	4	5	6	7	8	Всего
1	8 х 8	7 х 8	6 х 8	5 х 8	4 х 8	3 х 8	2 х 8	1 х 8	8 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 8 x 36
2	8 х 7	7 х 7	6 х 7	5 х 7	4 х 7	5 х 7	2 х 7	1 х 7	7 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 7 x 36
3	8 х 6	7 х 6	6 х 6	5 х 6	4 х 6	3 х 6	2 х 6	1 х 6	6 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} = 6 x 36
4	8 х 5	7 х 5	6 х 5	5 х 5	4 х 5	3 х 5	2 х 5	1 х 5	5 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
5	8 х 4	7 х 4	6 х 4	4 х 4	5 х 4	3 х 4	2 х 4	1 х 4	4 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
6	8 х 3	7 х 3	6 х 3	4 х 3	5 х 3	3 х 3	2 х 3	1 х 3	3 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
7	8 х 2	7 х 2	6 х 2	4 х 2	5 х 2	3 х 2	2 х 2	1 х 2	2 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
8	8 х 1	7 х 1	6 х 1	4 х 1	5 х 1	3 х 1	2 х 1	1 х 1	1 x (1 + 2 + 3 + 4 + 5 + 6 + 7 + 8}
									(1 + 2 + 3 + 4 + 5 + 6 + 7 + 8} x 36 = 362

Следовательно, общее количество прямоугольников в сетке 8 x 8 равно (1 + 2 + 3 +… + 8) 2

Общее количество прямоугольников в сетке n x n составляет (1 + 2 + 3 + … + п) 2 = (п2 (п + 1) 2) / 4. Это использует формула суммы первых n натуральных чисел, арифметическая прогрессия. Подробнее об этом см. В доказательстве. сортировщик (ссылка).

Количество квадратов: (12 + 22 + 32 + … n2) = (n (n + 1) (2n + 1)) / 6 (для доказательства см. телескопирование серия)

SA: Имеют ли кубы и квадраты те же свойства, что и сферы и круги?

Студенты-математики часто бывают заинтригованы, когда понимают, что производная формулы объема сферы по радиусу сферы является формулой поверхности сферы:.Они также очарованы тем фактом, что производная от формулы площади круга является формулой для его длины:. Эти результаты, кажется, неприменимы к кубам и квадратам, потому что площадь поверхности куба и периметр квадрата. Почему сферы и круги ведут себя так, а кубы и квадраты — по-другому?

Рассмотрим производную площади круга. Согласно определению производной:

Геометрически этот результат легко увидеть, потому что область между двумя концентрическими окружностями, одна с радиусом r , а другая с радиусом r + h , по существу представляет собой полосу шириной h и длиной 2π r , как показано на рисунке 1.

Аналогичное вычисление справедливо для производной объема сферы. Согласно определению производной:

Геометрически этот результат легко понять, потому что область между двумя концентрическими сферами, одна с радиусом r, а другая с радиусом r + h , по существу представляет собой полый шар толщиной h и площадью поверхности 4π r ².

Подобные результаты не верны для стандартной формулы для объема куба и площади квадрата, как показано в первом абзаце.Давайте рассмотрим разные формулы: Пусть s будет расстоянием от центра квадрата перпендикулярно противоположной стороне, как показано на рисунке 2. Тогда, поскольку s составляет половину длины края квадрата, мы имеем формула A = (2 s ) ² = 4 s ² и P = 8 s для площади квадрата и периметра квадрата соответственно.

Рассмотрим производные этой новой формулы площади квадрата.Так как A = 4 s ², что является нашей формулой для периметра квадрата. Аналогично, пусть s будет расстоянием от центра куба перпендикулярно противоположной стороне. Тогда, поскольку s составляет половину длины ребра куба, мы имеем формулу V = (2 s ) ³ = 8 s ³ для объема куба, и (2 с ) ² = 4 с ² для площади каждой грани.Поскольку V = 8 s ³, то, что в 6 раз больше площади грани куба, и, таким образом, это выражение равно площади поверхности куба. Записав формулы в терминах s , половина длины ребра, мы теперь имеем формулы, которые имеют свойства, согласующиеся со свойствами сфер и кругов.

Мы можем распространить этот результат на равносторонние треугольники. Пусть e будет длиной ребра треугольника, как показано на рисунке 3.

Площадь треугольника равна, а его периметр равен 3 e . Производная площади равна, что отдаленно не похоже на периметр треугольника. Давайте теперь изменим переменную и пусть s представляет собой перпендикулярное расстояние от центра треугольника до одной из сторон, как показано на рисунке 4.

Используя соотношение Пифагора, или. В терминах s площадь треугольника равна, а периметр равен. Поскольку производная площади равностороннего треугольника равна периметру треугольника.Рисунок 5 показывает, что разница между треугольными областями с использованием s и s + h , по сути, представляет собой трехстороннюю полосу шириной h и длиной, равной периметру треугольника, что геометрически подтверждает наш результат.

Случай равностороннего треугольника предлагает способ обобщения этого результата на другие правильные многоугольники. Отрезок s от центра многоугольника перпендикулярно стороне называется апофемой многоугольника.Тогда длина стороны многоугольника равна, где n — количество сторон, и, следовательно, периметр многоугольника равен. Площадь многоугольника — это длина апофемы, умноженная на половину длины периметра. В символах:

Теперь мы можем проверить это, периметр правильного многоугольника.

Предложите своим ученикам применить этот метод к правильному шестиугольнику. Они должны найти формулы для площади и периметра шестиугольника с точки зрения его апофемы.Затем они должны показать, что одно является производным от другого.

Мы также можем распространить наши результаты на трехмерные фигуры. Для правильных многогранников апофема — это радиус вписанной сферы. Рассмотрим тетраэдр.

Стандартные формулы для объема и площади поверхности тетраэдра обычно основаны на длине ребра, a , тетраэдра. Однако нетрудно переписать их в терминах длины r апофемы — радиуса вписанной сферы.

r = радиус вписанной сферы = апофема многогранника
R = радиус описанной сферы
a = длина края тетраэдра
S = площадь поверхности тетраэдра
V = объем тетраэдра

В пересчете на r вписанный радиус:

Таким образом, мы легко можем видеть, что в терминах апофемы производной формулы для объема тетраэдра является формула для его площади поверхности.

Аналогично, используя стандартные формулы для объема и площади поверхности октаэдра на основе длины ребра, a , октаэдра. Мы можем переписать их в терминах длины апофемы х .

Опять же, ясно, что производная формулы объема по отношению к r является формулой для площади поверхности.

Вот формулы для объема и площади поверхности двух других правильных многогранников через длину вписанного радиуса, r .

Додекаэдр:

Икосаэдр:

Вы можете поручить учащимся сложную задачу проверки того, что производная приведенной выше формулы для объема додекаэдра на самом деле является данной формулой для его площади поверхности.

Какова ценность этого результата? Это просто академическое упражнение? Фактически, эти формулы предоставляют простой способ найти формулу для площади поверхности обычных твердых тел, если вы знаете формулу для их объема, или наоборот.Просто напишите формулу в терминах апофемы твердого тела и дифференцируйте или антидифференцируйте соответственно, чтобы найти другую формулу.

Список литературы

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#octahedron

http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html

Джон Ф. Махони представил AP Statistics в средней школе Баннекер в 2002–2003 годах и обучил 59 студентов в этом году в рамках курса. Каждый из студентов сдал экзамен AP, и Махони считает, что у них, возможно, был самый высокий процент пожилых людей, сдавших статистику AP в стране.В этом году он также преподает вычисление AP уровня AB и BC. Он является консультантом AP и давним участником чтения AP Calculus. В настоящее время он является одним из руководителей экзаменов. Он также возглавляет редакционную коллегию журнала NCTM ON-Math: www.nctm.org/onmath. В средней школе Баннекера он является одним из наставников команды робототехники и помогает студентам проектировать приводные механизмы на основе зубчатых колес — так же, как сам Баннекер делал более 200 лет назад. Им помогают многие инженеры, в том числе из Университета Ховарда, расположенного через проспект Джорджии от средней школы.Он является одним из тренеров отмеченной наградами школьной команды It’s Academic. Когда он решил преподавать в средней школе Баннекера три года назад, после долгой карьеры в частных школах, он изучил математику Баннекера, и эта статья является результатом этой работы.

Сколько квадратов? | Квадрат и кубики | CBSE | Класс 5

Каждый прямоугольник состоит из 12 равных квадратов, поэтому все они имеют одинаковую площадь, но длина границы будет разной.

Какой из этих прямоугольников имеет самый длинный периметр?
Какой из этих прямоугольников имеет наименьший периметр?

От детей не требуется, чтобы они выучили определение термина «область», но они разовьют понимание этого понятия с помощью подходящих примеров. Дайте им много возможностей в классе сравнивать предметы по площади и угадывать, что больше. Такие вещи, как печати, листья, следы, стены класса и т. Д.можно сравнить.

Марки меры

Посмотри на эти интересные марки

Сколько квадратов со стороной в один сантиметр покрывает штамп А?
А штамп Б?
Какая марка имеет наибольшую площадь?
Сколько квадратов со стороной 1 см покрывает эта марка?
Сколько стоит самая большая марка? квадратные см.
Какие две марки имеют одинаковую площадь?
Сколько стоит каждая из этих марок? квадратные см.
Площадь наименьшего штампа — см кв.
Разница между площадью самого маленького и самого большого штампа составляет квадратный сантиметр. .

Соберите несколько старых марок. Разместите их на квадратной сетке и найдите их площадь и периметр.

Угадать

У кого больше площадь — у одного из ваших следов или страницы этой книги?
Какая из них имеет меньшую площадь — две банкноты по пять рупий вместе или банкнота в сто рупий?
Посмотрите на банкноту в 10 рупий.Его площадь больше ста квадратных сантиметров?
Площадь синей фигуры больше площади желтой фигуры? Почему?
Периметр желтой фигуры больше периметра синей фигуры? Почему?

Насколько велика моя рука?

Проведите рукой по квадратному листу на следующей странице.

Как вы решите, чья рука больше — ваша рука или рука вашего друга?

Какова площадь руки вашего друга? _______ квадратных см.

Мои следы

Чей след больше — твой или твой друг?
Как вы решите? Обсудить
У вас одинаковые следы?
Угадайте, след какого животного будет иметь такую же площадь, что и ваш. Обсуждать.
Вот следы животных в натуральную величину.Угадай площадь их следов

На этом этапе детям не нужно считать каждый квадрат. Попросите их определить самые большие квадраты и прямоугольники в пределах следа, чтобы узнать их площадь, а затем посчитать маленькие квадраты неправильной формы. Хотя область прямоугольника будет описана в главе 11, некоторые дети могут обнаружить, что они могут найти эту область быстрее посредством умножения.

Сколько во мне квадратов?

В этом упражнении дети должны заметить геометрическую симметрию фигур, чтобы определить свою область.Поощряйте детей разрабатывать собственные стратегии. В этих примерах округление не требуется.

Попробуйте треугольники

Помогите Садику найти еще несколько таких треугольников. Нарисуйте еще как минимум 5.

Завершите форму

Суручи нарисовал две стороны фигуры. Она попросила Асифа дополнить фигуру еще двумя сторонами, чтобы ее площадь составила 10 квадратных сантиметров.

Он прав? Обсуждать.
Объясните, что зеленая область составляет 4 см2, а желтая область — 6 см2.
Суручи прав? Сколько стоит синяя область? Объяснять.
Можете ли вы придумать другие способы завершения фигуры?
Попробуйте другие способы самостоятельно.
Теперь попросите своих друзей решить их.

Это одна из сторон фигуры. Завершите форму так, чтобы ее площадь составляла 4 см кв.
Здесь нарисованы две стороны фигуры. Завершите форму, нарисовав еще две стороны так, чтобы ее площадь была меньше 2 квадратных сантиметров.

Детей можно побуждать создавать фигуры с прямыми или изогнутыми краями, чтобы покрыть заданную область. Это упражнение можно расширить, попросив детей нарисовать на бумаге в квадрате столько фигур, сколько они могут на данной площади, и угадать самый большой или самый маленький периметр.Их также можно попросить проверить свои догадки, измерив размеры фигур. В случае изогнутых краев для измерения периметра можно использовать резьбу.

Вот прямоугольник площадью 20 кв.
1. Нарисуйте одну прямую линию в этом прямоугольнике, чтобы разделить его на два равных треугольника. Какова площадь каждого из треугольников?
2. Нарисуйте одну прямую линию в этом прямоугольнике, чтобы разделить его на два равных прямоугольника.Какова площадь каждого из меньших прямоугольников?
3. Нарисуйте в этом прямоугольнике две прямые линии, чтобы разделить его на один прямоугольник и два равных треугольника.
- Какова площадь прямоугольника?
- Какова площадь каждого из треугольников?

Пазлы с пятью квадратами

Измерьте сторону небольшого квадрата на квадратной бумаге, указанной ниже. Сделайте столько формы по возможности используя 5 таких квадратов.Для вас нарисованы три.

Сколько разных фигур вы можете нарисовать? ___________
Какая форма имеет самый длинный периметр? Сколько? _______ см
Какая форма имеет самый короткий периметр? Сколько? _______ см
Какова площадь фигур? _______ квадратных см. Все просто!

Вы получили все 12 фигур из 5 квадратов?

Нарисуйте все 12 фигур на листе картона и вырежьте их.

Попробуйте еще одну головоломку

Из этих 12 фигур нужно создать прямоугольник 5 * 12. Для этого существует более 1000 способов. Если ты найдешь хотя бы один — отлично!

Игровое время

Вот шахматная доска. Играйте в эту игру со своим партнером, используя один набор из 12 фигур.

Первый игрок выбирает одну фигуру из набора и кладет ее на доску, покрывающую любые пять квадратов.

Другой игрок выбирает другую фигуру и кладет ее на доску, но она не должна перекрывать первую фигуру.

Продолжайте по очереди, пока один из вас не перестанет идти дальше.

Выигрывает тот, кто поставит последнюю фигуру!

Сделайте свою плитку

Вспомните образцы пола из книги 4 по математике и магии (страницы 117-119). Вам нужно было выбрать правильную плитку, которую можно было повторить, чтобы создать узор, чтобы не оставалось зазоров.

Поощряйте детей попытаться решить эти головоломки «пентамино» дома.Такие упражнения могут быть разработаны для фигур с 6 квадратами (гексомино), и в этом случае будет возможно 35 различных форм.

Зири пошел в магазин и был удивлен, увидев разный узор плитки на полу.
Разве это не красиво!

Можете ли вы найти плитку, из которой повторяется каждый из этих рисунков пола?
Обведите по плитке в каждом узоре.

Посмотрев на узоры, Зири захотела сделать свою собственную желтую плитку.Вы тоже таким способом делаете плитку.

Сделайте узор из плитки.Обведите фигуру, чтобы она повторилась на странице, но помните, что между ними не должно быть промежутков.

Зири сделала узор из своих желтых плиток (вы знаете площадь ее плитки).

Сколько плиток она использовала?
Какова площадь рисунка пола, созданного Зири?

Зири пытался сделать другие плитки. Она начала с квадрата со стороной 2 см и сделала такие формы.
Посмотрите внимательно на них и узнайте:

Какая из этих форм укроет пол (без зазоров)? Обсуждать. Какова площадь этих фигур?
Создайте дизайн на своей копии, выложив эти фигуры плиткой.
Теперь вы создаете свои собственные новые плитки из квадрата. Можете ли вы сделать то же самое с треугольником? Попробуй это сделать.

В классах III и IV основные формы, такие как квадраты, прямоугольники, шестиугольники, треугольники, круги и т. Д., Использовались для проверки того, какие из них можно облицовывать, а какие нет, для создания рисунков пола.Теперь дети должны иметь возможность изменять основные формы для создания различных форм мозаики. В приведенном выше упражнении они могут создавать новые формы из квадрата, который не укладывается в мозаику, даже если их площадь остается такой же, как у квадрата, из которого они сделаны.

ГОЛОВОЛОМКИ с подвижным кубом

Можно, конечно, получить пять алфавитных блоков и с помощью реальной проверки определить, каким блоком он должен быть, но при правильном понимании нечетно-четной структуры системы правильный блок можно определить, просто изучив картинку.Более того, проверка на четность обеспечивает доказательство того, что эмпирический тест — нет. Тест просто показывает, что один блок в ряду мог быть центральным; это не доказывает, что никакой другой блок не мог бы быть, если бы была сделана правильная последовательность поворотов. Доказательство паритета будет объяснено в следующем месяце. Вот ответ из колонки за январь 1964 года: В прошлом месяце читателей попросили определить, какой из пяти блоков алфавита в ряд на шахматной доске был центральным блоком в предыдущем построении до того, как блоки были перемещены, переворачивая их через край от квадрата к квадрату.Очевидно, что если блок перемещается четное количество раз, он будет стоять на квадрате того же цвета, что и квадрат, на котором он был начат. Нечетное количество ходов помещает его на квадрат противоположного цвета. Не так очевиден способ, которым нечетное и четное применимо к ориентации каждого блока.
Представьте себе блок, окрашенный в красный цвет с трех сторон, которые встречаются в одном углу и размещенный так, чтобы вы могли видеть три его стороны. Есть четыре варианта: вы не видите ни одной красной стороны, одной красной стороны, двух красных сторон или трех красных сторон.Если вы видите одну или три красные стороны, мы говорим, что у блока нечетная четность; в противном случае — четность. Каждый раз, когда блоку дается четверть оборота в любом направлении, он обязательно меняет четность. (Это следует из того факта, что противоположные стороны блока имеют разные цвета. Каждая четверть оборота убирает одну сторону с вашей прямой видимости и показывает противоположную сторону. Таким образом, четверть оборота всегда изменяет один из видимых цветов. ) Думайте о блоке как о кубике, а не о блоке с цветными сторонами. В этом случае на его четность указывает то, является ли поворот трех видимых граней четным или нечетным.

Поскольку каждое движение блока дает ему четверть оборота, он меняет свою четность с каждым ходом. После четного числа ходов он окажется на квадрате того же цвета, что и квадрат, с которого он начал, и будет иметь ту же четность. После нечетного количества ходов изменится и цвет квадрата, и четность. Центральный блок изначально стоял на белом. Если он переместился нечетное количество раз, он окажется во втором построении на черном квадрате, его четность изменится. Но все блоки на черных квадратах во второй формации имеют одинаковую четность, поэтому центрального блока среди них нет.Должно быть, он двигался четное количество раз. Это поместит его на белый квадрат с той же четностью, что и раньше. Из двух блоков на белых квадратах только второй справа имеет неизменную четность. Следовательно, мы ищем именно этот блок.

Это выдержка из колонки Гарднера за ноябрь 1965 года: В прошлом математики-любители уделяли много внимания «турам» по шахматной доске, в которых шахматная фигура перемещается по доске, чтобы посетить каждую клетку один и только один раз, с соблюдением различных ограничений.В прошлом году Джон Харрис из Санта-Барбары, штат Калифорния, разработал увлекательный новый вид тура — «тур по кубу», который открывает множество возможностей.

Чтобы поработать над двумя лучшими задачами Харриса, возьмите небольшой деревянный кубик из набора детских кубиков или сделайте одну из картона. Его стороны должны быть примерно того же размера, что и квадраты вашей шахматной доски или шахматной доски. Покрасьте одну сторону в красный цвет. Куб перемещается из одного квадрата в соседний, наклоняя его за край, причем край упирается в линию, разделяющую две ячейки.Таким образом, за каждое движение куб делает четверть оборота в северном, южном, восточном или западном направлении.

Задача 1. Поместите куб в северо-западный угол доски красной стороной вверх. Совершите поездку по доске, отдыхая только один раз в каждой ячейке и заканчивая кубиком красной стороной вверх в северо-восточном углу. Однако во время экскурсии кубу не разрешается отдыхать красной стороной вверх. (ПРИМЕЧАНИЕ: невозможно совершить такой обход от угла до противоположного по диагонали угла.)

Проблема 2.Поместите кубик в любую ячейку неокрашенной стороной вверх. Сделайте «повторный тур» по доске (один, который посещает каждую ячейку один раз и возвращает куб в его начальную клетку) таким образом, чтобы ни в какой момент во время обхода, в том числе на финише, кубик не стал красным сторона быть вверх.

Обе проблемы имеют уникальные решения, не считая поворотов и отражений пути.

Вот ответ из декабрьской колонки 1965 года: Ниже показаны решения проблем с вращением куба.В первом решении красная сторона куба находится только на верхних угловых квадратах. Во втором случае точка отмечает начало тура красной стороной вниз.

Это выдержка из колонки Гарднера за март 1975 года: 8. Катящиеся кубики. Для этой красивой комбинаторной головоломки, придуманной Джоном Харрисом из Санта-Барбары, Калифорния, вы должны получить восемь единичных кубиков. На каждом кубе раскрасьте одну грань и сделайте противоположную грань черной. (Конечно, вы можете различать два лица любым другим способом.Поместите кубики в неглубокую коробку 3 на 3 (или на матрицу 3 на 3) с пустой средней ячейкой и черными кубиками сверху, как показано здесь:
Ход заключается в перекатывании куба в пустую ячейку путем его опрокидывания на одну из своих четыре нижних края. Задача состоит в том, чтобы перевернуть все восемь кубиков так, чтобы их цветные стороны были вверху, а центральная ячейка оставалась пустой, как и раньше. Это нужно сделать за минимальное количество ходов. Я был бы признателен за получение всех решений менее чем на 40 ходов. Ответ в следующем месяце даст лучшее решение Харриса (его меньше 40), но в следующей колонке я расскажу о читателях, которые справляются так же или лучше.Для единообразия в решениях для записи используйте U, D, L, R для прокрутки вверх, вниз, влево и вправо, и начинайте все решения с URD. (Любой другой способ запуска аналогичен симметричному.) Вот ответ из колонки за апрель 1975 года: 8. Решение Джона Харриса с 38 ходами для его головоломки с катящимся кубом: URDL, DRUL, LDRR, UULD, RUL; LDR, ULDD, RRUL, LDRU, LURD.

Буквы обозначают вверх, вниз, влево и вправо. Решение симметрично в том смысле, что вторая половина повторяет движения первой половины в обратном порядке, за исключением того, что движения вниз переходят в движение вверх и наоборот.(См. Статью Харриса «Проблемы вращающегося куба для одной вакансии», журнал «Рекреационная математика», том 7, лето, 1974 г., страницы 220–224. Стоимость журнала для индивидуальных подписчиков составляет 10 долларов в год, а для учреждений — 18 долларов. Он издается издательством Baywood Publishing). Компания, 43 Central Drive, Farmingdale, NY 11735.)

Харрис заканчивает свою статью сложной задачей, которая также включает восемь кубов на матрице третьего порядка. Раскрасьте кубики так, чтобы, когда они находятся на матрице с пустой центральной ячейкой, все открытые грани были красными, а все скрытые грани не окрашивались.Будет всего 24 красных стороны и 24 неокрашенных стороны. Проблема состоит в том, чтобы катить кубики, пока они не вернутся в те же восемь ячеек, при этом центральная ячейка пуста, но все красные стороны скрыты, а видимые стороны неокрашены. Возможно, читатель сможет превзойти решение Харриса о 84 ходах.

К лабиринтам катящегося куба

Вернуться на главную страницу

Складной куб

Цель

Поэкспериментировать с различными способами складывания шести соединенных квадратов в куб, а также определить, какие узоры складываются в куб, а какие — нет.

Базовая сложность

Easy ( № студент должен иметь проблемы с базовыми понятиями)

Концепт

Представьте, что вы держите шестигранный кубик или, что еще лучше, возьмите один из настольной игры и посмотрите на него. Матрица, скорее всего, должна иметь форму куба. Обратите внимание, что игральная кость состоит из шести квадратов. А теперь представьте, что вы развернули стороны кубика, пока у вас не осталось шести соединенных квадратов. Вы можете получить такое расположение:

Или ваше расположение может выглядеть примерно так:

Теперь представьте, что вы начали с конца, а не с начала; то есть представьте, что вы соединили шесть квадратов вместе.Сколько выкроек вы можете сделать? Они сделают куб? Чем они похожи на другие связанные паттерны, которые вы уже наблюдали? Насколько они разные? Сможете ли вы создать узоры, которые категорически нельзя сложить в куб?

Гипотеза:

Основываясь на ваших ответах на вопросы в разделе «Предпосылки и мотивация», думаете ли вы, что любую комбинацию из шести соединенных квадратов можно превратить в куб?

Материалы:

Материалы будут зависеть от вашего метода строительства:

Физическая конструкция:
- Строительная бумага
- Линейка
- Карандаш
- Ножницы
Виртуальная конструкция:
- Компьютер
- Среда программирования

Независимо от того, какой метод вы используете, вы должны хотя бы продемонстрировать все возможные варианты расположения шести соединенных квадратов, а затем начать обсуждение, какие из них работают, а какие нет.

Процедура:

Порядок действий следующий:

Обведите карандашом и линейкой узор из соединенных квадратов на бумаге
Вырежьте узор ножницами
Сделайте складку на всех линиях, соединяющих квадраты
Попытка сложить бумагу кубиком

Прежде всего, вам обязательно нужно сделать несколько примеров шаблонов и посмотреть, как их можно сложить в куб или как они не могут создать куб.Например, посмотрите на этот пример раньше и посмотрите, как он формируется в квадрат:

Важное примечание : Вы должны складывать только края квадратов, и вы должны быть осторожны, чтобы не складывать сами квадраты. Это изображение, например, показывает неправильную складку:

После того, как вы это сделаете, вы должны попытаться сформировать общее представление о том, как все шаблоны будут работать и что делает различные шаблоны потенциальными кубами по сравнению с другими, которые нельзя сложить в кубики.Сделав это, вы должны четко продемонстрировать, почему вы думаете, что ваши обобщения верны, глядя на различные шаблоны, применяя свои идеи, а затем фактически складывая их и проверяя, верны ли ваши идеи.

«Я не ошибся, я просто нашел 10 000 способов не делать лампочку».

— Томас Эдисон

Исследования

Хотя эта концепция очень проста, вам было бы полезно в вашем анализе, если бы вы понимали идеи симметрии как в двух, так и в трех измерениях.Это позволит вам просмотреть меньше примеров и все же прийти к полному выводу, поскольку информация, полученная из одного шаблона, может быть применена к другим шаблонам.

Анализ

Вам необходимо четко определить все возможные паттерны шести соединенных квадратов, объяснить, почему ваш список возможностей является полным, а затем показать, какие паттерны складываются в куб, а какие — нет. Затем вам необходимо представить свои обобщения, которые вы сделали из своих наблюдений, и объяснить, к каким шаблонам они применяются и почему сформированные вами обобщения позволяют быстро определить, является ли шаблон возможным кубом или нет.

Узор: Уникальные способы соединения квадратов. Вам нужно определить, что уникально.
Завершить: Выкройка завершена, если она складывается в куб без открытых граней
Обобщения: Это можно сделать, когда выяснили, что делает куб завершаемым. Постарайтесь сделать простое утверждение, охватывающее все квадратные узоры.
Производные: Вы найдете закономерности в своих наблюдениях.Вам нужно определить, что они означают.

Заключение

Как вы думаете, что произойдет? Этот раздел предназначен для вас и станет последним шагом в вашем эксперименте со складыванием.

Расширения

Вместо того, чтобы пробовать это с шестью соединенными квадратами, вы можете попробовать добавить сложность восьми соединенных треугольников и найти, какие узоры складываются вместе в октаэдр.

Картонный куб

Создание идеального картонного куба 3 «x 3»

Будьте осторожны, чтобы не порезать столы и не наклеить клей. их.

Соберите материалы, которые понадобятся вам для этого упражнения
- упаковка лезвий Exacto и нож Exacto
- металлическая прямая кромка
- твердая режущая поверхность (может быть режущая поверхность Exacto, деревянная доска, так далее)
- 30-60-90 или 45-45-90 треугольник
- клей белый
- лист картонный
Ознакомьтесь с используемым материалом, то есть с картоном.
- Посмотрите на картон и поймите
- Обратите внимание, как он устроен.Обратите внимание, что у него есть зернистость. Картон:
  - состоит из трех слоев: ребристая внутренняя структура, зажатая между двумя гладкими гранями;
  - — сильнейший, параллельный гребням; а также
  - — самый слабый перпендикуляр к гребням.
- Возьмите кусок картона. Используя металлическую линейку в качестве направляющей, разрезать картон новым лезвием.
  - Не применяйте сильное давление; Не пытайтесь прорезать картон все сразу.
  - Попробуйте прорезать только один слой, не разрезая другие слои.
  - Попробуйте разрезать всего два слоя, не разрезая третий слой.
  - Обратите внимание, как легко острое лезвие разрезает картон всего за несколько удары.
  - Подумайте, какая сторона разреза является хорошей, а какая сторона будет в утиль. Положите металлическую направляющую на хорошую сторону, чтобы что если ваш нож поскользнется, он порежет ту сторону, которая будет слом.
Сделайте куб
Когда вы закончите с шагами в этом разделе, у вас должен быть Картон 6 штук. Квадраты, которые будут 4 сторонами куб должен иметь вырезы 1/8 дюйма на 3 края. Верх и низ должны быть 3-дюймовыми квадратами без вырезов.
1. Постройте четыре стороны
  1. Замените лезвие Exacto.
  2. Сделайте чистый прямой пропил около одного из краев. Сделайте еще один чистый прямой надрез перпендикулярно первому надрезу и близко к соседнему краю.Убедитесь, что угол, образованный этими двумя разрезами, перпендикулярен.
    - Используйте треугольник, чтобы убедиться, что у вас прямой угол.
    - Примечание: этот шаг необходим, потому что края листа картона часто давятся. Мы хотим чисто, прямо края.
    - Примечание: Используйте только металлическую линейку при обрезке картон ножом Exacto. Не используйте треугольник как прямая кромка: острое лезвие испортит кромку треугольник (если вы не используете металлический треугольник).
  3. Из этого установленного угла вырежьте квадрат 3 дюйма
    - Обязательно отметьте две точки для каждого края, чтобы убедитесь, что вы делаете точный разрез.
    - Не используйте карандаш для пометок на картоне; Используйте Exacto лезвие, которое производит более точную отметку.
  4. Сделайте три надреза в этом квадрате, чтобы получилось чистый стык на краю куба.
    - Подумайте, с какой стороны картона вы хотите лицевой стороной наружу.
    - От каждого выбранного края отмерьте 1/8 дюйма и слегка отметьте с помощью лезвия Exacto.
    - Замените лезвие Exacto.
    - Удалите первые два слоя с каждого из трех краев. Сделайте несколько легких движений ножом, пока третий слой — неразрезанный.
    - Не обрезайте все три слоя картон. Вам нужно оставить бумагу, чтобы она закройте необработанный край лица, который к нему присоединяется.
  5. Снимите два слоя картона с трех краев.
2. Повторите эти шаги еще три раза, чтобы сделать четыре стороны куб. В частности, повторяйте этап смены лезвия каждый раз. раз вы начнете новую сторону.
3. Сделайте верхнюю и нижнюю грани
  1. Замените лезвие Exacto.
  2. На свежем краю листа картона вырежьте 3 дюйма квадрат из картона для вершины вашего идеального куба.
  3. Повторите то же самое для нижней грани.
4. Протестируйте сборку куба.
  1. Соберите стороны так, чтобы у вас была полочка сверху и нижние грани, и поэтому необработанные края все покрыты.
5. Склейте кубики вместе.
  1. Сделайте тестовую сборку без клея, чтобы убедиться, что вы знаете, как ваш куб идет вместе.
  2. Возьмите кусок картона (он же клейкую подушечку) и положите капля клея на нем.
  3. С помощью небольшой палочки или пальца перенесите клей с блокнот к вашей части.
  4. Нанесите тонкий слой клея на бумажную часть сустав. (На гофрированную часть не надевать — он капля и не прилипает.) Убедитесь, что у вас есть только тонкий слой клея и следите за тем, чтобы клей был только на стыке, а не на всех над вашим кубом.
  5. Удерживайте стык вместе примерно 10 секунд перед переход к следующему стыку.
  6. Большинство людей считают, что проще всего собрать стороны вокруг низ и добавить верх в качестве последнего шага.
Подпишите свой куб!

Советы по стрижке

Будьте осторожны и обращайте внимание — как на свои конечности, так и на те из людей вокруг вас.
Опустите линейку пробковой стороной вниз.
Дважды проверьте, что вы режете доску.
Порез на себя.Режьте медленно и осторожно.
Некоторым людям легче резать стоя, потому что угол и давление лучше.

Будьте осторожны, чтобы не порезать столы и не наклеить на них клей

sfinger@ri.