Сечение проводов и токи: Таблица допустимых токов для медных эмалированных проводов диаметром от 0.02 до 2.5 мм

Допустимые длительные токи для проводов, шнуров и кабелей с резиновой или пластмассовой изоляцией

1.3.10. Допустимые длительные токи для проводов с резиновой или поливинилхлоридной изоляцией, шнуров с резиновой изоляцией и кабелей с резиновой или пластмассовой изоляцией в свинцовой, поливинилхлоридной и резиновой оболочках приведены в табл. 1.3.4 — 1.3.11. Они приняты для температур: жил +65, окружающего воздуха +25 и земли +15 º С.

При определении количества проводов, прокладываемых в одной трубе (или жил многожильного проводника), нулевой рабочий проводник четырехпроводной системы трехфазного тока, а также заземляющие и нулевые защитные проводники в расчет не принимаются.

Данные, содержащиеся в табл. 1.3.4 и 1.3.5, следует применять независимо от количества труб и места их прокладки (в воздухе, перекрытиях, фундаментах).

Допустимые длительные токи для проводов и кабелей, проложенных в коробах, а также в лотках пучками, должны приниматься: для проводов — по табл. 1.3.4 и 1.3.5, как для проводов, проложенных в трубах, для кабелей — по табл. 1.3.6 — 1.3.8, как для кабелей, проложенных в воздухе. При количестве одновременно нагруженных проводов более четырех, проложенных в трубах, коробах, а также в лотках пучками, токи для проводов должны приниматься по табл. 1.3.4 и 1.3.5, как для проводов, проложенных открыто (в воздухе), с введением снижающих коэффициентов 0, 68 для 5 и 6; 0, 63 для 7 — 9 и 0, 6 для 10 — 12 проводов.

Для проводов вторичных цепей снижающие коэффициенты не вводятся.

1.3.11. Допустимые длительные токи для проводов, проложенных в лотках, при однорядной прокладке (не в пучках) следует принимать как для проводов, проложенных в воздухе.

Допустимые длительные токи для проводов и кабелей, прокладываемых в коробах, следует принимать по табл. 1.3.4 — 1.3.7, как для одиночных проводов и кабелей, проложенных открыто (в воздухе), с применением снижающих коэффициентов, указанных в табл. 1.3.12.

При выборе снижающих коэффициентов контрольные и резервные провода и кабели не учитываются.

Таблица 1.3.4.

Допустимый длительный ток для проводов и шнуров с резиновой и поливинилхлоридной изоляцией с медными жилами

Сечение токопроводящей жилы, мм2	Ток, А, для проводов, проложенных
	открыто	в одной трубе
		двух одно жильных	трех одно жильных	четырех одно жильных	одного двух жильного	одного трех жильного
0,5	11	—	—	—	—	—
0,75	15	—	—	—	—	—
1	17	16	15	14	15	14
1,2	20	18	16	15	16	14,5
1,5	23	19	17	16	18	15
2	26	24	22	20	23	19
2,5	30	27	25	25	25	21
3	34	32	28	26	28	24
4	41	38	35	30	32	27
5	46	42	39	34	37	31
6	50	46	42	40	40	34
8	62	54	51	46	48	43
10	80	70	60	50	55	50
16	100	85	80	75	80	70
25	140	115	100	90	100	85
35	170	135	125	115	125	100
50	215	185	170	150	160	135
70	270	225	210	185	195	175
95	330	275	255	225	245	215
120	385	315	290	260	295	250
150	440	360	330	—	—	—
185	510	—	—	—	—	—
240	605	—	—	—	—	—
300	695	—	—	—	—	—
400	830	—	—	—	—	—

Таблица 1.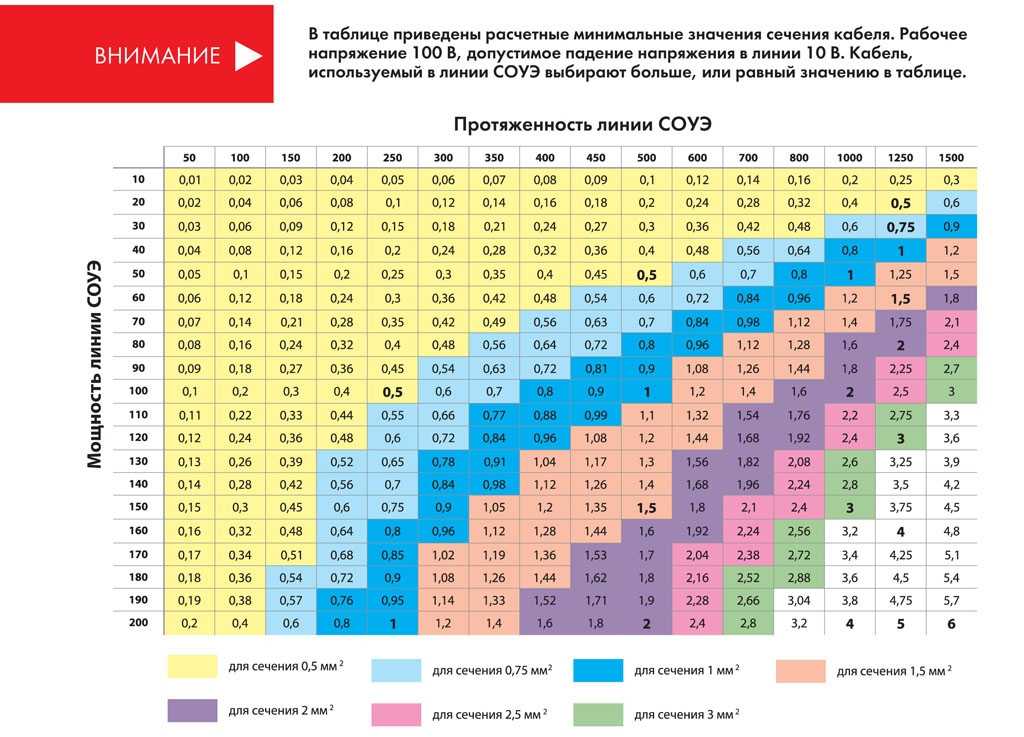 3.5.

Допустимый длительный ток для проводов с резиновой и поливинилхлоридной изоляцией с алюминиевыми жилами

Сечение токопроводящей жилы, мм2	Ток, А, для проводов, проложенных
	открыто	в одной трубе
		двух одножильных	трех одножильных	четырех одножильных	одного двухжильного	одного трехжильного
2	21	19	18	15	17	14
2,5	24	20	19	19	19	16
3	27	24	22	21	22	18
4	32	28	28	23	25	21
5	36	32	30	27	28	24
6	39	36	32	30	31	26
8	46	43	40	37	38	32
10	60	50	47	39	42	38
16	75	60	60	55	60	55
25	105	85	80	70	75	65
35	130	100	95	85	95	75
50	165	140	130	120	125	105
70	210	175	165	140	150	135
95	255	215	200	175	190	165
120	295	245	220	200	230	190
150	340	275	255	—	—	—
185	390	—	—	—	—	—
240	465	—	—	—	—	—
300	535	—	—	—	—	—
400	645	—	—	—	—	—

Таблица 1.

3.6.

Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией в металлических защитных оболочках и кабелей с медными жилами с резиновой изоляцией в свинцовой, поливинилхлоридной, найритовой или резиновой оболочке, бронированных и небронированных

Сечение токопроводящей жилы, мм2	Ток*, А, для проводов и кабелей
	одножильных	двухжильных		трехжильных
	при прокладке
	в воздухе	в воздухе	в земле	в воздухе	в земле
1,5	23	19	33	19	27
2,5	30	27	44	25	38
4	41	38	55	35	49
6	50	50	70	42	60
10	80	70	105	55	90
16	100	90	135	75	115
25	140	115	175	95	150
35	170	140	210	120	180
50	215	175	265	145	225
70	270	215	320	180	275
95	325	260	385	220	330
120	385	300	445	260	385
150	440	350	505	305	435
185	510	405	570	350	500
240	605	—	—	—	—

* Токи относятся к проводам и кабелям как с нулевой жилой, так и без нее.

Таблица 1.3.7.

Допустимый длительный ток для кабелей с алюминиевыми жилами с резиновой или пластмассовой изоляцией в свинцовой, поливинилхлоридной и резиновой оболочках, бронированных и небронированных^*

Сечение токопроводящей жилы, мм2	Ток, А, для проводов и кабелей
	одножильных	двухжильных		трехжильных
	при прокладке
	в воздухе	в воздухе	в земле	в воздухе	в земле
2,5	23	21	34	19	29
4	31	29	42	27	38
6	38	38	55	32	46
10	60	55	80	42	70
16	75	70	105	60	90
25	105	90	135	75	115
35	130	105	160	90	140
50	165	135	205	110	175
70	210	165	245	140	210
95	250	200	295	170	255
120	295	230	340	200	295
150	340	270	390	235	335
185	390	310	440	270	385
240	465	—	—	—	—

* Примечание. Допустимые длительные токи для четырехжильных кабелей с пластмассовой изоляцией на напряжение до 1 кВ могут выбираться по табл. 1.3.7., как для трехжильных кабелей, но с коэффициентом 0,92.

Таблица 1.3.8.

Допустимый длительный ток для переносных шланговых легких и средних шнуров, переносных шланговых тяжелых кабелей, шахтных гибких шланговых, прожекторных кабелей и переносных проводов с медными жилами

Сечение токопроводящей жилы, мм2	Ток*, А, для шнуров, проводов и кабелей
	одножильных	двухжильных	трехжильных
0,5	—	12	—
0,75	—	16	14
1,0	—	18	16
1,5	—	23	20
2,5	40	33	28
4	50	43	36
6	65	55	45
10	90	75	60
16	120	95	80
25	160	125	105
35	190	150	130
50	235	185	160
70	290	235	200

* Токи относятся к шнурам, проводам и кабелям с нулевой жилой и без нее.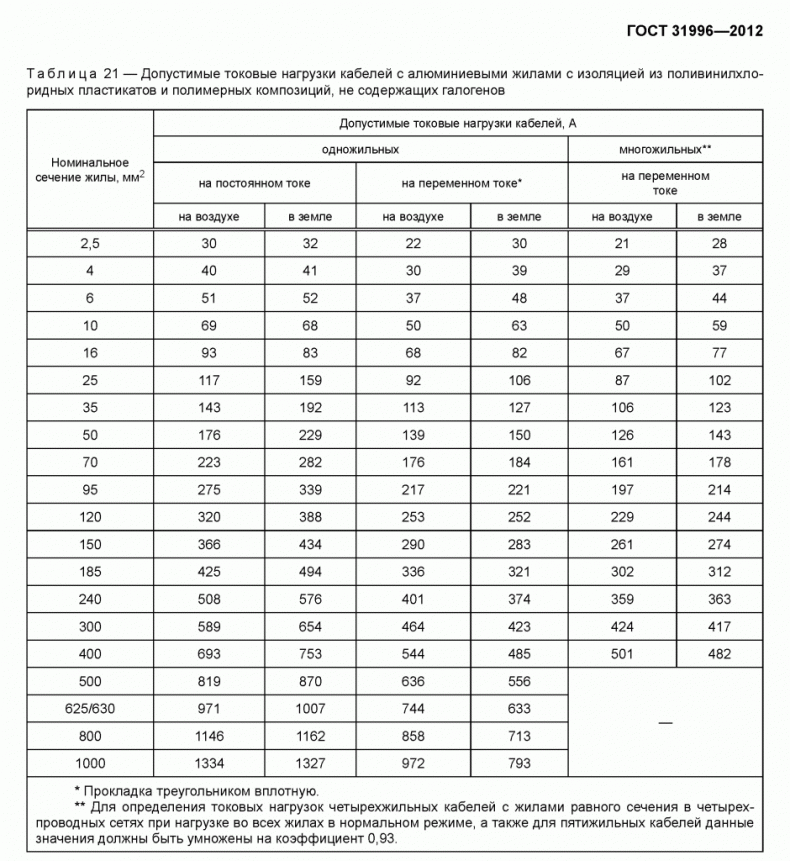

Таблица 1.3.9.

Допустимый длительный ток для переносных шланговых с медными жилами с резиновой изоляцией кабелей для торфопредприятий

Сечение токопроводящей жилы, мм2	Ток*, А, для кабелей напряжением, кВ
	0,5	3	6
6	44	45	47
10	60	60	65
16	80	80	85
25	100	105	105
35	125	125	130
50	155	155	160
70	190	195	—

* Токи относятся к кабелям с нулевой жилой и без нее.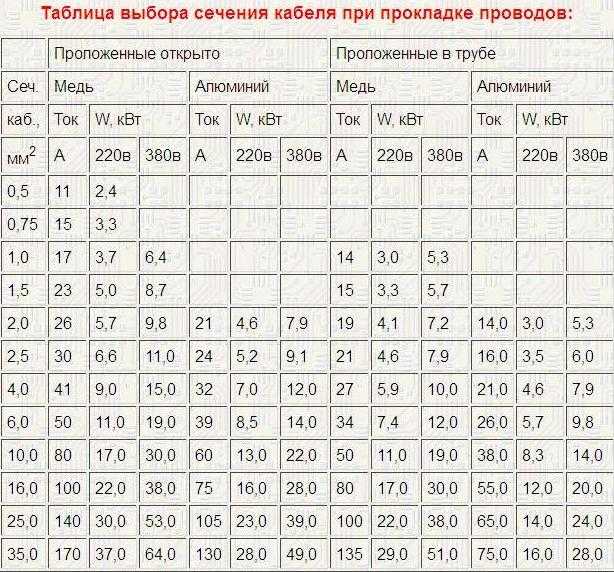

Таблица 1.3.10.

Допустимый длительный ток для шланговых с медными жилами с резиновой изоляцией кабелей для передвижных электроприемников

Сечение токопроводящей жилы, мм2	Ток*, А, для кабелей напряжением, кВ		Сечение токопроводящей жилы, мм2	Ток*, А, для кабелей напряжением, кВ
	3	6		3	6
16	85	90	70	215	220
25	115	120	95	260	265
35	140	145	120	305	310
50	175	180	150	345	350

* Токи относятся к кабелям с нулевой жилой и без нее.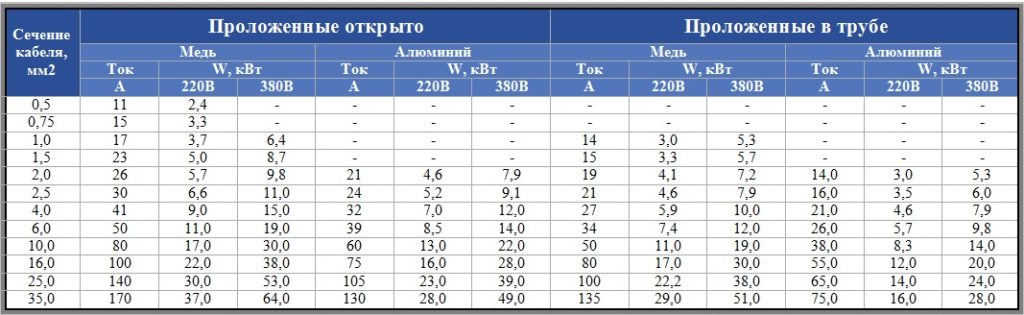

Таблица 1.3.11.

Допустимый длительный ток для проводов с медными жилами с резиновой изоляцией для электрифицированного транспорта 1, 3 и 4 кВ

Сечение токопроводящей жилы, мм2	Ток, А	Сечение токопроводящей жилы, мм2	Ток, А	Сечение токопроводящей жилы, мм2	Ток, А
1	20	16	115	120	390
1,5	25	25	150	150	445
2,5	40	35	185	185	505
4	50	50	230	240	590
6	65	70	285	300	670
10	90	95	340	350	745

Таблица 1.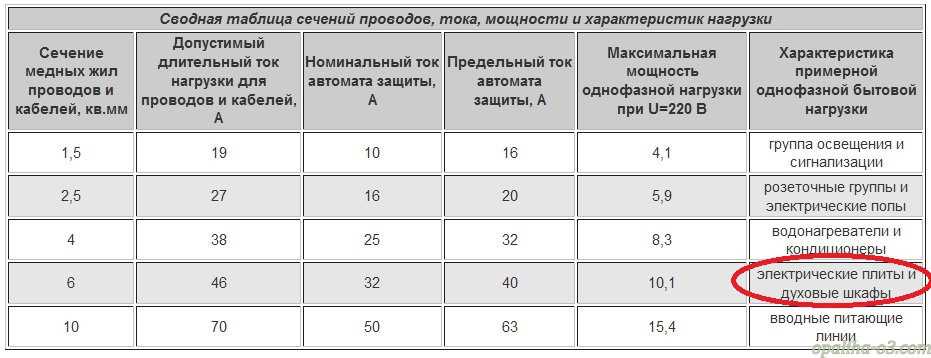 3.12.

Снижающий коэффициент для проводов и кабелей, прокладываемых в коробах

Способ прокладки	Количество проложенных проводов и кабелей		Снижающий коэффициент для проводов и кабелей, питающих
	одножильных	многожильных	отдельные электроприемники с коэффициентом использования до 0, 7	группы электроприемников и отдельные приемники с коэффициентом использования более 0, 7
Многослойно и пучками	—	До 4	1,0	—
	2	5-6	0,85	—
	3-9	7-9	0,75	—
	10-11	10-11	0,7	—
	12-14	12-14	0,65	—
	15-18	15-18	0,6	—
Однослойно	2-4	2-4	—	0,67
	5	5	—	0,6

 

Подбор сечения кабельной продукции по физическим параметрам, сила тока, мощность, напряжение

Термостойкие провода и кабели необходимы для любого электрооборудования и устройств питающихся от электросети. От их правильного подбора и расчета зависит насколько надежно, и долго будет функционировать электроприбор.

Высчитать потребляемый ток для термостойкого провода не сложно, для этого следует воспользоваться электротехнической формулой:

I = P / U

Как правило вычисления составляются для тока напряжением 220 В. Для примера предлагает рассмотреть расчет медного термостойкого провода. Чтобы провести расчёт сечения термостойкого медного провода нужно просуммировать токи всех потребителей, и за расчёт сечения принять:

Для открытой медной проводки: каждые 10 Ампер равно 1 мм кв. провода;

Для закрытой медной проводки: каждые 10 Ампер равно 1,25 мм кв. провода.

 

Сечение провода	Медные жилы
Токопроводящие жилы	Напряжение 220В		Напряжение 380В
мм. кв.	Ток, А	Мощность, кВт	Ток, А	Мощность, кВт
1,5	19	4,1	16	10,5
2,5	27	5,9	25	16,5
4	38	8,3	30	19,8
6	46	10,1	40	26,4
10	70	15,4	50	33,0
16	85	18,7	75	49,5
25	115	25,3	90	59,4
35	135	29,7	115	75,9
50	175	38,5	145	95,7
70	215	47,3	180	118,8
95	260	57,2	220	145,2
120	300	66,0	260	171,6

 

Данные из таблицы сечения по мощности и току очень полезны, когда необходимо правильно подобрать тип стабилизатора напряжения. Зачастую на практике возникает проблема в выборе стабилизатора из-за того, что, несмотря на требуемую мощность установить его с более мощным напряжением, чем позволяет вводный кабель невозможно. Кабель ограничивает максимальные показатели тока и в соответствии саму мощность.

В таком случае стоит просчитать данные с помощью специального калькулятора рассчитывающего сечение кабеля переменных и постоянных токов. Либо вы можете просто позвонить нам по телефону и наши менеджеры сами произведут расчеты и порекомендуют купить термостойкие провода из меди или никеля наиболее подходящих сечений.

На полученные значения стоит опираться и при изготовлении новой проводки. В расчётах обязательно нужно учитывать небольшой запас для предотвращения высокой нагрузки на кабель в течение длительного периода времени. При необходимости, например, соединения проводов из меди и алюминия стоит использовать мощные клеммные соединители со значительной площадью контакта разносоставных кабелей. В противном случае подобное соединение прослужит недолго.

 

Сечение медных жил	Длительная нагрузка	Номинальный авт. выкл.	Предельный авт. выкл.	Максимальная мощность	Характеристика однофазной бытовой нагрузки
мм.кв	ток, А	Ток, А	Ток, А	кВт, при 220В
1,5	19	10	16	4,1	освещение, сигнализация
2,5	27	16	20	5,9	розеточные группы, мелкая и средняя бытовая техника
4	38	25	32	8,3	водонагреватели и кондиционеры, электрические полы
6	46	32	40	10,1	электрические плиты и духовые шкафы
10	70	50	63	15,4	вводные питающие линии

 

Компания «ЭЛЕМАГ» поставляет высококачественные кабели и провода с высокой термозащитой для бытового и промышленного использования.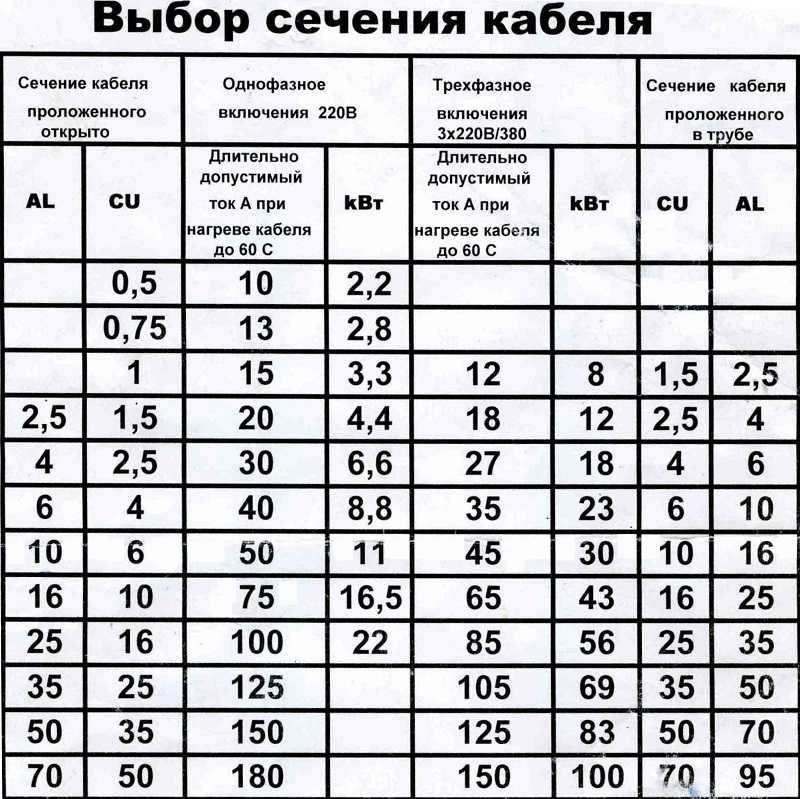 У нас Вы можете подобрать самый подходящий кабель по типу сплава и защитной оболочки с максимальной выдержкой до 400 градусов температуры.

электромагнетизм — Электрическое поле в поперечном сечении провода?

Задавать вопрос

спросил 8 лет, 9 месяцев назад

Изменено 8 лет, 9 месяцев назад

Просмотрено 2к раз

$\begingroup$ 9A \vec{E} \dot{}d\vec{l}$

Требование, чтобы двусторонняя разность потенциалов была равна нулю, означает, что $E_1$ и $E_2$ должны быть равны. Поэтому электрическое поле должны быть равномерными как по длине провода, так и по площади поперечного сечения провода. Поскольку скорость дрейфа пропорциональна $E$, мы находим, что ток действительно равномерно распределен по сечению. Этот результат верен только для однородного поперечного сечения и однородного материала в стационарном состоянии. Ток распределяется по поперечному сечению неравномерно в случае высокочастотных (нестационарных) переменных токов, потому что переменные во времени токи могут создавать некулоновские силы, как мы увидим в следующей главе, посвященной закону Фарадея. .

Допустим, поле неоднородное, но полностью продольное. Это привело бы к тому, что приведенный выше интеграл был бы отличен от нуля, что невозможно, поэтому поле всегда должно быть однородным, если оно продольное.

Если проволока изготовлена ​​из материалов разных типов, разные части будут действовать как диэлектрики, что приведет к поляризации материала и ослаблению электрического поля в разных точках, что приведет к тому, что электрическое поле будет неоднородным, но все же продольным , что противоречит сказанному в абзаце выше.

Как разрешить это кажущееся противоречие?

• электромагнетизм
• электричество
• электростатика

$\endgroup$

5

$\begingroup$

Если электрическое и магнитное поля постоянны, $\oint \mathbf{E}\cdot\mathrm{d}\mathbf{l} = 0$ является законом природы. Даже если вы измените материал проводника, электрическое поле все равно должно соответствовать $\oint \mathbf{E}\cdot\mathrm{d}\mathbf{l} = 0$ и, следовательно, должно быть однородным. По сути, это одно из граничных условий на диэлектрических границах раздела, если я правильно помню.

Однако по закону Ома, $\mathbf{J} = \sigma \mathbf{E}$, плотность тока уже не является однородной. Полный ток должен сохраняться, поэтому, если я вдруг создам интерфейс с другим проводником одинаковой толщины, электрическое поле $\mathbf{E}$ должно будет измениться, но при этом равномерно, так что $\oint \mathbf {E}\cdot\mathrm{d}\mathbf{l} = 0$ остается.

$\endgroup$

0

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

электрических цепей — Почему сила тока увеличивается при увеличении площади поперечного сечения?

$\begingroup$

Когда мы увеличиваем площадь поперечного сечения провода, мы обнаруживаем, что при том же напряжении, если через резистор проходит в два раза больше тока, чем раньше.

Либо вы думаете, что «это из-за того, что сопротивление обратно пропорционально площади резистора», либо что-то еще, объясните, почему это происходит.

Если ваш ответ такой же, как в цитате, тогда объясните, почему увеличение площади уменьшает сопротивление.

• электрические цепи
• электрические токовые
• электрические сопротивления

$\endgroup$

$\begingroup$

Простая интуиция состоит в том, что, когда мы увеличиваем площадь поперечного сечения, большее количество электронов может пройти через эту площадь по сравнению с исходным проводом.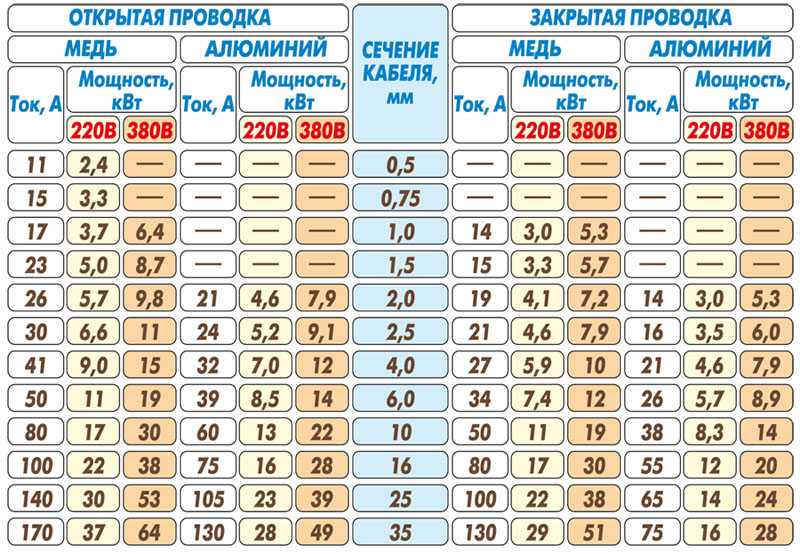 Больше электронов приводит к большему заряду, пересекающему поперечное сечение, и, следовательно, к большему току.

Теперь давайте посмотрим на это с помощью математики:

Сопротивление провода определяется как: $$R = \rho \frac{l}{A}$$ $R$ = сопротивление провода
$\rho$ = удельное сопротивление провода (зависит от материала провода)
$l$ = длина провода
$A$ = площадь поперечного сечения

Если мы возьмем провод одинаковой длины и из того же материала, то есть с одинаковым удельным сопротивлением, то: $$R\propto \frac{1}{A}$$

Таким образом, если увеличить площадь поперечного сечения, то сопротивление провода (при неизменной длине и удельном сопротивлении) уменьшится.
Также из закона Ома ( $V=iR$ ) мы можем сказать, что ток будет увеличиваться, если разность потенциалов на проводе одинакова в обоих случаях.

$\endgroup$

1

$\begingroup$

Не профессионал.