|
Раздел недели: Скоропись физического, математического, химического и, в целом, научного текста, математические обозначения. Математический, Физический алфавит, Научный алфавит. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Поиск на сайте DPVA Поставщики оборудования Полезные ссылки О проекте Обратная связь Ответы на вопросы. Оглавление Таблицы DPVA.ru — Инженерный Справочник |
Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация/ / Математический справочник / / Геометрические фигуры. Свойства, формулы: периметры, площади, объемы, длины. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Коды баннеров проекта DPVA.ru Консультации и техническая |
Проект является некоммерческим. Информация, представленная на сайте, не является официальной и предоставлена только в целях ознакомления. Владельцы сайта www.dpva.ru не несут никакой ответственности за риски, связанные с использованием информации, полученной с этого интернет-ресурса. Free xml sitemap generator
Free xml sitemap generator
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Расчет углов поворота пучков на 4, 6 и 8 путей
Начнем объединять пути сортировочного парка.
Найдем координаты центра второго стрелочного перевода
; . .
Если м, то м; если м, то м.
Допускается иметь м, тогда м.
Ответить на вопрос:
А как быть с минимальной величины междупутья в 4,80 метров?
С целью сокращения длины горочной горловины допускается начинать кривые непосредственно за торцом крестовины (т.е. за ). Уширение колеи в кривой в этом случае делают в пределах самой кривой, давая полное уширение в 4-х метрах от ее начала.
Расчет углов поворота пучка на 6 путей
Рисунок 2.1
Учитывая, что наиболее сложные по
вписыванию пути 1 и 2, угол
определяется из условия вписывания
этих двух путей.
Поставленную задачу можно решить двумя способами расчета (см. лекции за III курс):
1) Путем проецирования всех элементов трудного пути на вертикальную ось.
2) Путем построения двух вспомогательных прямоугольных треугольников с общей гипотенузой.
Решим поставленную задачу для пути 2 первым способом расчета.
Составим исходное уравнение всех элементов 2-го пути на вертикальную ось:
1,5e (1)
Вспомним, что:
Тогда:
;
,
или
;
Обозначим: ;
;
.
В окончательном виде уравнение имеет вид
.
Правильность расчета заключается в
том, что при подстановке в исходное
уравнение (1) мы
должны получить 1,5
e.
Задача. Определить правильность расчета величины в следующей пучкообразной стрелочной улице:
Рисунок 2.2
Обсудить возможность применения двойных стрелочных переводов для сокращения длины горочных горловин сортировочных горок.
Рисунок 2.3
Лекция №3 от 16.10.2012 Расчет углов поворота пучка на 8 путей
Поставленную задачу также можно решить двумя способами расчета:
Путем проектирования всех элементов наиболее трудного по вписыванию пути на вертикальную ось (для этого необходимо составить и решить исходное уравнение).
2) Путем построения двух вспомогательных прямоугольных треугольников с общей гипотенузой.
Рисунок 3.1
.
Решение этого уравнения
приведено в учебном пособии С. П. Вакуленко
и Е.И. Сычева «Расчет соединений путей
станции».
П. Вакуленко
и Е.И. Сычева «Расчет соединений путей
станции».
Преобразовав (см. предыдущую лекцию) это исходное уравнение, получим следующее решение данной задачи:
,
где .
Решим эту задачу вторым способом расчета.
.
Контроль правильности расчета заключается в том, что при подстановке значения угла в исходное уравнение должно получиться значение .
Задача.
Рисунок 3.2
По данным рисунка 3.2 определить правильность расчета величины в пучкообразной стрелочной улице на 8 сортировочных путей при междупутье м.:
Конструктивные элементы плана горочных горловин сортировочных парков
В пределах горочной горловины размещаются следующие конструктивные элементы:
– стрелочные переводы;
– изолированные участки ГАЦ и АЗСР;
– вагонные замедлители (а на
автоматизированных горках и измерительные
участки).
Изолированный участок стрелки состоит из предстрелочного участка и стрелочного от начала остряков до изолирующего стыка в конце рамного рельса. Длина предстрелочного участка должна быть достаточной для того, чтобы за время прохода вагона можно было гарантированно провести стрелку.
,
где – максимально возможная скорость движения вагона на стрелке, м/с;
– время перевода остряков стрелки , сек;
– время срабатывания устройств ГАЦ (0,2 сек).
При электрических приводах СПГБ-4М принята равной 6 метрам для всех стрелочных переводов.
Как это неправильно было пояснено при сдаче экзамена по ЖДСУ:
Рисунок 3.3 Симметричный стрелочный перевод
Калькулятор треугольника
Введите 3 значения, включая хотя бы одну сторону, в следующие 6 полей и нажмите кнопку «Рассчитать». Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.
Если в качестве единицы измерения угла выбран радиан, он может принимать такие значения, как пи/2, пи/4 и т. д.
Треугольник — это многоугольник с тремя вершинами. Вершина — это точка, в которой встречаются две или более кривых, линий или ребер; в случае треугольника три вершины соединены тремя отрезками, называемыми ребрами. Треугольник обычно называют его вершинами. Следовательно, треугольник с вершинами a, b и c обычно обозначается как Δabc. Кроме того, треугольники, как правило, описываются на основе длины их сторон, а также их внутренних углов. Например, треугольник, в котором все три стороны имеют одинаковую длину, называется равносторонним треугольником, а треугольник, в котором две стороны имеют одинаковую длину, называется равнобедренным. Когда ни одна из сторон треугольника не имеет одинаковой длины, он называется разносторонним, как показано ниже.
Засечки на ребрах треугольника — общепринятое обозначение, отражающее длину стороны, где одинаковое количество засечек означает одинаковую длину. Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Аналогичные обозначения существуют для внутренних углов треугольника, обозначаемых разным количеством концентрических дуг, расположенных в вершинах треугольника. Как видно из приведенных выше треугольников, длина и внутренние углы треугольника напрямую связаны, поэтому имеет смысл, что равносторонний треугольник имеет три равных внутренних угла и три стороны одинаковой длины. Обратите внимание, что треугольник, представленный в калькуляторе, показан не в масштабе; хотя он выглядит равносторонним (и имеет маркировку углов, которые обычно читаются как равные), он не обязательно является равносторонним и представляет собой просто изображение треугольника. При вводе фактических значений выходные данные калькулятора будут отражать форму входного треугольника.
Треугольники, классифицированные по их внутренним углам, делятся на две категории: прямоугольные и косоугольные. Прямоугольный треугольник — это треугольник, в котором один из углов равен 90°, и обозначается двумя отрезками, образующими квадрат в вершине, составляющей прямой угол. Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Самая длинная сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой. Любой треугольник, который не является прямоугольным, классифицируется как косоугольный и может быть либо тупоугольным, либо остроугольным. В тупоугольном треугольнике один из углов треугольника больше 90°, а в остроугольном треугольнике все углы меньше 90°, как показано ниже.
Факты, теоремы и законы треугольника
- Зная длины всех трех сторон любого треугольника, каждый угол можно вычислить с помощью следующего уравнения. Обратитесь к треугольнику выше, предполагая, что значения a, b и c известны.
Площадь треугольника
Существует несколько различных уравнений для расчета площади треугольника, в зависимости от того, какая информация известна. Вероятно, наиболее известное уравнение для вычисления площади треугольника включает его основание, b и высота h . «Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
«Основание» относится к любой стороне треугольника, где высота представлена длиной отрезка, проведенного от вершины, противоположной основанию, к точке на основании, образующей перпендикуляр.
Зная длину двух сторон и угол между ними, можно использовать следующую формулу для определения площади треугольника. Обратите внимание, что используемые переменные относятся к треугольнику, показанному в калькуляторе выше. Учитывая а = 9, b = 7 и C = 30°:
Другой метод вычисления площади треугольника использует формулу Герона. В отличие от предыдущих уравнений, формула Герона не требует произвольного выбора стороны в качестве основания или вершины в качестве начала координат. Однако для этого требуется, чтобы длины трех сторон были известны. Опять же, в отношении треугольника, представленного в калькуляторе, если a = 3, b = 4 и c = 5:
Медиана, внутренний радиус и радиус описанной окружности
Медиана
Медиана треугольника определяется как длина отрезка, проходящего от вершины треугольника до середины противоположной стороны. Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Треугольник может иметь три медианы, каждая из которых будет пересекаться в центре тяжести (среднее арифметическое положение всех точек треугольника) треугольника. Обратитесь к приведенному ниже рисунку для пояснения.
Медианы треугольника представлены отрезками m a , m b и m c . Длину каждой медианы можно рассчитать следующим образом:
Где a, b и c представляют длину стороны треугольника, как показано на рисунке выше.
Например, учитывая, что a=2, b=3 и c=4, медиана m a может быть рассчитана следующим образом: круг, который поместится внутри заданного многоугольника, в данном случае треугольника. Внутренний радиус перпендикулярен каждой стороне многоугольника. В треугольнике внутренний радиус можно определить, построив две биссектрисы угла, чтобы определить центр треугольника. Внутренний радиус — это расстояние по перпендикуляру между центром вписанной стороны и одной из сторон треугольника. Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Можно использовать любую сторону треугольника, если определено перпендикулярное расстояние между стороной и центром вписанной стороны, поскольку центр вписанной стороны по определению равноудален от каждой стороны треугольника.
Для целей этого калькулятора внутренний радиус рассчитывается с использованием площади (Area) и полупериметра (s) треугольника по следующим формулам:
| внутренний радиус = |
| с = |
|
где a, b и c — стороны треугольника
Радиус окружности
Радиус окружности определяется как радиус окружности, проходящей через все вершины многоугольника, в данном случае треугольника. Центр этой окружности, где встречаются все серединные перпендикуляры каждой стороны треугольника, является центром описанной окружности треугольника и является точкой, от которой измеряется радиус описанной окружности. Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Центр описанной окружности треугольника не обязательно должен находиться внутри треугольника. Стоит отметить, что у всех треугольников есть описанная окружность (окружность, проходящая через каждую вершину) и, следовательно, радиус описанной окружности.
Для целей данного калькулятора радиус описанной окружности рассчитывается по следующей формуле:
| радиус описанной окружности = |
|
Где а — сторона треугольника, а А — угол, противоположный стороне а
Хотя сторона а и угол А используются, в формуле можно использовать любую из сторон и соответствующие им противоположные углы.
Калькулятор угла прямоугольного треугольника
Этот калькулятор угла прямоугольного треугольника поможет вам определить, каковы углы прямоугольного треугольника, то есть если вы знаете измерения по крайней мере двух его сторон или хотя бы одной его сторон вместе с его площадью. Продолжайте читать, чтобы узнать о:
Продолжайте читать, чтобы узнать о:
- Как найти углы прямоугольного треугольника ;
- Как пользоваться этим калькулятором ; и
- Другие наши калькуляторы треугольников .
Как найти углы прямоугольного треугольника?
Поскольку сумма внутренних углов треугольника составляет 180°, то, если один угол имеет угол, равный 90°, это означает, что оставшиеся два других угла должны иметь в сумме 90°. При этом мы можем сказать, что два оставшихся угла α\alphaα и β\betaβ являются дополнительными углами. В форме уравнения мы выражаем это как:
α+β=90°\альфа + \бета = 90\градусα+β=90°
Итак, если мы знаем один из этих двух углов, как найти недостающие углы прямоугольного треугольника так же просто, как вычесть наш известный угол из 90° 🙂.
С другой стороны, если мы не знаем ни одного из двух углов, мы все равно можем найти их с помощью некоторых основных тригонометрических функций.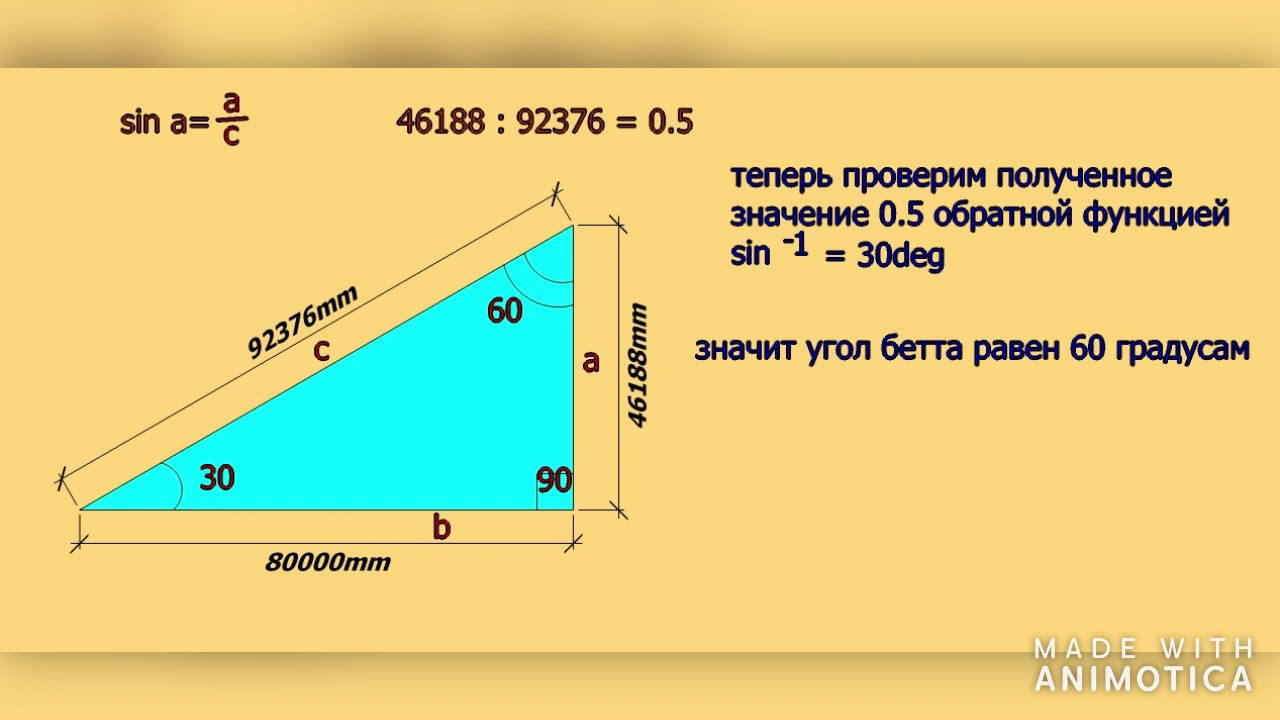
Чтобы найти угол α\alphaα, мы можем использовать следующие уравнения:
- α=arctan(a/b)\alpha = \arctan(a / b)α=arctan(a/b)
- α=arccos(b/c)\alpha = \arccos(b/c)α=arccos(b/c)
- α=arcsin(a/c)\alpha = \arcsin(a/c)α=arcsin(a/c)
Для определения угла β\betaβ можно использовать следующие уравнения:
- β=arctan(b/a)\beta = \arctan(b/a)β=arctan(b/a)
- β=arccos(a/c)\beta = \arccos(a/c)β=arccos(a/c)
- β=arcsin(b/c)\бета = \arcsin(b/c)β=arcsin(b/c)
С помощью этих уравнений мы можем видеть, что если у нас есть измерения по крайней мере двух сторон нашего прямоугольного треугольника, мы можем определить, каковы углы прямоугольного треугольника.
Что, если вы знаете размер только одной ноги? Для этого нужно хотя бы знать площадь вашего прямоугольного треугольника, чтобы получить другую сторону вашего треугольника, используя одно из следующих уравнений:
Чтобы найти aaa, зная площадь\текст{площадь}площадь и bbb:
a=2×area/ba = 2 \ times \text{area} / ba=2×area/b
Чтобы найти bbb по заданным \text{area} и aaa:
b=2×area/ab = 2 \times \text{area} / ab= 2×площадь/а
Затем вы можете использовать формулы, которые мы обсуждали ранее, чтобы найти недостающие углы вашего прямоугольного треугольника.
Самое интересное, что мы уже использовали эти уравнения в этом калькуляторе для вашего удобства. Перейдите к следующему разделу этого текста, чтобы узнать, как использовать этот инструмент для расчета угла прямоугольного треугольника 🙂.
🙋 Обратите внимание, что мы не можем найти углы прямоугольного треугольника, если мы знаем только его гипотенузу ccc и его площадь \ текст {площадь}, потому что разные прямоугольные треугольники могут иметь одну и ту же гипотенузу, но с разными площадями.
Как использовать наш калькулятор угла прямоугольного треугольника
Чтобы использовать наш калькулятор угла прямоугольного треугольника, все, что вам нужно сделать, это ввести любые две известные стороны вашего прямоугольного треугольника . Это могут быть измерения двух сторон вашего прямоугольного треугольника (aaa и bbb) или измерения одной стороны и гипотенузы (aaa и ccc или bbb и ccc). Вы также можете ввести одну из сторон вашего треугольника (aaa, bbb или ccc) и площадь\текст{площадь}прямоугольного треугольника .
После этого вы сразу увидите углы вашего прямоугольного треугольника: оба угла α\alphaα и угол β\betaβ. Это так просто!
Если вы хотите еще больше расширить свои знания о треугольниках, вот список других наших калькуляторов треугольников, которые вы можете проверить:
- Калькулятор стороны и угла прямоугольного треугольника;
- Калькулятор стороны треугольника;
- Калькулятор отсутствующей стороны треугольника;
- Калькулятор длины треугольника;
- Калькулятор градусов треугольника;
- Калькулятор стороны и угла треугольника;
- Калькулятор подобных прямоугольных треугольников;
- калькулятор треугольника abc;
- Это калькулятор прямоугольного треугольника; и
- Проверка подобия в калькуляторе прямоугольных треугольников.
Часто задаваемые вопросы
Каковы углы прямоугольного треугольника?
Допустим, прямоугольный треугольник имеет площадь 20 см² и один из его катетов равен 4 см. Чтобы найти углы этого прямоугольного треугольника:
Чтобы найти углы этого прямоугольного треугольника:
- Сначала мы найдем другую сторону треугольника , используя это уравнение:
b = 2 × площадь / a, гдеa = 4 см. Тогда у нас будетb = 2 × 20 см² / 4 см =10 см. - Затем мы вычисляем угол
αнапротивa, равныйα = arctg(a / b):α = arctg(4 см / 10 см) =21. 8°. - Наконец, мы можем вычесть
αиз 90° найтиβ:β = 90° - 21,8° =68,2°.
Каковы 3 угла прямоугольного треугольника?
Три угла прямоугольного треугольника: один угол 90° и два острых угла, которые являются дополнительными углами . Это означает, что если в прямоугольном треугольнике один из углов равен 30°, то его другой угол будет равен 60°.

 Треугольники, Прямоугольники и т.д. Градусы в радианы.
Треугольники, Прямоугольники и т.д. Градусы в радианы. ..)
..) 0875
0875 176
176 268
268 364
364 466
466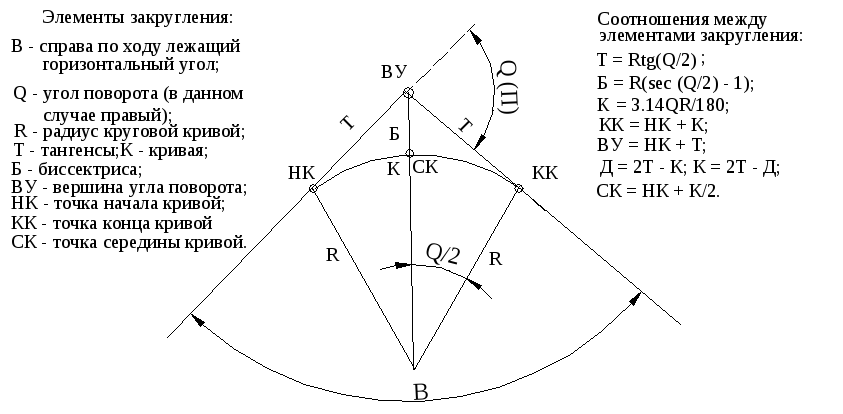 577
577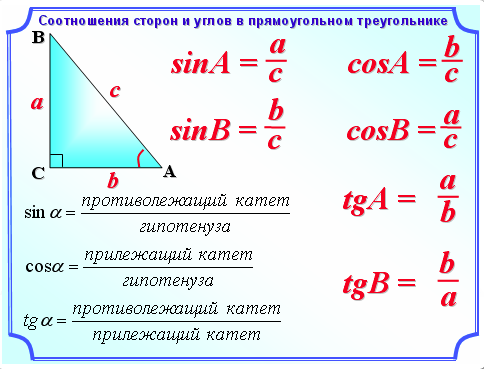
 839
839 41
41 Введите свой запрос:
Введите свой запрос: