Вес уголка – Калькулятор и таблицы
Стальной уголок – один из видов металлического проката, в виде L-образного профиля. Благодаря незначительной массе и высоким показателям устойчивости на изгиб, нашел широкое применение во всех отраслях хозяйства, в частности, наиболее распространен в строительстве для армирования бетона в монолитных конструкциях и перекрытиях. По форме сечения подразделяется на равнополочный и неравнополочный.
Калькулятор веса уголка стального от сервиса KALK.PRO позволяет определить массу металлопроката по известным характеристикам сторон и длине профиля. С используемыми марками стали можно ознакомиться в марочнике, в соответствующей вкладке интерфейса. Алгоритм программы производит расчеты на основании ГОСТ 8509-93 «Уголки стальные горячекатаные равнополочные», ГОСТ 8510-86 «Уголки стальные горячекатаные неравнополочные».
С помощью калькулятора можно найти вес всех возможных видов сортамента, например, уголок 40х40х4, 50х50х5, 63х63х5, 75х75х5 и т. д. При необходимости, вы сразу же можете воспользоваться марочником металлов или заглянуть в ГОСТы, в соответствующих вкладках инструмента.
д. При необходимости, вы сразу же можете воспользоваться марочником металлов или заглянуть в ГОСТы, в соответствующих вкладках инструмента.
Расчет веса уголка
- Выберите тип металла (по умолчанию Сталь).
- Подтвердите тип сортамента – Уголок.
- Выберите марку металла (по умолчанию Сталь Ст3сп).
- Укажите параметры уголка – ширина a, b (мм), толщина полки t (мм).
- Введите длину металлопроката L, м.
Расчет длины уголка (перевод из тонн в метры)
- Выберите тип металла (по умолчанию Сталь).
- Подтвердите тип сортамента – Уголок.
- Выберите марку металла (по умолчанию Сталь Ст3сп).
- Укажите параметры уголка – ширина a, b (мм), толщина полки t (мм).
- Введите массу металлопроката W, кг.
Произвести расчет стального уголка, также можно традиционным способом по математическим формулам и табличным значениям.
Уголок равнополочный – Таблица по ГОСТ 8509-93
| Наименование уголка | Размеры, мм | Толщина стенки, мм | Вес метра, кг | Метров в тонне | |
| a | b | ||||
| 20×3 | 20 | 20 | 3 | 0.89 | 1123.6 |
| 20×4 | 20 | 20 | 4 | 1.15 | 869.57 |
| 25×3 | 25 | 25 | 3 | 1.12 | 892.86 |
| 25×4 | 25 | 25 | 4 | 1.46 | 684.93 |
| 25×5 | 25 | 25 | 5 | 1.78 | 561.8 |
| 28×3 | 28 | 28 | 3 | 1.27 | 787.4 |
| 30×3 | 30 | 30 | 3 | 1.36 | 735.29 |
| 30×4 | 30 | 30 | 4 | 1. 78 78 | 561.8 |
| 30×5 | 30 | 30 | 5 | 2.18 | 458.72 |
| 32×3 | 32 | 32 | 3 | 1.46 | 684.93 |
| 32×4 | 32 | 32 | 4 | 1.91 | 523.56 |
| 35×3 | 35 | 35 | 3 | 1.6 | 625 |
| 35×4 | 35 | 35 | 4 | 2.1 | 476.19 |
| 35×5 | 35 | 35 | 5 | 2.58 | 387.6 |
| 40×3 | 40 | 40 | 3 | 1.85 | 540.54 |
| 40×4 | 40 | 40 | 4 | 2.42 | 413.22 |
| 40×5 | 40 | 40 | 5 | 2.98 | 335.57 |
| 40×6 | 40 | 40 | 6 | 3.52 | 284.09 |
| 45×3 | 45 | 45 | 3 | 2.08 | 480.77 |
| 45×4 | 45 | 45 | 4 | 2.73 | 366.3 |
| 45×5 | 45 | 45 | 5 | 3. 37 37 | 296.74 |
| 45×6 | 45 | 45 | 6 | 3.99 | 250.63 |
| 50×3 | 50 | 50 | 3 | 2.32 | 431.03 |
| 50×4 | 50 | 50 | 4 | 3.05 | 327.87 |
| 50×5 | 50 | 50 | 5 | 3.77 | 265.25 |
| 50×6 | 50 | 50 | 6 | 4.47 | 223.71 |
| 50×7 | 50 | 50 | 7 | 5.15 | 194.17 |
| 50×8 | 50 | 50 | 8 | 5.82 | 171.82 |
| 56×4 | 56 | 56 | 4 | 3.44 | 290.7 |
| 56×5 | 56 | 56 | 5 | 4.25 | 235.29 |
| 60×4 | 60 | 60 | 4 | 3.71 | 269.54 |
| 60×5 | 60 | 60 | 5 | 4.58 | 218.34 |
| 60×6 | 60 | 60 | 6 | 5.43 | 184.16 |
| 60×8 | 60 | 60 | 8 | 7. 1 1 | 140.85 |
| 60×10 | 60 | 60 | 10 | 8.7 | 114.94 |
| 63×4 | 63 | 63 | 4 | 3.9 | 256.41 |
| 63×5 | 63 | 63 | 5 | 4.81 | 207.9 |
| 63×6 | 63 | 63 | 6 | 5.72 | 174.83 |
| 65×6 | 65 | 65 | 6 | 5.91 | 169.2 |
| 65×8 | 65 | 65 | 8 | 7.73 | 129.37 |
| 70×4,5 | 70 | 70 | 4,5 | 4.87 | 205.34 |
| 70×5 | 70 | 70 | 5 | 5.38 | 185.87 |
| 70×6 | 70 | 70 | 6 | 6.39 | 156.49 |
| 70×7 | 70 | 70 | 7 | 7.39 | 135.32 |
| 70×8 | 70 | 70 | 8 | 8.37 | 119.47 |
| 70×10 | 70 | 70 | 10 | 10.29 | 97. 18 18 |
| 75×5 | 75 | 75 | 5 | 5.8 | 172.41 |
| 75×6 | 75 | 75 | 6 | 6.89 | 145.14 |
| 75×7 | 75 | 75 | 7 | 7.96 | 125.63 |
| 75×8 | 75 | 75 | 8 | 9.02 | 110.86 |
| 75×9 | 75 | 75 | 9 | 10.07 | 99.3 |
| 80×5,5 | 80 | 80 | 5,5 | 6.78 | 147.49 |
| 80×6 | 80 | 80 | 6 | 7.36 | 135.87 |
| 80×7 | 80 | 80 | 7 | 8.51 | 117.51 |
| 80×8 | 80 | 80 | 8 | 9.65 | 103.63 |
| 80×10 | 80 | 80 | 10 | 11.88 | 84.18 |
| 80×12 | 80 | 80 | 12 | 14.05 | 71.17 |
| 90×6 | 90 | 90 | 6 | 8.33 | 120.05 |
| 90×7 | 90 | 90 | 7 | 9. 64 64 | 103.73 |
| 90×8 | 90 | 90 | 8 | 10.93 | 91.49 |
| 90×9 | 90 | 90 | 9 | 12.2 | 81.97 |
| 90×10 | 90 | 90 | 10 | 13.48 | 74.18 |
| 90×12 | 90 | 90 | 12 | 15.96 | 62.66 |
| 100×6,5 | 100 | 100 | 6,5 | 10.06 | 99.4 |
| 100×7 | 100 | 100 | 7 | 10.79 | 92.68 |
| 100×8 | 100 | 100 | 8 | 12.25 | 81.63 |
| 100×10 | 100 | 100 | 10 | 15.1 | 66.23 |
| 100×12 | 100 | 100 | 12 | 17.9 | 55.87 |
| 100×14 | 100 | 100 | 14 | 20.63 | 48.47 |
| 100×15 | 100 | 100 | 15 | 21.97 | 45.52 |
| 100×16 | 100 | 100 | 16 | 23. 3 3 | 42.92 |
| 110×7 | 110 | 110 | 7 | 11.89 | 84.1 |
| 110×8 | 110 | 110 | 8 | 13.5 | 74.07 |
| 120×8 | 120 | 120 | 8 | 14.76 | 67.75 |
| 120×10 | 120 | 120 | 10 | 18.24 | 54.82 |
| 120×12 | 120 | 120 | 12 | 21.67 | 46.15 |
| 120×15 | 120 | 120 | 15 | 26.68 | 37.48 |
| 125×8 | 125 | 125 | 8 | 15.46 | 64.68 |
| 125×9 | 125 | 125 | 9 | 17.3 | 57.8 |
| 125×10 | 125 | 125 | 10 | 19.1 | 52.36 |
| 125×12 | 125 | 125 | 12 | 22.68 | 44.09 |
| 125×14 | 125 | 125 | 14 | 26.2 | 38.17 |
| 125×16 | 125 | 125 | 16 | 29. 65 65 | 33.73 |
| 140×9 | 140 | 140 | 9 | 19.41 | 51.52 |
| 140×10 | 140 | 140 | 10 | 21.45 | 46.62 |
| 140×12 | 140 | 140 | 12 | 25.5 | 39.22 |
| 150×10 | 150 | 150 | 10 | 23.02 | 43.44 |
| 150×12 | 150 | 150 | 12 | 27.39 | 36.51 |
| 150×15 | 150 | 150 | 15 | 33.82 | 29.57 |
| 150×18 | 150 | 150 | 18 | 40.11 | 24.93 |
| 160×10 | 160 | 160 | 10 | 24.67 | 40.54 |
| 160×11 | 160 | 160 | 11 | 27.02 | 37.01 |
| 160×12 | 160 | 160 | 12 | 28.35 | 35.27 |
| 160×14 | 160 | 160 | 14 | 33.97 | 29.44 |
| 160×16 | 160 | 160 | 16 | 38. 52 52 | 25.96 |
| 160×18 | 160 | 160 | 18 | 43.01 | 23.25 |
| 160×20 | 160 | 160 | 20 | 47.44 | 21.08 |
| 180×11 | 180 | 180 | 11 | 30.47 | 32.82 |
| 180×12 | 180 | 180 | 12 | 33.12 | 30.19 |
| 180×15 | 180 | 180 | 15 | 40.96 | 24.41 |
| 180×18 | 180 | 180 | 18 | 48.66 | 20.55 |
| 180×20 | 180 | 180 | 20 | 53.72 | 18.62 |
| 200×12 | 200 | 200 | 12 | 36.97 | 27.05 |
| 200×13 | 200 | 200 | 13 | 39.92 | 25.05 |
| 200×14 | 200 | 200 | 14 | 42.8 | 23.36 |
| 200×16 | 200 | 200 | 16 | 48.65 | 20.55 |
| 200×18 | 200 | 200 | 18 | 54. 4 4 | 18.38 |
| 200×20 | 200 | 200 | 20 | 60.08 | 16.64 |
| 200×24 | 200 | 200 | 24 | 71.26 | 14.03 |
| 200×25 | 200 | 200 | 25 | 74.02 | 13.51 |
| 200×30 | 200 | 200 | 30 | 87.56 | 11.42 |
| 220×14 | 220 | 220 | 14 | 47.4 | 21.1 |
| 220×16 | 220 | 220 | 16 | 53.83 | 18.58 |
| 250×16 | 250 | 250 | 16 | 61.55 | 16.25 |
| 250×18 | 250 | 250 | 18 | 68.86 | 14.52 |
| 250×20 | 250 | 250 | 20 | 76.11 | 13.14 |
| 250×22 | 250 | 250 | 22 | 83.31 | 12 |
| 250×25 | 250 | 250 | 25 | 93.97 | 10.64 |
| 250×28 | 250 | 250 | 28 | 104. 5 5 | 9.57 |
| 250×30 | 250 | 250 | 30 | 111.44 | 8.97 |
| 250×35 | 250 | 250 | 35 | 128.51 | 7.78 |
Уголок неравнополочный – Таблица по ГОСТ 8510-86
| Наименование уголка | Размеры, мм | Толщина стенки, мм | Вес метра, кг | Метров в тонне | |
| a | b | ||||
| 25х16х3 | 25 | 16 | 3 | 0,91 | 1098,90 |
| 30х20х3 | 30 | 20 | 3 | 1,12 | 892,86 |
| 30х20х4 | 30 | 20 | 4 | 1,46 | 684,93 |
| 32х20х3 | 32 | 20 | 3 | 1,17 | 854,70 |
| 32х20х4 | 32 | 20 | 4 | 1,52 | 657,89 |
| 40х25х3 | 40 | 25 | 3 | 1,48 | 657,68 |
| 40х25х4 | 40 | 25 | 4 | 1,94 | 515,46 |
| 40х25х5 | 40 | 25 | 5 | 2,37 | 421,94 |
| 40х30х4 | 40 | 30 | 4 | 2,26 | 442,48 |
| 40х30х5 | 40 | 30 | 5 | 2,46 | 406,50 |
| 45х28х3 | 45 | 28 | 3 | 1,68 | 595,24 |
| 45х28х4 | 45 | 28 | 4 | 2,2 | 454,55 |
| 50х32х3 | 50 | 32 | 3 | 1,9 | 526,32 |
| 50х32х4 | 50 | 32 | 4 | 2,4 | 416,67 |
| 56х36х4 | 56 | 36 | 4 | 2,81 | 355,87 |
| 56х36х5 | 56 | 36 | 5 | 3,46 | 289,02 |
| 63х40х4 | 63 | 40 | 4 | 3,17 | 315,46 |
| 63х40х5 | 63 | 40 | 5 | 3,91 | 255,75 |
| 63х40х6 | 63 | 40 | 6 | 4,63 | 215,98 |
| 63х40х8 | 63 | 40 | 8 | 6,03 | 165,84 |
| 65х50х5 | 65 | 50 | 5 | 4,36 | 229,36 |
| 65х50х6 | 65 | 50 | 6 | 5,18 | 193,05 |
| 65х50х7 | 65 | 50 | 7 | 5,98 | 167,22 |
| 65х50х8 | 65 | 50 | 8 | 6,77 | 147,71 |
| 70х45х5 | 70 | 45 | 5 | 4,39 | 227,79 |
| 75х50х5 | 75 | 50 | 5 | 4,79 | 208,77 |
| 75х50х6 | 75 | 50 | 6 | 5,69 | 175,75 |
| 75х50х7 | 75 | 50 | 7 | 6,57 | 152,21 |
| 75х50х8 | 75 | 50 | 8 | 7,43 | 134,59 |
| 80х50х5 | 80 | 50 | 5 | 4,49 | 222,72 |
| 80х50х6 | 80 | 50 | 6 | 5,92 | 168,92 |
| 80х60х6 | 80 | 60 | 6 | 6,39 | 156,49 |
| 80х60х7 | 80 | 60 | 7 | 7,39 | 135,32 |
| 80х60х8 | 80 | 60 | 8 | 8,37 | 119,47 |
90х56х5. 5 5 | 90 | 56 | 5,5 | 6,17 | 162,07 |
| 90х56х6 | 90 | 56 | 6 | 6,7 | 149,25 |
| 90х56х8 | 90 | 56 | 8 | 8,77 | 114,03 |
| 100х63х6 | 100 | 63 | 6 | 7,53 | 132,80 |
| 100х63х7 | 100 | 63 | 7 | 8,7 | 114,94 |
| 100х63х8 | 100 | 63 | 8 | 9,87 | 101,32 |
| 100х63х10 | 100 | 63 | 10 | 12,14 | 82,37 |
| 100х65х7 | 100 | 65 | 7 | 8,81 | 113,51 |
| 100х65х8 | 100 | 65 | 8 | 9,99 | 100,10 |
| 100х65х10 | 100 | 65 | 10 | 12,3 | 81,30 |
| 110х70х6.5 | 110 | 70 | 6,5 | 8,98 | 111,35 |
| 110х70х8 | 110 | 70 | 8 | 10,93 | 91,49 |
| 125х80х7 | 125 | 80 | 7 | 11,04 | 90,58 |
| 125х80х8 | 125 | 80 | 8 | 12,58 | 79,49 |
| 125х80х10 | 125 | 80 | 10 | 15,47 | 64,64 |
| 125х80х12 | 125 | 80 | 12 | 18,34 | 54,53 |
| 140х90х8 | 140 | 90 | 8 | 14,13 | 70,77 |
| 140х90х10 | 140 | 90 | 10 | 17,46 | 57,27 |
| 160х100х9 | 160 | 100 | 9 | 17,96 | 55,68 |
| 160х100х10 | 160 | 100 | 10 | 19,85 | 50,38 |
| 160х100х12 | 160 | 100 | 12 | 23,58 | 42,41 |
| 160х100х14 | 160 | 100 | 14 | 27,26 | 36,68 |
| 180х110х10 | 180 | 110 | 10 | 22,2 | 45,05 |
| 180х110х12 | 180 | 110 | 12 | 26,4 | 37,88 |
| 200х125х11 | 200 | 125 | 11 | 27,37 | 36,54 |
| 200х125х12 | 200 | 125 | 12 | 29,74 | 33,62 |
| 200х125х14 | 200 | 125 | 14 | 34,43 | 29,04 |
| 200х125х16 | 200 | 125 | 16 | 39,07 | 25,60 |
Как рассчитать нагрузку на металлический уголок
Металлический уголок – вид металлопроката, который представляет Г-образный профиль. Имеет несколько подвидов. Находит применение в строительстве и промышленности. Без данного изделия не обходится ни одна конструкция.
Имеет несколько подвидов. Находит применение в строительстве и промышленности. Без данного изделия не обходится ни одна конструкция.
Из чего изготавливается, где применяется?
Существует два способа катания: холодное и горячее. Во втором варианте сталь прокатывается через специальную форму горячих станков. Холодная прокатка проводится под давлением при низкой температуре 500-600°С. При этом металл вытягивается, приобретает прочность, снижает пластические свойства и магнитную проницаемость. Купить уголок металлический можно в любом строительном павильоне или магазине. Чеканится из обычной и низколегированной стали. Бывает неравнополочным и равнополочным.
Первый тип получается методом горячего проката. Используется для строительства зданий и в станкостроении. Второй тип является ведущим профильным прокатом. Отличается универсальностью и высокой прочностью в продольном сечении. Может легко свариваться, монтироваться любыми возможными способами. Используются в зависимости от:
- параметров жесткости;
- размеров полок;
- вида;
- типа стали.

По ГОСТу имеет регламентированный интервал толщины полок. Может усиливать бетонные конструкции, заменять прутки арматуры.
Для производства уголков подходит и углеродистый металл, что делает их оцинкованными. Употребляются для изготовления дверей, заборов, эстакад и мостов. Ими можно воспользоваться для строительства торговых павильонов, навесов, трубопроводов, огромных стоек для рекламных щитов. Задействуют при возведении линий электрических опор, в машиностроении.
Характеристика стального уголка
Продукт изготавливается высокой точности марки «А» и обычной – марки «В». Могут быть ограниченной длины, немерной, кратной и мерной. Готовый профиль допускает максимальную длину 12 метров. Неравнополочные бывают длиннее. Преимущества металлического изделия:
- возможное использование в местах со свободным пространством для оборудования и людей;
- стойкость к коррозии и атмосферному воздействию;
- высокое качество, прочность и жёсткость;
- большой срок службы;
- универсальность;
- отсутствие скручивания вокруг продольной оси.

Как провести расчёты нагрузки
Моменты нагрузки распределяются по признакам. Они могут быть:
- Постоянными, когда вес и давление с течением времени не изменяется.
- Временными длительными, которые учитывают вес дополнительных конструкций, включающих оборудование и мебель.
- Кратковременными поперечными, которые учитывают нагрузку от дождя, снега и ветра. При этом следует учитывать месторасположение объекта.
- Экстремальными и сейсмическими. Производятся специально для местности с сейсмической активностью.
Начало расчёта производится с учётом дополнительного давления на изделие. Нужно принимать во внимание вес металлического уголка и вес перекрытия. Нагрузки делятся на типы: нормативные и расчётные. Первые применяются для расчёта на прогиб, включая предельное состояние. Вторые – для расчёта на устойчивость и прочность. Определяются умножением первого типа на показатель нагрузки надёжности. В интернете можно найти онлайн-калькулятор для быстрого и лёгкого расчёта нагрузки.
Стальной профиль – популярное изделие металлопроката отечественной промышленности. Изготавливается из металла. Применяются для конструирования металлических систем с разной прочностью и жёсткостью при строительстве многоэтажных зданий, ремонте строительных сооружений и подвесных мостов.
Если Вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.
The Sumy Post в Telegram та Facebook. Цікаві й оперативні новини, фото, відео. Підписуйтесь на наші сторінки!
Реклама
comments powered by HyperComments| Меню инженерных расчетов Плоские пластины Напряжения, уравнения прогиба и калькуляторы : Следующие веб-страницы содержат калькуляторы инженерного проектирования, которые определяют величину прогиба и напряжения, которые плоская пластина известной толщины прогибается под действием указанной нагрузки и распределения. Многие уравнения и калькуляторы напряжения и прогиба ссылаются на формулы Рорка для напряжения и деформации. Обратите внимание, что для большинства калькуляторов требуется премиум-членство для полной функциональности. Поведение плоской пластины: пластина прогибается. Средняя поверхность (на полпути между верхней и нижней поверхностями) остается ненагруженной; в других точках имеются двухосные напряжения в плоскости пластины. Прямые линии на пластине, которые изначально были вертикальными, остаются прямыми, но становятся наклонными; поэтому интенсивность любого главного напряжения в точках любой такой линии пропорциональна расстоянию от срединной поверхности, а максимальные напряжения возникают на внешних поверхностях пластины. ** Искать ТОЛЬКО на этой СТРАНИЦЕ, нажмите на увеличительное стекло **
Родственный:
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Равномерно нагруженные прямоугольные пластины на трех угловых опорах (ошибка отклонения)
Аннотация
Численные решения теоретического решения для равномерно нагруженной прямоугольной пластины на трех угловых опорах, опубликованные в Journal of Structural Engineering, среди прочего , таблицы максимальных перемещений и максимальных главных моментов для использования инженером-практиком.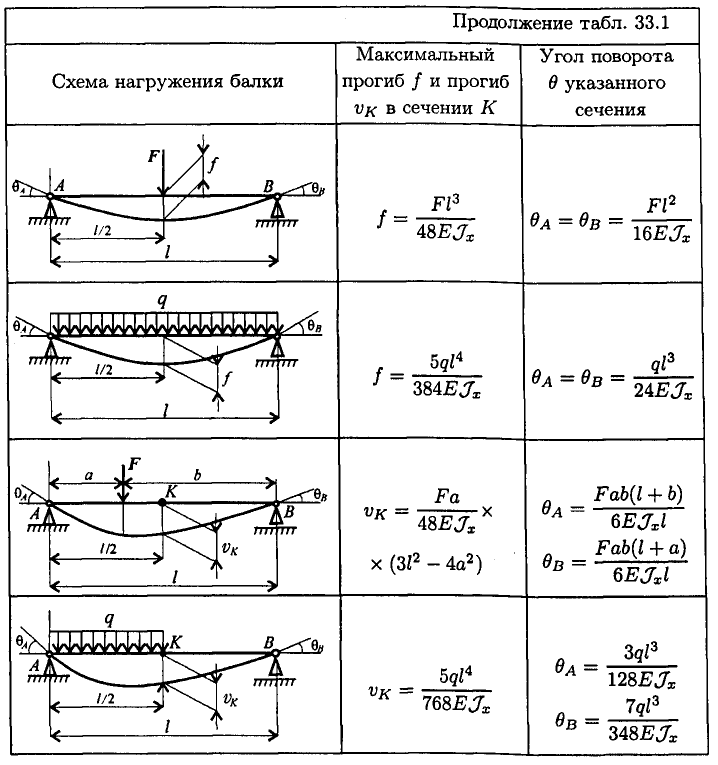 Предполагается, что максимальные смещения происходят в свободном углу пластины, и, хотя это справедливо для пластин с малым соотношением сторон, максимальное смещение перемещается от этого положения по мере увеличения отношения размеров. Конечные элементы используются в этом техническом примечании для получения независимого численного решения, которое согласуется с опубликованными значениями угловых смещений, а затем используется для получения максимального смещения. Для наибольшего рассматриваемого соотношения сторон (2,5) видно, что максимальное смещение занижено примерно на 10% в опубликованных результатах.
Предполагается, что максимальные смещения происходят в свободном углу пластины, и, хотя это справедливо для пластин с малым соотношением сторон, максимальное смещение перемещается от этого положения по мере увеличения отношения размеров. Конечные элементы используются в этом техническом примечании для получения независимого численного решения, которое согласуется с опубликованными значениями угловых смещений, а затем используется для получения максимального смещения. Для наибольшего рассматриваемого соотношения сторон (2,5) видно, что максимальное смещение занижено примерно на 10% в опубликованных результатах.
Введение
Во время недавнего проекта автору потребовалось для проверки модели конечных элементов (КЭ) теоретическое решение для прямоугольной пластины на трех угловых опорах, нагруженной точечной нагрузкой на неподдерживаемый угол. Теоретическое решение для этой конфигурации пластин не представлено в стандартных справочных текстах, таких как «Теория пластин и оболочек» Тимошенко, но довольно элегантное решение было найдено в [1], которое также включало случай, когда пластина равномерно нагружена, как показано на рис. 1.
1.
Для равномерно загруженной конфигурации пластины теоретическое перемещение в безопорном углу, w, было представлено в уравнении. (1) где q — равномерно распределенная нагрузка, D — жесткость на изгиб, а nu — коэффициент Пуассона.
Затем были представлены результаты для этой конфигурации плиты в виде безразмерных максимальных перемещений и максимальных главных моментов для диапазона соотношений сторон и коэффициентов Пуассона. Безразмерное смещение выражается как альфа-параметр в уравнении. (2) использование s=min(a,b) вместо a в знаменателе, чтобы сделать выражение более общим, чем в исходной публикации.
Используя КЭ-анализ с высокоточной сеткой из четырехузловых четырехугольных элементов Кирхгофа, автор смог проверить опубликованные результаты. В то время как при малых удлинениях максимальное смещение в пластине происходило в безопорном углу, с увеличением удлинения точка максимального смещения начинала удаляться от угла и вдоль верхнего свободного края и для наибольшего рассматриваемого удлинения, т. е. 2.5, фактическое максимальное смещение было примерно на 10% больше, чем в углу пластины.
е. 2.5, фактическое максимальное смещение было примерно на 10% больше, чем в углу пластины.
Результаты исследования автора показаны на рисунке 2 для коэффициента Пуассона 0,3. Нижняя кривая использует уравнение. (1) для смещения и опубликованных результатов, которые были получены из уравнения и согласуются с ним. (1), показаны на рисунке квадратами. Верхняя кривая представляет максимальные смещения от конечного элемента, полученные автором, и видно, что они расходятся с угловыми смещениями, когда соотношение сторон увеличивается примерно до 2.
Выводы
проверка результатов FE, если он/она сможет с уверенностью использовать их для проекта проектирования или оценки. Коммерческие системы КЭ содержат ошибки, и все инженеры способны их исправить.0558 Ошибка конечных элементов ! Хотя теоретические решения кажутся идеальным способом проверки, инженер должен следить за тем, чтобы эти решения были точными. Другими словами, теоретическое решение тоже нуждается в проверке! Если есть согласие между теоретическим и конечным решениями, тогда, хотя и не невозможно, весьма вероятно, что оба результата верны. В случае, показанном в этой технической заметке, автор получил почти идеальное соответствие между теорией и КЭ для углового смещения и, таким образом, смог представить результаты максимального смещения с уверенностью в их правильности.
В случае, показанном в этой технической заметке, автор получил почти идеальное соответствие между теорией и КЭ для углового смещения и, таким образом, смог представить результаты максимального смещения с уверенностью в их правильности.
В то время как недооценка максимального отклонения на 10 % может не угрожать структурной целостности пластины, это может привести к тому, что конструкция будет более чувствительной, чем ожидалось, например, к пешеходам. При проверке максимальных перемещений для этой конфигурации пластин автор также проверил опубликованные максимальные главные моменты и нашел их правильными.
Ошибка, раскрытая в этой статье, не первая обнаруженная автором – см., например, [2]. Таким образом, совет, предлагаемый практикующим инженерам, вполне может быть Предостережение emptor , когда дело доходит до принятия численных результатов даже из кажущихся достоверными результатов, представленных уважаемыми работниками в авторитетных публикациях.
Список литературы
[1] Азархин, А.

 программу Premium Publisher
программу Premium Publisher 

 пер. Формулы Рорка для напряжений и деформаций для плоских пластин с прямыми границами и постоянной толщиной
пер. Формулы Рорка для напряжений и деформаций для плоских пластин с прямыми границами и постоянной толщиной 
 Равномерная нагрузка по всей пластине. Уравнение напряжения и прогиба и калькулятор. пер. Формулы Роркса для напряжения и деформации
Равномерная нагрузка по всей пластине. Уравнение напряжения и прогиба и калькулятор. пер. Формулы Роркса для напряжения и деформации 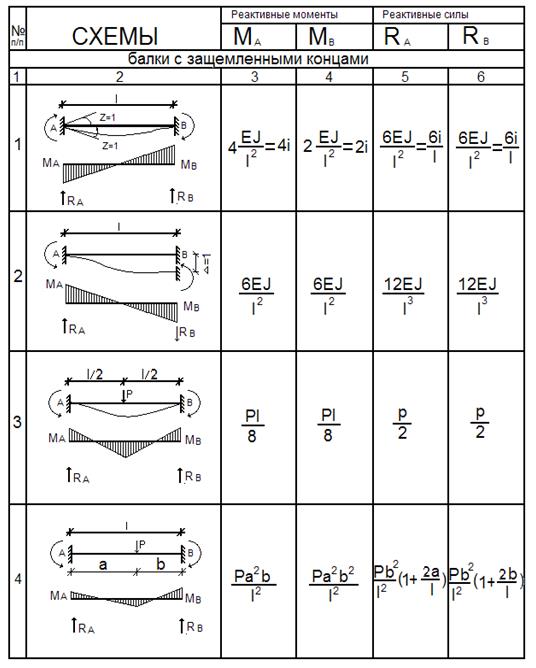 пер. Формулы Роркса для формул напряжений и деформаций
пер. Формулы Роркса для формул напряжений и деформаций  Равномерно уменьшается от фиксированной кромки до нуля при 2/3 b. Уравнение напряжения и прогиба и калькулятор. пер. Формулы Рорка для напряжения и деформации
Равномерно уменьшается от фиксированной кромки до нуля при 2/3 b. Уравнение напряжения и прогиба и калькулятор. пер. Формулы Рорка для напряжения и деформации  пер. Формулы Роркса для напряжения и деформации
пер. Формулы Роркса для напряжения и деформации  пер. Формулы Роркса для напряжения и деформации
пер. Формулы Роркса для напряжения и деформации  пер. Формулы Роркса для напряжения и деформации
пер. Формулы Роркса для напряжения и деформации  пер. Формулы Рорка для напряжения и деформации
пер. Формулы Рорка для напряжения и деформации 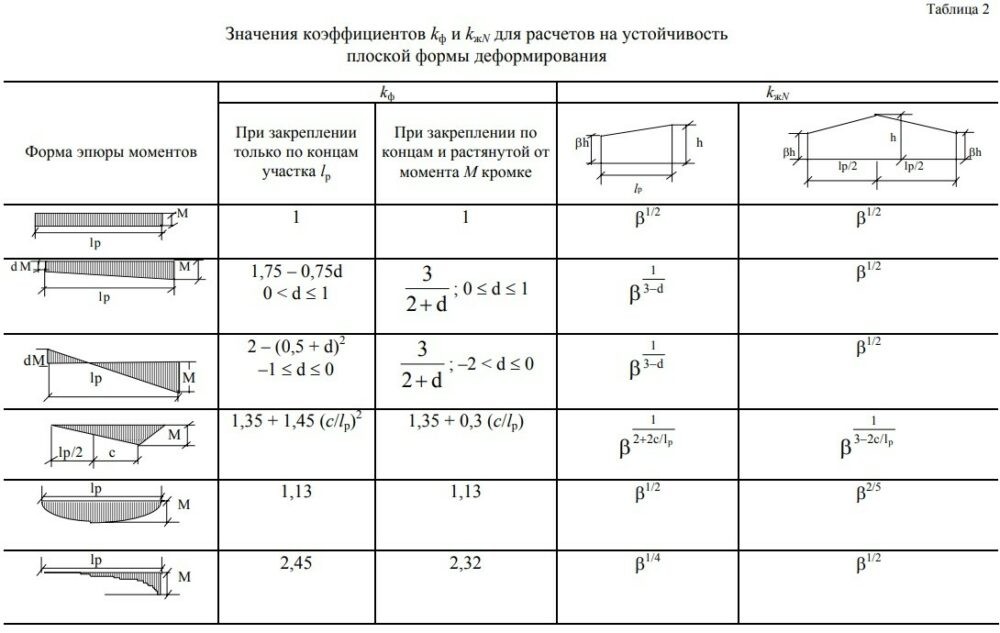 пер. Формулы Рорка для напряжения и деформации
пер. Формулы Рорка для напряжения и деформации 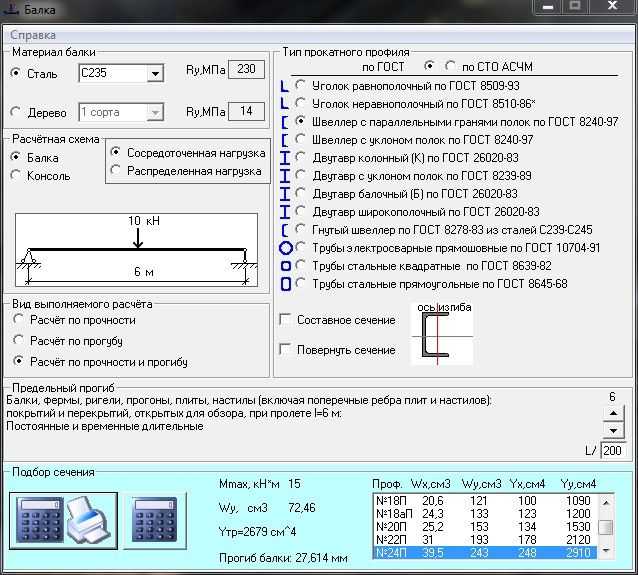 пер. Формулы Рорка для напряжения и деформации
пер. Формулы Рорка для напряжения и деформации  Равномерное нагружение по небольшой окружности радиусом r o , удаленной от краев. пер. Формулы Роркса для напряжения и деформации
Равномерное нагружение по небольшой окружности радиусом r o , удаленной от краев. пер. Формулы Роркса для напряжения и деформации  пер. Формулы Рорка для напряжения и деформации
пер. Формулы Рорка для напряжения и деформации 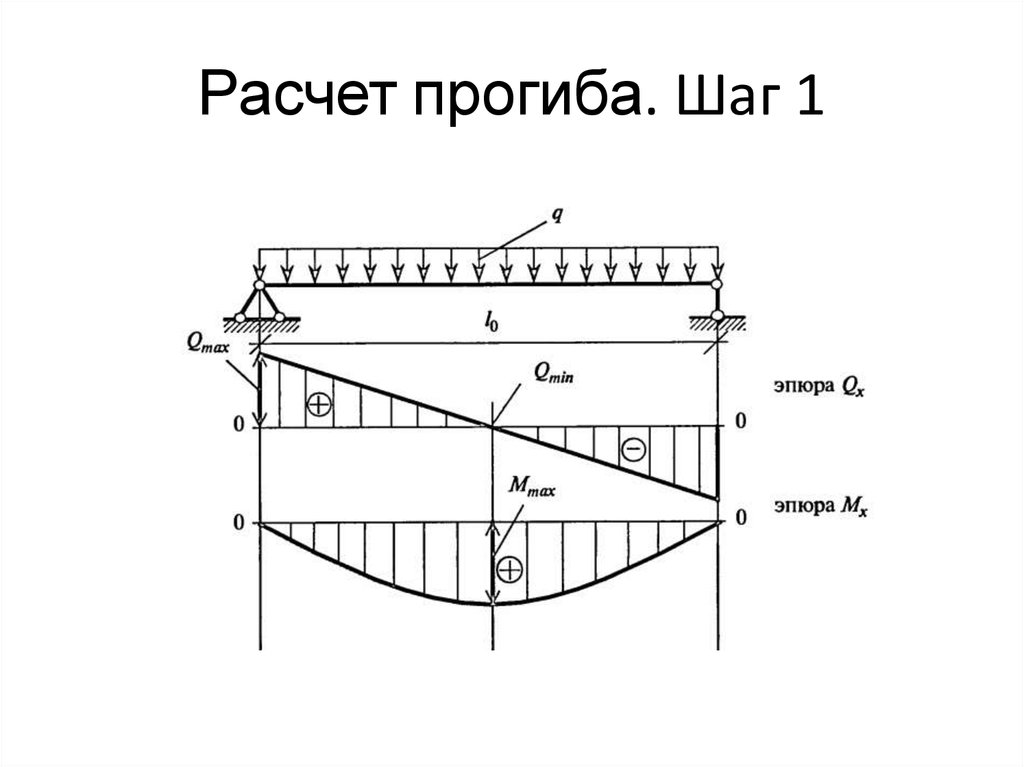 пер. Формулы Рорка для напряжения и деформации
пер. Формулы Рорка для напряжения и деформации  Предполагается, что нагрузка действует на небольшой площади радиусом e.
Предполагается, что нагрузка действует на небольшой площади радиусом e.  Таблицы предоставляют проектировщику быстрое и экономичное средство анализа конструкций в репрезентативных точках. Представленные данные, как указано на прилагаемом рисунке на фронтисписе, были рассчитаны для пяти наборов граничных условий, девяти соотношений поперечных размеров и одиннадцати типовых нагрузок, встречающихся при расчете.
Таблицы предоставляют проектировщику быстрое и экономичное средство анализа конструкций в репрезентативных точках. Представленные данные, как указано на прилагаемом рисунке на фронтисписе, были рассчитаны для пяти наборов граничных условий, девяти соотношений поперечных размеров и одиннадцати типовых нагрузок, встречающихся при расчете.