alexxlab Расчет балок онлайн. Примеры расчета
Расчет балки различается в зависимости от того, является она статически определимой, либо статически неопределимой. На сайте производится расчет любых балок, но подробное решение расписывается только для статически определимых балок, не имеющих промежуточных шарниров.
Балка на двух опорах. Построение эпюр
Для этого типа балок сервис позволяет определить и подробно расписывает:
- реакции опор
- эпюры поперечных сил и изгибающих моментов (эпюры Q и M)
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- по уравнениям метода начальных параметров вычисляются прогибы и углы поворота.
Посмотреть пример »
Консольная балка. Построение эпюр.
Для этого типа балок сервис позволяет определить и подробно расписывает:
- построение эпюр поперечных сил и изгибающих моментов
- подбор сечений — двутавр, прямоугольник, круг, квадрат, труба
- строятся эпюры нормальных и касательных напряжений
- вычисляются прогибы и углы поворота.
Посмотреть пример »
Статически неопределимая балка. Подбор сечения.
Для такого типа балок Вы можете получить
- только результаты расчета — (эпюры Q и M).
Естественно, по этим эпюрам можно легко найти реакции опор. Подробный ход расчета не расписывается,
но, имея результаты, Вы легко можете проверить все промежуточные итоги своего расчета.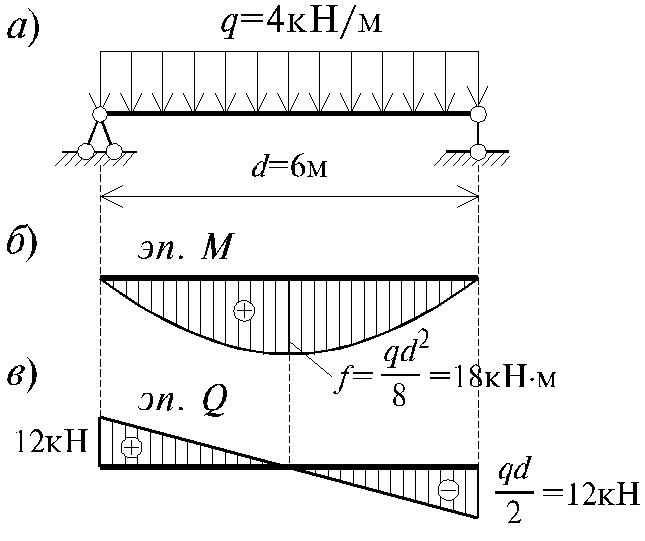
Посмотреть пример »
Балка с промежуточными шарнирами
Расчет балки с промежуточными шарнирами Вы должны производить, скорее всего, методом построения поэтажной схемы. Сервис, опять же, дает только конечный результат, но его наличие, естественно, очень упрощает проверку промежуточных этапов решения заданий.
Посмотреть пример »
Построение эпюр усилий онлайн
Інструкція.
Программа позволяет определить опорные реакции и построить эпюры внутренних усилий для двухопорной и консольной балки.
Дальнейшие инструкции будут приведены на примере балки на двух опорах.
1.
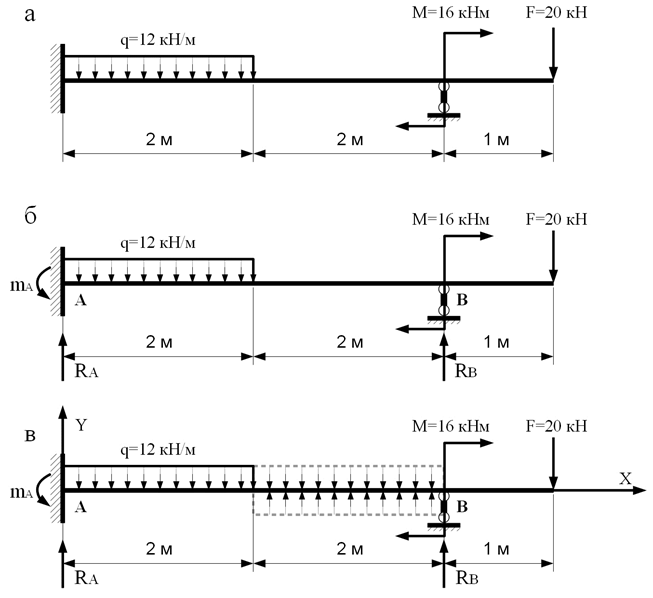Выберите условия крепления концов балки. Возможны варианты — свободный, шарнир и жесткое. В нашем примере левый и правый конец стержня не имеют креплений, поэтому выбираем вариант «свободный».
Если по ошибке был выбран другой вариант, нажимаем на кнопку «Новая схема».
2. Указываем длину балки и координаты опор. Длина балки равна «13», а координаты опор от левого конца балки, в соответствии к опоры A — «2» и к опоре B — «11».
3. Указываем нагрузку.
Выбираем количество сосредоточенных моментов — «2». В таблице вводим значения моментов и их координаты от левого конца балки. M1=40, a1=6 и M2=-20, a2=13
(момент который вращается против часовой стрелки — положительный, по — отрицательный).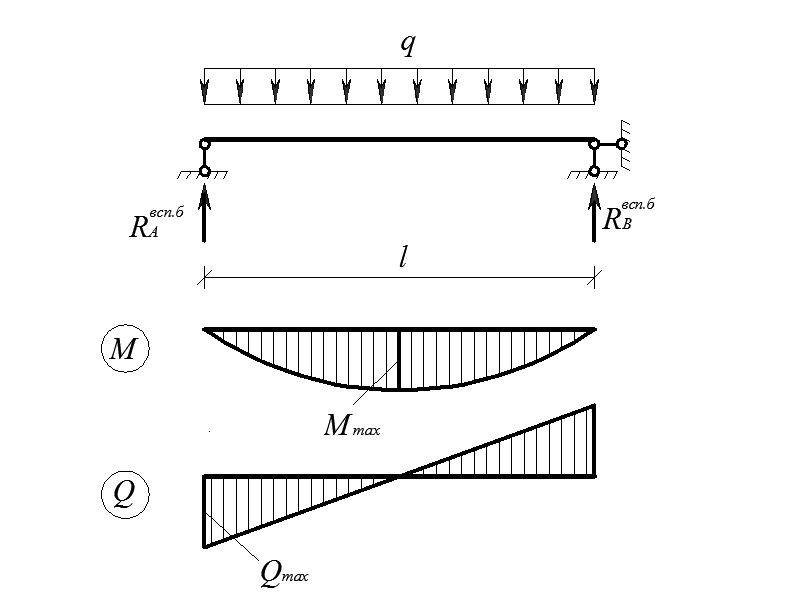
Выбираем количество сосредоточенных сил — «2». В таблице вводим значение сил и их координаты. F1=9, b1=0
и F2=6.93, b2=9 (сила направленная вниз — положительная, вверх — отрицательная).
Выбираем количество равномерно распределенной нагрузки — «1». В таблице вводим значение РРН, координаты начала
и конца РРН. q1=12, c1=2 та d1=8 (РРН направлена вниз — положительная, вверх — отрицательная).
4. Нажимаем на кнопку «Построить эпюры». После нажатия определяются опорные реакции и строятся эпюры усилий. Если нужно определить усилия в произвольном сечении, введите координату в форму. Если нужно, задайте точность расчета и выберите правое или левое сечение.
Скриншот к примеру:
Скриншот к примеру (эпюра поперечных сил):
Скриншот к примеру (эпюра изгибающих моментов):
Меню сайтаРасчет геометрических характеристик сечений он-лайн NEW — считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн — построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн. Расчет рам, ферм балок он-лайн NEW — эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы. Лекции — теория, практика, задачи… Примеры решения задач
Справочная информация — ГОСТы, сортамент проката, свойства материалов и другое. Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое). Форум сопромата и механики Книги — разная литература по теме. Заказать задачу Друзья сайта (ссылки) WIKIbetta Разработчикам (сотрудничество) Веб-мастерам (партнёрка) О проекте, контакты Подпроекты |
Добро пожаловать!!Сопротивление материалов , или просто сопромат. Считается, что сопромат — один из самых сложных предметов младших курсов. Cопротивление материалов является одной из наиболее систематизированных технических наук. Чтобы рассчитывать типовые инженерные задачи касающиеся проверки на прочность, прочностного проектирования нет необходимости каждый раз «ломать голову». Решение задач по сопромату сводится обычно к выбору подходящего метода для решения задачи, и последующему решению её. Для того, чтобы помочь решить задачи как можно большему числу людей всрок, на сайте есть: Подробнее о всех программах в разделе Программы. Как можно решить балку на паре?Есть 2 способа. Как можно рассчитать раму на паре?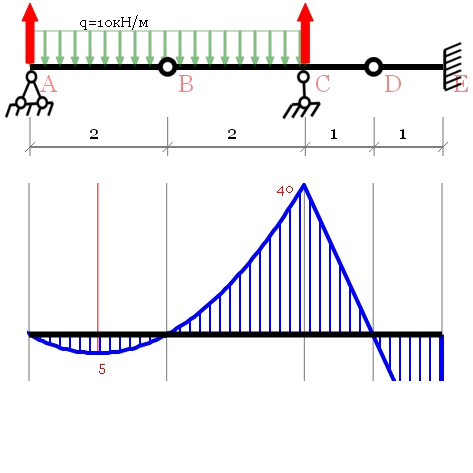 ЗаработайтеМини блогВертикальное перемещение точки в пространственной рамеhttps://ru.files.fm/thumb_show.php?i=afmduuvv&view Полностью… Консультация по динамической нагрузкеЗдравствуйте! Полностью… Нужен сопроматчик с хорошей математической подготовкойПривет. В команду проекта по разработке расчетного ПО для зданий ищем специалиста по сопромату с хорошей математической подготовкой для помощи нам в составлении расчетов, алгоритмов расчетов, поиска наилучших расчетов. Работа удаленная. Договор. Пишите, если интересно. Пообщаемся по деталям…. Полностью… нагрузка сверху вниз вдоль оси балкинадо найти максимальную нагрузку, которую может выдержать балка с нагрузкой сверху вниз вдоль оси балки, нагрузка 620 кг, длина балки 1030 мм ps Полностью… + Добавить статью или истрию (необходима авторизация) |
СообществоВходРешение задачРасчет редукторовДля Android (рекомендую)NEW Mobile Beam 2. 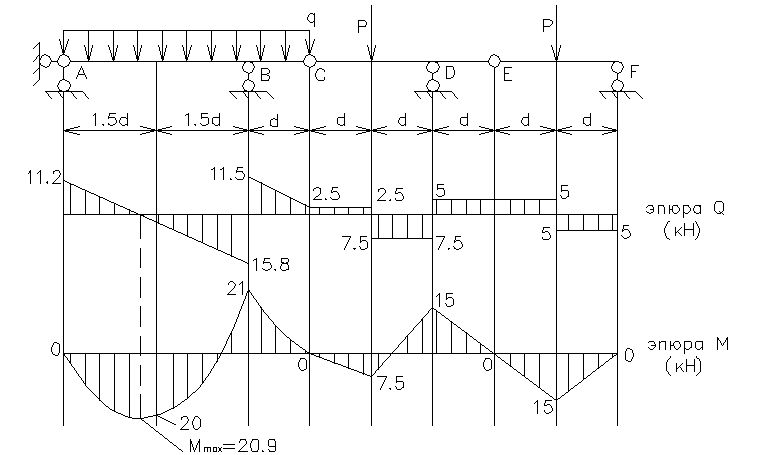 0Программа для расчета балок на прочность на Вашем Android устройстве… Java 2 ME |
Расчет балок, рам, ферм статически неопределимых и определимых
2. Наружный диаметр 357мм. Длина ремонтного участка 6м. Необходимо построить эпюры давлений…Расчет рамы по сопромату примеры и решения
Содержание:
- Аналитический расчет рам
- Пример решения задачи 2.1.1.
- Пример решения задачи 2.1.2
- Расчет рамы методом сил
- Выбор основной системы (ОС)
- Составление системы канонических уравнений
- Определение коэффициентов канонических уравнений
- Проверка коэффициентов каноническнх уравнений
- Статическая проверка
Рамы — это системы, состоящие из прямолинейных или криволинейных стержней, жестко или шарнирно связанных между собой по концам. Вертикальные и наклонные элементы рам называются стойками, горизонтальные и близкие к ним — ригелями. Рамы бывают несочлененными, то есть состоящими из одного диска, неподвижно закрепленного на плоскости, и сочлененными, состоящими из двух или нескольких дисков, соединенных между собой шарнирами.
В зависимости от способов образования и видов опорных закреплений рамы могут быть балочными (безраспорными) или арочными (распорными) системами. Расчет плоских, статически определимых рам выполняется с помощью уравнений равновесия статики и сводится к вычислению изгибающих моментов, поперечных и продольных сил в сечениях и построению эпюр внутренних усилий.
- Эпюрой называется график изменения изучаемой величины в различных сечениях от заданной неподвижной нагрузки.
Вычисление внутренних усилий в сечениях рамы выполняется статическим способом вырезания узлов и простых сечений. В аналитическом решении численные значения усилий определяются для каждого сечения из условий равновесия отсеченных частей рамы. Графическое решение удобно использовать при построении эпюр изгибающих моментов для простейших случаев загружения. Это позволяет определять общий характер распределения внутренних усилий, сечения с экстремальными и нулевыми изгибающими моментами.
Аналитический расчет рам
Аналитический расчет статически определимых рам сводится к следующему:
1.
Вычисление опорных реакций связей и проверка правильности их определения. Для однодисковых рам, прикрепленных к основанию тремя связями, реакции вычисляются из уравнений равновесия плоской произвольной системы сил в трех формах:
Перпендикулярно оси
не лежат на одной прямой
Для сочлененных рам необходимо к этим уравнениям дополнительно составить условия равновесия отдельных частей в виде
где -число простых шарниров.
Возможно вам будут полезны данные страницы:
Следовательно, для статически определимой рамы, имеющей простых шарниров, можно составить уравнения статики для определения опорных реакций.
2. Определение внутренних усилий — изгибающего момента поперечной силы продольной сил в характерных сечениях рамы.
Изгибающим моментом называется сумма статических моментов всех односторонних сил от рассматриваемого сечения относительно центральной оси рассматриваемого сечения перпендикулярной силовой плоскости.
Поперечной силой называется сумма проекций всех односторонних сил от рассматриваемого сечения на ось, перпендикулярную оси стержня и лежащую в силовой плоскости.
Поперечная сила считается положительной, если она вызывает вращение отсеченного элемента по часовой стрелке.
Продольной силой называется сумма проекций всех односторонних сил от рассматриваемого сечения на ось стержня.
Продольная сила считается положительной, если она вызывает растяжение отсеченного элемента, и отрицательной, если — сжатие.
На основании этих определений и способа простых сечений вычисление внутренних усилий в сечениях стержней производится из уравнений равновесия статики составленных для отсеченной части рамы, находящейся в
равновесии под действием внешних сил и внутренних усилий.
При рассмотрении равновесия той или иной отсеченной части системы неизвестный изгибающий момент принимается любого направления, а неизвестные поперечная и продольная силы только положительными.
Если в результате решения изгибающий момент получился отрицательным, то это значит, что растянуты противоположные волокна в стержне по отношению к первоначально принятому.
При определении усилий в сечениях отсеченной части рекомендуется рассматривать равновесие той системы, на которую действует меньшее число силовых факторов.
3. Построение эпюр изгибающих моментов, поперечных и продольных сил. При построении эпюр внутренних усилий по вычисленным в характерных сечениях значениям необходимо иметь в виду следующие особенности:
а) ординаты эпюр откладываются перпендикулярно оси стержня: в эпюре — со стороны растянутого волокна без указания знаков; в эпюре — с двух сторон от оси стержня; в эпюре — симметрично от оси стержня с указанием знаков;
б) каждый узел рамы должен находиться в равновесии;
в) на прямолинейном незагруженном участке рамы изгибающий момент всегда изменяется по линейному закону, а поперечная и продольная силы постоянны;
г) при действии на элемент равномерно распределенной нагрузки изгибающий момент изменяется по закону квадратной параболы, поперечная сила — по линейному закону, а продольная сила постоянна, если действующая нагрузка перпендикулярна оси стержня, и изменяется по линейному закону, если нагрузка не перпендикулярна оси стержня;
д) если на элемент системы действует нагрузка в виде сосредоточенной силы, то в том сечении, где она приложена, на эпюре будем иметь точку излома в сторону приложения силы; на эпюре скачок на величину этой силы, если она перпендикулярна оси стержня, и на величину проекции этой силы на ось; перпендикулярную оси стержня, если нагрузка не перпендикулярна оси элемента.
На эпюре скачок будет только в том случае, если нагрузка не перпендикулярна оси стержня, и его величина будет равна проекции этой силы на ось стержня.
е) если на элемент рамы действует нагрузка в виде сосредоточенного момента, то в том сечении, где он приложен, на эпюре будет скачок на величину этого момента с параллельными ветвями, очерчивающими эпюру; на эпюры эта
нагрузка влияния не оказывает;
ж) между изгибающим моментом и поперечной силой существует известная зависимость согласно которой, если эпюра на рассматриваемом участке нисходящая, то положительна, если эпюра восходящая, то отрицательна.
Построив эпюры необходимо выполнить статическую проверку, которая состоит в том, что любая отсеченная часть рамы должна находиться в равновесии и, таким образом, должны выполняться условия равновесия статики.
Пример решения задачи 2.1.1.
От заданной нагрузки определить внутренние усилия в сечениях рамы (рис.2.1) и построить эпюры изгибающих моментов поперечных и продольных сил.
При определении усилий направление осей проекций принято в соответствии с декартовой системой координат.
Решение:
1. Определяем опорные реакции и их составляющие.
2,Определяем значения изгибающих моментов, поперечных и продольных сил в характерных сечениях рамы, рассматривая равновесие отсеченных частей рамы (рис.2.2). Сечение А-А 2
(стержень сжат)
Сечение 1-1
(растянуты правые волокна)
(стержень сжат)
Сечение 2-2 (растянуты правые волокна),
(стержень сжат)
Сечение 3-3
(растянуты правые волокна),
(стержень сжат).
Сечение 4-4
(растянуты левые волокна),
(стержень сжат).
Сечение 5-5
(растянуты левые волокна),
(стержень сжат).
Сечение 6-6
(растянуты верхние волокна),
Сечение 7-7
Сечение 8-8
(растянуты нижние волокна),
сечение 9-9 ( растянуты нижние волокна)
Сечение 10-10 ( растянуты нижние волокна)
сечение 11-11 (растянуты левые волокна)
(стержень сжат)
сечение 12-12
(растянуты левые волокна)
(стержень сжат) сечение 13-13
(стержень сжат) Рис.
2.2
Сечение В-В
(стержень сжат)
3. Строим эпюры изгибающих моментов поперечных сил и продольных сил. Проверяем равновесие узлов (рис.2.3.).
3. Производим статическую проверку правильности расчета, рассматривая равновесие отсеченной сечением I-I части системы (рис.2.4).
Пример решения задачи 2.1.2
От заданной нагрузки определить аналитически внутренние усилия в сечениях рамы (рис.2.5) и построить эпюры изгибающих моментов поперечных сил и продольных сил. При определении усилий направление осей принято в соответствии с декартовой системой координат.
Решение:
1. Определяем опорные реакции и их составляющие:
Решая, получим
Проверка:
2. Определяем значения изгибающих моментов, поперечных и продольных сил в характерных сечениях рамы, рассматривая равновесие отсеченной частей рамы
Сечение А-А (растянуты правые волокна),
(стержень сжат)
Сечение 1-1
( растянуты правые волокна)
(стержень сжат).
Сечение D-D
(стержень сжат).
Сечение 2-2
(растянуты левые волокна),
(стержень сжат).
Сечение 3-3
(растянуты левые волокна),
(стержень сжат).
Сечение 4-4
(растянуты верхние волокна),
(стержень сжат),
Сечение Е-Е
(стержень сжат),
Сечение Е-Е
Сечение 5-5
(растянуты левые волокна),
Сечение 6-6
(растянуты правые волокна),
Сечение В-В
Сечение 7-7
( растянуты нижние волокна)
(стержень сжат)
Сечение 8-8
( растянуты нижние волокна)
(стержень сжат)
Сечение 9-9
( растянуты верхние волокна)
(стержень сжат)
Сечение 10-10
( растянуты правые волокна)
(стержень сжат)
Сечение С-С
(стержень сжат)
3.
Строим эпюры изгибающих моментов поперечных и продольных сил (рис. 2.8). Проверяем равновесие узлов.
4. Производим статическую проверку правильности расчета, рассматривая равновесие отсеченной части системы, 1-6-10 (рис.2.9).
Расчет рамы методом сил
Статически неопределимая система — это система, внутренние усилия которой нельзя определить из уравнений статики однозначно.
В отличие от статически определимых систем неопределимые системы:
- — более жесткие, то есть с меньшими перемещениями;
- — более надежные, так как выход из строя одного или нескольких элементов не обязательно приводит к разрушению сооружения;
- — более прочные, то есть с меньшими внутренними усилиями;
- — чувствительны к неточностям изготовления элементов конструкции, осадке опор, температурным воздействиям.
Подход, при котором неизвестными являются усилия, называют методом сил.
Ниже приведен алгоритм расчета статически неопределимых рам методом сил.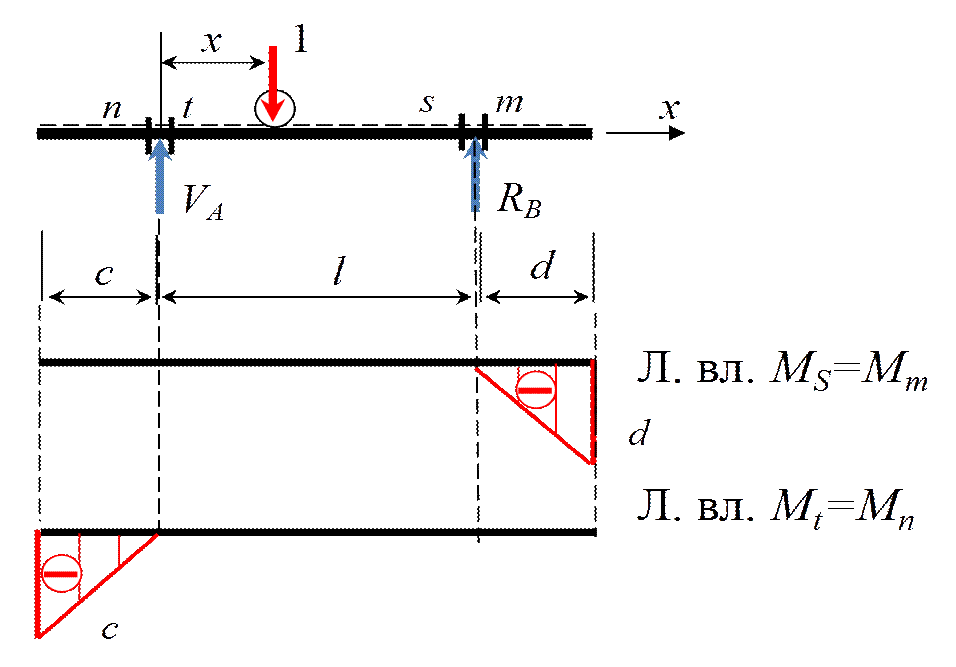
1. Определение степени статической неопределимости
Решение задач в строительной механике начинается с кинематического анализа. Статическая часть кинематического анализа отвечает на вопрос: является ли заданная система (ЗС) статически определимой или нет. Кинематическая часть — проверяет правильность расстановки связей. Система должна быть геометрически неизменяемой.
Для проведения кинематического анализа сооружение представляется в виде дискового аналога. Если система статически неопределима только за счет лишних опорных связей, то степень статической неопределимости определяется по формуле:
где число степеней свободы сооружений, количество дисков, число шарниров и стержней между дисками, — число опорных связей.
Выбор основной системы (ОС)
Сущность метода сил заключается в том, что статически неопределимая система сводится к решению нескольких статически определимых систем, которые получаются из заданной системы путём отбрасывания лишних (избыточных) связей.
Лишние связи — это связи, при удалении которых система остается геометрически неизменяемой. Линии действия оставшихся связей не должны быть параллельными и пересекаться в одной точке.
Степень статической неопределимости равна числу лишних связей, устранение которых приводит к статически определимой системе.
Основная система — это система, получающаяся из заданной системы путем удаления лишних связей и заменой их неизвестными усилиями. Как правило, выбирается статически определимой. В основной системе два вида воздействий: известные активные силы и неизвестные усилия в отброшенных связях. Количество неизвестных равно степени статической неопределимости заданной системы. Направления неизвестных реакций, принятые в основной системе, считаются положительными при расчетах.
На рис.1 изображена один раз статически неопределимая рама. Для получения основной системы (ОС) необходимо удалить одну связь. Удаление связи 2 приводит к механизму (оставшиеся три связи параллельны), удаление связи 4 — к мгновенно изменяемой системе (линии действия оставшихся трех реакций связей пересекаются в одной точке).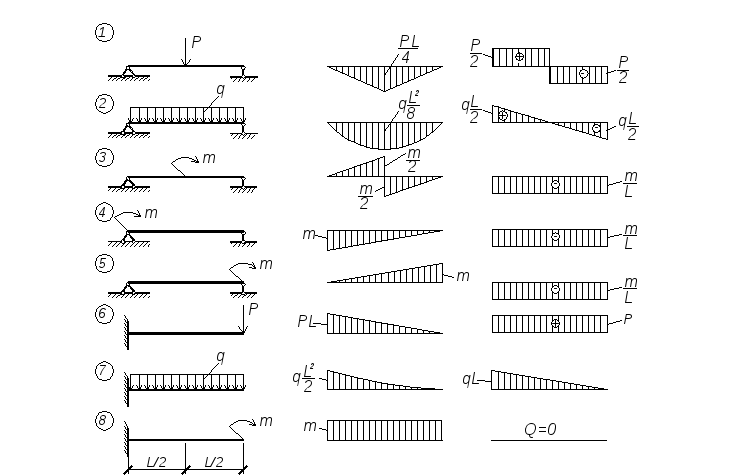
Таким образом, связи 2 и 4 не являются лишними. На рис. 16-1 г изображены варианты основной системы. За счет выбора в качестве неизвестного какого-либо внутреннего усилия (рис. 1г), основных систем может быть бесконечно много.
Критериями выбора основной системы являются простота построения эпюр в грузовом и единичных состояниях и минимум участков, на которые распространяются эпюры. Варианты на рис. 16, 1в, удовлетворяют этим
требованиям. Для заданных симметричных систем, при выборе основной системы выгодно сохранять симметрию (рис. 2).
На рис. 2а, 2в изображены рамы, содержащие замкнутый контур, и статически неопределимые внутренним образом. Для получения основной системы можно избавиться от контура, разрезав его (рис 26). Поскольку при этом возникает три неизвестных внутренних усилия в точке то замкнутый контур трижды статически неопределим. Внедрение шарнира в контур понижает его статическую неопределимость на единицу. Если система статически неопределима внутренним образом, то степень статической неопределимости определяется по формуле
где — количество контуров, — число шарниров в контурах.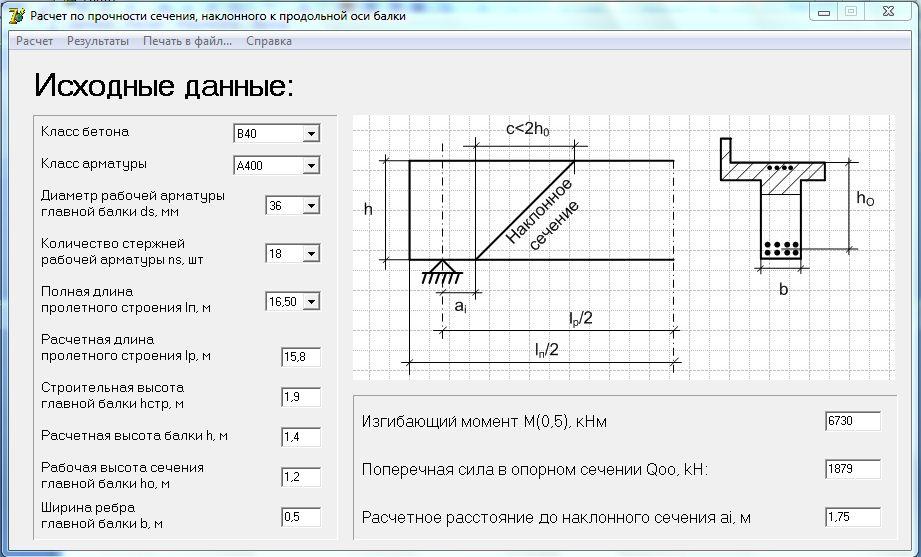
Для рамы на рис. 2в в точках в контур помещено два шарнира и для получения основной системы необходимо отбросить одну внутреннюю связь В качестве неизвестной выгодно выбрать усилие в ригеле, который представляет собой шарнирно опертый стержень. Для неразрезных балок (рис. 3) в качестве неизвестных усилий выбираются значения опорных моментов.
Составление системы канонических уравнений
Из выбранной статически определимой основной системы выделяют грузовое состояние (ГС) и единичные состояния (ЕС). В грузовом состоянии на основную систему действуют только внешние нагрузки. Для образования единичного состояния из основной системы убираются все внешние нагрузки, а в направлении отброшенной связи прикладывается приведённое единичное усилие. Если в качестве неизвестной выбрана сила, то усилие безразмерное, если — момент, то размерность единичного приведённого усилия (1/м).
Для один раз статически неопределимой балки (рис. 4а) выберем основную систему (рис.
46), заменив в заданной системе стержневую связь в точке на неизвестную реакцию Согласно принципу независимости действия сил, представим основную систему в виде суммы грузового и единичного состояния, в котором единичное усилие увеличено в раз (рис. 4в, 4г).
В направлении отброшенной связи в грузовом состоянии возможно перемещение (рис. 4в), в единичном состоянии — (рис. 4г).
Необходимо подобрать величину реакции так, чтобы суммарное
перемещение в основной системе от внешней нагрузки и
единичного усилия увеличенного в раз, было равно нулю, так как
в действительности в заданной системе в этом направлении наложена связь и перемещений нет, то есть:
Условие зависимости деформаций (2) называется каноническим уравнением и является условием эквивалентности заданной и основной систем. Число канонических уравнений совпадает с числом лишних отброшенных связей.
Определение коэффициентов канонических уравнений
По физическому смыслу коэффициенты канонических уравнений являются перемещениями, которые определяются с помощью интеграла Мора.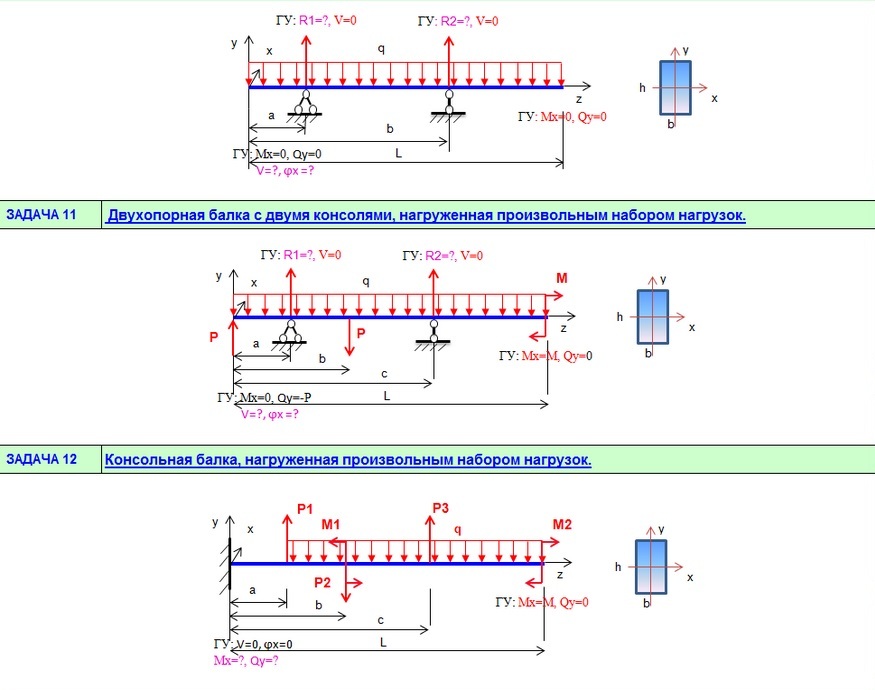
Операция интегрирования обычно называется перемножением эпюр и символически изображается знаком
где — функции моментов в единичных и грузовом состояниях,
— количество участков на эпюре, — изгибная жесткость стержней. Первый индекс обозначает номер отброшенной связи, второй — номер состояния.
Интеграл Мора может быть вычислен по формуле Симпсона (4) или Верещагина (5)
где — длина участка, на котором интегрируются («перемножаются») функции моментов, буквы «л», «с», «п» означают левое, среднее и правое значения моментов на участке (рис. 5а). Знак произведения положительный, если оба значения на эпюрах лежат по одну сторону от оси балки.
Согласно правилу Верещагина интеграл Мора равен произведению площади одной эпюры на ординату под её центром тяжести взятую
на другой эпюре. Если одна из эпюр является криволинейной, то вычисляется её площадь:
На рис. 56 показан пример перемножения двух треугольников, где площадь первого треугольника, — ордината второго треугольника, взятая под центром тяжести первого треугольника.
Суммирование ведётся по всем стержням, а интегрирование — по длине каждого участка эпюры моментов. По теореме Максвелла о взаимности перемещения коэффициенты, симметричные относительно диагонали, в канонических уравнениях равны между собой, то есть Для дважды статически неопределимой системы
Построим эпюры моментов в грузовом и единичном состояниях для задачи на рис. 4 и вычислим коэффициенты канонического уравнения (2):
Вычислим коэффициенты по формуле Симпсона:
или с помощью формулы Верещагина:
Проверка коэффициентов каноническнх уравнений
Для проверить правильность вычислений коэффициентов невозможно. Для перед решением канонических уравнений необходимо выполнить универсальные проверки:
где — суммарная эпюра, получается путем сложения ординат единичных эпюр.
6. Решение системы каноническнх уравнений
Для систем один раз статически неопределимых каноническое уравнение (2) одно и решение имеет вид:
Для систем два раза статически неопределимых необходимо решить систему из двух уравнений:
Решение имеет вид:
7.
Построение окончательной энюры изгибающих моментов
Окончательная эпюра в соответствии с принципом независимости действия сил получается путем сложения «исправленных» эпюр с грузовой:
«Исправленные» эпюры получаются путем увеличения всех ординат единичных эпюр раз. Если то измененные ординаты откладываются с другой стороны от оси стержня.
Для задачи на рис. 4 по формуле (7) получаем
После нахождения реакции в лишнеи связи статическая неопределимость считается раскрытой.
8. Проверка правильности построения энюры
Перед построением эпюр целесообразно убедиться в правильности эпюры Статическая проверка для не применима, поскольку равновесие узлов не нарушится в случае как при умножении эпюр на любое число так и при дальнейшем сложении уравновешенных
эпюр в формуле (9). Необходимо выполнить кинематическую (деформационную) проверку. Смысл проверки заключается в проверке отсутствия перемещений по направлению отброшенных связей в основной системе: где — число отброшенных связей.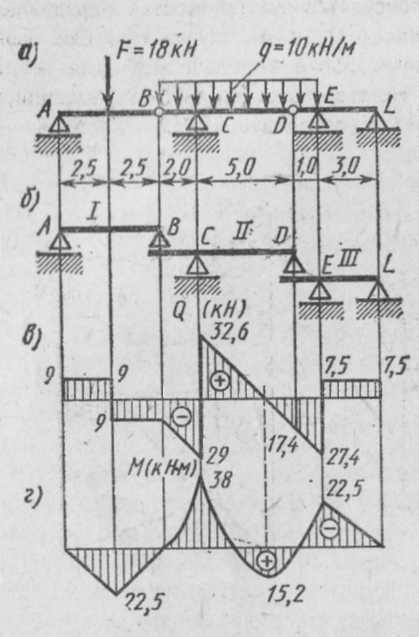
Эпюра построена верно, если перемещения по направлению отброшенных связей равны нулю,
поскольку в основной системе эти связи существуют.
Для проверки правильности эпюры для задачи на рис. 4 умножаем (рис. 7) на единичную эпюру (рис. 6), тем самым определяя
вертикальное перемещение точки Используя формулу Симпсона, получим:
9. Построение эпюр Предлагается два способа построения эпюр
1. Поскольку после определения усилий в лишних связях статическая неопределимость заданной системы считается раскрытой. В этом случае эпюры можно построить методом сечений. Алгоритм построения следующий:
1) из уравнений статики определить опорные реакции в основной системе с учетом найденных реакций лишних связей
2) на каждом участке реализовать метод сечения.
2. Если известна эпюра моментов, то можно построить эпюру поперечных сил по формуле Журавского (не прибегая к методу сечения):
Для линейных участков эпюры моментов формулу Журавского проще применять в следующем виде:
где — длина участка, в числителе отражено изменение момента на данном участке.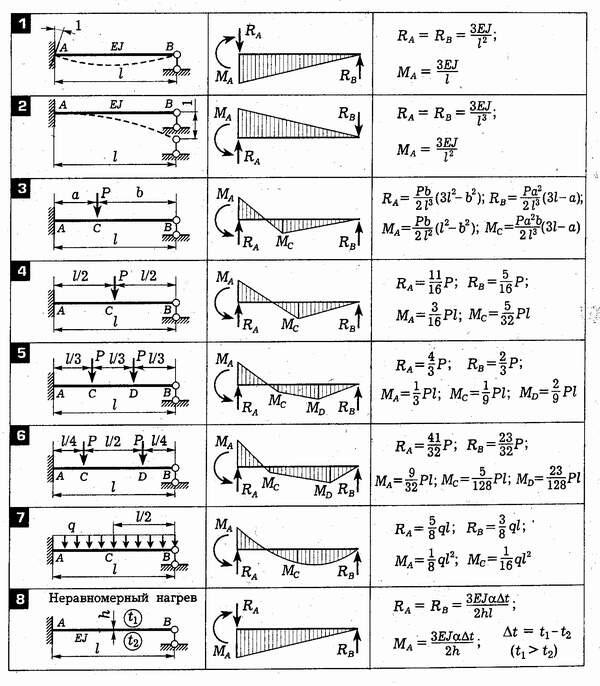
Поперечная сила если касательная к эпюре моментов совмещается с осью участка рамы при кратчайшем повороте против часовой стрелки.
Если на участок рамы действует равномерно распределенная нагрузка, то эпюра моментов имеет вид параболы, вогнутой в сторону действия нагрузки. В параболе нужно выделить квадратичную и линейную часть. Для каждой части по отдельности определить эпюру а полученные эпюры
сложить. Пусть для примера на рис (рис. 8). Тогда формула Журавского примет вид:
где балочное решение
По эпюре поперечных сил методом вырезания узлов строится эпюра продольных сил —
На вырезанный узел наносятся значения с эпюры с учетом базиса метода сечения, то есть положительные значения поперечных сил вращают узел по часовой стрелке, неизвестные положительные значения направляются от сечения. Затем из двух уравнений проекций определяются значения продольных сил и наносятся на эпюру с указанием знаков. Порядок вырезания узлов должен быть таким, чтобы в узле присутствовало не более двух неизвестных продольных сил.
В примере 1 эпюры получены первым способом, а в примере 2 -вторым.
Статическая проверка
Поскольку уравнения равновесия были использованы для первого способа при определении опорных реакций, то статическая проверка рамы заключается в проверке равновесия узлов. На вырезанных узлах отмечаются
значения, взятые из эпюр и проверяется тождество уравнений проекций.
Для второго способа из полученных эпюр определяются значения опорных реакций и составляются три уравнения равновесия, тождество которых подтверждает правильность решения задачи.
Расчетные схемы для статически неопределимых балок
18-01-2013: владимирв схеме 1 в формулах момента на опорах l не в квадрате?
18-01-2013: Доктор Лом
При сосредоточенной нагрузке в формулах момента длина в квадрате быть не может.
27-02-2013: Вадим
Уважаемый Доктор Лом! Как правильно рассчитать трехпролетную балку на шарнирных опорах от равномерной нагрузки, если все пролеты разные?
27-02-2013: Доктор Лом
Для расчета неразрезных балок с тремя пролетами и более проще составить уравнение трех моментов. Что это за уравнение в формате комментария объяснить не смогу, а статьи на эту тему у меня пока нет. Можете посмотреть статью: «Двухпролетные балки». Принципы, изложенные в указанной статье, можно применить и для трехпролетных балок.
11-05-2013: Дмитрий
«Таблица 2. Однопролетная балка с жестким защемлением на опоре А и шарнирной опорой В. Рисунок 1.2» Можно ли считать по данной схеме для x=a ?
Мне нужно знать как будет вал прогибаться в точке прикосновения резца.
11-05-2013: Доктор Лом
Можно. Однако в вашем случае более правильным будет расчет не только на изгибающий, но и на вращающий момент.
11-05-2013: Дмитрий
А можете выложить формулу для моего случая, когда x=a. Я боюсь, что погрешность расчёта выйдет больше за технологическую, от пересчета такой длинной формулы.
— В книге написано, что от вращательного момента валы прогибаются очень не значительно, поэтому не принимают в расчет обычно.
11-05-2013: Дмитрий
«Таблица 2. Однопролетная балка с жестким защемлением на опоре А и шарнирной опорой В. Рисунок 1.2» Можете выложить формулу,для частного случая x=a ? Имеется в виду, чтоб x=a было принято еще при интегрировании.
Тогда формула должна существенно упроститься.
Спасибо!
11-05-2013: Доктор Лом
х=а — частный случай приведенных формул, т.е. при расстоянии от начала балки равном а:
Ма = Аа + МА. С прогибом та же история.
Более того, если рассматривать участок балки при х>a, то формулы будут еще сложнее. Тут я ничего не могу поделать, но могу посоветовать следующее. Максимальный прогиб в вашем случае будет при приложении нагрузки приблизительно посредине вала, т.е. когда а?b, чем ближе вы будете смещать резец к одной или второй опоре, увеличивая расстояние а или b, тем меньше в итоге будет прогиб. Поэтому гораздо проще рассчитать максимальный прогиб по схеме 1.1, а для уверенности сделать дополнительный запас т.е. увеличить рассчитанный таким образом прогиб на 3-5% вряд ли полученный точным расчетом прогиб будет больше, но можно увеличить и на 10-15% для большей уверенности.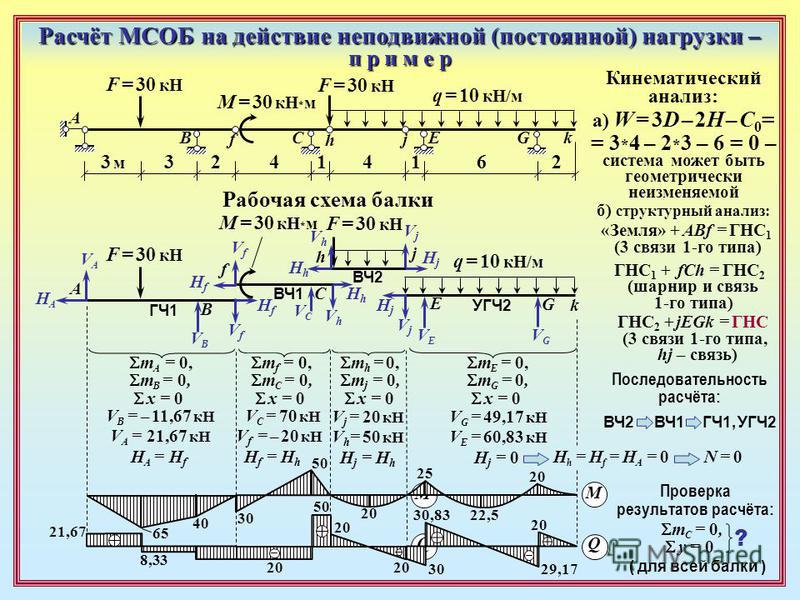
14-05-2013: Вера
Здравствуйте, можно ли где-то увидеть расчет (вывод формулы для изгибающего момента) для случая нагрузки таблица 1, п.2.5 по треугольнику?
14-05-2013: Доктор Лом
Все формулы, использованные для составления таблиц остались на бумаге (набирать их слишком долго). К тому же методик расчета статически неопределимых конструкций несколько. В данном случае использовалась методика, достаточно подробно расписанная в статье «Двухпролетные балки» (http://doctorlom.com/item230.html)
27-07-2013: Дмитрий
По Уважаемый Доктор Лом! Как правильно рассчитать трехпролетную балку на шарнирных опорах от равномерной нагрузки, если все пролеты разные?
27-02-2013: Доктор Лом
Для расчета неразрезных балок с тремя пролетами и более проще составить уравнение трех моментов.
Что это за уравнение в формате комментария объяснить не смогу, а статьи на эту тему у меня пока нет. Можете посмотреть статью: «Двухпролетные балки». Принципы, изложенные в указанной статье, можно применить и для трехпролетных балок.
Данный расчет имеет очень конкретное практическое применение — расчет нагрузок на оси фур. У фуры имеется прицеп с 4 опорами. 1-ая опирается на сцепное устройство тягача, три остальных — оси колес, расположенных на расстоянии (базы) от сцепки и на одинаковом расстоянии друг от друга. Равномерно/неравномерно распределенную нагрузку внутри кузова привести к точечной нагрузке с определенной координатой мне удалось. А вот распределение нагрузки между осями колес — увы. Будут благодарен за любую помощь/наводку на метериал.
27-07-2013: санитар Петрович
Э, батенька, вам в другую больницу надо, у нас и отделения такого нету.
27-07-2013: Доктор Лом
Петрович прав, расчет вращающихся валов и механизмов — отдельная история.
К тому же следует учитывать, что нагрузки будут не статические, но динамические и ударные, к тому же не только вертикальные, которые чаще всего и рассматриваются в строительстве, но и горизонтальные, возникающие при движении с ускорением.
Но вы можете посмотреть статьи «Многопролетные неразрезные балки». В них в частности рассматривается расчет трехпролетных балок. Правда, конкретно ваш случай не рассматривается, однако мастерство проектировщика в том и состоит, чтобы находить выход из сложных ситуаций, упрощая их. Например, в вашем случае при расчете на вертикальные нагрузки (от веса грузов) рассматривать сцепное устройство тягача, как опору вовсе не обязательно. Я конечно не специалист по автомобилестроению, но мне кажется большинство сцепных устройств рассчитывается на восприятие горизонтальных нагрузок, возникающих при ускоренном движении, при этом движение вверх-вниз вполне возможно, впрочем могу и ошибаться.
Таким образом у вас получится двухпролетная балка с двумя консолями.
И хотя у меня такой расчетной схемы нет, но тут можно воспользоваться принципом суперпозиции для равномерно распределенной нагрузки, т.е. можно отдельно рассчитать двухпролетную бесконсольную балку и две консоли, а затем полученные значения нужных параметров сложить. А если расчет будет производиться для сосредоточенной нагрузки внутри пролетов, то консоли вообще никакого значения не имеют.
Но все равно не забывайте совет Петровича, расчет вращающихся валов — это не ко мне.
29-07-2013: Дмитрий
санитар Петрович — интересует определение нагрузки на оси в статичном состоянии. В таком режиме реакция осей, сила тяжести груза и сила тяжести самого прицепа полностью соответствует схеме с балкой и реакциям опор.
29-07-2013: санитар Петрович
Оно конечно не мое дело — в дела дохтурские лезть, да пока оне отдыхают, я с вами покалякаю.
Ежели для статического состояния, так расчет ваш и бутылки выпитой не стоит, потому как рассчитывать надобно токмо две оси. Ведь на что третья ось надобна? — для страховки. Ежели у двухтонной легковушки колесо лопнет али отлетит — одно дело, а ежели у прицепа в коем 40 тонн, да на большой скорости — то веселья не обересси. А посему просчитайте себе неспешно все варианты однопролетной двухконсольной балки, а их всего два будет, да еще два для однопролетной одноконсольной, ежели сцепное устройство, как опору учитывать, да выбирайте самый нагруженый.
Так я себе это дело мыслю.
30-07-2013: Дмитрий
Петрович, на весовом контроле карают за перегруз на любую из конкретных осей.Так как их сзади три — нагрузка (неведомым пока способом) таки делится на все три оси.
Смогу посчитать — смогу паллеты с грузом так расставить, что все оси не будут перегружены.
30-07-2013: Дмитрий
Ведь на что третья ось надобна? — Вот тут http://www.packer3d.ru/online/veh-by-pal наглядно показано, что все оси задействованы
30-07-2013: санитар Петрович
Вона чего! Так бы и сказал сразу, все из вас пинцетом вытаскивать надо. Я-то себе другу картинку рисовал, ну да ладно.
Как понимаю, какулятор энтот для равномерно расставленных палет, дающих равномерно распределенную нагрузку. Ты, милок, кумекаешь так палеты расставить, чтобы нагрузку на оси равномерно распределить.
На то сразу скажу — плюнь ты на это дело. По-теоретически тако возможно, да для того половину груза, али более выбросить надобно.
К тому ж сумлеваюсь я, что есть весы такие, что на кажную ось нагрузку определяют, скорее отдельные весы на тягач и на прицеп. Так оно, нет?
Ежели так, то рецепт простой, с начала прицепа и до первой задней оси высота палет 2/3 от общей высоты, от 1 задней до 3 задней оси постепенно высоту палет увеличивать до полной высоты, дале — на всю высоту, ежели прицеп такой как в какуляторе.
И будет тебе более равномерное распределение нагрузки между осями. А точнее тебе и считать не надобно — размеры палет не позволят. К тому ж слишком много данных для расчета потребуется.
А ежели старик Петрович обшибся с высотой, то на весах тебе скажут, больше 2/3 надо, али меньше.
Ох, чевой-то в горле пересохло от энтих разговоров,надо бы пойти пивка попить, пока дохтура нету.
25-11-2013: Антон
Добрый день.У меня вопрос по формуле 1.2 в таблице 2. При расчете прогиба по данной формуле и подставлении в полученное выражение условия x=a=b=l/2 не получается выражения,данного в формуле выше.Разница заключается в отличие числа перед произведения EI. При подстановке получается не 107, а 109. Подскажите, в чем ошибка? Может ли этот метод вычиления являться приближенным?
25-11-2013: Доктор Лом
Дело в том, что, пользуясь формулой, вы определяете значение прогиба посредине пролета и внизу полученного выражения действительно будет 109.7. Между тем у балки с жестким защемлением на одной опоре и шарнирным закреплением на второй опоре максимальный прогиб будет смещен в сторону шарнирной опоры. В строке 1 таблицы 2 как раз и приведено это максимальное значение. Так как расстояние от опоры А до поперечного сечения с максимальным пролетом больше 0.5l, то для определения этого значения следует использовать формулы, учитывающие действие поперечной силы в точке приложения (или определять значение прогиба, ведя отсчет от опоры В с учетом угла поворота на опоре В). Не то, чтобы эти формулы такие уж сложные, но места занимают много, а потому в таблице не приводятся.
26-11-2013: Антон
Спасибо за ответ.Да,действительно, Вы правы.Точка максимального прогиба будет находиться чуть ближе от середины балки к шарнирной опоре.Но вот здесь у меня возник другой вопрос. Продифференцировав выражение для нахождения прогиба,найдя экстремум функции,получил тем самым х максимального прогиба.Подставив это значение х в формулу прогиба при тех же условиях a=b=L/2, получил в знаменателе 107,555.Не знаю в чем проблема,но и в других источниках находил такую же формулу для частного случая(a=b=L/2).Меня это интересует,потому что занимаюсь расчетом на работе и необходимо получить точный результат.
26-11-2013: Доктор Лом
А вот тут, когда речь идет о десятых долях процента и вообще о дробных числах, полученных в результате достаточно сложных вычислений, табличные значения действительно следует рассматривать как приближенные. Полученное вами значение является более точным, табличное значение дает больший прогиб, а потому способствует небольшому дополнительному запасу (0.2%) при расчете по 2 группе предельных состояний.
27-11-2013: Антон
Вы развеяли мои сомнения.Большое спасибо за объяснение и быстрые ответы!
06-12-2013: Максим
2 таблица, схема 3.1. В точке B получается значение момента на эпюре не равно значению приложенного момента в этой точке?
07-12-2013: Доктор Лом
Не получается, точнее значение момента на эпюре в точке В равно значению момента, приложенного в точке В. При таком направлении действия момент считается отрицательным (-M), соответственно при действии на опоре В отрицательного изгибающего момента на опоре А возникает положительный изгибающий момент, а вот опорная реакция на опоре А будет отрицательной. Если подставить в уравнение моментов все приведенные в таблице значения, то при х = l, на опоре В вы получите все тот же отрицательный момент Мb = -M.
07-12-2013: Максим
например, m=10, L=2.
тогда Ax = 3*10/2*2 = 7,5
Ma = 10/2=5
Mb= 5+ 7,5 = 12,5
07-12-2013: Доктор Лом
Вы не совсем правильно понимаете суть формул и не следите за знаками:
не Ax = 3*10/2*2 = 7,5 а просто опорная реакция А = 7.5. х — это переменная, означающая расстояние от начала балки до рассматриваемого поперечного сечения. В точке В значение х = L = 2.
Далее, если m = 10, то Ма = -5. Тогда на опоре В
Mb= -5 + 7,5х2 = 10
09-07-2014: Zarif
Уважаемый доктор.
Есть ли у Вас величина эпюры М для скатных крыш?
09-07-2014: Доктор Лом
Посмотрите статью » Примеры расчета стропил и обрешетки» там есть соответствующие расчету эпюры.
11-02-2015: Sanmart
Уважаемый Доктор Лом!
А нет ли у Вас формул для расчёта максимального прогиба и момента для двухпролётной балки полностью загруженной равномерно распределённой нагрузкой с пролётами разной длины?
Схема почти как на 2.3, но q распределена от A до C.
Если Вам лень забивать эти формулы в редактор, зашлите их как-нить так, типа в отсканированном формате, а я верну их Вам в редакторе.
11-02-2015: Доктор Лом
Дело в том, что изложить все возможные случаи загружения для всех возможных вариантов физически невозможно.4/768EI. Если для вас такие пределы являются слишком размытыми и требуется большая точность, то тогда только расчет.
12-02-2015: Валентин
Здравствуйте Доктор Лом. Хотел уточнить у Вас частный случай описанный в разделе «Таблица 3. Двухпролетная балка с шарнирными опорами. Рис.1.3» Есть ли у Вас возможность дополнить его исходя из того что в данном случае расстояния l не равны, а отличны, т.е. l1 и l2. Интересуют реакции в опорах и момент в опоре. Очень срочная просьба. Спасибо.
12-02-2015: Sanmart
Эх… Буду вспоминать давно забытый сопромат…
Всё равно спасибо!
12-02-2015: Доктор Лом
Я буквально вчера отвечал на подобный вопрос. В таблицах приводятся формулы для частных случаев, впрочем наиболее распространенных. Для общих случаев, подобных вашему, формулы становятся слишком громоздкими и наглядность теряется. В таких случаях необходимо выполнить полный расчет методом моментов или методом сил, так как у вас всего одна неизвестная опорная реакция.
Тем не менее приведенные таблицы очень удобны для предварительной оценки конструкций. Например, если ваш случай загружения подобен приведенному в Таблице 3, расчетная схема 1.3, то при уменьшении длины одного из пролетов расчетные значения и опорных реакций и момента на опоре и прочих величин будут однозначно меньше. Таким образом упрощенный расчет только увеличит запас прочности, этого знания при расчете конструкции, изготавливаемой в 1-2 экземплярах вполне достаточно. Ну а для массово производимых конструкций необходим точный расчет.
21-03-2015: Давид
Уважаемый Доктор Лом
У меня двухскатная крыша с одинаковыми сторонами с коньком без опоры, но жестко закрепленными стропилами (сварка),низ можно считать как шарнир. Можно ли применить для расчета прогибов формулу Таблица 2 2.1 или что-то другое если вас не затруднить напишите формулу или ссылку
22-03-2015: Доктор Лом
Это будет не совсем правильно, да и сварной шов должен быть рассчитан на соответствующие нагрузки, чтобы обеспечить жесткость. Возможно вашу конструкцию более правильно будет рассматривать как треугольную арку с затяжкой на опорах (смотрите соответствующую статью).
02-04-2015: Владимир
Таблица 1, схема 1.1 Формула для прогиба, по-моему неверна. По логике должно быть f(l) = 0. А в предложенной формуле такого не получается.
02-04-2015: Доктор Лом
Приведенная формула для определения прогиба, как и формула для определения момента справедлива для участка от 0 до l/2 (середины пролета, где приложена сосредоточенная сила).3/6.
03-04-2015: Владимир
Спасибо большое. Я не увидел, что 0<x<l/2 в графе для моментов. Можно эту же пометку перенести в графу с формулой для прогибов, тогда все вопросы отпадут.
03-04-2015: Доктор Лом
Я опубликовал статью больше двух лет назад, уже 3 компьютера с тех пор сменил и мне теперь проще сделать общее примечание в статье, чем найти и отредактировать картинку. Но попробую.
14-08-2015: Martin
Вопрос не в тему, но я бес понятия куда именно писать…
Проектируется мед. здание с помещением для МРТ, Здание планирует изначально поднять из металлокаркаса, а МРТ с металом не совместими в плане магнитных волн и притяжения, так вот вопрос, как защитить металл от МРТ???
14-08-2015: Доктор Лом
Я вообще-то не специалист по МРТ-оборудованию, но вроде бы ничего страшного в металлокаркасе нет (не будет металлокаркаса, будет арматура в ж/б конструкциях или еще чего). Поищите нормы по оборудованию МРТ-кабинетов, там вроде бы тоже нет ограничений по конструктиву стен и перекрытий.
09-09-2015: Yuriy
Уважаемый Доктор Лом
Помогите пожалуйста рассчитать силы и моменты действующие на 3 дверных навеса Учитывая то что расстояние третьего навеса между нижним и верхним можно изменять Заранее благодарен
09-09-2015: Yuriy
Я не могу решить проблемы с расчетом 3 и4 навесов на дверь Помогите пожалуйста
Н -высота двери 2,5м
ширина 1 м
нижний шарнир установлен на 0,2 м от низа двери
второй шарнир на 1,8 м от центра второго
масса двери 40 кг
Как расчитать силы и моменты
Буду очень признателен за помощ
[email protected]
09-09-2015: Доктор Лом
Подобная ситуация рассматривается в статье «Определение вырывающего усилия (почему дюбель не держится в стене)». Единственное отличие в том, что у вас сверху будут два навеса. Для упрощения расчетов можно допустить, что расстояние между верхними навесами значительно меньше расстояния между верхним и нижним навесами, тогда можно считать, что силы, действующие на верхние навесы, одинаковы и в сумме равны нижней силе. Но в любом случае нагрузка на верхний навес будет больше, чем на средний. При смещении среднего навеса к середине высоты двери роль его с точки зрения восприятия вырывающего усилия будет значительно уменьшаться, однако при этом будет повышаться устойчивость двери.
10-09-2015: Yuriy
Вы знаете
у меня получается сила на верхней петле -169
на второй петле 23
и на нижней петле 145
Где моя ошибка?
Как вы определяете силы?
С уважением
Юрий
10-09-2015: Yuriy
для двух петель у меня так и выходит силы равны только с противоположным знаком
А вот для трех петель получается что верхняя петля забирает на себя нагрузку которая в сумме составляет нагрузки двух других петель
Помогите пожалуйста с алгоритмом
Заранее благодарен
Юрий
10-09-2015: Доктор Лом
Ваша ошибка в выборе расчетной схемы. При 3 навесах вы рассматриваете дверь как двухпролетную балку с относительно малой жесткостью, другими словами как гибкую балку, которая под воздействием опорных реакций будет иметь некоторые деформации. Между тем в плоскости действия момента высота балки — это ширина двери 1 м, что значительно больше пролета между 2 верхними навесами. Т.е. дверь можно условно рассматривать как абсолютно жесткую балку, к которой расчетные схемы, приведенные в данной статье, не применимы. Дверь в данном случае можно рассматривать как некое поперечное сечение.
Кстати посмотрите еще статью «Расчет гвоздевого соединения кобылки со стропильной ногой. Теоретические предпосылки». Здесь же добавлю к сказанному ранее, опорный момент может быть разложен на любое количество разнонаправленных сил согласно диаграмме нормальных напряжений. При этом, если сверху две силы, а внизу одна, то сумма верхних сил равна нижней силе, но имеет обратный знак. Кроме того момент относительно центра тяжести условного поперечного сечения от нижней силы будет равен моменту от двух верхних сил. Таким образом задача сводится к определению центра тяжести условного сечения.
Как я уже говорил, при относительно небольшом расстоянии между верхними навесами их можно условно считать, как одно целое, т.е. разделить на 2 силу, действующую на как бы один верхний навес, однако использовать соответствующий коэффициент запаса.
15-10-2015: Сергей
Добрый день Доктор Лом. Извините мою необознаность. Подскажите пожалуйста, что обозначает Е в формуле расчета прогиба балки и как его (Е) определять
15-10-2015: Доктор Лом
Е — это модуль упругости материала, который вы собираетесь использовать для балки. Значения модулей упругости для различных строительных материалов можно посмотреть в статье «Расчетные сопротивления и модули упругости для различных строительных материалов».2/2. Сейчас попробую исправить. Спасибо за внимательность.
30-03-2016: Тимур
Здравствуйте!
Изучил несколько статей, но не совсем понятно как соотносятся несущая способность стальной однопролетной шарнирно-опёртой балки и балки с жестким защемлением на опорах? Зависит ли от длинны? Для конкретности например для пролётов 4,6,8,12 метров. По моим прикидкам о 2 до 5 должно быть…
30-03-2016: Доктор Лом
При действии равномерно распределенной нагрузки несущая способность жестко защемленной балки в 1.5 раза больше, чем такой же балки, но на шарнирных опорах. От длины это никак не зависит (если мы сравниваем шарнирно опертую и жестко защемленную балку одинаковой длины), а вот вид действующей нагрузки может влиять на значение разницы. А такая разница в несущей способности возникает из-за того, что максимальный момент для шарнирно опертой балки будет ближе к середине пролета, а для жестко защемленной балки — на одной из опор (или на обеих опорах, если нагрузка симметричная).
А от 2 до 5 — это к Корней Иванычу Чуковскому. Что вы в данном случае имели в виду под этим, я не понял.
31-03-2016: Тимур
Просто думал, что несущая способность увеличится скорее в 5 раз чем в 2. Это же по сути сталь на разрыв. По проволоке в пару миллиметров же можно ходить. Или со временем провисание произойдёт?
31-03-2016: Доктор Лом
В данной статье приведены расчетные схемы для относительно жестких балок. Как правило высота h таких балок составляет 1/10 — 1/20 от длины пролета l. А прогиб таких балок как правило не превышает f ? h/4 — h/2.
Стальные проволоки, канаты и прочие гибкие (я бы даже сказал абсолютно гибкие) нити рассчитываются совсем по другим формулам и эпюры будут иметь другой вид. Как правило прогиб f гибких нитей составляет не менее 5h — 6h. В гибких нитях напряжения, вызываемые действием изгибающего момента, крайне незначительны по сравнению с растягивающими напряжениями, возникающими в процессе столь значительной деформации. Эти растягивающие напряжения должны компенсироваться горизонтальными опорными реакциями. Впрочем, расчет гибких нитей — это отдельная тема.
15-04-2016: Станислав
Здравствуйте! Вопрос по таблице 1. «Однопролетная балка с жестким защемлением на опорах» по пункту 1.3. Момент на опорах Ma и Mb. Скажите пожалуйста в уравнении случайно двойка не лишняя?
15-04-2016: Доктор Лом
Нет, не лишняя. И проверить это достаточно просто. Если а = l/2, т.е. обе силы приложены в одной точке посредине балки, то уравнение моментов сведется к Ма = Мв = -2Ql/8 = -Ql/4. Такой же результат мы получим, сложив значения моментов при использовании расчетной схемы 1.1.
15-04-2016: Станислав
Прошу прощение. Вопрос, заданный мною ранее — не корректен. По Вашим таблицам (для шарнирных опор и для жестко закрепленных) я рассчитал максимальные прогибы в случае действия двух сосредоточенных сил с одинаковым расстоянием от опор (табл. 1 — пункт 1.3).в результате у меня получилось, что прогиб в случае шарнирных опор меньше, чем прогиб в случае жестко закрепленных. Хотя по логике должно быть наоборот. Прошу пояснить. Есть ли вероятность того, что в расчетной схеме для жестких опор 1.3 у вас ошибка?
15-04-2016: Доктор Лом
Не знаю, как это у вас получилось. Предполагаю, что вы подставили в формулу прогиба значение момента без учета знака «-«. Опять же, если а = l/2, т.е. обе силы приложены в одной точке посредине балки, то максимальный прогиб составит f = -Ql^3/96EI. Такой же результат мы получим, сложив значения прогибов при использовании расчетной схемы 1.1.
16-04-2016: Эмин
Где найти расчетную схему однопролетной балки с поворотным шарниром по середине.
16-04-2016: Доктор Лом
Что вы имеете в виду под поворотным шарниром посредине? Если это опора, препятствующая перемещению балки по вертикали, но не препятствующая изменению углов наклона поперечных сечений балки, то такую опору следует рассматривать как промежуточную опору двухпролетной балки, таблица 3. Если эта шарнирная опора расположена в перпендикулярной плоскости, то ее наличие влияет лишь на определение гибкости стержня в данной плоскости и при расчете на вертикальные нагрузки не учитывается.
16-12-2016: Михаил
Здравствуйте! Подскажите, как определить горизонтальные (вырывающие) реакции при схеме балки с двумя заделками?
16-12-2016: Доктор Лом
Вообще-то балки считаются достаточно жесткими стержнями (ограничения по максимально допустимому прогибу этому способствуют) и потому для упрощения расчетов горизонтальные опорные реакции, возникающие в результате деформации, принимаются равными нулю. Но вообще, если уж есть такая необходимость, то сначала определяется прогиб, строится эпюра. Потом определяется изменение длины нейтральной оси балки — процедура сама по себе достаточно сложная, а потом, в зависимости от модуля упругости материала балки определяются усилия, необходимые для такого изменения длины балки.
17-02-2017: ученик
Док, уж извините за тупые вопросы. Осваивал построение эпюр в ехеле, для балки защемление-шарнир, изгибающий момент в пролете М(х)(таб 2 п 2.1). Результат-в конце балки функция не равна 0. рис https://yadi.sk/i/Cal1RKes3EDm6W
Судя по результатам, если к Мх добавить значение опорной реакции В, то все приходит в норму, но увеличивается изгибающий момент на опоре А на значение реакции В. Там есть линии опор А и В,но это чистая визуализация уровней нагрузки и использование как постоянных в расчете. Расчет при: распред нагрузка 10, балка 4.
Док, еще вопрос. Можно ли найти функции поперечных сил для основных видов балок, сам не выведу-диф уравнения забыты напрочь.Хоть в расчетах как правило используются крайние значения. В графике я из опорной реакции А вычел нагрузку на плечо qx, но это чистой воды подгон результата. С уважением
17-02-2017: ученик
Док, для понимания чисто теоретически: можно ли в местах нулевого изгибающего момента в пролете балки не ставить или уменьшать арматуру? Или в этих точках сравнимы поперечные силы?
17-02-2017: Доктор Лом
Я уже говорил, что с exel не дружу, потому указать, где у вас вкралась ошибка, вряд ли смогу. А в целом, если в уравнение моментов, приведенное для данной расчетной схемы, подставить значения при x = l, то момент на опоре В равен нулю:
MB = Al + MA — ql^2/2 = 5ql^2/8 — ql^2/8 — ql^2/2 = 0
так что дерзайте.
По поводу необходимости наличия арматуры в сечениях с нулевым изгибающим моментом все верно, в таких сечениях продольная арматура по расчету не нужна. Вот только реальные условия работы конструкции могут значительно отличаться от принятой расчетной схемы, а кроме того должно быть обеспечено защемление арматуры для ее надежной работы. Больше подробностей смотрите в статье «Анкеровка арматуры».
18-02-2017: ученик
Пересчитал, теперь Мв на нуле, а остальной график не строится:). Поморщу репу в понедельник. Где у Вас из свежих статей можно подробнее посмотреть про поперечные силы?
18-02-2017: Доктор Лом
В разделе Напряженные состояния много статей, можете также посмотреть статьи «Влияние поперечных сил на прогиб», «Построение эпюр для балки».
07-05-2017: Vova
Помилка табл.3/6l.
22-08-2017: Иван
Добрый день! Допустимо ли для схемы со скользящими заделками по концам балки использовать расчетную формулу прогиба для варианта 1.1 (две жесткие заделки по концам)? Как я понял из комментариев горизонтальные опорные реакции приняты равными нулю, соответственно, жесткая заделка в этом случае и есть скользящая. Верно ли я понимаю?
23-08-2017: Доктор Лом
Да, допустимо, если балка имеет соответствующую жесткость. А вообще горизонтальные опорные реакции из-за распределения внутренних напряжений возникают всегда, просто чем больше жесткость балки, тем меньше их влияние на общую работу стержня. Поэтому как правило при расчетах жестких балок влиянием возможных горизонтальных опорных реакций в запас прочности пренебрегают, принимая их равными нулю. Ну а для гибких нитей скользящая заделка по умолчанию не годится, как опора.
02-10-2017: Студент
Добрый день! Подскажите пожалуйста, чему равно значение ?a в табл. 3 сх. 2.2 при определении прогиба балки.
03-10-2017: Марина
Не могли бы вы помочь с одной весьма ходовой в моём случае схемой: однопролётная балка с заделкой на опоре А и шарнирной опорой В; нагрузка по треугольнику: максимум «q» у заделки и ноль на расстоянии «а» от заделки. (т.е., если утрировать — это как бы смесь ваших пунктов 2.2 и 2.7) Очень нужен момент в заделке. Заранее спасибо.
20-11-2017: Nik
как выполняется расчет шарнирно опертой двухконсольной балки, методом начальных параметров. нагрузки расположены на консолях.
заранее благодарен
20-11-2017: Доктор Лом
Вы не указали количество пролетов балки.4. Подскажите почему так? Ошибка или я что то не учитываю?
28-05-2019: Доктор Лом
Скорее всего вы имели в виду расчетную схему 2.1, а не 2.2 в таблице 3. Это первое. Второе, я даю значение не для х = l/2 или 0.5l, а для х = 0.579l, т.е. максимально возможное значение прогиба для данной расчетной схемы. Возможно в этом причина. (т.е. прогиб посредине пролета не всегда бывает максимальным).
03-06-2019: Антон
Спасибо большое за ответ. Да, извиняюсь — расчетную схему 2.1 в таблице 3. Как я понимаю, определить в каком месте появится максимальный прогиб, можно построив Эпюру моментов?
03-06-2019: Доктор Лом
Не всегда так. Максимальный прогиб будет в той точке, в которой значение угла поворота в пролете будет равно 0. Правда, я в данной статье не приводил уравнений углов поворота на опорах, но их можно посмотреть в других статьях, например в «Двухпролетные балки» или «Статически неопределимые балки. Уравнения трех моментов».
07-07-2019: СергейЧ
Здравствуйте, Доктор! Почитал Ваш сайт, и сделал себе в Excel калькулятор неразрезных многопролетных балок, на шарнирных опорах, с консольными окончаниями. Длину балки разбил на отрезки по 1 см, задаю на получившихся отрезках и в точках нагрузки. В результате численного интегрирования, получаю моменты и прогибы. Промежуточные опоры добавляю методом сил (считаю прогибы в точках дополнительных опор, строю линейную комбинацию реакций, дающую нулевой прогиб на всех опорах). Полученные численные значения, совпадают с высокой точностью с теми, которые Вы выводили в статье про многопролетные балки. Большое спасибо за сайт!
Делал этот расчетный файл под деревянные балки, для собственного использования.
Теперь, хочется добавить в расчет подкосы, от столбов к балке. То, что есть на сайте про подкосы, ориентировано на проверку прочности подкоса. Меня же интересует, как добавление подкоса влияет на моменты, прогибы, и их максимальные значения. Как это реализовать? Направьте пожалуйста в нужную сторону.
07-07-2019: Доктор Лом
На ваш вопрос попробую ответить так: формально, что стойка, что подкос для расчета многопролетной балки значения не имеет. Т.е. и подкос и стойка рассматриваются как промежуточные опоры, на которых прогиб = 0.
07-07-2019: СергейЧ
Так для меня было бы проще всего, я могу хоть десяток неравномерно распределенных опор воткнуть.:) Но что-то меня тут смущает …
Например, у нас большой проем и перегруженная балка. Добавляем по краям проема два подкоса, пусть еще и под острым углом к балке. БОльшая часть нагрузки перенесется с первоначальных опор на точки крепления подкосов. А я поставлю на подкосы любой брусок, под любым углом, лишь бы проходил по гибкости и прочности, не разрушался. И, вуаля — мы уменьшили эффективную ширину пролета, напряжения в балке, прогибы и т.п. Два бруска заменили нам два дополнительных столба.
Балка у нас прогибается, а подкос — стоит как вкопанный :).В принципе, в точке крепления подкоса можно посчитать реакцию опоры (для случая дополнительной несжимаемой опоры), и ее изменение (уменьшение) при единичном смещении (деформации опоры). Если знать поведение подкоса под нагрузкой, зависимость изменения его длины от нагрузки, можно, с учетом геометрии, найти точку равновесия и величину смещения балки относительно случая несжимаемой опоры.
Но тут я упираюсь в то, что подкос не только сжимается, но и может, под действием случайных смещений нагрузки, неточного выполнения соединений и т.п., еще и прогибаться в направлении меньшего момента инерции. Как бы это достоверно посчитать?
Кстати, а как задающему вопрос выложить картинку?
09-07-2019: Доктор Лом
Посмотрите статью «Влияние осадки опор». Там рассматривается похожая ситуация.
07-05-2020: Станислав
Здраствуйте, не подскажите из первоисточник таблицы? Курсовая…
07-05-2020: Доктор Лом
Вот сейчас реально не подскажу. Статья писалась 7 лет назад. Что-то я брал из общедоступных источников (справочники по сопромату), а что-то рассчитывал сам, чтобы сделать таблицы более полными.
30-01-2021: Евгений
Рис. 2.2. Балка защемленная с двух сторон. Распределенная нагрузка на левой части балки. Ошибка в формуле для Мв. Начальный коэффициент не 1/6, а 1/3. Сначала проверил расчетом, а потом и влитературе нашёл.
09-03-2021: теано
Здравствуйте, Док. Я правильно понимаю: жесткая заделка и скользящая эквивалентны при расчетах прогибов?
09-03-2021: Доктор Лом
Да.
Моделирование разрезных и неразрезных балок
Изгибающие моменты во второстепенных балках появились над опорами, что характерно для неразрезных элементов. Шарниры из плоскости балок в схеме остались по тем же причинам, о которых я писал выше, что привело к разумному отсутствию изгибающих моментов из плоскости. Однако в нашей новой схеме появились новые моменты – крутящие в балках:
Связаны они с неравномерной загрузкой крайней балки Нагрузка на нее предается с одной стороны, а жесткое примыкания ведет к повороту сечения, который ограничен на колонне. Получается, что теперь колонна подвергается действию момента из плоскости, посмотрим в расчет:
Действительно, моменты в колоннах появились, что также неприемлемо, если вспомнить работу реальной конструкции. Модель необходимо доработать, сохранив при этом неразрезную работу конструкции. Рассмотрю два способа (хотя можно найти и больше):
1 . Расшивка узлов
В этом методе программа Лира 10.6 позволяет расшить конструкции в узле крепления балки второстепенной и главной, при этом, наложив вручную связь по заданным направлениям. Операция называется «Создание групп объединения перемещений».
Для разрыва соединений необходимо выделить элементы, которые подвергаются дальнейшему разъединению, а также узлы, в которых происходит расшивка. В этом узле после выполнения операций появится два узла (в одной координате), которые будут объединены по заданным направлениям (x,y,z).Сложность метода заключается в выделении балок и узлов в сложных схемах.
Результат работы привожу в эпюрах:
Появляются только те моменты, которые мы встречаем в реальных схемах.
2. Создание двух узловых конечных элементов упругой связи
Устранить недостаток первого метода (выделение элементов в сложных схемах) можно с помощью двухузловых конечных элементов упругой связи. Элементы можно копировать, а значит можно быстро размножать такие соединения по схеме. Для использования такого метода в схеме необходимо сперва сместить плоскость балок, и заполнить расстояние между узлами двухузловым конечным элементом упругой связи (КЭ55).
Жесткость таким элементам присваивается значительная, физически означающая смятие узла (поскольку жесткость упругой связи – это отношение силы на деформацию, при весьма малой деформации значение жесткости будет стремиться к бесконечности). Длина элементов упругой связи особой роли не играет, поскольку жесткость от длины не зависит. Закреплять направления необходимо ориентируясь на локальные оси элементов упругих связей, освобождая повороты из плоскости изгиба второстепенных балок, а так же кручение. Получим результаты:
Усилие момента из плоскости балок возникло из-за применения связи конечной жесткости, а не абсолютной как в первом случае, однако оно пренебрежимо мало, в сравнении с изгибающим моментом в плоскости изгиба. Метод можно считать приемлемым. У метода есть недостаток, например, при построении многоэтажной балочной клетки будет не просто учесть работу колонны выше уровня клетки. В таком случае можно попробовать балки «не довести» до колонн.
В результате можно сказать, что оба момента в схеме обеспечили реальную работу конструкции с неразрезными прогонами. Методы можно комбинировать в одной схеме, учитывая особенности работы обоих методов.
Моделирование полужесткой составной балки из древесины в виде поверхностной модели
Существует несколько вариантов расчета полужесткой составной балки. Они отличаются главным образом типом моделирования. Тогда как гамма-метод обеспечивает возможность простого моделирования, при применении других методов (например, аналогии сдвига) требуется более сложное моделирование, которое, однако, компенсируется гораздо более гибким применением в расчете по сравнению с гамма-методом.
Еще один вариант моделирования, со стержневой моделью, был пояснен в данной статье. В принципе, этот метод можно применить и для поверхностей. Поскольку моделирование, например, соединительных стержней требует много времени, рекомендуется соединить поверхность непосредственно со стержнем либо с другой поверхностью. Существует несколько вариантов:
- Соединение поверхность-поверхность с линейным шарнирном
- Соединение стержень-поверхность с линейным высвобождением
- Соединение поверхность-поверхность с контактным телом
Для пояснения взят пример из литературы [1] Глава E 8.6.2. Конструктивная система и размеры сечений показаны на рисунке 01. В расчете учтена податливость 133 Н/мм², что обусловлено расстоянием между крепежными элементами, равным 125 мм.
Pисунок 01 — Конструктивная система и размеры сечений по [1]
Соединение поверхность-поверхность с линейным шарнирном
Деревянная балка, а также бетон моделируются с помощью поверхностей, поверхность деревянной балки при этом перпендикулярна поверхности бетона. Так как поперечная деформация учитывается и для поверхностных элементов, у деревянной балки нужно выбрать ортотропную модель материала. В комбинированном соединении податливость может быть задана с помощью линейного шарнира путем задания пружины для степени свободы ux . В примере из литературы [1] она составляет 133 Н/мм².
Pисунок 02 — Соединение поверхность-поверхность с линейным шарниром
Преимущество этого метода заключается в том, что нам непосредственно отображается сдвиговой поток в комбинированном соединении. Мы можем выполнить разрез по вертикальной поверхности и проанализировать основные внутренние силы nxy. Полученные результаты идентичны результатам по методу аналогии сдвига из литературы [1]. Уменьшение сдвигового потока в области опоры до 0,040 МН/м является следствием сингулярности в этой области и может быть проигнорировано.
Pисунок 03 — Оценка сдвигового потока на уровне клеевого соединения
Одним из возможных недостатков является то, что напряжения и наложения должны быть рассчитаны с применением поверхностных внутренних сил. При этом расчет по стержням можно обеспечить с помощью результирующего стержня, который объединяет в себе результаты деревянной поверхности. Чтобы смоделировать одинаковое расстояние до центра тяжести у отдельных поперечных сечений, необходимо внецентренно переместить бетонную поверхность на 35 мм. Воздействие в этом случае очень мало, и поэтому оно не учитывается.
Соединение стержень-поверхность с линейным высвобождением
При применении этого метода деревянная балка моделируется в виде стержня и внецентренно соединяется с поверхностью. Так как поверхность, как правило, не соединена со стержнем, а продолжает его (эффект непрерывности), здесь нельзя применить линейный шарнир. В этом случае необходимо применить линейное высвобождение Таким образом можно высвободить один из компонентов и задать взаимодействие между ними с помощью соответствующего типа линейного высвобождения. В этом случае податливость можно учесть тем же способом, как у линейного шарнира, с помощью линейной пружины.
Pисунок 04 — Соединение стержень-поверхность с высвобождением линии
Недостатком данного метода является то, что сдвиговой поток не отображается напрямую. В этом случае необходимо выполнить разрез по линии соединения поверхности со стержнем. В результате мы получим сдвиговой поток слева и справа от линии. Значения результатов нужно суммировать вручную. После суммирования сдвиговой поток идентичен предыдущему методу.
Pисунок 05 — Оценка сдвигового потока на уровне клеевого соединения
Преимущество заключается в том, что расчет можно выполнить, например, в дополнительном модуле RF-TIMBER, который содержит внутренние силы.
Соединение поверхность-поверхность с контактным телом
Другим вариантом является соединение обеих поверхностей контактным телом. Обе поверхности моделируются параллельно друг другу, и между ними устанавливается контактное состояние в виде контактного тела. Деревянная балка должна быть также смоделирована в виде ортотропной поверхности. Податливость в этом случае задана с помощью пружины поверхности. В этом случае необходимо увеличить линейную пружину со значением 133 Н/мм² на одну плоскость, разделив значение на ширину контактной поверхности, т.е. на 120 мм. Пружина составляет:
Формула 1
C = 133 N/мм²120 мм = 1,108 N/мм³
Pисунок 06 — Соединение поверхности с поверхностью с контактным телом
В этом случае сдвиговой поток также не отображается напрямую и должен быть рассчитан по сдвиговым напряжениям контактного тела, снова умножив при этом напряжения на 120 мм = 0,12 м. Сечение с результатами можно экспортировать в Excel и проанализировать более подробно.
Pисунок 07 — Оценка касательных напряжений и сдвигового потока на уровне клеевого соединения
Поскольку поверхности расположены геометрически независимо друг от друга, нет необходимости определять эксцентриситет. Данный способ моделирования, безусловно, является наиболее сложным и имеет смысл только в том случае, если составные компоненты являются поверхностными элементами (например, в случае кросс-ламинированных деревянно-бетонных составных конструкций).
Расчет луча| MechaniCalc
Калькулятор балки позволяет анализировать напряжения и прогибы в прямых балках.
Опции
Пример загрузки
Очистить все данные
Входы
Введите данные балки, затем нажмите кнопку «Рассчитать результаты»:
—
Добавить ограничение
Удалить ограничение
Невозможно отобразить сюжет — браузер устарел.
Рассчитать результаты
Предупреждение — Перед решением необходимо исправить следующее:
Дисплейные блоки
Результаты
Результаты анализа пучка подробно описаны ниже. Задача решалась в виде конечно-элементной модели с использованием балочных элементов. Для получения дополнительной информации о том, как были получены эти результаты, обратитесь к справочнику по конечно-элементному анализу и справочнику по напряжению и прогибу балки.
Обзор результатов
Максимальный прогиб и наклон приведены ниже:
| Значение | Расположение | |
|---|---|---|
| Максимальный прогиб: | ||
| Максимальный наклон: |
Схема свободного тела (FBD) и деформированная сетка показаны ниже.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
См. Полную информацию о результатах на других вкладках (выше).
Обзор модели
Модель с приложенными силами и ограничениями показана ниже:
Невозможно отобразить сюжет — браузер устарел.
Свойства материала
Материал:
| Имущество | Значение |
|---|---|
| Предел текучести | |
| Максимальная прочность | |
| Модуль упругости | |
| Коэффициент Пуассона |
Характеристики поперечного сечения
Поперечное сечение:
| Имущество | Значение |
|---|---|
| Высота (Y) | |
| Ширина (X) | |
| Толщина полотна | |
| Толщина фланца | |
| Площадь | |
| Центроидное расстояние (в направлении первичного изгиба) | |
| Момент инерции, центроидный (относительно оси первичного изгиба) |
Диаграмма момента сдвига
Диаграммы сдвига и момента показаны ниже.Соблюдаются стандартные условные обозначения для диаграмм момента сдвига:
- Сдвиг: положительный сдвиг вызывает вращение балки по часовой стрелке, отрицательный сдвиг вызывает вращение против часовой стрелки.
- Момент: Положительный момент сжимает верхнюю часть балки и удлиняет нижнюю часть балки (т.е. заставляет балку «улыбаться»).
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Графики напряжений
Графики напряжений показаны ниже.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Напряжения рассчитываются на основе следующих уравнений:
| Осевое напряжение | Напряжение сдвига | Напряжение изгиба | Напряжение по Мизесу |
|---|---|---|---|
Графики прогиба
Графики прогиба показаны ниже.Условные обозначения прогибов:
.- X: положительный направо, отрицательный налево
- Y: положительный вверх, отрицательный вниз
- Наклон: линейка правой руки (положительное значение против часовой стрелки, отрицательное значение по часовой стрелке)
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Невозможно отобразить сюжет — браузер устарел.
Эта проблема была решена в виде конечно-элементной модели. На этой вкладке представлены результаты для отдельных узлов и элементов модели.
На приведенном ниже графике показана сетка с номерами элементов , помеченными:
Невозможно отобразить сюжет — браузер устарел.
Узловые результаты
Ниже приведены результаты для каждого узла. Следует отметить несколько моментов:
- Определенные узлы связаны с точками, и для этих узлов дается номер связанной точки.
- Сначала перечислены все узлы, связанные с точками, за ними следуют узлы, созданные как часть процесса построения сетки.
- Внешние реакции могут существовать для ограниченных степеней свободы. Любые узлы, не имеющие ограничений, не будут иметь внешних реакций.
Элементарные результаты
Ниже приведены результаты для каждого элемента. Следует отметить несколько моментов:
- Каждый элемент состоит из 2 узлов. В таблице эти узлы обозначаются как «Узел 1» и «Узел 2».
- Внутренние реакции даны в терминах глобальной системы координат (т.е. X и Y), а также в локальной системе координат (т.е. «осевой» вдоль оси элемента, «сдвиг» перпендикулярно элементу).
Загрузить результаты в Excel
Загрузите файл Excel на свой компьютер, содержащий узловые и элементарные результаты.
Скачать отчет
Сохраните отформатированный документ Word на свой компьютер с подробным описанием входных данных и результатов анализа.
Скачать входной файл
Сохранить все входные данные в файл. Позже вы можете загрузить этот файл, чтобы продолжить с того места, где вы остановились.
Требуется больше функциональности?
Зарегистрируйте учетную запись, чтобы получить полный доступ ко всем калькуляторам и другому контенту. Типы подписки описаны ниже вместе с преимуществами каждого из них.
- Цена
- Доступ к калькуляторам
- Логин
- Создание материалов
- Создание сечений
- Сохранить файлы
- Отчетность
- Бесплатно
Ограничено
Limited Доступ к калькуляторам
Предварительно определенные Поперечные сечения
- Учить больше »
39 долларов США.99 / месяц 249,99 долларов США в год Полный
Полный Доступ к калькуляторам
Плавающие лицензии
Плавающие лицензии
- Учить больше »
- Зарегистрироваться сейчас
— PolyBeam прост и удобен в использовании!
Простой в использовании калькулятор лучаПервое, что наши пользователи связывают с PolyBeam, — это простота.PolyBeam — это очень простой и интуитивно понятный калькулятор луча, который делает его очень простым в использовании, даже если вы не знакомы с ИТ и программным обеспечением. Опоры, нагрузки и свойства сечений вставляются с минимальным вмешательством пользователя. Одновременно PolyBeam построит графическое представление балки с приложенными нагрузками, вычислит поперечные силы и определит коэффициент использования балки.
Боковое продольное изгибание при крученииКритический изгибающий момент от поперечного продольного изгиба при кручении определяется на основе энергетического метода, который учитывает высоту атаки нагрузки, поперечные силы и ограничения.С помощью этого метода с высокой точностью определяется критический момент. Это часто приводит к более высокой несущей способности по сравнению с традиционными расчетами.
Упругие и пластические поперечные силыВ отличие от традиционного программного обеспечения для проектирования, PolyBeam определяет поперечные силы как упругими, так и пластическими методами. Это позволяет более эффективно использовать наиболее часто используемые стальные профили для статически неопределимых балок.
Расчет по предельным состояниям (ULS)Можно указать комбинацию нагрузок ULS.Если это будет сделано, PolyBeam проверит поперечные силы из расчета балки с грузоподъемностью выбранной секции и определит коэффициент использования. Для получения дополнительных сведений о том, что входит в проверку конструкции ULS, см. Вопрос «Что включает проверка конструкции?».
Расчет предельного состояния эксплуатационной пригодности (SLS)Можно указать два различных типа комбинаций нагрузок SLS: анализ собственной частоты или анализ прогиба. Анализ собственной частоты определяет первую собственную частоту балки и позволяет пользователю указать порог — это очень полезно при работе с требованиями к вибрации.аналогично можно указать порог отклонения, поскольку по умолчанию используется L / 400.
Противопожарное проектированиеЕсли указана комбинация пожарной нагрузки, PolyBeam рассчитывает температуру стали на основе продолжительности пожара и определяет несущую способность. Если секция не может выдержать нагрузку, можно определить критическую температуру стали и использовать ее для определения необходимой противопожарной изоляции.
Экспорт в PDFКогда вы закончите расчет балки, очень легко задокументировать свою работу.Просто нажмите на экспорт, выберите, какой контент вы хотите включить, и позвольте PolyBeam создать для вас короткий и элегантный документ PDF. Эта функция — одна из самых популярных среди наших пользователей. См. Пример.
Для всех калькуляторов требуется браузер с поддержкой JAVA. Дополнительная информация Примечание:
** СОВЕТ. Для поиска на этой веб-странице выберите «ctrl + F», затем введите ключевое слово во всплывающем окне.** Меню структурных прогибов и напряжений Уравнения и калькуляторы нагружения упругих каркасов на прогиб и противодействие в плоскости для Формулы реакции и прогиба и калькулятор для плоского нагружения упругих рам Уравнения и калькуляторы прогиба пластин и напряжений
Приложения общего назначения и математические калькуляторы Формулы для круглых колец, момента, кольцевой нагрузки, радиального сдвига и деформации
Свойства сечения Выбранные формы
Разработка и проектирование систем зубчатых передач и зубчатых передач
Теплообменная техника Калькуляторы для проектирования электроники Уравнения и калькуляторы IEEE 1584-2018 Производство Калькуляторы простых механических рычагов Конструкция пружины Уравнения и анализ трения Гражданское строительство Расчет напряжения / прочности при установке болта и резьбы Тензодатчик Анализ допусков с использованием допусков геометрических размеров с учетом требований GD&T и других принципов Дизайн управления движением Сосуд под давлением и конструкция цилиндрической формы Расчетные и инженерные уравнения и калькуляторы
Жидкости Допуск на изгиб листового металла Пластиковая защелка Конверсии, жидкости, крутящий момент, общие Решения для треугольников / тригонометрии Финансы и прочее. Калькуляторы для расчета сварочных и технических данных Главное меню Инженерная физика |
Простой калькулятор луча | calcresource
Предпосылки
Оглавление
Введение
Балка с простой опорой — одна из самых простых конструкций. У него всего две опоры, по одной с каждой стороны. Одна штифтовая опора и роликовая опора. Оба они препятствуют любому вертикальному движению, позволяя, с другой стороны, свободное вращение вокруг них.Роликовая опора также позволяет балке расширяться или сжиматься в осевом направлении, хотя свободному горизонтальному перемещению препятствует другая опора.
Удаление любой из опор или установка внутреннего шарнира приведет к тому, что балка с простой опорой перейдет в механизм, то есть тело перемещается без ограничений в одном или нескольких направлениях. Очевидно, это нежелательно для несущей конструкции. Следовательно, балка с простой опорой не обеспечивает избыточности с точки зрения опор. Если произойдет локальный сбой, вся конструкция рухнет.Эти типы структур, которые не обеспечивают избыточности, называются критическими или детерминантными структурами . Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией .
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов. Обычно для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M.Для балки с простой опорой, которая несет только поперечные нагрузки, осевая сила всегда равна нулю, поэтому ею часто пренебрегают. Результаты расчетов на странице основаны на следующих предположениях:
- Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно эластичный
- Нагрузки прикладываются статично (они не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольной оси, остается плоской и перпендикулярно отклоненной оси.Это тот случай, когда высота поперечного сечения намного меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.
Условные обозначения
Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:
- Осевая сила считается положительной, когда она вызывает натяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила, хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать им последовательно, также даст те же физические результаты.
Обозначения
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общий пролет балки
- R: опора реакция
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \ theta: slope
Балка с простой опорой и равномерно распределенной нагрузкой
Нагрузка w распределяется по всему пролету балки с постоянной величиной и направление. 3)} {24 EI} 91 960
Балка с простой опорой и точечной силой в середине
Сила сосредоточена в одной точке, расположенной в середине балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше длины пролета балки. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной в середине.2)} {16 E I} &, x> L / 2 \ end {align} \ right.
где:
\ строго {x} = L-x
Балка с простой опорой, с точечной силой в произвольном положении
Сила сосредоточена в одной точке, в любом месте пролета балки. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины пролета балки.В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от левого конца.
Балка с простой опорой и точечной нагрузкой в произвольном положении | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = {Pb \ over L} R_B = {Pa \ над L} |
| Концевые уклоны: | \ theta_A = — \ frac {P b (L ^ 2-b ^ 2)} {6E IL} \ theta_B = \ frac {P a (L ^ 2-a ^ 2)} {6E IL} |
| Предельный изгибающий момент: | M_u = {Pab \ over L} |
| Предельное усилие сдвига: | V_u = \ left \ {\ begin {Выровнено } & {Pb \ over L} &, \ textrm {if:} a \ le L / 2 \\ — & {Pa \ over L} &, \ textrm {if:} a> L / 2 \ end {выровнено} \Правильно. 3} {6EI} &, x> a \ end {align} \ right.2} {2 E I} &, x> a \ end {align} \ right. |
где: b = La \ строго {x} = Lx | |
Балка с простой опорой с точечным моментом
В этом случае момент накладывается на одну точку балки в любом месте пролета балки. С практической точки зрения, это может быть пара сил или элемент на кручение, соединенный из плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину луча, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке.Хотя в непосредственной близости от области применения ожидается, что результаты, предсказанные с помощью классической теории пучка, будут неточными (из-за концентраций напряжений и других локализованных эффектов), по мере того, как мы удаляемся, предсказанные результаты полностью верны, как заявил Святой -Венантный принцип.
В следующей таблице представлены формулы, описывающие статический отклик простой балки под действием сосредоточенного момента M точки, приложенного на расстоянии a от левого конца. 2 )} {6E IL}
где:
b = La
\ строго {x} = Lx
Балка с простой опорой и треугольной нагрузкой
Нагрузка распределяется по всему пролету балки, однако ее величина не константа, но изменяется линейно, начиная от нуля на левом конце до своего пикового значения w_1 на правом конце. Размеры w_1 — сила на длину. Общее количество силы, приложенной к балке, равно W = {1 \ over2} w L, где L — длина пролета.
Ориентация треугольной нагрузки важна! Формулы, представленные в этом разделе, были подготовлены для случая восходящей нагрузки (слева направо), как показано на схеме. Для нисходящей нагрузки вы можете отразить балку так, чтобы ее левый конец (точка A) был наименее нагруженным. Ось x и все результаты также будут отражены.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при линейно изменяющейся (треугольной) распределенной нагрузке, восходящей слева направо.4} {24EIL}
где:
C = \ sqrt {15- \ sqrt {120}} \ left (\ sqrt {15} + \ sqrt {50} \ right) \ приблизительно 22.01237
Балка с простой опорой и трапецеидальной нагрузкой
Нагрузка распределяется по всему пролету балки и имеет линейно изменяющуюся величину, начиная с w_1 на левом конце и заканчивая w_2 на правом конце. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина пролета.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при переменной распределенной нагрузке трапециевидной формы. 3} {24EI}
где:
w_x = w_1 + {(w_2-w_1) x \ over L}
900 53Балка с простой опорой и трапециевидным распределением нагрузки в виде плиты
Такое распределение нагрузки типично для балок по периметру плиты.Распределение имеет трапециевидную форму с максимальной величиной w внутри балки, а на двух ее концах становится равной нулю. Размеры (\ w \) — сила на длину. Общее количество силы, приложенной к балке, равно W = w (La / 2-b / 2), где L — длина пролета, а a, b — длины с левой и правой стороны балки соответственно, где распределение нагрузки равно разная (треугольная).
В следующей таблице представлены формулы, описывающие статический отклик простой балки при трапецеидальном распределении нагрузки, как показано на схеме выше.3
Балка с простой опорой и частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть пролета балки с постоянной величиной w, в то время как оставшийся пролет разгружен. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = \ left (L-a-b \ right) w, где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной равномерной нагрузке.2} {2 E I} &, x \ ge L-b \ end {align} \ right.
где:
\ острый {x} = Lx
x_a = xa
L_w = Lab
Балка с простой опорой и частично распределенной трапециевидной нагрузкой
Нагрузка распределяется на часть пролет балки, имеющий линейно изменяющуюся величину от w_1 до w_2, а оставшийся пролет разгружен. Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина пролета, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2. Кроме того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю.
В следующей таблице представлены формулы, описывающие статический отклик простой балки при частично распределенной трапециевидной нагрузке.3
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Калькулятор консольной балки | calcresource
Теоретические основы
Содержание
Введение
Консольная балка — одна из самых простых конструкций. Он имеет только одну опору на одном из концов. Опора представляет собой так называемую фиксированную опору , которая запрещает все движения, включая вертикальные или горизонтальные смещения, а также любые вращения.Другой конец не поддерживается, поэтому он может свободно перемещаться или вращаться. Этот свободный конец часто называют концом кантилевера.
Консоль имеет только одну фиксированную опору.Удаление единственной опоры или установка внутреннего шарнира превратят консольную балку в механизм: тело движется без ограничений в одном или нескольких направлениях. Это нежелательная ситуация для несущей конструкции. В результате консольная балка не обеспечивает избыточности с точки зрения опор.Если произойдет локальный сбой, вся конструкция рухнет. Эти типы структур, которые не обеспечивают избыточности, называются критическими или детерминантными структурами . Напротив, конструкция, которая имеет больше опор, чем требуется для ограничения ее свободного движения, называется избыточной или неопределенной конструкцией . Консольная балка — определяющая конструкция.
Допущения
Статический анализ любой несущей конструкции включает оценку ее внутренних сил и моментов, а также ее прогибов.Обычно для плоской конструкции с плоской нагрузкой интересующими внутренними воздействиями являются осевая сила N, поперечная поперечная сила V и изгибающий момент M. Для консольной балки, несущей только поперечные нагрузки, осевое усилие всегда равно нулю. при условии небольших прогибов. Поэтому осевыми силами часто пренебрегают.
Результаты расчетов на этой странице основаны на следующих предположениях:
- Материал однороден и изотропен (другими словами, его характеристики одинаковы во всех точках и в любом направлении)
- Материал линейно эластичный
- Нагрузки прикладываются статично (они не меняются со временем)
- Поперечное сечение одинаково по всей длине балки
- Прогибы небольшие
- Каждое поперечное сечение, которое изначально является плоским, а также перпендикулярно продольному ось, остается плоской и перпендикулярной отклоненной оси.Это тот случай, когда высота поперечного сечения намного меньше длины балки (в 10 и более раз), а также поперечное сечение не является многослойным (не сечение сэндвич-типа).
Последние два предположения удовлетворяют кинематическим требованиям теории пучка Эйлера-Бернулли, которая здесь также принята.
Условные обозначения
Для расчета внутренних сил и моментов при любом разрезе сечения балки необходимо условное обозначение. Здесь приняты следующие значения:
- Осевая сила считается положительной, когда она вызывает натяжение детали.
- Сила сдвига положительна, когда она вызывает вращение детали по часовой стрелке.
- Изгибающий момент является положительным, когда он вызывает растяжение нижнего волокна балки и сжатие верхнего волокна.
Эти правила, хотя и не являются обязательными, но достаточно универсальны. Другой набор правил, если следовать им последовательно, также даст те же физические результаты.
Положительный знак для внутренней осевой силы, N, поперечной силы, V и изгибающего момента, MОбозначения
- E: модуль упругости материала (модуль Юнга)
- I: момент инерции поперечного сечения вокруг упругой нейтральной оси изгиба
- L: общая длина балки
- R: реакция опоры
- d: прогиб
- M: изгибающий момент
- V: поперечная поперечная сила
- \ theta: наклон
Консольная балка с равномерно распределенной нагрузкой
Нагрузка w распределена по пролету консоли, имея постоянную величину и направление. 2)} {6 EI}
Консольная балка с точечной силой на конце
Сила сосредоточена в одной точке, расположенной на свободном конце балки.Однако на практике сила может распространяться на небольшую площадь, хотя размеры этой области должны быть существенно меньше, чем длина кантилевера. В непосредственной близости от приложения силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным. Однако это только местное явление. По мере удаления от места расположения силы результаты становятся действительными в силу принципа Сен-Венана.
В следующей таблице содержатся формулы, описывающие статический отклик балки кантилевера под действием сосредоточенной силы P, приложенной к наконечнику.2 (3L-x)} {6EI}
Консольная балка с точечной силой в произвольной позиции
Сила сосредоточена в одной точке в любом месте по длине консоли. Однако на практике сила может распространяться на небольшую площадь. Однако, чтобы считать силу сосредоточенной, размеры области приложения должны быть существенно меньше длины балки. В непосредственной близости от силы ожидаются концентрации напряжений, и в результате отклик, предсказываемый классической теорией балки, может быть неточным.Однако это только локальное явление, и по мере удаления от места расположения силы расхождение результатов становится незначительным.
Следующая таблица содержит формулы, описывающие статический отклик консольной балки под действием сосредоточенной точечной силы P, приложенной на случайном расстоянии a от неподвижной опоры.
Консольная балка с точечной нагрузкой в произвольном положении | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = P M_A = -Pa Наклоны |
\ theta_A = 0 \ theta_B = — {Pa ^ 2 \ over 2EI} | |
| Предельный изгибающий момент: | M_u = -Pa |
| Предельное усилие сдвига: | V_u = P |
| Предельный прогиб: | d_u = {Pa ^ 2 (3L-a) \ over 6EI} |
| Изгибающий момент в x: | M (x) = \ left \ {\ begin {align} — & P (ax) &, x \ le a \\ & 0 &, x> a \ end {align} \ right.2 (3x — a) \ over 6EI} &, x> a \ end {align} \ right. |
| Наклон в точке x: | \ theta (x) = \ left \ {\ begin {align} — & {Px (2a — x) \ over 2EI} &, x \ le a \\ & \ theta_B & , x> a \ end {выровнено} \ right. |
Консольная балка с точечным моментом
В этом случае момент прикладывается к одной точке балки в любом месте пролета. С практической точки зрения, это может быть пара сил или элемент на кручение, соединенный из плоскости и перпендикулярно балке.
В любом случае область приложения момента должна распространяться на небольшую длину консоли, чтобы ее можно было успешно идеализировать как сосредоточенный момент в точке. Хотя в непосредственной близости от области применения ожидается, что результаты, предсказанные с помощью классической теории пучка, будут неточными (из-за концентраций напряжений и других локализованных эффектов), предсказанные результаты становятся совершенно достоверными, когда мы удаляемся, как заявил Св. -Венантный принцип.
Следующая таблица содержит формулы, описывающие статический отклик консольной балки под действием сосредоточенного момента M точки, приложенного на расстоянии a от неподвижной опоры.
Консольная балка с острым моментом | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = 0 M_A = M |
| Торцевые уклоны: | |
| Торцевые уклоны \ theta_A = 0 \ theta_B = \ frac {M a} {EI} | |
| Предельный изгибающий момент: | M_u = M |
| Предельное усилие сдвига: | V_u = 0 |
| Ultimate прогиб: | d_u = — {Ma (2L-a) \ over 2EI} |
| Изгибающий момент в точке x: | M (x) = \ left \ {\ begin {align} & M &, x \ le a \\ & 0 &, x> a \ end {align} \ right.2} {2 E I} &, x \ le a \\ & — \ theta_B \ left (x- {a \ over2} \ right) &, x> a \ end {align} \ right. |
| Наклон в точке x: | \ theta (x) = \ left \ {\ begin {align} & \ frac {M x} {EI} &, x \ le a \\ & \ theta_B &, x> а \ конец {выровнено} \ право. |
Консольная балка с переменной распределенной нагрузкой
Нагрузка распределяется по длине консоли с линейно изменяющейся величиной, начиная с w_1 на неподвижной опоре и заканчивая w_2 на свободном конце.Размеры w_1 и w_2 — сила на длину. Общее количество силы, приложенной к балке, равно W = {L \ over2} (w_1 + w_2), где L — длина консоли.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Если w_1 = 0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с возрастающей величиной (пик на вершине).
Если w_2 = 0, формулы в следующей таблице соответствуют треугольной распределенной нагрузке с уменьшающейся величиной (пик на неподвижной опоре).3} {24EI}
где:
w_x = w_1 + {(w_2-w_1) \ over L} x
Консольная балка с трапециевидным распределением нагрузки в виде плиты
Такое распределение нагрузки является типичным для консольных балок, поддерживающих плиту. Распределение выглядит как прямая трапеция, с увеличивающейся частью рядом с неподвижной опорой и постоянной частью с величиной, равной w, на оставшейся длине до кончика. Размеры w — сила на длину.Общее количество силы, приложенной к балке, равно W = w (L-a / 2), где L — длина консоли, а a — длина, близкая к неподвижной опоре, где распределение нагрузки меняется (треугольное).
В следующей таблице содержатся формулы, описывающие статический отклик консольной балки при трапециевидном распределении нагрузки от плиты, как показано на схеме выше.
Консольная балка с трапециевидным распределением нагрузки (от плиты) | |
|---|---|
| Кол-во | Формула |
| Реакции: | R_A = w \ left (L- {a \ over 2 } \ right) M_A = — {w \ over 6} \ left (3L ^ 2 — a ^ 2 \ right) |
| Концевые уклоны: | \ theta_A = 0 \ theta_B = — \ frac {w (4L ^ 3 — a ^ 3)} {24EI} |
| Предельный изгибающий момент: | M_u = — {w \ over 6} \ left (3L ^ 2 — a ^ 2 \ right) |
| Предельная сила сдвига: | V_u = w \ left (L- {a \ over 2} \ right) |
| Максимальный прогиб: | d_u = \ frac {w (15L ^ 4 — 5La ^ 3 + a ^ 4)} {120EI} |
| Изгибающий момент в x: | M (x) = \ left \ {\ begin {align} & xR_A + M_A- {wx ^ 3 \ over 6a} &, x \ ле a \\ & — {w \ over 2} (Lx) ^ 2 &, x> a \ end {align} \ right.3} {6EI} &, x> a \ end {align} \ right. |
Консольная балка с частично распределенной равномерной нагрузкой
Нагрузка распределяется на часть длины консоли с постоянной величиной w, в то время как оставшаяся длина разгружается. Размеры w — сила на длину. Общее количество силы, приложенной к балке, равно W = w \ left (L-a-b \ right), где L — длина консоли, а a, b — длины без нагрузки с левой и правой стороны балки, соответственно.
В следующей таблице приведены формулы, описывающие статический отклик консольной балки при частично распределенной равномерной нагрузке.
Консольная балка с частично распределенной равномерной нагрузкой | |
|---|---|
| Количество | Формула |
| Реакции: | R_A = wL_w M_A = — wL_w \ left (a + over 2} \ right) |
| Концевые уклоны: | \ theta_A = 0 \ theta_B = — \ frac {w (L_b ^ 3- a ^ 3)} {6 EI} |
| Ultimate изгибающий момент: | M_u = M_A |
| Предельная сила сдвига: | V_u = V_A |
| Предельный прогиб: | d_u = \ frac {w \ left (3L ^ 4 — 8L ^ 3 b + 6L ^ 2 b ^ 2 — 4L a ^ 3 + a ^ 4 — b ^ 4 \ right)} {24 EI} |
| Изгибающий момент в точке x: | M (x) = \ left \ {\ begin {align} & R_A x + M_A &, x \ le a \\ & R_Ax + M_A- \ frac {w x_a ^ 2} {2} &, a {<} x {<} Lb \\ & 0 &, x \ ge Lb \ end { выровнено} \ вправо.3} {6EI} &, a {<} x {<} L-b \\ & \ theta_B &, x \ ge L-b \ end {align} \ right. |
где: x_a = xa L_w = Lab L_b = Lb | |
Консольная балка с частично распределенной трапециевидной нагрузкой
Нагрузка распределяется на часть длины консоли, имеющую длину линейно меняющаяся величина от w_1 до w_2, а оставшаяся длина не загружается. Размеры w_1 и w_2 — сила на длину.Общее количество силы, приложенной к балке, равно W = {L-a-b \ over2} (w_1 + w_2), где L — длина балки, а a, b — длины без нагрузки с левой и правой стороны балки соответственно.
Значения w_1 и w_2 могут быть присвоены произвольно. Первое не обязательно должно быть меньше второго. Они могут принимать даже отрицательные значения (одно или оба).
Это самый общий случай. Формулы для частично распределенных равномерных и треугольных нагрузок можно получить, соответствующим образом задав значения w_1 и w_2.Кроме того, соответствующие случаи для полностью нагруженного пролета можно получить, установив a и b равными нулю. 2} {6} &, a {<} x {<} Lb \\ & 0 &, x \ ge Lb \ end {align} \ right.3} {24EI} &, a {<} x {<} L-b \\ & \ theta_B &, x \ ge L-b \ end {align} \ right.
где:
x_a = xa
L_w = Lab
L_1 = L + ab
L_b = Lb
w_ {m} = {w_1 + w_2 \ over2}
w_x = w_1 + {(w_2 -w_1) \ over L_w} (xa)
Статьи по теме
Понравилась эта страница? Поделись с друзьями!
Непрерывная балка — опорные силы момента и реакции
Сплошная балка с распределенной нагрузкой
Для неразрезной балки с 3, 4 или 5 опорами и распределенной нагрузкой силы реакции опоры могут быть рассчитаны как
R = c r q L (1)
где
R = сила реакции опоры (Н, фунт f )
c r = коэффициент силы реакции опоры из рисунка выше
q = распределенная нагрузка (Н / м, фунт f / фут)
L = длина пролета (м, фут)
Моменты могут быть рассчитаны как
M = c м q L 2 (2)
где
M = момент балки (Нм, фунт f фут)
c м = коэффициент момента Пример из рисунка выше
Пример — Непрерывная балка с распределенной нагрузкой
Силы реакции в концевых опорах для неразрезной балки с 3 опорами и распределенной нагрузкой 1000 Н / м можно рассчитать как
R конец = (0.375) (1000 Н / м)
= 375 Н
= 0,38 кН
Силу реакции в центральной опоре можно рассчитать как
R центр = (1,250) (1000 Н / м)
= 1250 Н
= 1,25 кН
Моменты балки в середине пролета с длиной пролета 1 м можно рассчитать как
M конец = (0.070) (1000 Н / м) (1 м) 2
= 70 Нм
Момент балки в центральной опоре можно рассчитать как
M центр = (0,125) (1000 Н / м) (1 м) 2
= 125 Нм
Сплошная балка с точечными нагрузками
Для неразрезной балки с 3, 4 или 5 опорами и точечными нагрузками силы реакции опоры могут можно рассчитать как
R = c r F (3)
, где
c r = коэффициент опорной силы реакции из рисунка выше
F = точечная нагрузка (Н, фунт f )
Моменты могут быть рассчитаны как
M = c м FL (4)
, где
c м = моментный коэффициент из рисунка выше
Пример — Сплошная балка с точечными нагрузками
Силы реакции в концевых опорах для неразрезной балки с опорами 3 и точечными нагрузками 2 1000 Н можно рассчитать как
R конец = (0.313) (1000 Н)
= 313 Н
= 0,31 кН
Силу реакции в центральной опоре можно рассчитать как
R центр = (1,375) (1000 Н)
= 1375 Н
= 1,4 кН
Моменты балки при точечных нагрузках с длиной пролета 1 м можно рассчитать как
M конец = (0.156) (1000 Н) (1 м)
= 156 Нм
Момент балки в центральной опоре можно рассчитать как
M центр = (0,188) (1000 Н) (1 м )
= 188 Нм
Прогиб в App Store
Deflection — это самое интерактивное, быстрое и точное приложение, доступное для расчета несущих балок. Создавайте визуально и мгновенно получайте инженерные результаты, графики и уравнения!
Просто поместите нагрузки и опоры на балку и посмотрите, как она изгибается.Найдите поперечное сечение во встроенной библиотеке или определите индивидуальную форму. Прогиб, внутренние напряжения и другие полезные результаты обновляются автоматически.
Это программное обеспечение является результатом более чем шести лет непрерывных разработок и инноваций, направленных на машиностроение, гражданское строительство и строительство. Этот инструмент поможет вам применять теорию упругости балки с первого дня, когда вы изучаете Механику материалов, и в любое время в будущем он станет вашим карманным справочником.
РЕЗУЛЬТАТЫ
Получение результатов проектирования и диаграмм в режиме реального времени.
• Сила сдвига
• Изгибающий момент
• Расстояние прогиба
• Внутреннее напряжение изгиба
• Внутреннее напряжение сдвига
БАЗЫ ДАННЫХ ПОПЕРЕЧНОГО СЕЧЕНИЯ
Укажите значения напрямую или найдите общие формы и материалы с помощью встроенных баз данных.
• США
• Европа
• Япония
• Индия
• Россия
• Великобритания
• Канада
• Австралия
• Китай
РЕДАКТОР СЕЧЕНИЯ
Редактировать встроенные поперечные сечения.Свойства формы рассчитываются автоматически.
• Момент инерции
• Площадь
НЕОГРАНИЧЕННЫЕ НАГРУЗКИ И ОПОРЫ
Просто перетащите любой груз или опору на балку.
• Сосредоточенные точечные нагрузки
• Распределенные нагрузки
• Моментные нагрузки
• Простые опоры
• Фиксированные опоры
• Фиксированные петли
• Плавающие петли Gerber
ДРУГИЕ ХАРАКТЕРИСТИКИ
• Применить собственный вес балки по желанию
• Автоматическое определение локальных максимумы и минимумы на диаграммах
• Неограниченное количество файлов для проектирования
• Шаблоны для быстрого запуска
• Метрические и стандартные единицы измерения
КОНТАКТ
Мы хотим услышать от вас! Проблемы, вопросы или запросы? Отправьте отзыв или свяжитесь по электронной почте @ ketchep.com
.