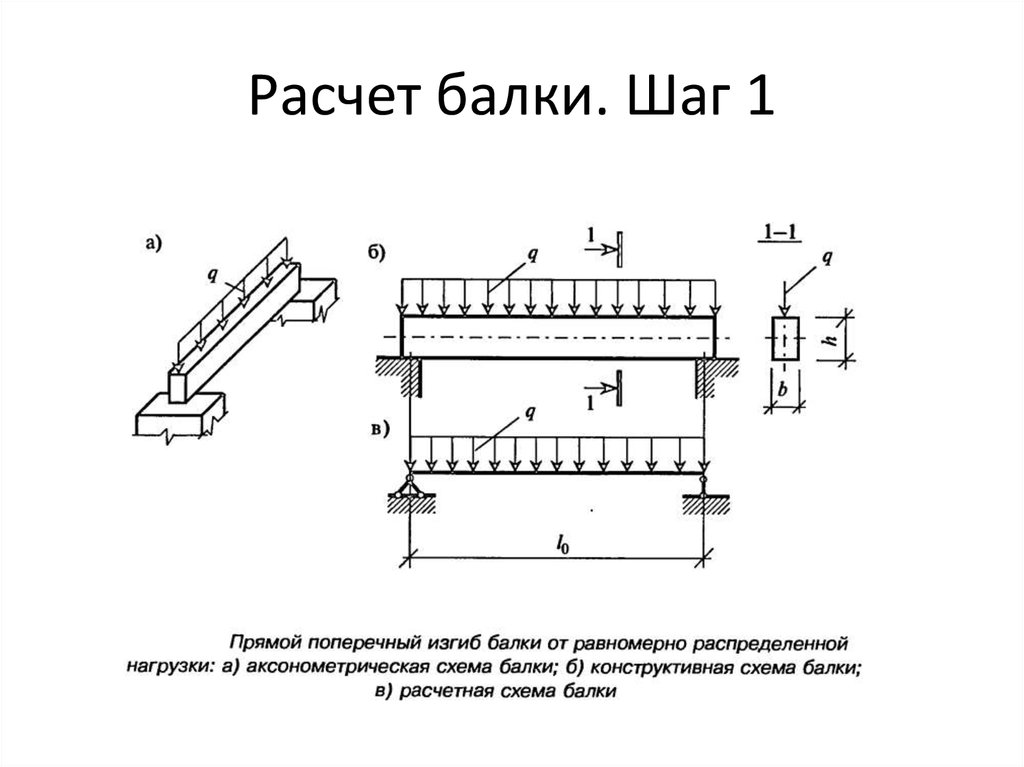
alexxlab Расчеты металлической балки перекрытия на прочность и прогиб, онлайн-калькулятор
Несмотря на бушующий в мире экономический кризис, который, к сожалению, затронул и нашу страну, строительство объектов различной важности продолжает производиться. При этом, в последнее время получило новый толчок развития именно промышленное строительство, однако, потребность жителей страны в жилых квадратных метрах не уменьшилось.
- Описание ↓
- Область применения ↓
- Расчет ↓
- Онлайн ↓
- Пример расчета ↓
Сегодня в строительстве промышленных и гражданских объектов повсеместно применяются металлические балки перекрытия, которые повышают несущую способность всей конструкции.
Описание
Стальные балки перекрытия представляют собой металлический брус определённой длины и определённой формы поперечного сечения. Как правило, металлические балки исполняются из высокопрочной стали марки Ст 5 с формой поперечного сечения типа двутавр и швеллер.
Балки производятся именно в таких формах поперечного сечения, потому что расчёт показывает, что такая форма является более экономически выгодной по сравнению с другими геометрическими фигурами.
Кроме того, расчёты показывают, что балка именно двутаврогого сечения лучше всего воспринимает давление и такие нагрузки, как изгиб, кручение и их совместное действие.
Продолжая перечислять преимущества двутавровых балок, можно отметить немаловажный факт того, что такая форма сечения помогает уменьшить вес конструкции.
Это помогает снизить нагрузку, например, на стены и фундамент здания, если в межэтажном перекрытии использовать металлические балки перекрытия. Также, из преимуществ можно отметить простоту монтажа любой конструкции из балок, скорость выполнения работ.
Для большей экономии использования металла и для облегчения всей конструкции существует сортамент балок двутаврового и швеллерного поперечного сечения. Площадь сечения изменяется от минимальной равной 12 кв.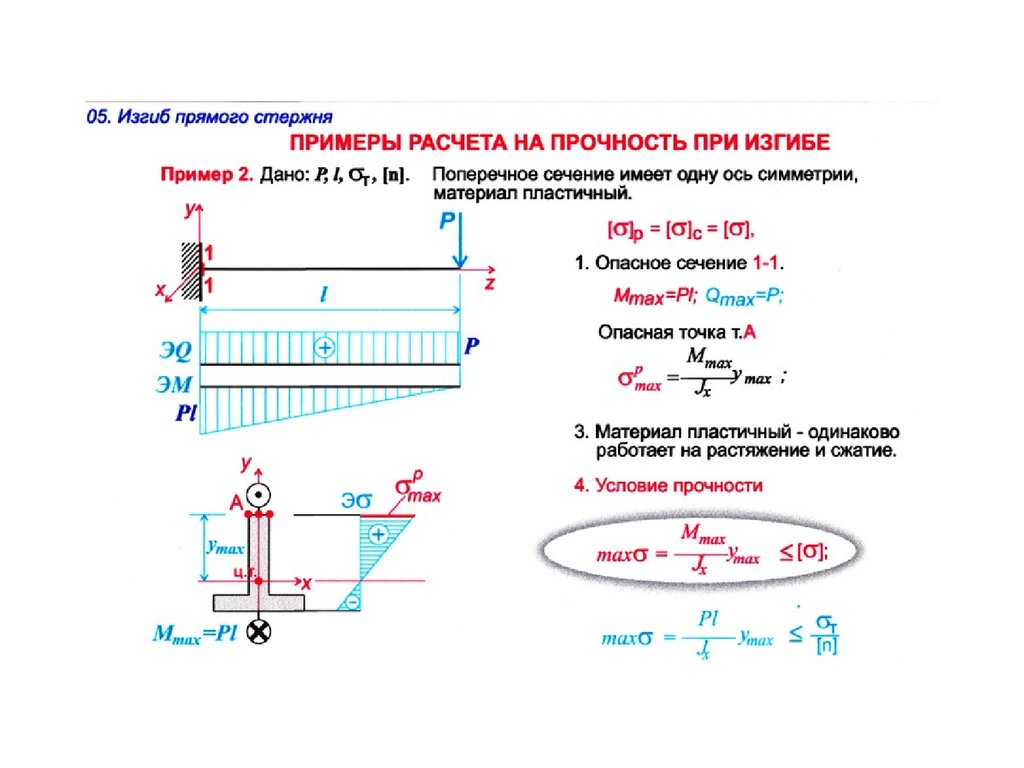
см до максимальной 234 кв. см, соответственно, для номеров профиля 10 и 70б.
Все значения площадей и массы профиля представлены в таблицах ГОСТ 8239-72. Чтобы её произвести, необходимо произвести расчёт профиля по прочностным характеристикам и вычислить подходящую площадь. Точная методика представлена ниже.
Таким образом, видно, что в качестве бруса перекрытия стоит использовать именно стальные балки, так как они во многом выигрывают по сравнению с конкурирующими материалами.
Область применения
Чаще всего, двутавровые балки применяются в промышленном строительстве, а именно, в случае возведения зданий с большими пролётами между опорами.
Благодаря своим механическим характеристикам и стойкости к динамическим воздействиям, металлический брус используют при возведении дорог и мостов и в других случаях необходимости возведения конструкций, выдерживающих большие нагрузки подобного характера.
В последнее время, стальные двутавровые балки стали применять в качестве элемента декора в квартирах и офисах.
После покраски, металлическая балка может выглядеть эстетично и иметь практическое применение в бытовом хозяйстве.
Расчет
Чтобы произвести выбор металлического бруса для той или иной конструкции, которая будет нести определённую нагрузку, необходимо произвести расчёт балки на прочность при изгибе. Это можно сделать, рассчитав все параметры самостоятельно по известной методике или воспользоваться онлайн-калькулятором.
Для выбора балки перекрытия, делают проверку из условия на прочность, где максимальная прочность стали должна быть больше суммы отношений максимального изгибающего момента в точке действия той или иной нагрузки к осевому моменту, и поперечных сил и площади поперечного сечения в максимально нагруженной точке.
Для определения всех неизвестных параметров этого условия, вычисления проводят поочерёдно.
Сначала определяют максимально нагруженный участок балки. Для этого, строят эпюру поперечных сил и изгибающих моментов. Чтобы построить эпюру, необходимо вычислить все суммарные изгибающие моменты и поперечные силы, действующие на балку, по участкам.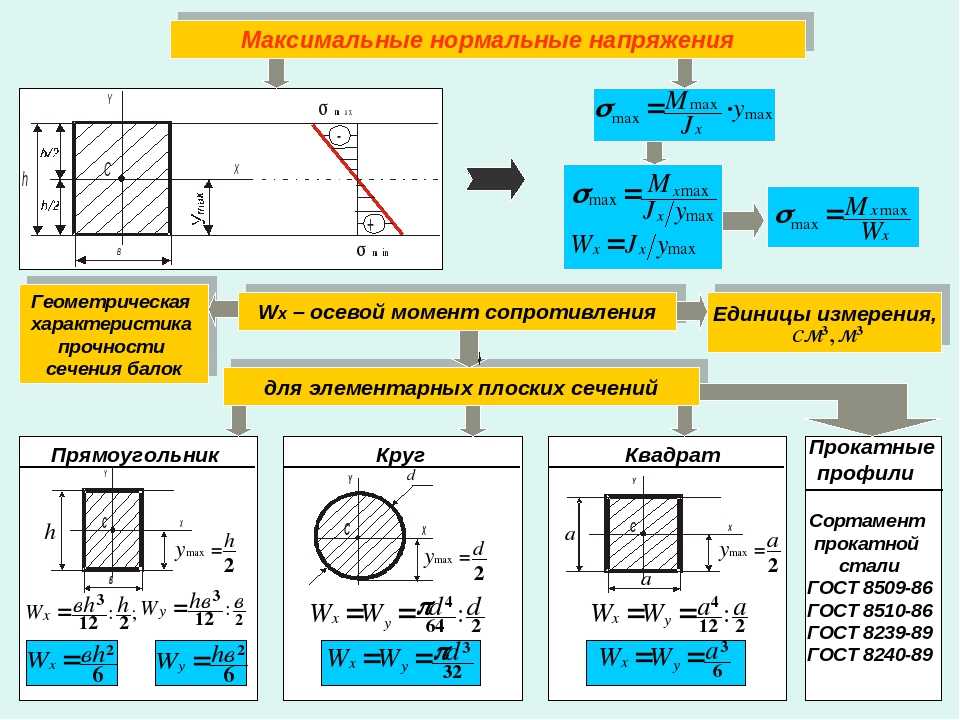
Как правило, в случае металлического бруса перекрытия, расчётную схему заменяют балкой, лежащей на двух шарнирных опорах. В этих опорах возникают реакции сопротивления, у которых необходимо определить их условия:
Когда реакции определены, балку разбивают на участки по опорам. Первый участок находится от одного конца балки до опоры, второй участок располагается между опорами, третий за последней опорой и так далее. Необходимо знать, что если на одном участке имеется точка изменения нагрузки, то её нужно выделить в отдельный участок.
После того, как участки определены, строятся эпюры поперечных сил и изгибающий моментов, и определяется нагруженный участок. Далее, вычисляется осевой момент сопротивления сечения:
По вычисленному параметру производят выбор номера двутавра из сортамента. На этом расчёт балки считается оконченным.
Онлайн
Рассчитывать металлическую балку и производить её выбор вручную довольно трудоёмко и занимает время, которое не всегда можно выделить занятому человеку.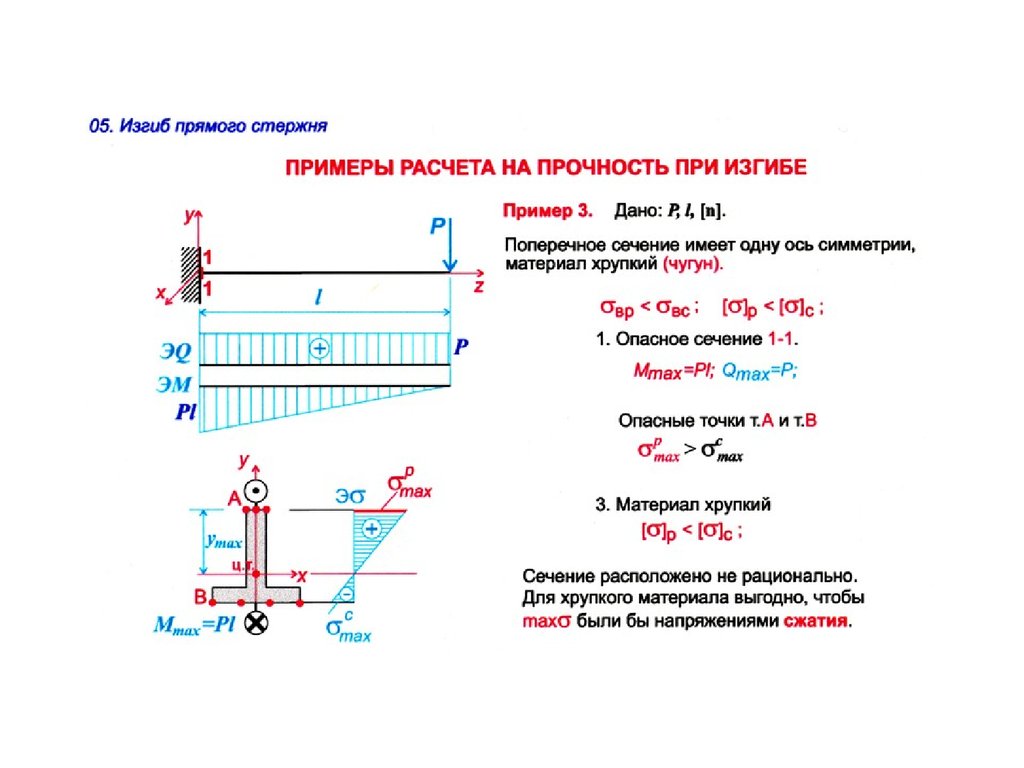
Поэтому, стоит довериться расчётам профессионалов.
Но, если заказчик строительства сомневается в экономической целесообразности произведённого строителями расчёта, можно произвести быстрый автоматический расчёт при помощи сайтов, предлагающих данный товар.
Одним из примеров такого калькулятора может быть портал http://svoydomtoday.ru/building-onlayn-calculators/111-raschet-metallicheskoy-balki-perekritiya.html, который предлагает, находясь на сайте, рассчитать расход материала и выбрать балку из сортамента.
Данный калькулятор требует введения следующих исходных данных:
- Сначала нужно ввести условия эксплуатации металлической балки.
- После этого характеристики предварительно выбранной металлической балки.
- Указать нормативную и расчётную нагрузку на балку и произвести расчёт.
В результате, получается минимально возможный при заданных условиях момент сопротивления балки. Из полученного момента можно выбрать балку по таблице сортамента.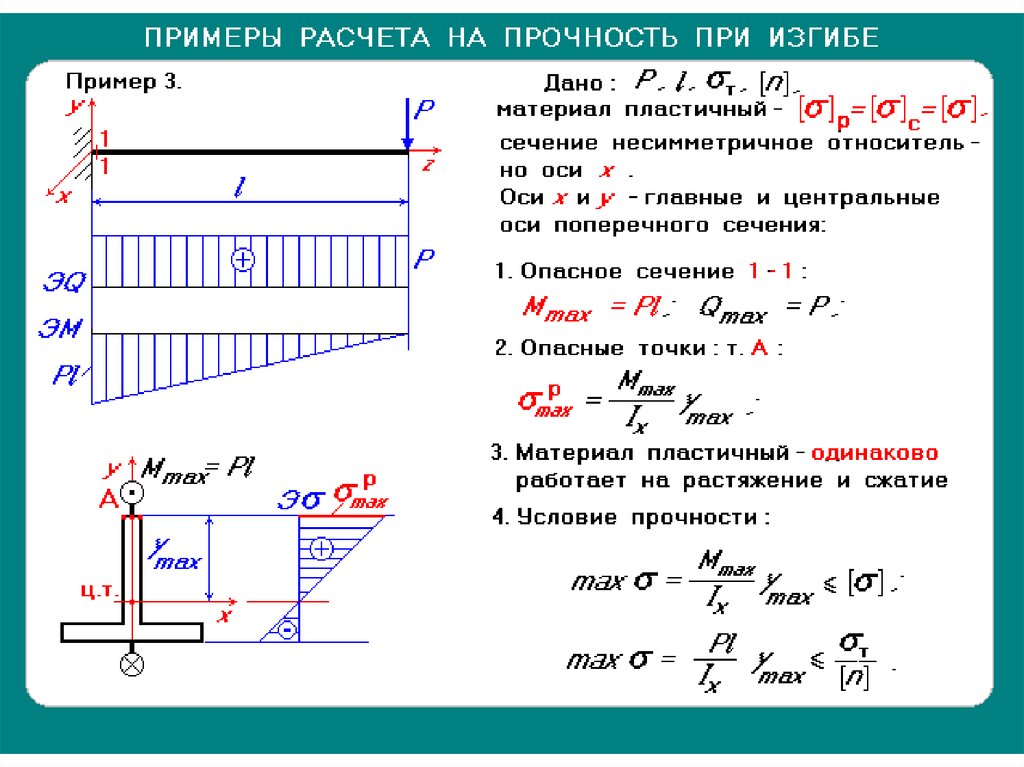
Так же определяется минимально допустимый момент инерции, по которому можно выбрать номер профиля из сортамента. Если для строительства в первую очередь важно не допустить прогиб балки, тогда стоит выбирать балку исходя из полученного момента инерции.
Пример расчета
Металлической балки перекрытия:
Расчет несущей способности:
- Чтобы рассчитать несущую способность одной балки нужно из таблицы сортамента выбрать момент осевого сопротивления и по формуле вычислить максимально допустимый изгибающий момент:
- Отсюда можно вычислить максимально допустимую равнораспределённую нагрузку на однопролётную балку.
Расчет сечения металлических балок:
- Для расчёта необходимого сечения металлической балки можно воспользоваться формулой расчёта момента сопротивления сечения.
- После вычисления результата, определить площадь сечения нужно по сортаменту фасонного профиля, выбрав при этом номер двутавра с ближайшим большим значением момента сопротивления.
При расчёте металлической балки пролёта необходимо отнестись ко всему ответственно и внимательно, потому что от расчёта зависит срок эксплуатации здания и его возможная нагрузка. Здания, построенные по ошибочным расчётам, могут разрушиться в любой момент, унеся за собой много жизней.
Статья была полезна?
0,00 (оценок: 0)
Расчет балки на изгиб — Favorit-TK.ru
Рассчитывать балку на изгиб можно несколькими вариантами:1. Расчет максимальной нагрузки, которую она выдержит
2. Подбор сечения этой балки
3. Расчет по максимальным допустимым напряжениям (для проверки)
Давайте рассмотрим общий принцип подбора сечения балки на двух опорах загруженной равномерно распределенной нагрузкой или сосредоточенной силой.
Для начала, вам необходимо будет найти точку (сечение), в которой будет максимальный момент.
Это зависит от опирания балки или же ее заделки. Снизу приведены эпюры изгибающих моментов для схем, которые встречаются чаще всего.
После нахождения изгибающего момента мы должны найти момент сопротивления Wx этого сечения по формуле приведенной в таблице:
Далее, при делении максимального изгибающего момента на момент сопротивления в данном сечении, мы получаем максимальное напряжение в балке и это напряжение мы должны сравнить с напряжением, которое вообще сможет выдержать наша балка из заданного материала.
Для пластичных материалов (сталь, алюминий и т.п.) максимальное напряжение будет равно пределу текучести материала, а для хрупких (чугун) – пределу прочности. Предел текучести и предел прочности мы можем найти по таблицам ниже.
1. Вы хотите проверить, выдержит ли вас двутавр №10 (сталь Ст3сп5) длиной 2 метра жестко заделанного в стену, если вы на нем повисните. Ваша масса пусть будет 90 кг.
Для начала нам необходимо выбрать расчетную схему.
На данной схеме видно, что максимальный момент будет в заделке, а поскольку наш двутавр имеет одинаковое сечение по всей длине, то и максимальное напряжение будет в заделке.
Давайте найдем его:
P = m * g = 90 * 10 = 900 Н = 0.9 кН
М = P * l = 0.9 кН * 2 м = 1.8 кН*м
По таблице сортамента двутавров находим момент сопротивления двутавра №10.
Он будет равен 39.7 см3. Переведем в кубические метры и получим 0.0000397 м3.
Далее по формуле находим максимальные напряжения, которые у нас возникают в балке.
б = М / W = 1.8 кН/м / 0.0000397 м3 = 45340 кН/м2 = 45.34 МПа
После того, как мы нашли максимальное напряжение, которое возникает в балке, то мы его может сравнить с максимально допустимым напряжением равным пределу текучести стали Ст3сп5 – 245 МПа.
45.34 МПа < 245 МПа – верно, значит данный двутавр выдержит массу 90 кг.
2. Поскольку у нас получился довольно-таки большой запас, то решим вторую задачу, в которой найдем максимально возможную массу, которую выдержит все тот же двутавр №10 длиной 2 метра.
Если мы хотим найти максимальную массу, то значения предела текучести и напряжения, которое будет возникать в балке, мы должны приравнять (б=245 Мпа = 245 000 кН*м2).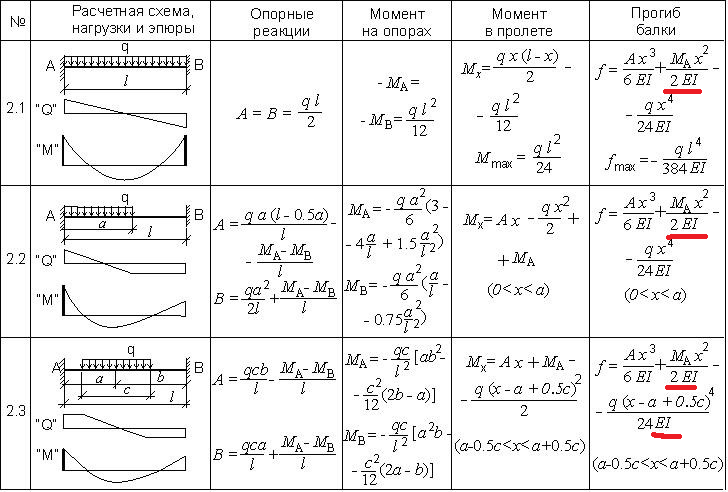
Далее по формуле б = М / W, находим максимальный момент.
М = б * W = 245 000 * 0.0000397 = 9.73 кН * м
Тогда по формуле M = P * L найдем P:
P = 9,73 кН/м / 2м = 4,87 кН = 487 кг
Итак, максимальная масса, которую выдержит двутавр №10 – 487 кг. Число это грубое, поскольку для простоты расчета мы не учитывали различные коэффициенты запаса, поэтому, чтобы подстраховаться, возьмите некий двукратный запас по прочности.
Онлайн Калькулятор | напряжение изгиба
Получить помощь
{CalQlata © 01.01.20}
Напряжение упругого изгиба в балках
Этот калькулятор основан на формуле упругого напряжения; σ/y = M/I = E/R
и поэтому предполагает, что ни один из материалов не подвергается пластической деформации.
Введите известные свойства:
| Свойство: | Входные данные | Выходные данные |
|---|---|---|
| напряжение @’y’ (σ): | ||
| нейтральная ось к внешнему слою (y): | ||
| изгибающий момент (М): | ||
| второй момент площади (I): | ||
| Модуль упругости при растяжении (E): | ||
| радиус изгиба на нейтральной оси (R): |
Напряжение изгиба пластика в балках
Этот калькулятор определяет величину пластической деформации в любой точке по длине нагруженной балки.
Предполагается, что сила приложена в середине длины балки (наихудший сценарий).
Введите известные свойства:
| Ввод: | Данные | Выход @ ‘x’: | Данные |
|---|---|---|---|
| расстояние до ‘Mₓ’ (x): | расстояние от нейтральной оси (y): | ||
| приложенная нагрузка на ½L (F): | изгибающий момент (М): | ||
| длина балки (L): | упругий изгибающий момент (Мₑ): | ||
| толщина балки (т): | пластиковый изгибающий момент (Mₚ): | ||
| Предел текучести (σy): | общий [проверочный] момент (Mₜ): |
Справка
Эти калькуляторы напряжения на изгиб доступны из любого места на веб-сайте с помощью сочетания клавиш; «Альт» + «н».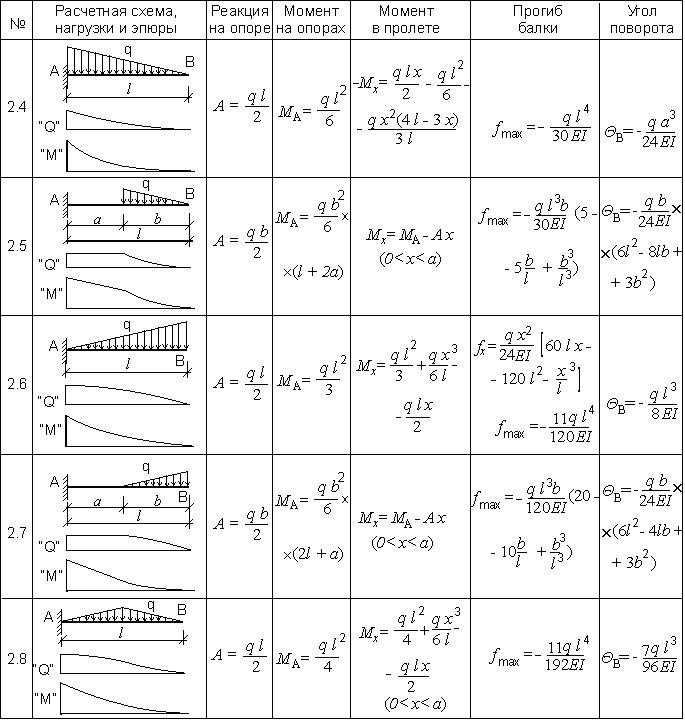
Кнопка « Reset » очищает все расчеты на странице и переустанавливает значения по умолчанию (эта кнопка может не реагировать в браузере FireFox).
Сброс также можно выполнить, нажав клавишу «F5».
Кнопка Calculate вычисляет только соответствующую опцию.
Наведите курсор на символы соответствующего описания.
Напряжение
Прямая балка (или пластина), изогнутая, как показано на изображениях выше, образует нейтральную ось в центре области [поперечного сечения].
Напряжение вдоль этой нейтральной оси [теоретически] равно нулю, если к балке не применяется одновременное осевое растяжение или сжатие.
Напряжение вне нейтральной оси является растягивающим, а напряжение внутри нейтральной оси — сжимающим.
Elastic Calculator
Этот метод расчета предполагает, что вся толщина материала упруго деформируется и что наибольшее напряжение возникает в плоскости материала, наиболее удаленной от нейтральной оси; ‘у’.
Расчет эластичности включает три группы свойств в зависимости от цвета: напряжение, раздел и форма.
Вам нужны оба свойства одной группы и одно из любого другого, чтобы вычислить свойство неизвестной группы.
Вы будете уведомлены, если вы предоставили недостаточно данных для расчета.
Калькулятор пластичности
Расчет пластичности определяет плоскость предела текучести (‘y’) через балку, нагруженную в середине ее длины.
Изгибающий момент (M), возникающий в результате действия нагрузки (F) и расстояния (x), включает упругую составляющую (Mₑ) и пластическую составляющую (Mₚ), которые вместе составляют общий момент (M).
Если зоны [растягивающего и сжимающего] пластического напряжения соприкасаются (y=0), вы создаете пластический шарнир, а если они перекрываются (y<0), вы рискуете сломать балку.
Если y больше t/2, все сечение балки упруго деформировано; в вашей балке не произошло пластической деформации.
Загружаемая версия
Полные загружаемые версии этих калькуляторов доступны на этом веб-сайте по адресу; Основы инженерии и пластическое напряжение.
Вернуться к началу страницы
Калькулятор напряжения при изгибе | Рассчитать напряжение при изгибе
✖Изгибающий момент — это реакция, возникающая в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента.ⓘ Изгибающий момент [M b ] | Грамм-сила СантиметрКилограмм-сила-метрКилоньютон-метрМикроньютон-метрМиллиньютон-метрНьютон-метрНьютон-миллиметрфунт-футфунт-дюймфунт-сила-футтонна-сила (длинная) метр-тонна-сила (метрическая) метр-тонна-сила (короткая) метр | +10% -10% | |
✖Расстояние от нейтральной оси определяется как расстояние от оси в поперечном сечении балки или вала, вдоль которого отсутствуют продольные напряжения или деформации .ⓘ Расстояние от нейтральной оси [y] | AlnAngstromArpentАстрономическая единица АттометрAU длиныЯчменное зерноМиллиард световых летBohr RadiusCable (International)Cable (UK)Cable (US)CalibreCentimeterChainCubit (Greek)Cubit (Long)Cubit (UK)EarthCubit (UK)DecimeterDecimeterDecimeter Decimeter from Moon SunEarth Equatorial RadiusEarth Polar RadiusElectron Radius (Classical)EllExameterFamnFathomFemtometerFermiFinger (Ткань)FingerbreadthFootFoot (US Survey)FurlongGigameterHandHandbreadthHectometerInchKenKilometerKiloparsekKiloyardLeagueLeague (Statute)Light YearLinkMegameterMegaparsecMeterMironicMileMicrometer Опрос)МиллиметрМиллион Светового ГодаГвоздь (Ткань)НанометрМорская Лига (внутренняя)Морская Лига ВеликобританииМорская Миля (Международная) Морская миля (Великобритания)ПарсекОкуньПетаметрПикаПикометрПланк ДлинаТочкаПолюсКварталТростник (Длинный)РодРоман АктусВеревкаРусский АрчинПротяженность (Ткань)Солнце РадиусТераметрТвипВара КастелланаВара КонукераВара Де ТареаЯрдЙоктометрЙоттаметрЗептометрЗеттаметр | +10% -10% | |
✖Момент инерции – это мера сопротивления тела угловому ускорению относительно заданной оси. Грамм Квадратный СантиметрГрамм Квадратный МиллиметрКилограмм Квадратный СантиметрКилограмм Квадратный МетрКилограмм Квадратный МиллиметрКилограмм-Сила Метр Квадратная СекундаУнция Квадратный ДюймУнция-Сила Дюйм Квадратный СекундаФунт Квадратный ФутФунт Квадратный ДюймФунт-Сила Фут Квадрат СекундаФунт-Сила Дюйм Квадрат СекундаСлаг Квадратный Фут | +10% -10% |
✖Напряжение при изгибе — это нормальное напряжение, возникающее в точке тела, подверженного нагрузкам, вызывающим его изгиб.ⓘ Напряжение при изгибе [σ b ] | ⎘ Копировать |
👎
Формула
Перезагрузить
👍
Решение напряжения изгиба
ШАГ 0: Сводка предварительного расчета
ШАГ 1: Преобразование входных данных в базовые единицы
Изгибающий момент: 52 ньютон-метра —> 52 ньютон-метра Преобразование не требуется
Расстояние от нейтральной оси: 4 миллиметра —> 0,004 метр (проверьте преобразование здесь)
ШАГ 2: Вычислите формулу
ШАГ 3: Преобразуйте результат в единицу измерения
Пакалей —> > Преобразование не требуется
< 16 калькуляторов стрессаНапряжение из-за ударной нагрузки
Идти Напряжение сдвига = Вес груза*(1+sqrt(1+((2*Площадь поперечного сечения*Напряжение при изгибе*Высота, на которую падает груз)/(Вес груза*Длина сварного шва))))/Площадь поперечного сечения
Термическое напряжение в коническом стержне
Идти Напряжение сдвига = (4*нагрузка*длина сварного шва)/(pi*диаметр большего конца*диаметр меньшего конца*напряжение при изгибе)
Напряжение сдвига балки
Идти Напряжение сдвига = (Общая сила сдвига * Первый момент площади) / (Момент инерции * Толщина материала)
Напряжение сдвига
Идти Напряжение сдвига = (сила сдвига * первый момент площади) / (момент инерции * толщина материала)
Тепловая нагрузка
Идти Напряжение сдвига = Коэффициент теплового расширения*Напряжение при изгибе*Изменение температуры
Напряжение сдвига в двойном параллельном угловом сварном шве
Идти Напряжение сдвига = нагрузка на параллельный угловой шов/(0,707*длина сварного шва*половина сварного шва)
Напряжение изгиба
Идти Напряжение при изгибе = Изгибающий момент * Расстояние от нейтральной оси / Момент инерции
Напряжение сдвига при кручении
Идти Напряжение сдвига = Крутящий момент * Радиус вала / Полярный момент инерции
Коэффициент запаса прочности при предельном напряжении и рабочем напряжении
Идти Коэффициент запаса прочности = напряжение разрушения/рабочее напряжение
Прямое напряжение
Идти Прямое напряжение = осевая нагрузка/площадь поперечного сечения
Касательное напряжение круглой балки
Идти Напряжение сдвига = 4*сила сдвига/(3*площадь)
Максимальное напряжение сдвига
Идти Напряжение сдвига = 1,5*сила сдвига/площадь
Напряжение сдвига
Идти Касательное напряжение = тангенциальная сила/площадь
Массовое напряжение
Идти Объемное напряжение = нормальная внутренняя сила/площадь
Стресс из-за внезапной нагрузки
Идти Напряжение сдвига = 2*сила/площадь
Стресс из-за постепенной нагрузки
Идти Касательное напряжение = сила/площадь
Формула напряжения изгиба
Напряжение при изгибе = Изгибающий момент * Расстояние от нейтральной оси / Момент инерции
σ b = M b *y/I
Что такое напряжение изгиба?
Напряжение изгиба — это нормальное напряжение, возникающее в точке тела, подвергающегося нагрузкам, вызывающим его изгиб.
Когда нагрузка приложена перпендикулярно длине балки (с двумя опорами на каждом конце), в балке индуцируются изгибающие моменты.
Как рассчитать напряжение изгиба?
Калькулятор напряжения изгиба использует Напряжение изгиба = Изгибающий момент * Расстояние от нейтральной оси/момент инерции для расчета напряжения изгиба. Формула напряжения изгиба определяется как нормальное напряжение, возникающее в точке тела, подверженного нагрузкам, вызывающим его сгибать. Напряжение изгиба обозначается символом σ b .
Как рассчитать напряжение на изгиб с помощью этого онлайн-калькулятора? Чтобы использовать этот онлайн-калькулятор для напряжения изгиба, введите изгибающий момент (M b ) , Расстояние от нейтральной оси (y) и Момент инерции (I) и нажмите кнопку расчета. Вот как можно объяснить расчет напряжения на изгиб с заданными входными значениями -> 0,059429 = 52*0,004/3,5 .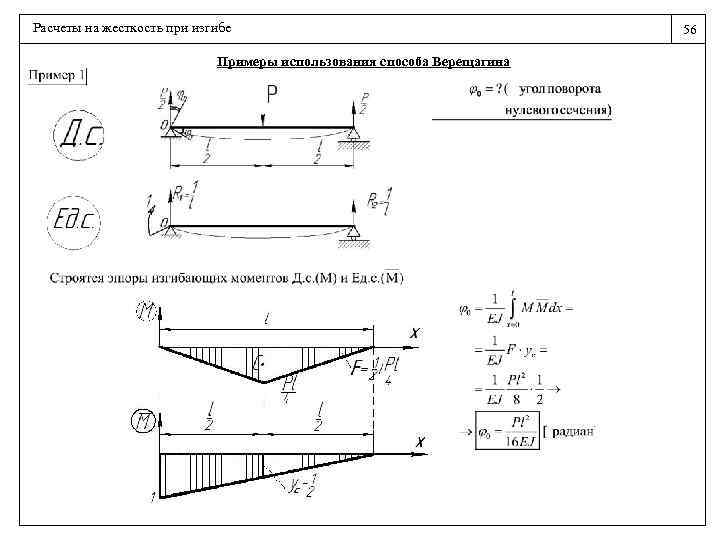
Часто задаваемые вопросы
Что такое напряжение при изгибе?
Формула напряжения при изгибе определяется как нормальное напряжение, возникающее в точке тела, подвергаемого нагрузкам, вызывающим его изгиб, и представляется как σ b = M b *y/I или Напряжение при изгибе = Изгибающий момент*Расстояние от нейтральной оси/момент инерции . Изгибающий момент — это реакция, возникающая в элементе конструкции, когда к элементу прилагается внешняя сила или момент, вызывающий изгиб элемента. Расстояние от нейтральной оси определяется как расстояние от оси в поперечном сечении балки или вал, вдоль которого нет продольных напряжений и деформаций & Момент инерции есть мера сопротивления тела угловому ускорению относительно данной оси.
Как рассчитать напряжение на изгиб?
Формула напряжения при изгибе определяется как нормальное напряжение, возникающее в точке тела, подверженного нагрузкам, вызывающим его изгиб, и рассчитывается по формуле Напряжение при изгибе = Изгибающий момент * Расстояние от нейтральной оси/момент инерции .