Прогиб от сосредоточенной нагрузки: Расчет балки на прогиб — деревянной и металлической, формулы

Расчет балок на прогиб. Максимальный прогиб балки: формула расчета

Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.

Типы

На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.

Деревянные балки

Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.

Допустимый прогиб балки формируется из двух факторов:

• Соответствие прогиба и допустимых значений.
• Возможность эксплуатации здания с учетом прогиба.

Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.

Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.

Расчет балок на прогиб. Алгоритм работы

На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

• Составляется расчетная схема.
• Определяются геометрические характеристики балки.
• Вычисляется максимальную нагрузку на данный элемент.
• В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
• Производится вычисление максимального прогиба.

Как видите, все действия достаточно просты и вполне выполнимы.

Составление расчетной схемы балки

Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.

Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.

Момент инерции

Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. Формула позволяет вычислить эту величину, мы приведем ее немного ниже.

При вычислении момента инерции нужно обращать внимание на то, что размер этой характеристики зависит от того, какова ориентация элемента в пространстве. При этом наблюдается обратно пропорциональная зависимость между моментом инерции и величиной прогиба. Чем меньше значение момента инерции, тем больше будет значение прогиба и наоборот. Эту зависимость достаточно легко отследить на практике. Каждый человек знает, что доска, положенная на ребро, прогибается гораздо меньше, чем аналогичная доска, находящаяся в нормальном положении.

Подсчет момента инерции для балки с прямоугольным сечением производится по формуле:

J=b*h^3/12, где:

b – ширина сечения;

h – высота сечения балки.

Вычисления максимального уровня нагрузки

Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. В этом случае нужный нам коэффициент составит 0,6. 3/48*E*J, где:

F – сила давления на брус.

Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.

Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.

Двутавровая балка

Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.

Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.

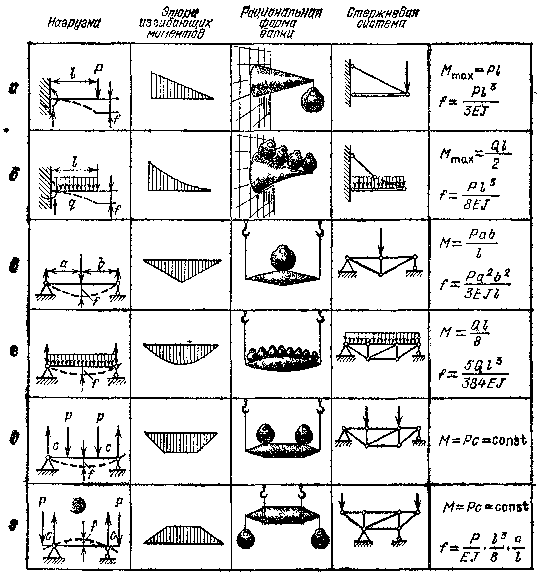
Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:

• Балка однопролетного типа с равномерно распределенной нагрузкой.
• Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
• Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
• Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
• Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
• Консоль с жесткой заделкой и сосредоточенной силой.

Металлические балки

Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.

Расчет максимального прогиба для балки с двумя опорами

В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.

Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости.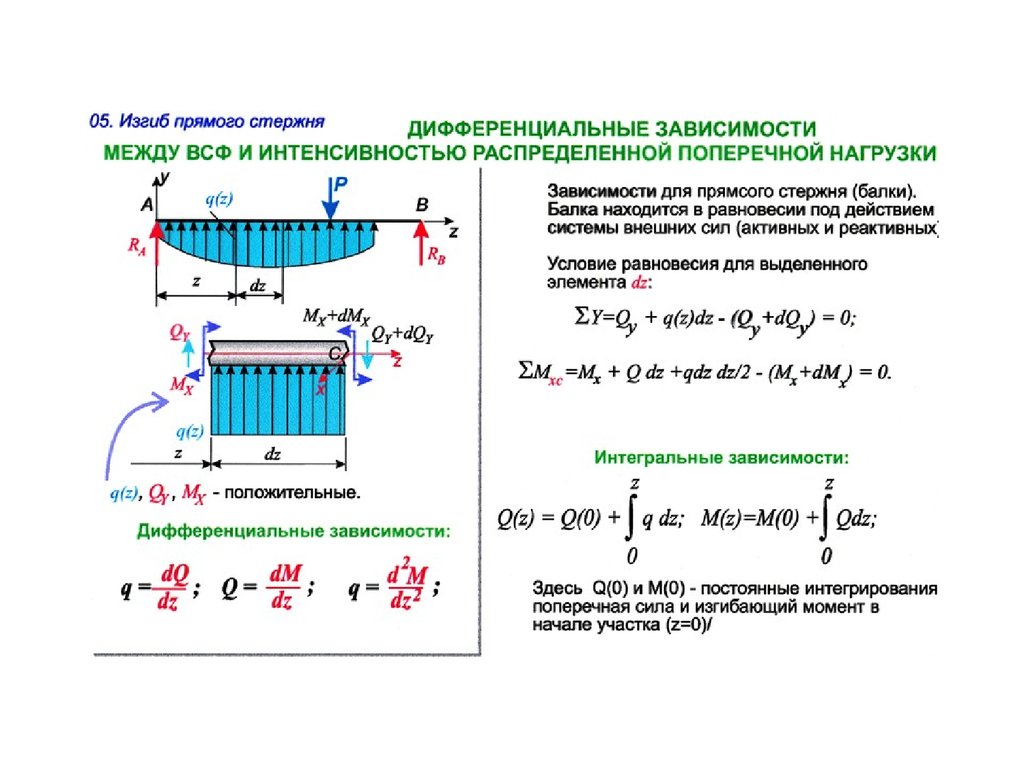 Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.

Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a

F(z)=(P*a²*b²)/(6E*J*l)*(2*z/a+z/b-z³/a²*b)

Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l

f(z)=(-P*a²*b²)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)³/a+b²), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.

В случае балки с двумя опорами момент инерции вычисляется следующим образом:

J=b₁h₁³/12, где b₁ и h₁ – значения ширины и высоты сечения используемой балки соответственно.

Заключение

В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.

Прогиб балки | Полный обзор и важные взаимосвязи — Lambda Geeks

Содержание: Отклонение луча

• Определение кривой прогиба
• Определение угла отклонения
• Определение отклонения
• Граничные условия прогиба балки
• Взаимосвязь между силами нагрузки, поперечной силой, изгибающим моментом, наклоном и прогибом
• Уравнения и соотношения изгиба балки
• Таблица прогиба балки и формулы для стандартных случаев нагружения
• Отклонение и наклон балки с примерами Случай I: выступающая балка
• Случай II: определение максимального прогиба балки без опоры с точечной нагрузкой в ​​центре.
• Случай III: определение максимального прогиба балки с простой опорой при сосредоточенной точечной нагрузке на расстоянии «а» от опоры А.
• Метод двойной интеграции
• Процедура метода двойного интегрирования
• Метод двойного интегрирования для нахождения прогиба балки на примере консольная балка с равномерно распределенной нагрузкой
• Метод двойного интегрирования для треугольной нагрузки

In инженерия, отклонение — степень смещения элемента конструкции под действием нагрузки (из-за его деформации). Это может относиться к углу или расстоянию. Расстояние прогиба элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон отклоненной формы элемента под этой нагрузкой. Существуют стандартные формулы для прогиба общих конфигураций балок и загружений в отдельных местах. В противном случае используются такие методы, как виртуальная работа, прямая интеграция, метод Кастильяно, метод Маколея или метод прямой жесткости.

Кривая отклонения

Когда балки нагружены поперечными или продольными нагрузками, начальная прямая продольная ось деформируется в кривую, известную как упругая кривая балки или кривая прогиба. Кривая прогиба — это деформированная ось выбранной балки.

Угол отклонения

Наклон можно определить как угол между продольной осью балки и касательной, построенной к кривой деформации балки в любом желаемом месте. Это угол поворота нейтральной оси луча. Измеряется в радианах.

прогиб

Отклонение — это поступление или смещение любой точки на оси балки, измеренное в направлении y от начальной прямой продольной оси до точки на кривой прогиба балки. Измеряется в миллиметрах. Прогиб представляет собой отклонение прямой продольной оси из-за поперечной нагрузки. Напротив, изгиб балки представляет собой отклонение начальной прямой продольной оси из-за осевой сжимающей нагрузки. Обычно он представлен как ‘у»

Если балка изгибается по дуге окружности, это называется изгибом по окружности; в противном случае это называется некруглым изгибом. Предположим, что на призматическую балку действует переменный изгибающий момент. В этом случае это приводит к изгибу некруглого типа, а если он подвергается постоянному изгибающему моменту, приводит к круговому изгибу балки.

Граничные условия прогиба балки

1. y равен нулю на опоре штифта или ролика.
2. y равен нулю на встроенной или консольной опоре.
3. Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:

• 1. y для левой части должен быть равен y для правой части.
• 2. Уклон левого участка должен быть равен уклону правого участка.

Взаимосвязь между силами нагрузки, поперечной силой, изгибающим моментом, наклоном и прогибом

Рассмотрим горизонтальную балку AB в ненагруженном состоянии. Если AB отклоняется под нагрузкой, новое положение будет A’B ‘.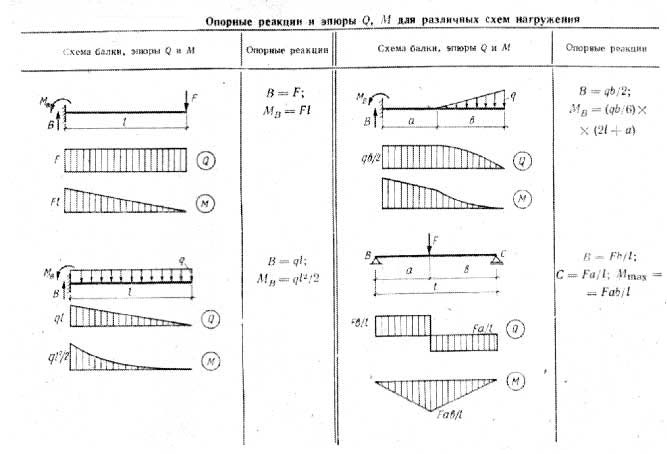 4}

Таблица прогиба балки и формулы для стандартных случаев нагружения:

• Максимальный наклон и прогиб консольной балки происходит на свободном конце балки, в то время как на зажатом конце консольной балки не наблюдается наклона или прогиба.
•  Для балки без опоры с симметричными условиями нагружения максимальный прогиб может быть найден в середине пролета. Максимальный уклон наблюдается у опор балки. Максимальный прогиб возникает при нулевом уклоне.

https://www.pinterest.it/pin/711076228644344940/Наклон и прогиб для балки с простой опорой при различных условиях нагрузки

Прогиб и наклон балки с примерами

Случай I: Свисающая балка

Рассмотрим выступающую стальную балку, несущую сосредоточенную нагрузку P = 50 кН на конце C.

Для выступающей балки: (a) определить наклон и максимальное отклонение, (b) оценить наклон на расстоянии 7 м от точки A и максимальное отклонение по заданным данным. {- 3} \; m = -8.93 \; мм

Метод двойной интеграции

Если жесткость на изгиб EI постоянна, а момент является функцией расстояния x, интегрирование EI (d² y) / (dx² ) = M даст наклон

EI \ frac {dy} {dx} = \ int M dx + C_1

EIy = \ int \ int Mdxdx + C_1x + C_2

где С₁ и C₂ являются константами. Они определяются с помощью граничных условий или других условий на балке. Вышеприведенное уравнение дает отклонение y как функцию от x; это называется уравнением кривой упругости или деформации.

Вышеупомянутый метод анализа прогиба и наклона балки известен как метод двойного интегрирования для расчета прогибов балки. Если изгибающий момент и жесткость на изгиб являются непрерывными функциями x, одно дифференциальное уравнение может быть записано для всей балки. Для статически определенной балки существует две опорные реакции; каждая из них накладывает определенный набор ограничений на наклон упругой кривой. Эти ограничения называются граничными условиями и используются для определения двух постоянных интегрирования.

Граничные условия метода двойного интегрирования

1. y равен нулю на опоре штифта или ролика.
2. y равен нулю на встроенной или консольной опоре.
3. Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:

• 1. y для левой части должен быть равен y для правой части.
• 2. Уклон левого участка должен быть равен уклону правого участка.

Процедура метода двойного интегрирования

• Нарисуйте упругую кривую балки и примите во внимание все необходимые граничные условия, такие как y равен нулю на опоре пальца или ролика и y равен нулю на встроенной или консольной опоре.
• Определите изгибающий момент M на произвольном расстоянии x от опоры методом сечений. Используйте соответствующие правила изгибающего момента при нахождении момента М. для разрывного момента, уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке между сегментами: 1. y для левой части должно быть равно y для правой секции. 2. Уклон левого участка должен быть равен уклону правого участка.
• Проинтегрируйте уравнение дважды, чтобы получить наклон и прогиб, и не забудьте найти постоянное интегрирование для каждого сечения с использованием граничных условий.

Примеры метода двойного интегрирования для определения прогиба балки

Рассмотрим консольную балку длиной L, показанную на рисунке ниже, с равномерно распределенной нагрузкой. В консольной балке один конец зафиксирован, а другой конец может свободно двигаться. Мы выведем уравнение для наклона и изгибающего момента для этой балки, используя метод двойного интегрирования. 4}{120}

у = -0.01758 \; м

Чтобы узнать о прочности материала (нажмите сюда)и метод площади момента Открыть.

Формула прогиба балок с диаграммами для всех условий.

15.05.2021 19.07.2020 от Вики

когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что это отклонение балок . Максимальный прогиб балок происходит там, где уклон равен нулю.

Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.

Общие и стандартные уравнения для отклонения балок приведены ниже:

Где,
M = изгибающий момент,
E = Модуль Янга,
I = Moment Inertia.

Продукт E. I известен как жесткость на изгиб .

Существует много типов балок, и для этих разных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.

1. Свободно опертая балка с центральной точечной нагрузкой:

Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки при °C. Прогиб при точка C будет:

2. Свободно опертая балка с внецентренной точечной нагрузкой:

Свободно опертая балка AB длиной2 l2 несет нагрузку2 l 90 в центральной точке.0009 C как показано на рис. Отклонение балки определяется следующим образом:

Поскольку b > a , поэтому максимальное отклонение происходит в CB , а его расстояние от B определяется как:

, а максимальное отклонение определяется как :

3. Свободно опертая балка с равномерно распределенной нагрузкой :

Свободно опертая балка AB с равномерно распределенной нагрузкой w /единица длины показана на рисунке ,

Максимальное отклонение происходит в средней точке C и определяется как:

4 Постепенно меняющаяся нагрузка:

Свободно поддерживаемая балка из AB длиной l , несущая постепенно изменяющуюся нагрузку от нуля на B до веса на единицу длины на A , показана на рисунке ниже,

Максимальное отклонение луча возникает, когда x = 0,519 L , и его значение определяется как:

5. Консольная луча с точечной нагрузкой на свободном конце:

балка AB длиной l , несущая на свободном конце точечную нагрузку, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:

Максимальный отклонение происходит на свободном конце (когда x = 0 ), и его значение определяется

6. Консольный луч с равномерной распределенной нагрузкой:

99. балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, показана на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением

Максимальное отклонение происходит на свободном конце (когда x = 0), и его значение определяется

, когда консоль частично загружается, как показано на рис. расстояние от фиксированного конца) определяется как:

и максимальное отклонение происходит на B чьи значения определяется

7. Консольный луч с постепенно изменяющейся нагрузкой:

Кантилеверная луча AB длины л . на единицу длины A показан на рис. Прогиб в любом сечении X на расстоянии x от B определяется как

Максимальный прогиб происходит на свободном конце (при x = 0) и его значение определяется как

8.

Неподвижная балка, несущая центральную точечную нагрузку:

Неподвижная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , а его значение определяется формулой

9. Неподвижная балка, несущая внецентренную нагрузку:

загрузить в C , как показано на рис. Прогиб в любом сечении X на расстоянии x от A равен

Максимальное расстояние возникает, когда

и прогиб под нагрузкой при C ,

10. Фиксированная балка, несущая равномерно распределенную нагрузку:

A09 фиксированная балкаAB длиной л , несущий равномерно распределенный груз на единицу длины, как показано на рис. Отражение в любом разделе x при A Расстояние x от A дается

Максимальное отклонение луча происходит в центре луча, и его значение определяется

….

Читайте также : Кривая напряжения и деформации для низкоуглеродистой стали
Также читайте : Анализ тарифов на строительные работы

Нравится:

Нравится Загрузка…

Точечная нагрузка

и равномерная распределенная нагрузка

Являясь лидером рынка наземных опор, мы постоянно учитываем грузоподъемность. При разработке новых продуктов в первую очередь мы думаем о грузоподъемности и связанном с ней коэффициенте прогиба. Конечно, сила, прикладываемая к брекету, имеет много характеристик. Эти характеристики имеют равное количество влияний на результирующий прогиб. Все нагрузки вызывают некоторое отклонение, но распределение этой нагрузки может сильно повлиять на степень отклонения. Этот ресурс покажет, как размещение нагрузки может повлиять на прогиб и общую грузоподъемность. Также будет указано, как планировать это в определенных приложениях.

Существует два основных типа нагрузки, которые наиболее часто используются при определении прогиба опорной скобы: Точечная нагрузка (PL) и Равномерно распределенная нагрузка (UDL).

В следующих примерах будут использоваться опоры с одним закрепленным концом (консольные балки).

Точечная нагрузка

Точечная нагрузка — это сила, приложенная к сосредоточенной точке опоры. Примером может служить человек, стоящий на свободном конце трамплина.

Равномерно распределенная нагрузка

Равномерно распределенная нагрузка — это сила, приложенная равномерно по всей длине опоры. Для наименьшего возможного прогиба эта нагрузка распределяется по всей длине опоры. Примером может служить транспортировочный ящик на вилочном погрузчике.

В строительстве UDL предпочтительнее точечных нагрузок. При равномерно распределенной нагрузке вероятность изгиба и/или разрушения опоры значительно снижается по сравнению с ситуацией точечной нагрузки. Сосредоточенные нагрузки чаще вызывают изгиб. Ниже приведены изображения реального эксперимента с обоими упомянутыми типами нагрузки, а также с размещением нагрузки, показывающие, как эти факторы влияют на прогиб.

Консоль, используемая в этом эксперименте, представляет собой простую металлическую линейку, прикрепленную одним концом к опорной конструкции. Магниты с равномерным весом использовались для обозначения типов нагрузки на линейке. Это простой способ показать визуальные изменения прогиба.

PL — Свободный конец

Проиллюстрированное размещение точечной нагрузки на свободном конце кантилевера вызовет наибольшее отклонение из всех показанных конфигураций. Не так много случаев, когда вы хотели бы поместить свой тяжелый груз на самый дальний конец вашей опоры. Примером того, когда это может произойти, может быть человек, наклонившийся или сидящий на краю нависающей барной стойки.

PL — Средний

Как показано на этом рисунке, точечная нагрузка, приложенная на половине расстояния от опоры, фактически приводит к приблизительно ⅓ максимального прогиба в результате точечной нагрузки на свободный конец. Это показывает, что по мере того, как вы приближаете PL к фиксированному концу, отклонение уменьшается экспоненциально.

PL — Фиксированный конец

Размещение точечной нагрузки в непосредственной близости от фиксированного конца опоры приведет к значительному уменьшению максимального прогиба. С конструктивной точки зрения это самое безопасное место для применения PL к консольной опоре.

UDL — по всей длине

Как показано выше, равномерно распределенная нагрузка при том же весе показанного ранее PL, равномерно распределенная по всей длине опоры, приведет примерно к ⅜ прогиба PL в свободном конец.

Сравнение размещения нагрузки

При разработке распорок и опор для поддержки каменных стоек, рабочих мест и других плавающих поверхностей мы проводим испытания несущей способности распорок, чтобы убедиться, что они будут эффективно и надежно поддерживать необходимый вес. Чтобы помочь нашим клиентам в выборе распорок для своих проектов, мы ссылаемся на грузоподъемность, полученную в результате этих испытаний. Говоря о грузоподъемности любого продукта Federal Brace, следует отметить, что грузоподъемность основана на использовании с равномерно распределенной нагрузкой.