Натяжка для тросов: Талрепы для натяжки троса DIN1480 купить в Москве не дорого с доставкой, цена, фото, гарантия производителя.

Натяжка проводов и тросов (канатов) ВЛ | Монтаж электрических установок | Архивы

• 6кВ
• 0,4кВ
• кабель
• монтаж
• ВЛ
• подстанция
• 10кВ
• шины и провод
• заземление

Содержание материала

• Монтаж электрических установок
• Маркировка цепей в электрических схемах
• Управление электромонтажным производством
• СПУ
• Организация и подготовка электромонтажных работ
• Производство электромонтажных работ
• Материально техническое-обеспечение бригады
• Бригадный подряд, оплата труда
• Научная организация труда, нормирование
• Материалы для электромонтажных работ
• Электромонтажные изделия
• Опрессовка жил проводов и кабелей
• Сварка жил проводов и кабелей, контактных соединений шин
• Пайка жил проводов и кабелей, контактных соединений шин
• Соединение алюминия с медью, сплав АВ—Е
• Контактные соединения и присоединения к контактным выводам электрооборудования
• Виды сварок в электромонтажном производстве
• Сварка шин в электромонтажном производстве
• Сварка алюминиевых гибких шин
• Сварка стальных заземляющих проводников
• Сварка пластмассовых оболочек кабеля
• Назначение заземляющих устройств
• Заземляющие устройства
• Монтаж заземляющих устройств
• Монтаж распределительных устройств до 1 кВ
• Аппараты распределительных устройств
• Шинопроводы напряжением до 1 кВ
• Монтаж шинопроводов до 1 кВ
• Оборудование распределительных устройств и подстанций выше 1 кВ
• КТП
• ГПП
• ЗРУ
• Силовые выключатели на 6—10 кВ
• Выключатели нагрузки
• Разъединители, предохранители 6, 10 кВ
• Разрядники, измерительные трансформаторы 6, 10 кВ
• Конденсаторы, фильтры, изоляторы 6, 10 кВ
• Монтаж распределительных устройств и подстанций
• Монтаж РЗА и вторичных цепей
• Монтаж токопроводов напряжением выше 1 кВ
• Осветительные установки
• Монтаж осветительных установок
• Устройства для обслуживания светильников, освещение строительных площадок
• Провода и кабели, применяемые в электропроводках
• Общие требования к монтажу электропроводок
• Открытые электропроводки плоскими проводами
• Открытые электропроводки незащищенными изолированными проводами
• Открытые тросовые электропроводки
• Открытые электропроводки защищенными проводами и кабелями
• Скрытые электропроводки
• Электропроводки на лотках и в коробах
• Выбор труб для электропроводок в трубах
• Правила монтажа труб для электропроводок
• Монтаж труб для электропроводок
• Монтаж проводов в трубах
• Электропроводки за подвесными потолками, на чердаках по станкам механизмам и наружные
• Кабельные линии
• Подготовка к прокладке кабелей внутри и вне зданий
• Прокладка кабелей в траншее
• Прокладка кабелей в производственных помещениях
• Прокладка кабелей в кабельных сооружениях
• Прокладка кабеля при низких температурах
• Маркировка кабельных линий после монтажа
• Соединение и оконцевание силовых кабелей
• Удаление изоляции и заполнителей кабеля
• Соединение и оконцевание кабелей с пластмассовом изоляцией
• Соединение кабелей с бумажной изоляцией в свинцовых муфтах
• Оконцевание и монтаж кабелей и муфт
• Подготовительные работы при монтаже ВЛ
• Определения, габариты ВЛ
• Котлованы, фундаменты, опоры ВЛ
• Провода и изоляторы ВЛ
• Защита проводов ВЛ от вибрации (пляски)
• Установка опор ВЛ
• Монтаж изоляторов ВЛ
• Монтаж проводов и тросов ВЛ
• Натяжка проводов и тросов (канатов) ВЛ
• Закрепление проводов и канатов ВЛ
• Заземление опор и траверс ВЛ
• Проверка качества работ при сдаче электроустановок в эксплуатацию
• Сдача электроустановок в эксплуатацию
• Техника безопасности при производстве электромонтажных работ
• Сокращения и использованная литература

Страница 77 из 83

Раскатку проводов и тросов производят, как правило, одновременно. Провес провода, натянутого между двумя опорами (стрела провеса), зависит от массы провода и усилия, с которым он натянут (тяжения провода). Стрелы провеса для данной линии при данных температурах воздуха указывают в проекте.
При натяжке проводов и тросов должны выполняться следующие требования [2]: при визировании проводов и канатов стрелы провеса должны быть установлены согласно рабочим чертежам по монтажным таблицам или кривым в соответствии с температурой провода или каната во время монтажа. При этом фактическая стрела провеса провода или каната не должна отличаться от проектной величины более чем на ±5 % при условии соблюдения требуемых габаритов до земли и пересекаемых объектов; разрегулировка проводов различных фаз и канатов относительно друг друга должна составлять не более 10 % проектной величины стрелы провеса провода или каната; разрегулировка проводов в расщепленной фазе должна быть не более 20 % для ВЛ 330—500 кВ и 10 % для ВЛ 750 кВ; угол разворота проводов в фазе должен быть не более 10°; визирование проводов и канатов ВЛ напряжением выше 1 кВ до 750 кВ включительно следует проводить в пролетах, расположенных в каждой трети анкерного участка при его длине более 3 км.

При длине анкерного участка менее 3 км визирование разрешается производить в двух пролетах: наиболее отдаленном и наиболее близком от тягового механизма; отклонение поддерживающих гирлянд вдоль ВЛ от вертикали не должно превышать, мм: 50 — для ВЛ 35 кВ, 100 — для ВЛ 110 кВ, 150 — для ВЛ 150 кВ и 200 — для ВЛ 220 — 750 кВ.
Натяжку проводов ВЛ до 10 кВ производят лебедкой при помощи полиспастов или автомашиной, а линий 35 кВ и выше с большими пролетами — трактором. Провод с алюминиевыми жилами зажимают в монтажном зажиме (рис. 13.38). Натяжку проводов и тросов производят между анкерными опорами.
На линиях 35 кВ и выше обычно производят натяжку нескольких проводов (двух, трех и более). На рис. 13.39 показано приспособление для одновременного натягивания трех проводов.

Рис. 13 38. Зажим монтажный клиновой; 1 — корпус; 2 — планка; 3 — клин

Рис 13 39 Приспособление для одновременного натягивания трех проводов
Оргэнергострой Минэнерго разработал прогрессивный способ монтажа проводов под тяжением с помощью комплекта специальных механизмов и приспособлений.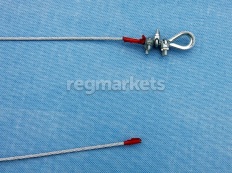 Разработана технология монтажа проводов под тяжением с одновременной раскаткой до трех проводов В комплекте раскатного оборудования использованы серийная базовая техника и комплектующие детали. Навесная тяговая лебедка для перематывания тягового каната сконструирована на базе трактора Т-130Г, лебедка с гидроприводом от трактора для сматывания тягового каната и тормозная установка на три провода — на базе прицепов типа МАЗ, раскаточные устройства для барабанов с проводом — на базе одноосных прицепов. Комплект обеспечивает длину раскатываемых за один цикл проводов до 5 км. Общее тяговое усилие 75 кН, тяговое усилие максимальное: для трех проводов — 60 кН, для одного провода — 40 кН. Применение комплекта механизмов и приспособлений при сооружении ВЛ 500 кВ показало его высокую эффективность [77].

Стрелу провеса проводов и тросов выверяют визированием в соответствии с указанными выше требованиями [2].
Для визирования на опорах визировочных пролетов укрепляют визирные
рейки (рис. 13 40). Высоту установки визирных реек определяют по монтажным кривым или таблицам стрел провеса, приведенным в проекте, с учетом длины поддерживающих гирлянд (или высоты штыревых изоляторов). Таким образом, визирные рейки устанавливают на высоте от земли, соответствующей наинизшей точке провисания провода в пролете для условий монтажного режима. На одну из указанных промежуточных опор поднимается визировщик. По его команде провод сначала перетягивают на 0,3—0,5 м, а затем, выдержав 2 — 3 мин, отпускают до линии визирования. Линия визирования представляет собой прямую линию, проведенную между визирными рейками, установленными на опорах визировочного пролета При горизонтальном расположении проводов вначале обычно визируют средний провод по линии, проходящей через накрест расположенные рейки, после чего визируют крайние провода по рейке и среднему проводу При одновременной натяжке трех проводов визирование производят по верхнему проводу при вертикальном расположении проводов и по среднему проводу — при горизонтальном При плохой видимости стрелу провеса допускается устанавливать по динамометру по тяжению по проводу или тросу, соответствующему монтажному режиму По заданной стреле провеса определяют тяжения Т, Н, по формуле

] — стойка металлической опоры, 2 — окуляр 3 — рейка с уровнем, 4 — струбцина для крепления

Рис 13 40 Приспособление для визирования проводов
где I — длина пролета, м, F — площадь поперечного сечения провода или троса, мм², f — стрела провеса для монтажного режима, м; k — коэффициент, равный для алюминиевых проводов 0,00337, для сталеалюминиевых 0,0044, для стальных проводов и тросов 0,01
По окончании визирования (приема стрелы провеса) на проводе у анкерной опоры, находящейся на противоположном от тягового механизма конце анкерного пролета, наносят метку места установки натяжного зажима После этого провод может быть опущен на землю для удобства монтажа зажима.
Стрелу провеса в анкерном пролете для всех проводов устанавливают одну и ту же. На BЛ до 1 кВ, когда на одной и той же опоре закрепляют провода разных сечений, стрелу провеса для всех проводов также устанавливают одну — по проводу с большим сечением. Стрелы провеса проводов указывают в проектах.
Выше, были указаны наименьшие допустимые расстояния (габариты) от проводов ВЛ до земли, пересекаемых дорог и т. п. В частности, для ВЛ до 1 кВ расстояние от провода до земли должно быть не менее 6 м. Для ВЛ выше 1 кВ и до 110 кВ эти расстояния должны быть не менее: в населенной местности — 7 м; в ненаселенной — 6 м; в труднодоступной — 5 м. Эти расстояния должны быть соблюдены при наивысшей температуре воздуха без учета нагрева провода электрическим током, а также при гололеде, но без ветра [3].

• Назад
• Вперед

• Назад
• Вперед

• Вы здесь:  
• org/ListItem»> Главная
• Книги
• Архивы
• Испытание мощных трансформаторов и реакторов

Читать также:

• Электрические сети промышленных предприятий
• Электромонтажные материалы
• Монтаж сельских электроустановок
• Наладка электроустановок
• Монтаж, эксплуатация и ремонт сельскохозяйственного электрооборудования

Натяжение канатов | Компания «СТЭФС»

Несущие тросы – одни из наиболее ответственных элементов грузоподъемной техники и специальных конструкций. Высокая структурная прочность тросов позволяет использовать их в самых сложных условиях, в том числе на открытом воздухе, при подверженности воздействию агрессивных сред и т. д.

Натяжение канатов – технологическая операция, которая необходима для придания изделиям необходимых характеристик. Она основана на особенностях напряженно-деформированного состояния тросов. В результате большего натяжения канатов увеличивается стойкость несущих элементов (в среднем на 40-60 %).

Для данных целей, как правило, используются спиральные тросы, отличающиеся высоким коэффициентом заполнения металлом поперечного сечения. Это обуславливает минимальное упругое и остаточное удлинение во время эксплуатации. Стальные канаты, которые используются в качестве несущих, необходимо выбирать в соответствии с требованиями ДНАОП 0.00-1.03-93.

Применение натяжения канатов

Процедура требуется при использовании тросов на строительных и металлургических кранах, подъемных установках шахтового типа, кабель-кранах, скреперах и экскаваторах, а также на подвесных дорогах.

Кроме того, натяжение канатов является экономически и технологически обоснованным в следующих случаях:

1. Обустройство фасадов. Несущие тросы с заливными втулками позволяют избежать использования больших талрепов, создавая легкие и эстетичные сталебетонные конструкции.
2. Строительство стадионов. Натяжение канатов дает возможность сооружать уникальные конструкции крыш для таких объектов, используя при этом минимальное количество строительных материалов.
3. Создание мембранных кровель – сложных и креативных конструкций, предусматривающих использование текстильных материалов. Правильное натяжение канатов позволит создать облегченное сооружение, которое быстро собирается и просто демонтируется.
4. Строительство транспортных и пешеходных мостов. Для этого натягиваются витые многожильные тросы.
5. Многие другие специальные проекты.

Все операции, которые проводятся с применением технологических процедур натяжения канатов, проходят строгий и постоянный контроль.

Регулировка натяжения несущих канатов кранов

Регулирование осуществляется после монтажа конструкции при помощи домкратного оборудования, а также подкладных шайб и домкратов. Выполнение операций возможно на всех типах кранов и лифтов, в том числе с качающимися опорами.

Для регулировки натяжения канатов к грузовой тележке подвешивают максимальный груз, после чего устанавливают ее ближе к середине пролета. При этом раскачивающаяся опора получает максимальный наклон в сторону и отделяется от тумбы. В этом положении кран необходимо передвинуть, после чего разгрузить грузовую тележку и сместить ее к головке опоры, которая не раскачивается. В таком положении осуществляется проверка соответствия действительного противовеса несущего троса исходному проектному провесу, а также регулировка натяжения посредством досыпки балласта в противовес опоре.

Затем необходимо проверить положение задней стойки качающейся опоры: если оно не соответствует исходным параметрам, указанным в проекте, то его нужно поправить при помощи специальных домкратных приспособлений.

Процедура натяжения канатов является достаточно сложной с технологической точки зрения, поскольку требует множества статических и динамических расчетов. Поэтому доверять ее выполнение следует исключительно профессионалам.

8.5: Натяжение веревки

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

24470

• Питер Дурмашкин
• Массачусетский технологический институт через MIT OpenCourseWare

Определение натяжения веревки

Вернемся к нашему примеру очень легкой веревки (объект 2 с \(m_{2} \simeq 0\)), прикрепленной к блоку (объект 1) в точке B , и тянется приложенной силой в точке A \(\overrightarrow{\mathbf{F}}_{\mathrm{A}, 2}\) (рис. 8.18а).

Рисунок 8.18a Безмассовая веревка, тянущая блок mathbf{i}}\) — единичный вектор, указывающий в положительном направлении x (рис. 8.18b). Диаграммы сил для системы, состоящей из каната и блока, показаны на рис. 8.19., а для веревки и блока отдельно на рис. 8.20, где \(\overrightarrow{\mathbf{F}}_{2,1}\) сила, действующая на блок (объект 1) от веревки (объект 2), и \(\overrightarrow{\mathbf{F}}_{1,2}\) — сила, действующая на веревку из-за блока.

Рисунок 8.18b Силы, действующие на систему, состоящую из блока и каната

Силы, действующие на канат и блок, должны в сумме равняться нулю. Поскольку веревка не ускоряется, второй закон Ньютона, примененный к веревке, требует, чтобы \(F_{\mathrm{A}, 2}-F_{1,2}=m_{2} a\) (где мы используем величины для все силы).

Рисунок 8.19 Отдельные диаграммы сил для веревки и блока

Поскольку мы предполагаем, что масса веревки пренебрежимо мала, поэтому

\[F_{\mathrm{A}, 2}-F_{1,2}=0 ; \quad \text { (безмассовая веревка) } \nonumber \]

Если рассматривать случай, когда веревка очень легкая, то силы, действующие на концах веревки, почти горизонтальны. Тогда, если система канат-блок движется с постоянной скоростью или в состоянии покоя, второй закон Ньютона теперь равен

\[F_{\mathrm{A}, 2}-F_{1,2}=0 \nonumber \]

Второй закон Ньютона, примененный к блоку в \(+\hat{\mathbf{i}}\)-направлении, требует, чтобы \(F_{2,1}-f=0\) Третий закон Ньютона, примененный к пара взаимодействия блок-веревка требует, чтобы \(F_{1,2}=F_{2,1}\). Следовательно,

\[F_{\mathrm{A}, 2}=F_{1,2}=F_{2,1}=f \nonumber \]

Таким образом, приложенная тяговая сила передается через веревку на блок так как она имеет ту же величину, что и сила веревки на блоке. Кроме того, приложенная тянущая сила также равна силе трения о блок.

Как определить «натяжение» в какой-либо точке веревки? Предположим, сделайте воображаемый срез веревки в точке P, на расстоянии \(x_{P}\) от точки B, где веревка прикреплена к блоку. Воображаемый срез делит веревку на две секции, обозначенные буквами L (левая) и R (правая), как показано на рис. 8.20.

Рис. 8.20 Воображаемый разрез веревки

Теперь между левой и правой частями веревки действует пара сил третьего закона. Обозначим силу, действующую на левую секцию, через \(\overrightarrow{\mathbf{F}}_{\mathrm{R}, \mathrm{L}}\left(x_{P}\right)\), а силу, действующую на правом участке \(\overrightarrow{\mathbf{F}}_{\mathrm{L}, \mathrm{R}}\left(x_{P}\right)\) Третий закон Ньютона требует, чтобы силы в эти пары взаимодействия равны по величине и противоположны по направлению.

\[\overrightarrow{\mathbf{F}}_{\mathrm{R}, \mathrm{L}}\left(x_{p}\right)=-\overrightarrow{\mathbf{F}}_{ \mathrm{L}, \mathrm{R}}\left(x_{P}\right) \nonumber \]

Диаграммы сил для левой и правой секций показаны на рис. 8.21, где \(\overrightarrow{\mathbf {F}}_{1, \mathrm{L}}\) — сила, действующая на левый отрезок каната за счет взаимодействия блока с канатом. (Ранее мы обозначали эту силу через \(\overrightarrow{\mathbf{F}}_{1,2}\)) Теперь обозначим силу на правом отрезке стороны веревки, вызванную тянущей силой в точке A, через \(\overrightarrow{\mathbf{F}}_{\mathrm{A}, \mathrm{R}}\) (которые мы ранее обозначали как \(\overrightarrow{\mathbf{F}}_{\mathrm{ А}, 2}\)).

Рисунок 8.21 Диаграмма сил для левой и правой секций каната

Натяжение \(T\left(x_{P}\right)\) в точке P каната, лежащей на расстоянии x от левого конца каната, есть величина пары сил действие-противодействие, действующих в точке P ,

\[T\left(x_{p}\right)=\left|\overrightarrow{\mathbf{F}}_{\mathrm{ R}, \mathrm{L}}\left(x_{P}\right)\right|=\left|\overrightarrow{\mathbf{F}}_{\mathrm{L}, \mathrm{R}}\ влево(x_{P}\вправо)\вправо| \номер \]

Для веревки незначительной массы, натянутой, как в предыдущем случае (даже если веревка ускоряется), сумма горизонтальных сил, приложенных к левому и правому участкам веревки, равна нулю , и поэтому натяжение равномерно и равно приложенной силе тяги,

\[T=F_{\mathrm{A}, \mathrm{R}} \nonumber \]

Пример 8. 3 Натяжение массивной веревки

Рис. 8.22a Массивная веревка, тянущая блок

Рассмотрим блок массы \(m_{1}\), лежащий на горизонтальной поверхности. Коэффициент кинетического трения между блоком и поверхностью равен \(\mu_{k}\). К блоку привязана однородная веревка массы \(m_{2}\) и длины d. Веревку тянут со стороны, противоположной блоку, с приложенной силой величины \(\left|\overrightarrow{\mathbf{F}}_{\mathrm{A}, 2}\right|=F_{\mathrm{A }, 2}\). Поскольку веревка стала массивной, сила тяги образует угол \(\phi\) по отношению к горизонтали, чтобы уравновесить силу тяжести на веревке (рис. 8.22а). Определить натяжение веревки в зависимости от расстояния x от блока.

Решение: В следующем анализе мы будем предполагать, что угол \(\phi\) очень мал, и изображать тянущие и растягивающие силы как действующие в основном в горизонтальном направлении, хотя должна быть некоторая небольшая вертикальная составляющая, чтобы уравновесить гравитационные силы.

Ключевым моментом, который необходимо понять, является то, что веревка теперь массивна, и мы должны учитывать инерцию веревки при применении второго закона Ньютона. Рассмотрим воображаемый разрез веревки на расстоянии х от блока (рис. 8.22б), разделяющий веревку на две части. Правый участок имеет длину \(d-x\) и массу \(m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\). \begin{уравнение}m_{\mathrm{R}}=\left(m_{2} / d\right)(dx)\end{уравнение}. Левая часть имеет длину x и массу \(m_{\mathrm{L}}=\left(m_{2} / d\right)(x)\).

Рисунок 8.22b Воображаемый разрез веревки

Диаграммы силы свободного тела для двух секций веревки показаны на рисунке 8.22c, где T (x) — натяжение веревки на расстоянии x от блока, а \ (F_{1, \mathrm{L}}=\left|\overrightarrow{\mathbf{F}}_{1, \mathrm{L}}\right| \equiv\left|\overrightarrow{\mathbf{F} }_{1,2}\right|\) — величина силы, действующей на левый отрезок каната из-за взаимодействия каната с блоком.

Рисунок 8.22c Диаграмма сил для левой и правой частей каната

Применить второй закон Ньютона к правому отрезку веревки, что даст

\[F_{\mathrm{A}, \mathrm{R}}-T(x)=m_{\mathrm{R}} a_{\mathrm{ R}}=\frac{m_{2}}{d}(dx) a_{\mathrm{R}} \nonumber \]

, где \(a_{\mathrm{R}}\) — x -компонента ускорения правого участка каната. Примените второй закон Ньютона к левому отрезку веревки, получив

\[T(x)-F_{1, \mathrm{L}}=m_{\mathrm{L}} a_{\mathrm{L}}=\ слева (m_ {2} / d \ справа) x a _ {\ mathrm {L}} \ nonumber \]

где \(a_{\mathrm{L}}\) — x -компонента ускорения левого отрезка веревки.

Рисунок 8.23 ​​Диаграмма усилия на скользящем блоке

Диаграмма усилия на блоке показана на рисунке 8.23. Второй закон Ньютона для блока в направлении \(+\hat{\mathbf{i}}\)- равен \(F_{\mathrm{L}, 1}-f_{k}=m_{1} a_{1 }\) и в направлении \(+\hat{\mathbf{j}}\)- \(N-m_{1} g=0\) Кинетическая сила трения, действующая на блок, равна \(f_{k }=\mu_{k} N=\mu_{k} m_{1} g\) Второй закон Ньютона для блока в направлении \(+\hat{\mathbf{i}}\) становится равным

\[F_{\mathrm{L}, 1}-\mu_{k} m_{1} g=m_{1} a_{1} \nonumber \]

Третий закон Ньютона для взаимодействия блока с канатом: определяется выражением \(F_{\mathrm{L}, 1}=F_{1, \mathrm{L}}\). Уравнение (8.5.8) тогда принимает вид

\[T(x)-\left(\mu_{k} m_{1} g+m_{1} a_{1}\right)=\left(m_{2} / d\right) x a_{\mathrm{L}} \nonumber \]

Поскольку веревка и блок движутся вместе, ускорения равны, что мы обозначаем символом \(a \equiv a_{1}=a_{ \mathrm{L}}\). Тогда уравнение (8.5.10) становится

\[T(x)=\mu_{k} m_{1} g+\left(m_{1}+\left(m_{2} / d\right) x\right) a \nonumber \]

Этот результат не является неожиданным, поскольку натяжение ускоряет как блок, так и левую секцию и противодействует силе трения.

В качестве альтернативы диаграмма сил на систему, состоящую из каната и блока, показана на рис. 8.24.

Рисунок 8.24 Диаграмма сил в системе блок-веревка

Второй закон Ньютона принимает вид

\[F_{\mathrm{A}, \mathrm{R}}-\mu_{k} m_{1} g=\left(m_{ 2}+m_{1}\right) a \nonumber \]

Решите уравнение (8.5.12) для \(F_{\mathrm{A}, \mathrm{R}}\) и подставьте в уравнение (8.5.7), а затем решите уравнение текучести на растяжение (8.5.11) .

Пример 8.4 Натяжение подвешенной веревки

Однородная веревка массы M и длины L подвешена к потолку (рис. 8.25). Величина ускорения свободного падения равна g. а) Найдите натяжение веревки на верхнем конце, где веревка прикреплена к потолку. б) Найдите натяжение веревки в зависимости от расстояния до потолка. (c) Найдите уравнение для скорости изменения натяжения по отношению к расстоянию от потолка через M , L и g .

Рис. 8.26 Система координат для подвешенной веревки

Решение: (a) Начните с выбора системы координат с началом на потолке и положительным направлением y, указывающим вниз (рис. 8.26). Для того чтобы найти натяжение на верхнем конце веревки, выберем в качестве системы всю веревку. Силы, действующие на веревку, — это сила при y = 0, удерживающая веревку, T (y = 0), и сила тяжести, действующая на всю веревку. Диаграмма силы свободного тела показана на рис. 8.27.

Рисунок 8.27 Диаграмма сил на канате

Поскольку ускорение равно нулю, второй закон Ньютона для веревки равен \(Mg-T(y=0)=0\). Следовательно, натяжение на верхнем конце равно \(T(y=0)=Mg\).

(б) Напомним, что напряжение в точке есть величина пары сил действие-противодействие, действующих в этой точке. Сделайте воображаемый разрез веревки на расстоянии y от потолка, разделив веревку на верхний отрезок 1 и нижний отрезок 2 (рис. 8.28а). Выберем верхний отрезок как систему с массой \(m_{1}=(M / L) y\). Силы, действующие на верхний отрезок, — это сила тяжести, сила T ( y = 0), удерживающая веревку вверх, и натяжение T(y) в точке y, которое тянет верхний отрезок вниз. Диаграмма силы свободного тела показана на рис. 8.28б.

Рис. 8.28 (a) Воображаемый разрез разделяет веревку на две части. (b) Диаграмма силы свободного тела на верхнем отрезке веревки

. Применим второй закон Ньютона к верхнему отрезку: \(m_{1} g+T(y)-T(y=0)=0\). Следовательно, натяжение на расстоянии y от потолка равно \(T(y)=T(y=0)-m_{1}g\). Поскольку \(m_{1}=(M / L) y\) — это масса сегмента, а Mg — натяжение на верхнем конце, второй закон Ньютона принимает вид

\[T(y)=M g(1 -y / L) \nonumber \]

В качестве проверки отметим, что при \(y=L\) натяжение \(T(y=L)=0\), что мы и ожидаем, поскольку силы нет действует на нижний конец веревки.

(c) Дифференцируйте уравнение (8.5.13) по y, получая

\[\frac{d T}{d y}=-(M / L) g \nonnumber \]

Скорость изменяется с постоянной скоростью по отношению к расстоянию от вершины каната.

Непрерывные системы и второй закон Ньютона как дифференциальные уравнения

Мы можем определить натяжение на расстоянии y от потолка в примере 8.4 альтернативным методом, который можно обобщить на многие типы «непрерывных систем». Выберите систему координат с началом на потолке и положительным направлением y, указывающим вниз, как показано на рис. 8.25. Рассмотрим в качестве системы небольшой элемент веревки между точками y и \(y+\Delta y\). Этот маленький элемент имеет длину \(\Delta y\) Малый элемент имеет массу \(\Delta m=(M / L) \Delta y\) и показан на рис. 8.29..

\[\Delta m=(M / L) \Delta y \nonumber \]

Силы, действующие на малый элемент, это натяжение T(y) при y, направленное вверх, натяжение \(T( y+\Delta y)\) при \(y+\Delta y\) направлена ​​вниз, а сила тяжести \(\Delta m g\) направлена ​​вниз. Натяжение \(T(y+\Delta y)\) равно натяжению T ( y) плюс небольшая разница \(\Delta T\)

\[T(y+\Delta y)=T(y)+ \Delta T \nonumber \]

Небольшая разница в общем случае может быть положительной, нулевой или отрицательной. Диаграмма силы свободного тела показана на рис. 8.30.

Рис. 8.30 Диаграмма силы свободного тела на элементе малой массы

Теперь применим второй закон Ньютона к элементу малой массы

\[\Delta m g+T(y)-(T(y)+\Delta T)=0 \nonumber \ ]

Тогда разница в натяжении равна \(\Delta T=-\Delta m g\). Подставим теперь наш результат на массу элемента \(\Delta m=(M / L) \Delta y\) и найдем, что

\[\Delta T=-(M / L) \Delta y g \ nonumber \]

Разделить на \(\Delta y\), получив \(\Delta T / \Delta y=-(M / L) g\). Теперь возьмем предел, при котором длина маленького элемента стремится к нулю, \(\Delta y \rightarrow 0\)

\[\lim _{\Delta y \rightarrow 0} \frac{\Delta T}{\Delta y}=-(M / L) g \nonumber \]

Напомним, что левая часть уравнения ( 8.5.18) является определением производной натяжения по y , поэтому мы приходим к уравнению (8.5.14),

\[\frac{d T}{d y}=-(M / L) g \nonumber \]

Мы можем решить дифференциальное уравнение (8.5.14) с помощью метода, называемого разделением переменных. {\prime}=T(y):\ ) 9{\prime} \nonumber \]

После интегрирования и подстановки пределов имеем

\[T(y)-T(y=0)=-(M / L) g y \nonumber \]

Используя тот факт, что натяжение в верхней части веревки равно \(T(y=0)=M g\), найдем, что

\[T(y)=M g(1-y / L) \nonumber \]

в соответствии с нашим предыдущим результатом, уравнением (8.5.13).

---

Эта страница под названием 8.5: Tension in a Rope распространяется в соответствии с лицензией CC BY-NC-SA 4.0. Автором, ремиксом и/или куратором был Петр Доурмашкин (MIT OpenCourseWare) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Петр Доурмашкин

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Программа OER или Publisher

   MIT OpenCourseWare

   Показать оглавление

   нет

2. Теги

   1. источник@https://ocw. mit.edu/courses/8-01sc-classical-mechanics-fall-2016/

Калькулятор натяжения

Создано Кеннетом Аламбра

Отзыв от Bogna Szyk и Jack Bowater

Последнее обновление: 21 декабря 2022 г.

Содержание:

• Что такое сила натяжения?
• Второй закон движения Ньютона
• Как рассчитать натяжение канатов, подвешивающих объект
• Как найти натяжение канатов при вытягивании объекта
• Часто задаваемые вопросы веревка или веревка, используемая для подъема объекта. В этой статье вы также узнаете, как найти натяжение веревок, которыми тянут объект на поверхности без трения. Вы также увидите в этом калькуляторе натяжения веревки или струны различные диаграммы свободного тела, чтобы лучше понять, как рассчитать силы натяжения. Если вы хотите узнать больше о натяжении и формуле силы натяжения, читайте дальше!

  Что такое сила натяжения?

  Представьте, что вы поднимаете с земли баскетбольный мяч. Вы почувствуете вес мяча в своих руках из-за силы тяжести, действующей на массу мяча. Теперь представьте, что вы обвязываете мяч веревкой, которую затем используете, чтобы снова поднять мяч. Вы по-прежнему чувствовали бы вес мяча через веревку. В этой ситуации канат теперь находится в состоянии натяжения . То, что удерживает веревку вместе, называется силой натяжения . Разрезание веревки ослабит силу натяжения и отправит мяч в свободное падение.

  Сила натяжения — это осевая сила, действующая на объект, который тянет, например веревку, веревку или цепь. Мы также можем наблюдать силу натяжения в других материалах, таких как стержни и стержни, при условии, что они подвергаются внешнему растяжению или растяжению. Материалы с высокой прочностью на растяжение делают лучшие стержни и стержни, так как они не ломаются под действием сил растяжения. Вы можете проверить наш калькулятор напряжения, в котором обсуждается эластичность, чтобы узнать больше о прочности на растяжение.

  Сила натяжения также является прекрасным примером Третьего закона движения Ньютона . Третий закон движения Ньютона гласит, что когда одно тело воздействует на другое тело, то второе тело действует с такой же силой в противоположном направлении обратно на исходное тело. Сила натяжения представляет собой реактивную силу, противодействующую внешней силе притяжения.

  Второй закон движения Ньютона

  Чтобы вычислить натяжение, действующее на веревку, нам сначала нужно понять Второй закон движения Ньютона . Второй закон Ньютона гласит, что сумма сил, действующих на объект постоянной массы, равна массе этого объекта, умноженной на его ускорение. Мы также можем выразить это утверждение в виде уравнения:

  ΣF = m × a

  , где:

  • Σ (сигма) обозначает сумму сил F ;
  • м — масса объекта; и
  • a это ускорение.

  Для объекта, подвешенного на веревке, мы можем использовать ускорение свободного падения g в качестве его ускорения. Гравитационное ускорение дает нам значение его веса с точки зрения силы, например, ньютонов или фунт-сила . Если объект движется с другим ускорением, мы должны использовать его фактическое ускорение для расчета. Однако этот калькулятор натяжения определяет силы натяжения только в случаях статического равновесия .

  Это утверждение означает, что этот инструмент рассматривает только объектов в покое в данной системе. В этом калькуляторе натяжения мы также предполагаем, что веревки не имеют массы и, следовательно, не вносят никакого вклада в силы натяжения. Мы также предполагаем, что массы или объекты находятся в вакууме и не испытывают трения или сопротивления воздуха по отношению к окружающей их среде.

  Как рассчитать натяжение канатов, подвешивающих объект

  На приведенном ниже рисунке видно, что сила F, необходимая для подъема объекта, равна весу объекта W. Эта идея является фундаментальной концепцией, лежащей в основе нашей формулы силы натяжения. Ниже также показана диаграмма свободного тела объекта, которая показывает силы натяжения T, действующие на струну. Как видите, силы натяжения приходят парами и в противоположных направлениях:

  Следуя второму закону движения Ньютона, мы можем выразить сумму сил, используя диаграмму свободного тела объекта, как показано в правой части иллюстрации выше. Мы используем диаграммы свободного тела , чтобы показать различные направления и величины сил, действующих на тело. В равновесии все эти силы должны равняться нулю. Считая все восходящие силы положительными, а направленные вниз отрицательными, получаем следующее уравнение:

  ΣF↑ = 0 = T + (-W)

  T = W

  где вес W становится отрицательным, поскольку он направлен вниз. Перенося W в другую часть уравнения, мы теперь видим, что сила натяжения веревки равна весу предмета, который она несет, как это также показано выше.

  Если мы используем больше веревок для подъема объекта, общая сила натяжения делится на веревки. Сила натяжения каждой веревки зависит от ее угла по отношению к направлению силы, которой она противодействует. Чтобы лучше понять это, давайте рассмотрим другую диаграмму свободного тела объекта, подвешенного на двух веревках, как показано ниже:0034

  На диаграмме свободного тела, показанной выше, мы можем видеть горизонтальную и вертикальную составляющие сил натяжения, T₁ и T₂. Силы являются векторами, а это значит, что они всегда имеют как величин, так и направлений. Как и все векторы, силы могут быть выражены в этих компонентах, которые дают влияние силы вдоль горизонтальной и вертикальной осей. T₁ₓ и T₂ₓ — вертикальные компоненты T₁ и T₂ соответственно. С другой стороны, T _1y и T _2y являются вертикальными составляющими одних и тех же сил соответственно. Поскольку гравитация действует на объект по вертикальной оси, нам необходимо учитывать вертикальные составляющие сил натяжения для нашего суммирования сил следующим образом:

  σf ↑ = 0 = T _1Y + T _2Y + (-W)

  W = T _1Y + T _2Y

  3 + T _2Y

  3 3533353 + T _2Y

  333333333331 годы. , мы можем выразить T _1y и T _2y через T₁ и T₂ соответственно с помощью тригонометрических функций: = T₂ × sin(β)

  W = T₁ × sin(α) + T₂ × sin(β)

  Можно также сказать, что для того, чтобы система находилась в равновесии, объект не должен двигаться ни горизонтально, ни вдоль оси x. Следовательно, горизонтальные компоненты T₁ и T₂ должны равняться нулю. Также с помощью тригонометрии мы можем выразить T₁ₓ и T₂ₓ через T₁ и T₂ соответственно:

  T₁ₓ = T₂ₓ

  T₁ × cos(α) = T₂ 3 × cos(β)

  0 делим обе части на cos(α) , получаем уравнение, в котором T₁ выражается через T₂ и углы:

  T₁ = T₂ × cos(β) / cos(α)

  Затем мы можем использовать это уравнение для решения T₂, подставив T₂ × cos(β) / cos(α) в качестве T₁ в нашем суммировании уравнения сил, как показано ниже:

  Вт = T₁ × sin(α) + T₂ × sin(β)

  Вт = T₂ × [cos(β) / cos(α)] × sin(α) + T₂ × sin(β)

  W = T₂ × [cos(β) × sin(α) / cos(α) + sin(β)]

  T₂ = W / [cos(β) × sin(α) / cos(α) + sin(β)]

  Наконец, если мы умножим все это уравнение на cos(β) / cos(α) , поскольку мы получили значение T₁ через T₂, а затем все упростим, мы получим следующее уравнение:

  T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

  T₁ = W / [cos(β) × sin(α) / cos(α) + sin(β)] × [cos(β) / cos(α)]

  T₁ = W / [cos(α) × sin(β) / cos( β) + sin(α)]

  Теперь все, что вам нужно знать, это углы натяжения канатов относительно горизонтали. Если задан угол от вертикали, просто вычтите этот угол из 90°. Это даст вам угол от горизонтали. Однако, если вам даны другие значения углов, которые могут быть больше 90° или даже 180°, вы можете воспользоваться нашим калькулятором эталонного угла, который поможет вам определить нужный угол. После определения значений переменных в наших формулах силы натяжения мы теперь можем найти силы натяжения.

  Как найти натяжение веревки при вытягивании объекта

  Как найти силу натяжения на объекте, который тянут так же, как когда объект подвешен. Единственное отличие состоит в том, что сначала нам нужно вычислить ускорение всей системы и сумма всех сил по горизонтали. Если веревка находится под углом к ​​уровню пола, нам также необходимо вычислить горизонтальную составляющую тягового усилия.

  Давайте рассмотрим пример ниже, чтобы лучше понять, как найти силу натяжения веревки, тянущей один или два объекта. В этом примере два объекта тянутся одной приложенной силой тяги. Другая веревка тянет второй объект, который прикреплен к первому объекту, как показано ниже:

  На этом рисунке показано, что массы m₁ и m₂ равны 3 кг и 2 кг соответственно. Сумма этих двух масс дает общую массу системы 5 кг . Нам также необходимо определить горизонтальную составляющую силы тяги, T = 24 N , то есть под углом θ = 60° . Если снова использовать тригонометрические функции, то можно сказать, что горизонтальная составляющая силы тяги равна 24 Н × cos(60°) , что равно 12 Н . Теперь, когда мы знаем горизонтальную составляющую тяговой силы и полную массу системы, мы можем рассчитать ускорение системы a следующим образом:

  F = m × a → a = F / m

  a = 12 Н / 5 кг = 2,4 м/с²

  После того, как мы нашли ускорение системы, мы можем снова использовать второй закон Ньютона для расчета натяжения веревки или струны системы. Для этого умножьте ускорение на массу, которую тянет веревка. Для T₂ его диаграмма свободного тела показывает нам, что он отвечает только за массу m₂; мы можем сказать, что Т₂ = а × м₂ . При этом T₂ = (2,4 м/с²) × (2 кг) = 4,8 Н . С другой стороны, T₁ — это сила натяжения, которая притягивает вес m₁ и m₂. Однако у нас уже есть значение T₁, которое просто равно T = 24,0 Н. Следовательно, T₁ = 24,0 Н .

  В нашем примере, если бы левая и правая веревки были просто одной веревкой, мы могли бы сравнить эту установку с системой шкивов. Блок — это простая машина, которая использует силы натяжения канатов для получения механического преимущества. Вы можете воспользоваться нашим калькулятором шкивов и калькулятором длины ремня (который представляет собой систему с двумя шкивами), чтобы узнать больше о механических преимуществах и натяжении.

  Часто задаваемые вопросы

  Как рассчитать натяжение веревки под углом?

  Чтобы рассчитать натяжение веревки под углом:

  1. Найдите угол от горизонтали, на которую установлена ​​веревка.
  2. Найдите горизонтальную составляющую силы натяжения, умножив приложенную силу на косинус угла.
  3. Рассчитайте вертикальную составляющую силы натяжения, умножив приложенную силу на синус угла.
  4. Сложите эти две силы вместе, чтобы найти общую величину приложенной силы.
  5. Учитывайте любые другие приложенные силы , например, другую веревку, силу тяжести или трение, и решайте уравнение силы обычным образом.

  Как рассчитать натяжение, создаваемое 10-килограммовым ящиком на двух веревках, подвешенных под углом 60 градусов?

  Для определения натяжения в этом случае:

  1. Определение вертикальной и горизонтальной составляющих растягивающих усилий на канатах:
     • Т₁ = Т₁ sin(60) + Т₁ cos(60)
     • T₂ = T₂ sin(60) + T₂ cos(60)
  2. Вертикальные (синусоидальные) составляющие уравновешивают вес :
     • T₁ sin(60) + T₂ sin(60) = √3 (T₁ + T₂)/2 = 98 Н
  3. Горизонтальные (косинусные) составляющие силы натяжения уравновешивают друг друга :
     • T₁ cos(60) = T₂ cos(60) или T₁ = T₂
  4. Решите уравнения:
     • 98 Н = √3 Т₁ или, Т₁ = Т₂ = 56,58 Н

  Как найти натяжение двух канатов при одинаковом угле подвески?

  Когда углы подвески (α) одинаковы для двух веревок, величина натяжения (T) становится одинаковой для обеих веревок.