Максимальный прогиб балки: Предельный прогиб

Содержание

Прогиб балки | Полный обзор и важные отношения —

Содержание: Отклонение луча

Определение кривой прогиба
Определение угла отклонения
Определение отклонения
Граничные условия прогиба балки
Взаимосвязь между силами нагрузки, поперечной силой, изгибающим моментом, наклоном и прогибом
Уравнения и соотношения изгиба балки
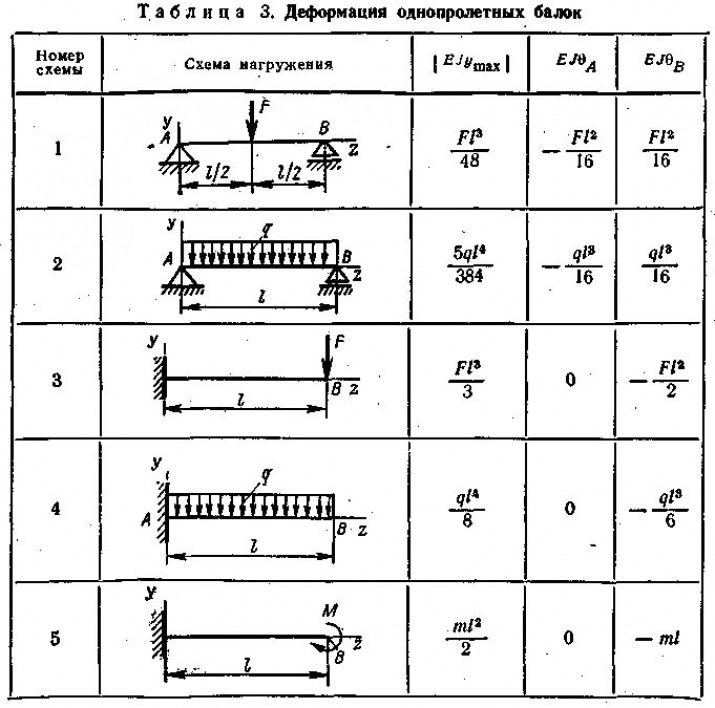
Таблица прогиба балки и формулы для стандартных случаев нагружения
Отклонение и наклон балки с примерами Случай I: выступающая балка
Случай II: определение максимального прогиба балки без опоры с точечной нагрузкой в центре.
Случай III: определение максимального прогиба балки с простой опорой при сосредоточенной точечной нагрузке на расстоянии «а» от опоры А.
Метод двойной интеграции
Процедура метода двойного интегрирования
Метод двойного интегрирования для нахождения прогиба балки на примере консольная балка с равномерно распределенной нагрузкой
Метод двойного интегрирования для треугольной нагрузки

In инженерия, отклонение — степень смещения элемента конструкции под действием нагрузки (из-за его деформации). Это может относиться к углу или расстоянию. Расстояние прогиба элемента под нагрузкой можно рассчитать путем интегрирования функции, которая математически описывает наклон отклоненной формы элемента под этой нагрузкой. Существуют стандартные формулы для прогиба общих конфигураций балок и загружений в отдельных местах. В противном случае используются такие методы, как виртуальная работа, прямая интеграция, метод Кастильяно, метод Маколея или метод прямой жесткости.

Кривая отклонения

Когда балки нагружены поперечными или продольными нагрузками, начальная прямая продольная ось деформируется в кривую, известную как упругая кривая балки или кривая прогиба. Кривая прогиба — это деформированная ось выбранной балки.

Угол отклонения

Наклон можно определить как угол между продольной осью балки и касательной, построенной к кривой деформации балки в любом желаемом месте. Это угол поворота нейтральной оси луча. Измеряется в радианах.

прогиб

Отклонение — это поступление или смещение любой точки на оси балки, измеренное в направлении y от начальной прямой продольной оси до точки на кривой прогиба балки. Измеряется в миллиметрах. Прогиб представляет собой отклонение прямой продольной оси из-за поперечной нагрузки. Напротив, изгиб балки представляет собой отклонение начальной прямой продольной оси из-за осевой сжимающей нагрузки. Обычно он представлен как ‘у»

Если балка изгибается по дуге окружности, это называется изгибом по окружности; в противном случае это называется некруглым изгибом. Предположим, что на призматическую балку действует переменный изгибающий момент. В этом случае это приводит к изгибу некруглого типа, а если он подвергается постоянному изгибающему моменту, приводит к круговому изгибу балки.

Граничные условия прогиба балки

y равен нулю на опоре штифта или ролика.
y равен нулю на встроенной или консольной опоре.
Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:

1. 4}
Таблица прогиба балки и формулы для стандартных случаев нагружения:
- Максимальный наклон и прогиб консольной балки происходит на свободном конце балки, в то время как на зажатом конце консольной балки не наблюдается наклона или прогиба.
- Для балки без опоры с симметричными условиями нагружения максимальный прогиб может быть найден в середине пролета. Максимальный уклон наблюдается у опор балки. Максимальный прогиб возникает при нулевом уклоне.
https://www.pinterest.it/pin/711076228644344940/Наклон и прогиб для балки с простой опорой при различных условиях нагрузки
Прогиб и наклон балки с примерами
Случай I: Свисающая балка
Рассмотрим выступающую стальную балку, несущую сосредоточенную нагрузку P = 50 кН на конце C.
Для выступающей балки: (a) определить наклон и максимальное отклонение, (b) оценить наклон на расстоянии 7 м от точки A и максимальное отклонение по заданным данным. {- 3} \; m = -8.93 \; мм
Метод двойной интеграции
Если жесткость на изгиб EI постоянна, а момент является функцией расстояния x, интегрирование EI (d² y) / (dx² ) = M даст наклон
```
EI \ frac {dy} {dx} = \ int M dx + C_1
```
```
EIy = \ int \ int Mdxdx + C_1x + C_2
```
где С₁ и C₂ являются константами. Они определяются с помощью граничных условий или других условий на балке. Вышеприведенное уравнение дает отклонение y как функцию от x; это называется уравнением кривой упругости или деформации.
Вышеупомянутый метод анализа прогиба и наклона балки известен как метод двойного интегрирования для расчета прогибов балки. Если изгибающий момент и жесткость на изгиб являются непрерывными функциями x, одно дифференциальное уравнение может быть записано для всей балки. Для статически определенной балки существует две опорные реакции; каждая из них накладывает определенный набор ограничений на наклон упругой кривой. Эти ограничения называются граничными условиями и используются для определения двух постоянных интегрирования.
Граничные условия метода двойного интегрирования
1. y равен нулю на опоре штифта или ролика.
2. y равен нулю на встроенной или консольной опоре.
3. Предположим, что изгибающий момент и жесткость на изгиб являются разрывными функциями x. В этом случае невозможно написать одно дифференциальное уравнение для всей балки; уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке сегментов:
- 1. y для левой части должен быть равен y для правой части.
- 2. Уклон левого участка должен быть равен уклону правого участка.
Процедура метода двойного интегрирования
- Нарисуйте упругую кривую балки и примите во внимание все необходимые граничные условия, такие как y равен нулю на опоре пальца или ролика и y равен нулю на встроенной или консольной опоре.
- Определите изгибающий момент M на произвольном расстоянии x от опоры методом сечений. Используйте соответствующие правила изгибающего момента при нахождении момента М. для разрывного момента, уравнения кривой для двух соседних сегментов должны удовлетворять данным двум условиям на стыке между сегментами: 1. y для левой части должно быть равно y для правой секции. 2. Уклон левого участка должен быть равен уклону правого участка.
- Проинтегрируйте уравнение дважды, чтобы получить наклон и прогиб, и не забудьте найти постоянное интегрирование для каждого сечения с использованием граничных условий.
Примеры метода двойного интегрирования для определения прогиба балки
Рассмотрим консольную балку длиной L, показанную на рисунке ниже, с равномерно распределенной нагрузкой. В консольной балке один конец зафиксирован, а другой конец может свободно двигаться. Мы выведем уравнение для наклона и изгибающего момента для этой балки, используя метод двойного интегрирования. 4}{120}
```
у = -0.01758 \; м
```
Чтобы узнать о прочности материала (нажмите здесь.)и метод площади момента Открыть.
Расчет балок на прогиб. Максимальный прогиб балки: формула расчета
Балка – элемент в инженерии, представляющий собой стержень, который нагружают силы, действующие в направлении, перпендикулярном стержню. Деятельность инженеров зачастую включает в себя необходимость расчета прогиба балки под нагрузкой. Этой действие выполняется для того, чтобы ограничить максимальный прогиб балки.
Типы
На сегодняшний день в строительстве могут использоваться балки, изготовленные из разных материалов. Это может быть металл или дерево. Каждый конкретный случай подразумевает под собой разные балки. При этом расчет балок на прогиб может иметь некоторые отличия, которые возникают по принципу разницы в строении и используемых материалов.
Деревянные балки
Сегодняшнее индивидуальное строительство подразумевает под собой широкое применение балок, изготовленных из дерева. Практически каждое строение содержит в себе деревянные перекрытия. Балки из дерева могут использоваться как несущие элементы, их применяют при изготовлении полов, а также в качестве опор для перекрытий между этажами.

Узнаем от чего зависит устойчивость конструкции. Расчет….
Строительством объектов различного назначения человек занимается всегда. Возводимые сооружения…
Ни для кого не секрет, что деревянная, так же как и стальная балка, имеет свойство прогибаться под воздействием нагрузочных сил. Стрелка прогиба зависит от того, какой материал используется, геометрических характеристик конструкции, в которой используется балка, и характера нагрузок.
Допустимый прогиб балки формируется из двух факторов:
- Соответствие прогиба и допустимых значений.
- Возможность эксплуатации здания с учетом прогиба.
Проводимые при строительстве расчеты на прочность и жесткость позволяют максимально эффективно оценить то, какие нагрузки сможет выдерживать здание в ходе эксплуатации. Также эти расчеты позволяют узнать, какой именно будет деформация элементов конструкции в каждом конкретном случае. Пожалуй, никто не будет спорить с тем, что подробные и максимально точные расчеты – это часть обязанностей инженеров-строителей, однако с использованием нескольких формул и навыка математических вычислений можно рассчитать все необходимые величины самостоятельно.

Балка металлическая в строительстве
Балка металлическая относится к особому виду сортового металлопроката и применяется в основном для…
Для того чтобы произвести правильный расчет прогиба балки, нужно также брать во внимание тот факт, что в строительстве понятия жесткости и прочности являются неразрывными. Опираясь на данные расчета прочности, можно приступать к дальнейшим расчетам относительно жесткости. Стоит отметить, что расчет прогиба балки – один из незаменимых элементов расчета жесткости.
Обратите ваше внимание на то, что для проведения таких вычислений самостоятельно лучше всего использовать укрупненные расчеты, прибегая при этом к достаточно простым схемам. При этом также рекомендуется делать небольшой запас в большую сторону. Особенно если расчет касается несущих элементов.
Расчет балок на прогиб. Алгоритм работы
На самом деле алгоритм, по которому делается подобный расчет, достаточно прост. В качестве примера рассмотрим несколько упрощенную схему проведения расчета, при этом опустив некоторые специфические термины и формулы. Для того чтобы произвести расчет балок на прогиб, необходимо выполнить ряд действий в определенном порядке. Алгоритм проведения расчетов следующий:

Монолитное перекрытие в доме из газобетона. Расчет и…
Монолитное перекрытие в доме из газобетона может быть выполнено с использованием железобетонной…
- Составляется расчетная схема.
- Определяются геометрические характеристики балки.
- Вычисляется максимальную нагрузку на данный элемент.
- В случае возникновения необходимости проверяется прочность бруса по изгибающему моменту.
- Производится вычисление максимального прогиба.
Как видите, все действия достаточно просты и вполне выполнимы.
Составление расчетной схемы балки
Для того чтобы составить расчетную схему, не требуется больших знаний. Для этого достаточно знать размер и форму поперечного сечения элемента, пролет между опорами и способ опирания. Пролетом является расстояние между двумя опорами. К примеру, вы используете балки как опорные брусья перекрытия для несущих стен дома, между которыми 4 м, то величина пролета будет равна 4 м.
Вычисляя прогиб деревянной балки, их считают свободно опертыми элементами конструкции. В случае балки перекрытия для расчета принимается схема с нагрузкой, которая распределена равномерно. Обозначается она символом q. Если же нагрузка несет сосредоточенный характер, то берется схема с сосредоточенной нагрузкой, обозначаемой F. Величина этой нагрузки равна весу, который будет оказывать давление на конструкцию.
Момент инерции
Геометрическая характеристика, которая получила название момент инерции, важна при проведении расчетов на прогиб балки. 3/12, где:
b – ширина сечения;
h – высота сечения балки.
Вычисления максимального уровня нагрузки
Определение максимальной нагрузки на элемент конструкции производится с учетом целого ряда факторов и показателей. Обычно при вычислении уровня нагрузки берут во внимание вес 1 погонного метра балки, вес 1 квадратного метра перекрытия, нагрузку на перекрытие временного характера и нагрузку от перегородок на 1 квадратный метр перекрытия. Также учитывается расстояние между балками, измеренное в метрах. Для примера вычисления максимальной нагрузки на деревянную балку примем усредненные значения, согласно которым вес перекрытия составляет 60 кг/м², временная нагрузка на перекрытие равна 250 кг/м², перегородки будут весить 75 кг/м². Вес самой балки очень просто вычислить, зная ее объем и плотность. Предположим, что используется деревянная балка сечением 0,15х0,2 м. В этом случае ее вес будет составлять 18 кг/пог.м. Также для примера примем расстояние между брусьями перекрытия равным 600 мм. 3/48*E*J, где:
F – сила давления на брус.
Также обращаем внимание на то, что значение модуля упругости, используемое в расчетах, может различаться для разных видов древесины. Влияние оказывают не только порода дерева, но и вид бруса. Поэтому цельная балка из дерева, клееный брус или оцилиндрованное бревно будут иметь разные модули упругости, а значит, и разные значения максимального прогиба.
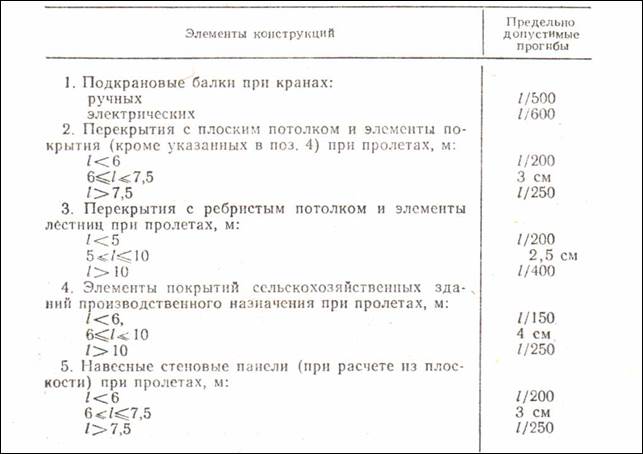
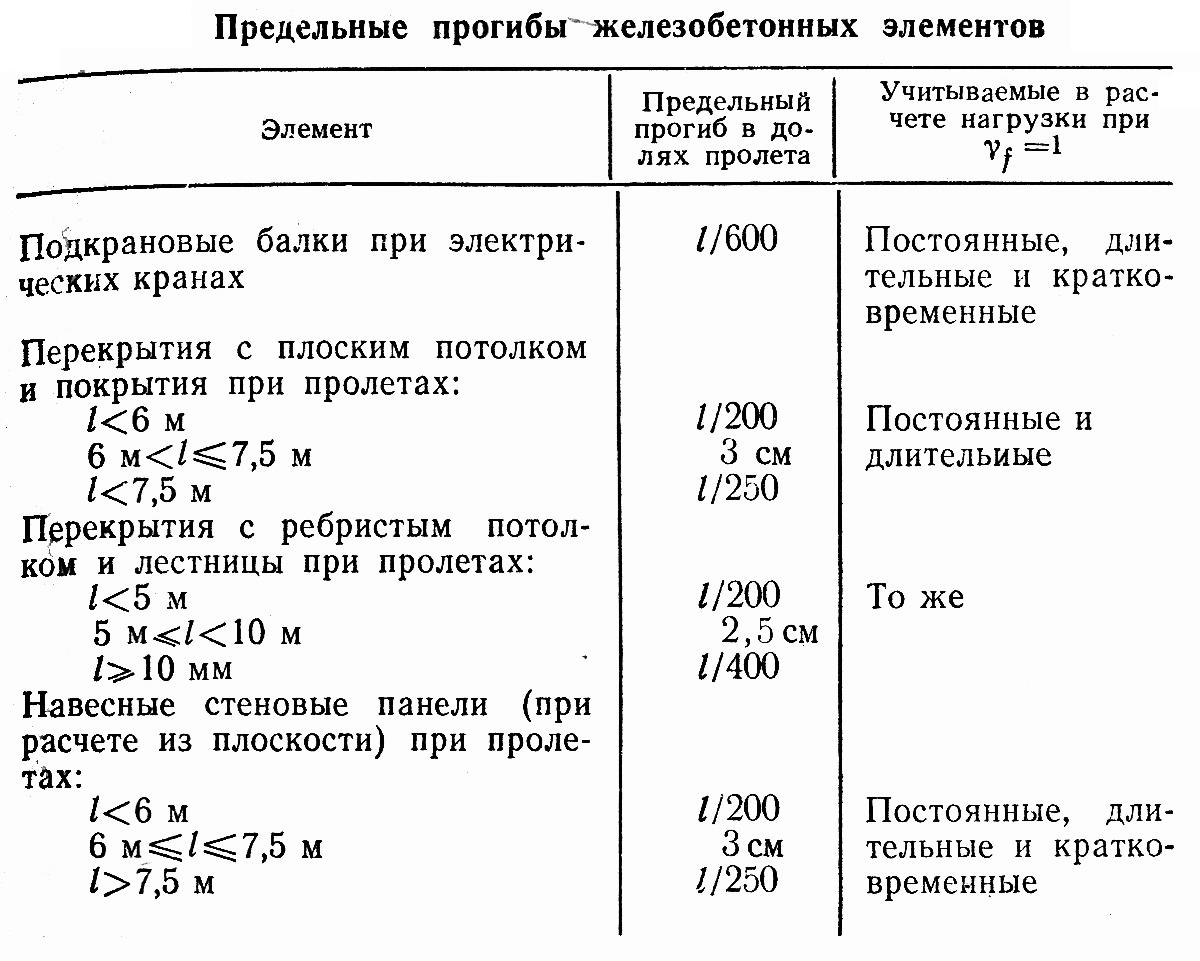
Вы можете преследовать разные цели, совершая расчет балок на прогиб. Если вы хотите узнать пределы деформации элементов конструкции, то по завершении расчета стрелки прогиба вы можете остановиться. Если же ваша цель – установить уровень соответствия найденных показателей строительным нормам, то их нужно сравнить с данными, которые размещены в специальных документах нормативного характера.
Двутавровая балка
Обратите внимание на то, что балки из двутавра применяются несколько реже в силу их формы. Однако также не стоит забывать, что такой элемент конструкции выдерживает гораздо большие нагрузки, чем уголок или швеллер, альтернативой которых может стать двутавровая балка.
Расчет прогиба двутавровой балки стоит производить в том случае, если вы собираетесь использовать ее в качестве мощного элемента конструкции.
Также обращаем ваше внимание на то, что не для всех типов балок из двутавра можно производить расчет прогиба. В каких же случаях разрешено рассчитать прогиб двутавровой балки? Всего таких случаев 6, которые соответствуют шести типам двутавровых балок. Эти типы следующие:
- Балка однопролетного типа с равномерно распределенной нагрузкой.
- Консоль с жесткой заделкой на одном конце и равномерно распределенной нагрузкой.
- Балка из одного пролета с консолью с одной стороны, к которой прикладывается равномерно распределенная нагрузка.
- Однопролетная балка с шарнирным типом опирания с сосредоточенной силой.
- Однопролетная шарнирно опертая балка с двумя сосредоточенными силами.
- Консоль с жесткой заделкой и сосредоточенной силой.
Металлические балки
Расчет максимального прогиба одинаковый, будь это стальная балка или же элемент из другого материала. Главное — помнить о тех величинах, которые специфические и постоянные, как к примеру модуль упругости материала. При работе с металлическими балками, важно помнить, что они могут быть изготовлены из стали или же из двутавра. Прогиб металлической балки, изготовленной из стали, вычисляется с учетом, что константа Е в данном случае составляет 2·105Мпа. Все остальные элементы, вроде момента инерции, вычисляются по алгоритмам, описанным выше.
Расчет максимального прогиба для балки с двумя опорами
В качестве примера рассмотрим схему, в которой балка находится на двух опорах, а к ней прикладывается сосредоточенная сила в произвольной точке. До момента прикладывания силы балка представляла собой прямую линию, однако под воздействием силы изменила свой вид и вследствие деформации стала кривой.
Предположим, что плоскость ХУ является плоскостью симметрии балки на двух опорах. Все нагрузки действуют на балку в этой плоскости. В этом случае фактом будет то, что кривая, полученная в результате действия силы, также будет находиться в этой плоскости. Данная кривая получила название упругой линии балки или же линии прогибов балки. Алгебраически решить упругую линию балки и рассчитать прогиб балки, формула которого будет постоянной для балок с двумя опорами, можно следующим образом.
Прогиб на расстоянии z от левой опоры балки при 0 ≤ z ≤ a
F(z)=(P*a²*b²)/(6E*J*l)*(2*z/a+z/b-z³/a²*b)
Прогиб балки на двух опорах на расстоянии z от левой опоры при а ≤ z ≤l
f(z)=(-P*a²*b²)/(6E*J*l)*(2*(l-z)/b+(l-z)/a-(l-z)³/a+b²), где Р – прикладываемая сила, Е – модуль упругости материала, J – осевой момент инерции.
В случае балки с двумя опорами момент инерции вычисляется следующим образом:
J=b₁h₁³/12, где b₁и h₁– значения ширины и высоты сечения используемой балки соответственно.
Заключение
В заключение можно сделать вывод о том, что самстоятельно вычислить величину максимального прогиба балки разных типов достаточно просто. Как было показано в этой статье, главное — знать некоторые характеристики, которые зависят от материала и его геометрических характеристик, а также провести вычисления по нескольким формулам, в которых каждый параметр имеет свое объяснение и не берется из ниоткуда.
Прогиб балки — BOLD
«Перегруженные балки могут привести к остановке вашей работы. Узнайте, как обезопасить своих сотрудников и максимально повысить производительность склада».

Основы отклонения балки
По мере того, как компании максимизируют потенциал хранения на своих складах, перегруженные системы являются общей проблемой. Во время складских инспекций наши инженеры регулярно выявляют отклоненные балки, представляющие угрозу безопасности сотрудников и продукции.
Когда отклоненный луч становится опасным?
Стандартная отраслевая формула для определения перегруженной балки рассчитывается путем деления длины балки на 180. Например, максимальное отклонение балки 96 дюймов не должно превышать 0,53 дюйма.
Почему это должно беспокоить мой бизнес?
- Правильно установленные балки с надлежащими предохранительными замками рассчитаны на отклонение под нагрузкой. Слишком большой прогиб может нарушить целостность балки и создать ненужный риск.
- Когда перегруженные балки и последующие отклонения превышают отраслевые стандарты, поддоны начинают опускаться к центру балки, что приводит к поломке материала и травмам операторов вилочных погрузчиков во время установки и удаления поддонов.
Что можно сделать, чтобы предотвратить отклонение балки?
- Регулярные проверки безопасности обеспечивают надлежащий контроль и соблюдение отраслевых стандартов стеллажей.
- Текущие инженерные расчеты и знаки грузоподъемности помогают сотрудникам лучше понять ограничения системы.
- Обучение сотрудников правильной вместимости стоек и использованию каждого уровня имеет решающее значение для максимального использования системы, сохраняя при этом безопасность в качестве приоритета.
Как мы можем поддерживать соответствие между проверками?
- Балки рассчитаны на отклонение под нагрузкой, но важно понимать, когда отклонение становится опасным. Ниже приведен быстрый метод выборочной проверки отклонения.
- Выборочная проверка прогиба:
  1. Измерьте длину балки и разделите ее на 180, чтобы определить максимальный предел
  2. Прикрепите шнур от одного соединителя к другому вдоль нижней части балки
  3. Измерьте расстояние от натянутой струны до нижней части балки
  4. Определите любые балки, которые отклоняются или близки к отклонению больше, чем рекомендуется
Для получения дополнительной информации посетите веб-сайт: www.mhi.org/rmi/faq
Насколько допустимо отклонение?
При нормальных расчетных рабочих нагрузках балки обычно проектируются с учетом вертикальных отклонений, не превышающих 1/180 (или 0,55 процента) горизонтальной длины балки, измеренной относительно концов балок.
Некоторые пользователи могут указать требование меньшего отклонения для внешнего вида или косметических целей. Тем не менее, другие пользователи с системами, предназначенными для использования более точного автоматизированного оборудования для хранения и извлечения, могут указывать требования к меньшему отклонению. (См. Спецификацию ANSI/RMI, раздел 5.3, комментарий к разделу 5.3).
https://www.mhi.org/rmi/faq
Похожие сообщения
| 16 сентября 2021 г.
Подробнее
| 11 сентября 2021 г.
Подробнее
| 13 августа 2021 г.
Подробнее
| 13 июля 2021 г.
Подробнее
| 10 мая 2021 г.
Подробнее
|
10 мая 2021 г.
Подробнее
| 10 мая 2021 г.
Подробнее
| 10 мая 2021 г.
Подробнее
| 10 мая 2021 г.
Подробнее
| 4 марта 2021 г.
Подробнее
Формула прогиба балок с диаграммами для всех условий.
15.05.2021 19.07.2020 Вики
когда есть вертикальное смещение в любой точке нагруженной балки, говорят, что это отклонение балок . Максимальный прогиб балок происходит там, где уклон равен нулю.
Наклон луча определяется как угол между отклоненным лучом и фактическим лучом в той же точке.

Общие и стандартные уравнения для прогиба балок приведены ниже: = Модуль Юнга,
I = Момент инерции .
Продукт E. I известен как жесткость на изгиб .
Существует много типов балок, и для этих различных типов балок или случаев формула не будет одинаковой. Он должен быть изменен в зависимости от случая или типа луча. Теперь давайте рассмотрим следующие случаи.
1. Свободно поддерживаемая балка с центральной точечной нагрузкой:
Свободно опертая балка AB длиной l несет точечную нагрузку в центре балки в точке C. отклонение в точка C будет:
2. Свободно опертая балка с внецентренной точечной нагрузкой:
Свободно опертая балка AB длиной 9012 8 л несет внецентренную точечную нагрузку на C , как показано на рис. Отклонение балки определяется следующим образом:
Поскольку b > a , поэтому максимальное отклонение происходит в CB , а его расстояние от B определяется как:
а максимальное отклонение определяется выражением :

3. Свободно опертая балка с равномерно распределенной нагрузкой :
Свободно опертая балка AB при равномерно распределенной нагрузке w /единица длины показана на рисунке ,
Максимальное отклонение происходит в средней точке C и определяется как:
90 129 4. Свободно поддерживаемая балка с Постепенно меняющаяся нагрузка:
Свободно поддерживаемая балка из AB длиной l , несущая постепенно изменяющуюся нагрузку от нуля в B до w/единицы длины в A , показана на рисунке ниже. ,
Максимальное отклонение балки происходит, когда x = 0,519 l и его значение определяется как:
5. Консольная балка с точечной нагрузкой на свободном конце:
Консоль балка АВ длиной l , несущая на свободном конце точечную нагрузку, показана на рис. Прогиб в любом сечении х на расстоянии х от свободного конца определяется как:
Максимальный прогиб происходит на свободном конце (когда x = 0 ) и его значение определяется выражением
6. Консольная балка с равномерно распределенной нагрузкой:
90 055

Консоль балка AB длиной l , несущая равномерно распределенную нагрузку на единицу длины, показана на рис. Прогиб в любом сечении х на расстоянии х от В определяется выражением
Максимальное отклонение происходит на свободном конце (когда x = 0), а его значение определяется

, когда консоль частично загружается, как показано на рис. расстояние от фиксированного конца) определяется как:
и максимальное отклонение происходит на B , значение которого определяется как
7. Консольная балка с постепенно изменяющейся нагрузкой:
Консольная балка AB длиной 901 28 л с постепенно меняющейся нагрузкой от нуля до B на единицу длины A показан на рис. Прогиб в любом сечении X на расстоянии x от B определяется как
Максимальный прогиб происходит на свободном конце (при x = 0) и его значение определяется как
8. Неподвижная балка, несущая центральную точечную нагрузку:
Неподвижная балка AB длиной l , несущая точечную нагрузку в центре балки C , как показано на рис. Максимальное отклонение балки происходит при C , и его значение определяется как
9. Неподвижная балка, несущая внецентренную нагрузку:
Фиксированная балка AB длиной л с эксцентриком загрузить в C , как показано на рис. Прогиб в любом сечении X на расстоянии x от A определяется как
Максимальное расстояние возникает, когда

90 298 Отсюда Максимальное отклонение луча,
и прогиб под нагрузкой при C ,
10.