Как отмерить угол 45 градусов без транспортира: Угол 45 градусов

Измерения и построение углов при проведении различных работ. Золотой египетский треугольник.

Часто домашнему мастеру необходимо срочно произвести какое либо измерение или сделать разметку под определенным углом, а под рукой нет либо угольника, либо транспортира. В этом случае его выручат несколько простых правил.

Угол 90 градусов.

Если нужно срочно построить прямой угол, а угольника нет, можно воспользоваться любым печатным изданием. Угол бумажного листа — очень точный прямой угол ( 90 град.). Резательные (вырубочные) машины в типографиях настроены очень точно. Иначе исходный рулон бумаги начнет резаться вкривь и вкось. Поэтому вы можете быть уверены, что этот угол — именно прямой.

А если нет даже печатного издания или необходимо построить угол на местности, например при разметке фундамента или листа фанеры с неровными краями? В этом случае нам поможет правило золотого (или египетского) треугольника.

Золотым (или египетским, или Пифагоровым) треугольником называется треугольник со сторонами, которые соотносятся друг с другом как 5:4:3.

По теореме Пифагора, у прямоугольного треугольника квадрат гипотенузы равен сумме квадратов катетов. Т.е. 5х5 = 4х4 + 3х3. 25=16+9 и это неоспоримо.

Поэтому для построения прямого угла достаточно на заготовке провести прямую линию длиной 5 (10,15,20 и т.д. кратной 5 см). А затем, из краев этой линии начать отмерять с одной стороны 4 (8,12,16 и т.д кратно 4 см), а с другой — 3 (6,9,12,15 и т.д. кратно 3 см) расстояния. Должны получиться дуги с радиусом 4 и 3 см. Где эти дуги пересекутся между собой и будет прямой (90 градусов) угол.

Угол 45 градусов.

Такие углы обычно применяют при изготовлении прямоугольных рамок. Материал из которого делается рамка (багет) пилится под углом 45 градусов и стыкуется. Если под рукой нет стусла или транспортира, получить шаблон угла в 45 градусов можно следующим образом. Необходимо взять лист писчей бумаги или любого печатного издания и согнуть его так, что бы линия сгиба проходила точно через угол, а края загнутого листа совпадали.

Получившийся угол и будет равен 45 градусам.

Угол 30 и 60 градусов.

Угол в 60 градусов требуется для построения равносторонних треугольников. Например, вам надо напилить такие треугольники для декоративных работ или точно установить силовой укос. Угол в 30 градусов редко применяется в чистом виде. Однако с его помощью (и с помощью угла в 90 градусов) строится угол 120 градусов. А это угол, необходимый для построения равносторонних шестиугольников, фигуры весьма популярной у столяров.

Для построения весьма точного шаблона этих углов в любой момент необходимо запомнить константу (число) 173. Они вытекает из соотношений синусов и косинусов этих углов.

Возьмите лист бумаги из любого печатного издания. Его угол равен точно 90 градусам. От угла по одной стороне отмерьте 100 мм (10 см.), а по другой — 173 мм (17,3 см). Соедините эти точки. Таким образом мы и получили шаблон, у которого один угол 90 градусов, один 30 градусов и один 60 градусов. Можете проверить на транспортире — все точно!

Запомните это число — 173, и вы всегда сможете построить углы в 30 и 60 градусов.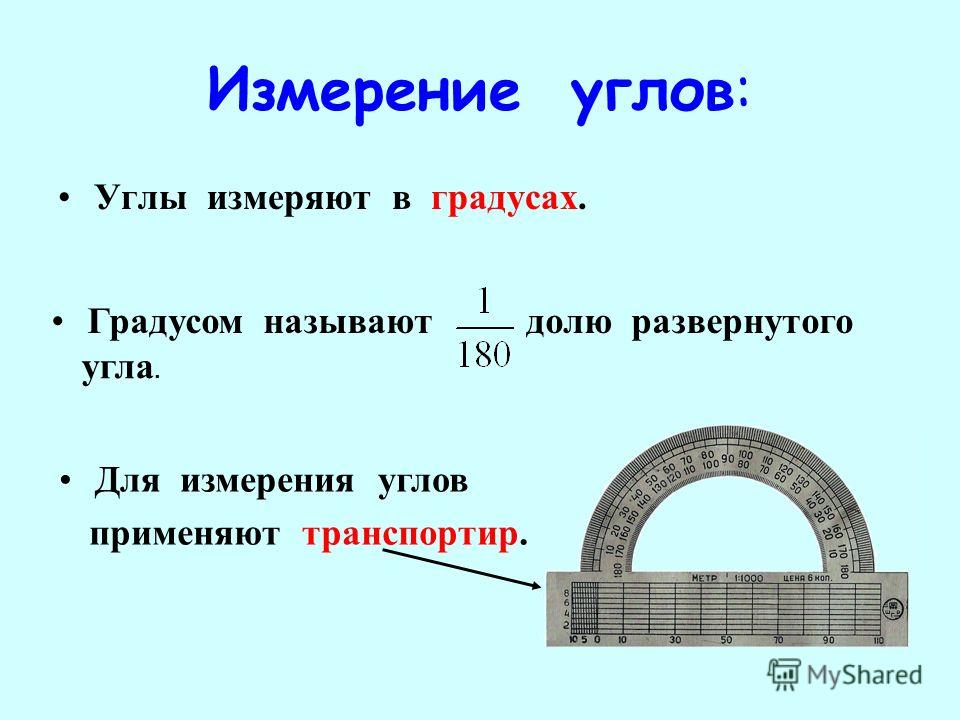

Прямоугольность заготовки.

При разметке заготовок или построений на деталях кроме самих углов весьма важно и их соотношение. Особенно это важно при изготовлении прямоугольных деталей или например при разметке фундамента, раскрое больших листов материала. Неправильное построение или разметка приносит впоследствии много лишней работы или к появлению большого числа отходов.

К сожалению, даже весьма точные разметочные инструменты, даже профессиональные, всегда имеют определенную погрешность.

Между тем, существует весьма простой метод определения прямоугольности детали или построения. В прямоугольнике диагонали абсолютно равны! Значит, после построения необходимо измерить длины диагоналей прямоугольника. Если они равны, все в порядке, это действительно прямоугольник. А если нет — вы построили параллелограмм или ромб. В этом случае следует немного «поиграть» смежными сторонами, что бы добиться точного (для данного случая) равенства диагоналей размечаемого прямоугольника.

К. Тимошенко

Как проверить прямой угол без угольника

При отделочных работах и строительстве бывает нужна четкая геометрия: перпендикулярные стены и иные конструкции, требующие прямого угла в 90 градусов. Обыкновенный угольник не может позволить проверить или разметить углы со сторонами в несколько метров. Описываемый же метод превосходно подходит для разметки или проверки любых углов — длинна сторон не ограничена. Основной инструмент для измерений — рулетка.

Мы будем рассматривать точную разметку прямого угла, а также метод проверки уже размеченных углов на стенах и других объектах.

Теорема Пифагора

Теорема основана на утверждении, что у прямоугольного треугольника сумма квадратов длин катетов равна квадрату длины гипотенузы. В виде формулы записывается это так:

a²+b²=c²

Стороны a и b — катеты, между которыми угол равен ровно 90 градусов.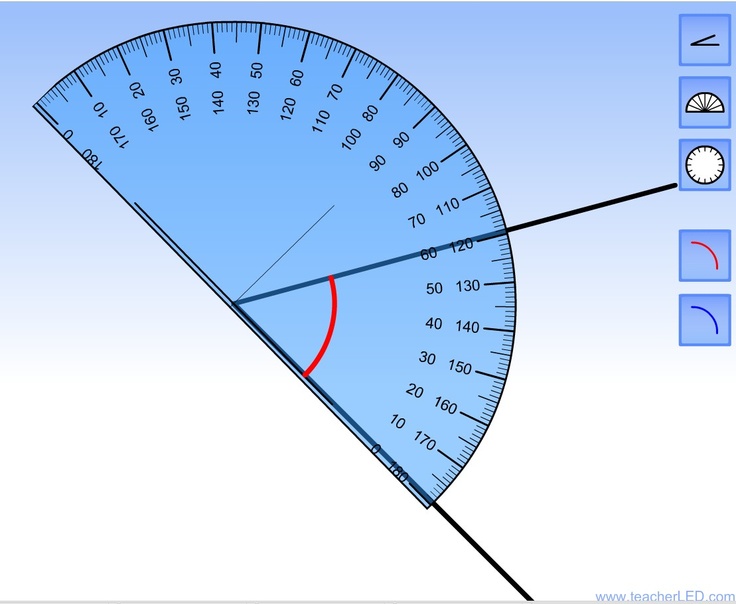 Следовательно, сторона c — гипотенуза. Подставляя в эту формулу две известные величины, мы можем вычислить третью, неизвестную. А следовательно можем размечать прямые углы, а также проверять их.

Теорема Пифагора известна еще под названием «египетский треугольник». Это треугольник со сторонами 3, 4 и 5, причем совершенно не важно, в каких единицах длинны. Между сторонами 3 и 4 — ровно девяносто градусов. Проверим данное утверждение вышеприведенной формулой: a²+b²=c² = (3×3)+(4×4) = 9+16 = (5×5) = 25 — все сходится!

А теперь применим теорему на практике.

Проверка прямого угла

Начнем с самого простого — проверки прямого угла с помощью теоремы Пифагора. Самым частым примером в отделке и строительстве является проверка перпендикулярности стен. Перпендикулярные стены — это стены, расположенные друг к другу под прямым углом 90°.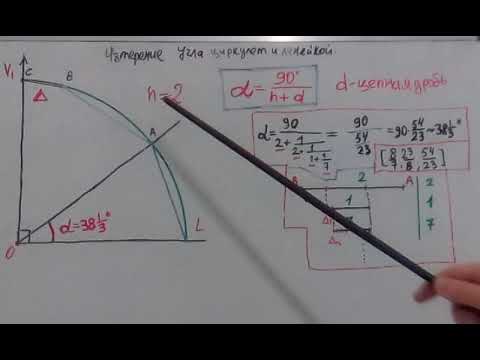

Итак, берем любой проверяемый внутренний угол. На стенах (на одной высоте) или на полу отмечаем на обоих стенах отрезки произвольных длин. Длинна этих отрезков произвольная, по возможности нужно отмечать как можно больше, но чтобы между отметками на стенах удобно было мерить диагональ. Например, мы отметили 2,5 метра (или 250 см.) на одной стене и 3 метра (или 300 см.) на другой. Теперь длину отрезка каждой стены возводим в квадрат (умножаем саму на себя) и получившиеся произведения складываем. Выглядит это так: (2,5×2,5)+(3×3)=15,25 — это диагональ в квадрате. Теперь нужно извлечь из этого числа квадратный корень √15,25≈3,90 — 3,9 метра должна составлять диагональ между нашими отметками. Если измерение рулеткой показывает другую длину диагонали — проверяемый угол развернут и имеет отклонение от 90°.

Калькулятор расчета диагонали прямого угла

Внимание! Для работы калькулятора необходимо включить поддержку JavaScript в вашем браузере!

Длина a

Длина b

Диагональ c

Извлечение квадратного корня никогда меня не привлекало — простому человеку не обойтись без калькулятора, к тому же, не на всех мобильных устройствах калькуляторы умеют извлекать его. Поэтому можно пользоваться упрощенным методом. Нужно лишь запомнить: у прямого угла со сторонами ровно 100 сантиметров, диагональ равна 141,4 см. Таким образом, у прямого угла со сторонами 2 м. — диагональ равна 282,8 см. То есть на каждый метр плоскости приходится 141,4 см. У этого метода один недостаток: от измеряемого угла нужно откладывать одинаковые расстояния на обеих стенах и отрезки эти должны быть кратны метру. Не буду утверждать, но по моей скромной практике — это гораздо удобнее. Хотя не стоит забывать о первоначальном способе совсем — в некоторых случаях он очень актуален.

Сразу же возникает вопрос: какое отклонение от вычисленной длинны диагонали считать нормой (погрешностью), а какое нет? Если проверяемый угол с отмеченными сторонами по 1 м. будет 89°, то диагональ уменьшится до 140 см. Из понимания этой зависимости можно сделать объективный вывод, что погрешность диагонали 141,4 см. в несколько миллиметров не даст отклонения в один целый градус.

Как проверить внешний угол? Проверка внешнего угла по сути не отличается, нужно лишь продлить линии каждой стены на полу (или земле, при помощи шнура) и получившийся внутренний угол измерить обычным способом.

Как разметить прямой угол рулеткой

Разметка может основываться как на общей теореме Пифагора, так и на принципе «египетского треугольника». Однако это только в теории линии просто чертятся на бумаге, «ловить» же все выбранные размеры растянутыми шнурами или линиями на полу — задача посложнее.

Поэтому я предлагаю упрощенный способ, основанный на диагонали 141,4 см. у треугольника со сторонами 100 см. Вся последовательность разметки изображена на картинках ниже. Важно не забывать: диагональ 141,4 см. нужно умножать на количество метров в отрезке А-Б. Отрезки А-Б и А-В должны быть равны и соответствовать целому числу в метрах. Картинки увеличиваются по клику!

Как разметить острый угол

Гораздо реже возникает надобность в создании острых углов, в частности 45°. Для формирования подобных фигур формулы более сложные, однако это не самое проблематичное. Гораздо сложнее свести все линии, начерченные или натянутые шнурами — дело это непростое. Поэтому я предлагаю использовать упрощенный метод. Сначала размечается прямой угол 90°, а затем диагональ 141,4 делится на нужное количество равных частей. Например, чтобы получить 45°, диагональ нужно поделить пополам и от точки А провести линию через место деления. Таким образом мы получим два угла по 45 градусов. Если поделить диагональ на 3 части, то получится три угла по 30 градусов. Думаю алгоритм вам понятен.

Собственно я рассказал все, что мог рассказать, надеюсь все изложил понятным языком и у вас больше не возникнет вопросов как размечать и проверять прямые углы. Стоит добавить, что уметь делать это должен любой отделочник или строитель, ведь полагаться на строительный угольник небольшого размера — непрофессионально.

Смотрите также другие статьи

измерения и изготовления углов-Dummies

BY: Марк Райан и

Обновлены: 12-21-2021

Из книги: Геометрия для Dummies

Геометрия для Dummies

Exploore Book на Amast

На карте вы прокладываете свой маршрут и подходите к развилке дорог. Две расходящиеся дороги выходят из общей точки и образуют угол . Точка, в которой дороги расходятся, — это вершина . Угол отделяет область вокруг себя, известную в геометрии как 9.0018 плоскость , на две области. Точки внутри угла лежат во внутренней области угла, а точки вне угла лежат во внешней области угла.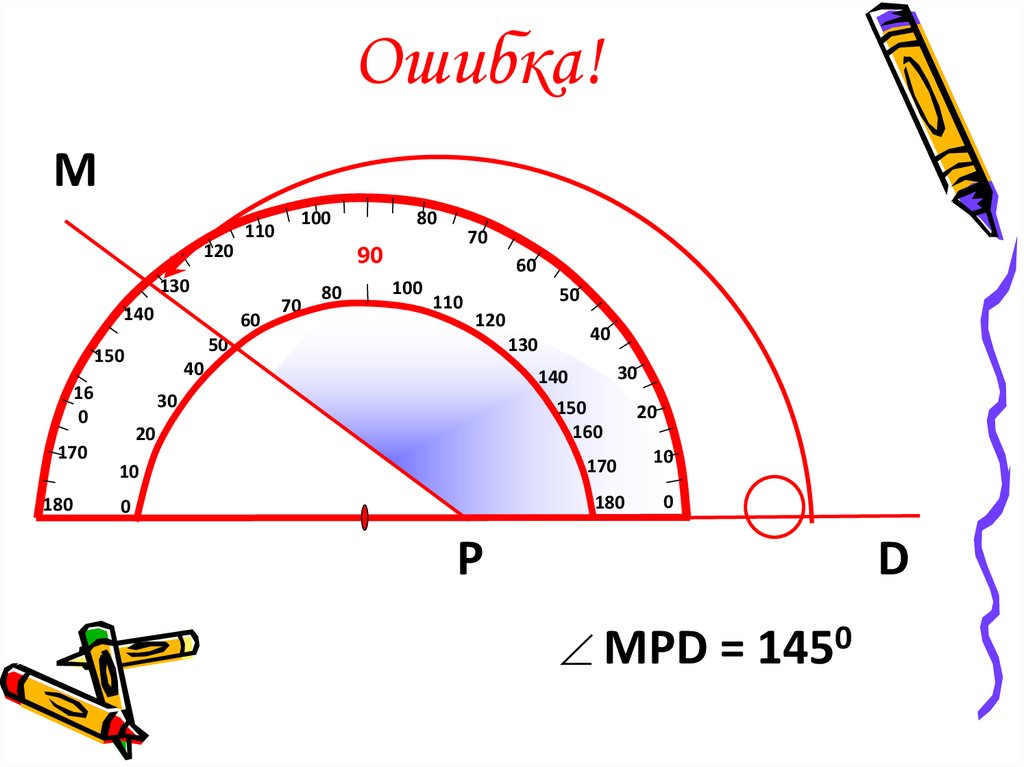

Как только вы узнаете типы углов и способы их измерения и создания, вы приобретете ценные навыки геометрии, которые помогут вам решить даже самые сложные геометрические головоломки.

Для выполнения обеих задач вы используете транспортир, очень полезный инструмент, который всегда под рукой (см. рис. 1).

Рис. 1. Удобный транспортир

Выбирая транспортир, постарайтесь найти его из прозрачного пластика. Вычислить меру угла проще, потому что вы можете видеть линию угла через транспортир.

Породы англов

Существует несколько различных угловых пород или типов. Определить, какая у вас порода угла, можно по его мерке. Наиболее распространенной мерой угла является градусов . Вот краткое введение в четыре типа углов:

• Прямой угол. С таким ракурсом вы никогда не ошибетесь. Прямой угол — один из самых легко узнаваемых углов. Он имеет форму буквы L и образует прямой угол (см. рис. 2). Он имеет меру 90 градусов.

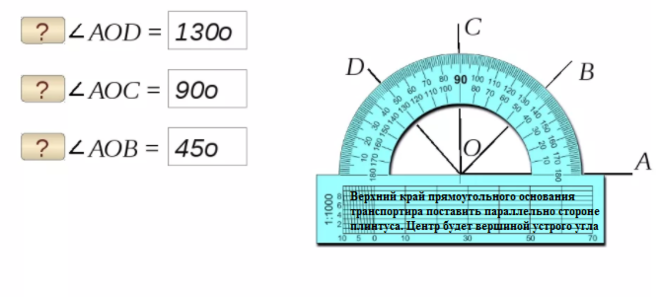
Рисунок 2: Прямой угол

• Угол прямой. Знаешь что? На самом деле это прямая линия. Большинство людей даже не думают об этом типе как об угле, но это так. Прямой угол состоит из противоположных лучей или отрезков, имеющих общий конец (см. рис. 3). Этот угол имеет меру 180 градусов.

Прямые и прямые углы довольно легко определить, просто взглянув на них, но никогда не делайте поспешных выводов о величине угла. Лучше всего быть осторожным. Если информация не написана на странице, ничего не предполагайте. Мера.

Рисунок 3: Прямой угол

• Острый угол. Это очаровательный угол .

На самом деле, это всего лишь щепотка. Это любой угол, который больше 0 градусов, но меньше 90 градусов. Острый угол находится где-то между несуществующим и прямым углом (см. рис. 4).

Рисунок 4: Острые углы при 45° (рис. a), 60° (рис. b) и 30° (рис. c)

• Тупой угол. Этот тип просто не так захватывающий, как острый угол. Его мера находится где-то между прямым углом и прямым углом (см. рисунок 5). Это холм, на который вы должны подняться, гора, на которую вы должны взойти. Он имеет меру больше 90 градусов, но меньше 180 градусов.

Рис. 5. Тупые углы при 95° (рис. a), 125° (рис. b) и 175° (рис. c)

Измерение углов

Углы чаще всего измеряются в градусах, но те из вас, кто является приверженцем точности, могут использовать даже более мелкие единицы измерения: минуты и секунды. Такие минуты и секунды подобны часам — минута больше секунды. Так что думайте о градусе как о часе, и вы поняли: один градус равен 60 минутам. Одна минута равна 60 секундам.

Прежде чем измерять угол, определите его и оцените, к какому типу, по вашему мнению, он относится. Это прямой угол? Прямой угол? Острый или тупой? После того, как вы его оцените, измерьте угол. Следуй этим шагам:

1. Поместите выемку или центральную точку транспортира в точку, где сходятся стороны угла (вершина).
2. Поместите транспортир так, чтобы одна из линий угла, который вы хотите измерить, была равна нулю (на самом деле это 0°). Использование нулевой линии не обязательно, потому что вы можете измерить угол, получив разницу в градусах одной линии по отношению к другой. Однако проще измерить угол, когда одна его сторона находится на нулевой линии. Наличие одной линии на нулевой линии позволяет вам считывать измерения непосредственно с транспортира без необходимости выполнять дополнительные математические операции. (Но если вы готовы принять вызов, нокаутируйте себя.)
3. Считайте число с транспортира там, где вторая сторона угла встречается с транспортиром.

Еще несколько советов:

• Убедитесь, что ваша мера близка к вашей оценке. Это говорит вам, правильно ли вы выбрали шкалу. Если вы ожидали измерения острого угла, но получили серьезно тупой угол, вам нужно переосмыслить используемую вами шкалу. Попробуйте другой.
• Если стороны вашего угла не достигают шкалы транспортира, удлините их так, чтобы они соответствовали. Это повысит точность измерения.
• Помните, что мера угла всегда является положительным числом.

Так что же делать, если ваш угол не совсем соответствует масштабу транспортира? Посмотрите на рисунок 6 для примера. Угол на этом рисунке имеет меру больше 180°. Что теперь? Извините, но в этом случае вам придется потратить немного больше энергии. Да, вам нужно заняться математикой. Эти углы известны как углы рефлекса, и их величина превышает 180°.

Рис. 6. Углы отражения не укладываются в шкалу транспортира, поэтому для их измерения необходимо выполнить некоторые математические действия.

Нарисуйте линию так, чтобы получилась прямая линия (см. вытянутые точки на рис. 6). Эта часть угла равна 180°, потому что это прямой угол. Теперь измерьте угол, образованный выносной линией, которую вы только что сделали, и второй стороной исходного угла, который вы хотите измерить. (Если вы запутались, просто посмотрите на рисунок 6.) Как только вы получили меру второго угла, прибавьте это число к 180. Результатом будет общее количество градусов угла. На рисунке 6 180° + 45° = 225°.

Об этой статье

Эта статья взята из книги:

• Геометрия для чайников,

Об авторе книги:

Марк Райан — основатель и владелец Математического центра в районе Чикаго, где он занимается репетиторством. по всем математическим предметам, а также при подготовке к экзаменам. Марк является автором книг «Исчисление для чайников», рабочей тетради по математическому анализу для чайников и рабочей тетради по геометрии для чайников .

Этот артикул находится в категории:

• Геометрия,

Что такое угол 45 градусов? Определение, построение, примеры

Определение угла

Когда два луча пересекаются в общей конечной точке, они образуют угол.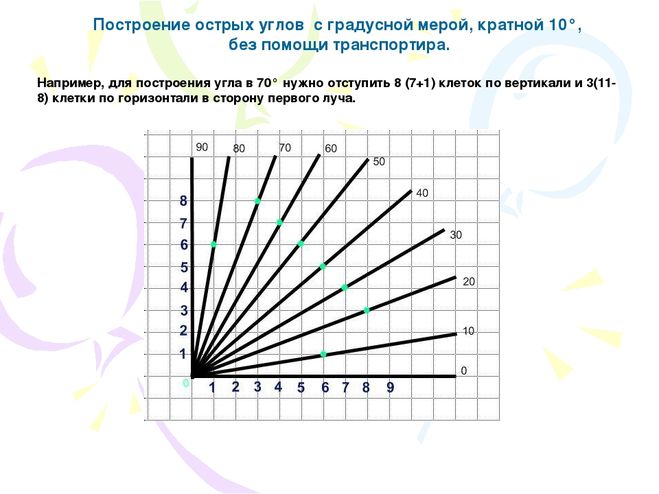 Общий конец называется вершиной, а лучи — плечами угла.

Угол измеряется в градусах или радианах. Если две стороны угла направлены в противоположные стороны, то это прямой угол. Прямой угол равен 180°. Угол можно измерить с помощью транспортира, а угол измерения в 90 градусов называется прямым углом. Под прямым углом две руки перпендикулярны друг другу.

Рекомендуемые рабочие листы:

Что такое угол 45 градусов?

Когда прямой угол делится на две равные части, каждый угол равен 45°.

Угол 45 градусов является острым углом. Это половина прямого угла или угол 90 градусов. Взгляните на изображение угла 45 градусов.

Рекомендуемые игры:

Реальные примеры угла 45 градусов

Мы можем видеть угол 45 градусов в различных местах вокруг нас. Например, если экран ноутбука правильно изогнут, он образует с клавиатурой угол в 45 градусов.
Точно так же, если дверь открыта наполовину, она образует со стеной угол в 45 градусов.

Рассмотрим следующие примеры углов в 45 градусов, встречающихся в нашей среде:

• Угол в 45 градусов позволяет солнечным лучам проходить наибольшее расстояние. Вот почему некоторые солнечные панели расположены под углом 45 градусов, в зависимости от их географического положения.
• При броске мяча угол в 45 градусов является оптимальным, потому что он достигает самого дальнего расстояния.
• В архитектуре угол 45 градусов используется для создания дизайнерских дверей и оконных решеток.

Интересные факты об угле 45 градусов

• Диагонали квадрата образуют угол 45 градусов с его сторонами.
• В равнобедренном прямоугольном треугольнике один прямой угол и два угла по 45 градусов.

Построение угла 45°:

• а) Использование транспортира

Шаги формирования угла в 45 градусов следующие:

Шаг 1 : Нарисуйте луч и назовите его AB.

Шаг 2 : Держите центр транспортира в точке A. Поскольку угол открывается вправо, выберите 45° в списке, который начинается справа и движется против часовой стрелки. Отметьте точку C.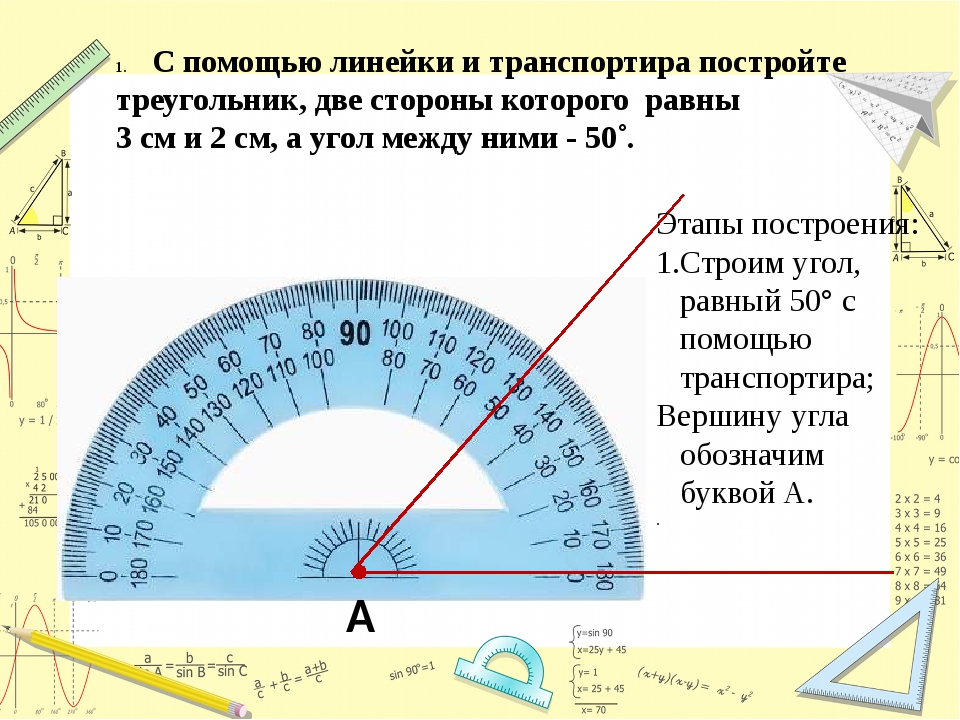

Шаг 3 : Соедините A и C. Вот меры.

а) Использование компаса

Порядок формирования угла 45 градусов следующий:

Шаг 1: Отметьте точку A, чтобы получился угол 45°.

Шаг 2: Сначала создайте угол 90°. Расширьте свой компас за пределы половины длины АВ. Отметьте дугу выше и ниже отрезка AB острым концом.

Шаг 3: Сохраняя исходную ширину циркуля, поместите его острый конец в точку B и проведите дуги выше и ниже отрезка AB, чтобы пересечься с дугами, нарисованными на шаге 2.

Шаг 4: Нарисуйте прямую линия, соединяющая две точки пересечения дуг. Эта прямая перпендикулярно делит AB пополам. P — середина AB.

Шаг 5: Разделите угол 90 градусов пополам, чтобы получился угол 45 градусов.

Вкратце, этапы построения угла 45° следующие:

1. Создайте перпендикулярные линии, чтобы получился угол 90°.
2. Разделите угол 90° пополам, чтобы получить угол 45°.

Решенные примеры

Пример 1: Чему равна четвертая часть угла 180°?

Решение:

Одна четвертая угла 180° = 180/4 = 45

Четвертая часть угла 180° составляет угол 45°.

Пример 2: Тим нарисовал горизонтальную линию на листе бумаги. Нарисовав вертикальную линию, Рон разделил ее пополам. По прибытии Джек разделил две половины еще на четыре равные половины.

Сколько углов в 45 градусов нарисовано на бумаге?

Решение:

Нарисовав вертикальную линию на горизонтальной, Тим получил два угла по 90°.

Разделение каждого 9Угол 0° пополам дает два угла 45°.

Всего имеется четыре угла по 45°..

Практические задачи

1

Примером какого типа угла является угол в 45 градусов?

Острый угол

Прямой угол

Прямой угол

Тупой угол

Правильный ответ: Острый угол
Углы меньше 90 градусов являются острыми углами.

2

Какая из следующих мер не является прямым углом?

(2 x 45) степень

90 градусов

(2 x 90) градусов

(3 x 30) градусов

Правильный ответ: (2 x 90) градусов
(2 x 90) градусов дает 180 градусов, что образует прямую линию.

3

Тупой угол _____, чем прямой угол.

Меньше

Больше

Равно

Ничего из вышеперечисленного

Правильный ответ: Больше
Углы больше 90 градусов являются тупыми.

4

Два прямых угла составляют _____ угол.

Рефлекторный угол

Прямой угол

Полный угол

Прямой угол

Правильный ответ: Прямой угол
Два прямых угла образуют угол в 180 градусов, который дает прямую линию.

5

Время на аналоговых часах, когда часовая и минутная стрелки образуют угол, который больше прямого угла, равно

15:00

23:00

17:00

14:00

17:00
Время на аналоговых часах, когда часовая и минутная стрелки образуют угол, который больше прямого угла среди заданных вариантов, составляет 17:00.

Заключение
Мы надеемся, что в этом уроке мы попытались охватить некоторые основные определения, геометрию угла 45 градусов и примеры из жизни, которые должны дать вам хотя бы базовое представление о том, что такое угол 45 градусов. -градусный угол есть. С помощью SplashLearn вы можете научиться учиться лучше. Вы можете загрузить приложение SplashLearn сегодня, которое поможет вам развеять сомнения. Установив приложение, вы сможете развеять все свои сомнения по поводу угла 45 градусов, тригонометрии и других подобных тем на своем телефоне.

Часто задаваемые вопросы

Что такое угол 45 градусов?

Угол 45 градусов — острый угол, равный 45 градусам.

Если провести биссектрису угла в 90 градусов, каждый из меньших углов будет равен 45 градусам.

Как составить угол 45 градусов?

На листе бумаги можно провести две перпендикулярные линии. Затем разделите полученный прямой угол на две равные части.