Естественная конвекция это: Чем отличается естественная конвекция от вынужденной

Естественная конвекция для горизонтально расположенного цилиндра

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 11 из 18Следующая ⇒   Расчет теплоотдачи в случае горизонтального цилиндра ( ) выполняется в соответствии с уравнением . В этой формуле к качестве определяющего размера используется диаметр цилиндра. За определяющую температуру принимается температура окружающей среды (жидкости) .     Рис. Изотермы у горизонтального цилиндра при свободной конвекции. Интерферограмма демонстрирует тепловые пограничные слои, сливающиеся сверху и создающие стационарный ламинарный факел   Естественная конвекция на тонких нагретых проволоках Средний коэффициент теплоотдачи на тонких нагретых проволоках (пленочный режим имеющий место при очень малых значениях ):   при .       Рис. Плоский конвективный факел поднимающийся от нагретой проволоки   Естественная конвекция в узких щелях, плоских и кольцевых каналах   Плотность теплового потока рассчитывается по формуле: . Эквивалентный коэффициент теплопроводности :   Рис. Изотермы в конвективном движении между соосными цилиндрами   Естественная конвекция в узких щелях, плоских и кольцевых каналах   Для воздушной прослойки, образованной двумя концентрическими сферами, уравнение для определения числа Нуссельта имеет вид , где d=δ — характерный размер. Определяющая температура равна .     Вынужденная тепловая конвекция   Общие сведения   Вынужденной конвекцией называется теплообмен, при котором движение жидкости и газа осуществляется принудительным путем. К внешним побудителям можно отнести дымовые трубы печей, насосы, вентиляторы и др. Как и в случае свободной тепловой конвекции, теплообмен происходит между жидкостью (газам) и твердой поверхностью (вынужденное обтекание пластины, цилиндра, шара, трубных пучков и др.) По характеру движения жидкости теплообмен подразделяют на два режима: ламинарное течение жидкости; турбулентное течение жидкости. Поскольку четкая граница между указанными режимами зависит от целого ряда факторов, выделяют переходную область движения жидкости. Характер движения жидкости влияет на интенсивность передачи теплоты. При ламинарном режиме и отсутствии естественной конвекции теплота передается только теплопроводностью. При турбулентном режиме перенос теплоты наряду с теплопроводностью происходит в результате перпендикулярного к поверхности перемещения частиц. Количественное определение коэффициентов теплоотдачи является одной из основных задач теории конвективного теплообмена . Для увеличения коэффициента теплоотдачи необходимо использовать жидкости с высоким значением коэффициента теплопроводности и принимать меры, приводящие к сокращению толщины теплового пограничного слоя (увеличение скорости течения жидкости, плотности, шероховатости поверхности, внешних возмущений, уменьшение вязкости жидкости).   ⇐ Предыдущая6789101112131415Следующая ⇒ Читайте также:  Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры 

Последнее изменение этой страницы: 2017-02-19; просмотров: 575; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.014 с.)

Convection — Wikipedia

Not to be confused with Conviction.

Simulation of thermal convection in the Earth’s mantle. Hot areas are shown in red, cold areas are shown in blue. A hot, less-dense material at the bottom moves upwards, and likewise, cold material from the top moves downwards.

Convection

is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow.

Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see Convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth’s atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often categorised or described by the main effect causing the convective flow, e.g. Thermal convection.

Thermal image of a newly lit Ghillie kettle. The plume of hot air resulting from the convection current is visible.

Convection cannot take place in most solids because neither bulk current flows nor significant diffusion of matter can take place. Granular convection is a similar phenomenon in granular material instead of fluids. Advection is fluid motion created by velocity instead of thermal gradients. Convective heat transfer is the intentional use of convection as a method for heat transfer.

Contents

• 1 Terminology
• 2 Mechanisms
  • 2.1 Natural convection
  • 2.2 Gravitational or buoyant convection
  • 2.3 Solid-state convection in ice
  • 2.4 Thermomagnetic convection
  • 2.5 Combustion
• 3 Examples and applications
  • 3.1 Demonstration experiments
  • 3.2 Double diffusive convection
  • 3.3 Convection cells
  • 3.4 Atmospheric convection
    • 3.4.1 Atmospheric circulation
    • 3.4.2 Weather
  • 3.5 Oceanic circulation
  • 3.6 Mantle convection
  • 3.7 Stack effect
  • 3.8 Stellar physics
  • 3.9 Water convection at freezing temperatures
  • 3.10 Nuclear reactors
• 4 Mathematical models of convection
  • 4.1 Onset
  • 4.2 Turbulence
  • 4. 3 Behavior
• 5 Natural convection from a vertical plate
• 6 Pattern formation
• 7 See also
• 8 References
• 9 External links

Terminology[edit]

The word convection has different but related usages in different scientific or engineering contexts or applications. The broader sense is in fluid mechanics, where

convection refers to the motion of fluid driven by density (or other property) difference.^[1][2]

In thermodynamics «convection» often refers to heat transfer by convection, where the prefixed variant Natural Convection is used to distinguish the fluid mechanics concept of Convection (covered in this article) from convective heat transfer.^[3]

Some phenomena which result in an effect superficially similar to that of a convective cell may also be (inaccurately) referred to as a form of convection, e.g. thermo-capilliary convection and Granular convection.

Mechanisms[edit]

Convection may happen in fluids at all scales larger than a few atoms. There are a variety of circumstances in which the forces required for convection arise, leading to different types of convection, described below. In broad terms, convection arises because of body forces acting within the fluid, such as gravity.

Natural convection[edit]

Rayleigh–Bénard cells.

This color schlieren image reveals thermal convection originating from heat conduction from a human hand (in silhouette) to the surrounding still atmosphere, initially by diffusion from the hand to the surrounding air, and subsequently also as advection as the heat causes the air to start to move uppwards.

Natural convection is a type of flow, of motion of a liquid such as water or a gas such as air, in which the fluid motion is not generated by any external source (like a pump, fan, suction device, etc.) but by some parts of the fluid being heavier than other parts. In most cases this leads to natural circulation, the ability of a fluid in a system to circulate continuously, with gravity and possible changes in heat energy. The driving force for natural convection is gravity. For example if there is a layer of cold dense air on top of hotter less dense air, gravity pulls more strongly on the denser layer on top, so it falls while the hotter less dense air rises to take its place. This creates circulating flow: convection. As it relies on gravity, there is no convection in free-fall (inertial) environments, such as that of the orbiting International Space Station. Natural convection can occur when there are hot and cold regions of either air or water, because both water and air become less dense as they are heated. But, for example, in the world’s oceans it also occurs due to salt water being heavier than fresh water, so a layer of salt water on top of a layer of fresher water will also cause convection.

Natural convection has attracted a great deal of attention from researchers because of its presence both in nature and engineering applications. In nature, convection cells formed from air raising above sunlight-warmed land or water are a major feature of all weather systems. Convection is also seen in the rising plume of hot air from fire, plate tectonics, oceanic currents (thermohaline circulation) and sea-wind formation (where upward convection is also modified by Coriolis forces). In engineering applications, convection is commonly visualized in the formation of microstructures during the cooling of molten metals, and fluid flows around shrouded heat-dissipation fins, and solar ponds. A very common industrial application of natural convection is free air cooling without the aid of fans: this can happen on small scales (computer chips) to large scale process equipment.

Natural convection will be more likely and more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection or a larger distance through the convecting medium. Natural convection will be less likely and less rapid with more rapid diffusion (thereby diffusing away the thermal gradient that is causing the convection) or a more viscous (sticky) fluid.

The onset of natural convection can be determined by the Rayleigh number (Ra).

Note that differences in buoyancy within a fluid can arise for reasons other than temperature variations, in which case the fluid motion is called gravitational convection (see below). However, all types of buoyant convection, including natural convection, do not occur in microgravity environments. All require the presence of an environment which experiences g-force (proper acceleration).

The difference of density in the fluid is the key driving mechanism. If the differences of density are caused by heat, this force is called as «thermal head» or «thermal driving head.» A fluid system designed for natural circulation will have a heat source and a heat sink. Each of these is in contact with some of the fluid in the system, but not all of it. The heat source is positioned lower than the heat sink.

Most materials that are fluid at common temperatures expand when they are heated, becoming less dense. Correspondingly, they become denser when they are cooled. At the heat source of a system of natural circulation, the heated fluid becomes lighter than the fluid surrounding it, and thus rises. At the heat sink, the nearby fluid becomes denser as it cools, and is drawn downward by gravity. Together, these effects create a flow of fluid from the heat source to the heat sink and back again.

Gravitational or buoyant convection[edit]

Gravitational convection is a type of natural convection induced by buoyancy variations resulting from material properties other than temperature. Typically this is caused by a variable composition of the fluid. If the varying property is a concentration gradient, it is known as solutal convection.^[4] For example, gravitational convection can be seen in the diffusion of a source of dry salt downward into wet soil due to the buoyancy of fresh water in saline.^[5]

Variable salinity in water and variable water content in air masses are frequent causes of convection in the oceans and atmosphere which do not involve heat, or else involve additional compositional density factors other than the density changes from thermal expansion (see thermohaline circulation). Similarly, variable composition within the Earth’s interior which has not yet achieved maximal stability and minimal energy (in other words, with densest parts deepest) continues to cause a fraction of the convection of fluid rock and molten metal within the Earth’s interior (see below).

Gravitational convection, like natural thermal convection, also requires a g-force environment in order to occur.

Solid-state convection in ice[edit]

Ice convection on Pluto is believed to occur in a soft mixture of nitrogen ice and carbon monoxide ice. It has also been proposed for Europa,^[6] and other bodies in the outer solar system.^[7]

Thermomagnetic convection[edit]

Main article: Thermomagnetic convection

Thermomagnetic convection can occur when an external magnetic field is imposed on a ferrofluid with varying magnetic susceptibility. In the presence of a temperature gradient this results in a nonuniform magnetic body force, which leads to fluid movement. A ferrofluid is a liquid which becomes strongly magnetized in the presence of a magnetic field.

Combustion[edit]

In a zero-gravity environment, there can be no buoyancy forces, and thus no convection possible, so flames in many circumstances without gravity smother in their own waste gases. Thermal expansion and chemical reactions resulting in expansion and contraction gases allows for ventilation of the flame, as waste gases are displaced by cool, fresh, oxygen-rich gas. moves in to take up the low pressure zones created when flame-exhaust water condenses.

Examples and applications[edit]

Systems of natural circulation include tornadoes and other weather systems, ocean currents, and household ventilation. Some solar water heaters use natural circulation. The Gulf Stream circulates as a result of the evaporation of water. In this process, the water increases in salinity and density. In the North Atlantic Ocean, the water becomes so dense that it begins to sink down.

Convection occurs on a large scale in atmospheres, oceans, planetary mantles, and it provides the mechanism of heat transfer for a large fraction of the outermost interiors of our sun and all stars. Fluid movement during convection may be invisibly slow, or it may be obvious and rapid, as in a hurricane. On astronomical scales, convection of gas and dust is thought to occur in the accretion disks of black holes, at speeds which may closely approach that of light.

Demonstration experiments[edit]

Thermal circulation of air masses

Thermal convection in liquids can be demonstrated by placing a heat source (e.g. a Bunsen burner) at the side of a container with a liquid. Adding a dye to the water (such as food colouring) will enable visualisation of the flow.^[8][9]

Another common experiment to demonstrate thermal convection in liquids involves submerging open containers of hot and cold liquid coloured with dye into a large container of the same liquid without dye at an intermediate temperature (eg. a jar of hot tap water coloured red, a jar of water chilled in a fridge coloured blue, lowered into a clear tank of water at room temperature).^[10]

A third approach is to use two identical jars, one filled with hot water dyed one colour, and cold water of another colour. One jar is then temporarily sealed (eg. with a piece of card), inverted and placed on top of the other. When the card is removed, if the jar containing the warmer liquid is placed on top no convection will occur. If the jar containing colder liquid is placed on top, a convection current will form spontaneously.^[11]

Convection in gases can be demonstrated using a candle in a sealed space with an inlet and exhaust port. The heat from the candle will cause a strong convection current which can be demonstrated with a flow indicator, such as smoke from another candle, being released near the inlet and exhaust areas respectively.^[12]

Double diffusive convection[edit]

Main article: Double diffusive convection

Convection cells[edit]

Main article: Convection cell

Convection cells in a gravity field

A convection cell, also known as a Bénard cell, is a characteristic fluid flow pattern in many convection systems. A rising body of fluid typically loses heat because it encounters a colder surface. In liquid, this occurs because it exchanges heat with colder liquid through direct exchange. In the example of the Earth’s atmosphere, this occurs because it radiates heat. Because of this heat loss the fluid becomes denser than the fluid underneath it, which is still rising. Since it cannot descend through the rising fluid, it moves to one side. At some distance, its downward force overcomes the rising force beneath it, and the fluid begins to descend. As it descends, it warms again and the cycle repeats itself.

Atmospheric convection[edit]

Main article: Atmospheric convection

Atmospheric circulation[edit]

Main article: Atmospheric circulation

Idealised depiction of the global circulation on Earth

Atmospheric circulation is the large-scale movement of air, and is a means by which thermal energy is distributed on the surface of the Earth, together with the much slower (lagged) ocean circulation system. The large-scale structure of the atmospheric circulation varies from year to year, but the basic climatological structure remains fairly constant.

Latitudinal circulation occurs because incident solar radiation per unit area is highest at the heat equator, and decreases as the latitude increases, reaching minima at the poles. It consists of two primary convection cells, the Hadley cell and the polar vortex, with the Hadley cell experiencing stronger convection due to the release of latent heat energy by condensation of water vapor at higher altitudes during cloud formation.

Longitudinal circulation, on the other hand, comes about because the ocean has a higher specific heat capacity than land (and also thermal conductivity, allowing the heat to penetrate further beneath the surface ) and thereby absorbs and releases more heat, but the temperature changes less than land. This brings the sea breeze, air cooled by the water, ashore in the day, and carries the land breeze, air cooled by contact with the ground, out to sea during the night. Longitudinal circulation consists of two cells, the Walker circulation and El Niño / Southern Oscillation.

Weather[edit]

See also: Cloud, Thunderstorm, and Wind

How Foehn is produced

Some more localized phenomena than global atmospheric movement are also due to convection, including wind and some of the hydrologic cycle. For example, a foehn wind is a down-slope wind which occurs on the downwind side of a mountain range. It results from the adiabatic warming of air which has dropped most of its moisture on windward slopes.^[13] Because of the different adiabatic lapse rates of moist and dry air, the air on the leeward slopes becomes warmer than at the same height on the windward slopes.

A thermal column (or thermal) is a vertical section of rising air in the lower altitudes of the Earth’s atmosphere. Thermals are created by the uneven heating of the Earth’s surface from solar radiation. The Sun warms the ground, which in turn warms the air directly above it. The warmer air expands, becoming less dense than the surrounding air mass, and creating a thermal low.^[14][15] The mass of lighter air rises, and as it does, it cools by expansion at lower air pressures. It stops rising when it has cooled to the same temperature as the surrounding air. Associated with a thermal is a downward flow surrounding the thermal column. The downward moving exterior is caused by colder air being displaced at the top of the thermal. Another convection-driven weather effect is the sea breeze.^[16][17]

Stages of a thunderstorm’s life.

Warm air has a lower density than cool air, so warm air rises within cooler air,^[18] similar to hot air balloons.^[19] Clouds form as relatively warmer air carrying moisture rises within cooler air. As the moist air rises, it cools, causing some of the water vapor in the rising packet of air to condense.^[20] When the moisture condenses, it releases energy known as latent heat of condensation which allows the rising packet of air to cool less than its surrounding air,^[21] continuing the cloud’s ascension. If enough instability is present in the atmosphere, this process will continue long enough for cumulonimbus clouds to form, which support lightning and thunder. Generally, thunderstorms require three conditions to form: moisture, an unstable airmass, and a lifting force (heat).

All thunderstorms, regardless of type, go through three stages: the developing stage, the mature stage, and the dissipation stage.^[22] The average thunderstorm has a 24 km (15 mi) diameter. Depending on the conditions present in the atmosphere, these three stages take an average of 30 minutes to go through.^[23]

Oceanic circulation[edit]

Main articles: Gulf Stream and Thermohaline circulation

Ocean currents

Solar radiation affects the oceans: warm water from the Equator tends to circulate toward the poles, while cold polar water heads towards the Equator. The surface currents are initially dictated by surface wind conditions. The trade winds blow westward in the tropics,^[24] and the westerlies blow eastward at mid-latitudes.^[25] This wind pattern applies a stress to the subtropical ocean surface with negative curl across the Northern Hemisphere,^[26] and the reverse across the Southern Hemisphere. The resulting Sverdrup transport is equatorward.^[27] Because of conservation of potential vorticity caused by the poleward-moving winds on the subtropical ridge’s western periphery and the increased relative vorticity of poleward moving water, transport is balanced by a narrow, accelerating poleward current, which flows along the western boundary of the ocean basin, outweighing the effects of friction with the cold western boundary current which originates from high latitudes.^[28] The overall process, known as western intensification, causes currents on the western boundary of an ocean basin to be stronger than those on the eastern boundary.^[29]

As it travels poleward, warm water transported by strong warm water current undergoes evaporative cooling. The cooling is wind driven: wind moving over water cools the water and also causes evaporation, leaving a saltier brine. In this process, the water becomes saltier and denser. and decreases in temperature. Once sea ice forms, salts are left out of the ice, a process known as brine exclusion.^[30] These two processes produce water that is denser and colder. The water across the northern Atlantic ocean becomes so dense that it begins to sink down through less salty and less dense water. (This open ocean convection is not unlike that of a lava lamp.) This downdraft of heavy, cold and dense water becomes a part of the North Atlantic Deep Water, a southgoing stream.^[31]

Mantle convection[edit]

Main article: Mantle convection

An oceanic plate is added to by upwelling (left) and consumed at a subduction zone (right).

Mantle convection is the slow creeping motion of Earth’s rocky mantle caused by convection currents carrying heat from the interior of the earth to the surface. ^[32] It is one of 3 driving forces that causes tectonic plates to move around the Earth’s surface.^[33]

The Earth’s surface is divided into a number of tectonic plates that are continuously being created and consumed at their opposite plate boundaries. Creation (accretion) occurs as mantle is added to the growing edges of a plate. This hot added material cools down by conduction and convection of heat. At the consumption edges of the plate, the material has thermally contracted to become dense, and it sinks under its own weight in the process of subduction at an ocean trench. This subducted material sinks to some depth in the Earth’s interior where it is prohibited from sinking further. The subducted oceanic crust triggers volcanism.

Convection within Earth’s mantle is the driving force for plate tectonics. Mantle convection is the result of a thermal gradient: the lower mantle is hotter than the upper mantle, and is therefore less dense. This sets up two primary types of instabilities. In the first type, plumes rise from the lower mantle, and corresponding unstable regions of lithosphere drip back into the mantle. In the second type, subducting oceanic plates (which largely constitute the upper thermal boundary layer of the mantle) plunge back into the mantle and move downwards towards the core-mantle boundary. Mantle convection occurs at rates of centimeters per year, and it takes on the order of hundreds of millions of years to complete a cycle of convection.

Neutrino flux measurements from the Earth’s core (see kamLAND) show the source of about two-thirds of the heat in the inner core is the radioactive decay of ⁴⁰K, uranium and thorium. This has allowed plate tectonics on Earth to continue far longer than it would have if it were simply driven by heat left over from Earth’s formation; or with heat produced from gravitational potential energy, as a result of physical rearrangement of denser portions of the Earth’s interior toward the center of the planet (i. e., a type of prolonged falling and settling).

Stack effect[edit]

Main article: Stack effect

The Stack effect or chimney effect is the movement of air into and out of buildings, chimneys, flue gas stacks, or other containers due to buoyancy. Buoyancy occurs due to a difference in indoor-to-outdoor air density resulting from temperature and moisture differences. The greater the thermal difference and the height of the structure, the greater the buoyancy force, and thus the stack effect. The stack effect helps drive natural ventilation and infiltration. Some cooling towers operate on this principle; similarly the solar updraft tower is a proposed device to generate electricity based on the stack effect.

Stellar physics[edit]

Main articles: Convection zone and granule (solar physics)

An illustration of the structure of the Sun and a red giant star, showing their convective zones. These are the granular zones in the outer layers of these stars.

The convection zone of a star is the range of radii in which energy is transported primarily by convection.

Granules on the photosphere of the Sun are the visible tops of convection cells in the photosphere, caused by convection of plasma in the photosphere. The rising part of the granules is located in the center where the plasma is hotter. The outer edge of the granules is darker due to the cooler descending plasma. A typical granule has a diameter on the order of 1,000 kilometers and each lasts 8 to 20 minutes before dissipating. Below the photosphere is a layer of much larger «supergranules» up to 30,000 kilometers in diameter, with lifespans of up to 24 hours.

Water convection at freezing temperatures[edit]

Water is a fluid that does not obey the Boussinesq approximation.^[34] This is because its density varies nonlinearly with temperature, which causes its thermal expansion coefficient to be inconsistent near freezing temperatures.^[35][36] The density of water reaches a maximum at 4 °C and decreases as the temperature deviates. This phenomenon is investigated by experiment and numerical methods.^[34] Water is initially stagnant at 10 °C within a square cavity. It is differentially heated between the two vertical walls, where the left and right walls are held at 10 °C and 0 °C, respectively. The density anomaly manifests in its flow pattern.^{[34][37][38][39]} As the water is cooled at the right wall, the density increases, which accelerates the flow downward. As the flow develops and the water cools further, the decrease in density causes a recirculation current at the bottom right corner of the cavity.

Another case of this phenomenon is the event of super-cooling, where the water is cooled to below freezing temperatures but does not immediately begin to freeze.^[36][40] Under the same conditions as before, the flow is developed. Afterward, the temperature of the right wall is decreased to −10 °C. This causes the water at that wall to become supercooled, create a counter-clockwise flow, and initially overpower the warm current. ^[34] This plume is caused by a delay in the nucleation of the ice.^[34][36][40] Once ice begins to form, the flow returns to a similar pattern as before and the solidification propagates gradually until the flow is redeveloped.^[34]

Nuclear reactors[edit]

In a nuclear reactor, natural circulation can be a design criterion. It is achieved by reducing turbulence and friction in the fluid flow (that is, minimizing head loss), and by providing a way to remove any inoperative pumps from the fluid path. Also, the reactor (as the heat source) must be physically lower than the steam generators or turbines (the heat sink). In this way, natural circulation will ensure that the fluid will continue to flow as long as the reactor is hotter than the heat sink, even when power cannot be supplied to the pumps. Notable examples are the S5G ^[41][42][43] and S8G^[44][45][46]United States Naval reactors, which were designed to operate at a significant fraction of full power under natural circulation, quieting those propulsion plants. The S6G reactor cannot operate at power under natural circulation, but can use it to maintain emergency cooling while shut down.

By the nature of natural circulation, fluids do not typically move very fast, but this is not necessarily bad, as high flow rates are not essential to safe and effective reactor operation. In modern design nuclear reactors, flow reversal is almost impossible. All nuclear reactors, even ones designed to primarily use natural circulation as the main method of fluid circulation, have pumps that can circulate the fluid in the case that natural circulation is not sufficient.

Mathematical models of convection[edit]

A number of dimensionless terms have been derived to describe and predict convection, including the Archimedes number, Grashof number, Richardson number, and the Rayleigh number.

In cases of mixed convection (natural and forced occurring together) one would often like to know how much of the convection is due to external constraints, such as the fluid velocity in the pump, and how much is due to natural convection occurring in the system.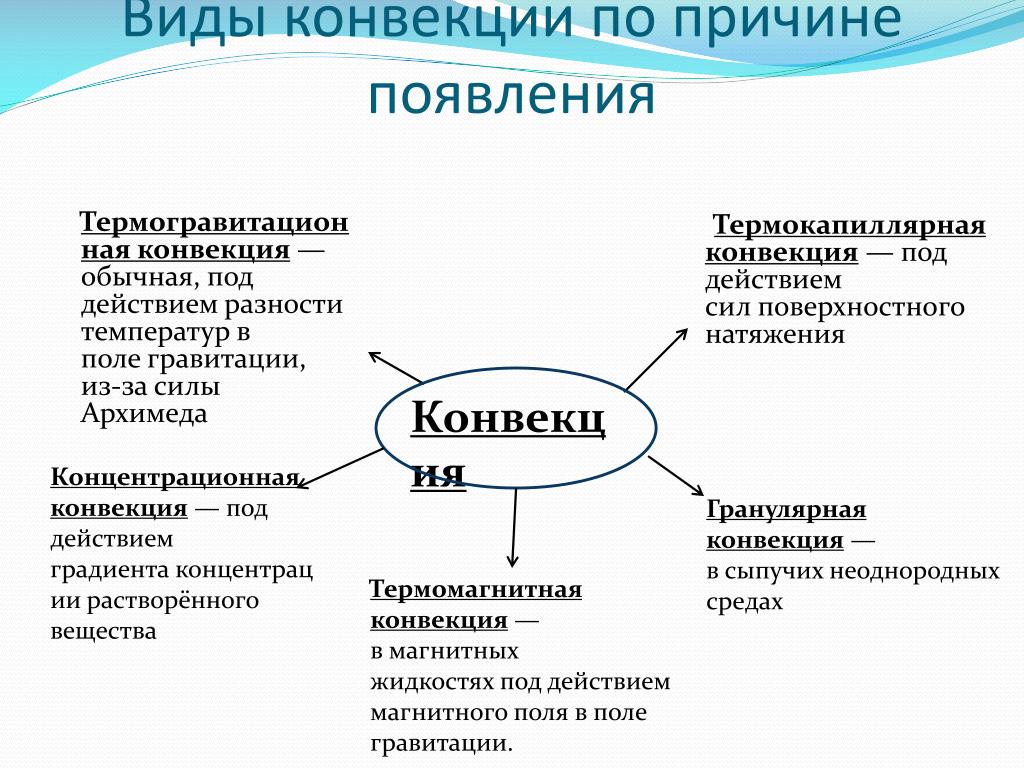 {3}}{D\mu }}}

where

• Δρ{\displaystyle \Delta \rho } is the difference in density between the two parcels of material that are mixing
• g{\displaystyle g} is the local gravitational acceleration
• L{\displaystyle L} is the characteristic length-scale of convection: the depth of the boiling pot, for example
• D{\displaystyle D} is the diffusivity of the characteristic that is causing the convection, and
• μ{\displaystyle \mu } is the dynamic viscosity.

Natural convection will be more likely and/or more rapid with a greater variation in density between the two fluids, a larger acceleration due to gravity that drives the convection, and/or a larger distance through the convecting medium. Convection will be less likely and/or less rapid with more rapid diffusion (thereby diffusing away the gradient that is causing the convection) and/or a more viscous (sticky) fluid.

For thermal convection due to heating from below, as described in the boiling pot above, the equation is modified for thermal expansion and thermal diffusivity.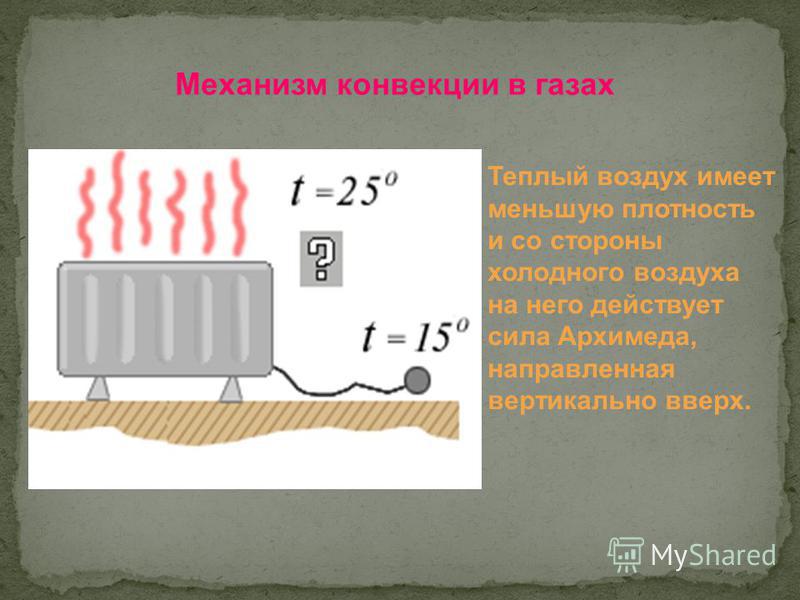 {\frac {-16}{9}}}

Nu is the Nusselt number and the values of Nu₀ and the characteristic length used to calculate Ra are listed below (see also Discussion):

Geometry	Characteristic length	Nu0
Inclined plane	x (Distance along plane)	0.68
Inclined disk	9D/11 (D = diameter)	0.56
Vertical cylinder	x (height of cylinder)	0.68
Cone	4x/5 (x = distance along sloping surface)	0.54
Horizontal cylinder	πD/2{\displaystyle \pi D/2} (D = diameter of cylinder)	0.36π{\displaystyle \pi }

Warning: The values indicated for the Horizontal cylinder are wrong; see discussion.

Natural convection from a vertical plate[edit]

One example of natural convection is heat transfer from an isothermal vertical plate immersed in a fluid, causing the fluid to move parallel to the plate. {2}T}^[49][50]

where

• g = gravitational acceleration (m/s²)
• L = distance above the lower edge (m)
• t_s = temperature of the wall (K)
• t∞ = fluid temperature outside the thermal boundary layer (K)
• v = kinematic viscosity of the fluid (m²/s)
• T = absolute temperature (K)

When the flow is turbulent different correlations involving the Rayleigh Number (a function of both the Grashof number and the Prandtl number) must be used.^[50]

Note that the above equation differs from the usual expression for Grashof number because the value β{\displaystyle \beta } has been replaced by its approximation 1/T{\displaystyle 1/T}, which applies for ideal gases only (a reasonable approximation for air at ambient pressure).

Pattern formation[edit]

A fluid under Rayleigh–Bénard convection: the left picture represents the thermal field and the right picture its two-dimensional Fourier transform.

Convection, especially Rayleigh–Bénard convection, where the convecting fluid is contained by two rigid horizontal plates, is a convenient example of a pattern-forming system.

When heat is fed into the system from one direction (usually below), at small values it merely diffuses (conducts) from below upward, without causing fluid flow. As the heat flow is increased, above a critical value of the Rayleigh number, the system undergoes a bifurcation from the stable conducting state to the convecting state, where bulk motion of the fluid due to heat begins. If fluid parameters other than density do not depend significantly on temperature, the flow profile is symmetric, with the same volume of fluid rising as falling. This is known as Boussinesq convection.

As the temperature difference between the top and bottom of the fluid becomes higher, significant differences in fluid parameters other than density may develop in the fluid due to temperature. An example of such a parameter is viscosity, which may begin to significantly vary horizontally across layers of fluid. ^{a b c d e} Bennett (1962). Momentum, Heat and Mass Transfer. McGraw-Hill. ISBN 978-0-07-004667-2.

External links[edit]

Portals:

 Physics Astronomy Solar System Weather

Вынужденная конвекция — Большая Энциклопедия Нефти и Газа, статья, страница 1

Cтраница 1

Вынужденная конвекция осуществляется за счет внешнего перепада давления, создаваемого в потоке за счет затраты механической работы.  [1]

Вынужденная конвекция, например, при движении нагретой жидкости под действием разности давлений на концах трубы сопровождается ее охлаждением.  [2]

Вынужденная конвекция наблюдается при движении, вызванном внешними силами ( насос, вентилятор), и зависит главным образом от скорости и режима движения теплоносителя. Увеличение скорости обычно приводит к повышению коэффициента теплоотдачи ак.  [3]

Вынужденная конвекция происходит под действием внешних сил, приложенных к жидкости, например, со стороны лопаток насоса или вентилятора. Естественная конвекция ( свободное движение) осуществляется под действием неоднородности температурного поля в жидкости, что приводит к возникновению архимедовой силы.  [4]

Вынужденная конвекция возникает под действием посторонних возбудителей: насоса, вентилятора, дымовой трубы, ветра.  [5]

Вынужденная конвекция может и не сопровождаться теплообменом ( изотермическое течение), в атом случае осуществляется конвективный перенос только массы.  [6]

Вынужденная конвекция происходит под действием внешней движущей силы, здесь жидкость обтекает поверхность, имеющую более высокую или более низкую температуру, чем температура самой жидкости. Скорость движения жидкости при вынужденной конвекции больше, чем при свободной, поэтому в этом случае при заданном перепаде температур может быть передано больше теплоты. Возрастание теплового потока связано с необходимостью расхода энергии, затрачиваемой для приведения жидкости в движение.  [7]

Вынужденная конвекция кипящей воды в вертикальных каналах широко используется для охлаждения ядерных реакторов и других высоконапряженных теплогенерирующих систем. Одним из наиболее важных факторов, ограничивающих теплонапряжен-ность таких систем, является критический тепловой поток. Критические условия характеризуются резким уменьшением теплоотдачи от нагретой поверхности, что может привести к повреждению этой поверхности. До недавнего времени большая часть экспериментальных исследований, посвященных этой проблеме, была направлена на испытание секций с постоянным по длине тепловым потоком. Следовательно, большое количество имеющихся экспериментальных данных, строго говоря, не может быть непосредственно использована для расчета реакторов, так как распределение теплового потока в реакторах является неравномерным. Кроме того, немногочисленные данные, полученные для случая неравномерного теплового потока, показывают, что критический тепловой поток в подобных условиях может оказаться существенно ниже, чем для постоянного по длине теплового потока, при одинаковых гидродинамических условиях. Таким образом, проведенное экспериментальное и аналитическое исследование [1] было предпринято с целью определения влияния аксиальной неравномерности теплового потока на критический тепловой поток в пароводяных смесях.  [8]

Теплопроводность веществ 1 — органические газы и пары. 2 — аморфные теплоизоляционные материалы. 3 — масла.  [9]

Вынужденной конвекцией называется такое движение жидкости или газа, которое возникает под действием посторонних возмущений, например, под действием. В общем случае наряду с вынужденным одновременно может быть и свободное движение. При больших скоростях влияние свободного движения становится пренебрежительно малым.  [10]

Теплопроводность веществ 1 — органические газы и пары. 2 — аморфные теплоизоляционные материалы. 3 — масла.  [11]

Вынужденной конвекцией называется такое движение жидкости или газа, которое возникает под действием посторонних возмущений, например, под действием ветра, насоса, компрессора или вентилятора. В общем случае наряду с вынужденным одновременно может быть и свободное движение. При больших скоростях влияние свободного движения становится пренебрежительно малым.  [12]

Влияние вынужденной конвекции на естественную, которое выражается граничным условием для и на бесконечности, учитывается в анализе с помощью функций Риф.  [13]

Обобщение данных по скрытым теплотам ( а и по.  [14]

При вынужденной конвекции такой характеристикой является скорость вынужденного потока ш, при свободной конвекции — тепловая нагрузка ( или температура стенки), в случае смешанной конвекции — оба эти фактора.  [15]

Страницы:      1    2    3    4

Тепловая конвекция: естественная и принудительная конвекция

Тепловая конвекция: основа теплопередачи

В большинстве решений по управлению температурным режимом мы используем тепловую конвекцию как средство отвода тепла от наших чувствительных компонентов и устройств. В редких случаях мы не используем конвекцию, потому что у нас практически нет жидкости для работы. Конкретные приложения, такие как аэрокосмическая промышленность, лишены жидкости и не могут использовать тепловую конвекцию. В противном случае это самый популярный способ получить тепло от продуктов.

Но в промышленности вы, наверное, слышали термины «принудительная конвекция» и «естественная конвекция». Хотя может показаться, что это не имеет большого значения между ними, это оказывает большое влияние на то, как разработано ваше решение для управления температурным режимом. Итак, давайте посмотрим на естественную конвекцию и принудительную конвекцию и разберемся в различиях.

Конвекция: рассказ о двух процессах

Процесс конвекции, как мы его называем в тепловом менеджменте, на самом деле является комбинацией двух процессов. Первый процесс технически является теплопроводностью, когда тепло от поверхности радиатора передается любой жидкости, контактирующей с этой поверхностью. Вторым процессом считается адвекция, представляющая собой объемный поток жидкости, нагретой устройством, от источника тепла. То, что мы делаем, вместо того, чтобы обращаться к обоим по отдельности, мы объединяем их в один термин: конвекция.

Важно понимать две части конвекции, когда мы пытаемся улучшить тепловые характеристики наших растворов. Когда мы понимаем части конвекции, у нас появляется больше возможностей разрушить и улучшить каждую из этих частей, чтобы улучшить нашу общую теплопередачу.

Естественная конвекция против принудительной

Мы классифицируем тип конвективного потока как естественный или вынужденный. Мы сделали это обозначение, поскольку каждое из них по-своему влияет на приложение и продукт в целом. Эти разные типы потока имеют разные проектные ограничения и проблемы, которые необходимо решать индивидуально.

Это естественно (поток)

Естественная конвекция – это когда естественная плавучесть приводит в движение адвективный поток. Вы, наверное, слышали термины «шлейф» или «эффект дымохода» для описания естественной конвекции. По сути, когда жидкость внутри или рядом с источником тепла и радиатором нагревается выше температуры окружающей среды, она имеет меньшее давление. Здесь, на Земле, у нас есть гравитация, поэтому меньшее давление означает большую плавучесть. Этот перепад давления создает движение более горячего воздуха вверх, в сторону от источника гравитации. Затем более холодная окружающая жидкость заполняет место, откуда выходит горячий воздух, создавая поток внутрь, а затем вверх.

Плывите по течению: рекомендации по проектированию естественной тепловой конвекции

Сверхнадежность решений с естественной тепловой конвекцией

В тех случаях, когда надежность имеет решающее значение, естественная конвекция является предпочтительным типом потока в решении по управлению температурным режимом. Полагаясь на естественные силы для придания движения вашей жидкости, ключевые компоненты, такие как вентиляторы или насосы, не требуются. Эти компоненты, хотя и тщательно спроектированы и протестированы, со временем изнашиваются. Пока у вас есть фрикционные детали, такие как двигатели вентиляторов или насосов, вы будете обеспокоены надежностью ваших двигателей.

Варианты жидкости для естественной тепловой конвекции

Естественная конвекция легче в системах с воздушным охлаждением, чем в системах с жидкостным охлаждением. Жидкость должна быть локализована, и если система не погружена в воду, а большая часть электроники плохо работает с жидкостями, весь маршрут жидкости должен быть спланирован и локализован. Это требует больше инженерного времени, особенно на этапах проектирования и проверки разработки продукта. С другой стороны, мы окружены воздухом, и любое движение воздуха от системы будет быстро заменено другим окружающим воздухом.

Расстояние между ребрами естественной тепловой конвекции

Когда вы говорите о радиаторах с естественной и принудительной конвекцией, вы увидите разницу в общей структуре радиатора. Независимо от жидкости, мы хотим оптимизировать наш радиатор, чтобы максимизировать эффект дымохода. Это означает, что между ребрами радиатора достаточно места, чтобы они могли «дышать». Вам нужно достаточно места для нагрева рядом с ребрами в пределах их пограничного слоя с каждой стороны зазора, а также дополнительное пространство посередине для потока воздуха вверх. Вы увидите, что меньшее расстояние между ребрами на тепловых контурах внизу слева позволяет более холодному воздуху проходить гораздо дальше вверх по зазорам ребер, чем к радиатору справа. Вот почему вы заметите, что некоторые радиаторы имеют гораздо больший зазор между ребрами, чем другие. Те, у которых зазор между ребрами около 1/4 дюйма и больше, обычно предназначены для естественной конвекции.0009

Принуждение субъекта к принудительной тепловой конвекции

Когда этот адвективный поток создается не только естественной плавучестью, но и другим механизмом, мы называем его вынужденной конвекцией. В этих случаях мы обычно используем что-то вроде вентилятора или насоса для управления потоком жидкости. Вынужденная конвекция также может быть вызвана такими вещами, как кто-то, кто дует на кожу, чтобы охладить ожог, или слуги, вооруженные пальмовыми ветвями. Дело в том, что есть какой-то механизм, помимо физики, управляющий потоком, это называется вынужденная конвекция.

Влияние конструкции на принудительную конвекцию

Избавься от жары!

Большим преимуществом принудительной конвекции по сравнению с естественной конвекцией является повышенная теплопередача. Имея возможность перемещать больше жидкости через систему за тот же период времени, больше тепла, поглощаемого жидкостью, может быть отведено от вашего источника тепла. Это не позволяет теплу задерживаться и накапливаться, а в управлении температурой это последнее, чего мы хотим.

Что принудительная конвекция означает для надежности

К сожалению, недостатком принудительного потока через вашу систему является то, что он может выйти из строя. Фрикционные детали в наших насосах и вентиляторах изнашиваются, у легкого ожога кружится голова от всего этого дуновения, или слуги идут есть или спать. Эти вещи не могут продолжаться бесконечно. Именно здесь инженеры-конструкторы должны учитывать надежность своих компонентов и убедиться, что конечный продукт достаточно исправен, чтобы заменить сломанные детали, или что детали могут прослужить дольше, чем ожидаемый срок службы конечного продукта. Это особенно верно для критических устройств, которые поддерживают жизнь или безопасность.

Движущиеся части и шум

Поскольку принудительная конвекция требует движущихся частей для ускорения потока жидкости, она также производит звук. Двигатели вентиляторов или насосов производят больше шума по сравнению с естественной конвекцией. Для некоторых приложений это может быть настоящим недостатком. Я имею в виду, что это действительно выводит вас из вашего захватывающего опыта с видеоиграми или фильмом, когда вентилятор включает высокую передачу и начинает громко напевать. Вам все еще нужен вентилятор, так как вы хотите играть в игры и смотреть фильмы на долгие годы. Но этот вентилятор может включиться в те напряженные моменты вашего аудио/визуального опыта.

Значение конструкции для принудительной конвекции

Когда дело доходит до вашего дизайна и требований к конечному продукту, вы и ваш конечный покупатель являетесь экспертами. Вы должны быть в состоянии определить предпочитаемый тип потока на основе вашей надежности и требований конечного пользователя. Но помните, вы не одиноки. Aavid Genie может помочь пройти процесс сравнения естественной и вынужденной конвекции для вашего приложения. Если вы обнаружите, что вам нужна дополнительная помощь, инженеры-конструкторы Boyd разработали решения для сложных ситуаций с высокой мощностью естественной конвекции или создали решения для принудительной конвекции, отвечающие жестким требованиям надежности. Каким бы ни было ваше приложение, будь то естественное или принудительное, Бойд может помочь вам с тем, что вам нужно.

Удачного проектирования!

Сопутствующие товары и ресурсы

Авид Джинн

Радиаторы

Проектирование

Осевой вентилятор

Есть вопросы? Мы готовы помочь!

СВОБОДНАЯ КОНВЕКЦИЯ

Свободная конвекция, или естественная конвекция , представляет собой самопроизвольное течение, возникающее под действием неоднородных полей объемных (массовых) сил (гравитационных, центробежных, кориолисовых, электромагнитных и др.):

Если изменение плотности Δρ обусловлено пространственной неоднородностью температурного поля, то течение, возникающее в гравитационном поле Земли, называется термогравитационной конвекцией . Изменчивость плотности может быть вызвана также неравномерным распределением концентрации какого-либо компонента в смеси или химическими реакциями, различием плотностей фаз или силами поверхностного натяжения на границе раздела фаз (в этом случае подразумевается концентрационная диффузия или конвекция).

Свободноконвективные течения могут быть ламинарными и турбулентными. Обтекание твердой поверхности, температура которой выше (ниже) температуры окружающей обтекаемой среды, является наиболее распространенным видом свободной конвекции. На рис. 1 и 2 схематично показаны характерные примеры свободной конвекции. В начале нагрева вертикальной поверхности (х = 0) (рис. 1а) формируется ламинарный пограничный слой. Толщина слоя растет вдоль направления потока и на некотором расстоянии, соответствующем x _c1 течение жидкости становится неустойчивым, изменяясь в диапазоне от x _c1 до x _c2 от ламинарного до турбулентного. Такому характеру изменения структуры течения соответствует изменение коэффициента теплоотдачи α _x , который в случае развитого турбулентного ТК остается постоянным по длине пластины, где характеристики тепловой турбулентности становятся статистически равными. Картины развития ТЭ при обтекании горячей сферы или горизонтального цилиндра качественно аналогичны (рис.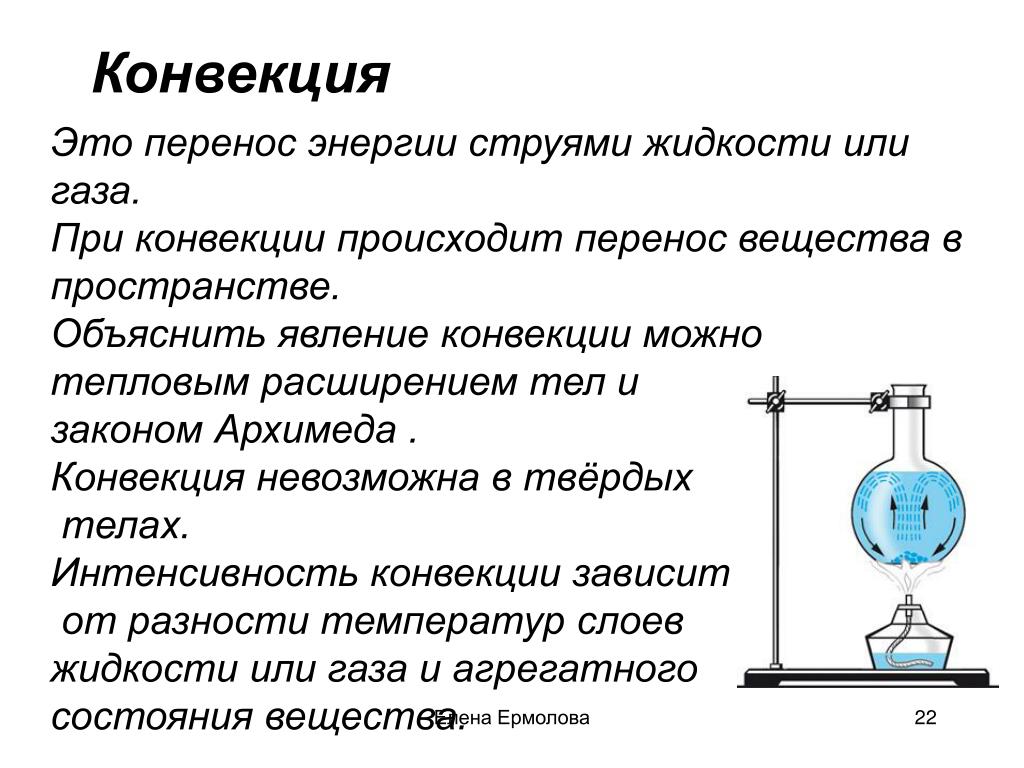 1б, в). На телах больших диаметров (рис. 1в) развивается турбулентный пограничный слой, формирующий восходящий турбулентный тепловой шлейф в задней кромке. От горячих тел малых диаметров поднимается ламинарный тепловой шлейф (рис. 1б), который на некотором расстоянии от тела становится турбулентным. В узких и замкнутых полостях течение ТЭ значительно сложнее (рис. 2) из-за взаимодействия пристеночных потоков жидкости, образующихся на теплообменных поверхностях. При обогреве одной вертикальной стенки (температура Т _h ) и охлаждающий другой (температура T _c1 ) возможны режимы с общим течением жидкости через всю полость с участием локальных вторичных течений вблизи вертикальных стенок, как это показано на рис. Течение в узких щелях между параллельными вертикальными пластинами формируется в виде периодических циркуляций (рис. 2б). В горизонтальном слое жидкости между холодной верхней (T _c1 ) и горячей нижней (T _h ) стенками течение жидкости имеет ячеистый вид с шестиугольными ячейками ( ячейки Бенара ), в центре которых жидкость поднимается с горячей поверхности на холодную, а на периферии опускается (рис. 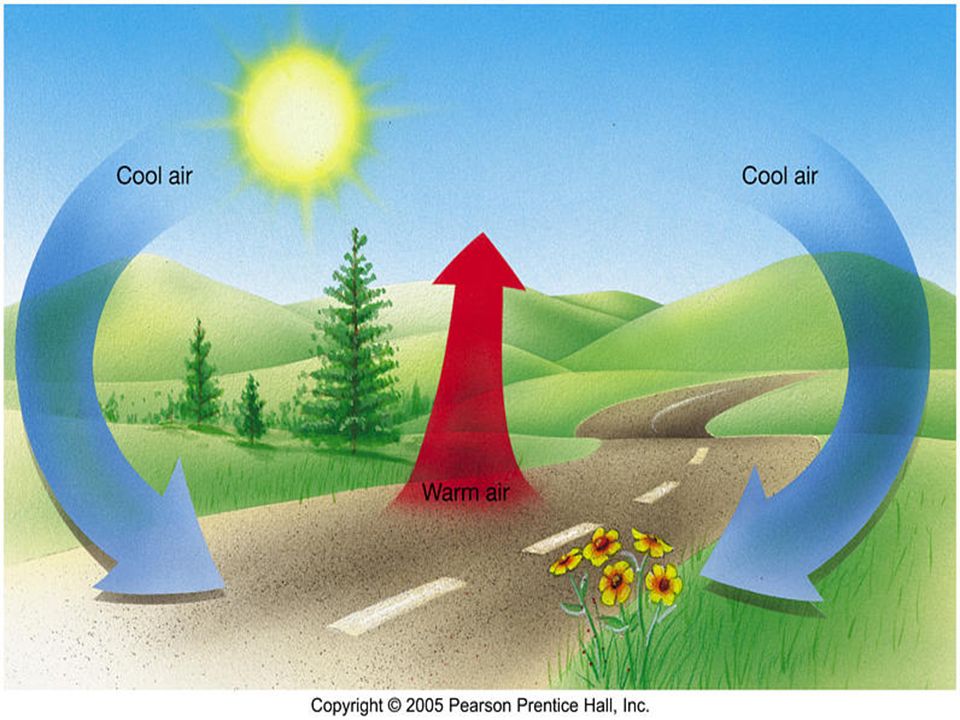2, в, г). Такую форму течения жидкости впервые наблюдал Бенар в 1901 г. При увеличении теплового потока происходит разрушение ячеек и течение переходит в турбулентное.

Рисунок 1. Развитие древовидного конвекционного пограничного слоя на поверхностях.

Рис. 2. Свободная конвекция в полостях.

При теоретическом анализе течений и теплообмена ТЭ используются законы сохранения импульса, массы и энергии при определенных граничных условиях. Широко применяется приближение Буссинеска «слабой» тепловой конвекции, т. е. отклонения плотности от среднего значения считаются пренебрежимо малыми во всех уравнениях, кроме уравнения движения, где они учитываются в члене силы плавучести. При малых перепадах температуры в потоке зависимость ρ(T) можно считать линейной

где ρ ₀ – плотность жидкости при температуре T ₀ , β = − [∂ρ/∂T] _p /p – объемный коэффициент теплового расширения.

Численные значения β обычно малы (вода: β = 1,5 × 10 ⁻⁴ , воздух: β = 3,5 × 10 ⁻³ при T = 273 K), поэтому изменение плотности учитывается только в этих случаях.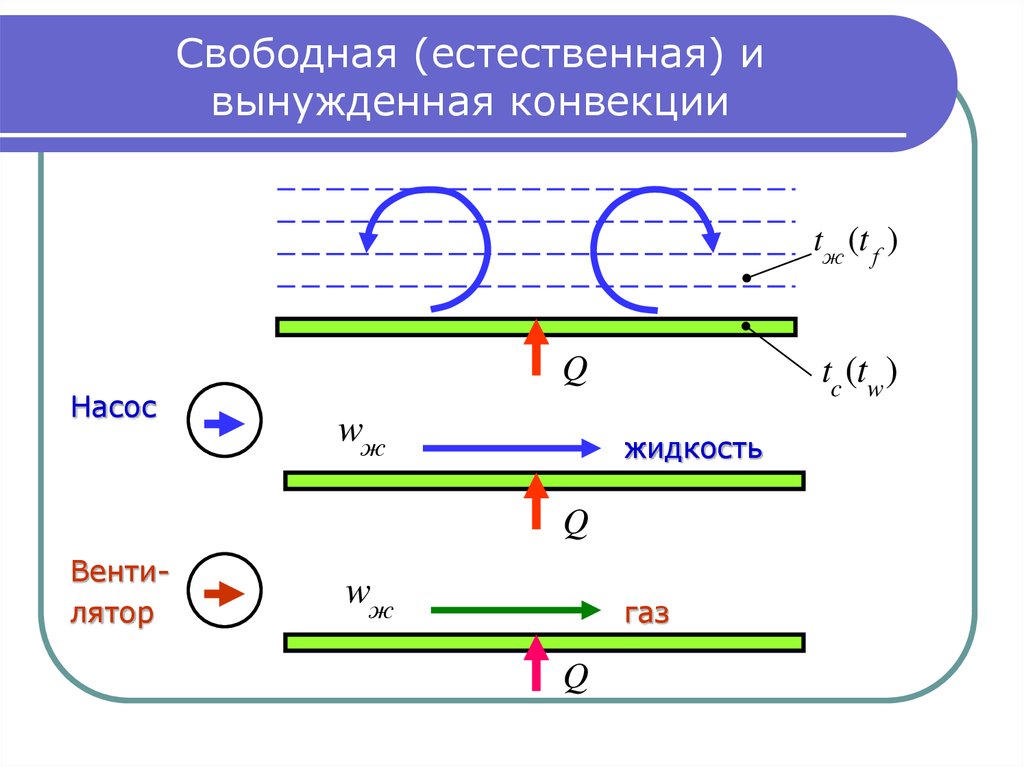 где на него действуют гравитационные силы. Приближение Буссинеска связывает коэффициент объемного расширения среды β с ускорением свободного падения g; они входят в управляющие уравнения только как произведение. Физическое обоснование приближения Буссинеска основано на малости ускорений в течениях ТЭ по сравнению с ускорением свободного падения.

Сравнение с обширным экспериментальным материалом свидетельствует о том, что приближение Буссинеска хорошо отражает основные особенности термогравитационной конвекции в широком классе реальных конвективных течений.

Как показывают экспериментальные данные, во многих случаях ТЭ основные вариации характеристик тепловых и гидродинамических полей сосредоточены в относительно узких пограничных слоях вблизи поверхности теплообмена, где вязкие силы соизмеримы с инерционными и объемными силами. Малость толщины пограничного слоя по сравнению с характерными размерами тел позволяет внести дополнительные упрощения в уравнения движения и теплообмена.

Понятие пограничного слоя для ТЭ гораздо сложнее, чем для вынужденной конвекции, поскольку тепловая и гидродинамическая задачи не могут рассматриваться отдельно из-за того, что течение жидкости полностью определяется теплообменом. Основная движущая сила (разность температур стенки и окружающей среды) заметно проявляется только в тонкой пристеночной зоне. Эта область температурного поля толщиной δ _T называется тепловым пограничным слоем.

Разность температур в пограничном слое создает объемную выталкивающую силу, вызывающую движение. На поверхности жидкость неподвижна (условие «прилипания»). По мере удаления от стенки скорость u постепенно возрастает до максимума, а затем под действием вязкого трения обращается в нуль (рис. 1а). За пределами этого динамического пограничного слоя находится область невязкого (потенциального) течения. Расстояние по нормали от стены до места, где скорость отличается от нуля на 1 процент от значения u _max , принимается за толщину динамического пограничного слоя δ.

При δ _T < δ движение вне теплового слоя, где сила плавучести отсутствует, определяется силами динамического и турбулентного взаимодействия между отдельными слоями жидкости.

При δ < δ _T вне динамического пограничного слоя и в пределах теплового слоя δ _T течение можно рассматривать как потенциальное.

Течение в пограничном слое вносит основной вклад в процессы переноса, тогда как индуцированное внешнее течение является второстепенным и дает поправку только более высокого порядка. В этом проявляется вторичное влияние пограничного слоя на течение в окружающей среде.

Из размерного анализа следует, что относительная толщина пограничного слоя δ/x имеет порядок Gr ^−0,25 , где Gr = gβ(T _w – T _∞ )x ³ /ν ² . При очень больших числах Грасгофа, характерных для практических приложений теории ФК-пограничного слоя, толщина пограничного слоя обычно очень мала по сравнению с размерами тела. Сравнительно толстые пограничные слои имеют место для сред с малыми числами Прандтля (Pr) и малыми перепадами температур тела и окружающей среды.

В приближении Буссинеска для несжимаемой жидкости и стационарного режима уравнения сохранения импульса, массы и энергии для ламинарного ТЭ в плоском пограничном слое имеют вид

Система уравнений (1) позволяет определить как компоненты скорости (u, v), так и поле температуры (T) для различных граничных условий.

Для обобщения результатов решения или экспериментальных данных, а также для уменьшения количества параметров задачи используется теория подобия.

Некоторые параметры задачи заменяются их комбинациями, так называемыми обобщенными переменными. Их структура зависит от вида дифференциальных операторов, входящих в уравнения. (1). Приведем уравнения к безразмерному виду. В качестве масштабов редукции удобно использовать величины, входящие в условия однозначности (граничные условия). В качестве линейной шкалы возьмем некоторый характерный размер тела L, для температуры удобно использовать, например, соотношение θ = (T – T _∞ )/(T _w – T _∞ ), где T _w – температура поверхности тела, T _∞ – температура окружающей среды, T – локальная температура. Характеристическую скорость можно получить из сравнения объемной силы и силы вязкости u ₀ = βgΔTL ² /ν или из оценок типа u ₀ = L/τ ₀ , где τ ₀ равно шкала времени.

Размерность дает

Число Грасгофа Gr = βgΔTL ³ /ν ² – основной определяющий критерий и важнейшая характеристика теплообмена ТЭ. Это мера отношения между силами плавучести в неизотермическом потоке и силами молекулярной вязкости. Он также определяет режим движения среды по поверхности теплообмена. По своему физическому смыслу оно аналогично числу Рейнольдса для вынужденного течения.

При малых числах Gr течение FC отсутствует и теплообмен осуществляется за счет молекулярной теплопроводности. В частности, в горизонтальном слое (рис. 2в) это происходит при Ra _δ = Gr _δ Pr = βg(T _h – T _c )δ ³ /νa < 1708. При Ra _{FC δ} = 1708 устойчивость горизонтального слоя нарушается и течение жидкости развивается в виде ячеек Бенара (рис. 2, в, г). При Ra _x = Gr _x Pr ≈ 10 ⁹ на вертикальной пластине происходит переход от ламинарного течения к турбулентному (рис. 1а).

Свободноконвективный теплообмен, как и при вынужденной конвекции, характеризуется числом Нуссельта Nu = αL/λ. Обычно это неизвестная величина, поскольку она связана с коэффициентом теплопередачи α, который необходимо найти. Таким образом, безразмерная форма коэффициента теплоотдачи Nu зависит от безразмерных чисел Pr, Gr и координаты X = x/L

В теории пограничного слоя FC широко используются интегральные соотношения, полученные усреднением уравнений движения и энергии по толщине пограничного слоя. Для стационарных условий, в которых пренебрегают работой диссипации и сжатия, эти уравнения имеют вид

Система уравнений (3) не пригодна для использования в приближенных расчетах. Умножая уравнения пограничного слоя на скорость и интегрируя, получаем баланс механической энергии

последующая интеграция. Например, уравнения первого момента имеют вид

Наиболее распространенным методом обработки результатов расчетов и экспериментов является применение экспоненциальной функции между критериями подобия

где C, m и n — постоянные безразмерные числа. Если в логарифмических координатах все точки попадают на прямую, то это составляет основу практического метода построения показательной функции. Если контрольные точки попадают на кривую, то одиночная линия заменяется сегментированной линией. Для отдельных участков такой кривой значения C, m, n различны.

Для расширения области применимости соотношения типа (4) его можно представить в виде суммы

Если физические свойства среды зависят от температуры, то среди основных уравнений должны быть уравнения, определяющие вид этих зависимостей. В этом случае критерий подобия следует трактовать как аргументы корреляций. Здесь применение обобщенного анализа невозможно и приходится ограничиваться приближенными решениями. В частности, если теплофизические характеристики могут быть представлены экспоненциальными функциями температуры, то дополнительный параметрический критерий, вводимый в соотношение (4), представляется в виде отношения температур окружающей среды к температуре стенки, а именно: (T _∞ /T _w ) ^{1 l} . Физические параметры следует отнести к одной из двух характеристических температур. Этот метод применим к газам.

Зависимость теплоотдачи жидкости от направления теплового потока и разности температур приближенно учитывается введением в уравнение подобия дополнительного множителя (Pr _∞ /Pr _w ) _{1 2} . Для нагрева жидкости Pr _∞ /Pr _w > 1; для охлаждения Pr _∞ /Pr _w < 1. Отношение Pr _∞ /Pr _w тем больше отличается от нуля, чем выше температурный напор. Изменчивость физических параметров может быть учтена параметрическими симплексами типа /c _pw и т. д., а также введением определяющей для данного процесса температуры.

Нуссельт предложил усреднение физических параметров по уравнению

и рассчитать определяющую температуру как среднелогарифмическую

Когда , соотношение (5) представляется в виде степенного ряда отношения T _∞ /T _w . Если ограничиться первым членом ряда, то ; в случае ограничения двумя членами T = (T _∞ + T _w )/2. В задачах ТС определяющую температуру часто выбирают в виде линейной комбинации температур стенки и окружающей среды:

где a и b — коэффициенты, меняющиеся от 0 до 1: (a + b) = 1.

Определяющим линейным размером обычно считается тот, который в большей степени соответствует физической сущности процесса (например, высоте пластины, диаметру цилиндра или сферы, толщине зазора или пограничного слоя и т. д.). Остальные размеры входят в уравнение подобия в виде симплексов P _Lk = L _k /L (ширина и толщина пластины, высота вертикали или длина горизонтального цилиндра, высота зазора). В ряде случаев комбинация разнородных физических величин, входящих в условия однозначности (масштаб длины в асимптотической теории L/Gr _1/4 , линейный размер в случае струйной конвекции) принимается за определяющий линейный размер. Для универсализации расчетных отношений и устранения параметрических критериев вводится общая характеристическая размерность. В качестве примера приведем: 1/L = 1/a + 1/b для горизонтальной пластины; πD для горизонтального цилиндра; πD/2 для сферы; D _hyd = 4S/P _l — гидравлический диаметр для горизонтального канала произвольного поперечного сечения (S — площадь поперечного сечения, P _l — смоченный периметр).

Для прикладных задач расчета теплоотдачи от поверхностей произвольной формы в безграничной жидкости уравнение

предлагается, или в размерной форме

где величины C, A и n зависят от Ra _L ( = L ³ gp(T _∞ – T _w )β/η ² ) и формы тела. В качестве определяющей температуры принимается средняя температура пограничного слоя. Вводятся поправочные коэффициенты для наклонных и горизонтальных поверхностей.

Особенностью ламинарного ТЭ на вертикальной пластине при постоянной температуре стенки (рис. 1а) является то, что он допускает автомодельное решение при введении в уравнения новой переменной. (1) в виде

Граничные условия

Представив функцию тока и безразмерную температуру в виде

мы получаем уравнения (1) в виде

где f'(η _с ) = df/dη _с .

Граничные условия

Локальная скорость теплоотдачи на расстоянии x от края пластины может быть определена по формуле Nu _x = αx/λ = (Gr _x /4) ^1/4 H(Pr) (где H(Pr) = 0,75Pr ^1/2 /(0,609 + 1,22Pr ^1/2 + 1,28Pr) ^1/4 ) действительно для 0 ≤ Pr < ∞. Представленная корреляция отражает два заслуживающих внимания физических факта:

1. В случае ламинарного ТЭ коэффициент теплоотдачи вдоль вертикальной поверхности изменяется по закону α(x) = Ax ^−1/4 .

2. В предельных случаях Pr → 0 и Pr → ∞ зависимость безразмерного коэффициента теплоотдачи от числа Прандтля носит различный характер, а именно: когда Pr → 0 и когда Pr → ∞.

Случай больших чисел Прандтля соответствует очень высокой вязкости и, следовательно, медленному течению, обычно называемому ползущим течением. Для таких течений инерционными членами в уравнении движения можно пренебречь и соотношение для числа Нуссельта Nu имеет вид F(GrPr). Случай Pr → 0 соответствует малой вязкости, что позволяет пренебречь вязкими эффектами в уравнении движения, а соотношение для числа Нуссельта принимает вид F(Gr Pr ² ).

Среднее число Нуссельта на пластине длиной x = L равно

или же .

Постоянство теплового потока на стенку ( ), что соответствует постоянному подводу тепла к теплообменной поверхности (например, в электронагревательных устройствах, в элементах радиоэлектронной аппаратуры), является важным практически граничным условием. Этот случай легко реализуется на практике при нагреве электрическим током тонкой металлической фольги постоянной толщины, поэтому его часто используют в экспериментах. В этих задачах температура стенки T _w — неизвестная величина. В силу вышеизложенного модифицированное число Грасгофа, вычисляемое по тепловому потоку на стенку, а именно: принимается за определяющий безразмерный параметр вместо традиционного . Здесь разность температур, входящая в обычное число Грасгофа, заменена множителем . Температура стенки растет по течению как (T _w – T _∞ ) ~ x ^1/5 и, следовательно, безразмерный коэффициент теплоотдачи – число Нуссельта при зависит от в качестве что сравнивается с отношением для Т _w = const (что также видно из подстановки ). Для данного случая на рис. 3 и 4 приведены примеры распределений скорости и температуры в ламинарном пограничном слое при различных числах Прандтля, построенные по результатам Сперроу и Грегга (J. Heat Transfer . 1956, т. 78, с. 435). Эти теоретические результаты находятся в хорошем согласии с экспериментальными данными.

Рис. 3. Безразмерные профили скорости в свободно конвективных пограничных слоях на плоских пластинах с постоянным тепловым потоком.

Рис. 4. Безразмерные профили температуры в свободно конвективных пограничных слоях на плоской пластине с постоянным тепловым потоком.

Многие течения ТЦ, встречающиеся в природе и технике, являются турбулентными, т. е. имеют нерегулярный пульсирующий характер. По сравнению с большим объемом теоретических и экспериментальных исследований турбулентности в вынужденных турбулентных течениях турбулентность с ФК изучена значительно меньше. Однако основные механизмы турбулентного течения весьма схожи. Основное их отличие состоит в том, что в FC-течениях значения осредненных скоростей меньше, а уровни возмущений выше, чем в вынужденных течениях. Поле течения связано с полем температуры, и для изучения турбулентности с помощью FC требуется одновременная диагностика обоих полей. Это соотношение сильно усложняет как теоретический анализ, так и измерения. Экспериментальные данные по локальному теплообмену с развитой турбулентный FC на вертикальных и наклонных поверхностях при в диапазоне описаны Улиттом и Россом ( J. Heat Transfer . 1975, v. 97, p. 549) как

где γ — угол наклона поверхности к вертикальной плоскости. Из приведенного уравнения следует, что коэффициент теплоотдачи при турбулентном ПЧ не зависит от х. Некоторые данные указывают на возможность наличия слабой зависимости α(x).

Для инженерных расчетов теплообмена от тел различной геометрии и ориентации в пространстве предложено множество безразмерных эмпирических соотношений.

Для поверхности вертикальной пластины (рис. 1а) при числах Рэлея Ra _L = Gr _L Pr, изменяющихся в пределах от 10 ⁴ до 10 ¹³ и охватывающих как ламинарную, так и турбулентную зоны течения, длина среднее число Нуссельта равно

Это уравнение можно использовать для жидких металлов (Pr < 0,1) при замене Ra _L на Gr _L Pr ² согласно рассмотренному выше случаю предельных значений Pr. Это выражение для может применяться для определения средней теплоотдачи от вертикального цилиндра высотой H, если толщина пограничного слоя много меньше диаметра цилиндра D, т. е. D/H ≥ 35/Gr ^1/4 . Эффекты, вызванные искривлением тела, особенно существенны при малых и средних числах Грасгофа.

Для горизонтального цилиндра (рис. 1б, в) среднюю теплоотдачу можно определить по формуле

что справедливо для Ra _D < 10 ¹² .

При наклоне цилиндра под некоторым углом j к горизонту появляется осевая составляющая скорости и течение становится трехмерным. Рост пограничного слоя при наклоне цилиндра ослабляет конвективный теплообмен. Теплообмен у нижнего конца наклонного цилиндра конечной длины определяется соотношениями, характерными для течения вдоль цилиндра. В верхней части цилиндра течение приближается к обтеканию горизонтального цилиндра. При малых углах наклона этот эффект незначителен. Например, уменьшается на 8 % при увеличении φj от 0° до 45°. При приближении к оси цилиндра нормальная теплоотдача от цилиндра резко уменьшается.

Соотношение для расчета осредненной теплопередачи от шара к окружающей среде представляется в следующем виде

для Pr = 0,7 – 6, Ra _D = 10 ⁻⁶ – 10 ⁴ , .

Теплоотдача от горизонтальной плоской поверхности сильно зависит от ее положения (вверх или вниз) относительно направления выталкивающей силы, а также от размеров тела. Наибольший коэффициент теплоотдачи при свободном течении вблизи горизонтальной пластины следует ожидать в местах максимального расхода, т. е. на торцах пластины. При достаточно больших размерах пластин средний коэффициент теплопередачи перестает зависеть от торцевого эффекта. Средний коэффициент теплоотдачи можно определить по формулам

Если горячая поверхность теплообмена обращена вниз, то результирующий поток происходит от центра к краям и усредненные значения коэффициента теплопередачи рассчитываются по выражению

Кинг ( Mech. Eng. 1932, т. 54, с. 347) получил практически важный результат и предложил общее уравнение для приближенного определения теплоотдачи от тела произвольной формы, найденное при обобщенных исследованиях теплоотдачи из пластин, цилиндров, стержней, сфер и тел других геометрических форм. Это уравнение по форме аналогично формуле для ламинарного течения вблизи вертикальных поверхностей. Эту формулу можно использовать при отсутствии более определенных данных для тела данной формы. Формула короля

Характерный размер тела L находится из соотношения

где L _h и L _v — размеры кузова по горизонтали и вертикали. Так, для вертикальной пластины она равна высоте, а для сферы – радиусу.

В жидкости, заключенной между двумя вертикальными поверхностями (рис. 2а, б), теплообмен при малых числах Грасгофа (примерно до 2000) осуществляется в основном теплопроводностью и число Нуссельта равно 1. При больших числах Грасгофа 10 ₆ < Pr < 10 ⁹ , 1 < Pr < 20 при аспектном отношении полости H/δ = l – 40 осредненный теплообмен между вертикальными поверхностями (горизонтальные стороны полости теплоизолированы) описывается выражением отношение

В жидкости между горизонтальными поверхностями при малых числах Грасгофа (Gr < 1700) устанавливается режим теплопроводности и число Нуссельта равно единице как в случае, когда нагреваемая поверхность находится внизу, так и в случае, когда она находится вверху. При больших числах Грасгофа, соответствующих турбулентному режиму течения, начинающемуся при Gr ≈ 5 × 10 ⁴ зависимость от δ отсутствует, а средний теплообмен между верхней нагреваемой и нижней охлаждаемой пластинами описывается соотношением

что справедливо для 0,02 < Pr < 8750, 3 10 ⁵ < Ra < 7 10 ⁹ .

Изучение динамики теплового факела ТЭ над нагретыми элементами является особым разделом теории ТЭ. Рассмотрены две идеализированные модели (рис. 5): в виде двумерного факела (2) от линейного источника тепла (1) или в виде осесимметричного факела (2) от точечного источника (1). Плюмы возникают в результате непрерывного подвода тепла. Если теплота выделяется только в течение короткого промежутка времени, то возникающий при этом поток называется термическим.

Рисунок 5. Формирование теплового плюма при свободной конвекции.

На практике часто приходится сталкиваться с проблемой взаимодействия восходящих потоков, имеющих свободные границы, с другими потоками и поверхностями. В частности, это относится к охлаждению элементов электронной аппаратуры при взаимодействии потоков, создаваемых источниками тепла, размещенными в разных местах. Поэтому важно расположить эти источники в таком порядке, чтобы можно было получить максимальный отвод тепла. Элементы с источниками тепла могут располагаться на поверхности, обычно теплоизолированной, а результирующее течение обусловлено взаимодействием потоков, образованных источниками, расположенными в разных местах (рис. 6). Во многих производственных процессах, связанных с отоплением, приходится иметь дело и с взаимодействием потоков, создаваемых системой нагревательных элементов, в частности, градирнями, трубопроводами для транспортировки горячей жидкости. На рисунках 7а и б показано взаимодействие факелов с одинаковыми и разными подводами тепла, а на рисунках 7в и г показано влияние вертикальных и криволинейных поверхностей на течение в примыкающем к ним плоском факеле.

.

Джалурия Ю. (1980) Естественная конвекция. Тепломассоперенос. Пергамон Пресс.

Разница между естественной и принудительной конвекцией

Ключевое различие между естественной и принудительной конвекцией заключается в том, что при естественной конвекции на движение жидкости влияют естественные средства, тогда как при принудительной конвекции на движение жидкости влияют внешние средства. Разница между естественной и вынужденной конвекцией, связанная с теплопередачей, заключается в том, что нет внешних факторов, влияющих на теплопередачу при естественной конвекции, в то время как внешние факторы могут вызывать теплопередачу при принудительной конвекции.

Конвекция — это метод передачи тепла посредством объемного движения молекул в жидкости (такой как газ или жидкость). По способу инициирования движения жидкости она бывает двух видов: естественная и вынужденная конвекция.

СОДЕРЖАНИЕ

1. Обзор и ключевые отличия
2. Что такое естественная конвекция
3. Что такое принудительная конвекция
4. Сравнение бок о бок — естественная и вынужденная конвекция в табличной форме
5. Резюме

Что такое естественная конвекция?

Естественная конвекция – это метод теплопередачи, при котором естественные средства влияют на движение жидкости. Нет влияния внешних фактов. Это движение молекул в жидкости обусловлено различиями в плотности различных областей одной и той же жидкости. Плотность жидкости уменьшается при нагревании и наоборот. Это происходит из-за теплового расширения жидкости (скорость молекул увеличивается с повышением температуры, что приводит к увеличению объема жидкости. Хотя объем увеличивается, масса остается постоянной. Следовательно, плотность уменьшается).

Когда мы нагреваем жидкость в сосуде со дна, плотность нижнего слоя жидкости уменьшается. Затем область с более низкой плотностью имеет тенденцию перемещаться к верхней части контейнера. Затем более холодная жидкость в верхней части контейнера заменяет нижнюю часть. Это продолжается, в результате происходит конвекция.

Рисунок 01: Механизм естественной конвекции

Примеры естественной конвекции включают охлаждение вареного яйца при хранении на обычном воздухе, охлаждение банки с прохладительным напитком и т. д. При рассмотрении механизма естественной конвекции сначала , температура снаружи горячего объекта (находящегося на холодном воздухе) падает. При этом температура воздуха, прилегающего к объекту, будет повышаться за счет теплообмена. Затем плотность этого соседнего слоя воздуха уменьшается. В результате воздух поднимается вверх. Холодный воздух заменит этот регион. Затем конвекция продолжается. В конце концов, объект остынет.

Что такое принудительная конвекция?

Принудительная конвекция — это метод теплопередачи, при котором внешние средства влияют на движение жидкости. Там внешние источники, такие как насосы, вентиляторы, всасывающие устройства и т. д., полезны для создания движения жидкости. Этот метод очень ценен, поскольку позволяет эффективно передавать тепло от нагретого объекта. Некоторые распространенные примеры этого механизма включают кондиционирование воздуха, паровые турбины и т. д.

При рассмотрении механизма принудительной конвекции он имеет более сложный механизм, чем естественный. Это потому, что в этом методе мы должны регулировать два фактора; движение жидкости и теплопроводность. Эти два фактора тесно связаны, поскольку движение жидкости может усиливать теплопередачу. Пример: выше скорость движения жидкости, выше теплопередача.

В чем разница между естественной и принудительной конвекцией?

Естественная конвекция – это метод теплопередачи, при котором на движение жидкости влияют естественные средства. Вынужденная конвекция — это метод теплопередачи, при котором на движение жидкости влияют внешние факторы. При рассмотрении факторов, влияющих на теплообмен, не существует внешних факторов, влияющих на теплообмен при естественной конвекции, в то время как внешние факторы могут вызывать теплообмен при вынужденной конвекции.

Движение жидкости при естественной конвекции возникает в результате изменения плотности жидкости при нагревании. Однако движение жидкости при вынужденной конвекции создается за счет внешнего источника, такого как насосы, вентиляторы, всасывающие устройства. Охлаждение вареного яйца при хранении на обычном воздухе, потеря охлаждения банки с прохладительным напитком и т. д. могут быть включены в качестве примеров естественной конвекции, а кондиционирование воздуха, паровые турбины и т. д. являются примерами принудительной конвекции.

Резюме – Естественная и принудительная конвекция

Конвекция бывает двух видов: естественная конвекция и вынужденная конвекция. Разница между естественной и принудительной конвекцией заключается в том, что при естественной конвекции естественные средства влияют на движение жидкости, тогда как при принудительной конвекции внешние средства влияют на движение жидкости.

Артикул:

1. «Естественная конвекция». Википедия, Фонд Викимедиа, 17 апреля 2018 г.