Расчёт балки, рамы бесплатно онлайн
Не пришёл код Послать сообщение Заказать решение Поддержать проект
-
Операции
-
С чего начать построение расчётной модели — видео / видео откроется в отдельной панели данного окна /
Узлы — это основа для создания стержней и всей расчётной модели.
Введите
координаты узлаX, м: Y, м: - на узле на стержне
- на узле на стержне
-
на узле
на стержне
Для выполнения данной операции необходимо сначала создать один или несколько стержней.
 Для создания стержней
используйте пункт меню «Стержень» в данной панели.
Для создания стержней
используйте пункт меню «Стержень» в данной панели.
Номер стержня: Узел для отсчёта смещения: Смещение, м: Величина силы, кН: для смены направления силы поменяйте её знак Вариант ориентации Угол поворота, град.  :
:
Вариант изображения -
на узле
на стержне
Для выполнения данной операции необходимо сначала создать один или несколько стержней. Для создания стержней используйте пункт меню «Стержень» в данной панели.
Номер стержня: Узел для отсчёта смещения: Смещение, м: Момент, кН·м: для смены направления момента измените знак его величины Угол поворота, град.  :
:
090180270 - на узле на стержне
- на узле на стержне
-
Жёсткость предназначена для определения перемещения, для чего необходимо задать контрольную точку. Так как контрольная точка в расчёте не определена, задание жесткости смысла не имеет.
Задайте коэффициент жёсткости № 2 : {EJ}2 = ∗EJ
-
-
Объекты
В данном расчёте не задано ни одного объекта.
Для создания объектов модели перейдите в раздел «Операции»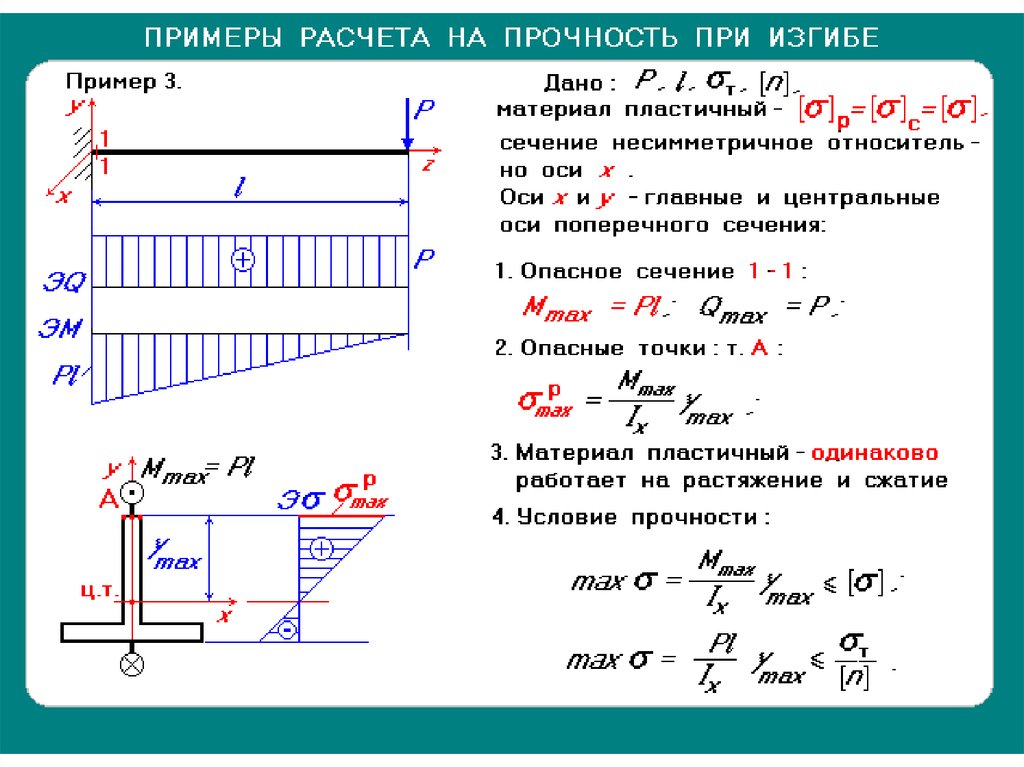
Задание 3 расчет балки на прочность и жесткость
Целью задания является расчет балки на прочность при плоском изгибе и исследование влияния формы поперечного сечения на ее металлоемкость.
Для заданной балки (рис. 18):
1) определить реакции опор;
2) записать уравнения поперечной силы и изгибающего момента для всех участков и построить эпюры поперечной силы и изгибающего момента;
3) подобрать балку двутаврового поперечного сечения из условия прочности по нормальным напряжениям и проверить балку на прочность по касательным напряжениям;
4) произвести анализ изменения веса балки в зависимости от формы ее поперечного сечения (рис. 17), приняв за единицу вес двутавровой балки;
5) построить эпюры распределения нормальных и касательных напряжений по высоте двутавровой балки в произвольном ее сечении, в котором ни поперечная сила, ни изгибающий момент не равны нулю;
6) записать уравнения углов поворота и прогибов сечений балки для всех участков и построить эпюры углов поворота и прогибов;
7) графическая
часть задания должна содержать чертеж
балки в стандартном масштабе с указанием
размеров балки и нагрузки (под чертежом
балки расположить эпюры поперечных
сил, изгибающих моментов, углов поворота
и прогибов сечений балки), эпюры
распределения нормальных и касательных
напряжений по высоте сечения балки.
Материал балки – сталь Ст.3. При расчетах принять: допускаемые напряжения adm = 160 МПа, adm = 100 МПа, модуль упругости Е = = 2105 МПа.
Для построения эпюр углов поворота и прогибов сечений балки необходимо подсчитать соответствующие величины в 4-6 сечениях на каждом участке.Разрешается ординаты эпюр углов поворота и прогибов сечений балки увеличить в EI раз.
Исходные данные взять из табл. 3.
Таблица 3
|
Номер строки |
l, м |
l1, м |
l2, м |
F, кН |
M, кНм |
q, кН/м |
|
а |
б |
в |
|
а |
б | |
|
1 |
2,0 |
4,0 |
3,0 |
50 |
10 |
40 |
|
2 |
2,5 |
5,0 |
3,5 |
45 |
20 |
30 |
|
3 |
3,0 |
6,0 |
4,5 |
40 |
30 |
20 |
|
4 |
3,5 |
7,0 |
1,5 |
35 |
40 |
10 |
|
5 |
4,0 |
6,0 |
2,0 |
30 |
50 |
15 |
|
6 |
1,5 |
5,0 |
2,5 |
25 |
15 |
25 |
|
7 |
2,0 |
4,0 |
3,0 |
20 |
25 |
35 |
|
8 |
3,0 |
3,0 |
3,5 |
15 |
35 |
45 |
|
9 |
4,0 |
2,0 |
4,0 |
10 |
45 |
20 |
|
0 |
2,5 |
7,0 |
2,0 |
60 |
55 |
30 |
Рассчитать балку
(рис. 19) постоянного поперечного сечения
на прочность при плоском поперечном
изгибе и исследовать влияние формы
поперечного сечения на ее весовые
характеристики.
19) постоянного поперечного сечения
на прочность при плоском поперечном
изгибе и исследовать влияние формы
поперечного сечения на ее весовые
характеристики.
Исходные данные: l = 2 м, l1 = 5 м, l2 = 2 м, F = 30 кН, М = 30 кНм, q = 20 кН/м, adm = 160 МПа; adm = 100 МПа.
Решение
1. Определим опорные реакции из условия равновесия балки:
, НА =0;
, ;
= = -57,14 кН.
, ;
== 27,14 кН.
Проверка правильности определения реакций опор:
, ;
27,14 — 57,14 — 20·2 + 30 + 202 = 0;
0 = 0.
2.
Запишем выражения поперечной силы Q
и изгибающего момента Mz
по участкам, используя
метод сечений. Определим значения
поперечных
сил Q
и изгибающих моментов Мz
в характерных точках по длине балки
и построим эпюры Q
и Mz.
Определим значения
поперечных
сил Q
и изгибающих моментов Мz
в характерных точках по длине балки
и построим эпюры Q
и Mz.
1-й участок: 0 ≤х1≤ 2 м (рис. 20)
;
= = 10.
При х1 = 0 Q = 0, Mz = 0; при х1 = 3 м Q = -40 кН, -40 кНм.
2-й участок: 2 м ≤ х2 ≤ 7 м
= 27,14 — 202 = -12,86 кН;
.
При х2 = 2 м -10 кНм, при х2 = 7 м -74,3 кНм.
3-й участок: 7 м ≤ х3 ≤ 9 м
При х3
= 7 мQy
= 17,14 кН,
= -74,3 кНм,
при х3
= 13 м 0,
Qy
=57,14 кН.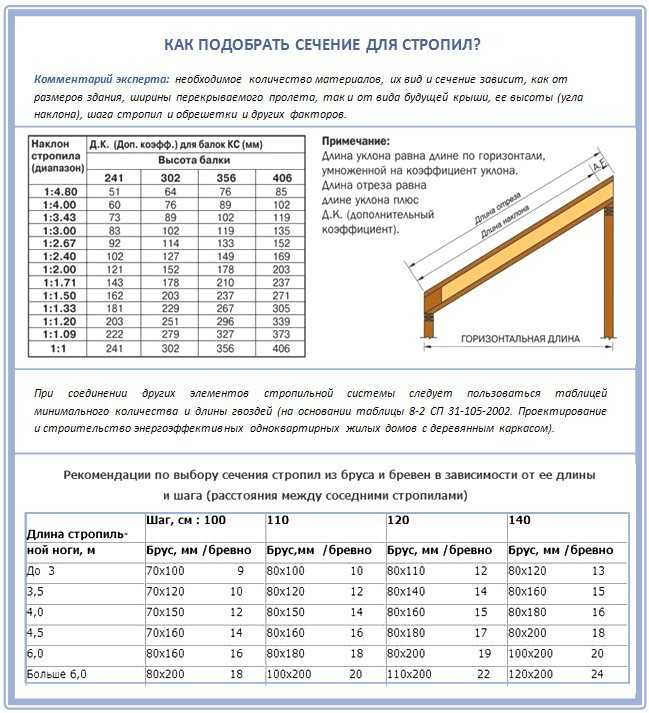
По результатам расчета построим эпюры поперечных сил Q и изгибающих моментов Mz (рис. 19).
3. Определим опасное сечение: из эпюр поперечных сил и изгибающих моментов = 57,14 кН,74,3 кНм.
4. Подбираем двутавровую балку из условия прочности по нормальным напряжениям
,
Откуда
см3.
По величине осевого момента сопротивления выбираем двутавр №30 по ГОСТ 8239-72, у которого Wzтабл = 472 см3. Вычисляем фактическое максимальное напряжение
фmax = == 157,4 МПа.
Вычисляем недонапряжение по нормальным напряжениям
=100%=100 = 1,6 % < 5 %.
При расчетах
допускается недонапряжение и
перенапряжение до 5 %.
Выбранный двутавр № 40 удовлетворяет
условию прочности по нормальным
напряжениям. Из таблицы балок двутавровых
выписываем геометрические характеристики:
Wz
= 472 см3,
h
= 30 см, b
= 13,5 см, А1
= =46,5 см2;
7080
см4,
=
268 см3,
s
= 0,65 см, t
=1,02 см.
Из таблицы балок двутавровых
выписываем геометрические характеристики:
Wz
= 472 см3,
h
= 30 см, b
= 13,5 см, А1
= =46,5 см2;
7080
см4,
=
268 см3,
s
= 0,65 см, t
=1,02 см.
Проверяем балку на прочность по касательным напряжениям
max = = МПа аdm = 100 МПа.
Таким образом, выбранная двутавровая балка удовлетворяет условию прочности по касательным напряжениям.
5. Определим размеры поперечных сечений балки различной формы:
а) коробчатое сечение (рис. 23)
;
= 10,6 см, 0,7210,62 = 80,9 см2;
б) прямоугольное сечение (рис. 24)
= 464,4, = 8,9 см,
28,92 = 158,4 см2;
в) квадратное
сечение (рис. 25)
25)
464,4, а = = 14,1 см,198,8 см2;
г) круглое сечение (рис. 26)
= 464,4, см,
= 221,6 см2;
д) трубчатое сечение (рис. 27)
, ;
ymax = d/2, =464,4,см,
= 113 см2;
е) квадратное сечение с углами по осям координат (рис. 28)
, 0,707 a, (для квадратного сечения моменты инерции относительно любых центральных осей одинаковы),
464,4, а = = 15,8 см,
= 249,6 см2.
6. Производим анализ изменения веса балки в зависимости от формы ее сечения, приняв за единицу вес двутавровой балки. Вес балки определим по формуле .
Обозначим отношение веса балки различной формы сечения к весу двутавровой балки:
Таким образом,
сечения балки в порядке возрастания ее
веса выстроятся в ряд: двутавр, коробчатое
сечение, трубчатое сечение, прямоугольное
сечение, квадратное сечение, круглое
сечение, квадратное сечение с углами
по осям координат.
7. Строим эпюры распределения нормальных и касательных напряжений по высоте двутавровой балки для сечения, где приложена сила F. В этом сечении Q = 17,14 кН, Мz = 74,3 кНм.
Нормальные напряжения определяются по формуле
= .
Подсчитаем нормальные напряжения в характерных точках сечения:
y1 = h / 2, 1 = = 157,4 МПа;
y4 = 0, 4 = 0.
Эпюра нормальных напряжений показана на рис. 29.
Касательные напряжения определяются по формуле Журавского
= .
У двутаврового сечения ширина b сечения и статический момент отсеченной части сечения меняются по высоте, поэтому вычисляем касательные напряжения в характерных точках сечения:
Точка 1:
;.
Точка 2: 199,5 см3.
В точке 2 ширина волокон равна ширине полки b, поэтому
0,35 МПа.
Точка 3: = 199,5 см3, ширина волокон равна толщине стенки s, поэтому
7,4 МПа.
Точка 4: 268 см3, ширина волокон равна толщине стенки s, поэтому
10 МПа.
Эпюра касательных напряжений показана на рис. 29.
8. Определим углы поворота и прогибы сечений балки методом начальных параметров. Уравнения углов поворота и прогибов сечений пометоду начальных параметровимеют вид:
;
,
где ,- угол поворота и прогиб сечения балки в начале координат (на левом конце балки).
Запишем уравнения углов поворота и прогибов сечений балки для различных участков:
1-й участок: 0 ≤ х1 ≤ 2 м
,
.
2-й участок: 2 м ≤ х2 ≤ 7 м
,
.
3-й участок: 7 м ≤ х3 ≤ 9 м
Постоянные интегрирования C и D определяем из граничных условий — прогибы на опорах равны нулю:
при x = l = 2 м yA= y1 = y2 = 0;
при x2 = l + l1 + l2 = L = 9 м yB = y3 = 0.
Получаем систему уравнений
или
Решая систему
уравнений, получаем С
= 159,1 кНм2,
D
= -304,8 кНм3.
Вычислим значения углов поворота и прогибов сечений балки в 3-4 точках на каждом участке. Результаты расчета приведены в табл. 4.
Таблица 4
|
№ участка, i |
1 |
2 | ||||
|
xi, м |
0 |
1 |
2 |
2 |
3 |
5 |
|
, кНм2 |
159,1 |
155,8 |
132,4 |
132,4 |
101,0 |
44,6 |
|
EIzyi, кНм3 |
-304,8 |
-146,5 |
0 |
0 |
125,4 |
294,5 |
Продолжение
табл. 4
4
|
№ участка, i |
2 |
3 | |||
|
xi, м |
6 |
7 |
7 |
8 |
9 |
|
,кНм2 |
-10,4 |
-78,3 |
-78,3 |
-140,7 |
-166,0 |
|
EIzyi, кНм3 |
312,6 |
269,3 |
269,3 |
157,5 |
0 |
Определим экстремальное (максимальное) значение прогиба на 2-м участке:
Решая уравнение
методом последовательных приближений,
получим х2
= 5,827 м,
313,5 кН· м3.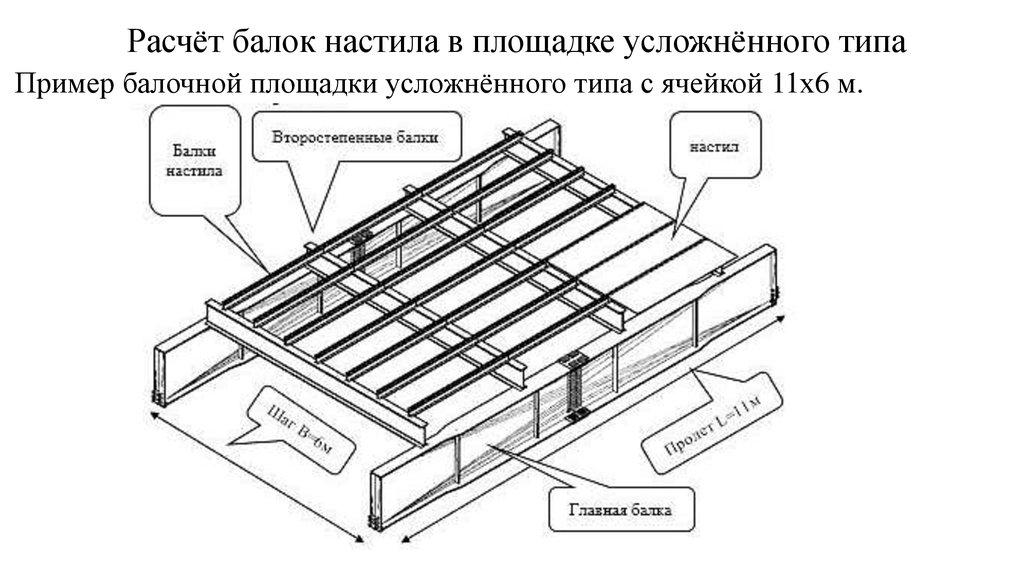
На основе полученных результатов строим эпюры углов поворота и прогибов сечений балки (рис. 21).
Лечить учить и судить умеют все, а вот рассчитать несущую балку? — Обсуждай
Лечить учить и судить умеют все, а вот рассчитать несущую балку? — ОбсуждайМари
Лечить учить и судить умеют все, а вот рассчитать несущую балку? балка
1039
155
2
Ответы
МИ
Мурат Ибраев
Рассматриваемая балка воспринимает постоянные нагрузки от собственного веса опирающихся на нее железобетонных ребристых плит покрытия, кровли, конструкций светового фонаря, а также временную нагрузку от веса снегового покрова.
Основные характеристики балки Б-1 по ОСТ 10016-39:
– поперечное сечение: двутавр №45
– момент инерции: J = 27450 см4
– момент сопротивления: W = 1220 см3
– расчетный пролет балки: L = 9,15 м
– собственный вес балки: P = 65,2 кг/м
– ширина площади сбора нагрузок: b = 6,0 м (см.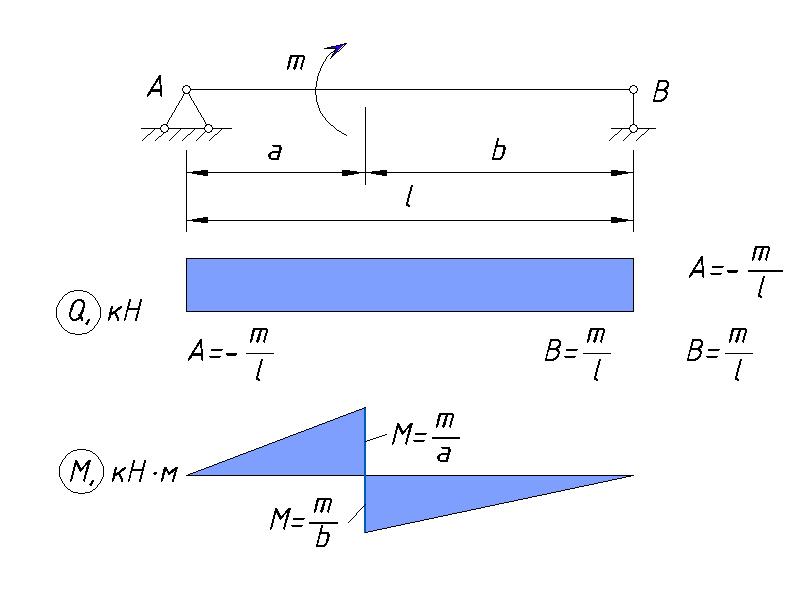 Рис.1,2).
Рис.1,2).
Схемы для сбора нагрузок на балку Б-1 приведены на Рис.1, 2. Расчетная схема балки Б-1, соответствующая реальной схеме нагружения, представлена на Рис.3.
расчет двутавровой балки
0
Мари
O_o
1
МИ
Мурат Ибраев
разве не верно ?
1
Николай Гарипов
а где Рис.1,2,3 😕
1
ОП
Охотник Пустынный
Смотря какие силы воздействуют на нее. Либо изгиб, либо изгиб с кручением. Либо что-то еще, а если есть выступающая консоль, тогда ее тоже рассчитывать нужно. Нагрузки воздействуют на всю балку. Ах, да. Какой модификации опоры под этой балкой? Подвижные или полуподвижные? Или же не подвижные.
Нагрузки воздействуют на всю балку. Ах, да. Какой модификации опоры под этой балкой? Подвижные или полуподвижные? Или же не подвижные.
0
АС
Александр Степанов
а оно нам надо — рассчитывать эту самую балку??????
я, например, и без неё себя совершенно прекрасно чувствую!) ))
к тому же невозможно объять необъятное!..
а вот лечить, воспитывать, судить… и ещё много, чего, нам в жизни
приходится очень часто ))
0
Сергей Лоскутов
Да сопромат и теорию упругости в житейской суете забывать стали. Нам все схему аль чертеж, сотворим тады что хош.. А чтобы в расчетах увольте грамотешки не хватает. Вот если кто подучил?
0
Серёга Парфёнов
А вот это могут только люди хорошо учившиеся на строительной специальности. А судить легко других,но порой такие люди в своей жизни разобраться не могут
А судить легко других,но порой такие люди в своей жизни разобраться не могут
0
Александр Баштан
Не все! Но я умею. Может быть я Вам подойду? Млодой человек спрашивает: «Девушка, а Вы любите животных?» Да, отвечает. А возьмите меня себе, я такая скотина!
0
Мари
1
ПУ
Павел Угаров
Это вопрос по сопромату там надо эпюры чертить и расчитывать несущую балку. Мы в шахте столько балок таскаем ужас.
0
Михаил Карепанов
Или потерю напряжения на расстоянии один километр в алюминиевом проводе сечением 20 квадратных миллиметров ?
0
Горностаева Татьяна
Дааааааа. ….Сопромат штука серьёзная. Подозреваю, что сейчас мне будет это сделать легче, чем 35 лет назад)))
….Сопромат штука серьёзная. Подозреваю, что сейчас мне будет это сделать легче, чем 35 лет назад)))
0
По
Полтергейст
Тут смотря как это понимать. Тут два варианта балки:1) Балка сухая — т.е. не сущая. 2) Балка несуществующая
0
Мари
1
Евгений Томеев
Всё зависит от последующей ответственности. Если она отсутствует, то и балку так же легко рассчитают
0
ГМ
Григорий Макеев
Мари,обращайтесь, я не только балку расчитаю, ну расчитаю время посещения туалетной комнаты.
0
ПС
Предельно Серьёзен
Лечить и судить тоже мало кто умеет, просто берутся за это кому не лень. В отличие от.
0
николай К
все лезут управлять государством… а управлять пароходом все боятся… учиться надо
0
Света Абильдина
может некоторые и смогут,но как правило выбирают то что легче и без напряга
0
ЛГ
Латиф Гасанов
Могу на глаз, т.к. нет строительного образования. Хотя построил 3 дома.
Хотя построил 3 дома.
0
Владимир Максимов
Да так, чтоб она потом вместе с крышей не рухнула на свою же голову!…
0
Михаил Бардов
Идите в технический ВУЗ.Изучайте сопромат и техническую механику.
0
ЯО
Япарова Ольга
Может любой строитель или человек интересующийся строительством!
0
Валерий М
Да, с сопроматом у многих немалые сложности, не то, что в медицине!
0
Мари
1
Следующая страница
Расчеты деревянных балок перекрытия — онлайн расчет по формуле
В любом здании имеются перекрытия. В собственных домах при создании опорной части, применяются деревянные балки, которые обладают рядом потребительских свойств:
В собственных домах при создании опорной части, применяются деревянные балки, которые обладают рядом потребительских свойств:
- доступность на рынке;
- лёгкость обработки;
- цена значительно ниже, нежели на стальные или бетонные конструкции;
- высокая скорость и удобство монтажа.
Но, как и всякий строительный материал, деревянные балки имеют определённые прочностные характеристики исходя из которых производится расчёт на прочность, определяются необходимые размеры силовых изделий.
- Основные виды балок ↓
- Нагрузки на горизонтальное перекрытие ↓
- Как рассчитать нагрузку на балку перекрытия ↓
- Пример расчёта ↓
- Как рассчитать необходимое количество балок ↓
- Пример расчёта ↓
- Как рассчитать необходимое сечение традиционной деревянной балки перекрытия ↓
- Пример расчёта ↓
Основные виды балок
При бытовом строительстве используются несколько типов монтажа опорных элементов перекрытий:
- Простая балка, — представляет собой перекладину, имеющую две опорные точки на своих концах.
 Расстояние между опорами называется пролёт. Соответственно, при наличии нескольких точек крепления, бывают двух–, трёх–, и более пролётные неразрезные балки. В конструкции частного дома в этом качестве выступают промежуточные стеновые перегородки.
Расстояние между опорами называется пролёт. Соответственно, при наличии нескольких точек крепления, бывают двух–, трёх–, и более пролётные неразрезные балки. В конструкции частного дома в этом качестве выступают промежуточные стеновые перегородки. - Консоль, — брус жёстко закреплён одним концом в стене или имеет один свободный конец, с длиной более чем двукратный поперечный размер. Наличие двух свободных свисающих частей говорит о том, что наличествует двухконсольная конструкция. На практике – это горизонтальные балки, входящие в состав крыши и образующие навес.
- Заделанное изделие, — оба окончания жёстко вмонтированы в стену. Такая схема встречается при возведении вышерасположенных перегородок и стен, при этом балка получается вмонтированной в вертикальную конструкцию.
Нагрузки на горизонтальное перекрытие
Для расчёта на прочность необходимо знать нагрузки, возникающие в процессе эксплуатации перекрытия. Самые значительные величины возникают на первом этаже жилого здания. Меньшие значения получаются для мансардных конструкций и чердачных помещений. Напряжения в балке возникают:
Самые значительные величины возникают на первом этаже жилого здания. Меньшие значения получаются для мансардных конструкций и чердачных помещений. Напряжения в балке возникают:
- от внутренних строительных конструкций, например, перегородок, лестниц;
- от веса бытовой техники, мебели;
- от массы людей.
Статическую нагрузку определяет два основных вида напряжения, – прогиб по всей длине и изгиб в месте опоры.
- Прогиб, – получается от веса вышерасположенных элементов. Максимальная стрелка отклонения получается в точке местонахождения объекта с самой большой массой и (или) посередине между опорами.
- Изгиб или излом, – это разрушение перекладины в точке заделки. Возникает от вертикальной нагрузки, а сама балка, воспринимающая это напряжение, выступает в роли рычага. С определённой величины усилия начинается критический изгиб, приводящий к разрушению поперечной опоры.
Для уменьшения влияния на прочность деревянного поперечного изделия от внутренних конструкций, их стараются располагать в местах нахождения нижних опор. Бытовую технику и мебель по возможности, целесообразно размещать вдоль стен или около разгрузочных конструкций.
Существует достаточно много типов деревянных балок, но наиболее доступны для широкой массы населения – это изделия прямоугольного или овального сечения. В последнем случае, балка представляет собой оцилиндрованное бревно, обрезанное с двух противоположных сторон.
Как рассчитать нагрузку на балку перекрытия
Общая нагрузка на элементы перекрытия складывается из собственного веса конструкции, веса от внутренних строительных изделий, опирающихся на балки, а также массы людей, мебели, бытовой техники и прочей хозяйственной утвари.
Полный расчёт, учитывающий все технические нюансы, достаточно сложен и выполняется специалистами при проектировании жилого дома. Для граждан, возводящих жильё по принципу «самостроя», более удобна упрощённая схема, в которую заложены требования СНиП, оговаривающие условия и технические характеристики деревянных материалов:
- длина опорной части балки, контактирующей с фундаментом или стеной, не должна быть меньше 12 см;
- рекомендуемое соотношение сторон прямоугольника 5/7, — ширина меньше высоты;
- допустимый прогиб для чердачного помещения составляет не более 1/200, межэтажные перекрытия – 1/350.

По СНиП 2.01.07–85 эксплуатационная нагрузка на чердачную конструкцию с лёгким утеплителем из минеральной ваты составит:
Пример расчёта
Дано:
- чердак в жилом доме, использующийся для хранения различного хозяйственного инвентаря;
- для утепления применён керамзит с лёгкой бетонной стяжкой.
Общая нагрузка составит G = 50 кг/м² + 150 кг/м² * 1,3 = 245 кг/м².
Исходя из практики, средние усилия на мансардном этаже не превышают значений в 300–350 кг/м².
Для межэтажных перекрытий величины находятся в диапазоне 400–450 кг/м², причём большее значение следует принимать при расчётах первого этажа.
Совет. При выполнении перекрытий целесообразно принимать значения нагрузок, превышающие расчётные на 30–50%. Это повысит надёжность конструкции в целом и увеличит общий срок эксплуатации.
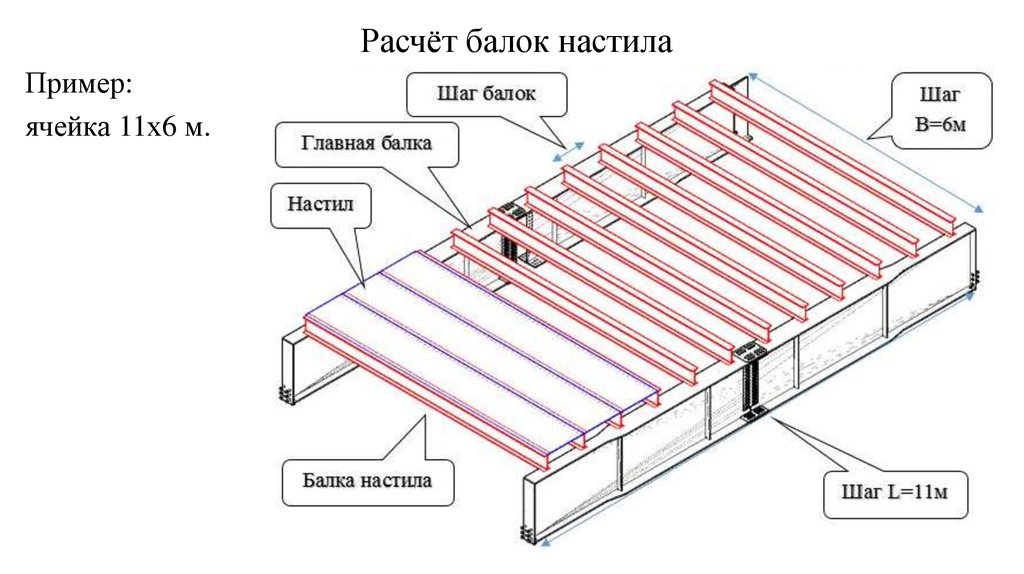
Как рассчитать необходимое количество балок
Число поперечных опор определяется нагрузками, приходящиеся на них, и максимальным прогибом чернового покрытия, выполненного, например, из доски или фанеры. На их жёсткость влияет собственная толщина изделий и шаг между точками опоры, то есть, расстояние от соседних балок.
На их жёсткость влияет собственная толщина изделий и шаг между точками опоры, то есть, расстояние от соседних балок.
Для помещения с малой эксплуатацией (чердак), допускается использовать доску толщиной не менее 25 мм, при шаге между опорами 0,6–0,75 метра. Межэтажное перекрытие жилой зоны целесообразно осуществлять половой доской с размером не менее 40 мм и расстоянием по ближайшим точкам крепления не более 1 метра.
Пример расчёта
Чердачное пространство. Длина между стенами составляет 5 метров. Слабая эксплуатационная нагрузка, – хранение всякой утвари. Настил осуществляется из обрезной сухой доски хвойных пород толщиной 25 мм. Принимая максимальный шаг в 0,75 метра, количество опорных точек должно составить:
5 м / 0,75 м = 6,67 шт., округляя до целого числа в большую сторону – 7 балок.
Тогда уточнённый шаг равен:
5 м / 7 шт = 0,715 м.
Межэтажное перекрытие. Длина между стенами 5 метров. Первый этаж с максимальной нагрузкой. Черновой пол выполняется из изделия с размером 40 мм. Шаг по опорам принимается в 1 метр.
Первый этаж с максимальной нагрузкой. Черновой пол выполняется из изделия с размером 40 мм. Шаг по опорам принимается в 1 метр.
Количество точек крепления составляет: 5 м / 1 м = 5 шт.
Совет. Несмотря на невысокую нагрузку, приходящуюся на чердачное пространство, целесообразно применять требования, относящиеся к межэтажным перекрытиям, — в будущем может появиться вероятность перестройки в жилое мансардное помещение.
Как рассчитать необходимое сечение традиционной деревянной балки перекрытия
Прочностные характеристики опорного элемента определяются геометрическими параметрами, – длиной и поперечным сечением. Длина, как правило, даётся из внутренних размеров межстенного пространства и закладывается на стадии проектирования здания. Второй параметр, – сечение, можно изменять в зависимости от предполагаемых нагрузок в процессе строительства.
Пример расчёта
Чтобы избежать достаточно мудрёных математических выкладок, приводим рекомендуемые данные, которые сведены в таблицу.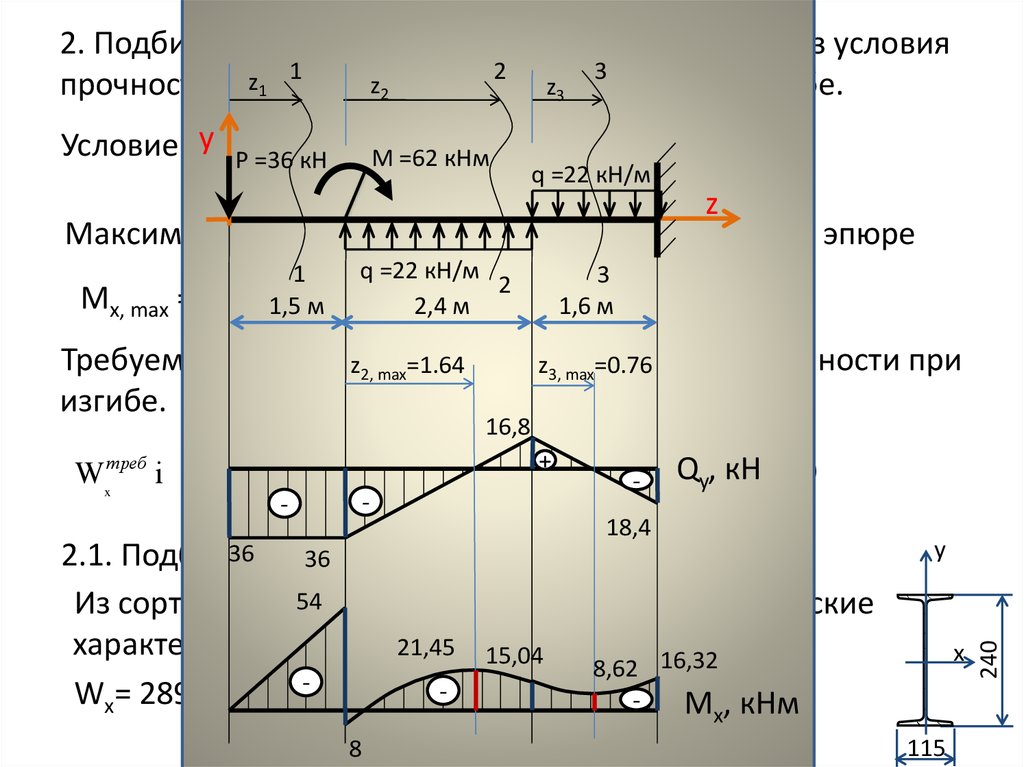 При имеющихся размерах пролёта и шага, можно определить примерное сечение бруса или диаметр бревна. Расчёт осуществлялся исходя из усреднённой нагрузки в 400 кг/м²
При имеющихся размерах пролёта и шага, можно определить примерное сечение бруса или диаметр бревна. Расчёт осуществлялся исходя из усреднённой нагрузки в 400 кг/м²
Таблица 1
Сечение прямоугольного бруса:
| Шаг, метр | Пролёт, метр | ||||
| 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | |
| 0,6 | 75 х 100 | 75 х 200 | 100 х 200 | 150 х 200 | 150 х 225 |
| 1,0 | 75 х 150 | 100 х 175 | 125 х 200 | 150 х 225 | 175 х 250 |
Таблица 2
Диаметр оцилиндрованного бревна:
| Шаг, метр | Пролёт, метр | ||||
| 2,0 | 3,0 | 4,0 | 5,0 | 6,0 | |
| 0,6 | 110 | 140 | 170 | 200 | 230 |
| 1,0 | 130 | 170 | 210 | 240 | 270 |
Примечание: В таблицах приведены минимальные допустимые размеры. При проектировании собственного здания, необходимо принимать те размеры деревянных изделий, которые присутствуют на местном строительном рынке региона, причём значения требуется округлять в большую сторону.
При проектировании собственного здания, необходимо принимать те размеры деревянных изделий, которые присутствуют на местном строительном рынке региона, причём значения требуется округлять в большую сторону.
Совет. При отсутствии необходимого бруса, его можно заменить досками, скреплёнными между собой посредством столярного клея и саморезов. Ещё один вариант усиления – увеличить сечение бруса, добавив к его боковым сторонам доски определённой толщины.
Совет. Продлить срок службы и снизить показатель горючести поможет обработка специальными огне– и биозащитными средствами. Кроме этого, такая операция способствует небольшому увеличению прочности деревянных изделий.
Совет. Тем, кто всё-таки желает провести математические изыскания, по расчётам деревянных балок, для перекрытий, целесообразно заглянуть в интернет с этим вопросом, — имеется достаточное количество сайтов, на которых выложены электронные калькуляторы по определению параметров элементов силовых конструкций.
Статья была полезна?
0,00 (оценок: 0)
Расчёт балок на прочность при изгибе
Задача 1
В некотором сечении балки прямоугольного сечения 20×30см М=28 кНм, Q=19 кН.
Требуется:
а) определить нормальное и касательное напряжения в заданной точке К, отстоящей от нейтральной оси на расстоянии 11 см,
б) проверить прочность деревянной балки, если [σ]=10 МПа, [τ]=3 МПа.
Решение
а) Для определения σ(К), τ(К) и maxσ,maxτ потребуется знать величины осевого момента инерции всего сечения IН.О., осевого момента сопротивления WН.О., статического момента отсечённой части и статического момента половины сечения Smax:
Тогда:
б) Проверка прочности:
— по условию прочности нормальных напряжений:
— по условию прочности касательных напряжений:
Задача 2
В некотором сечении балки М=10кНм, Q=40кН. Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
Поперечное сечение – треугольное. Найти нормальное и касательное напряжения в точке, отстоящей от нейтральной оси на расстоянии 15 см.
где
Тогда
где:
Тогда
Задача 3
Подобрать сечение деревянной балки в двух вариантах: круглое и прямоугольное (при h/b=2), если [σ]=10 МПа, [τ]=3 МПа, и сравнить их по расходу материала.
Задаёмся направлениями опорных реакций А и В и составляем уравнения статики:
(1) ∑М(В) = F·8 – М – А·6 + (q·6)·3 =0,
откуда
(2) ∑М(А) = F·2 – М + В·6 — (q·6)·3 =0,
откуда
Iучасток
∑М(С) = М(z1) +F·z1=0,
ММ(z1) = —F·z1= — 30 ·z1 —
– уравнение прямой.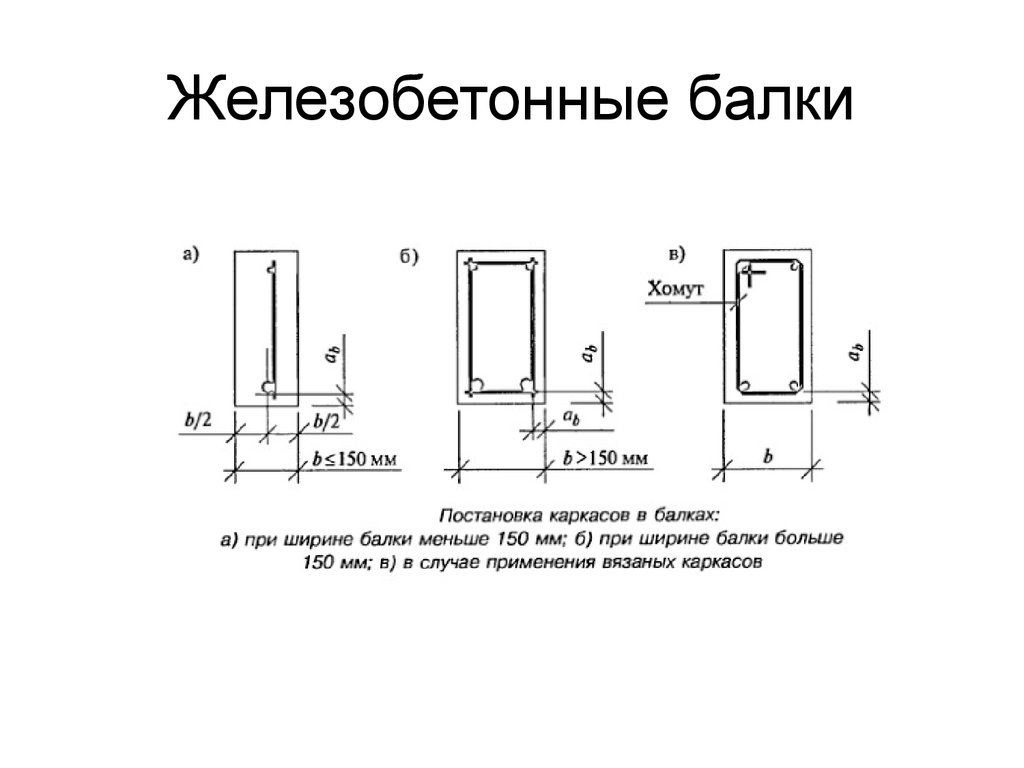
При z1 = 0: М = 0,
z1 = 2: М =- 60 кНм.
∑у= — F — Q(z1) = 0,
Q(z1) = — F = -30 кН – постоянная функция.
II участок
откуда
— уравнение параболы.
При z2=0: М = 0,
z2=3м: М = 30 · 3 – 5 · 32 = 90 — 45 = 45кНм,
z2=6м: М = 30 · 6 – 5 · 62 = 180 — 180 = 0.
∑у= Q(z2) — q·z2 + B= 0,
Q(z2) = q·z2 — B= 10·z2 – 30 – уравнение прямой,
при z2 = 0: Q = -30,
z2 = 6м: Q = 10·6 – 30 = 30.
Определение аналитического максимума изгибающего момента второго участка:
из условиянаходим :
И тогда
Заметим, что скачок в эп.М расположен там, где приложен сосредоточенный момент М = 60кНм и равен этому моменту, а скачок в эп.Q – под сосредоточенной силой А = 60 кН.
Подбор сечения балок производится из условия прочности по нормальным напряжениям, куда следует подставлять наибольший по абсолютной величине изгибающий момент из эпюры М.
В данном случае максимальный момент по модулю М = 60кНм
откуда: :
а) сечение круглой формы d=?
б) сечение прямоугольной формы при h/b = 2:
тогда
Размеры сечения, определенные из условия прочности по нормальным напряжениям, должны удовлетворять также условию прочности по касательным напряжениям:
Для простых форм сечений известны компактные выражения наибольшего касательного напряжения:
— для круглого сечения
— для прямоугольного сечения
Воспользуемся этими формулами.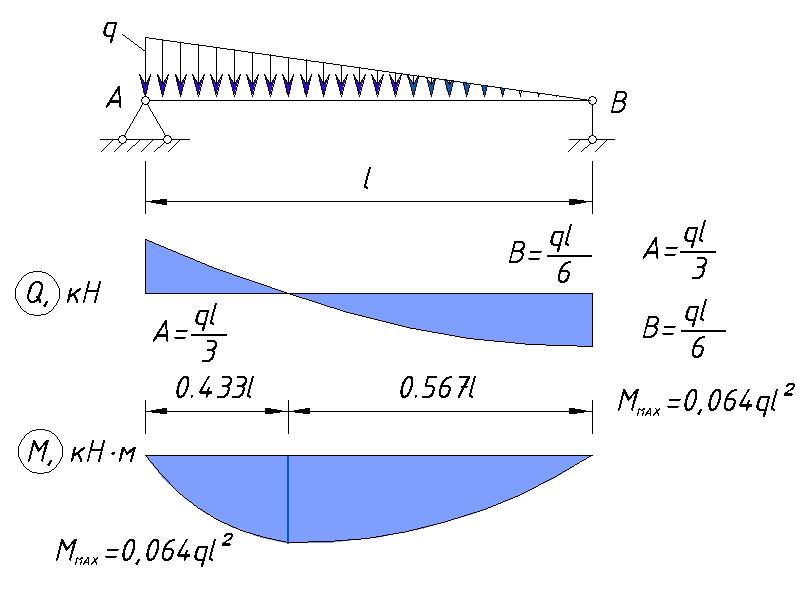 Тогда
Тогда
— для балки круглого сечения при :
— для балки прямоугольного сечения
Чтобы выяснить, какое сечение требует меньшего расхода материала, достаточно сравнить величины площадей поперечных сечений:
Апрямоугольного = 865,3см2 < Акруглого = 1218,6см2, следовательно, балка прямоугольного сечения в этом смысле выгоднее, чем круглого.
Задача 4
Подобрать двутавровое сечение стальной балки, если [σ]=160МПа, [τ]=80МПа.
Задаёмся направлениями опорных реакций А и В и составляем два уравнения статики для их определения:
(1) ∑М(А) = – М1– F ·2 — (q·8)·4 + М2 + В·6 =0,
откуда
(2) ∑М(В) = – М1– А · 6 + F · 4 + (q·8)·2 + М2 =0,
откуда
Проверка:
∑у = А – F – q · 8 + В = 104 – 80 – 20 · 8 +136 = 240 – 240 ≡ 0.
∑М(С) = М(z1) — М1=0,
М(z1) = М1= 40 кНм – постоянная функция.
∑у= — Q(z1) = 0,
Q(z1) = 0.
II участок
— парабола.
Приz2=0: М = 40 кНм,
z2=1м: М = 40 + 104 – 10=134кНм,
z2=2м: М = 40+ 104 · 2 – 10 · 22 = 208 кНм.
∑у=А — q·z2 — Q(z2) = 0,
Q(z2) =А— q·z2 = 104 – 20·z2 – уравнение прямой,
при z2 = 0: Q = 104кН,
z2 = 6м: Q = 104 – 40 = 64кН.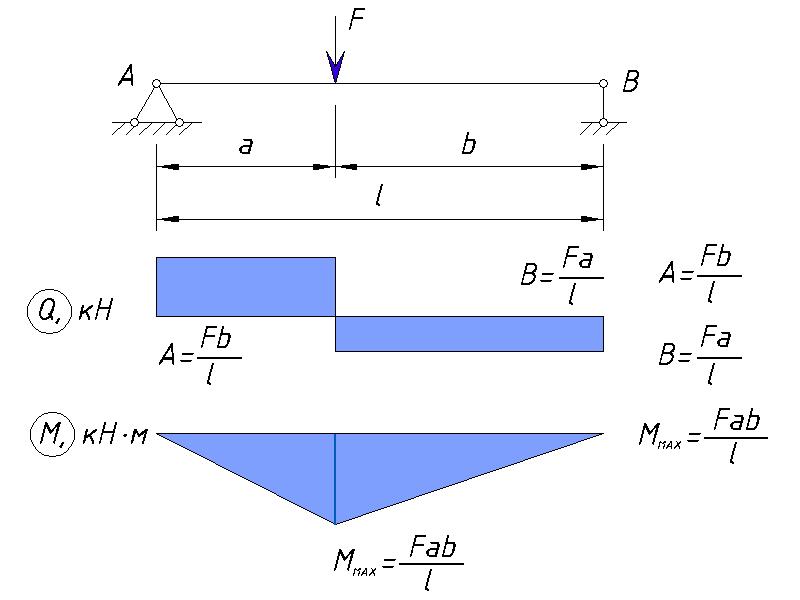
III участок
— парабола.
Приz3=0: М = 24+40=-16 кНм,
z3=2м: М = 24 + 136·2 — 10 (2+2)2 = 24 + 272 – 160 = 136кНм,
z3=4м: М = 24 + 136·4 – 10 (2+4)2 = 24 + 544 – 360 = 208 кНм.
∑у=В — q(2+z3 ) + Q(z3) = 0,
Q(z3) =- В + q(2+z3 ) = -136 + 20 (2+z3 ) – уравнение прямой,
при z3 = 0: Q = -136 + 40 = — 94кН,
z3 = 4м: Q = — 136 + 20 (2+4) = — 136 + 120 = — 16кН.
IV участок
— парабола.
z4=0: М = 0кНм,
z4=1м: М = – 10кНм,
z4=2м: М = — 40кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 20·z4 – уравнение прямой.
Приz4 = 0: Q = 0,
z4 = 2м: Q = 40кН.
Проверяем скачки в эпюрах:
а) В эпюре М скачок на правой опоре величиной 24кНм (от 16 до 40) равен сосредоточенному моменту М2=24, приложенному в этом месте.
б) В эпюре Q три скачка:
первый из них на левой опоре соответствует сосредоточенной реакции А=104кН,
второй – под силой F=80кН и равен ей (64+16=80кН),
третий – на правой опоре и соответствует правой опорной реакции 136кН (94+40=136 кН)
Наконец, проектируем двутавровое сечение.
Подбор его размеров производится из условия прочности по нормальным напряжениям :
В сортаменте двутавровых профилей профиля с точно таким моментом сопротивления Wх нет.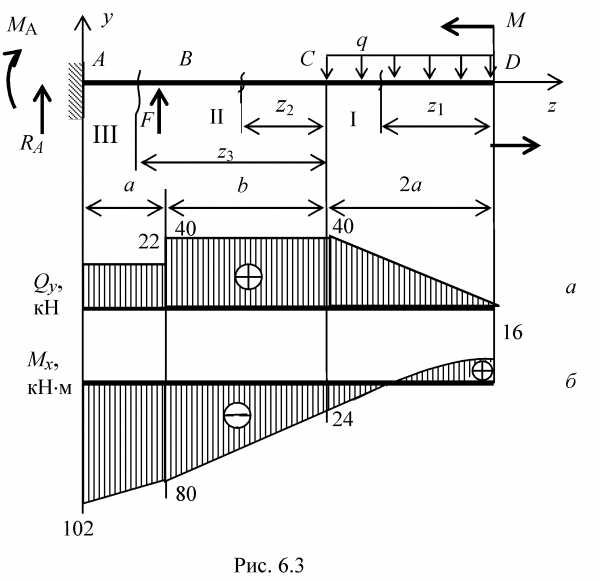 Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Есть № 40а с Wх=1190 см3 и № 45а с Wх=1430 см3
Попробуем меньший из них. Если принять двутавр № 40а, у которого Wх=1190 см3 , то наибольшее напряжение в опасном сечении будет:
и перенапряжение составитчто превышает рекомендуемую величину отклонения, равную 5%.
Поэтому приходится принимать ближайший больший размер двутавра, а именно №45а, у которого Wх=1430 см3. В этом случае балка будет работать с недонапряжением:
что меньше [σ]=160МПа на
Итак, принимается двутавр №45а, у которого: Wх=1430 см3, Iх=32240см4, Iх: Sх=38,6см, d=11,5мм.
Далее необходима проверка прочности по касательным напряжениям с помощью условия прочности :
Это условие прочности выполняется, даже с избыточным запасом.
Задача 5
Подобрать сечение балки, рассмотрев шесть вариантов форм и три вида материалов (древесина, чугун, сталь).
Решение
1.Определение опорных реакций
∑М(А) = F · 2 + М1 — М2— q·6·7 + В · 8 =0,∑М(В) = F · 10 + М1— М2 – А · 8 + q·6·1 =0,Проверка:
∑у = – 20 – 40 ·6 +50+210 = — 260 + 260 ≡ 0.
2.Построение эпюр изгибающих моментов и поперечных сил.
I участок
∑М(С) = М(z1) + F·z1=0,
М(z1) = — F·z1= -20·z1.
При z1=0: М = 0,
z1=2м: М = – 40кНм,
∑у= — F— Q(z1) = 0,
Q(z1) = — 20кН.
II участок
z2=0: М = — 20 – 40 = -60 кНм,
z2=4м: М = 200 — 20 – 120 = 200 — 140 = 60кНм.
∑у=- F + А — Q(z2) = 0,
Q =- F + А= -20+50=30кН.
III участок
— парабола.
Приz3=0: М = — 20·4= — 80 кНм,
z3=2м: М = 210·2 — 20·(2+2)2 = 420 – 320 = 100кНм,
z3=4м: М = 210·4 – 20 · (2+4)2 = 840 – 720 = 120кНм.
∑у= Q(z3) + В — q·(2+z3) = 0,
Q(z3) = — В + q·(2+z3) = — 210 + 40·(2+z3) – уравнение прямой.
Приz3 = 0: Q = -130кН,
z3 = 4м: Q = 30кН.
Q(z0) = — 210 + 40·(2+z0) = 0,
— 210 + 80 + 40·z0 = 0,
40·z0 = 130,
z0 =3,25м,
IV участок
парабола.
Приz4=0: М = 0 кНм,
z4=1м: М = – 20кНм,
z4=2м: М = — 80кНм.
∑у=- q·z4 + Q(z4) = 0,
Q(z4) =q·z4 = 40·z4 – уравнение прямой,
z4 = 0: Q = 0,
z4 = 2м: Q = 80кН.
3. Подбор сечений (опасное сечение по σ: |maxМ|=131,25кНм,
опасное сечение по τ: |maxQ|=130кН).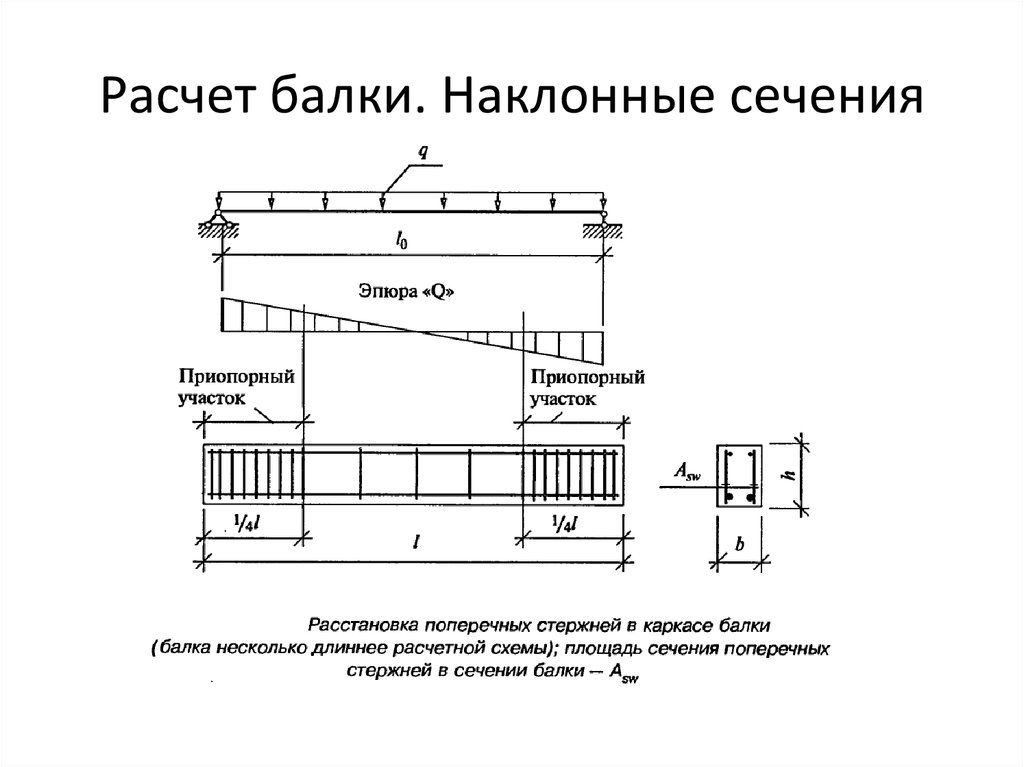
Вариант 1. Деревянное прямоугольное ([σ]=15МПа, [τ]=3МПа)
Принимаем: В=0,24м,
Н=0,48м.
Проверяем по τ:
Вариант 2. Деревянное круглое
Принимаем d=0,45м,
Проверяем по τ:
Вариант 3. Чугун : ([σР]=30МПа, [σс]=120МПа, [τ]=15МПа)
Принимаем b=0,19м, тогда h=0,38м, d=0,076м.
Проверка по τ:
b(у)= b — d= 0,19 — 0,076 = 0,114м
Вариант 4. Сталь, двутавр : ([σ]=160МПа, [τ]=80МПа).
по сортаменту Wх=953см3. Это №40: Ix=19062см4, Sх=545см3, d=0,83см.
Проверка по τ:
Вариант 5. Сталь, круглая труба
Сталь, круглая труба
Принимаем D=0,22м → d = 0,6·D =0,132м.
Проверка по τ:
Вариант 6. Сталь, прямоугольная труба
b1= b — 2t = b — 2·0,1b = 0,8b,
h1= h — 2t = 0,8h,
Принимаем b=0,13м, h=0,26м.
Проверка по τ:
Кстати: какое из сечений стальной балки выгодней по расходу материала?
Двутавр — А = 72,6см2 = 72,6·10-4 = 0,00726м2,
круглая труба –
прямоугольная труба —
Самый лёгкий: двутавр → самый выгодный с точки зрения изгиба.
какова максимальная длина и толщина, как рассчитать (пример сбора нагрузок, определения внутренних усилий, предельного прогиба, подбора высоты и ширины, шага)?
Конструктивный раздел рабочего проекта жилого или общественного здания является важной частью комплекта технической документации.
Инженер разрабатывает комплекс решений, выполнение которых гарантирует безопасную эксплуатацию объекта.
Перед разработкой чертежей несущих элементов здания требуется провести общий и локальный расчёт каждого из них с подбором оптимальных сечений.
Проектировщики уделяют повышенное внимание конструктивным решениям перекрытий, и, при необходимости, добавляет в конструкцию балки, повышающие прочность и компенсирующие прогибы конструкции.
О расчете балок перекрытия поговорим в статье.
Содержание
- 1 Для чего требуется?
- 2 Исходные данные
- 3 Как рассчитать?
- 3.1 Сбор нагрузок
- 3.2 Определение внутренних усилий
- 3.3 Подбор высоты и ширины
- 3.4 Подбор шага
- 3.5 Определение предельного прогиба
- 4 Классические ошибки
- 5 Заключение
Для чего требуется?
Балки перекрытия – это горизонтальные линейные несущие элементы здания, расположенные в пролёте между вертикальными конструкциями. Работают на изгиб под действием постоянных и временных нагрузок.
Работают на изгиб под действием постоянных и временных нагрузок.
Расчёт балок перекрытия является неотъемлемым этапом разработки раздела проекта «Конструктивные решения», и он выполняется по следующим причинам:
- Подбор оптимального поперечного сечения элемента, воспринимающего внутренние усилия, которые образуются под действием внешних сил.
- Определение шага балок и их количества, исходя из условий предельного равновесия перекрытия и объёмно-планировочных ограничений помещения.
- В случае конструирования железобетонного перекрытия – определение минимального процента армирования в зонах повышенных напряжений, в соответствии со значениями эпюр момента и поперечной силы.
- Назначение минимального запаса прочности и устойчивости в случае непредвиденного увеличения эксплуатационных нагрузок.
При корректном расчёте балочных конструкций, по завершении монтажных работ и приложения всех расчётных нагрузок, перекрытие не разрушается, а его деформации остаются в пределах нормативных значений.
Исходные данные
Расчёт балок проводится в два этапа – определение внутренних усилий в стержневом элементе и подбор сечений конструкции для последующего конструирования. Для выполнения первой части расчёта потребуются следующие исходные данные:
- длина пролёта, вдоль которого располагается стержневой элемент;
- характер опирания балки на вертикальную конструкцию – шарнирное, либо жёсткое защемление;
- вес вышележащих конструкций перекрытия и полов – постоянные нагрузки;
- временная нагрузка, равномерно распределённая по площади, принимаемая по СНиП, исходя из эксплуатационных характеристик помещения;
- штамповые нагрузки, при наличии технологических особенностей при эксплуатации.
Когда усилия известны, инженер начинает подбор ширины и высоты, а, при необходимости, конструирование элемента. Для этого также потребуются некоторые данные:
- материал стержневого элемента – как правило, железобетон, металлический профиль или деревянный брус;
- архитектурные ограничения, например, предельная высота балки;
- жёсткость материала – класс железобетона, марка стали, порода дерева и т.
 д.;
д.; - дополнительные ограничения, связанные с особенностями эксплуатации здания – наличие инженерных коммуникаций под потолком.
Подбор сечения сводится к назначению его габаритов в произвольном порядке с последующей проверкой условий прочности и устойчивости.
Как рассчитать?
Все балки перекрытий, вне зависимости от их количества, материала, высоты и условий работы, рассчитываются в строгом соответствии с определённым алгоритмом.
Сбор нагрузок
Большинство нагрузок, прикладываемых к перекрытию, являются равномерно распределёнными по площади, и их необходимо привести к линейным значениям. Чтобы собрать все нагрузки на балку, необходимо выполнить следующие шаги:
- Определить величину промежуточного пролёта между стержнями.
- Выделить в перекрытии расчётную полосу. Ширина этого гипотетического элемента составляет ½ пролёта между стержневыми элементами, отложенную в каждую сторону от центральной оси рассматриваемой балки.
- Вычислить массу расчётной полосы перекрытия, путём умножения её объёма на плотность материала.
- Таким же образом определить загружение от веса полов.
- Привести временную эксплуатационную нагрузку из распределённой по площади на стержневой элемент.
- Добавить особые штамповые, либо точечные загружения при наличии специальных условий эксплуатации.
- Если речь идёт о плите покрытия, то в качестве временной нагрузки принимается нормативный вес снегового покрова для конкретного региона страны. Например, в Москве этот показатель составляет 180 кг/м2.
Пример: если стержни уложены в пролёте 6 м, а расстояние между ними составляет 2 м, перекрытие – монолитная железобетонная плита толщиной 180 мм, вес полов 150 кг/м2, а временная нагрузка в жилом здании – 100 кг/м2, на стержневой элемент собираются следующие загружения:
- масса участка плиты: 6 м х 2 м х 0,18 м х 2500 кг/м3 (r – плотность железобетона) = 5400 кг;
- масса полов: 150 кг/м2 х 6 м х 2 м = 1800 кг;
- временная нагрузка: 100 кг/м2 х 6 м х 2 м = 1200 кг;
- суммарная нагрузка на деталь составит: 5400 кг + 1800 кг + 1200 кг = 8400 кг;
- учитывая, что стержневой элемент имеет длину 6 м, то прикладываемая равномерно распределённая нагрузка q = 8400 кг / 6 м = 1400 кг/м, или 14 кН/м.

В зависимости от условий работы, назначается повышающий коэффициент, принимаемый по СНиП – от 1,05 до 1,2.
Определение внутренних усилий
Когда известны все нагрузки, длина и характер защемления, проектировщик определяет внутренние усилия в стержневом элементе:
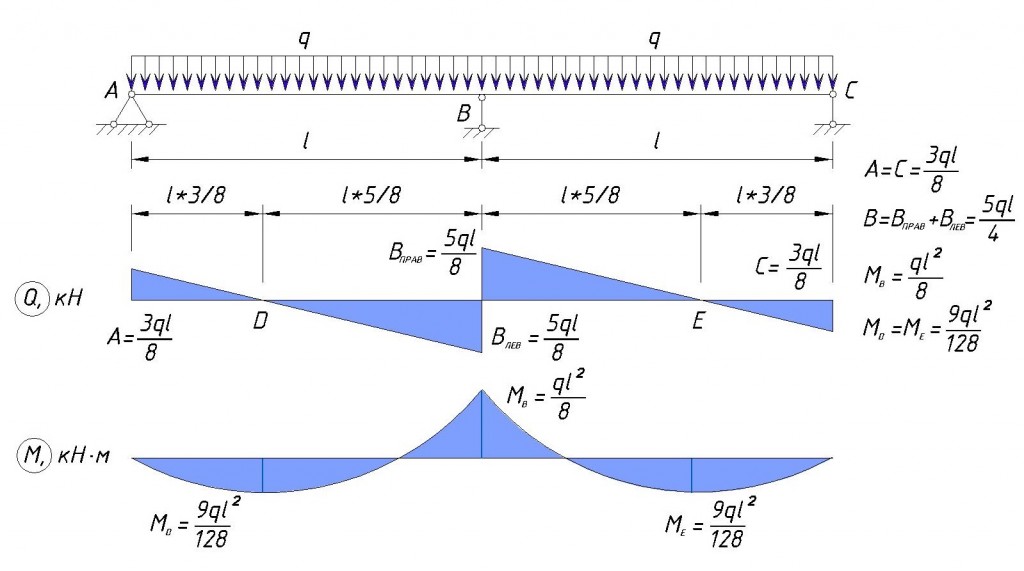
- Изгибающий момент, являющийся основной характеристикой изгибаемого элемента, определяется по формуле M = ql2 / 8, при стандартном опирании детали на вертикальные опоры. l – длина пролёта. Таким образом, M = 14 кН/м * 62 / 8 = 63 кН*м. Максимальное значение момента оказывается в центре полёта.
- Поперечное усилие Q, называется также перерезывающей силой, которая имеет предельную величину около опор. Q = ql / 2 = 14 кН/м * 6 / 2 = 42 кН.
Исходя из полученных значений, инженер строит 2 эпюры с графическим отображением данных усилий.
Подбор высоты и ширины
Определив значения внутренних усилий и владея информацией о материале конструкции, инженер начинает подбор поперечного сечения.
Исходя из объёмно-планировочных показателей и опыта в проектировании, инженер самостоятельно назначает предварительное сечение, например, h = 45 cм, b = 20 cм, где h – высота, b – ширина.
Высота железобетонной балки складывается из двух величин: h = h0 + a, где h0 – рабочая высота от центра растянутой арматуры в нижней зоне до верхней кромки, а – величина защитного слоя бетона от грани арматуры до низа элемента + 1/2 диаметра рабочего стержня. Принимая a = 5 см, можно определить h0 = 45 см – 5 см = 40 см.
Далее проверяются условия равновесия по двум формулам: Rs As = Rbbx и M = Rbbx (h0 – x/2), где Rs и Rb – расчётные сопротивления арматуры и бетона, соответственно, зависящие от классов материалов, х – высота сжатой зоны бетона. Чаще всего, в конструкцию закладывают арматурную сталь А500s, а бетон для перекрытий принимается класса В25. Таким образом, в соответствии со СНиП, Rs = 43,5 кН/см2, а Rb = 1,45 кН/см2.
Высота сжатой зоны составляет х = Rs Аs / gb1 Rbb, где As – площадь рабочей арматуры, gb1 – коэффициент условий работы бетона, принимаемый в стандартных конструкциях 0,9.
Площадь рабочей арматуры Аs = gb1Rbbeh0/Rs, где e – относительная высота сжатой зоны бетона, определяемая по формуле e = (1 – (1 – 2am)1/2), а безразмерная величина am = M / (gb1 Rbbh02) = 6300 кНсм / (0,9 * 1,45 * 20 * 1600) = 0,15. e = (1 – (1 – 2 * 0,15) 1/2) = 1 – 0,837 = 0,163. Таким образом, в конкретно взятом примере, Аs = 0,9 * 1,45 * 20 * 0,163 * 40 /43,5 = 3,91 см2.
По факту принимается арматура большего сечения, чем показал расчёт. 2d16 имеют площадь 4,02 см2. Высота сжатой зоны, исходя из 1 условия предельного равновесия, составит х = 43,5 * 4,02 / (0,9 * 1,45 * 20) = 6,7 см.
Предельно допустимый момент, который может воспринять сечение, выводится из 2 условия предельного равновесия и составляет M = gb1 Rbbx(h0 – x/2) = 0,9 * 1,45 * 20 * 6,7 * (40 – 6,7/2) = 6409 кНсм < M = 6300 кНсм. В данном примере условие прочности полностью выполняется.
Если прочность и устойчивость конструкции не обеспечивается, проектировщик должен вернуться к началу алгоритма и назначить другие габариты сечения, а затем провести проверку ещё раз.
Подбор шага
Если высота и ширина подобраны верно, необходимо определить количество элементов в перекрытии, которое зависит от следующих критериев:
-
Объёмно-планировочные решения помещения.
Если подобранное сечение детали, удовлетворяющее условиям прочности и устойчивости, значительно сокращает высоту комнаты в чистоте, то проектировщику придётся уменьшать сечение, добавляя количество деталей с более частым шагом.
- Шаг и количество балок должны быть подобраны таким образом, чтобы свободный пролёт плиты между ними обеспечивал условиям предельного равновесия. Для расчёта конструктивного элемента необходимо принять расчётную полосу шириной 1 м, собрать на неё нагрузки и полностью повторить алгоритм.
При корректно подобранном шаге, удовлетворяющим условиям равновесия, эксплуатации перекрытия обеспечит полную безопасность людей, пребывающих в здании.
Определение предельного прогиба
Помимо прочности, балочная система должна отвечать условиям предельных деформаций.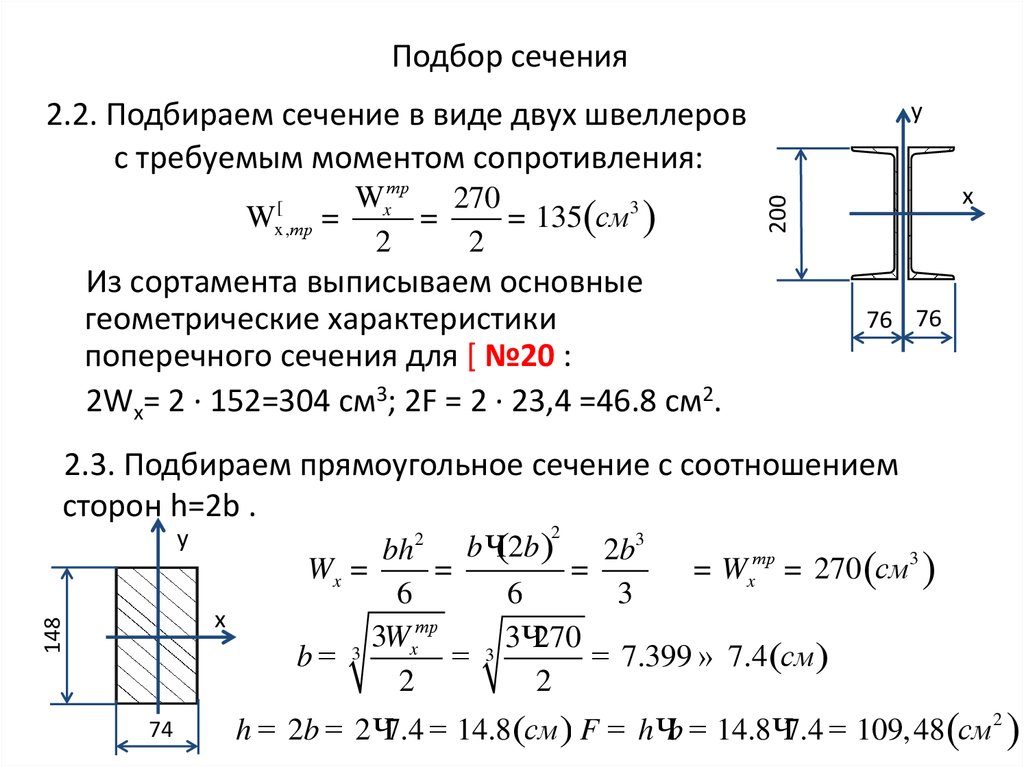 Если линейный элемент имеет вертикальные перемещения под действием суммарной нагрузки, не превышающие нормативных значений, то сечение подобрано верно.
Если линейный элемент имеет вертикальные перемещения под действием суммарной нагрузки, не превышающие нормативных значений, то сечение подобрано верно.
Алгоритм выглядит следующим образом:
- Определяется фактический прогиб конструкции по формуле f = 5/384 * qnl4/EI, где qn – суммарная нагрузка, l – величина пролёта, Е – модуль упругости материала, принимаемый по таблице СНиП (для бетона класса В25 он составляет 30000 кгс/см2), I – момент инерции сечения.
- I – это переменная величина, которая зависит от формы сечения. В случае, с прямоугольником I = bh4/12, а в конкретном примере I = 20 * 91125 / 12 = 151875 см4.
- Реальный прогиб составит f = 5/384 * 6300 * 6004 / 30000 * 151875 = 2,3 см.
- Полученное значение сравнивается с предельно допустимой нормативной величиной, которая для стандартных стержней в жилых и общественных зданиях составляет 1/250l, а в случае пролёта 6 м = 600 см, 1/1250 *600 = 2,4 см. То есть, конструкция удовлетворяет условиям предельных деформаций.

В случае, когда данное условие не выполняется, проектировщику необходимо принимать другой класс бетона, уменьшать шаг или изменять габариты сечения.
Классические ошибки
Инженеры, не имеющие должного опыта, часто допускают некоторые ошибки при расчёте балок, а именно:
- Слишком малое сечение, даже если оно и проходит по условиям прочности, может прогнуться больше нормативных значений, из-за чего перекрытие перестанет удовлетворять эксплуатационным требованиям.
- Наоборот, слишком большое сечение приведёт к перерасходу материалов и повышенным затратам при строительстве.
- Неверно выбранное защемление балки повлияет на результат расчёта.
- При расчёте необходимо приводить все единицы к единому модулю, а, в противном случае, результат окажется далёким от истины.
Чтобы не совершать типичные ошибки, следует выполнять расчёт в соответствии с алгоритмом и фиксировать все промежуточные результаты.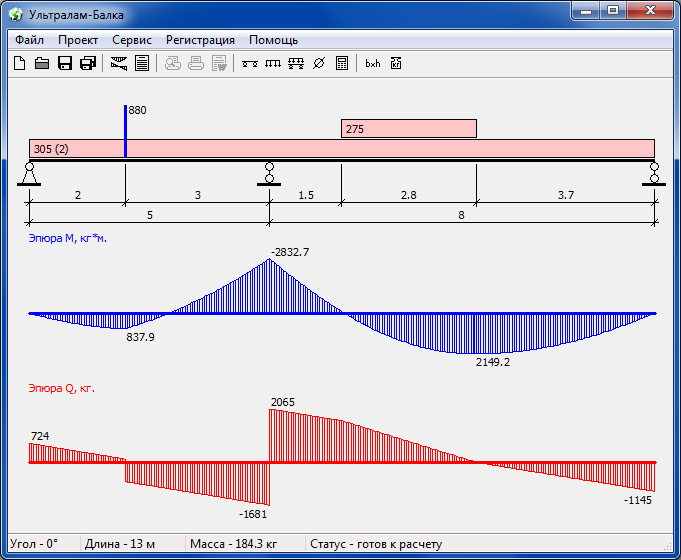 После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.
После выполнения расчёта следует несколько раз проверить результат. Если возникают сомнения, лучше сравнить подобранное сечение балки с аналогичными примерами.
Заключение
Расчёт балок перекрытия – кропотливый процесс, требующий повышенного внимания, знаний формул и алгоритма. Перед началом выполнения чертежа нужно определить 4 главных параметра – нагрузки на балку, оптимальное сечение элемента, шаг стержней в перекрытии и фактический прогиб конструкции.
Бесплатный онлайн-калькулятор луча | Civils.ai
Создание диаграмм изгибающих моментов, диаграмм поперечной силы и измерение прогиба для неопределенного пролета балки.
Рассчитайте изгибающий момент, поперечную силу, силы реакции и прогиб, используя свойства реального стального сечения.
Этот инструмент оптимизирован для настольного использования
Длина балки: 10,0 м
Второй момент площади: 473,0 см 4
Модуль Юнга: 210,0 ГПа
Загрузка. ..
..
Условия поддержки неудовлетворительны, добавьте другую поддержку.
Загрузка…
Макс. БМ: Мин. BM:
Макс. SF: Мин. SF:
Макс. отклонение:
Мин. отклонение:
Как работает этот анализ?
Введение
Балки бывают самых разных форм и размеров, понимание того, как рассчитать силы, действующие на конструкционную балку, может быть затруднено. Но здесь мы дадим вам краткое введение в теорию того, как они устроены. Начиная с теории напряжение балки .
Что такое напряжение балки и как рассчитать напряжение балки?
Когда мы прикладываем силу где-то вдоль пролета балки, мы создаем внутренние напряжения. Существует два типа напряжений, которые создаются:
Существует два типа напряжений, которые создаются:
- Нормальное напряжение: Возникает из-за сил, действующих по длине балки при сжатии или растяжении.
- Напряжение сдвига: Возникает из-за сил, действующих параллельно направлению нагрузки.
Происхождение этих двух компонентов напряжения можно разделить на два компонента силы, которые мы называем Изгибающий момент и Сила сдвига .
Типы внешней нагрузки
Простейшие нагрузки, прикладываемые к балке, можно разделить на три категории:
- Точечные нагрузки: Это сила, приложенная к одной точке балки.
- Распределенные нагрузки: Эта сила распределяется по определенной длине и действует как форма давления.
- Сосредоточенный момент: Это чистый момент, действующий на балку в заданном положении.
Типы опор
Простейшие опоры для балки можно разделить на три категории:
- Штифтовая опора: Удерживает балку как в горизонтальном, так и в вертикальном направлениях, не ограничивая ее вращение.

- Роликовая опора: Опора балки только в одном направлении, без ограничения изгиба или вращения.
- Фиксированная опора: Эти опоры обеспечивают фиксацию балки во всех направлениях и препятствуют вращению.
Диаграмма сил свободного тела
Чтобы найти силы, действующие на балку, мы должны следовать процессу создания диаграммы сил свободного тела.
Как рассчитать силы реакции опор на пролет балки?
Сначала мы рисуем балку в масштабе с указанием силовых составляющих приложенных нагрузок, а затем рассчитываем силы реакции опоры.
Для расчета реакций необходимо использовать уравнения равновесия для разрешения внешних сил:
- Σ Приложенные вертикальные силы = 0 кН
- Σ Приложенные горизонтальные силы = 0 кН
- Σ Прикладываемые моменты = 0 кНм
Существует два типа случаев при разрешении внешних условий балки:
- Статически определяемые: Где количество уравнений равно количеству неизвестных, и расчеты могут быть решены с помощью ручных вычислений в закрытой форме.

- Статически неопределимое: Когда количество неизвестных превышает количество уравнений и необходимо использовать более продвинутые методы, такие как теория сопротивления момента.
Как нарисовать диаграмму поперечной силы?
Чтобы создать диаграмму поперечной силы, вы работаете слева направо поперек балки, суммируя приложенные силы и реакции в каждой точке приложения. Консоли являются наиболее простым примером этого с единственной реакцией на одном конце пролета балки с нулевой силой сдвига на неподдерживаемом конце.
Как нарисовать диаграмму изгибающего момента?
Чтобы создать диаграмму изгибающего момента, вы снова должны работать слева направо поперек балки и вычислять момент слева от каждой интересующей вас точки. наш расчет стальной балки для расчета в соответствии с Еврокодом 3.
Проектировщик стальных профилей
Расчет бетонной балки
Результаты этого анализа затем можно использовать в нашем расчете бетонной балки для расчета в соответствии с Еврокодом 2.
Конструктор бетонных секций
Внесите свой вклад в этот код
Этот код является открытым исходным кодом, и вы можете внести свой вклад в его разработку.
Вы можете найти исходный код на GitHub здесь:
IndeterminateBeamСпециальные кредиты: Джесси Бонанно
Что такое Beam Calculation? (с картинками)
`;
Д. Пупон
Расчет балки — это измерение напряжения и прогиба конструкционной балки при приложении к ней заданной нагрузки. На способность балки сопротивляться изгибу влияют многие факторы, такие как характеристики балки, нагрузка и опоры. Вычисление смещения нагрузки одиночной балки с использованием уравнения балки Эйлера-Бернулли несложно, но в большинстве практических приложений используется программное обеспечение балки. Расчеты луча используются для обеспечения безопасности и предотвращения чрезмерной застройки в различных дисциплинах, таких как строительство и аэронавтика.
На способность балки сопротивляться изгибу влияют многие факторы, такие как характеристики балки, нагрузка и опоры. Вычисление смещения нагрузки одиночной балки с использованием уравнения балки Эйлера-Бернулли несложно, но в большинстве практических приложений используется программное обеспечение балки. Расчеты луча используются для обеспечения безопасности и предотвращения чрезмерной застройки в различных дисциплинах, таких как строительство и аэронавтика.
Необходимо рассчитать несущую способность балки, чтобы построить конструкции из самых легких и недорогих материалов при соблюдении требований безопасности и сохранении эстетических качеств конструкции. Вся дисциплина строительной инженерии посвящена этому анализу и проектированию, гарантируя, что крыши не рухнут под тяжестью снега, что подземные гаражи будут безопасны, когда движение транспорта над головой и что небоскребы, построенные вдоль линий разлома, отвечают требованиям сейсмостойкости. Расчет балки также имеет применение в машиностроении при проверке сопротивления отдельных частей машины нагрузке, например нагрузке, которую может выдержать крыло самолета до развития потенциально опасных напряжений. Наконец, архитекторы должны учитывать деформацию балок при строительстве и ремонте домов из стоек и балок, а также при рассмотрении визуального воздействия провисающих полов, крыш и балконов.
Вся дисциплина строительной инженерии посвящена этому анализу и проектированию, гарантируя, что крыши не рухнут под тяжестью снега, что подземные гаражи будут безопасны, когда движение транспорта над головой и что небоскребы, построенные вдоль линий разлома, отвечают требованиям сейсмостойкости. Расчет балки также имеет применение в машиностроении при проверке сопротивления отдельных частей машины нагрузке, например нагрузке, которую может выдержать крыло самолета до развития потенциально опасных напряжений. Наконец, архитекторы должны учитывать деформацию балок при строительстве и ремонте домов из стоек и балок, а также при рассмотрении визуального воздействия провисающих полов, крыш и балконов.
Одним из наиболее важных факторов при расчете несущей способности балки является выбор материалов. Обычно балки изготавливаются из дерева, стали, железобетона или алюминия. Каждый материал имеет различную склонность к упругой деформации, называемую модулем упругости, который относится к способности материала возвращаться на место. В пределе текучести материал будет пластически деформироваться, сохраняя деформацию после снятия приложенной силы.
Обычно балки изготавливаются из дерева, стали, железобетона или алюминия. Каждый материал имеет различную склонность к упругой деформации, называемую модулем упругости, который относится к способности материала возвращаться на место. В пределе текучести материал будет пластически деформироваться, сохраняя деформацию после снятия приложенной силы.
Форма поперечного сечения балки — вторая характеристика, учитываемая при расчете балки. Балки могут быть прямоугольными, круглыми или полыми, а также иметь множество типов боковых сторон, таких как двутавровые, Z-образные или тавровые балки. Каждая форма имеет свой момент инерции, также известный как второй момент площади, который предсказывает жесткость балки.
Каждая форма имеет свой момент инерции, также известный как второй момент площади, который предсказывает жесткость балки.
Усилие на единицу длины — это еще один параметр, используемый при расчете балки, и он зависит от типа нагрузки. Постоянные нагрузки — это просто вес конструкции, а вынужденные или временные нагрузки — это силы, которым конструкция будет периодически подвергаться, например, снег, движение транспорта или ветер. Большинство нагрузок являются статическими, но особое внимание следует уделять динамическим нагрузкам, землетрясениям, волнам и ураганам, которые повторяются в течение длительного времени. Нагрузка может быть распределена, как правило, равномерно или асимметрично, например, снегопад или куча грязи. Он также может быть сконцентрирован в точке, в центре или с различными интервалами.
Нагрузка может быть распределена, как правило, равномерно или асимметрично, например, снегопад или куча грязи. Он также может быть сконцентрирован в точке, в центре или с различными интервалами.
Граничные условия для расчета балки зависят от типа опоры балки. Балка может просто поддерживаться с обоих концов, как балка пола между двумя несущими стенами. Он может быть консольным или поддерживаться на одном конце, как балкон или крыло самолета. Граничные условия применяются ко всем точкам по длине балки.
Связь между прогибом балки и статической нагрузкой описывается уравнением балки Эйлера-Бернулли. Другое уравнение, уравнение балки Эйлера-Лагранжа, описывает это соотношение для динамической нагрузки, но из-за сложности его применения обычно используются статические приближения. Можно рассчитать прогиб, изгибающие моменты и поперечную силу балки с учетом приложенной нагрузки. На практике для обобщения этой информации используются диаграммы нагрузки, в которых перечислены распространенные материалы, отвечающие требованиям безопасности для известной нагрузки. Для более сложных приложений калькуляторы балок легко доступны на веб-сайтах компаний и в качестве надстроек для программного обеспечения автоматизированного проектирования (САПР).
Другое уравнение, уравнение балки Эйлера-Лагранжа, описывает это соотношение для динамической нагрузки, но из-за сложности его применения обычно используются статические приближения. Можно рассчитать прогиб, изгибающие моменты и поперечную силу балки с учетом приложенной нагрузки. На практике для обобщения этой информации используются диаграммы нагрузки, в которых перечислены распространенные материалы, отвечающие требованиям безопасности для известной нагрузки. Для более сложных приложений калькуляторы балок легко доступны на веб-сайтах компаний и в качестве надстроек для программного обеспечения автоматизированного проектирования (САПР).
Расчет нагрузки на балку, как для рамы прицепа — механические элементы
В качестве упрощенного введения в нагрузку на балку в этой статье обсуждаются сложности расчета напряжений и прогиба.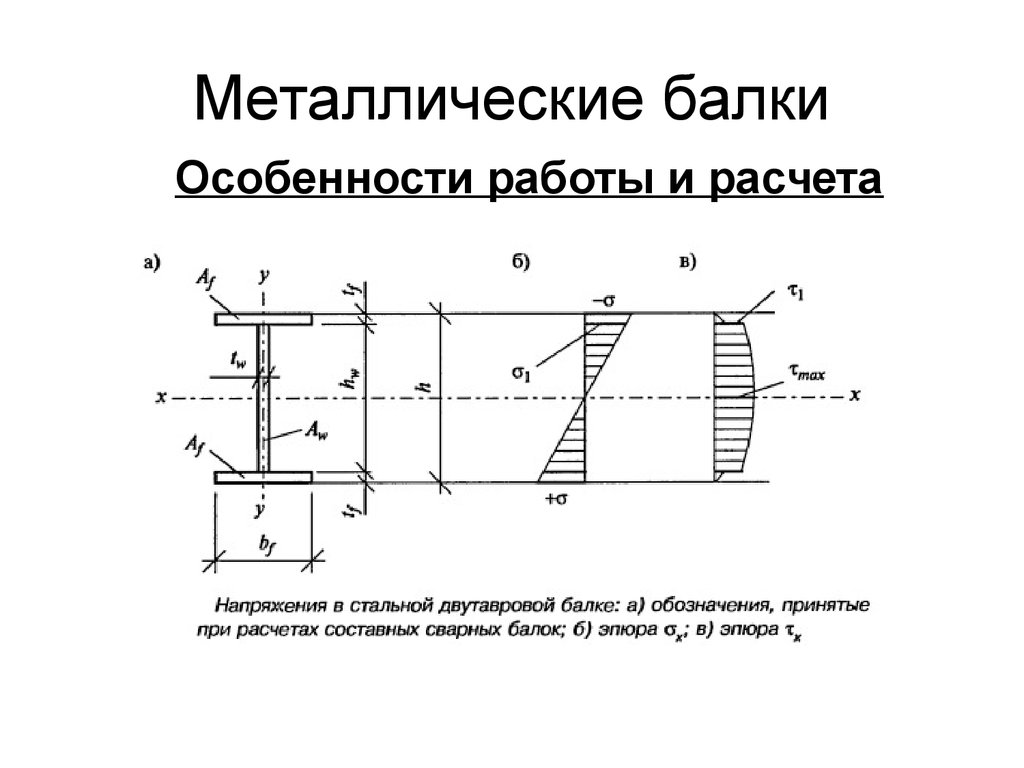 Несмотря на то, что рассчитать нагрузку на балку для простых теоретических случаев довольно легко, очень немногие балки на самом деле являются простыми. Рама прицепа, например, представляет собой ряд простых балок, но когда мы собираем их все вместе, она становится намного сложнее.
Несмотря на то, что рассчитать нагрузку на балку для простых теоретических случаев довольно легко, очень немногие балки на самом деле являются простыми. Рама прицепа, например, представляет собой ряд простых балок, но когда мы собираем их все вместе, она становится намного сложнее.
Даже кажущиеся простыми балки, например, верхняя балка козлового крана, не так уж и просты. Изображение из предыдущей статьи, посвященной сравнению стали и алюминия. На нем видно, что напряжение увеличивается вблизи концов главной балки, где простая теория говорит, что напряжение снижается. Дополнительная нагрузка возникает из-за того, что прогиб верхней балки пытается согнуть ногу. Хотя связь достаточно проста, она, безусловно, усложняет точный полный анализ.
Не расстраивайтесь. Даже со всеми сложностями реальности есть способы подобраться «достаточно близко», и в большинстве случаев это «достаточно хорошо».
Начните с концепции нагрузки на балку
Подчеркнем, что это упрощенное введение. Хотя реальность обычно сложна, базовые теоретические концепции по-прежнему применимы, поэтому мы начнем с основ расчета нагрузки на балку. Мы коснулись многих из этих концепций в других статьях, поэтому перейдите по ссылкам для получения дополнительных объяснений.
Хотя реальность обычно сложна, базовые теоретические концепции по-прежнему применимы, поэтому мы начнем с основ расчета нагрузки на балку. Мы коснулись многих из этих концепций в других статьях, поэтому перейдите по ссылкам для получения дополнительных объяснений.
Нагрузка
Во-первых, разберитесь с нагрузками на балку. Какие силы «пытаются» воздействовать на балку? В то время как обсуждение находится в разделе «Выбор лучшего материала для рамы прицепа», это изображение изгиба, сдвига и скручивания показывает концепции. Чтобы начать расчет нагрузки на балку, нужно знать силы и их направления. Они «изгибают» луч? Перекрутить луч? Или попробовать «подстричь» его? Часто это комбинация.
Форма
Во-вторых, что делает форма балки, чтобы сопротивляться силам. Как и в обсуждении «Формы балок для строительства», форма имеет большое значение в том, как она справляется с силами.
Один пример. Двутавровая балка широко известна своей прочностью, и это правильно. Это инженерная форма, позволяющая выдерживать большие нагрузки при меньшем общем весе. ОДНАКО, это утверждение вводит в заблуждение. Двутавровая балка действительно очень хорошо справляется с изгибающими нагрузками (в вертикальном направлении, если смотреть на это изображение), но не так хорошо справляется с боковыми нагрузками (горизонтальными на изображении) или скручивающими нагрузками. Направление и тип нагрузки имеют значение для каждой формы. 93. Это означает, что стальной блок размером 1 метр на 1 метр на 1 метр весит 7800 кг. Блок алюминия того же размера весит около 2700 кг. Магния больше похоже на 1700 кг. Плотность — это свойство материала, и это просто так.
Это инженерная форма, позволяющая выдерживать большие нагрузки при меньшем общем весе. ОДНАКО, это утверждение вводит в заблуждение. Двутавровая балка действительно очень хорошо справляется с изгибающими нагрузками (в вертикальном направлении, если смотреть на это изображение), но не так хорошо справляется с боковыми нагрузками (горизонтальными на изображении) или скручивающими нагрузками. Направление и тип нагрузки имеют значение для каждой формы. 93. Это означает, что стальной блок размером 1 метр на 1 метр на 1 метр весит 7800 кг. Блок алюминия того же размера весит около 2700 кг. Магния больше похоже на 1700 кг. Плотность — это свойство материала, и это просто так.
«Модуль упругости» — это свойство, которое мы используем при нагружении балки для расчета прогиба (изгиба). Мы часто видим его как «Е» в уравнениях. Чтобы сравнить жесткость материалов, мы смотрим на это число. Например, «модуль упругости» стали составляет примерно 30 000 000 фунтов на квадратный дюйм. Алюминий примерно 10 000 000 фунтов на квадратный дюйм. Магний составляет 6 500 000 фунтов на квадратный дюйм. (Английские единицы.) В этих статьях, посвященных сравнению «Сравнить: сталь и алюминий» и особенно в «– Часть 2», показано, как прогиб является важной частью расчета нагрузки на балку.
Магний составляет 6 500 000 фунтов на квадратный дюйм. (Английские единицы.) В этих статьях, посвященных сравнению «Сравнить: сталь и алюминий» и особенно в «– Часть 2», показано, как прогиб является важной частью расчета нагрузки на балку.
Прочность
Мы выражаем механическую «прочность» через «напряжение». Силы, воздействующие на балку, создают реакцию, которую мы рассчитываем как напряжение. Если напряжение превышает прочность, то форма материала изменяется. Иногда это хорошо, например, если мы изготавливаем кронштейны и нам нужна новая форма, но иногда это плохо, например, когда балка выходит из строя. (См. эти проблемы с отказом крана.)
Свойства материала (см. выше) не меняются в зависимости от размера или формы. Они также не сильно меняются с различными сплавами. Например, необработанная сталь имеет примерно такую же плотность, как высокопрочная инструментальная сталь. То же самое для алюминиевых сплавов. С другой стороны, прочность у разных сплавов сильно различается.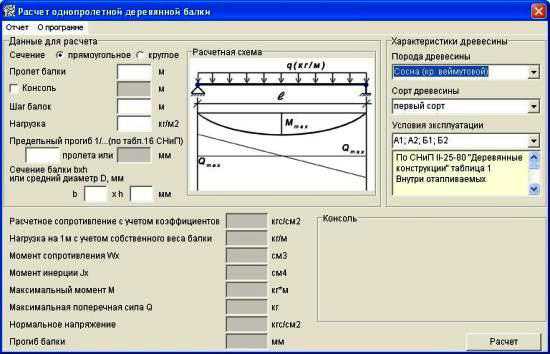 Он также меняется в зависимости от состояния — мы обсуждали ослабление материала вблизи сварного шва.
Он также меняется в зависимости от состояния — мы обсуждали ослабление материала вблизи сварного шва.
Чтобы рассчитать нагрузку на балку, нам нужно знать прочность материала и, в частности, прочность, которая важна для нашей ситуации с нагрузкой. Например, предел прочности или предел прочности при растяжении не так важен при анализе рамы прицепа. Элементы рамы будут изгибаться задолго до того, как сломаются, поэтому ключевым моментом является знание предела текучести (изгибной прочности).
Еще одна сила, «Усталость», со временем становится важной. К сожалению, показатели усталости не публикуются, поскольку они зависят от многих факторов, помимо самой балки или материала. Хотя мы должны знать об этом, расчет усталости выходит за рамки этой статьи.
Размер
Это может показаться очевидным. Размер важен для расчета напряжения нагрузки на балку, и он взаимодействует с формой .
Итак, как определить размер для расчетов? Мы делаем это с 2 свойствами.
Первое и самое простое для понимания — это «у» или расстояние от нейтральной оси. Для изгибающих нагрузок, характерных для рамы прицепа, можно использовать это изображение (из статьи о сварке кронштейнов рессор). Глядя на стрелки силы (красная и синяя), мы видим, что центр балки не имеет изгибающей нагрузки. В этом луче, поскольку он симметричен, «нейтральная ось» является центром луча. Это не всегда так, и уголки — хороший тому пример.
«y» (в некоторых источниках используется другая переменная) — это расстояние от нейтральной оси до точки анализа. Поскольку самые высокие силы находятся в самой дальней точке (если смотреть на сечение балки), мы обычно анализируем там. Мы называем это «у-макс».
Во-вторых, это «момент инерции площади», или иногда называемый «секундным моментом площади». Часто в уравнениях мы видим его как «I» (заглавная i). Мы не будем вдаваться в подробности (вы можете найти математические подробности здесь), потому что это сложно, но это связано с количеством материала и его расстоянием от нейтральной оси.
Для двутавровой балки основная часть материала находится на крайних точках (около y-max), что придает форме большую букву «I» для ее общего веса и размера.
Помните, это сочетание формы и размера. Ширина тоже имеет значение, толщина тоже. Кроме того, если вы складываете лучи, «момент инерции площади» изменяется, чтобы принять полный стек.
Простые инженерные уравнения
Теперь рассмотрим расчет нагрузки на балку. У нас есть немного знаний о нагрузке, свойствах материала, прочности, размере и форме.
Поскольку для начала лучше всего использовать простое, мы будем использовать сплошную балку на простых концевых опорах. Затем одна центральная нагрузка. В верхней части рисунка показаны балка и нагрузки.
Графика включает некоторые уравнения для расчета нагрузки на балку. График сдвига (синий) показывает, как мы представляем, что происходит с силами вдоль балки.
На следующем графике представлены моменты или изгибающие силы вдоль балки.
Наконец, график отклонения. (Между расчетами моментов и отклонениями есть несколько шагов, но они здесь не рассматриваются.)
Это очень простой случай. На самом деле слишком просто для большинства реальных жизненных ситуаций, но дает представление. Итак, что это значит? Если эта балка из титана, 1 ″ x 1 ″ сплошная (25,4 мм x 25,4 мм), длина 6 футов (~ 2 м), с пределом текучести 35 000 фунтов на квадратный дюйм (241 МПа), то она выдержит нагрузку 324 фунта. (147 кг) перед постоянным сгибанием. Центр будет отклоняться чуть более чем на 1,7 дюйма (43 мм) до выхода из строя. Это, конечно, теоретическое, потому что оно основано на опубликованных цифрах. На самом деле это может быть немного больше или немного меньше, потому что вещи никогда не бывают идеальными, но это близко.
Конечно, простые основы не учитывают движения, подпрыгивания или аномалии, которые случаются в реальной жизни.
Расчет нагрузки на балку рамы прицепа
Теперь вопрос, который нам задают довольно часто. Как рассчитать нагрузку на балку прицепа?
Как рассчитать нагрузку на балку прицепа?
Для простоты воспользуемся примером из статьи «Куда идет ось», так как в ней уже есть уравнения для расчета сил и положения. Вот обзор.
Сводка загрузки:
Длина дышла = 42 дюйма
Длина станины = 96 дюймов
Вес рамы = 450 фунтов
Распределенная нагрузка = 2250 фунтов
Вес ящика для инструментов = 300 фунтов
Нагрузка на дышло = 360 фунтов (12%)
Нагрузка на ось = 2644. ″ из мяча.
Подробная информация по этим номерам находится в статье «Куда идет ось».
Итак, это состояние нагрузки. Теперь, вот график (ниже), показывающий, как указанная выше нагрузка применяется к прицепу. Это похоже на графики загрузки выше, но здесь 3 графика вместе с масштабированием, поэтому их легко сравнивать от строки к строке.
Для краткости мы пропустим уравнения для этих графиков. Они похожи на приведенные выше уравнения, но с большей сложностью, с несколькими нагрузками, различными типами нагрузок, а не только на концах.
На этом втором графике мы не показываем отклонение, но показываем «Напряжение» для рамы прицепа. Линия Stress выделяет области перехода, например, место, где дека встречается с языком. Поскольку напряжение зависит от размера и формы балки, на этом графике уже учтены балки. Тем не менее, это шаг вперед.
На самом деле мы используем силы и моменты для выбора балок. Применяя свойства балки и материала, мы можем выбрать балки, которые будут выдерживать нагрузки. Строка «Стресс» предназначена для балок в этом примере, но процесс выбора не так прост и поэтому выходит за рамки этой статьи.
Понимание техники
Приведенные выше расчеты являются началом. Начнем с графика нагрузки, показывающего силы. Силы ВВЕРХ должны быть равны силам ВНИЗ. (См. диаграмму сдвига.) Силы также должны суммироваться с НУЛЕМ при расчете силы на соответствующем расстоянии. (См. расчеты в статье о положении оси.) Мы называем это суммированием моментов. Если эти два условия выполняются, то, вероятно, мы все сделали правильно, и остальные расчеты сработают.
Далее идет сила сдвига. Это своего рода проверка правильности расчета нагрузки. (Синяя линия на графике.) Использование графика — это простой способ увидеть относительную величину сил, и он является хорошим ориентиром при анализе загрузки прицепа.
Затем график моментов. (Зеленая линия) Вы можете думать об этом как о сгибании, но это не совсем так. Для таких балок, как на прицепе, изгиб является основным условием, поэтому мы должны быть очень внимательны. Хотя заманчиво просто посмотреть на высокие точки, области, где нагрузка переходит от одного набора лучей к другому, очень важны. Например, место, где заканчивается кровать, а продолжается язык. По нашему опыту, это самое слабое место для большинства прицепов.
Хотя приведенное выше — хороший способ взглянуть на силы, на самом деле все гораздо сложнее. Даже при загрузке, потому что пример статичен (не двигается). Когда все движется, динамика действительно меняет игру.
Еще для расчета нагрузки на балку
Все вышеперечисленное является первым шагом к выбору балок рамы прицепа. Мы сказали, что следующим шагом будет выбор подходящих лучей, но это не совсем так. Следующим шагом является повторение этого процесса для всех возможных условий нагрузки. Мы сделали простую статическую равномерно распределенную нагрузку — например, заполнив прицеп водой, когда нагрузка равномерно распределяется по всей платформе. Это интересно, но не так реалистично. Даже когда вы перевозите песок, обычно в середине есть горб, из-за которого нагрузка распределяется не совсем равномерно.
Мы сказали, что следующим шагом будет выбор подходящих лучей, но это не совсем так. Следующим шагом является повторение этого процесса для всех возможных условий нагрузки. Мы сделали простую статическую равномерно распределенную нагрузку — например, заполнив прицеп водой, когда нагрузка равномерно распределяется по всей платформе. Это интересно, но не так реалистично. Даже когда вы перевозите песок, обычно в середине есть горб, из-за которого нагрузка распределяется не совсем равномерно.
А как насчет перевозки RZR? Маленький трактор? Или квадроцикл? Поскольку шины соприкасаются с платформой прицепа только в 4 точках, это создает очень разные силы. Мы должны рассчитать нагрузку на балку и для этого случая. Если он загоняет его на прицеп, весь вес приходится на заднюю часть, а это еще один случай нагрузки. Нам нужно сделать еще один расчет нагрузки на балку.
Список загрузки можно продолжить. Как насчет того, чтобы в передней части трейлера стоял холодильник, а рядом с ним стиральная машина и сушилка? (Ничего сзади.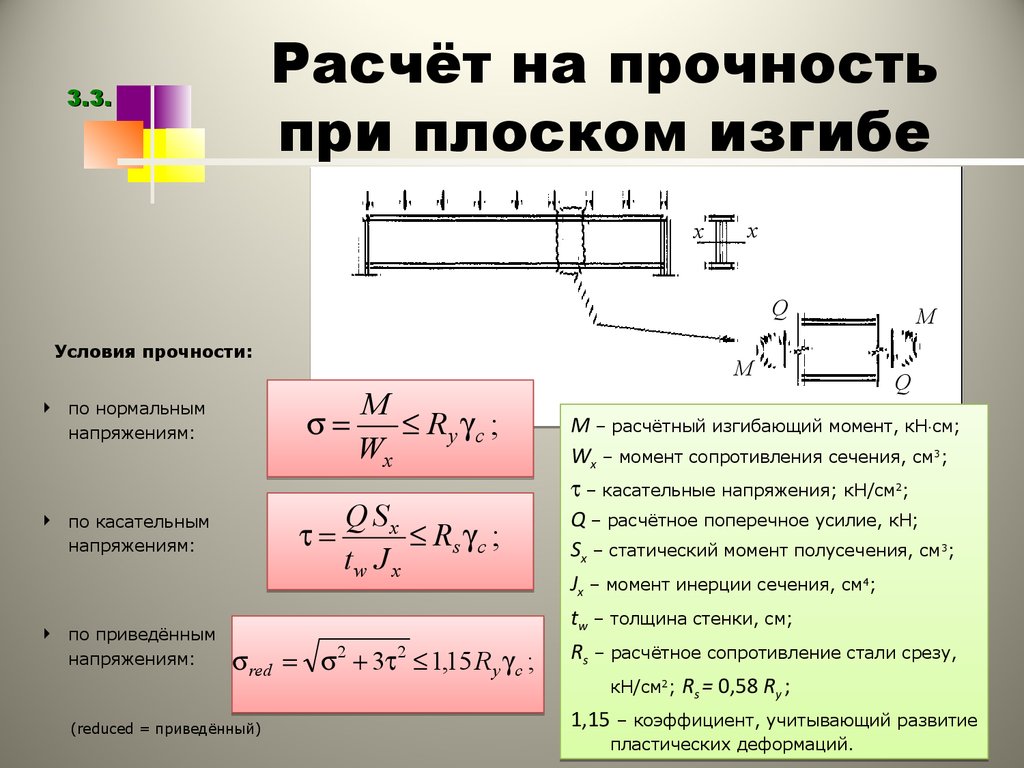 ) Ага, еще один набор расчетов.
) Ага, еще один набор расчетов.
Когда расчеты завершены, следующим шагом будет подумать о том, насколько они реалистичны и какие модификаторы применяются. Например, при перевозке песка вы, скорее всего, наткнетесь на кочку во время движения по дороге. Нам нужно компенсировать динамическими расчетами. Мы, вероятно, не наткнемся на кочку при загрузке квадроцикла. Однако, вероятно, есть некоторый отскок, поэтому наши динамические расчеты для этого отличаются.
Еще один момент: приведенный выше анализ представляет собой 2D-анализ, но большинство трейлеров — 3D . . . Надеюсь, вы уловили идею.
Выбор балок
Как бы нам не хотелось, чтобы это было просто, это не так. К сожалению, именно поэтому многие производители прицепов не занимаются проектированием. Да, это правда. Большинство просто соединяют балки вместе, основываясь на опыте, копировании и том, что «чувствует» себя хорошо. Это работает для большинства, пока это не работает.
Как инженер, занимающийся этим долгое время, я, вероятно, вижу худшее из этого. Люди связываются со мной, поэтому я это вижу, но мало что могу сделать. Как только балка изгибается или сварной шов рвется, время для проектирования уже давно прошло. Что подчеркивает необходимость действительно убедиться, что он достаточно силен в первую очередь.
Люди связываются со мной, поэтому я это вижу, но мало что могу сделать. Как только балка изгибается или сварной шов рвется, время для проектирования уже давно прошло. Что подчеркивает необходимость действительно убедиться, что он достаточно силен в первую очередь.
В общем, мы отклонились от темы. Выбор балки включает в себя объединение всех загружений с соответствующей динамикой и ситуационными модификациями. Да, факторы безопасности также имеют значение. Все это устанавливает потребности, затем мы можем выбрать балки. По сути, мы рассчитываем напряжение любой заданной балки (форма, размер, материал), а затем сравниваем напряжение с прочностью материала. Если напряжение ниже прочности, то, наверное, сработает. Если прогнозируемое напряжение выше, балка может выйти из строя.
В этом суть расчета нагрузки на балку. В то время как для простых балок и единичных вариантов использования это достаточно просто, сложности возникают быстро, когда накладываются динамические и загруженные варианты.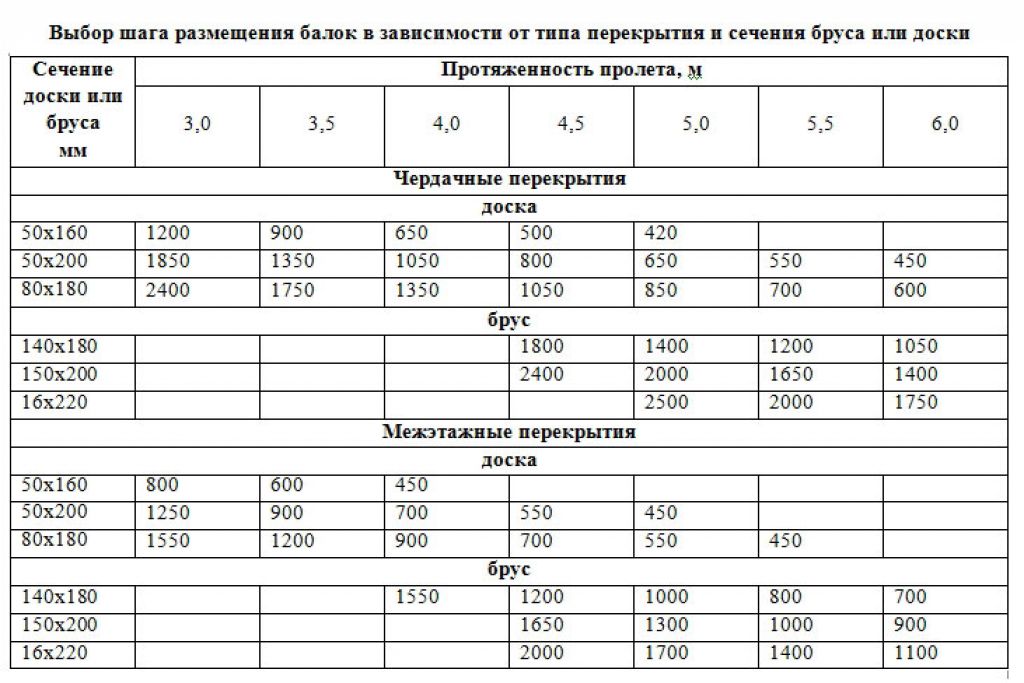
Оптимизация для упрощения
Одно предостережение. Частой целью при проектировании прицепов является минимизация веса. Это хорошая цель, но она обманчива. Если варианты использования хорошо определены, то целесообразна большая оптимизация. Однако оптимизация для одного варианта использования оставит уязвимыми другие области. Я видел много «слишком легких» трейлеров, которые не были сняты. Если вы ищете легкий вес, убедитесь, что вы не жертвуете функциональностью ради восприятия «легкости». Есть способы достичь цели, не прибегая к коротким путям.
Также подумайте о реальных преимуществах. Довольно легко увлечься цифрами, такими как вес, в дизайне. Спросите себя о ценности, например, какова ценность 50 фунтов? Если в этом разница между рамой, в которой вы уверены, и «легкой» рамой, которая может показаться схематичной, то стоит ли это 50 фунтов? А 100 фунтов? Для прицепа, предназначенного для перевозки 3500 фунтов, небольшое увеличение веса рамы незначительно по сравнению со стоимостью неисправной рамы.
Я предлагаю дизайн для решения сложных задач, которые неизбежно возникнут. Всегда есть практический баланс, так что имейте это в виду, если вам нужен легкий вес.
Пусть компьютер рассчитает нагрузку на балку
Примеры здесь простые и двумерные. На самом деле анализ рамы прицепа намного сложнее, поэтому мы используем специальные инструменты САПР.
Иногда на нашем сайте можно увидеть такие цветные изображения. Они получены из FEA, анализа методом конечных элементов, который выполняет для нас все сложные расчеты балки. К сожалению, это загружается одновременно, поэтому полный анализ занимает много времени, особенно с учетом итераций для оптимизации.
Большим преимуществом является то, что он позволяет рассчитать нагрузку на балку так, как это невозможно сделать с помощью описанных выше методов. Это делает сложное легким. Хотя это отличный инструмент, у него есть один существенный недостаток — мусор на входе равен мусору на выходе. Это легко даст красивые картинки, но входные данные должны быть правильными, иначе выходные данные будут мусором.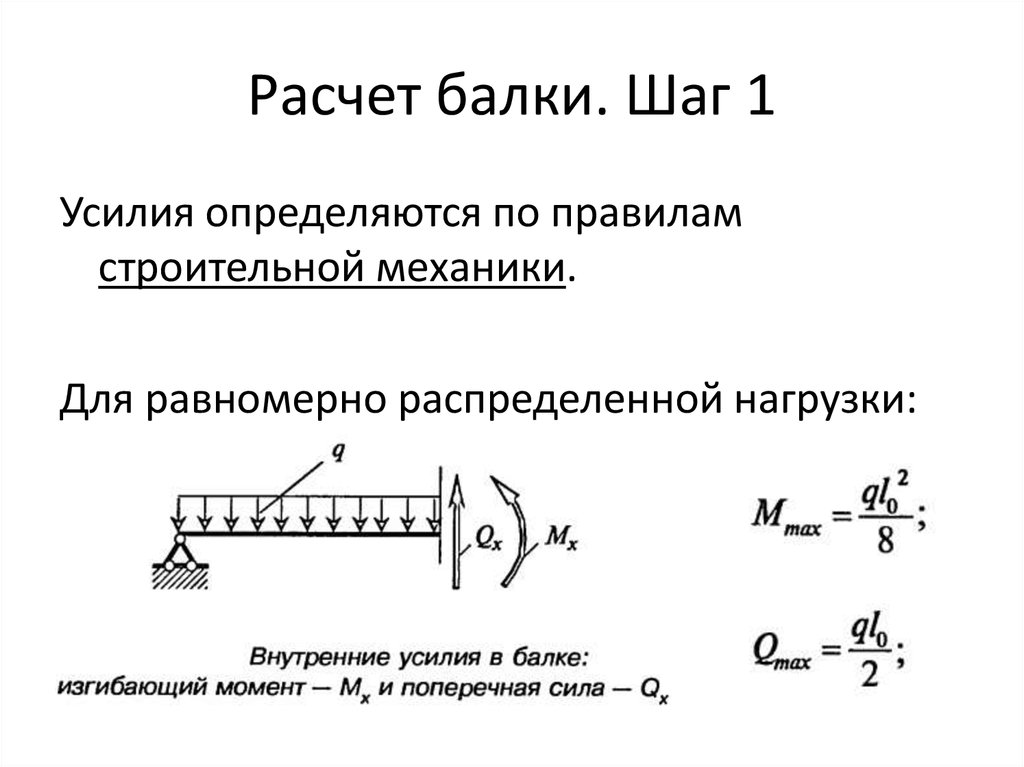 Просто пища для размышлений.
Просто пища для размышлений.
Используя инструменты и инженерные знания, мы производим лучшие чертежи прицепов на рынке. Мы делаем это для планов трейлеров на этом сайте, потому что это правильный способ проектирования. Мы делаем это и для всех нестандартных прицепов, которые мы проектируем. Это одна из ценностей, которую вы получаете в Mechanical Elements.
Кстати, один из наших конкурентов утверждает, что у них есть «единственные» проектные чертежи трейлеров — теперь вы знаете правду. Они продаются на нескольких сайтах, но это все одни и те же планы. Я не буду бить инженеров других, но скажем так, эти планы не соответствуют моим стандартам.
Стройте уверенно, вот что мы говорим. Удачи вам в ваших дизайнерских начинаниях.
Реакции и диаграммы балок. Дополнение по сопротивлению материалов для энергетики
Основной корпус
Диаграммы
Цели обучения
По окончании этой главы вы должны уметь:
- Определять реакции свободно опертых, выступающих и консольных балок
- Рассчитайте и начертите диаграммы поперечных усилий и изгибающих моментов балок, подверженных сосредоточенным нагрузкам, равномерным распределенным нагрузкам и их комбинациям.

Обзор балок
Балки — это конструктивные элементы различного инженерного назначения, такие как крыши, мосты, механические узлы и т. д. В общем случае балка представляет собой тонкую, прямую, жесткую конструкцию, изготовленную из изотропных материалов и, что наиболее важно, подвергается нагрузкам, перпендикулярным их продольной оси. Если бы вместо перпендикулярных нагрузок тот же элемент конструкции подвергался бы продольным нагрузкам, его называли бы колонной или стойкой. Если бы тот же элемент подвергался крутящему моменту, его называли бы и рассматривали как вал. Поэтому при идентификации механических или конструктивных компонентов очень важно учитывать способ нагрузки.
Обратите внимание, что когда дело доходит до ориентации, балки могут быть горизонтальными, вертикальными или с любым промежуточным наклоном (например, погруженные в воду плиты, анализируемые в гидромеханике)… при условии, что нагрузка перпендикулярна их главной оси.
Опоры балки:
| Тип опоры | Похоже на | Символ | Реакции |
Ролик, также называемый
|
|
|
|
Штифтовой, также называемый
|
|
|
|
| Фиксированный |
|
Нагрузки на балку [1] :
| Нагрузки | Символ | Примеры | Закрытый |
Точка, также называемая
|
|
Да | |
| Униформа Распределенная |
|
Да | |
| Распределенная переменная |
|
Да | |
| Концентрированные моменты |
|
№ |
Типы балок:
| Типы | Схема | Примеры | Закрытый |
| Простые балки или просто поддерживаемые |
|
Да | |
| Нависающие балки |
|
|
Да |
| Консольные балки |
|
Да | |
| Составные балки |
|
№ | |
| Неразрезные балки |
|
№ |
Решение для балочных реакций
При нахождении реакций рекомендуется выполнить следующие шаги:
- Нарисуйте схему корпуса без балки
- Заменить равномерную распределенную нагрузку (если есть) эквивалентной точечной нагрузкой
- Решите ΣM A = 0 (сумма моментов относительно опоры A).
 Это даст вам R B (реакция на поддержке B).
Это даст вам R B (реакция на поддержке B). - Решите ΣM B = 0. Это даст вам R A .
- Используя R A и R B , найденные на шагах 3 и 4, проверьте, выполняется ли ΣV = 0 (сумма всех вертикальных сил).
- Обратите внимание, что шаги 4 и 5 можно поменять местами.
- Для консольной балки используйте ΣV = 0, чтобы найти вертикальную реакцию на стене, и ΣM , стена = 0, чтобы найти реакцию момента на стене. Нет никакого другого уравнения для проверки ваших результатов.
Диаграммы поперечных сил и изгибающих моментов
Обратите внимание:
«Сдвиговые силы — это внутренние силы, возникающие в материале балки для уравновешивания внешних сил, чтобы обеспечить равновесие всех частей балки.
Изгибающие моменты — это внутренние моменты, возникающие в материале балки, чтобы уравновесить стремление внешних сил вызвать вращение любой части балки». [3]
[3]
Перерезывающую силу в любом сечении балки можно найти путем суммирования всех вертикальных сил слева или справа от рассматриваемого сечения.
Аналогично, изгибающий момент в любом сечении балки можно найти, сложив моменты слева или справа рассматриваемого сечения. Опорной точкой момента является рассматриваемое местоположение.
По соглашению внутренние силы сдвига, действующие вниз, считаются положительными. Они противодействуют восходящим внешним силам. Следовательно, при представлении поперечных сил их можно рисовать в направлении внешних сил. Это визуально проще, чем следовать соглашению о знаках.
Моменты по часовой стрелке обычно считаются отрицательными, а моменты против часовой стрелки считаются положительными. При представлении изменения изгибающего момента обратитесь к следующей таблице, показывающей качественные кривые изгибающего момента в зависимости от формы графиков поперечной силы.
.
При построении диаграмм поперечной силы и изгибающего момента, несмотря на то, что соглашение о знаках важно, постоянство имеет решающее значение. Например, рассмотрим простую балку, нагруженную точечной нагрузкой, приложенной к нагрузке UD. Запустив диаграммы на опоре А, глядя на страницу, вы получите следующее:
Теперь переверните луч по горизонтали на 180º (или измените точку наблюдения, глядя на луч с противоположной стороны) и нарисуйте диаграммы, начиная с той же точки A. Диаграммы будут выглядеть следующим образом:
Обратите внимание, что хотя диаграммы поперечной силы выглядят как зеркальные изображения (перевернутые по горизонтали), диаграмма изгибающего момента не затрагивается. Кроме того, наиболее важный результат этого анализа показывает, что максимальная сила сдвига и величина изгибающего момента всегда будут одинаковыми.
Контрольные точки диаграммы направленности
При построении диаграммы направленности учитывайте следующее:
Диаграммы поперечной силы:
- На концах свободно опертой балки поперечная сила равна нулю.

- На стене консольной балки поперечная сила равна вертикальной реакции на стене. На свободном конце балки поперечная сила равна нулю.
- На любом сегменте балки, к которому не приложены нагрузки, поперечная сила остается постоянной (горизонтальная линия).
- Точечная нагрузка или реакция на диаграмме поперечной силы вызывает резкое изменение графика в направлении приложенной нагрузки.
- Равномерная распределенная нагрузка, действующая на балку, представлена прямолинейной поперечной силой с отрицательным или положительным наклоном, равной нагрузке на единицу длины.
Диаграмма изгибающих моментов:
- На концах свободно опертой балки изгибающие моменты равны нулю.
- На стенке консольной балки изгибающий момент равен реакции момента. На свободном конце изгибающий момент равен нулю.
- В месте, где поперечная сила пересекает нулевую ось, соответствующий изгибающий момент имеет максимальное значение.

- Форма кривой изгибающего момента между двумя точками балки показана в двух приведенных выше таблицах.
- Изменение изгибающего момента между двумя точками на балке равно площади под диаграммой поперечной силы между теми же двумя точками.
Приведенные выше рекомендации помогут вам в создании диаграмм балок; они также служат проверкой.
При решении диаграмм балок в классе и дома вы можете проверить свои ответы с помощью этого бесплатного онлайн-калькулятора балок: SkyCiv Cloud Engineering Software
Задача 1: Укажите максимальные значения поперечной силы и изгибающего момента.
Задача 2: Укажите максимальные значения поперечной силы и изгибающего момента.
Задача 3: Балка длиной 24 м свободно поддерживается на расстоянии 3 м от каждого конца. Балка несет точечную нагрузку 18 кН на левом конце и 22 кН на правом конце балки. Балка весит 400 кг/м. Нарисуйте диаграммы балок и определите место на балке, где изгибающий момент равен нулю.
Балка весит 400 кг/м. Нарисуйте диаграммы балок и определите место на балке, где изгибающий момент равен нулю.
Задача 4: Простая выступающая балка длиной 112 футов выступает над левой опорой на 14 футов. Балка несет сосредоточенную нагрузку в 90 тысяч фунтов на расстоянии 12 футов от правого конца и равномерно распределенную нагрузку в 12 тысяч фунтов на фут на высоте 40 футов. участок с левого конца. Нарисуйте диаграммы балки и определите поперечную силу и изгибающий момент в сечении на расстоянии 50 футов от левого конца.
Проблема 5: Предложите улучшение этой главы.
- Щелкните на диаграмме, чтобы развернуть ↵
Таблица угла луча светодиодов » Калькулятор угла луча
Угол луча светодиодных светильников и осветительных приборов определяет, насколько большим будет световой конус в помещении. Здесь вы можете узнать, что означает угол наклона леща в градусах и на что следует обратить внимание при выборе направленного светодиодного фонаря. Вы также найдете калькулятор для определения оптимального угла луча для вашего случая использования.
Вы также найдете калькулятор для определения оптимального угла луча для вашего случая использования.
- Пояснение к углу светодиодного луча
- Угол луча и угол поля зрения
- Угол луча и расстояние
- Угол луча и яркость
- Какой угол луча для какого места?
- Угол луча для светодиодных прожекторов
- Угол луча для светодиодов GU10
- Значение угла луча 15°, 60° или 120° градусов
- Расчет угла луча
- Формула угла луча
- Заключение: важно визуальное впечатление
Объяснение угла наклона светодиодного луча
Светодиодные светильники и источники света имеют как всенаправленные , так и направленные источники света. Всенаправленные прожекторы излучают свет равномерно во всех направлениях. Светодиодные прожекторы, с другой стороны, являются направленными источниками света. Они излучают весь свой световой поток только в одном определенном направлении.
Угол луча указывает угол, под которым световой поток выходит из светодиодного прожектора. В зависимости от расстояния между светильником и полом или освещаемой поверхностью создается световой конус соответствующего диаметра. Угол луча оказывает прямое влияние на то, насколько большим будет световой конус в помещении. Математические отношения между углом луча, расстоянием и диаметром можно найти ниже.
Угол светового пучка указан в градусах.
Раньше галогенные прожекторы обычно имели угол светового пучка 35°. Впервые были доступны светодиодные прожекторы с аналогичными углами луча в диапазоне 30°. Со встроенными призмами или рассеивающими линзами современные светодиодные прожекторы теперь доступны с углами луча от 10° до 120°.
Угол луча и угол поля зрения
Помимо угла луча существует также так называемый угол поля зрения . В световом круге угол луча определяет область, в которой лампа излучает не менее половины (50%) своей максимальной силы света. Полная сила света (100 %) достигается только точно в центре светового круга.
Полная сила света (100 %) достигается только точно в центре светового круга.
Угол поля определяет внешнюю область светового круга, где лампа излучает до одной десятой (10%) своей максимальной силы света. Даже за пределами угла поля не совсем темно, небольшие части силы света все еще излучаются здесь в виде рассеянного света.
Угол и расстояние луча
Угол луча определяет, насколько большой световой круг появляется на освещаемом объекте. Важным фактором здесь также является расстояние между источником света и освещаемым объектом. Например, если светодиодный прожектор находится недалеко от стены, будет виден только небольшой точечный световой кружок. Но если прожектор отвести от стены, световой контур становится все больше и больше.
Угол луча и яркость
Существует также прямая зависимость между углом луча и яркостью светодиодной лампы. Яркость светодиодных ламп указывается в люменах. Если сравнить два светодиодных спота с одинаковой светоотдачей 600 люмен, то по техпаспорту они вроде бы имеют одинаковую яркость. Однако, если оба прожектора имеют разные углы луча, около 15° и 60°, это дает представление о воспринимаемой яркости.
Однако, если оба прожектора имеют разные углы луча, около 15° и 60°, это дает представление о воспринимаемой яркости.
Прожектор с углом луча 60° должен освещать гораздо большую площадь с такой же светоотдачей, что и прожектор 15°. По этой причине освещенная поверхность кажется больше, но и намного темнее. Поэтому угол луча всегда следует выбирать в сочетании с желаемой яркостью в зависимости от освещаемой поверхности.
Какой угол луча для какого места?
Угол луча в первую очередь интересен для направленных источников света. К ним относятся светодиодные прожекторы или светодиодные прожекторы и светильники GU10. Угол луча следует выбирать в зависимости от местоположения или варианта использования перед покупкой светодиодной лампы. В жилой зоне в основном используются следующие три варианта освещения:
- Основное освещение
- Акцентное освещение
- Декоративное освещение
Угол луча 120° является хорошим выбором для основного освещения помещения. Для коридоров и дорожек внутри помещения рекомендуется угол луча 90°.
Для коридоров и дорожек внутри помещения рекомендуется угол луча 90°.
Акцентное освещение используется для выделения определенных зон в комнате. Это может быть зона отдыха или цветная стена. Здесь угол луча нужно подбирать индивидуально, в зависимости от размера акцентируемой области.
Декоративное освещение часто используется для выделения определенных объектов в помещении. Это может быть арт-объект или картина. Также здесь угол луча зависит от диаметра объекта и расстояния до источника света.
Расчет угла луча
Калькулятор угла луча поможет вам определить правильный угол.
Угол луча для светодиодных прожекторов
Светодиодные прожекторы доступны в различных вариантах, например, для установки на потолке или на поверхности. Они предлагаются со многими различными углами луча. Угол следует выбирать в соответствии с применением, как описано выше.
Угол луча для светодиодов GU10
Светодиоды GU10 также доступны с различными углами луча. Здесь играет роль не только угол луча источника света. Также важно состояние светильника или стекла лампы, где используется лампа ГУ10. Лампа GU10 с углом луча 120°, вероятно, будет экранирована небольшим отверстием в стекле лампы. Фактический угол луча этой лампы, следовательно, будет меньше.
Здесь играет роль не только угол луча источника света. Также важно состояние светильника или стекла лампы, где используется лампа ГУ10. Лампа GU10 с углом луча 120°, вероятно, будет экранирована небольшим отверстием в стекле лампы. Фактический угол луча этой лампы, следовательно, будет меньше.
Значение угла луча 15°, 60° или 120° градусов
Таблица дает вам обзор диаметра светового круга с различными углами луча и высотой потолка 8 футов. Для расчета с вашими индивидуальными значениями вы можете использовать онлайн-калькулятор.
| Beam Angle | Diameter of Light Circle |
|---|---|
| 15° | 2.1 feet |
| 30° | 4.3 feet |
| 45° | 6. 6 feet 6 feet |
| 60° | 9.2 feet |
| 90° | 16 feet |
| 120° | 27.7 feet |
Calculate beam angle
Значение угла луча иногда кажется немного неинформативным. Оценка часто затруднена, особенно из-за влияния расстояния между лампой и полом или стеной. Следующая формула и калькулятор помогут вам определить наилучший угол луча.
Формула угла луча
С помощью следующей тригонометрической функции (функция угла) вы можете самостоятельно рассчитать угол луча со всеми параметрами.
Описание переменных:
- α: угол луча
- Ø: диаметр освещаемого объекта или поверхности
- d: расстояние между лампой и объектом или поверхностью
- arctan: функция, обратная касательной для расчета угла
Онлайн-калькулятор угла луча
Калькулятор поможет вам рассчитать точный угол луча. Здесь можно рассчитать прямую зависимость между углом луча, диаметром светового круга и расстоянием до освещаемого объекта (пола, стола, рабочей поверхности, стены, картины). Таким образом, вы можете рассчитать оптимальный угол луча для вашего приложения и использовать его при принятии решения о покупке.
Здесь можно рассчитать прямую зависимость между углом луча, диаметром светового круга и расстоянием до освещаемого объекта (пола, стола, рабочей поверхности, стены, картины). Таким образом, вы можете рассчитать оптимальный угол луча для вашего приложения и использовать его при принятии решения о покупке.
Калькулятор угла луча
Инструменты на этом веб-сайте предоставляются «как есть» без каких-либо гарантий.
Заключение: важно визуальное впечатление
Угол луча светодиодного пятна определяет диаметр генерируемого светового круга на освещаемой поверхности или объекте. Идеальный угол луча обычно очень индивидуально зависит от места использования лампы и от вашего собственного варианта использования. Это можно очень хорошо определить с помощью калькулятора угла луча.
В основном, большие углы луча 90° или 120° хорошо подходят для освещения комнаты на большой площади. Небольшие углы луча от 15° до 35° — хороший выбор для декоративного освещения.
Как рассчитать нагрузку на балку
Простой взгляд вокруг покажет нам простой, но интересный факт, что каждый объект, живой или неживой, постоянно прикладывает определенную нагрузку к определенному основанию и одновременно подвергается действию равной и противоположной величины силы со стороны поддерживаемого основания.
Автомобиль, припаркованный над местом, оказывает на землю силу или оказывает нагрузку, которая может быть равна его весу; однако земля также оказывает равную, но противоположную силу на автомобиль, так что он остается на месте неповрежденным. Поскольку автомобиль удерживается в одном постоянном положении, это означает, что две силы должны быть равны и действовать в противоположных направлениях.
Обычно на любой объект, представляющий собой нагрузку, обычно действуют следующие две силы:
- Вес объекта, действующий на землю
- Реакция земли или основания, действующая вверх на объект
Прежде чем мы Чтобы перейти к деталям расчета нагрузки на балку, важно сначала узнать о типах нагрузок, которые могут действовать на балку, поддерживаемую на ее концах.
Нагрузку можно разделить на следующие важные типы:
- Точечная нагрузка, резко ограниченная одной точкой,
- Равномерно или равномерно распределенная нагрузка и,
- Равномерно изменяющаяся нагрузка.

Давайте разберем их по порядку.
Точечная нагрузка: Нагрузка или вес, воздействующий на точечную площадь, называется точечной нагрузкой . Однако с математической точки зрения точечная нагрузка не выглядит осуществимой просто потому, что любая нагрузка должна иметь определенную площадь удара и не может балансировать в точке, но если площадь удара слишком мала по сравнению с длиной балки, может приниматься как определено.
Равномерно распределенная нагрузка: Как следует из названия, нагрузка, равномерно распределенная по всей балке, называется равномерно распределенной нагрузкой .
Равномерно изменяющаяся нагрузка: Нагрузки, распределенные по балке и создающие равномерно увеличивающийся градиент нагрузки по всей балке от конца до конца, называются равномерно изменяющейся нагрузкой .
Балка может быть подвергнута одной из вышеуказанных нагрузок или их комбинациям.
Лучевые реакции
На следующем простом рисунке мы познакомимся с формулами, относящимися к расчету нагрузки на балку или, точнее, реакции балки: буквами А и В соответственно.
Пусть на балку действуют точечные нагрузки в точках, отмеченных как W1, W2 и W3.
Также пусть,
RA = Реакция на конце A балки.
RB = Реакция на конце B балки.
В основном существует пара сил (эффект поворота), которые действуют на концы балки A и B, а именно. по часовой стрелке и против часовой стрелки момент силы.
Так как момент силы, действующей на опорную балку, равен произведению Силы (здесь вес) и ее расстояния от опоры или оси вращения, общий момент по часовой стрелке, действующий в точке A, может быть равен:
W1. a + W2.b + W3.c,
Кроме того, против часовой стрелки момент силы, действующей на точку B, должен быть:
RB.1
Теперь, поскольку балка находится в равновесии, подразумевается, что два вышеуказанных момента силы должны быть равны по величине, поэтому приравнивание двух выражений дает:
W1.a + W2.b + W3.c = RB.l
RB = W1.a + W2.b + W3. c / l
c / l
Равновесие с балкой также означает, что:
RA + RB = W1.a + W2.b + W3.c
RA = ( W1.a + W2.b + W3.c) — RB
Теперь согласно условиям равновесия алгебраическая сумма всех горизонтальных компонент в приведенное выше выражение становится несущественным и может быть обнулено (ƩH = 0.)
Таким образом, окончательное уравнение принимает вид
RA = (W1 + W2 + W3) — RB
Приведенную выше формулу можно использовать для определения реакции нагруженной балки относительно ее концевых опор.
Расчет поперечной силы и изгибающего момента
Двумя важными параметрами, которые также используются при расчете нагрузки на балку, являются поперечная сила (SF) и изгибающий момент (BM).
Выведем их с помощью следующей простой иллюстрации:
Ссылаясь на рисунок рядом, рассмотрим балку, нагруженную равномерно распределенной нагрузкой Вт на единицу длины. Также рассмотрим некоторый участок балки RS, имеющий длину δx на расстоянии x от левой опоры балки.
Нагрузка, действующая на сечение RS балки, будет равна Вт. δx ( момент Силы).
Теперь предположим, что сила сдвига в точке R равна F,
Тогда в точке S она будет равна F + δF .
Кроме того, если изгибающий момент при R = M , то при S он становится M + δM.
Так как балка находится в равновесии, то приложенный момент также должен подчиняться законам равновесия, поэтому приравнивая два неуравновешенных выражения при S получаем:
Или δF/δx = W,
Приведенные выше выражения показывают, что скорость изменения силы сдвига равна давлению нагрузки или интенсивности.
Аналогично моменты в точке S можно приравнять: , δM/δx = – F
Приведенное выше соотношение показывает, что скорость изменения изгибающего момента равна поперечной силе сечения RS.
Данные (формула реакции, соотношение поперечной силы и изгибающего момента), описанные в этой статье, могут использоваться при расчете нагрузки на балку для дальнейшего определения качества и типа материала, который будет использоваться для безопасной нагрузки на балку.
