alexxlab Ноутбуки-монстры. Вспоминаем лаптопы с диагональю 20 дюймов / Хабр
В предыдущей статье я рассказал о необычных «карманных» ноутбуках, отличающихся очень компактными размерами, благодаря чему они и завоевали популярность у пользователей. Однако в галактике ноутбуков встречаются не только «карлики», но и настоящие «гиганты». О самых больших мобильных компьютерах, конечно же, необычных и интересных с конструктивной точки зрения, мы сегодня и поговорим.
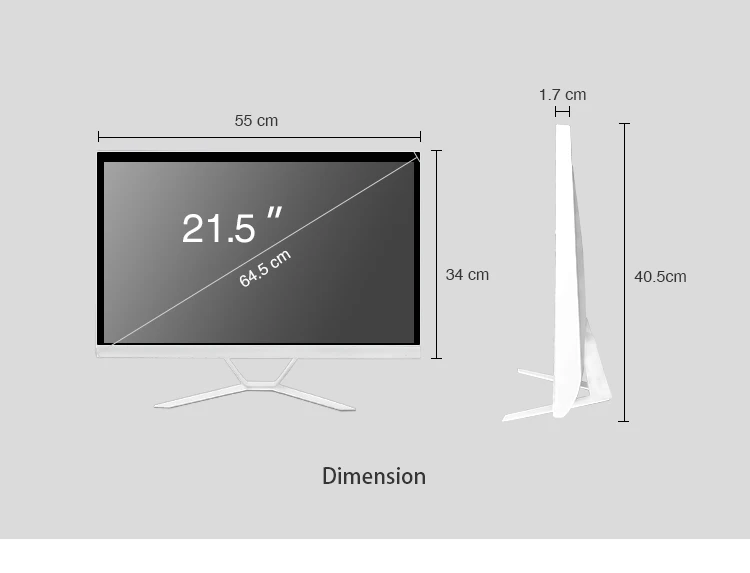
Когда-то давно я считал свой 18-дюймовый игровой Toshiba Satellite с процессором Pentium IV, занимавший примерно половину рабочего стола, очень громоздким аппаратом. В те времена я еще подозревал, что по сравнению с некоторыми другими моделями эта машина — просто верх изящества и миниатюрности. Куда ему, например, до Dell XPS M2010, диагональ экрана которого составляет целых 20,1 дюймов (51.054 см)!
Самым любопытным в этом ноутбуке был даже не большой экран, а необычный форм-фактор: в «боевом положении» ноут превращался в некое подобие полноценной рабочей станции — с полноформатным монитором, отдельной Bluetooth-клавиатурой с мышью, а в сложенном состоянии умещался в довольно компактный, хотя и тяжелый кейс — массой 8,3 кг.
Dell XPS M2010 был оборудован двумя жесткими дисками, объединенными в массив RAID 0, дискретной видеокартой ATI и очень мощным по тем временам процессором Core 2 Duo T7600. Этой мощности вполне хватало для обработки графики, монтажа видео и весьма ресурсоемких игр. А запускать игры на этой машине было крайне интересно: в нижней части монитора разработчики смонтировали целых 8 широкополосных динамиков, плюс еще один низкочастотный динамик с фазоинвертором в корпусе самого ноутбука! Самое то, чтобы пугать соседей панк-роком. В общем, это был ноут для сильных программистов, способных таскать эту тяжеленную бандуру с места на место, не надорвав себе спину.
Такую же диагональ — 20,1 дюймов — имел Acer Aspire 9920G. Дисплей поддерживал разрешение до 1680×1050 пикселов (WSXGA+), что до сих пор считается очень неплохим показателем. В отличие от Dell XPS M2010 эта машина представлена в традиционном для ноутбуков исполнении, просто она ну очень здоровая.
Компания Hewlett Packard решила, видимо, не отставать от прямых конкурентов и в середине «нулевых» выпустила свою версию 20,1-дюймового ноутбука под названием HP Pavilion HDX 9000. Этот аппарат имел необычное «шарнирное» крепление дисплея, благодаря которому представлял собой нечто среднее между диковинным Dell XPS M2010 и традиционным Acer Aspire 9920G. Шарнир позволял регулировать экран не только по «вылету», но и по высоте, чем не может похвастаться ни один другой похожий ноутбук.
Из других интересных конструктивных особенностей HP Pavilion HDX 9000 следует отметить наличие дополнительного ряда сенсорных клавиш, расположенного над основной клавиатурой. Машина оснащена 3 Гбайтами оперативки в базовой комплектации против 2 у прямых конкуретов. В корпусе предусмотрено место для установки второго жесткого диска формата 2,5” SATA, хотя с завода ноутбук поставлялся с одним винчестером объемом 160 Гбайт. Из всех перечисленных 20-дюймовых моделей этот ноут имеет, пожалуй, самую высокую яркость дисплея — 261 кд/м2.
Еще одним представителем «двадцатидюймовой братии» был практически неизвестный в России CLEVO M590KE (он же SAGER NP5960). Этот монстр оборудован двухъядерным AMD Turion и аж двумя видеокартами GeForce Go 7950 GTX (во второй модели — Quadro FX Go 2500M), объединенными в режим SLI. В остальном аппарат соответствовал характеристикам других схожих ноутбуков 2007 года: 2 жестких диска, работающих в массиве RAID 1, 2 Гбайта оперативки, широкоформатный 20,1-дюймовый WSXGA+ дисплей с поддержкой экранного разрешения 1680×1050.
Стоил этот ноут, правда, весьма недешево: от 3795 до 6395 долларов США в зависимости от комплектации. Машина для своего времени была очень мощной и производительной, позволяла уверенно работать с видеоредакторами и 3D-пакетами. Да и играть на CLEVO было клево: в корпусе ноутбука прятались 4 мощные колонки и один сабвуфер. В общем, достойный конкурент HP, Dell и Acer.
В наши дни ноутбуков с большой диагональю, за исключением совсем уж монструозного Aurora 7, практически не выпускают. Ближайшим современным наследником 20.1-дюймовых ноутбуков из середины «нулевых» является, пожалуй, ROG Mothership GZ700 от компании ASUS. До 20 дюймов этот агрегат все-таки не дотягивает, но, тем не менее, он большой и о-о-очень мощный!
Этот ноутбук имеет отсоединяемую клавиатуру, он оборудован процессором Intel Core i9, видеокартой GeForce RTX 2080 и ценой от звездолета. Ну, а поскольку «ROG» расшифровывается как «Republic Of Games», назначение этого агрегата в целом понятно.
Старые добрые HP, Dell и Acer еще можно отыскать на досках бесплатных объявлений, аукционах и барахолках, очистить от пыли и водрузить на них какую-нибудь винтажную игру.
Knipex 74-21-200 8-дюймовые бокорезы с высоким рычагом, угол 12 градусов
Бесплатная доставка свыше 75 долларов США *
ПРИМЕЧАНИЕ. Название и описание продукта заменяют изображенное на нем изображение. Картинка, предоставленная производителем, не всегда точна. Мы можем использовать одно и то же изображение для разных размеров товара.
Цена по прейскуранту: $56,10
Цена продажи: $38,43
- Артикул:
- 7421200
- Наличие:
- 1
- Описание
- Информация о гарантии
- Атрибуты
На 20 % меньше усилий по сравнению с обычными бокорезами той же длины
Со встроенной кованой шарнирной осью.
Для длительного использования в тяжелых условиях
Высокая режущая способность при минимальных усилиях благодаря оптимальному согласованию угла режущей кромки, передаточного числа и эргономичной формы рукоятки проволока в том числе рояльная струна
Наконечник под углом 12 градусов обеспечивает зазор для захвата с черным покрытием
Полированная головка
Рукоятки с пластиковым покрытием
| Артикул № | 44 мм4 мм 047 Стиль | Плоскогубцы | Головка | Ручки | Режущие способности (мм) | | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 25 | 9000 048 | ||||||||||||||
| 74 01 140 | 140 | 0 | черный атраментированный 0090 | пластиковое покрытие | 3. 1 | 2.0 | 1.5 | 131 | |||||||
| 74 01 160 | 160 | 3,4 | 2,5 | 2,0 | 178 | ||||||||||
| 74 01 90 180 908190 80 89 3,8 | 2,7 | 2,2 | 241 | ||||||||||||
| 74 01 200 | 200 | 4,2 | 3,0 | 2,5 7 09090 | 2 04674 01 250 | 250 | 4,6 | 3,5 | 3,0 | 391 | |||||
| 74 02 140 | 140 | 0 | чернение | полировка | с многокомпонентными ручками | 90 90 90 89 8,0 90 901,5 | 157 | ||||||||
| 74 02 160 | 160 | 3,4 | 2,5 | 2,0 | 209 | 7082690 9 180 | 180 | 3,8 | 2,7 | 2,2 | 273 | ||||
| 74 02 200 | 200 | 4,2 | 3,0 | 2,5 | 304 | ||||||||||
| 74 02 900 90 90892 90 89 4,6 | 3,5 | 3,0 | 437 | ||||||||||||
| 74 05 200 | 200 | 0 | хромированный | с многокомпонентными ручками | 90 90890 90890 0089 2,5 | 304 | |||||||||
| 74 06 160 | 160 | 0 | хромированный | изолированный с многокомпонентными ручками, проверен VDE | 3,4 | 2,5 | 2,0 | 180 | 3,8 | 2,7 | 2,2 | 280 | |||
| 74 08 200 | 6090 9029 200 900 276 0 | черный, атраментированный | изолированный, с многокомпонентными ручками, проверен VDE | 4. 2 | 3.0 | 2.5 | 303 | ||||||||
| 74 08 250 | 250 | 909 90890 90 89 3,0 | 437 | ||||||||||||
| 74 12 160 | 160 | 1 | черная атраментированная | полированная | с многокомпонентными ручками | 3,4 | 902 900 8 0209 | ||||||||
| 74 12 180 | 180 | 3,8 | 2,7 | 2.2 | 273 | ||||||||||
| 74 21 160 | 160 | 2 | 909389 черн. 0с пластиковым покрытием | 3,4 | 2,5 | 2,0 | 181 | ||||||||
| 74 21 180 | 180 | 9009902 9008 902 9008 0 | 2,2 | 235 | |||||||||||
| 74 21 200 | 200 | 4,2 | 3,0 | 2,5 | 258 | ||||||||||
| 74 21 250 | 250 | 4,6 | 3,5 | 90 390 8 90 390 8 90 3 90 8 90 90 90 90||||||||||||
| 74 22 200 | 200 | 2 | черный, атраментированный | полированный | с многокомпонентными ручками | 4,2 | 3,0 | 2,5 | 300 | 250 | 4,6 | 3,5 | 3,0 | 437 | |
К сожалению, ваш браузер не поддерживает мультимедиа HTML5.
Knipex-Werk производит, а Knipex Tools LP распространяет инструменты высочайшего качества для промышленного и коммерческого использования. Инструменты KNIPEX поставляются с Пожизненная ограниченная гарантия . В том маловероятном случае, если инструмент точного типа больше не будет доступен, Knipex может решить заменить инструмент сопоставимым инструментом равной или большей стоимости, или, по усмотрению Knipex Tools LP, Knipex Tools LP может принять решение о возврате покупной цены. за неисправный инструмент. Вышеуказанные средства правовой защиты являются единственными и исключительными средствами правовой защиты, доступными в рамках настоящей гарантии, и ни при каких обстоятельствах Knipex-Werk или Knipex Tools LP не несут ответственности за случайные, особые или косвенные убытки, упущенную выгоду или другие экономические потери. Настоящая гарантия распространяется только на первоначального конечного пользователя, купившего инструмент, и никоим образом не распространяется на неисправности, вызванные неправильным использованием, неправильным использованием, модификацией, несчастным случаем или износом инструментов в результате использования.
Для получения гарантийного обслуживания обратитесь в компанию Knipex Tools LP или к ближайшему авторизованному дилеру компании Knipex.
Гарантийные претензии требуют возврата неисправного инструмента, подтверждения покупки и подтверждения от вас, что вы являетесь первоначальным конечным покупателем инструмента. Все расходы по доставке и транспортировке исключены из настоящей гарантии.
НАСТОЯЩАЯ ГАРАНТИЯ ЯВЛЯЕТСЯ ЕДИНСТВЕННОЙ ГАРАНТИЕЙ КОМПАНИИ KNIPEX-WERK И KNIPEX TOOLS LP НА ИХ ИНСТРУМЕНТЫ И ЗАМЕНЯЕТ ВСЕ ДРУГИЕ ГАРАНТИИ И УСЛОВИЯ, ЯВНЫЕ ИЛИ ПОДРАЗУМЕВАЕМЫЕ. KNIPEX-WERK и KNIPEX TOOLS LP ОТКАЗЫВАЮТСЯ ОТ ВСЕХ ДРУГИХ ЯВНЫХ ИЛИ ПОДРАЗУМЕВАЕМЫХ ГАРАНТИЙ И УСЛОВИЙ, ВКЛЮЧАЯ ПОДРАЗУМЕВАЕМЫЕ ГАРАНТИИ ИЛИ УСЛОВИЯ ТОВАРНОГО КАЧЕСТВА, КОММЕРЧЕСКОЙ ПРИГОДНОСТИ И ПРИГОДНОСТИ ДЛЯ ОПРЕДЕЛЕННОЙ ЦЕЛИ.
Knipex-Werk и Knipex Tools LP не принимают на себя и не уполномочивают какое-либо лицо принимать на себя любые другие гарантии, условия или обязательства, выраженные или подразумеваемые.
2 отзыва Написать обзор
Knipex
Knipex 74-21-200 8-дюймовые боковые кусачки с высоким рычагом, изогнутые под углом 12 градусов — пластиковая рукоятка
Рейтинг Обязательно Выберите Рейтинг1 звезда (худший)2 звезды3 звезды (средний)4 звезды5 звезд (лучший)
Имя Обязательно
Электронная почта Обязательно
Тема отзыва Требуется
Комментарии Обязательно
- сопутствующие товары
- Клиенты также просмотрели
Площадь прямоугольника размером 24 x 21 и геометрические свойства, такие как симметрия, периметр прямоугольника, диагонали
w3.org/1999/xhtml» cellspacing=»0″>Нам дано, что длина прямоугольника = 24,0 единицы, а ширина = 21,0 единица.
AD = BC = 24,0 ед.
А АВ = CD = 21,0 ед.
Единицами могут быть любые единицы длины: дюймы, см, футы, мили, км и т. д.
Геометрические свойства, которые мы вычислимВычислим площадь, периметр, длину диагонали, радиус описанной окружности, площадь описанной окружности и углы, образуемые диагональю со сторонами.
Вычисление площади прямоугольника
Площадь этого прямоугольника = длина х ширина (длина х ширина) = 24,0 х 21,0 = 504,0 квадратных единиц
Вычисление периметра прямоугольникаПериметр этого прямоугольника = 2 * (длина + ширина) = 2 * (24,0 + 21,0) = 90,0 единиц
Диагональ этого прямоугольника может быть вычислена с помощью теоремы Пифагора (или теоремы Пифагора).
Треугольники ADC (или BDC) являются прямоугольными треугольниками.
Итак, диагональ(и) можно рассматривать как гипотенузу прямоугольного треугольника. Таким образом, квадрат длины диагонали равен сумме квадратов длины и ширины.
Длина диагоналей AC и BD = (24,0 2 + 21,0 2 ) (1/2)
Итак, длина диагонали = 31,89 единицы
Вычисление радиуса и площади описанной окружностиНа самом деле у прямоугольника нет вписанной окружности, которая касается каждой стороны. Это возможно только в предельном случае, когда длина и ширина равны и это квадрат.
Однако действительно возможно нарисовать окружность, проходящую через все 4 вершины прямоугольника. Обе диагонали являются диаметрами окружности.
Угол в полуокружности является прямым углом: каждый из 4 углов прямоугольника становится углом полукруга, когда мы рисуем описанную окружность.
Радиус описанной окружности = половина длины диагонали = 31,89/2 единицы = 15,95 единицы
Площадь описанной окружности = PI x радиус окружности2 = PI * 15,95 * 15,95 = 798,75 квадратных единиц
Симметрия и оси симметрии
Прямоугольник имеет 2 оси симметрии: прямую, проходящую через середины сторон AB и CD, и другую прямую, проходящую через середины сторон AD и BC.
Оба проходят через точку E. Прямоугольник также является «изогональным» по своей природе, хотя это понятие вы, возможно, изучите или столкнетесь с ним позже.
Вычисление угла между диагональю и сторонами
Мы можем использовать немного тригонометрии, чтобы вычислить это.
Тангенс угла CAD = Тангенс угла ACB = ширина прямоугольника / длина прямоугольника = 21,0/24,0 = 0,88
Угол CAD = Угол ACB = tan -1 0,88 = 0,72 радиана = 41,19градусов
и угол BAC = угол ACD = 90 градусов — угол CAD = 0,85 радиана = 48,81 градуса
Примеры конгруэнтности и конгруэнтных треугольников
Каждая диагональ делит прямоугольник на пару конгруэнтных треугольников.
ДиагональBD делит прямоугольник на равные треугольники BAD и BCD.
Доказательство:
(a) Угол BAD = угол BCD = 90 градусов (прямой угол)
(b) BD общая сторона обоих (гипотенуза)
(c) BA = CD = 21,0 единицы (противоположные стороны прямоугольника равны)
(d) AD = BC = 24,0 единицы (противоположные стороны прямоугольника равны)
Используя (a) (b) и (c), два треугольника конгруэнтны, используя конгруэнтность RHS или HL (гипотенуза-каттер).
Или, используя (c) (a) и (d), два треугольника конгруэнтны, используя конгруэнтность SAS (сторона-угол-сторона)
Аналогично можно доказать, что АС делит прямоугольник на два равных треугольника.
Кроме того, две диагонали делят прямоугольник на две пары конгруэнтных треугольников
(Треугольник AEB и треугольник CED равны, треугольник BEC и треугольник AED равны)
Чтобы доказать, что треугольник AEB и треугольник CED конгруэнтны:
(a) AB = CD = 21,0 единиц (Противоположные стороны прямоугольника равны)
(б) Угол ABD = Угол CDB (AB параллелен CD, а BD — секущая их секущая, это противоположные углы, значит, они равны)
(c) Угол BAC = угол DCA (по той же причине, что и выше)
(d) Угол BEA = угол CED (противоположные или вертикальные углы равны)
Таким образом, мы можем доказать конгруэнтность двух треугольников с помощью ASA-конгруэнтности (используя (c) (a) (b))
Или мы можем доказать конгруэнтность двух треугольников с помощью Конгруэнтности AAS (используя (d)(b)(a))
Аналогичным образом мы можем доказать, что треугольники BEC и AED равны.
Помните: прямоугольник — это четырехугольник с 4 прямыми углами. Противоположные стороны равны. Все свойства, применимые к параллелограммам, применимы и к прямоугольникам.
Квадрат можно рассматривать как частный случай прямоугольника, у которого все стороны равны.
Каждый прямоугольник представляет собой выпуклый многоугольник и вписанный четырехугольник, диагональ которого представляет собой диаметр описанной окружности.
Несколько примеров, иллюстрирующих похожие прямоугольники, преобразование размеров, коэффициент масштабирования и геометрическое сходство.
Эти учебные пособия по подобным треугольникам, масштабному коэффициенту и преобразованию размеров также могут быть полезны.
Несколько примеров для иллюстрации похожих прямоугольников, преобразования размеров, масштабного коэффициента и геометрического подобияПример:
Пусть текущий прямоугольник (с размерами 24,0 x 21,0) будет прямоугольником A.
Теперь рассмотрим другой прямоугольник B (размерами 8,0 x 7,0)
Оба эти прямоугольника геометрически подобны, потому что отношения длин соответствующих сторон равны.
Длина прямоугольника A : Длина прямоугольника B = Ширина прямоугольника A : Ширина прямоугольника B
24,0 : 8,0 = 21,0 : 7,0 = 3,0 : 1
А отношение их площадей:
Площадь прямоугольника A : Площадь прямоугольника B = 504,0 : 56,0 = 9,0 : 1
Масштабный коэффициент между A:B = длина прямоугольника A : длина прямоугольника B = 24,0 : 8,0 = 3,0
Обратите внимание, что отношение площадей равно квадрату отношения соответствующих сторон (или масштабному коэффициенту).
Это пример преобразования размера в 2D-фигурах:
, когда все стороны фигуры умножаются на отношение R , площадь новой фигуры в R 2 умножается на площадь исходной фигуры.
Еще несколько примеров:
Геометрические свойства прямоугольника размером 25 x 21.